Abstract
In the much-studied Centipede Game, which resembles the Iterated Prisoners’ Dilemma, two players successively choose between (1) cooperating, by continuing play, or (2) defecting and terminating play. The subgame-perfect Nash equilibrium implies that play terminates on the first move, even though continuing play can benefit both players—but not if the rival defects immediately, which it has an incentive to do. We show that, without changing the structure of the game, interchanging the payoffs of the two players provides each with an incentive to cooperate whenever its turn comes up. The Nash equilibrium in the transformed Centipede Game, called the Reciprocity Game, is unique—unlike the Centipede Game, wherein there are several Nash equilibria. The Reciprocity Game can be implemented noncooperatively by adding, at the start of the Centipede Game, a move to exchange payoffs, which it is rational for the players to choose. What this interchange signifies, and its application to transforming an arms race into an arms-control treaty, are discussed.
1. Introduction
Since Rosenthal [1] introduced what has come to be called the Centipede Game, there has been controversy about what constitutes rational play in it, which we discuss in the next section. We begin by describing an abbreviated form of this game and show that it bears some resemblance to Iterated Prisoners’ Dilemma (IPD).
In the Centipede Game, like IPD, there is a tension between a Pareto-inferior subgame-perfect equilibrium outcome and a Pareto-optimal nonequilibrium outcome. However, unlike IPD, in the Centipede Game, players do not make simultaneous choices, in ignorance of each other, in a stage game, which is then repeated. Instead, they make sequential choices in a game of perfect information, in which the players’ strategic situation may change after every move.
Interchanging the two players’ payoffs at each stage of the Centipede Game transforms it into a new game we call the Reciprocity Game. The latter game makes it rational, via backward induction, for each player not to defect at any opportunity to do so but, instead, to cooperate until the end of play, whether or not the endpoint is known (the game is assumed to be finite).
To implement the Reciprocity Game, we give the players at the outset of the Centipede Game the choice of playing this game or switching to the Reciprocity Game. Because the payoff from continuing play to the end in the Reciprocity Game outweighs the benefit at each stage of defecting, the players will rationally choose to play the Reciprocity Game over the Centipede Game. Since the roles of the players are reversed on each round of the Reciprocity Game, both players, when they make their choices, find it in their mutual interest to cooperate until the end, whether it is fixed or probabilistic.
It is no surprise that, if a game changes, its equilibria may also change. What is striking in going from the Centipede Game to the Reciprocity Game is that no feature of the Centipede Game changes—including the players’ choices, their payoffs (except for the switch between the players), and the sequence of moves—which benefits not the player who defects on a round but its rival, who can then reciprocate on the next round.
Because the sum of the payoffs to the players on each round remains the same in the two games, it is the redistribution that transforms the Pareto-inferior subgame-perfect equilibrium in the Centipede Game into a more compelling Pareto-optimal subgame-perfect equilibrium in the Reciprocity Game.1 We will return to this feature, and its implications for reciprocity, in Section 3, using an arms-control treaty, and a brief case study of the aftermath of the Cuban missile crisis and the period of détente that followed, as an example.
2. The Centipede Game
In the Centipede Game, two players, P1 and P2, take turns choosing whether to take some payoff (defect), which terminates play, or not take it (cooperate), in which case the other player is given the same choice in the following round. If neither player defects in a round, play continues for 100 rounds, reflecting the many pairs of legs of a centipede (not necessarily 100). The amount that each player receives steadily accumulates if neither defects, until it is divided equally between the two players when play terminates after 100 rounds.
In the Centipede Game we analyze next (there are different versions—see Section 3), we limit play to two choices each for P1 and P2 over four rounds (see Figure 1 for the game in extensive form). Starting at the top of the game tree, P1 chooses between defecting, d, and cooperating, c. If P1 defects, the game ends. If P1 cooperates, play passes to P2, who has the same choice as P1 did on the first round. Play continues as long as neither player defects, until the fourth round, when play terminates whether or not P2 chooses d or c.
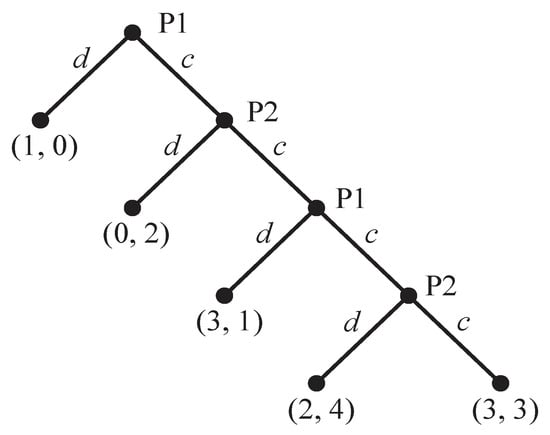
Figure 1.
The Centipede Game in Extensive Form.
We show the payoffs to P1 and P2 at each terminal node, where either P1 or P2 defects (by moving to the left) or when both players cooperate throughout (on the bottom right). These payoffs show that both players benefit equally at (3, 3) if they cooperate over the entire course of play. If one player defects at any point, its payoff is greater than its rival’s payoff.
Although a player who defects receives an immediate bonus from defecting, the accumulating payoffs of both players from cooperating to the end are at least as good as, and sometimes better than, those they would receive if either player had defected earlier. More specifically, if both players cooperated through the fourth round, their payoffs of (3, 3) are equal to or greater than their payoffs of (1, 0), (0, 2), and (3, 1) if one player had defected earlier.
To be sure, P2 would have done even better at (2, 4) than (3, 3) if it had defected on the fourth round, which makes it rational for P2 to defect on this round. However, if P1 anticipates this choice—as it would in a game of complete and perfect information—it would do better to defect on the third round, when it would receive 3 rather than 2, which it would receive on the fourth round when P1 defects. This logic carries back to the first round in a finite game, which makes it rational for P1 to defect on this round rather than to continue play.
This is the logic of backward induction, which ends up giving the players (1, 0) when P1 defects initially, rather than (3, 3) if both players cooperate to the end. The Centipede Game is shown in normal form in Table 1, wherein P1 chooses c or d on the first and third rounds, and P2 makes the same choices on the second and fourth rounds. Each player has four strategies, indicated by the Roman numerals in Table 1, depending on whether it chooses c or d on the two rounds when it can make a choice.

Table 1.
The Centipede Game in Normal Form.
After the successive elimination of weakly dominated strategies in this game, only strategies I and II of each player remain undominated: first, strategy IV of each player is weakly dominated; then strategy III of P2 is weakly dominated; finally, strategy III of P1 is weakly dominated. Although no strategy dominates any other for either player, the three outcomes around the upper left outcome of (1, 0), indicated by the superscript b, are all Nash equilibria.
But only the choice of strategy I by both players, which leads to the upper left outcome and is indicated by the superscript a in Table 1, is subgame perfect for the reason given earlier: working backwards from the bottom node in Figure 1 when P2 makes a second choice, each player would choose d whenever it has the opportunity to do so, which means that the game ends with P1’s initial choice of d.
By contrast, the three Nash equilibria that are not subgame-perfect involve P1 and P2 choosing strategy I or strategy II, with at least one of them choosing II. In effect, P1’s initial defection precludes either player from doing better than (1, 0) by switching to a different strategy.
The payoffs of the players in Figure 1 are the smallest non-negative numbers (1, 2, 3, etc.) that satisfy the following minimality condition for a Centipede Game: a defector does minimally better than it would do if the other player defected on the next round. For example, P1 receives 1 for defecting in the first round; if P1 cooperates and P2 then defects in the second round, P1 receives 0. Similarly, P2 receives 2 for defecting in the second round; if P2 cooperates and P1 then defects in the third round, P2 receives 1.
We also assume that the defector on the first round, P1, does minimally better than its rival at (1, 0), and that both players receive the equal payoffs of (3, 3) if they cooperate to the end. Of course, there are infinitely many Centipede-like games with larger payoffs that do not satisfy the minimality condition or the aforementioned assumptions, some of which are given in Garcia-Pola, Iriberri, and Kovárík [2] and discussed in Section 3.
In summary, the Centipede Game poses a conflict between the self-interest of one player—the defector on a round—and the mutual interest of both players. Each player would prefer that both cooperate throughout the entire game, except for P2 on the fourth round that triggers earlier defections. However, each player’s apprehension that if it cooperates on a round, its rival has an incentive to defect on the next round to its detriment interferes with the players maximizing their equal rewards at the end of play. We next propose a solution to their dilemma and show how it can be implemented.
3. The Reciprocity Game
What happens if the players’ payoffs are interchanged on each round—if P1 receives P2’s payoff, and P2 receives P1’s, as shown in the Figure 2 game tree, which defines the Reciprocity Game? Working backwards from the bottom node, P2 prefers (3, 3) to (4, 2) on the fourth round, so (3, 3) moves up as the outcome that would be chosen on this round. Then, because
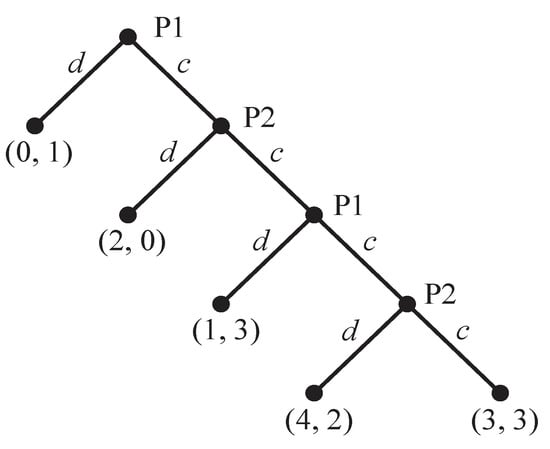
Figure 2.
The Reciprocity Game in Extensive Form.
- P1 prefers (3, 3) to (1, 3) on the third round,
- P2 prefers (3, 3) to (2, 0) on the second round,
- P1 prefers (3, 3) to (1, 0) on the first round,
both players would prefer to continue to cooperate on each round, eventually reaping the rewards of (3, 3) on the fourth round. Like (1, 0) in the Centipede Game, (3, 3) in the Reciprocity Game is the unique outcome supported by backward induction and is, therefore, the unique subgame-perfect equilibrium.
Unlike the Centipede Game, in which there are four Nash equilibria, including one that is subgame-perfect, the subgame-perfect equilibrium that results in the (3, 3) outcome is the only Nash equilibrium in the Reciprocity Game. Moreover, its implementation requires only that the players choose their weakly dominant IV strategies, as shown in the normal form of the game in Table 2. This renders the (3, 3) outcome of the Reciprocity Game more compelling than the (1, 0) outcome of the Centipede Game: although both are supported by unique subgame-perfect equilibria, the former is associated with weakly dominant strategies, whereas the latter competes with three other Nash equilibria.

Table 2.
The Reciprocity Game in Normal Form.
But how does one get the players to agree to play the Reciprocity Game if they start with the Centipede Game? Let each player be given the choice—independently and at the start of play—to switch or not switch to the Reciprocity Game. If either one or both players agree to switch, then the Reciprocity Game replaces the Centipede Game. The players’ rational choices, based on the anticipated outcomes of each game, would be to switch, showing how they could voluntarily replace the Centipede Game with the Reciprocity Game.2
Experiments with the Centipede Game show that the subgame-perfect equilibrium outcome is generally not the choice of subjects (McKelvey and Palfrey [3]; Nagel and Tang [4]). Neither are the other Nash-equilibrium outcomes, all of which involve the defection of P1 on the first round, terminating future play, so no later rounds are ever reached.
There are, of course, other Centipede Games besides the one shown in Figure 1; Garcia-Pola, Iriberri, and Kovárík [2] analyze 16 such games. Reciprocity works in all of these with increasing payoff sums (which increase by 2 on each successive round in Figure 1) but fails in all those with constant or decreasing sums. In our view, the latter games violate the spirit of a Centipede Game in which continuing cooperation brings increasing benefits to the players. The payoff sums are variable in four games, wherein the benefits of cooperation are at best partial when payoffs are switched to yield a Reciprocity Game.
In a standard Centipede Game like that in Figure 1, the unique subgame-perfect Nash equilibrium that gives (1, 0) is not the choice of subjects, including of chess grandmasters, in numerous experiments with the Centipede Game. Like most other players, they cooperate in the beginning but, toward the end of play, cooperation breaks down.3 To encourage cooperation throughout play, it seems desirable to distribute payoffs so that both players find it in their interest not to defect on any round, including the last, which is exactly what the Reciprocity Game rationalizes. Even if the time of occurrence of the last round is uncertain, it is still rational for the players to cooperate until it does, because the dominant subgame-perfect equilibrium of cooperation holds for every possible endpoint of a finite game.
Note that reciprocity in the Reciprocity Game takes the form of rewarding—not immediately, but eventually—the player who cooperates on a round instead of the player who defects. On each successive round, each player can reciprocate the cooperation shown to it by the rival player, which is always rational for it to do in the Reciprocity Game. Thereby, both players cooperate throughout the game and, in the end, equally benefit at (3, 3) in the Reciprocity Game.
The Reciprocity Game suggests a way in which an arms race, modeled as a Centipede Game, may be transformed into an arms-control treaty. If there is an endpoint, as there often is in a treaty, countries may lapse into an arms race before the end because of the temptation to defect, as in the Centipede Game. However, the Reciprocity Game reverses this temptation by turning the immediate advantage of defection into a reward to the rival player for abiding by the treaty’s terms, perhaps by a good will gesture or possibly a threat that would make abrogation of the treaty costly. This seems a sturdier way to undergird trust than to hope, in the Centipede Game, that the temptation to defect will not undermine compliance with the treaty.
The reward for cooperating rather than defecting is what, in international relations, Lebow and Stein [7] refer to as “reassurance.” This involves countries taking measures that discourage a rival from cheating on a treaty or considering a surprise attack. These measures are not just cheap talk, such as pronouncements of good will, but concrete actions to build up trust and stabilize cooperation. For example, the countries may develop peaceful means to settle any dispute that may arise.
This happened between the United States and the Soviet Union after the Cuban missile crisis in October 1962. To be sure, the arms race continued, but the two superpowers established a “hot line” in 1963 to enable electronic communication that could forestall a future crisis that might escalate to nuclear war. They also agreed to other reciprocal agreements, including a treaty on the nonproliferation of nuclear weapons in the late 1960s. Indeed, a period of détente between the superpowers, which began in 1969 and lasted until the Soviet invasion of Afghanistan in 1979, was characterized by reciprocal agreements that bore the earmarks of cooperation in the Reciprocity Game.
True, negotiations that lead to a treaty, or concrete measures that offer reassurance to an opponent that one intends to do no harm, may not follow the strict protocol of P1 and P2 making alternating choices that yield the payoffs shown in the Reciprocity Game in Figure 2. Nonetheless, this game may approximate the players’ give-and-take in negotiating a treaty. Most importantly, it demonstrates that the redistribution of payoffs in the Centipede Game leads to cooperation rather than conflict in the Reciprocity Game.
4. Conclusions
The Reciprocity Game does not provide the only “solution” to the Centipede Game. Some analysts have posited an aversion to the loss of the surplus from cooperation as well as cultural and social preferences for fairness or altruism that may overcome distrust.
Still others have argued, based on some form of forward induction, that past choices can serve as a harbinger of future choices and, consequently, as a reason for revising one’s beliefs about the behavior of a rival. These differing views are summarized in Levitt, List, and Sadoff [5] that includes several references.
In the case of belief revision, if P1 at the outset does not defect, this may justify P2’s cooperating next, because, by setting an example in choosing c, P1 has provided a reason for rejecting the logic of backward induction and hence for P2 also to choose c, especially if the game has many rounds. But we know that rarely, if ever, do players follow this logic to the very end by always cooperating in the Centipede Game, both in experiments and real life.
Axelrod [8] argued that being “nice” at the outset of an IPD game offers dividends, giving several examples of its occurrence. We do not dispute the advantage of this feature of tit-for-tat—cooperating at the outset but defecting in response to an opponent’s defection—which defeated other strategies in two tournaments and tends to foster the evolution of cooperation in IPD.
The problem is that players, especially toward the end of a repeated game with a definite termination point, also see the advantage of defecting near the end and may well do so (Embre, Fréchette, and Yuksel [9]). Not surprisingly, if there is no fixed endpoint, cooperation is more likely to persist, but it is not a dominant strategy in IPD (Bó and Fréchette [10]), as it is in the Reciprocity Game, whether repeated or not.
The ability to transform the Centipede Game into the Reciprocity Game—by interchanging the payoffs of the players on a round without adding anything to their total value or otherwise altering the structure of the game—would not be possible if the Centipede Game were zero-sum. Because there is a growing surplus available to the players if the game continues, the players may well be induced to cooperate by redistributing it in a way that transforms a “bad” subgame-perfect equilibrium into a “good” one.4
The surplus need not come from an outside party. The players themselves may recognize the benefits of continuing cooperation and come to a joint recognition that doing good deeds is a better way of settling a dispute, and cementing an agreement, than trying to seize a quick advantage that ultimately may backfire.
The player who makes this choice on each round of the Reciprocity Game boosts the later payoffs that both players will ultimately realize, thereby stabilizing cooperation throughout the game.5 It is this reciprocity, which is rationally based, that locks the players into the cooperative outcome in the Reciprocity Game.
Author Contributions
Conceptualization, S.J.B. and D.M.K.; methodology, S.J.B. and D.M.K.; formal analysis, S.J.B. and D.M.K.; investigation, S.J.B. and D.M.K.; writing—original draft preparation, S.J.B. and D.M.K.; writing—review and editing, S.J.B. and D.M.K. The authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rosenthal, R.W. Games of Perfect Information; Predatory Pricing and the Chain-Store Paradox. J. Econ. Theory 1981, 23, 92–100. [Google Scholar] [CrossRef]
- García-Pola, B.; Iriberri, N.; Kovárí, J. Non-Equilibrium Play in Centipede Games. Games Econ. Behav. 2020, 120, 391–433. [Google Scholar] [CrossRef]
- McKelvey, R.; Palfrey, T. An Experimental Study of the Centipede Game. Econometrica 1992, 60, 803–836. [Google Scholar] [CrossRef]
- agel, R.; Tang, F.F. Experimental Results on the Centipede Game in Normal Form: An Investigation on Learning. J. Math. Psychol. 1998, 42, 356–384. [Google Scholar]
- Lebow, R.N.; Stein, J.G. Beyond Deterrence. J. Soc. Issues 1987, 43, 5–71. [Google Scholar] [CrossRef]
- Palacio-Huerta, I.; Volij, O. Field Centipedes. Am. Econ. Rev. 2009, 99, 1619–1635. [Google Scholar] [CrossRef]
- Levitt, S.D.; List, J.A.; Sadoff, S.E. Checkmate: Exploring Backward Induction among Chess Players. Am. Econ. Rev. 2011, 101, 975–990. [Google Scholar] [CrossRef]
- Axelrod, R. A. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1984. [Google Scholar]
- Embrey, M.; Fréchette, G.R.; Yuksel, S. Cooperation in the Finitely Repeated Prisoner’s Dilemma. Q. J. Econ. 2018, 133, 509–551. [Google Scholar] [CrossRef]
- Bó, D.P.; Fréchette, G.R. On the Determinants of Cooperation in Infinitely Repeated Games: A Survey. J. Econ. Lit. 2018, 56, 60–114. [Google Scholar] [CrossRef]
- Press, H.W.; Dyson, F.J. Iterated Prisoner’s Dilemma Contains Strategies that Dominate an Evolutionary Opponent. Proc. Acad. Natl. Sci. USA 2012, 109, 10409–10413. [Google Scholar] [CrossRef] [PubMed]
| 1 | The Reciprocity Game equilibrium is more compelling in the sense that it is a dominant-strategy Nash equilibrium, whereas the Centipede Game equilibrium is not, as we will show later. |
| 2 | Requiring only one player rather than both to agree to the switch is “safer” in the following sense: If one player, perhaps mistakenly, does not agree, both players still benefit from receiving (3, 3) when they choose the subgame-perfect dominant strategies in the Reciprocity Game. The one exception to this statement is that P2 can benefit more from (2, 4) than from (3, 3) in the Centipede Game if it defects on the fourth round—should that round be reached—but P1 can, by itself, ensure that this does not happen by agreeing to play the Reciprocity Game. As an alternative decision rule, one could require that both P1 and P2 must agree to switch to the Reciprocity Game for it to happen, thereby ensuring that there is a consensus for switching rather than letting only one player determine this choice. |
| 3 | This was the finding in Levitt, List, and Sadoff [5], though an earlier study by Palacio-Huerta and Volij [6] found that chess grandmasters generally chose the subgame-perfect equilibrium. We hypothesize that not only chess grandmasters but also other subjects would elect to switch to the Reciprocity Game, if given the choice, and cooperate throughout in the latter game. |
| 4 | Benefits also accrue in IPD if the players continue to cooperate but, without changing the stage game, we know of no transformation of IPD that would render cooperation rational at every stage. In fact, Press and Dyson [11] showed IPD is vulnerable to an exploitive strategy they call “extortion.” |
| 5 | In international relations, requiring players to achieve milestones before the next phase of a treaty goes into effect often promotes cooperation. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).