Consider the infinitely repeated interaction between a
Homo oeconomicus, player 1, and an emotional player, player 2.
9 The set of feasible payoff vectors (utility vectors) in a stochastic game is the convex hull of the range of the present values from the pure stationary Markov strategy profiles.
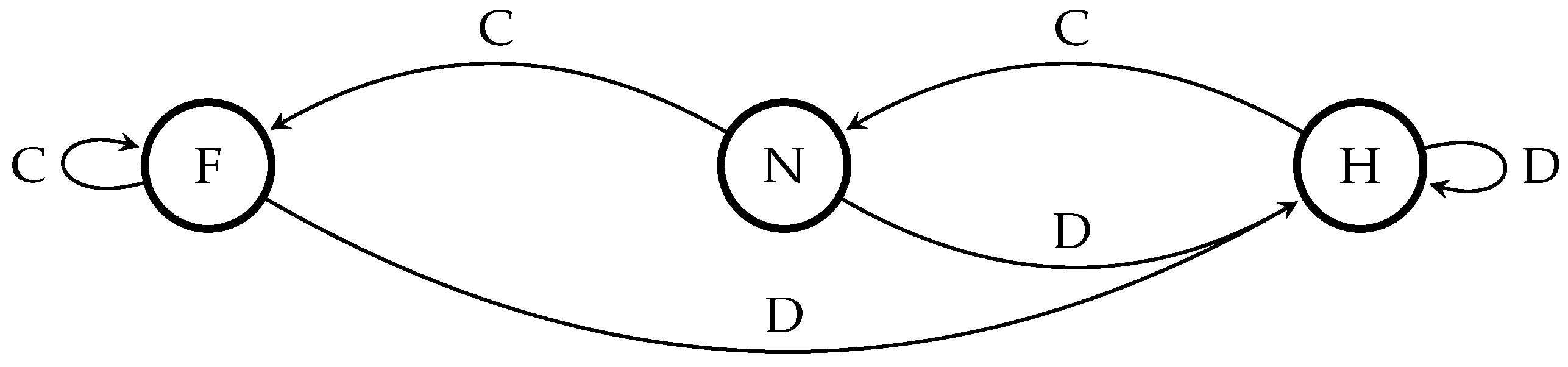
10 The two players have eight pure stationary Markov strategies each: Choose
C regardless of state; choose
C in the friendly and neutral states and
D in the hostile; choose
C in the friendly state and
D in the neutral and hostile states; choose
C in the friendly and hostile states and
D in the neutral; choose
D in the friendly state and
C in the neutral and hostile states; choose
D in the friendly and neutral state and
C in the hostile state; choose
D in the friendly and hostile states and
C in the neutral state; and choose
D regardless of state.
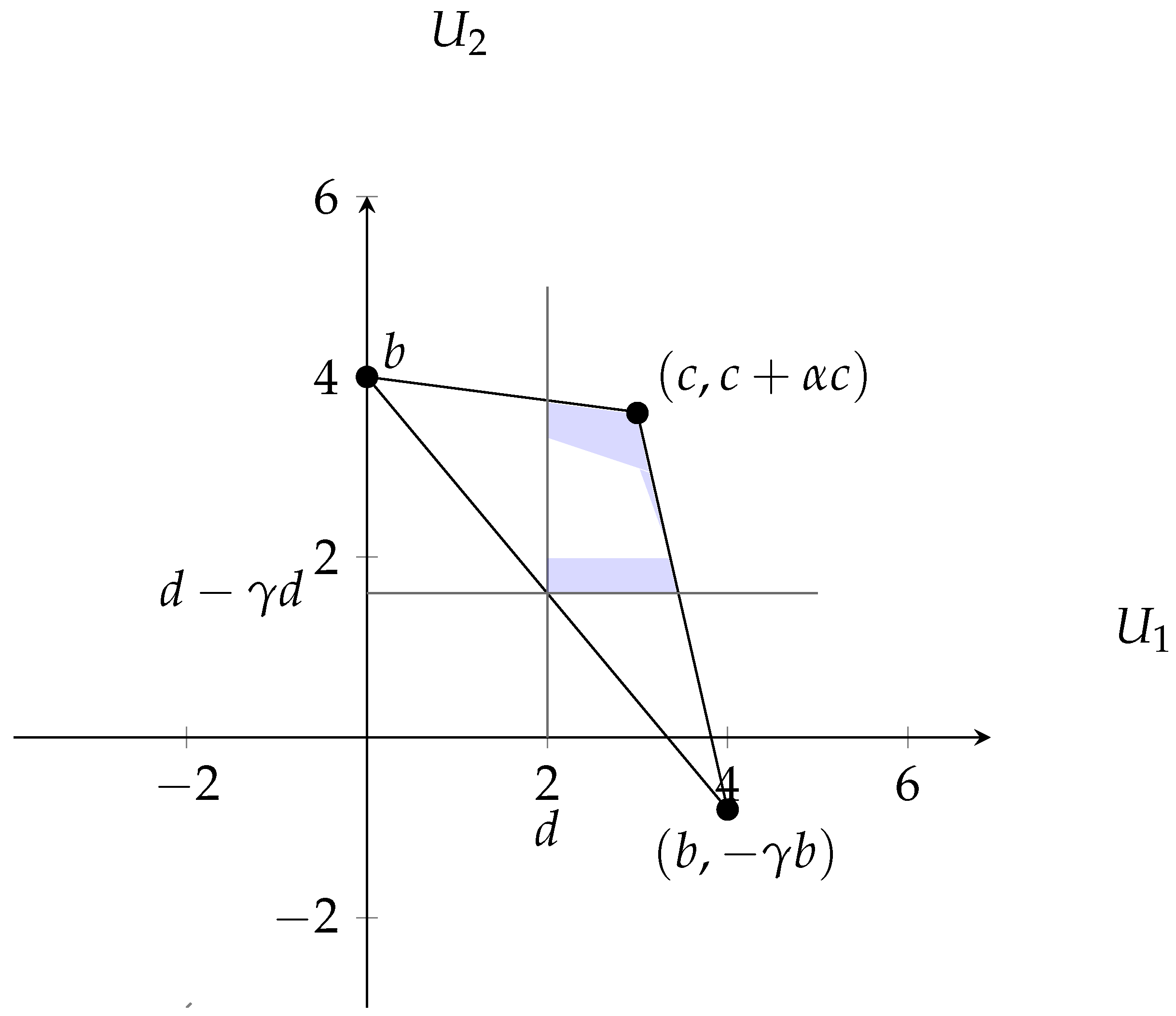
In addition, there is a subset of feasible and individually rational utility vectors in which both players receive a higher utility than what is possible for two Homo oeconomicus. This is because player 2’s positive concern for the material payoff of player 1 increases the maximum utility that can be received in each period. If , , , then the maximum utility for any player in the benchmark case is , and the cooperative utility vector is . If, in addition, , the maximum utility player 1 can receive from the interaction with the emotional player is , and the maximum utility the emotional player can receive is . The maximum symmetric utility vector is .
3.2.1. Grim Trigger
In a standard repeated game the one-shot deviation principle is used to verify that a strategy profile is a subgame perfect equilibrium. In a stochastic game the players have two reasons to deviate from a strategy. As in the repeated game they may do so for the immediate payoff, but there is also an incentive to deviate in order to influence future state transitions. As the players become more patient the second incentive becomes more important. In a stochastic game with either a finite set of states or a deterministic transition function, a strategy
is a one-shot deviation for player
i, from strategy
, if there is only one history at which the strategies disagree. A strategy profile
in such a game is subgame perfect if, and only if, there are no profitable one-shot deviations [
14].
First consider the game between one Homo oeconomicus, player 1, and one emotional player, player 2. The Grim Trigger strategy profile is subgame perfect if neither of the two players has a profitable one-shot deviation. Player 1 has no incentive to deviate if the normalized discounted utility from using the strategy, c, is higher than the sum of the normalized discounted utilities from player 1’s best one-shot deviation, , and from continued play of the Nash equilibrium, .
Player 1 has no incentive to deviate iff
This condition is identical to the corresponding one in the benchmark case. Note that player 2 cannot hurt player 1 more than by choosing D, and since player 1 only cares for own material payoff, player 1 is unaffected by player 2’s state of mind.
Now turn to the emotional player, player 2. Assume that player 2 uses the strategy. In the first period player 2 is in the neutral state of mind and receives a normalized discounted utility of before transitioning to the friendly state of mind and remaining there for the rest of the interaction, receiving a normalized discounted utility of .
Player 2 can deviate either in the neutral or in the friendly state of mind. It is most profitable for player 2 to deviate already in the first period because the immediate benefit from cooperation is lower in the neutral state. The normalized discounted utility in the first period is then . In the second period the Nash equilibrium action profile is played. Player 2 is in the friendly state of mind since player 1 choose C in the first period. Player 2’s normalized discounted utility in that period is . In the third period, player 2 has transitioned to the hostile state of mind and will stay there for the remaining interaction, receiving a normalized discounted utility of .
If
, then player 2 has no profitable one-shot deviation from the Grim Trigger strategy profile iff
When
, (
4) is identical to (
3). An increase in either
or
decreases player 2’s profitability of deviating. Player 2’s positive concern for the other player’s material utility increases the benefit from cooperation, and the negative concern increases the cost of deviating. Player 2 requires less patience than player 1 not to deviate, and the common discount factor required for Grim Trigger to be subgame perfect is determined by the condition for player 1.
Let and be the minimal discount factors required for the Grim Trigger strategy profile to be subgame perfect in the case of play between one Homo oeconomicus and one emotional player, and in the benchmark case respectively.
Proposition 4. Suppose that both players use the Grim Trigger strategy. Then .
Next consider the game between two emotional players. Note that an emotional player receives no utility from the state of mind of the other player, only from their material payoff. Therefore the condition for an emotional player not to deviate from a strategy profile does not depend on the type of the other player.
Thus, in the infinitely repeated interaction between two identical emotional players, the Grim Trigger strategy profile is subgame perfect iff (
4) holds. An increase in either
or
decreases the patience required not to deviate; both states of mind facilitate cooperation when the Grim Trigger strategy is used.
Let be defined as before and let be the minimal discount factor required for the Grim Trigger strategy profile to be subgame perfect in the game between two emotional players.
Proposition 5. Suppose that both players use the Grim Trigger strategy. Then , and is decreasing in α and γ.
To summarize, two emotional players can sustain cooperation easier than two Homo oeconomicus if they use the Grim Trigger strategy. With that strategy, both the friendly and the hostile state of mind facilitate cooperation.
3.2.2. Mutual Minmax
Consider next the mutual minmax strategy profile in which the players choose C as long as both have always chosen C; they choose C also if the history contains L consecutive periods of mutual play of D after which only C has been played; they play the mutual minmax action, D, for L consecutive periods after all other histories. Let any history after which the players choose C be denoted the cooperative phase, and any history after which the players choose D be denoted the punishment phase.
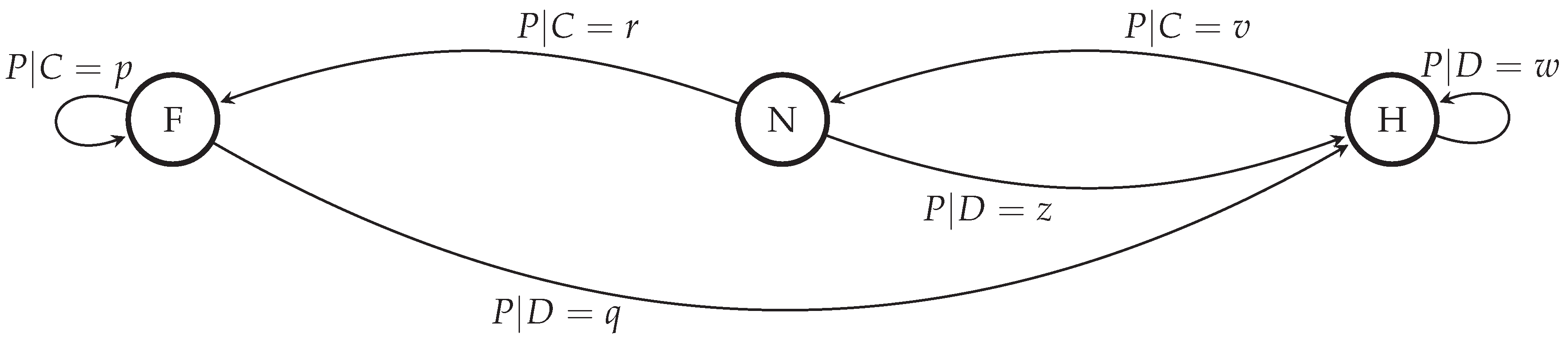
A noteworthy implication of the transition probabilities in
Figure 1 is that two players who punish each other by choosing
D will both transition to the hostile state of mind. When the punishment period is over, the players are still in a hostile state of mind.
11In the benchmark case the players may have an incentive to deviate either during the cooperative phase or during the punishment phase. The players have no incentive to deviate during the punishment phase since the mutual minmax action profile,
, coincides with the unique Nash equilibrium. In the cooperative phase the players have no incentive to deviate iff
The normalized discounted utility from deviating is the sum of three terms: The one-shot deviation utility of , the utility received during the punishment phase of L periods, , and the utility received from returning to choosing C after the punishment period, .
The above condition can also be presented as a cost-benefit calculation. The benefit of deviating is the utility from the one-period deviation,
b, minus the one-period utility from using the strategy,
c. The cost of deviating is the utility received if no one had deviated,
c, minus the utility received during the punishment phase,
d, for the
L consecutive periods of punishment. Thus (
5) can be rewritten as
Now consider the case of one Homo oeconomicus and one emotional player. The condition required for the Homo oeconomicus not to deviate is the same as the condition in the benchmark case. The reasoning is similar to the case of the Grim Trigger strategy profile.
Now turn to player 2, the emotional player. Player 2 can either deviate during the cooperative phase or during the punishment phase. Moreover, the incentives to deviate are affected by player 2’s states of mind.
First consider the equilibrium path history, in which no player thus far has chosen D. Start with assuming a punishment phase of length one, . On the equilibrium path, player 2 can either deviate in the neutral or in the friendly state of mind, and it is most profitable to deviate in the neutral state. Player 2’s benefit from the best one-shot deviation is . After the deviation the players punish each other for L periods. In the first punishment period, however, player 2 is in the friendly state of mind since player 1 cooperated in the previous period, and incurs a normalized discounted cost of . Player 2 then transitions to the hostile state of mind, and therefore receives a smaller utility from choosing C during the two periods required to transition to the friendly state of mind. This implies a additional cost of .
Suppose that
and
, then player 2 has no profitable one-shot deviation in the cooperative phase iff
When
, (
7) is identical to (
6). When
, player 2 has a higher cost of deviating than player 1.
Now assume . Player 2’s one-period benefit from deviating is as before, and so is the cost in the first punishment period. In the second period of the punishment phase, player 2 has transitioned to the hostile state of mind, and incurs a normalized discounted cost of . In addition, player 2 also incurs the cost pf transitioning back to the friendly state of mind once the players return to cooperation.
Suppose that
and
, then player 2 has no profitable one-shot deviation in the cooperative phase iff
For punishment phases of length
, the above condition can be generalized to
When
, (9) is identical to (
6). An increase in either
or
increases the cost of deviation and thus decreases the patience required to use this strategy.
Player 2’s states of mind have three effects on the profitability of deviating in the neutral state of mind. First, the utility from continued cooperation is larger because of the, in the friendly state of mind, positive concern for the other player’s material payoff. Second, the utility during the punishment phase is smaller if , due to the negative concern for the other players material payoff. Third, it takes time for player 2 to calm down and transition back to a friendly state of mind once the players have returned to cooperation.
Next consider the off the equilibrium path histories. If one player deviated in the previous period, the players are supposed to play the mutual minmax action profile, , for L consecutive periods. If player 1 deviated then player 2 is in the hostile state of mind and has no incentive to deviate from the punishment. However, if player 2 deviated and player 1 cooperated, player 2 has transitioned to the friendly state of mind and might be less inclined to punish the other player. If player 2 deviates from punishment, the immediate benefit is: . After this deviation, the players are supposed to restart the punishment phase, and now player 2 has transitioned to the hostile state of mind. The normalized discounted utility from the extra period of punishment is . Player 2 would have received from using the strategy. In addition, player 2 also faces the delayed cost of transitioning back to the friendly state of mind.
If
, then player 2 has no profitable one-shot deviation from punishment iff
The friendly state of mind has two effects on the profitability of deviating during the punishment phase. It increases the cost of punishing the other player due to the positive concern for the other player’s material payoff, but also increases the cost of deviating due to the cost of transitioning back to the friendly state of mind after the punishment phase. When the first effect dominates and an increase in increases the cost of punishing the other player.
Further, the hostile state of mind also has two effects on the cost of punishing the other player. It increases the cost of deviating from punishment by increasing the cost of remaining in the hostile state, but also decreases the cost of deviating by decreasing the difference in utility between cooperation and punishment. If player 2 is sufficiently patient, , the first effect dominates, and an increase in increases the cost of deviating from the punishment. Thus, while player 2’s positive concern for the other player’s material payoff can make threats of punishment less credible, the possibility of transitioning to the hostile state of mind offsets this effect.
Finally, after a punishment phase the players are supposed to return to cooperation, but once in the hostile state of mind, player 2 may require more patience to do so.
First suppose , and that player 2 is in the hostile state of mind. Player 2’s immediate benefit from deviating is . Since player 1 cooperated player 2 transitions to the neutral state of mind, and the cost of the single punishment period is . Following the punishment period player 2 transitions to the hostile state of mind. Once cooperation is resumed, player 2 also faces the cost of transitioning from the hostile to the friendly state of mind.
If
, and
, then player 2 has no profitable one-shot deviation from cooperation iff
When
, (
11) is identical to (
6). An increase in
increases player 2’s cost of deviating, and an increase in
increases player 2’s benefit from deviating. Player 2 might thus require more patience than player 1 for the strategy profile to be subgame perfect.
Now suppose . Then player 2’s one-period benefit from deviating is as before, and so is the cost in the first period of the punishment phase. In the second period of the punishment phase, player 2 has transitioned to the hostile state of mind. In the hostile state of mind player 2 receives a lower utility, , than in the friendly state of mind. After the punishment phase has ended, player 2 faces the cost associated with transitioning back to the friendly state of mind.
For punishment phases of length
, the condition in (
11) can be generalized to
When
, (
12) is identical to (
6). An increase in
increases player 2’s cost of deviating, whereas an increase in
now increases both the benefit and the cost of deviating. The cost increase dominates if
If this inequality holds, then the Homo oeconomicus has the binding restriction on the minimal discount factor required for the mutual minmax strategy profile to be subgame perfect.
Given that
is sufficiently small, such that player 2 has no incentive to deviate during the punishment phase, and that (
13) holds, player 2 requires less patience than player 1 not to deviate from the mutual minmax strategy profile. The minimal discount factor required is therefore determined by the condition for player 1.
Let and be the minimal discount factors required for the mutual minmax strategy profile to be subgame perfect in the case of play between one Homo oeconomicus and one emotional player, and in the benchmark case resepectively.
Proposition 6. Suppose that both players use the mutual minmax strategy with a punishment length . If , and (13) does not hold, then . Next consider the case of two emotional players. Both the positive and the negative concern for the other player’s material payoff has conflicting effects on cooperation. The friendly state of mind makes it more costly to deviate from cooperation, but also more costly to punish the other player for deviating. The hostile state of mind can obstruct cooperation by making it more difficult to return to cooperation after a punishment phase, but can at the same time facilitate cooperation by making threats of punishment more credible. When
, the mutual minmax strategy profile is subgame perfect iff (
7), (
10), and (
11) hold. When
, it is subgame perfect iff (9), (
10), and (
12) hold.
Only if
is sufficiently small, such that the players have no incentive to deviate during the punishment phase, and the players are sufficiently patient, such that (
13) holds, can two emotional players sustain cooperation easier than in the benchmark case when using the mutual minmax strategy.
Let be defined as before and let be the minimal discount factor required for the mutual minmax strategy profile to be subgame perfect in the game between two emotional players.
Proposition 7. Suppose that both players use the mutual minmax strategy with a punishment length . If , and (13) hold, then , and is decreasing in γ. If (13) does not hold, then . To summarize, two emotional players who use the mutual minmax strategy may find it either easier or more difficult to sustain cooperation than two Homo oeconomicus. Both the hostile and the friendly state of mind have conflicting effects on cooperation.