1. Introduction
People have varying degrees of expertise and views of the facts. Nevertheless, they often need to come to a decision without the help of some leader who imposes her view. Is the developed product ready to be launched? Should the UK leave the EU? While people are free to discuss facts and what to make of them with a colleague or a friend, the joint time of all involved is a scarce resource, especially if the group is large. Not every team member can elaborate on the chances of a successful launch. Asking every UK citizen to describe the perceived benefits and costs of leaving the EU and then agreeing on what these contributions imply seems absurd. Instead, communication is restricted—in the extreme case to an expression of opinion by a vote on a proposal that reduces potentially rich information to the rather coarse “yea,” “nay,” or “nil.”
When group communication is restricted, holding back less valuable information can become optimal—a notion that has been formalized by Feddersen et al. [
1] as the “swing voter’s curse.” Talking about a minor detail in a team meeting may bury potentially important contributions of others. Voting on whether to leave the EU based on one’s gut feeling dilutes the voices of those who correctly foresee the implications and consequences of such a step. Individuals do not always realize that withholding information may improve the group’s decision. In practice, people frequently talk or vote without much to go on. For such groups to improve information aggregation, individuals would have to learn about the benefits of restraining themselves and let the expert be heard.
While direct communication can help small groups in coordinating for better outcomes, (for examples, see [
2,
3,
4,
5]) such coordination may be hampered by three features in our initial examples. First, a large group size directly complicates coordination. Second, if others are unaware of the efficient strategy, trying to coordinate on this strategy with them seems less promising. Third, coordination is difficult if those involved cannot talk to each other. Communication may even be detrimental when it is local. Someone who has the insight to restrain herself may realize, while conversing with others, that ignorance is prevalent. If she believes that group behavior is unlikely to change for the better, it becomes optimal for her to no longer restrain herself and contribute the little that she knows. On the other hand, local communication may foster learning and people may trust that others are independently reaching similar conclusions and restrain themselves. Can a large group learn to withhold inferior information? Is local communication helpful in achieving this goal?
Answering these questions in the field is difficult because we cannot observe the quality of information that is withheld. In an experimental study, however, the quality of information can be controlled by the experimenter. We opted to run the experiment in a first-year class with more than 500 participants. We did so to capture the three above-mentioned features of real-life situations. First, we can have several groups of 36 members jointly deciding on an issue, while not being able to reach out to one another and coordinate because they are randomly dispersed across the auditorium. In an economics laboratory that seated 20–30 people, this would have been very hard to do. Second, while subjects in the laboratory seem to be aware of the benefits of holding back to such a degree that Morton et al. [
6] speak of a norm of “letting the experts decide,” our experience suggested that participants in a large lecture might not. Third, the classroom setting allows us to have “rich” local communication, while that on the group level is restricted to voting: students sit next to those whom they are likely to know and trust, but they decide together with other students who are scattered across the room.
One out of the 36 group members received expert knowledge: she was perfectly informed about the most frequent color in an urn with blue and green balls. For the other 35, we drew balls from the urn without replacement and showed them the colors of their individual draws on a mobile device. In order to introduce some uncertainty about the value of one’s own information, one of the 36 individuals was randomly excluded from the group. The perfectly informed individual was thus not certain but very likely to remain in the group. Every remaining individual could then either abstain or vote for or against the color that they saw. If the majority voted for the right color, all in the group received €10. Otherwise, they got nothing.
This game featured an
all-vote equilibrium, where everybody votes for their information, but also an
only-expert-votes equilibrium, in which everyone but the expert abstained. We parameterized it so that the only-expert-votes equilibrium was substantially more efficient: the probability of identifying the correct state was more than 30 percentage points higher than when all voted. Our game is similar to that by Morton et al. [
6], so our experiment can be regarded as an extension and robustness check bringing in the above features.
As we expected and hoped for, participants initially overwhelmingly voted for their own color (78.1%). This is not only a coordination problem. In a post-experimental questionnaire, we asked participants the hypothetical question: If you would interact with a group of robots, how would you program them? More than half of the people programmed the robots to always vote and only a quarter to play the efficient strategy. This suggests that they were unaware of the efficient strategy. Moreover, participants were more likely to vote against their own color (15.5%) than to abstain (6.4%). Given this behavior, voting one’s own color is optimal.
Taking inspiration from Cason et al. [
7], who found that local communication among students reduces misconceptions in an individual decision task, we gave students five minutes to talk to their immediate neighbors before repeating our interactive decision task with a newly filled urn and in new teams. While individual changes in voting behavior had little impact, a coordinated response by the group could improve its performance by five percentage points if the few people who voted against their color and abstained could be convinced to vote in line with their color. Alternatively, the group could obtain a gain of over 40 percentage points if almost everybody in the group but the expert abstained. As pointed out, voting one’s own color is the best response to the initial behavior of others. Given that direct communication with the other group members was not possible, these circumstances were unlikely to change and an increase in voting thus seemed likely.
Still, we found that abstentions increased in the second run from 6% to 13%. This increased by more than 100% was not only economically but also highly statistically significant. It documents, to our knowledge for the first time, that self-governed groups are not trapped but make a tentative step toward the more efficient use of information. Put differently, we may have been observing the birth of a “norm of abstention”. The increase is all the more surprising because it is (predictably) too small to improve information aggregation: if anything, the majority is now less likely to identify the right color.
One possible explanation for why abstentions increase is that participants teach each other about the sophisticated strategy. Consistent with this notion, people who program the sophisticated strategy are significantly more likely to start abstaining in the second round (86%) than those who do not (33%). Moreover, abstention spreads locally. With a neighbor who abstained in the first round the probability that a voter abstains in the second round increases by 13%.
In our setting, communication occurs naturally, without interference, structure, or observation. The downside of this is that we are unable to use the content of conversations to decide whether people really learn about the sophisticated strategy or whether they already know this strategy and only learn to trust that coordination can be successful. It is even possible that the increase in abstention had nothing to do with communication at all but instead resulted from locally correlated independent learning. More able participants are more likely to find the sophisticated strategy either in the first or the second round than less able ones. If people of similar ability are more likely to sit next to each other, having a neighbor who abstained in the last round is associated with a higher probability to switch to abstention in the second round—even without communication. We cannot exclude this explanation because participants were not seated randomly but (as is typical for lectures) chose their seats themselves.
1 Our design can also not exclude that people learn to trust in successful coordination. We can, however, examine whether these alternative explanations are consistent with the data.
Both alternative explanations, local but independent learning and learning to trust in the success of coordination, imply that having more abstaining neighbors in the first round is associated with a stronger increase in abstentions in the second round. The more neighbors of an individual have abstained in the previous round, the more likely appears a successful coordination to that individual. She becomes more willing to abstain. A participant with more able independent learners around is more likely to discover the sophisticated strategy and to abstain.
These alternative explanations, however, are not borne out by the data. How many neighbors previously abstained is not associated with a higher probability to abstain. The explanations of local independent learning and learning to trust in the success of coordination are thus not consistent with what we observed. Our tentative conclusion is that people teach each other the sophisticated behavior—although this is lowering the group’s probability of success.
The remainder of the paper is organized as follows. The next section describes our contribution to the literature.
Section 3 derives the best-reply and some equilibria of the game.
Section 4 explains the design of the study.
Section 5 presents our findings and
Section 6 concludes.
2. Contribution to the Literature
Our paper relates to three strands of the literature: (i) optimal extraction of information in groups, (ii) choice of equilibrium when there is communication, and (iii) learning in experiments.
The proposition that more people know more has fascinated social philosophers at least since Galton conducted his famous analysis showing that the average guess of visitors at a fair was closer to the true weight of an ox than that of an expert [
8]. De Condorcet [
9] asserts that more (at least partially) independent and informative viewpoints lead to better decisions. Here, we check whether crowds are not only wise in the sense of available information but also whether they wisely aggregate this information.
How groups aggregate information has received quite a bit of attention in the literature. One of the best established results in this regard is that markets work extremely well in extracting and pooling private information from individual traders. This power of markets to collect and disseminate information has been demonstrated by Plott et al. [
10]. In the presence of complete markets,
2 the price swiftly converges to the rational expectation’s benchmark. Plott et al. [
11] and Camerer et al. [
12] examined the role of “expertise” (or perfectly informed insider) in experimental asset markets. They show that the experts’ information quickly takes a hold and the prices converge to the underlying fundamental value.
3 In contrast, information is shared in our study by voting.
There is a sizable literature examining information aggregation when voting. For instance, Guarnaschelli et al. [
14] examined the strategic voting incentives in ad hoc committees of various sizes under the majority and unanimity rule. Ali et al. [
15] further extended this work to standing committees that interact repeatedly. In line with assertions of Austen et al. [
16] and Feddersen et al. [
1], these studies found that strategic voting is prevalent. Under the unanimity rule, as predicted, a substantial fraction of subjects vote against their signal.
4 These findings demonstrate that in laboratory voting games, subjects are capable of acting with a high degree of sophistication.
5 In our case, there are no incentives to vote against one’s own signal. On the other hand, strategic abstention is central to the efficient information aggregation strategy that we focus on.
Unlike in our study, a high degree of coordination on abstention by non-experts is observed in laboratory experiments. Exploring Feddersen et al. [
1,
20] in a series of experiments, Battaglini et al. [
21,
22] and Morton et al. [
6] found that a large fraction of subjects withheld their information if there was a high chance of a better informed expert. In Morton et al. [
6] some learning of abstention seemed to be going on, which suggested that we might see the emergence of a “norm of abstention.” This, however, was by no means certain. In all these experiments, standard procedures ensure common knowledge of the game and the problem that we are interested in studying, i.e., whether abstention can propagate in a group where many are unaware of the value of abstention, does not arise.
The sophistication of individuals when extracting information in common value environments can reach its limits. If public and private information is available, members of a group can, for example, be prone to updating biases. In Mengel et al. [
23], inefficiencies arise because subjects trust available expert information too much and then vote too often against their signal. In Kawamura et al. [
24], subjects are locked in a situation where they vote too often for their own uninformative signal rather than abstain. Following Charness et al. [
25], who inquired into whether beliefs or cognitive difficulty are at the heart of overbidding in auctions, Esponda et al. [
26] addressed this issue in a voting context and identified a subject’s difficulty to engage in hypothetical thinking as the root of non-strategic voting.
6 Neither of these contributions examines how behavior develops if subjects have the opportunity to communicate and hence to learn from each other.
The second strand of literature to which we relate is coordination between differently efficient equilibria when there is communication. A sizable literature documents the positive impact of pre-play communication on the ability of the group to coordinate on Pareto efficient equilibrium; e.g., Cooper et al. [
2], Charness [
3], Duffy et al. [
4], Blume et al. [
5], Cason et al. [
28], and Blume et al. [
29]. Goeree et al. [
30] examined the role of free communication on the behavior in a subsequent experimental voting game. They found that subjects not only truthfully and publicly revealed their private information to each other but they also discussed what to do with that information (i.e., how to vote) to achieve the best outcome.
7 This decentralized process uniformly improves group decision making and diminishes the role of strategic incentives presented by different voting institutions. Palfrey et al. [
34] found a significant positive impact of intra-party communication on turnout in laboratory elections. Contrary to Nash equilibrium predictions, the higher turnout primarily benefits the majority party.
8 In both these contributions, communication was public (within the relevant group of voters) and could thus be used to establish common knowledge. In our study, we were interested in a situation wherein communication does not extend to the whole group, so that common knowledge cannot be achieved.
Finally, our paper offers a contribution to learning in experiments. Various experiments examine how subjects learn individually in interactive situations, e.g., in Cournot or Bertrand competition (see, e.g., [
36,
37]), social-dilemma games (see, e.g., [
38,
39,
40]), and coordination games [
41,
42]. In other contributions, subjects learn from others in individual decision problems [
7,
43,
44]. We looked at a situation in which individuals could learn from others but in an interactive situation.
3. Model and Analysis
The game that is played by participants involves 36 players . Each player receives a signal about an unknown state of nature which represents whether the majority of balls in an urn are blue or green. Signals are of different quality . One of the signals is perfect and reveals the true state . All others are relatively noisy because they are drawn from the urn which contains 99 balls of which 50 have one color and 49 the other color. One randomly drawn player is excluded, so that 35 players remain and it is very likely that one of these is perfectly informed (%).
The remaining 35 players can vote blue, green or abstain depending on the content s and type t of the signal. Once signals are realized, strategies result in a voting outcome v, where v measures how many more people voted for the true than the other state . Let us standardize the payoff in the case that the majority voted for the actual state, to one and for to zero.
Player i’s vote is decisive in two situations: in the case of a tie, , and in the case of a one-vote lead for the true state, where is the voting outcome without i’s vote. In the first case, a vote for the true state generates a majority for the true state and gains of one. In the second case, a vote against the true state destroys the majority and leads to losses of one. These situations may never occur. If, for example, all other players always vote blue irrespective of their signal, player i’s vote will never make a difference. In our setting of a large class, however, such a coordinated response is very unlikely. This is why we assume the following.
Assumption 1 (Strategic uncertainty assumption). From player i’s perspective, it cannot be excluded that her vote affects results: and .
This strategic uncertainty means that player i’s behavior matters and gives her a reason to contemplate her choice in the first place. The assumption has several consequences. First, voting for one’s own signal strictly dominates voting against it (see Lemma A1). The reason is that the signal is informative and voting against it is hence more likely to cause harm whenever the player can make a difference. Moreover, for perfectly informed players () voting strictly dominates abstaining (see Lemma A2). Since they are perfectly informed, they will never destroy a one-vote lead for the true state by voting for their signal but they may resolve a tie in the right way.
For imperfectly informed players (
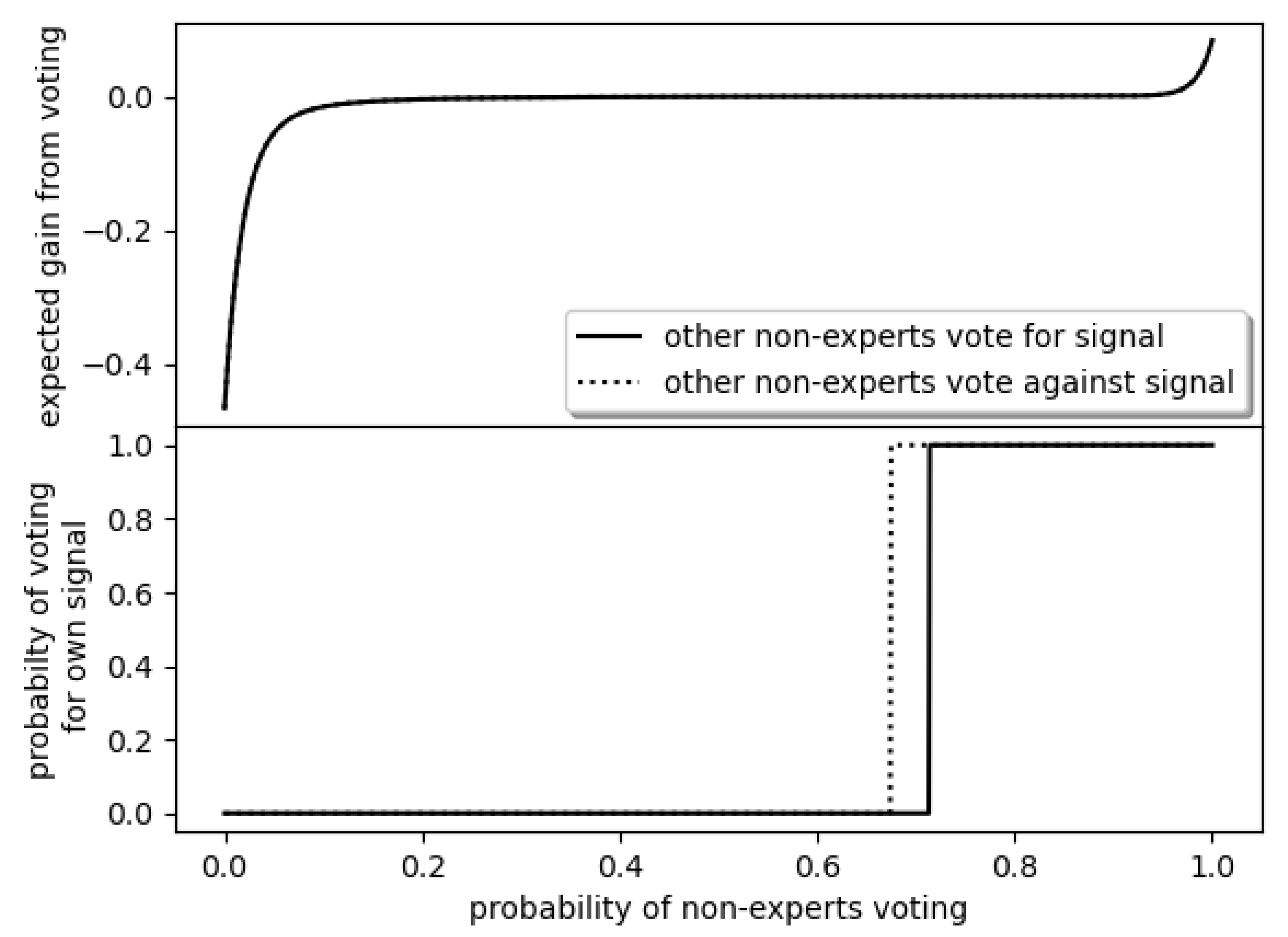
), the situation is more interesting. On the one hand, voting for one’s own signal can resolve a tie. On the other hand, it may destroy a one-vote lead. The gains from voting one’s signal thus depend on the likelihood that these pivotal situations occur. The top panel in
Figure 1 shows the gains from voting relative to abstaining under the assumptions that players with perfect information vote for their signal and given a probability
q that other imperfectly informed players (non-experts) vote. The figure actually contains both extreme cases, i.e., when non-experts vote for and against their signals. The difference, however, is so small that they do not show in the graph. The reason is that the expert is very likely to be present. Hence, the question whether others abstain or vote is more important than the relatively small difference in getting it right when voting.
Player i’s best reply in the lower panel shows that the likelihood that other imperfectly informed players vote is crucial. If it is unlikely, abstention is better to not dilute the expert’s vote. If it is likely, the expert’s vote is already so diluted that voting is the best reply.
The share for which it becomes optimal to vote rather abstain depends on the behavior of the other non-experts: if they all vote against their signal, voting for the signal becomes more valuable in comparison to abstaining and the share drops. The best reply function reveals the following equilibria of the game (the proof is in
Appendix A).
Proposition 1. Under the strategic uncertainty assumption, there are two Nash equilibria in pure strategies:
In the only-expert-votes equilibrium, only the perfectly informed expert votes and all others abstain.
In the all-vote equilibrium, everyone votes.
In addition, there is a Nash equilibrium in mixed strategies, wherein the expert votes and non-experts are likely to vote for their color (in around 70% of the cases) but sometimes abstain (in around 30% of the cases).
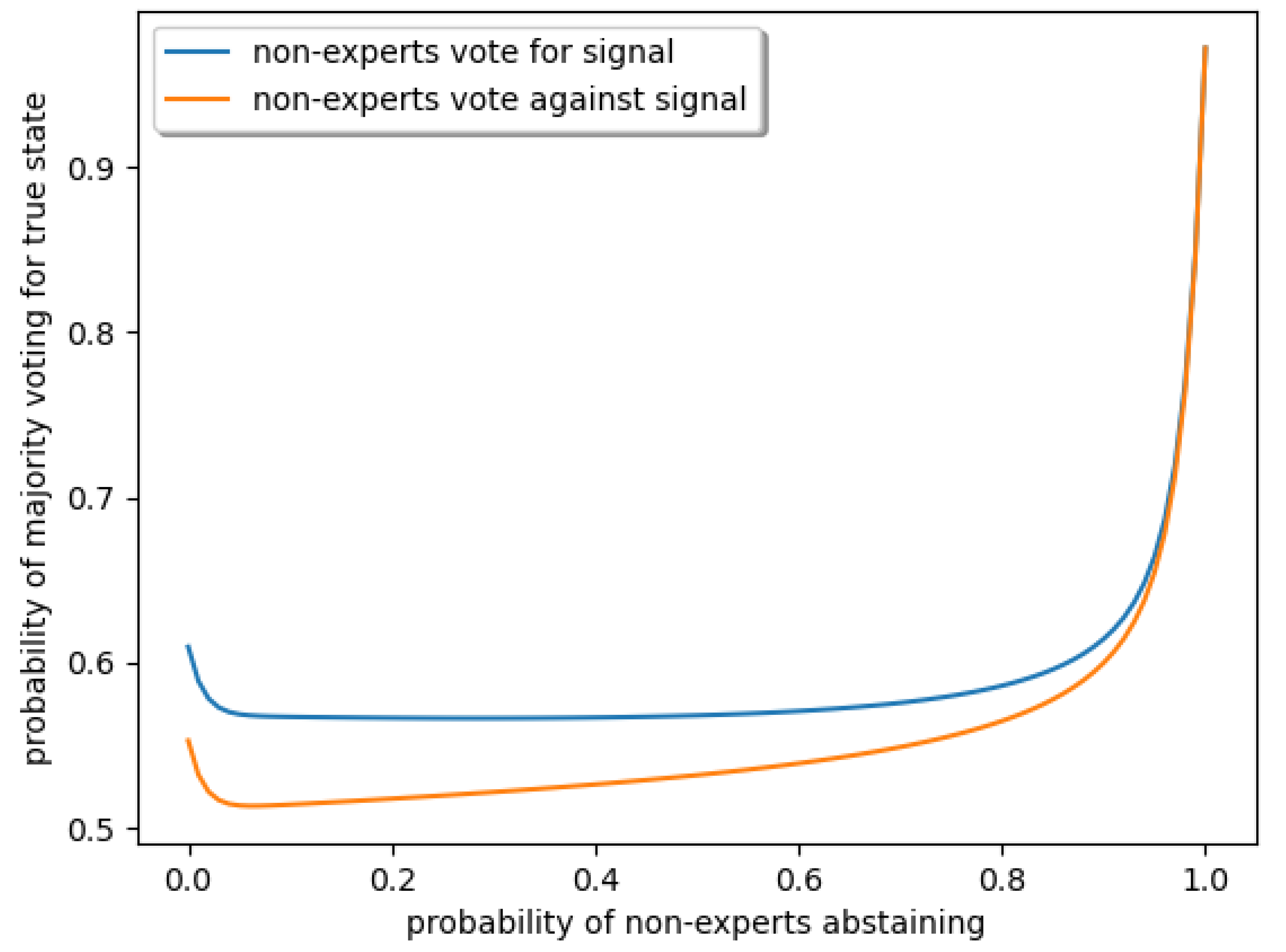
Figure 1 shows that apart from extreme situations in which nearly everyone either abstains or votes, the individual decision to vote or abstain has very little impact on the group’s probability of identifying the right color. The non-expert’s joint decisions, however, can have a sizable impact (see
Figure 2), so that it matters which equilibrium will be played (the proof is in
Appendix A).
Proposition 2. The only-expert-votes equilibrium Pareto-dominates the all-vote and mixed-strategy equilibrium by more than 30 percentage points.
Since perfectly informed players vote in both equilibria, which of them is reached depends on the behavior of imperfectly informed players. This is why we focus on their behavior when discussing results, later.
4. Experimental Design
When introducing the game in the lecture, we used physical props to render it easy for subjects to comprehend the problem. Before the lecture, we filled two urns with 49 blue and 49 green balls, and added another (blue or green) ball to generate a majority and a dice of the same color (to represent the perfect information). We then drew the dice and 35 balls from the urn, numbered them, and placed them into a small cardboard box that was sealed and put on display during the whole lecture. After the complete experiment, the box was opened and students were allowed to inspect them.
Each participant in the lecture theater received the information about the color of one object from the cardboard box on an Internet capable device,
9 i.e., a mobile phone, tablet, or laptop. The ball (imperfect information) was represented on the screen by a circle of the appropriate color; the dice (perfect information) was represented by a square of the respective color. For logging in, subjects had an access code taped to their desk, which could only be used once.
Subjects were told that they would be matched in groups of 35 members who were dispersed throughout the auditorium. Each member of the group had a unique piece of information corresponding to the color of one of the 36 objects from the cardboard box. Subjects were assigned randomly rather than with their immediate neighbors in order to prevent direct communication within the voting group. For practical reasons, the matching of participants into groups was carried out after all decisions were made. One group was selected for payout and each member of this group received €10 in case that the color with most votes was actually the majority color in the urn.
With 35 group members and 36 objects in the box, one object was left unassigned. This physically conveys the idea that it is unlikely (but possible) that none of the group members might have received the perfect information without having to rely on probabilities.
Before sending out information about colors, we asked subjects several control questions in order to get some indication of their comprehension. We did not provide feedback about correct answers in order to maintain the “natural” heterogeneity. At the end of the round, subjects received information on their mobile device about the voting outcome of their group, whether this outcome was correct, and whether their group was selected for payout. Then, we surprised subjects with the announcement that the voting would be repeated with a new urn and a new draw of 36 objects. A second sealed cardboard box containing the 36 draws from the second urn was presented and placed on the desk next to the box from the first round.
Before starting the second round, we gave subjects 5 min to freely discuss with their neighbors. After the five minutes, subjects were again put under the exam protocol, i.e., no talking or looking around. They then received their signals and cast their votes.
At the very end, we sent subjects a brief questionnaire on their devices in which we inquired about their gender and age. In addition, we wanted to assess whether they were aware of the efficient strategy. We did so by asking subjects to imagine that they would play with robots that could be programmed to follow a certain behavior. We then wanted to know how they would program these robots. They could specify whether robots should vote for blue or green or abstain depending on the information received by the robot.
5. Results
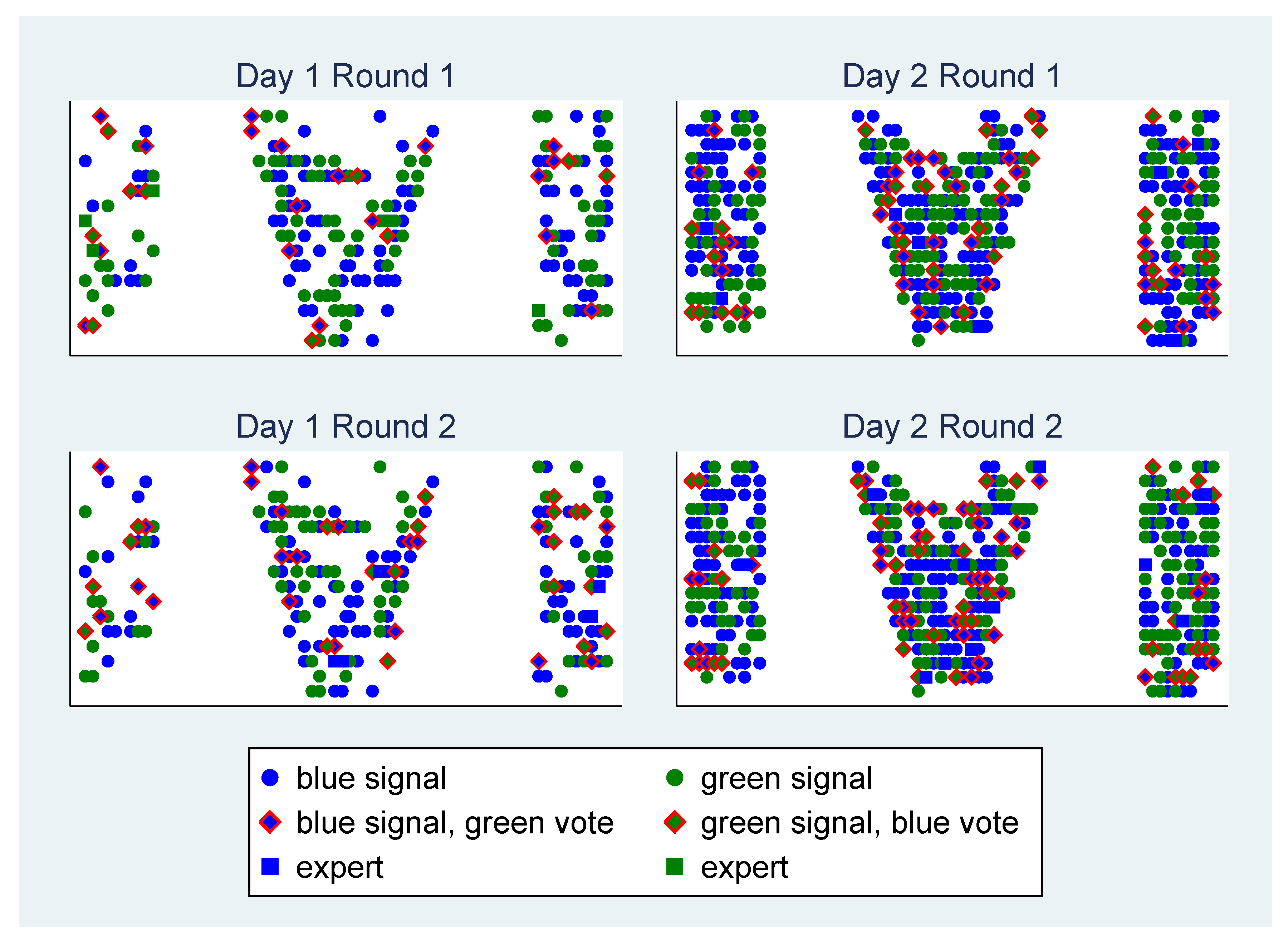
The participants in this study were almost 600 students from a large first-year class (“Introduction to Business Administration”) at Paderborn University. It was run on two consecutive days and the overwhelming majority of those present participated. Participants were able to “leave” and “enter” the study at any time by disconnecting from or reconnecting to the server. Still, only 3% were lost during the actual experiment, which might be expected for purely technical reasons (network interruptions, low battery). Attrition during the ex-post questionnaire was larger, particularly on the first day, for many participants had to move on to the next lecture. Our analysis will focus on the around 590 participants with imperfect information whose behavior determined whether or not the efficient equilibrium was played. (Numbers for perfectly informed subjects were too low for a meaningful analysis.) The whole experiment took between 20–27 min and average earnings among subjects in groups selected for payout were €7.50.
5.1. Prerequisites
If we want to study whether a group can overcome the problems of unawareness about the efficient strategy and evolve to a more sophisticated use of information, we need to check whether the starting point exhibits such unawareness and whether there is still room for sophistication.
Some evidence for unawareness comes from the control questions. About 6% incorrectly believed that green was more likely to be the majority color when their signal was blue. Around 3% claimed that voting blue meant that blue became less likely to be the majority color in their group; 30% said that them voting blue would not affect the outcome of the vote.
10More importantly, participants did not agree on how to optimally behave. The majority programmed their voting robots to vote regardless of whether they were perfectly or imperfectly informed, which suggests that they are unaware of the efficient only-expert-votes equilibrium. Slightly more than a quarter restricted the robots to voting only when information was perfect and is hence likely to be aware of the efficient equilibrium.The remaining quarter’s programming was all over the place—see
Table 1. This shows disagreement on how to optimally behave even at the end of the experiment, i.e., after people had the chance to talk to each other. It thus seems likely that these disagreements were more pronounced before subjects communicated.
Subjects not only expressed disagreement in the un-incentivized question on how to program voting robots; the discrepancy was also reflected in actual behavior. As expected and hoped for, first-round voting was far from the efficient only-expert-votes equilibrium. On both days and in both rounds, almost 80% of non-experts voted for their color—see
Table 2. The group was not capable of reaping the efficiency gains from holding back and letting the expert decide. The probability that the majority in a group coincides with the true state in the first round can be computed to be 51.1% (using the actual behavior in the respective formula in
Appendix B) and is hence only slightly better than mere guessing. The expert-vote and even the all-vote benchmark of 97.2% and 61.0% were thus missed by a wide margin. The bad performance was also due to a considerable number of imperfectly (and even some perfectly) informed subjects who voted against their signal, which (as we argue in
Appendix F) can be traced back to people who misunderstood the game.
Summarizing these observations, initial behavior in our setting exhibits heterogeneity and leaves room for better coordination and sophistication.
5.2. Changes in Voting Behavior
The best-reply to the actual first-round behavior of only around 6% abstaining was to vote for one’s signal—recall
Figure 1. On the one hand, one might thus expect the share of votes to rise. On the other hand, abstaining becomes optimal if participants believe that sufficiently many of them will start abstaining after communicating (as limited as this communication may be).
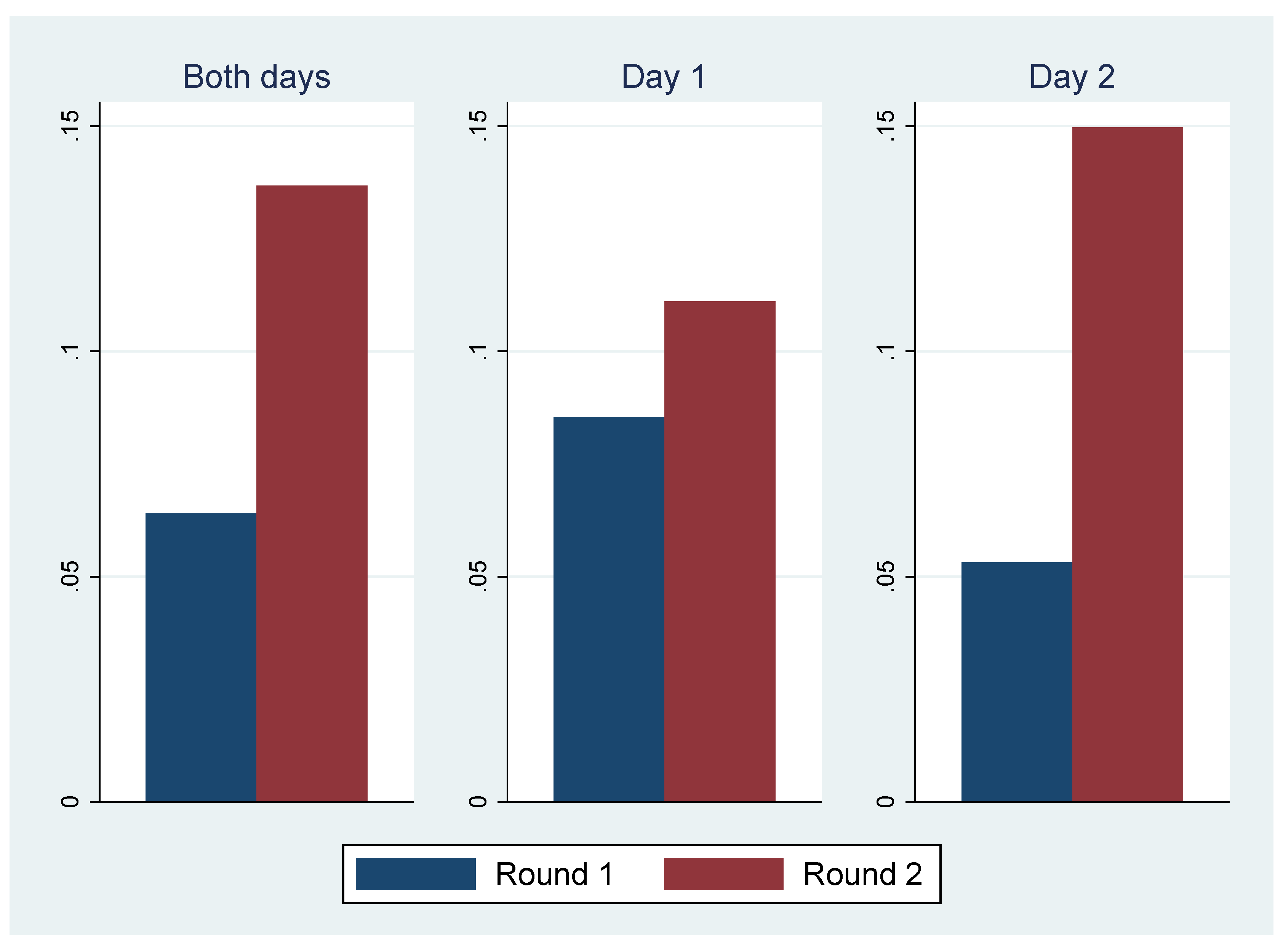
From the first to the second round, the number of abstention increased from 6.4% to 13.8%—see
Figure 3. The number of participants who switched to abstention was much higher than those who switched away from abstention, an increase that is highly significant (
p-value for McNemar test was below 0.001)—although it was much smaller (and not statistically significant) on the first day.
The increase in abstentions was not large enough to improve performance. Holding the shares of participants who voted against their signal constant, the probability that the majority in a group voted for the true state computed from the observed behavior slightly dropped to 51.0% (this was true for both days). The increase simply did not push abstentions to a level at which gains could be expected—recall
Figure 2. If participants started abstaining in the hopes that sufficiently many others would also do so, this hope was not fulfilled.
Result 1. Subjects are more likely to abstain in the second round, although this was not the best response to actual behavior.
5.3. Explanations for the Switch to Abstention
There are three reasons why people might switch from voting to abstaining between the first and second round. First, they learn the efficient strategy during the discussion. Second, they already know about this strategy but do not dare to act on it because they are afraid that others might be voting. The group discussion could then reduce the fear in so far as it becomes clear that others also know the strategy and are willing to act on it. Third, they discover the strategy by pondering the situation without the help of others during the discussion time. This may seem unlikely because apart from the discussion, there is no helpful new information from which to learn. Still, it cannot be excluded.
If the increase is related to learning about the only-expert votes equilibrium between the rounds either individually or from others, the increase should be associated with knowledge about the efficient strategy. This seems to be the case. People who later programmed their robot to that equilibrium were more likely to have switched to abstention (86%) than away from it (14%). On the other hand, people who did not program their robots to the equilibrium were more likely to have switched away from abstention (66%) than to it (33%)—see
Table 3. The difference between the two groups is significant at any conventional level. That switchers are more likely to later know about the equilibrium suggests that they learned about it between the rounds.
We can distinguish more systematically between the reasons by examining how the number of abstaining neighbors in the first round affects abstention in the second round. If participants already know about the strategy but start believing that other members will act on it, their individual beliefs should increase the number of neighbors who abstain around them. With respect to individual learning between the rounds, one would a priori perhaps expect that there is no correlation with the number of neighbors who abstained. If people sit together with friends whose abilities are correlated with their own, however, one would also observe a spurious correlation between the number of abstaining neighbors (indicating a higher ability in this local area) and the likelihood to start abstaining in the second round. If participants learn the efficient strategy from their neighbor, one abstaining neighbor who is willing to share the strategy suffices. The last two channels assume that abstention in the first round is an indicator for knowing about the efficient strategy. This assumption is plausible since the two are highly correlated—see
Appendix E.
In order to find out about the relationship between switches to abstention and the number of neighbors who abstained before, we regress the change to abstention after either voting in line with or against one’s own signal on dummies indicating whether one, two, or many neighbors abstained in the previous round. In our preferred specification (G2SLS), we allow for local correlation in the dependent variable as well as in the error term.
11 We only used the 525 subjects who did not abstain in the first round.
The presence of one neighbor who abstained in the first round was highly significantly correlated with abstention in the next round—see
Table 4. With such a neighbor, it was 13% more likely that an individual changed from voting to abstaining in the next round.
Result 2. Having a neighbor who previously abstained is associated with a higher probability of abstention. Having several abstaining neighbors is not associated with a further increase in the likelihood to abstain.
This result is consistent with learning the sophisticated strategy from a neighbor but not with learning independently or learning to trust that others abstain.
5.4. Reasons for the Difference between the Days
There was a marked difference between both days. Participants were much less likely to switch to abstention on the first than on the second day—recall
Figure 3.
Attributing this difference to a specific feature is difficult because the two days differed in many ways, including starting time (whether a lecture is at Monday 7:30 or Tuesday 9:15 is important to many students, leading to potential selection effects) and study programs to which students signed up. There were also substantially fewer students on the first day, which in principle can facilitate coordination. On the other hand, students were less densely seated on the first day: only about a third of seats were filled and participants were widely dispersed throughout the auditorium. Some did not even have the opportunity to discuss with their neighbors because they had no neighbors—see
Figure 4. Information could thus travel less well in the room on this day.
While we cannot identify which of these confounding factors caused the difference, there is a hint. Examining the regression, we see that switches to abstention are not related to the day in itself. The coefficient of the day dummy is small and insignificant—see
Table 4. This suggests that we are not dealing with a direct effect of the day. Instead, abstention seemed to be less contagious on the first day. While on the second day, having an abstaining neighbor was associated with an increase of abstention of 13%, the increase was 15 percentage points lower on the first day; the respective coefficient of the interaction term of whether one neighbor abstained and the day 1 dummy was statistically significant (albeit at the 10% level). This is consistent with people not bothering to explain the sophisticated strategy to their neighbors when information cannot travel well.
6. Conclusions
Organisations, states, or companies can be in turmoil if they lack a functioning culture or understanding of how to act appropriately, i.e., a system of self-enforcing rules. The reason is diverging views of the facts and what to make of them and no central entity to guide the group. Some rule systems are more efficient but require sophisticated reasoning and trust, whereas others are more resilient in that they are robust to errors and confusion. Given the chance to talk but only locally, is there any chance that the more efficient system might emerge? Or will the organization take the path toward the resilient but less efficient equilibrium, which does not require a common understanding, trust, and communication?
Here, we studied this question using a voting game in a setting that included not only diverging views of the facts but also naturally occurring differences in what to make of them: a large first-year undergraduate class. The situation was not favorable for the efficient but sophisticated equilibrium to arise in. The initial behavior was already very close to the more resilient but less efficient equilibrium. Surprisingly, we found that after the opportunity to communicate, the group started moving in the direction of the more sophisticated equilibrium.
Using econometric analysis, we tentatively concluded that the increase came from students teaching each other about the more sophisticated strategy—even though this strategy was not the best response to what they experienced. This is a sign that it is possible for a group without central agency to move in a promising direction.