The Role of Suggestions and Tips in Distorting a Third Party’s Decision
Abstract
:1. Introduction
2. Theoretical Framework
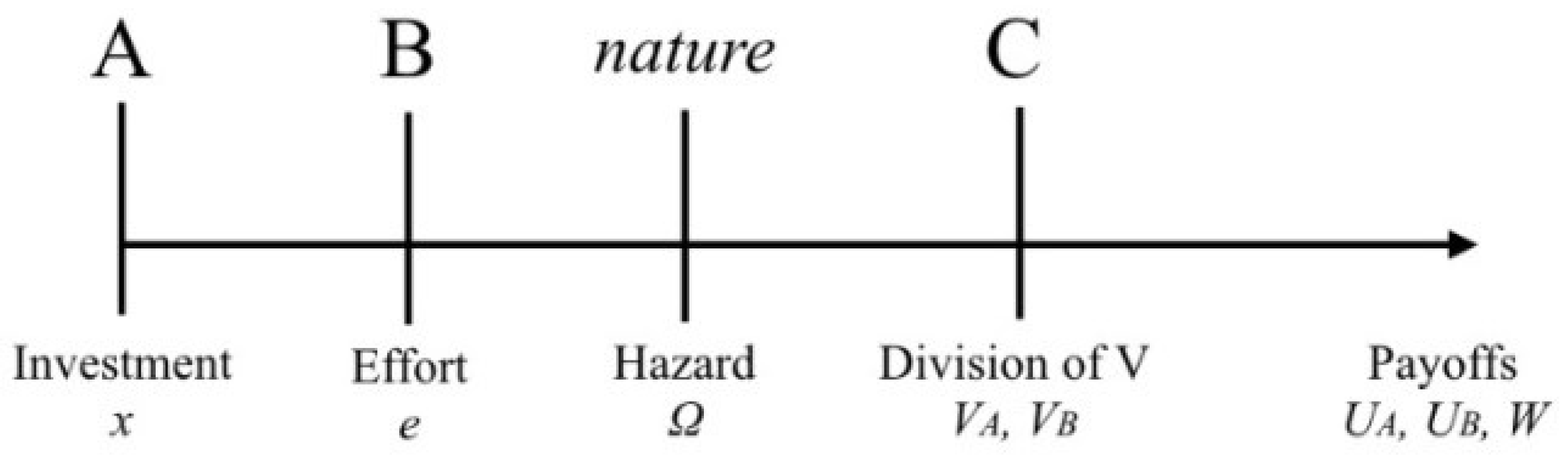
2.1. Influence Game and Equilibrium Characterization
2.2. The Third-Party Decision
3. Experimental Design
3.1. Treatments
3.1.1. Baseline Treatment (FREE)
3.1.2. Advice Treatment (AD)
3.1.3. Tipping Treatment (TIP)
3.2. Procedures
4. Results
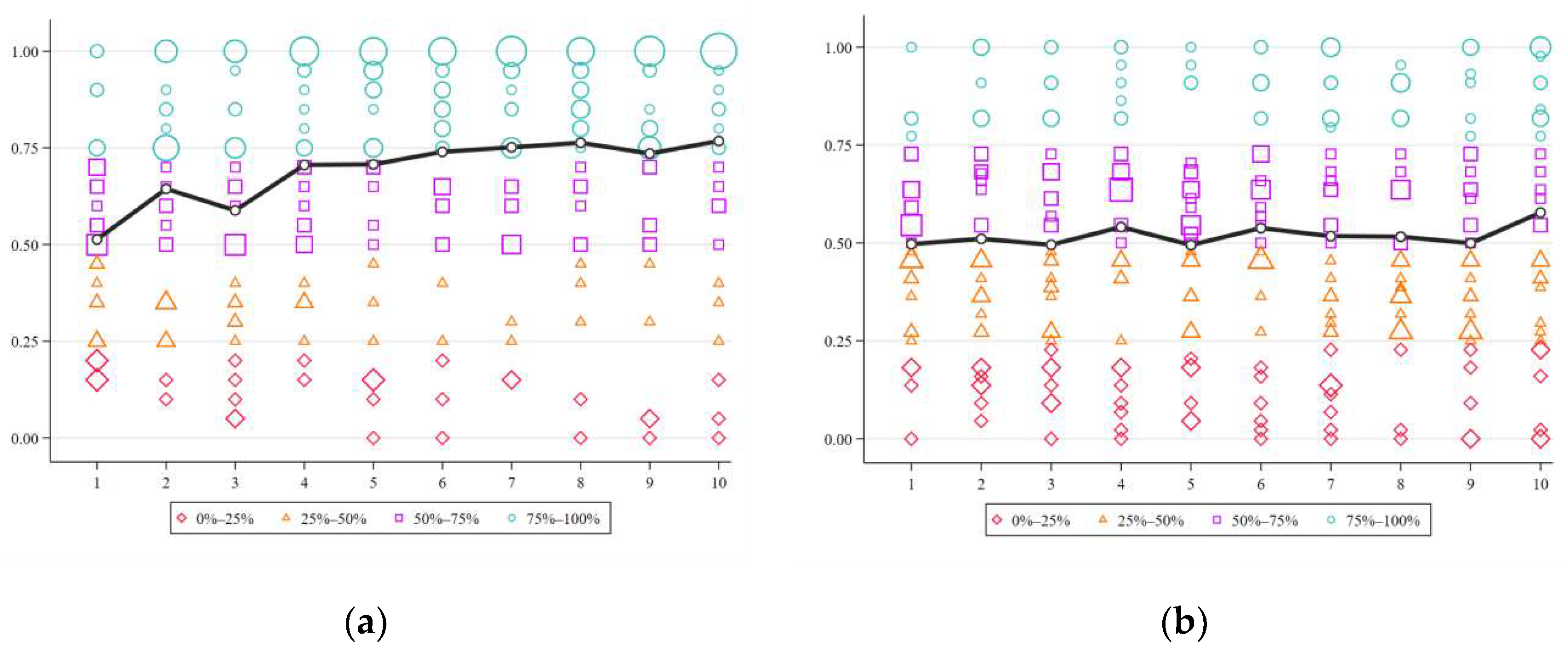
4.1. The Free of Influence Game
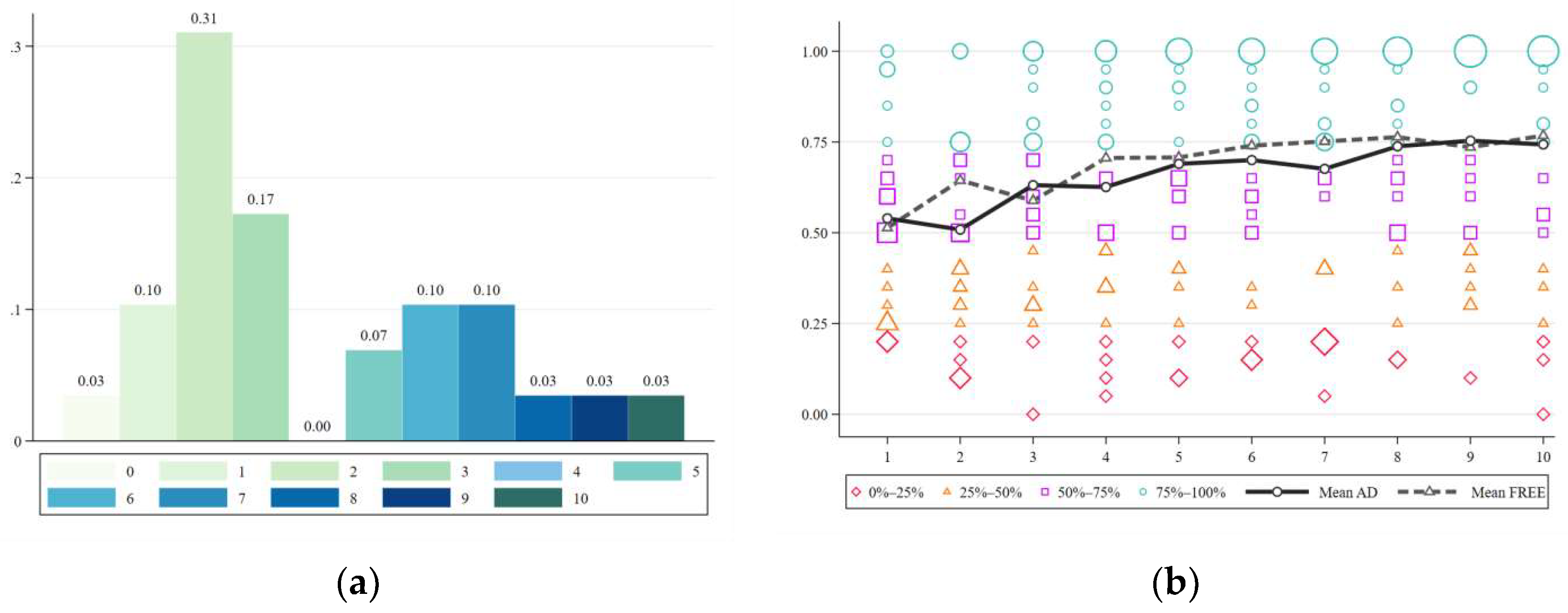
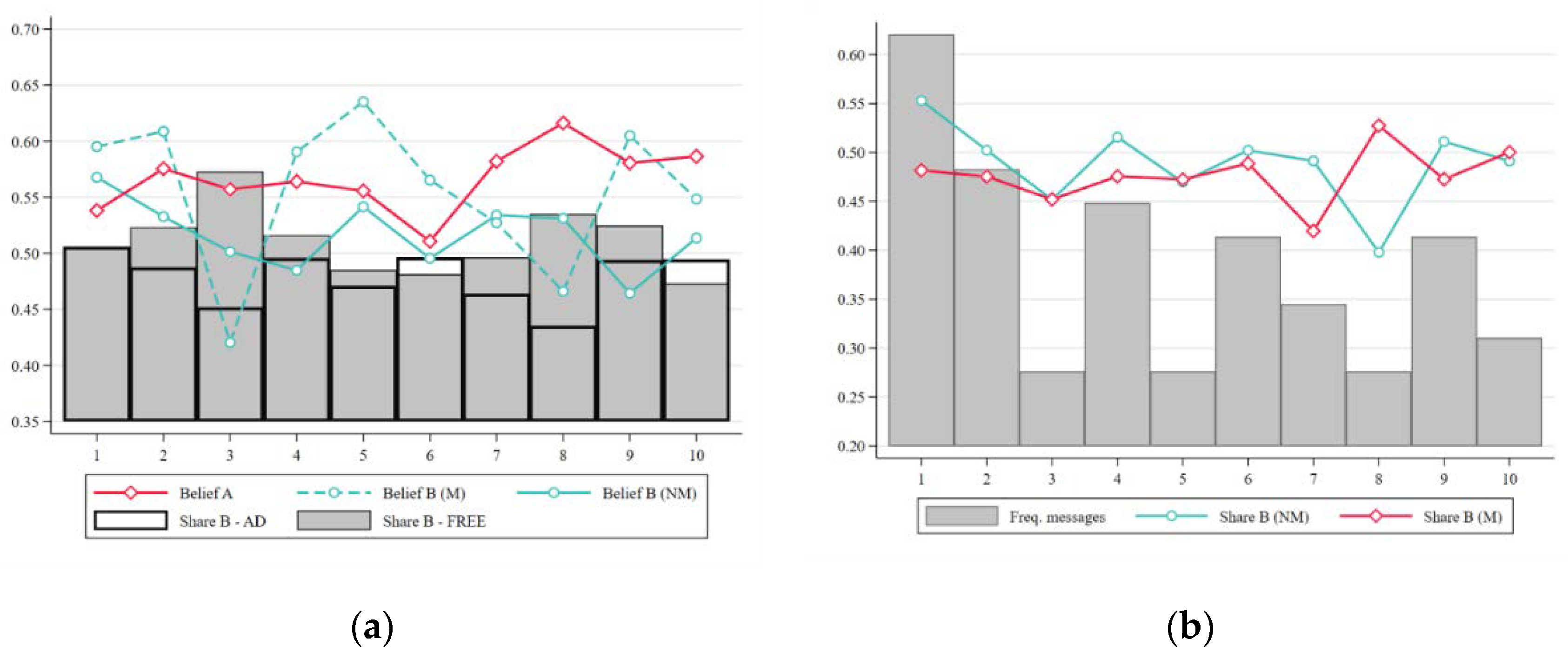
4.2. The Effect of Messages
4.3. The Effect of Tips
5. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof Proposition 1
Appendix B. Instructions
- 1.
- Participant A chooses an integer, s, between 0 and 20.
- 2.
- Participant B chooses a number, c, between 0 and 11 (both integers and decimals are allowed). Then, nature randomly selects a number, h, between −4 and +4. The sum of c and h is the score obtained by participant B, which is equal to n: or n = h + c.
- 3.
- Participant C chooses how to share the value of the project, v, between participants A and B. The value, v, results from participants A’s and B’s choices, and nature’s random number. This corresponds to the multiplication of n by s. Let v = n s.
- 4.
- Finally, all participants, A, B, and C, are informed of values of s, n, v, and the shares that participants A and B received.
- Your gain in a randomly chosen period (out of 10 in part 1). You will be informed of which period is chosen for pay at the end of the experiment.
- Your gain obtained in one of the 44 (2 times 22) choices in part 2:
- With a 1/2 chance you (and the other participant) get the payment from the choice you made.
- With a 1/2 chance you (and the other participant) get the payment from the choice the other participant made.
- The show-up fee of 5 for your participation in this experiment.
Appendix C. Creation of Inequality Aversion Variables
| Choice # | Option A | Option B | |||
|---|---|---|---|---|---|
| 1 | 5 | 5 | 2 | 2 | |
| 2 | 4.44 | 5.56 | 2 | 2 | 2.18 |
| 3 | 4.42 | 5.58 | 2 | 2 | 2.09 |
| 4 | 4.39 | 5.61 | 2 | 2 | 1.96 |
| 5 | 4.36 | 5.64 | 2 | 2 | 1.84 |
| 6 | 4.32 | 5.68 | 2 | 2 | 1.71 |
| 7 | 4.29 | 5.71 | 2 | 2 | 1.61 |
| 8 | 4.24 | 5.76 | 2 | 2 | 1.47 |
| 9 | 4.19 | 5.81 | 2 | 2 | 1.35 |
| 10 | 4.14 | 5.86 | 2 | 2 | 1.24 |
| 11 | 4.07 | 5.93 | 2 | 2 | 1.11 |
| 12 | 3.92 | 6.08 | 2 | 2 | 0.89 |
| 13 | 3.86 | 6.14 | 2 | 2 | 0.82 |
| 14 | 3.81 | 6.19 | 2 | 2 | 0.76 |
| 15 | 3.68 | 6.32 | 2 | 2 | 0.64 |
| 16 | 3.53 | 6.47 | 2 | 2 | 0.52 |
| 17 | 3.33 | 6.67 | 2 | 2 | 0.40 |
| 18 | 2.85 | 7.15 | 2 | 2 | 0.20 |
| 19 | 2.72 | 7.28 | 2 | 2 | 0.16 |
| 20 | 2.22 | 7.78 | 2 | 2 | 0.04 |
| 21 | 1.43 | 8.57 | 2 | 2 | −0.08 |
| 22 | 0.1 | 9.9 | 2 | 2 | −0.19 |
| Choice # | Option A | Option B | |||
|---|---|---|---|---|---|
| 1 | 10 | 0 | 0.0 | 0.0 | 1 |
| 2 | 10 | 0 | 0.5 | 0.5 | 0.95 |
| 3 | 10 | 0 | 1.0 | 1.0 | 0.9 |
| 4 | 10 | 0 | 1.5 | 1.5 | 0.85 |
| 5 | 10 | 0 | 2.0 | 2.0 | 0.8 |
| 6 | 10 | 0 | 2.5 | 2.5 | 0.75 |
| 7 | 10 | 0 | 3.0 | 3.0 | 0.7 |
| 8 | 10 | 0 | 3.5 | 3.5 | 0.65 |
| 9 | 10 | 0 | 4.0 | 4.0 | 0.6 |
| 10 | 10 | 0 | 4.5 | 4.5 | 0.55 |
| 11 | 10 | 0 | 5.0 | 5.0 | 0.5 |
| 12 | 10 | 0 | 5.5 | 5.5 | 0.45 |
| 13 | 10 | 0 | 6.0 | 6.0 | 0.4 |
| 14 | 10 | 0 | 6.5 | 6.5 | 0.35 |
| 15 | 10 | 0 | 7.0 | 7.0 | 0.3 |
| 16 | 10 | 0 | 7.5 | 7.5 | 0.25 |
| 17 | 10 | 0 | 8.0 | 8.0 | 0.2 |
| 18 | 10 | 0 | 8.5 | 8.5 | 0.15 |
| 19 | 10 | 0 | 9.0 | 9.0 | 0.1 |
| 20 | 10 | 0 | 9.5 | 9.5 | 0.05 |
| 21 | 10 | 0 | 10.0 | 10.0 | 0 |
| 22 | 10 | 0 | 10.5 | 10.5 | −0.05 |
Appendix D. Additional Regressions
| (1) Investment | (2) Effort | (3) Effort (NM) | (3) Belief A | (4) Belief B | |
|---|---|---|---|---|---|
| Period | 0.0248 *** | 0.00317 | 0.00284 | 0.00433 | −0.00110 |
| (4.55) | (1.01) | (0.89) | (1.59) | (−0.37) | |
| AD | −0.0359 | −0.0979 | −0.107 * | 0.0256 | 0.00998 |
| (−0.55) | (−1.95) | (−2.15) | (0.97) | (0.22) | |
| Men | 0.00814 | 0.0284 | 0.0221 | −0.0450 | −0.00998 |
| (0.16) | (0.73) | (0.50) | (−1.46) | (−0.33) | |
| Age | 0.0279 * | 0.0108 | 0.00713 | −0.00485 | 0.0167 |
| (2.03) | (0.87) | (0.51) | (−0.52) | (1.72) | |
| Message sent | 0.120 ** | 0.0394 *** | |||
| (2.74) | (5.09) | ||||
| Constant | −0.0408 | 0.259 | 0.341 | 0.651 ** | 0.164 |
| (−0.14) | (1.05) | (1.16) | (3.00) | (0.74) | |
| N | 630 | 630 | 518 | 573 | 572 |
| (1) Investment | (2) Effort | (3) Belief A | (4) Belief B | (5) Probit Tipping | |
|---|---|---|---|---|---|
| Period | 0.0238 *** | 0.00577 | 0.00324 | 0.00413 | −0.102 ** |
| (9.46) | (1.71) | (1.03) | (1.44) | (−3.04) | |
| Tipping | 0.113* | 0.0673 | −0.0751 *** | 0.0787 ** | |
| (2.13) | (1.33) | (−3.95) | (2.77) | ||
| Men | −0.0175 | 0.135 ** | −0.0130 | 0.00585 | 0.483 *** |
| (−0.36) | (2.95) | (−0.77) | (0.11) | (22.74) | |
| Age | −0.00830 | −0.0138 | 0.00496 *** | 0.00425 | −0.0257 |
| (−0.88) | (−1.07) | (3.89) | (0.52) | (−1.88) | |
| Value of the Project | 0.00660 | ||||
| (1.23) | |||||
| Share to B | 3.904 * | ||||
| (2.43) | |||||
| Alpha F&S | 1.138 *** | ||||
| (77.28) | |||||
| Beta F&S | 0.863 | ||||
| (1.30) | |||||
| Constant | 0.746 *** | 0.708 ** | 0.434 *** | 0.389 * | −3.223 *** |
| (3.48) | (2.81) | (9.61) | (2.00) | (−5.67) | |
| lnsig2u | −1.774 *** | ||||
| (−4.31) | |||||
| N | 480 | 480 | 442 | 441 | 111 |
| (1) Baseline (1–5) | (2) Baseline (6–10) | (3) All (1–5) | (4) All (6–10) | |
|---|---|---|---|---|
| Period | 0.0190 | 0.00669 | 0.0127 | 0.00927 |
| (1.68) | (0.69) | (1.68) | (0.76) | |
| Investment | −0.0250 *** | −0.0182 *** | −0.0218 *** | −0.0137 ** |
| (−16.85) | (−9.12) | (−6.88) | (−3.20) | |
| Player B output | 0.00685 | 0.0338 *** | 0.00429 | 0.0375 *** |
| (1.43) | (8.00) | (0.49) | (4.55) | |
| Value of the project | 0.000684 * | −0.000264 | 0.000911 * | −0.000738 |
| (2.29) | (−0.81) | (2.02) | (−1.12) | |
| Men | 0.0117 | 0.0274 | 0.0255 | 0.0540 |
| (0.28) | (0.76) | (0.83) | (1.52) | |
| Age | 0.00485 | −0.00584 | −0.000479 | 0.00470 * |
| (0.48) | (−1.01) | (−0.24) | (1.99) | |
| Alpha F&S | −0.00509 | −0.0413 | −0.0100 | −0.0301 * |
| (−0.36) | (−1.61) | (−0.97) | (−2.00) | |
| Beta F&S | 0.0897 | 0.0119 | 0.0145 | 0.0393 |
| (1.51) | (0.09) | (0.47) | (0.70) | |
| AD | −0.0251 | −0.00988 | ||
| (−1.35) | (−0.20) | |||
| Tipping | 0.0992 *** | 0.165 *** | ||
| (9.02) | (4.60) | |||
| Constant | 0.529 ** | 0.657 *** | 0.645 *** | 0.339 *** |
| (2.76) | (6.13) | (8.82) | (3.79) | |
| N | 133 | 134 | 308 | 313 |
References
- Gneezy, U.; Saccardo, S.; Van Veldhuizen, R. Bribery: Behavioral drivers of distorted decisions. J. Eur. Econ. Assoc. 2018, 17, 917–946. [Google Scholar] [CrossRef]
- Campos, N.; Giovannoni, F. Lobbying, corruption and political influence. Public Choice 2007, 131, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Moore, D.; Tetlock, P.; Tanlu, L.; Bazerman, M. Conflicts of interest and the case of auditor independence: Moral seduction and strategic issue cycling. Acad. Manag. Rev. 2006, 31, 10–29. [Google Scholar] [CrossRef]
- Bennedsen, M.; Feldmann, S.E.; Dreyer Lassen, D. Strong firms lobby, weak firms bribe: A survey-based analysis of the demand for influence and corruption. EPRU Work. Pap. Ser. 2009. [Google Scholar] [CrossRef] [Green Version]
- Abbink, K. Laboratory experiments on corruption. In Handbook on the Economics of Corruption; Edward Elgar Publishing: Northampton, MA, USA, 2006. [Google Scholar]
- Abbink, K.; Irlenbusch, B.; Renner, E. The moonlighting game: An experimental study on reciprocity and retribution. J. Econ. Behav. Organ. 2000, 42, 265–277. [Google Scholar] [CrossRef]
- Abbink, K.; Irlenbusch, B.; Renner, E. An experimental bribery game. J. Law Econ. Organ. 2002, 18, 428–454. [Google Scholar] [CrossRef]
- Bobkova, N.; Egbert, H. Corruption investigated in the lab: A survey of the experimental literature. Int. J. Latest Trends Financ. Econ. Sci. 2012, 2, 337–349. [Google Scholar]
- Austen-Smith, D. Information and influence: Lobbying for agendas and votes. Am. J. Political Sci. 1993, 37, 799. [Google Scholar] [CrossRef] [Green Version]
- Potters, J.; Van Winden, F. Lobbying and asymmetric information. Public Choice 1992, 74, 269–292. [Google Scholar] [CrossRef]
- Schultze, T.; Mojzisch, A.; Schulz-Hardt, S. On the inability to ignore useless advice. Exp. Psychol. 2017, 64, 170–183. [Google Scholar] [CrossRef]
- Rankin, F. Communication in ultimatum games. Econ. Lett. 2003, 81, 267–271. [Google Scholar] [CrossRef]
- Andersson, O.; Galizzi, M.; Hoppe, T.; Kranz, S.; Van der Wiel, K.; Wengström, E. Persuasion in experimental ultimatum games. Econ. Lett. 2010, 108, 16–18. [Google Scholar] [CrossRef] [Green Version]
- Ben-Ner, A.; Putterman, L.; Ren, T. Lavish returns on cheap talk: Two-way communication in trust games. J. Sociol. Econ. 2011, 40, 1–13. [Google Scholar] [CrossRef]
- Fehr, E.; Gächter, S.; Kirchsteiger, G. Reciprocity as a contract enforcement device: Experimental evidence. Econometrica 1997, 65, 833–860. [Google Scholar] [CrossRef]
- Fehr, E.; Kirchsteiger, G.; Riedl, A. Does fairness prevent market clearing? An experimental investigation. Q. J. Econ. 1993, 108, 437–459. [Google Scholar] [CrossRef]
- Abbink, K. Staff rotation as an anti-corruption policy: An experimental study. Eur. J. Political Econ. 2004, 20, 887–906. [Google Scholar] [CrossRef]
- Weisel, O.; Shalvi, S. The collaborative roots of corruption. Proc. Natl. Acad. Sci. USA 2015, 112, 10651–10656. [Google Scholar] [CrossRef] [Green Version]
- Malmendier, U.; Schmidt, K. You owe me. Am. Econ. Rev. 2017, 107, 493–526. [Google Scholar] [CrossRef] [Green Version]
- Austen-Smith, D.; Wright, J.R. Counteractive lobbying. Am. J. Political Sci. 1994, 38, 25. [Google Scholar] [CrossRef]
- You, H.Y. Ex post lobbying. J. Politics 2017, 79, 1162–1176. [Google Scholar] [CrossRef] [Green Version]
- Schotter, A.; Weigelt, K. Asymmetric tournaments, equal opportunity laws, and affirmative action: Some experimental results. Q. J. Econ. 1992, 107, 511–539. [Google Scholar] [CrossRef]
- Bull, C.; Schotter, A.; Weigelt, K. Tournaments and piece rates: An experimental study. J. Political Econ. 1987, 95, 1–33. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.M. Adding a stick to the carrot? The interaction of bonuses and fines. Am. Econ. Rev. 2007, 97, 177–181. [Google Scholar] [CrossRef] [Green Version]
- Camerer, C.F. Behavioral Game Theory: Experiments in Strategic Interaction; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Cappelen, A.W.; Hole, A.D.; Sørensen, E.Ø.; Tungodden, B. The pluralism of fairness ideals: An experimental approach. Am. Econ. Rev. 2007, 97, 818–827. [Google Scholar] [CrossRef] [Green Version]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition, and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Azar, O.H. The social norm of tipping: Does it improve social welfare? J. Econ. Z. Für Natl. 2005, 85, 141–173. [Google Scholar] [CrossRef]
- Abbink, K. Fair Salaries and the Moral Costs of Corruption; No. 1/2000. Bonn Econ Discussion Papers; Universität Bonn: Bonn, Germany, 2000. [Google Scholar]
- Charness, G.; Rabin, M. Understanding social preferences with simple tests. Q. J. Econ. 2002, 117, 817–869. [Google Scholar] [CrossRef] [Green Version]
- Azar, O.H. The implications of tipping for economics and management. Int. J. Soc. Econ. 2003, 30, 1084–1094. [Google Scholar] [CrossRef]
- Fischbacher, U. z-Tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar] [CrossRef] [Green Version]
- Crawford, V. A survey of experiments on communication via cheap talk. J. Econ. Theory 1998, 78, 286–298. [Google Scholar] [CrossRef]
- Roth, A.; Murnighan, J.; Schoumaker, F. The deadline effect in bargaining: Some experimental evidence. Am. Econ. Rev. 1988, 78, 806–823. [Google Scholar]
- Cohen, J. Statistical power analysis. Curr. Dir. Psychol. Sci. 1992, 1, 98–101. [Google Scholar] [CrossRef]
- Blanco, M.; Engelmann, D.; Normann, H.T. A within-subject analysis of other-regarding preferences. In Games and Economic Behavior; Elsevier Inc.: Amsterdam, The Netherlands, 2011; Volume 72, pp. 321–338. [Google Scholar]
- Yang, Y.; Onderstal, S.; Schram, A. Inequity aversion revisited. J. Econ. Psychol. 2016, 54, 1–16. [Google Scholar] [CrossRef]
| 1 | In the experiment, the names of the players were S, C, and B. However, for the ease of the presentation here, the labels were changed to A, B, and C. |
| 2 | This functional form is commonly used, e.g., by Schotter et al. [22]. |
| 3 | The cost function, c(e), is also corrected to the transformed cost, , by combining it. The following sequence shows the cost for various levels of effort in the experiment by way of illustration: c(e) = [0(0), 0.06(0.25), …, 0.89(1), 1.39(1.25), …, 3.56(2), …, 8(3), 9.39(3.25), …, 32(6), …, 72(9), …, 107.56(11)]. |
| 4 | The beliefs were not incentivized. However, given that the answer was not binding, it was considered that there were no reasons for player B to misreport their true beliefs. |
| 5 | From here on, F&S is used to mention Fehr and Schmidt’s model. |
| 6 | Using the variables in the actual levels would not change any result. |
| 7 | From here on, r is used to report the statistic for the Pearson’s correlation tests. |
| 8 | A power analysis using a two-sided t-test shows that a sample size of 523 observations per treatment would be needed to detect a significant effect if the power is set to 80%, the significance level is set to 5%, and given the decisions taken by the participants [35]. |
| 9 | The letter in the superscript represents the option (A or B). |
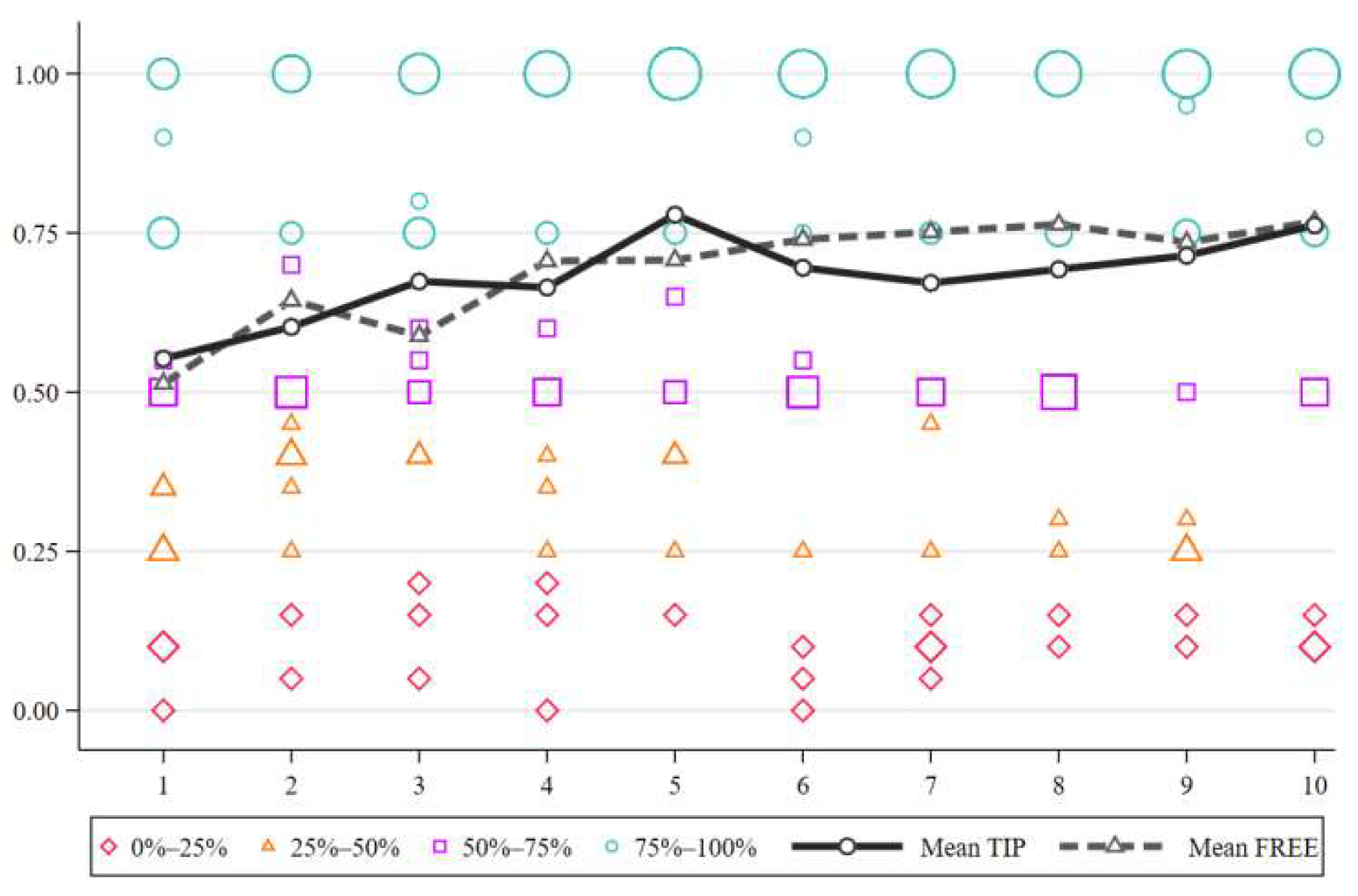
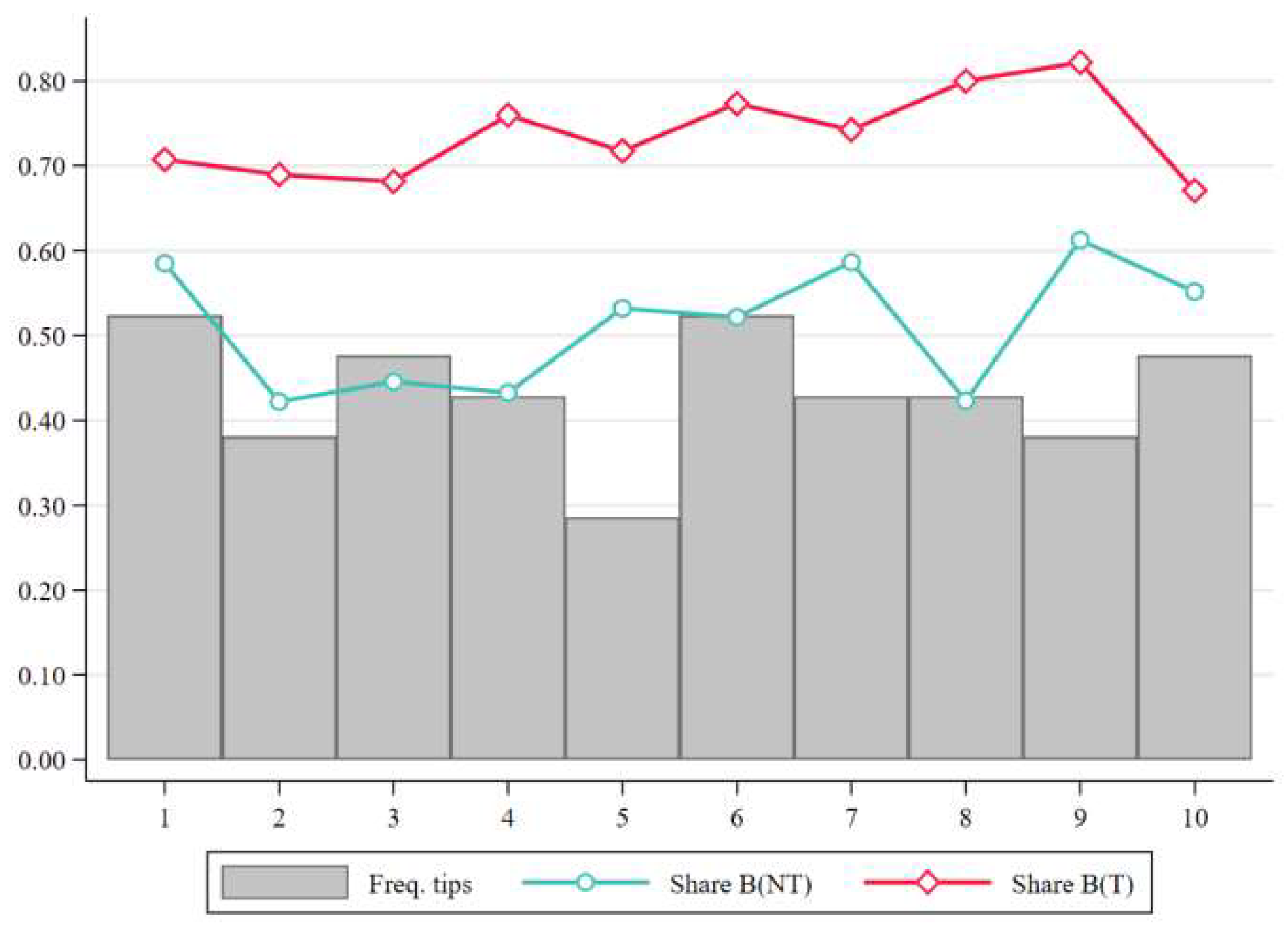
| FREE | AD | TIP | EQUIL | |
|---|---|---|---|---|
| Investment | 0.69 (340) | 0.66 (290) | 0.68 (210) | 1 |
| Effort | 0.52 (340) | 0.47 (290) | 0.57 (210) | 0.51 |
| Value of the project | 0.29 (340) | 0.25 (290) | 0.31 (210) | 0.375 |
| Belief A | 0.55 (340) | 0.57 (290) | 0.47 (210) | |
| Belief B | 0.51 (340) | 0.54 (290) | 0.59 (210) | |
| Advice from B | 0.62 (112) | |||
| Share for B | 0.51 (340) | 0.48 (290) | 0.62 (210) | 0.5 |
| Tip from B | 0.19 (91) |
| (1) All Periods | (2) Periods 2 to 9 | |
|---|---|---|
| Period | 0.0089 | 0.0097 |
| (1.68) | (1.40) | |
| Investment | −0.022 *** | −0.0256 *** |
| (−11.04) | (−8.74) | |
| Player B output | 0.0145 *** | 0.0115 * |
| (3.33) | (2.45) | |
| Value of the project | 0.0005 *** | 0.0008 ** |
| (5.09) | (3.19) | |
| Sex | 0.0239 | 0.0348 |
| (0.57) | (0.97) | |
| Age | −0.0000 | 0.0036 |
| (0.00) | (0.63) | |
| Alpha F&S | −0.0224 | −0.0209 |
| (−1.12) | (−1.34) | |
| Beta F&S | 0.0585 | 0.0584 |
| (0.68) | (0.72) | |
| Constant | 0.599 *** | 0.564 ** |
| (3.86) | (3.26) | |
| N | 267 | 213 |
| (1) All Treatments | (2) All Treatments (2–9) | (3) Advice | (4) Advice (2–9) | |
|---|---|---|---|---|
| Period | 0.0095 * | 0.0118 * | 0.0065 | 0.0050 |
| (2.36) | (2.48) | (0.74) | (0.83) | |
| Investment | −0.0191 *** | −0.0227 *** | −0.0191 *** | −0.0224 *** |
| (−7.76) | (−9.03) | (−4.72) | (−4.24) | |
| Player B output | 0.0148 ** | 0.0105 | 0.0045 | −0.0009 |
| (2.72) | (1.74) | (0.39) | (−0.07) | |
| Value of the project | 0.0004 | 0.0007 * | 0.0009 | 0.0013 |
| (1.20) | (2.25) | (1.22) | (1.88) | |
| AD | −0.0169 | −0.0285 | ||
| (−0.71) | (−1.22) | |||
| TIP | 0.133 *** | 0.126 *** | ||
| (6.59) | (7.47) | |||
| Sex | 0.0406 | 0.0404 | 0.0192 | 0.0286 * |
| (1.22) | (1.46) | (1.27) | (2.25) | |
| Age | 0.0018 | 0.0024 | −0.0209 *** | −0.0276 *** |
| (0.87) | (1.13) | (−3.62) | (−4.14) | |
| Alpha F&S | −0.0192 | −0.0263 * | −0.0152 * | −0.0246 ** |
| (−1.62) | (−2.06) | (−2.46) | (−2.93) | |
| Beta F&S | 0.0262 | 0.0182 | −0.0312 | −0.0122 |
| (0.93) | (0.63) | (−0.66) | (−0.20) | |
| Message sent | −0.0067 | −0.0068 | ||
| (−0.27) | (−0.23) | |||
| Constant | 0.527 *** | 0.563 *** | 1.068 *** | 1.252 *** |
| (5.34) | (5.39) | (4.85) | (4.77) | |
| N | 621 | 494 | 235 | 187 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parra, D. The Role of Suggestions and Tips in Distorting a Third Party’s Decision. Games 2020, 11, 23. https://doi.org/10.3390/g11020023
Parra D. The Role of Suggestions and Tips in Distorting a Third Party’s Decision. Games. 2020; 11(2):23. https://doi.org/10.3390/g11020023
Chicago/Turabian StyleParra, Daniel. 2020. "The Role of Suggestions and Tips in Distorting a Third Party’s Decision" Games 11, no. 2: 23. https://doi.org/10.3390/g11020023
APA StyleParra, D. (2020). The Role of Suggestions and Tips in Distorting a Third Party’s Decision. Games, 11(2), 23. https://doi.org/10.3390/g11020023




