Routing-Proofness in Congestion-Prone Networks
Abstract
1. Introduction
- Efficiency: the minimum total cost of connecting all agents to their target nodes;
- Stand-alone core stability: no groups of agents pay more than the cost of a subnetwork meeting all connection needs of the group;
- Routing-proofness: no agent can lower its cost by reporting as several agents along an alternative path connecting her target nodes.
1.1. Innovation of the Paper and Overview of the Results
1.2. Related Literature
2. The Model
3. Efficiency, Stand-Alone Core Stability and LRP
3.1. A New Egalitarian Mechanism
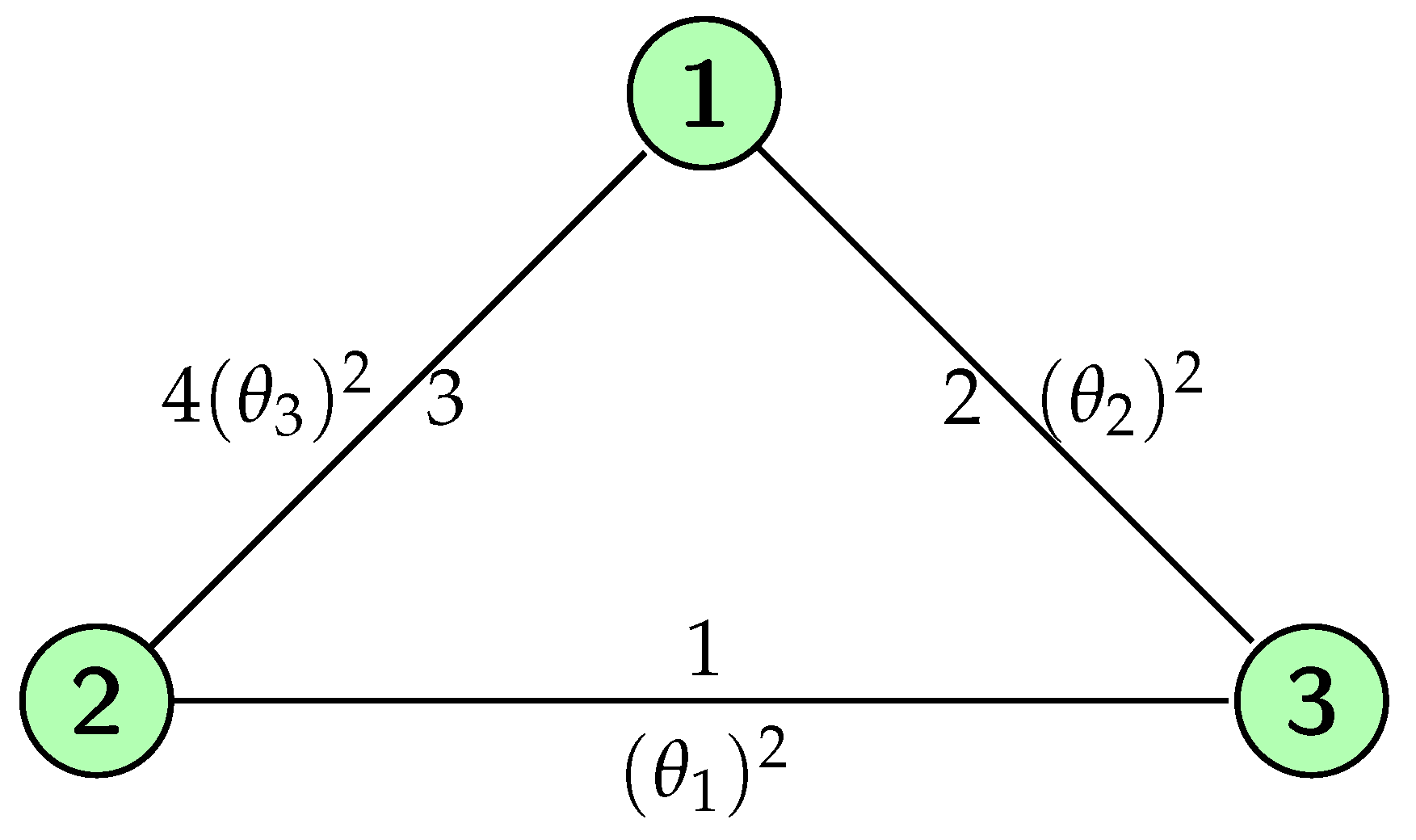
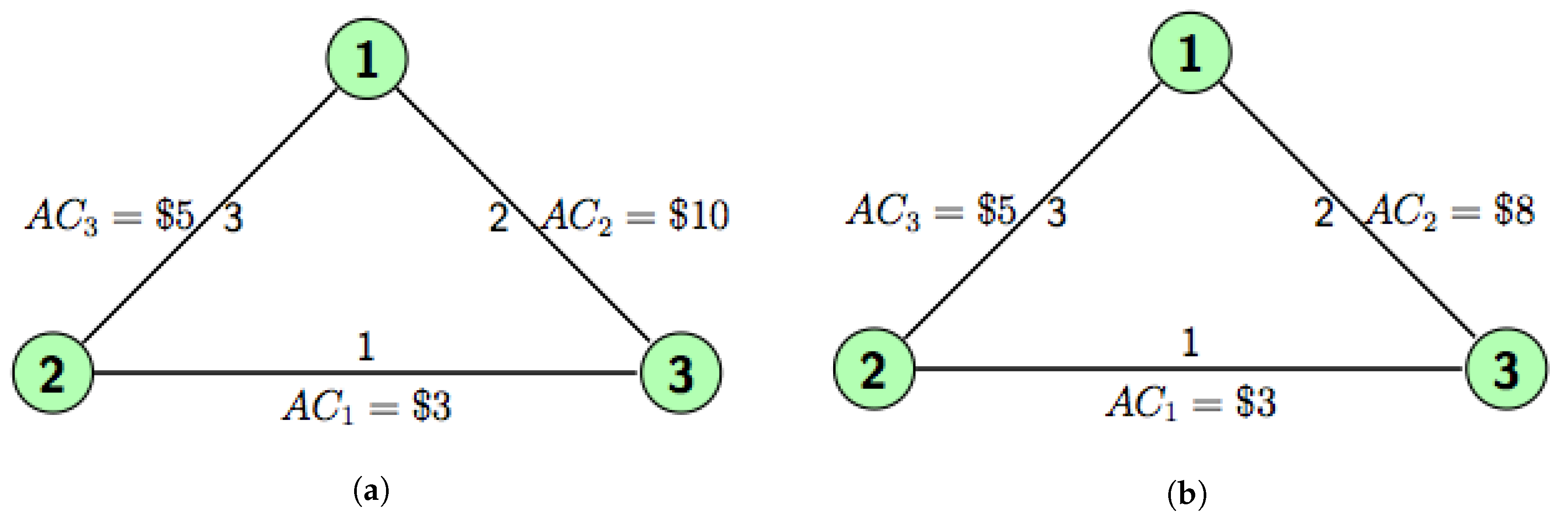
3.2. A Numerical Example of EG
3.3. An Example for Problem Where EG does not Exists
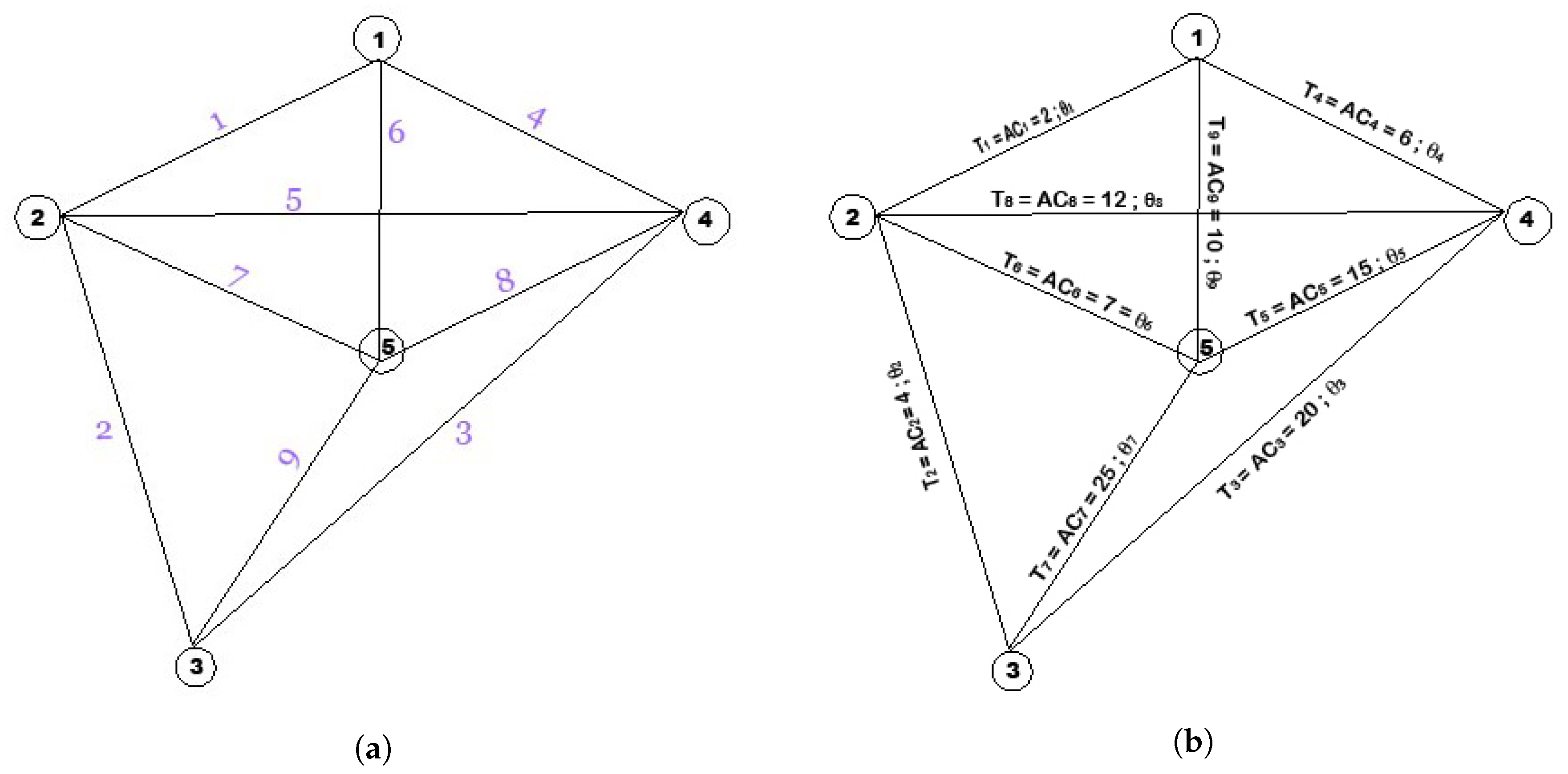
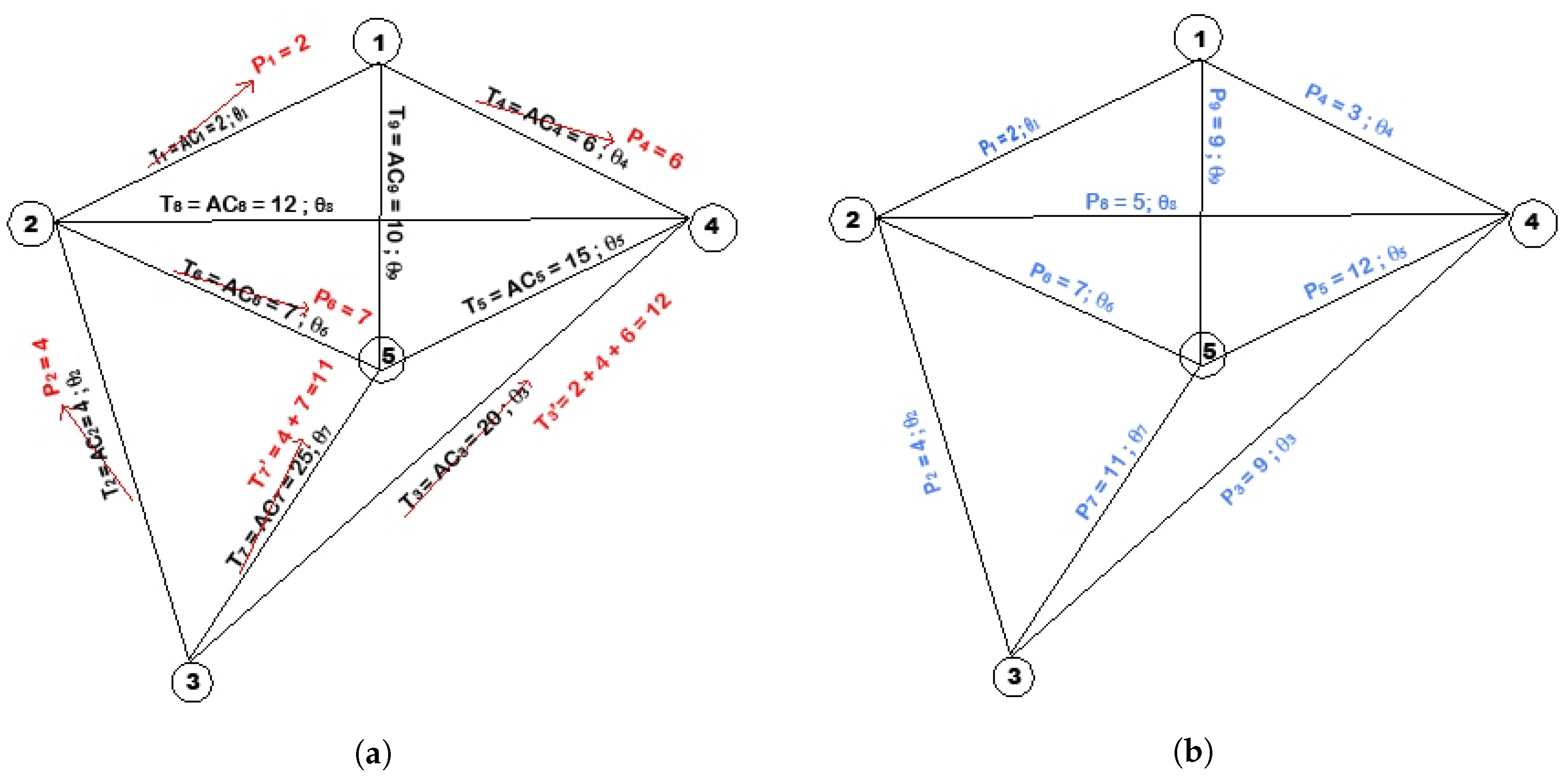
4. The RP Algorithm
- Step 0. We start from a network N and assign temporary prices to every link i in the network. Continue to step 1.
- Step 1. The algorithm ends when all the assigned prices are permanent. For a given set of prices, replace the smallest temporary price with a permanent price of the same value. The rest of the prices are unchanged. If the new prices generate a semi-cycle, then we continue to step 2. Otherwise, we repeat step 1 with the new prices.
- Step 2. For every semi-cycle with link i that has attached a temporary price , we replace their temporary price with a new temporary price Moreover, if every path is a semi-cycle, then becomes permanent. We continue to step 1 with the new set of prices.
Example of RP Algorithm
5. Main Results
- a.
- Let agent j* be the last agent in the RP algorithm. A stand-alone core stable, efficient and limit routing-proof price vector exists if and only if one of following conditions is satisfied:
- i
- , where is the set of all feasible alternative paths of ;
- ii
- b.
- The egalitarian solution exists if and only if either condition (i) or (ii) is satisfied.
6. Conclusions and Open Questions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proofs
Appendix A.1. Proof of Proposition 1
Appendix A.2. Proof of Theorem 1
Appendix A.3. Proof of Corollary 1
References
- Han, L.; Juarez, R. Free intermediation in resource transmission. Games Econ. Behav. 2018, 111, 75–84. [Google Scholar] [CrossRef]
- Juarez, R.; Kumar, R. Implementing efficient graphs in connection networks. Econ. Theory 2013, 54, 359–403. [Google Scholar] [CrossRef]
- Frederick, H.; Gerald, L. Introduction to Operations Research; McGraw-Hill: Columbus, OH, USA, 2009. [Google Scholar]
- Moulin, H. Cost sharing in networks: Some open questions. Int. Game Theory Rev. 2013, 15, 1340001. [Google Scholar] [CrossRef]
- Dominique, H.; Moulin, H. Traffic-based cost allocation in a network. RAND J. Econ. 1996, 27, 332–345. [Google Scholar]
- Juarez, R. Group strategyproof cost sharing: The role of indifferences. Games Econ. Behav. 2013, 82, 218–239. [Google Scholar] [CrossRef]
- Melo, E. Congestion pricing and learning in traffic network games. J. Public Econ. Theory 2011, 13, 351–367. [Google Scholar] [CrossRef]
- Roughgarden, T. The Price of anarchy is independent of the network topology. J. Comput. Syst. Sci. 2003, 67, 341–364. [Google Scholar] [CrossRef]
- Fotakis, D.; Spirakis, P. Cost-balancing tolls for atomic network congestion games. In Proceedings of the 3rd International Conference on Internet and Network Economics (WINE’07), San Diego, CA, USA, 12–14 December 2007; pp. 179–190. [Google Scholar]
- Moulin, H. Pricing traffic in a spanning network. In Proceedings of the 10th ACM Conference on Electronic Commerce (EC09), Stanford, CA, USA, 6–10 July 2009. [Google Scholar]
- Juarez, R.; Ko, C.Y.; Xue, J. Sharing sequential values in a network. J. Econ. Theory 2018, 77, 734–779. [Google Scholar] [CrossRef]
- Chakrabarty, D.; Mehta, A.; Nagarajan, V. Fairness and optimality in congestion games. In Proceedings of the 6th ACM Conference on Electronic Commerce (EC ’05), Vancouver, BC, Canada, 5–8 June 2005; pp. 52–57. [Google Scholar]
- Joel, S. Linear Programming Note X Integer Programming; Mimeo University of California: San Diego, CA, USA, 2007. [Google Scholar]
- Sprumont, Y. The division problem with single-peaked preferences: A characterization of the uniform allocation rule. Econ. J. Econ. Soc. 1991, 59, 509–519. [Google Scholar] [CrossRef]
- Benassy, J.P. The Economics of Market Disequilibrium (No. 330.1/B45e); Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Bogomolnaia, A.; Holzman, R.; Moulin, H. Sharing the cost of a capacity network. Math. Oper. Res. 2010, 35, 173–192. [Google Scholar] [CrossRef]
- Dutta, B.; Mishra, D. Minimum cost arborescences. Games Econ. Behav. 2011, 74, 120–143. [Google Scholar] [CrossRef]
- Dong, B.; Guo, G.; Wang, Y. Highway toll pricing. Eur. J. Oper. Res. 2012, 220, 744–751. [Google Scholar] [CrossRef]
- Hougaard, J.L.; Tvede, M. Truth-telling and nash equilibria in minimum cost spanning tree models. Eur. J. Oper. Res. 2012, 222, 566–570. [Google Scholar] [CrossRef]
- Hougaard, J.L.; Tvede, M. Minimum cost connection networks: Truth-telling and implementation. J. Econ. Theory 2015, 157, 76–99. [Google Scholar] [CrossRef]
- Kumar, R. Secure implementation in production economies. Math. Soc. Sci. 2013, 66, 372–378. [Google Scholar] [CrossRef]
- Hougaard, J.L.; Moreno-Ternero, J.D.; Tvede, M.; sterdal, L.P. Sharing the proceeds from a hierarchical venture. Games Econ. Behav. 2017, 102, 98–110. [Google Scholar] [CrossRef]
- Moulin, H.; Laigret, F. Equal-need sharing of a network under connectivity constraints. Games Econ. Behav. 2011, 72, 314–320. [Google Scholar] [CrossRef]
- Juarez, R.; You, J.S. Optimality of the uniform rule under single-peaked preferences. Econ. Theory Bull. 2018, 1–10. [Google Scholar] [CrossRef]
- Hougaard, J.L. An Introduction to Allocation Rules; Springer: Heidelberg/Berlin, Germany, 2009. [Google Scholar]
| 1. | See [8] for more POAs of different classes of functions such as the quadratic, M/M/1 delay functions and M/G/1 delay functions. |
| 2. | |
| 3. | A path is a sequence of consecutive nodes in the network. We say that a path has no cycles if the nodes do not repeat. We say that a path connects link i if the path starts in one of the nodes of link i and ends in the other. When there is no confusion, we also refer to a path by its links instead of its nodes. |
| 4. | For brevity, we do not repeat the formal definition of these mechanisms already discussed in Juarez and Kumar [2]. |
| 5. | |
| 6. | Moulin [4] suggests that if no simple algorithm can characterize the cost minimization outcomes, then we will have no choice but to drop the cost minimization requirement and turn to the exogenously given suboptimalities. |
| 7. | Note that if a simple triangular network is analyzed here, then the routing-proofness constraint is just a set of triangle inequalities. |
| 8. | If it happens that is the maximum revenue that EG can achieve, then and the allocation EG coincides with EG. |
| 9. | Similar to EG, the RP algorithm might not satisfy the efficiency property, but for any revenue (regardless of whether efficiency is achievable), it always generates prices that maximize the possible revenue. |
| 10. | Depending on the configuration of the networks, a temporary price may be replaced more than once before it finally becomes a permanent price. |
| 11. | Note that this does not necessary have to be a triangle, it can be a “n-cycle” inequality where n is the number of links in the cycle. |
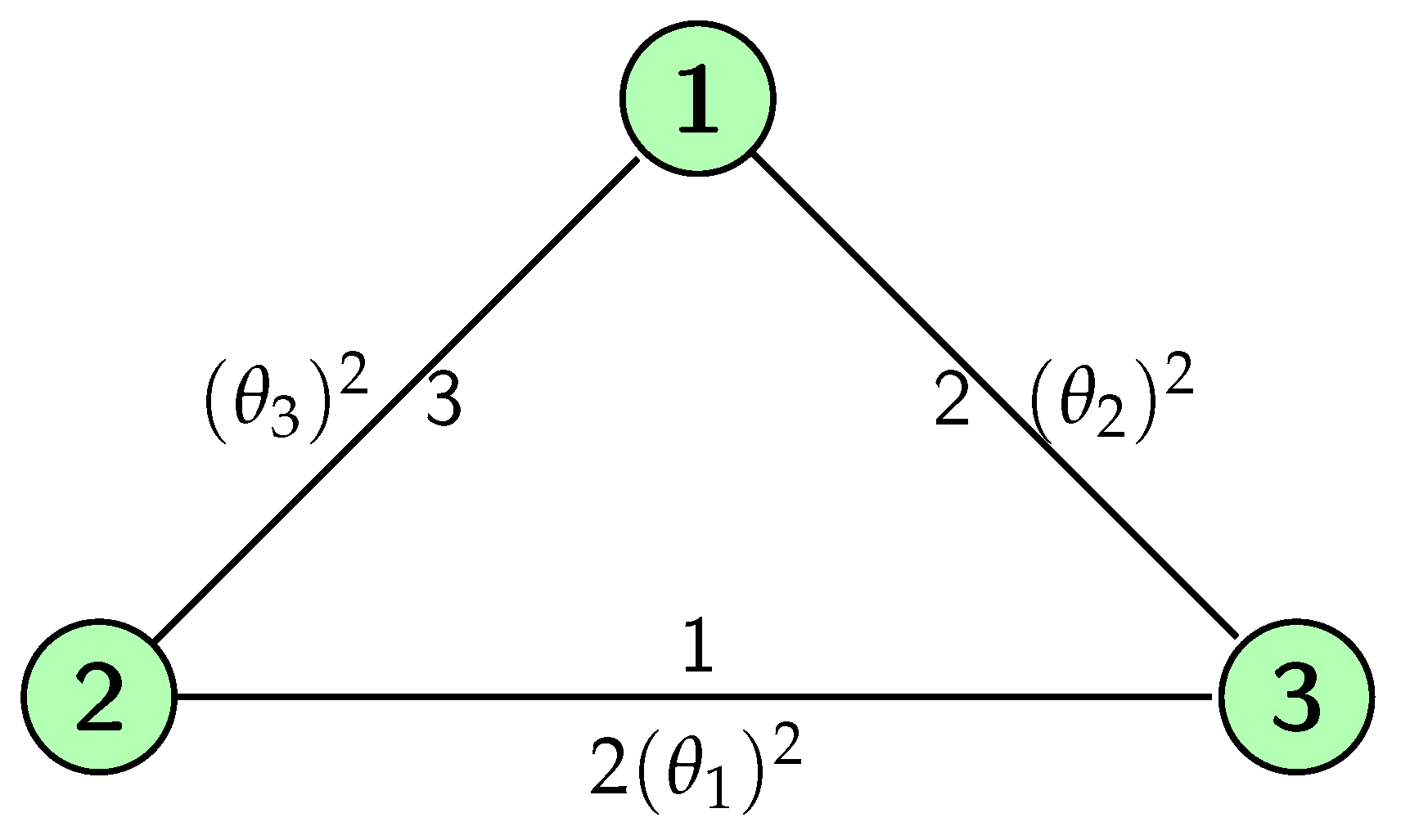
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juarez, R.; Wu, M. Routing-Proofness in Congestion-Prone Networks. Games 2019, 10, 17. https://doi.org/10.3390/g10020017
Juarez R, Wu M. Routing-Proofness in Congestion-Prone Networks. Games. 2019; 10(2):17. https://doi.org/10.3390/g10020017
Chicago/Turabian StyleJuarez, Ruben, and Michael Wu. 2019. "Routing-Proofness in Congestion-Prone Networks" Games 10, no. 2: 17. https://doi.org/10.3390/g10020017
APA StyleJuarez, R., & Wu, M. (2019). Routing-Proofness in Congestion-Prone Networks. Games, 10(2), 17. https://doi.org/10.3390/g10020017




