Effectiveness Evaluation Method for Hybrid Defense of Moving Target Defense and Cyber Deception

Abstract

Moving Target Defense (MTD) has been proposed as a dynamic defense strategy to address the static and isomorphic vulnerabilities of networks. Recent research in MTD has focused on enhancing its effectiveness by combining it with cyber deception techniques. However, there is limited research on evaluating and quantifying this hybrid defence framework. Existing studies on MTD evaluation often overlook the deployment of deception, which can expand the potential attack surface and introduce additional costs. Moreover, a unified model that simultaneously measures security, reliability, and defense cost is lacking. We propose a novel hybrid defense effectiveness evaluation method that integrates queuing and evolutionary game theories to tackle these challenges. The proposed method quantifies the safety, reliability, and defense cost. Additionally, we construct an evolutionary game model of MTD and deception, jointly optimizing triggering and deployment strategies to minimize the attack success rate. Furthermore, we introduce a hybrid strategy selection algorithm to evaluate the impact of various strategy combinations on security, resource consumption, and availability. Simulation and experimental results demonstrate that the proposed approach can accurately evaluate and guide the configuration of hybrid defenses. Demonstrating that hybrid defense can effectively reduce the attack success rate and unnecessary overhead while maintaining Quality of Service (QoS).

1. Introduction

With the growing complexity and diversity of cyberattacks, traditional static defense mechanisms face significant limitations due to their inherent characteristics of isomorphism [1,2,3]. To address this limitation in defense, MTD has become a prominent research focus in network security. MTD changes the asymmetry between attackers and defenders by continually varying system configurations and attributes. In recent years, research has gradually focused on hybrid defense frameworks combining MTD with cyber deception techniques [4,5,6]. These frameworks’ defence performance is superior to single MTD approaches, enhancing resistance against sophisticated attacks and mitigating the impact on QoS. Consequently, the hybrid defense framework of MTD and cyber deception is rapidly emerging as a key area of research in MTD.

Implementing MTD technologies effectively depends on a rigorous and scientific evaluation of their effectiveness. However, various approaches have been proposed for assessing the performance of MTD mechanisms, including performance evaluation models for both single MTD technology [7,8] and a mixture of multiple MTD technologies [9,10]. Research on evaluating hybrid defense strategies that integrate MTD with cyber deception remains limited. Existing studies evaluating the role of cyber deception in MTD [11] overlook the deployment of cyber deception, which may expand the attack surface, and fail to consider the impact of cyber deception on reliability and cost. Moreover, current evaluation frameworks have not comprehensively investigated how deception techniques can substitute for traditional MTD mechanisms in terms of system reliability and resource overhead. Therefore, there is a pressing need to develop a comprehensive performance evaluation model for hybrid defense technologies that can systematically assess the potential trade-offs between defense efficiency, system robustness, and defense cost.

A trade-off exists between performance and security when deploying MTDs, as with any other security mechanism [12]. Although frequent MTD adaptation can effectively improve system security, it inevitably has an adverse effect on system reliability. In addition, excessive defense deployment will also increase the cost of system resources. Most existing evaluation and qualification models focus primarily on security and reliability [13,14], often overlooking a comprehensive assessment of defense costs. Invalid defense mechanisms occupy shared resources, which may not reduce QoS [15]. Although some prior studies have attempted to integrate defense costs into reliability evaluations [16], such approaches neglect the resource inefficiency and waste introduced by defense mechanisms. Consequently, there is a compelling need for a comprehensive evaluation framework that considers security performance, system reliability, and defense costs.

To address the problems mentioned above, in this context, we propose a hybrid defense framework effectiveness evaluation model grounded in evolutionary game theory and queuing theory. The system is modeled as an M/M/c queuing system, wherein system reliability is assessed through indicators such as request packet loss rate and average queuing time. We define effective service rate as the defense cost metric. Then, we develop an evolutionary game model to optimize MTD and cyber deception deployment strategies, constructing replicator dynamic equations for evolutionary games to find the optimal strategy that balances security, reliability, and costs. By considering system reliability and defense costs, MTD and cyber deception are competing strategies within the defensive architecture. Furthermore, a hybrid strategy selection algorithm is designed to analyze the effects of various combinations of MTD triggering strategies and deception deployment schemes on system security, resource consumption, and service availability. The contributions of this paper are as follows.

• We propose a hybrid defense framework that combines MTD and cyber deception effectiveness evaluation models based on queuing theory, aiming to achieve an optimal balance among security, reliability, and defense costs by defining defense resource cost indicators.
• We develop an evolutionary game model to assess the impact of various combinations of MTD and cyber deception strategies on system security, resource overhead, and reliability. By treating MTD and cyber deception as competitive strategies regarding reliability and defense costs, the model aims to enhance system security while maintaining reliability and controlling defense costs.
• Validation of the analytic model through simulation and experimentation demonstrates that the method can accurately evaluate the effectiveness of the hybrid defense framework, which combines MTD and cyber deception.

The remainder of this paper is organized as follows. We survey the related works in Section 2. We present our evaluation model in Section 3. The results of the experiments and analysis are presented in Section 4. Finally, Section 5 concludes this article.

2. Related Work

This section surveys the state-of-the-art works, including the MTD and cyber deception hybrid defense framework and methods for evaluating the effectiveness of MTD techniques.

Table 1. Survey of MTD-related Literature and Study Areas.

Year	Literature	Study Areas
		S	D	R	Hybrid
2021	Evaluating the effectiveness of shuffle and redundancy MTD techniques in the cloud [17]	✓		✓
2022	A Practical Security Evaluation of a Moving Target Defence against Multi-Phase Cyberattacks [18]	✓
2022	Evaluating Performance and Security of a Hybrid Moving Target Defense in SDN Environments [19]				✓
2022	Performability evaluation of switch-over Moving Target Defence mechanisms in a Software Defined Networking using stochastic reward nets [16]	✓
2023	Spatial-Temporal Decisions for Moving Target Defense Game Subject to Quality of Service Constraints [20]	✓
2024	Proactive defense mechanism: Enhancing IoT security through diversity-based MTD and cyber deception [6]	✓	✓		✓
2025	Evaluation of time-based virtual machine migration as moving target defense against host-based attacks [21]	✓
2025	Evaluating Moving Target Defense Methods Using Time-to-Compromise and Security Risk Metrics in IoT Networks [10]	✓
2025	Effectiveness of Moving Target Defenses for Adversarial Attacks in ML-Based Malware Detection [22]	✓			✓
2025	Vulnerability defence using hybrid moving target defence in Internet of Things systems [9]				✓

summarizes the research on performance evaluation methods for MTD and they relate to shuffle-based MTD technology (S), diversity-based MTD technology (D), redundant-based MTD technology (R), and hybrid MTD technology (Hybrid).

2.1. Mobile Target Defense(MTD) and Cyber Deception Hybrid Defense Framework

The hybrid defense framework combining MTD and cyber deception misleads attackers by deploying decoys, maximizing the time attackers spend on these decoys while using MTD as an additional layer of protection to enhance overall system security. Ref. [4] proposed a hybrid defense framework for the ICS reconnaissance phase, integrating MTD with cyber deception. On an SDN platform, optimal network shuffling and diversified decoy coordination are employed, alongside dual heterogeneous subnets and adaptive decision-making (active/passive mode), to increase network uncertainty and ensure system availability. Ref. [5] introduced a dynamic defense architecture, DOLOS, combining MTD with cyber deception technology. By integrating fake services and resources into real production systems, it effectively misleads and delays attackers. The system employs a multi-layer isolation mechanism to bolster security, and its efficacy in enhancing the system’s resilience against attacks and prolonging attack duration has been validated across various attack scenarios.

2.2. Methods for Evaluating the Effectiveness of MTD Techniques

There are several classification methods for evaluating the effectiveness of MTD. Reference [11] categorizes these methods into metric-based [10,23], mathematical model-based [8,16,24], and simulation-based [13,25]. We primarily focus on research based on mathematical models. Ref. [8] proposes a quantitative analysis model for MTD under the constraint of concurrent reconfiguration, addressing the lack of unified quantitative indicators and the trade-off between performance and security. Using Continuous-Time Markov Chains (CTMCs) to evaluate resource availability, response time, and attack success probability, the model determines the optimal reconfiguration rate through a utility function, providing a unified analysis framework for comparing different MTD technologies and scenarios. To achieve a balance between system security and availability through time-based virtual machine migration scheduling in cloud environments, ref. [21] proposes a stochastic Petri net model and PyMTDEvauator tool to optimize MTD policy selection.

2.3. Efficiency Evaluation of Hybrid MTD Technology

With the advancement of hybrid MTD technology research, various evaluation methods have emerged to assess combinations of standard MTD techniques (shuffling, diversity, and redundancy). Ref. [17] addresses the lack of a unified and comparable effectiveness evaluation for multiple MTD combinations in cloud environments. It proposes a formal evaluation method based on the graphical security model HARM to assess hybrid defense techniques involving shuffling and redundancy, analyzing the trade-off between security and reliability. Ref. [10] proposes a series of security metrics to measure shuffling or diversity-based MTD methods. Ref. [6] also introduces a series of metrics to evaluate the effectiveness of the diversity-based MTD technique combined with honeypot defense models.

However, these performance analysis models for MTD are limited to single or multiple MTD technologies and are unsuitable for the hybrid defense framework combining MTD with cyber deception. The proposed model can demonstrate the advantages of a hybrid defense framework from three aspects: security, reliability, and defense costs.

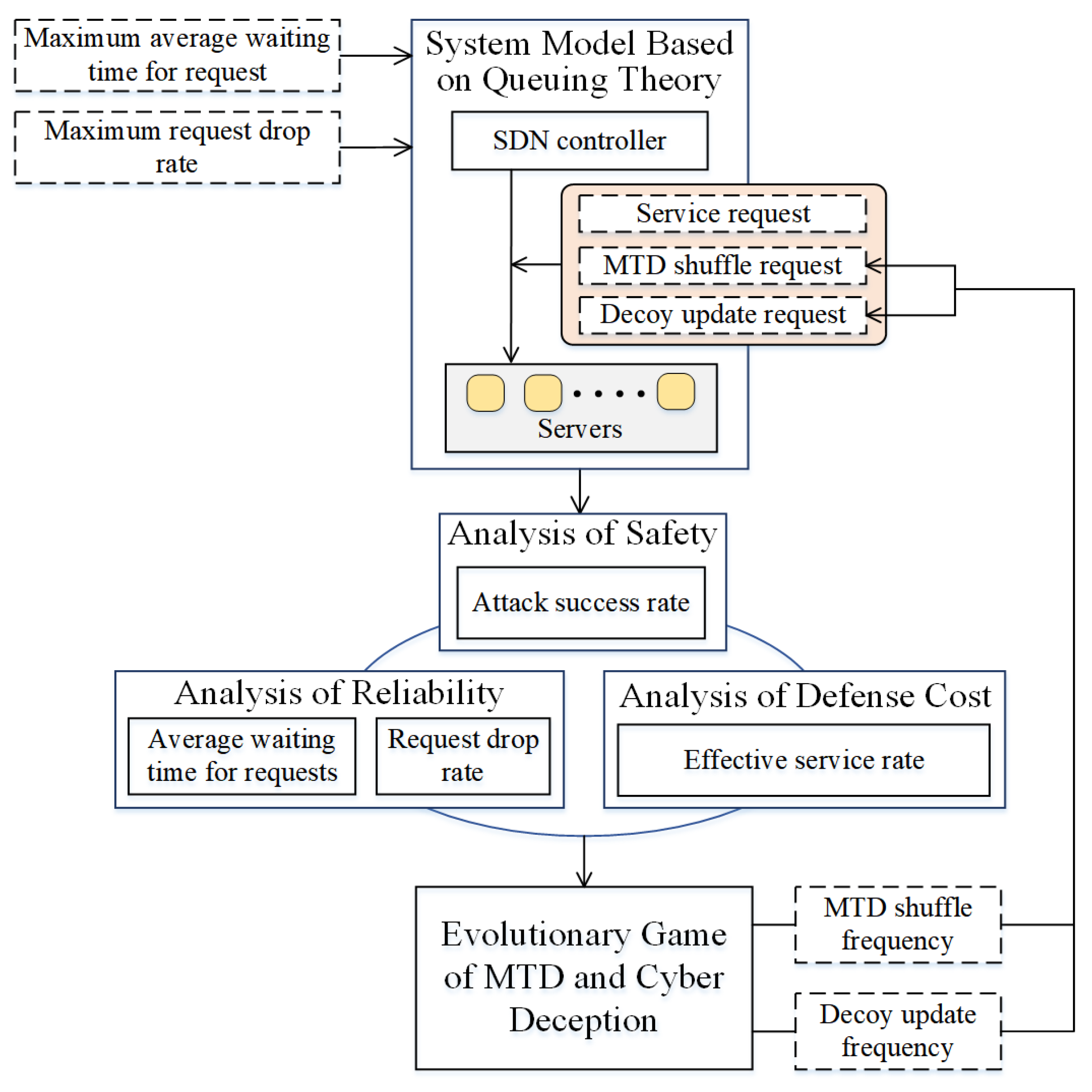
3. Hybrid Defense Evaluation Model

This section presents the evaluation model used to evaluate the effectiveness of our hybrid defense framework that combines MTD and cyber deception, as shown in Figure 1. We first model the system, the defense mechanisms, and the behaviour of the attacker, and quantify security, reliability, and service quality. We then detail the evolutionary game model and analyze the competitive interaction between the two defenses. Finally, we design an algorithm to evaluate how different defense strategies affect the system.

3.1. The Quantitative Model of MTD and Cyber Deception

3.1.1. MTD Shuffle Model

The defender uses MTD to reconfigure the attack surface, such as IP address, port, and service fingerprint, thereby disrupting reconnaissance and hindering the progression of the attack chain [2,26]. Specifically, At each interval ${\iota }_m$(${\iota }_m>t_R$, where $t_R$ is the service recovery time), reconfiguration commands are send to n($n\in \left\{1,\dots ,C\right\}$) servers. The frequency of the shuffle is:

$$f_m={\displaystyle \frac{1}{{\iota }_m}}$$

(1)

and the achievement rate of MTD requests per unit time is:

$${\lambda }_m=n\ast f_m$$

(2)

3.1.2. Cyber Deception Model

The defender deceives and misleads the attacker by deploying and periodically updating decoys. Decoys are first deployed to mislead the attacker [27,28], and then updated every interval ${\iota }_d$ to reduce detectability; r decoys are updated each time. The frequency of the update is:

$$f_d={\displaystyle \frac{1}{{\iota }_d}}$$

(3)

The decoy update request arrival rate is:

$${\lambda }_d=r\ast f_d$$

(4)

The time since the defender’s last ’decoy update’ is:

$$\tau \left(t\right)=t-{\displaystyle \frac{1}{f_d^{\prime }}}\ast ⌊f_d^{\prime }\ast t⌋,0\le \tau \left(t\right)<{\displaystyle \frac{1}{f_d^{\prime }}}$$

(5)

We can obtain the probability of attackers accessing each decoy server:

$$\gamma \left(t\right)={\gamma }_0\left(1-f_d^{\prime }\ast \tau \left(t\right)\right),0\le {\gamma }_0\le 1$$

(6)

3.2. System Model Based on Queuing Theory

We model the system as an M/M/C queue with a Poisson arrival process for data packets [29]. The SDN controller handles three requests: legitimate service ${\lambda }_l$, MTD transformation ${\lambda }_m$, and bait update ${\lambda }_d$. All requests have equal priority and are processed in first come, first served (FCFS) order. The system comprises C parallel servers with average service rates $\mu$. We denote the average queueing delay by W and the system utilization by $\rho$. We present our assumptions below.

• Requests queued at the server will be discarded after waiting for $W_0$.
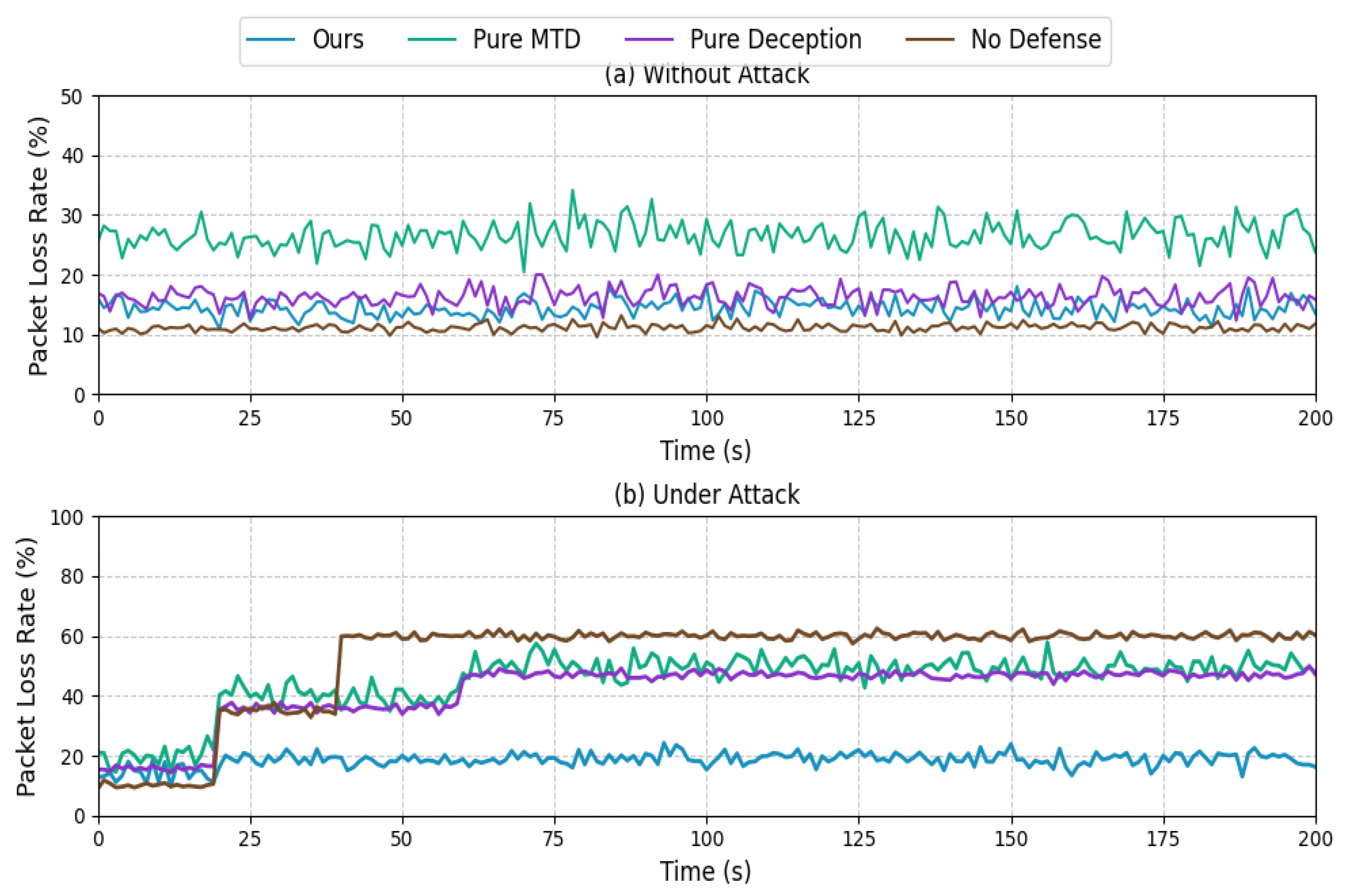
• When the packet loss rate of the system reaches $R_0$, we consider the system unusable.
• After performing MTD shuffle on the server, the connection will be interrupted, making the server temporarily unavailable and requiring waiting for time $t_R$ to restore the connection.
• The average processing time for service requests by the server is $t_A$.

Three types of requests obtain the total arrival rate of system requests:

$${\lambda }_{total}={\lambda }_l+{\lambda }_m+{\lambda }_d$$

(7)

We can obtain the utilization rate of the system:

$$\rho ={\displaystyle \frac{{\lambda }_{total}}{C\ast \mu }},\rho <1$$

(8)

And the load of the system:

$$a={\displaystyle \frac{{\lambda }_{total}}{\mu }}$$

(9)

The probability of all servers being busy is represented by the waiting and dropping formula (Erlang C):

$$P\left(C,a\right)={\displaystyle \frac{\frac{a^C}{C!\left(1-\rho \right)}\ast \frac{C}{C-a}}{{\sum }_{k=0}^{C-1}\frac{a^k}{k!}+\frac{a^C}{C!\left(1-\rho \right)}\frac{1}{1-\rho }}}$$

(10)

The decay rate of waiting time when all servers are busy:

$$\eta =\mu \ast C-{\lambda }_{total}$$

(11)

Due to the request drop after timeout, the waiting time $W=min\left(W_q,W_0\right)$, where $W_q$ is the queue waiting time. We can calculate the probability of requesting immediate service and the probability of requesting waiting:

$$P\left(W_q=0\right)=1-P\left(C,a\right)$$

(12)

$$P\left(W_q>t\right)=P\left(C,a\right)\ast e^{-\eta \ast t}$$

(13)

In summary, the average waiting time is calculated as follows:

$$W={\int }_0^{W_0}P\left(W_q>t\right)dt=P\left(C,a\right)\ast {\displaystyle \frac{1-e^{-\eta \ast W_0}}{\eta }}$$

(14)

Due to the request dropout occurring after the timeout, the dropout rate of requests is:

$$R_d=P\left(W>W_0\right)=P\left(C,a\right)\ast e^{-\eta \ast W_0}$$

(15)

When MTD transformation and bait update requests arrive at the server, they will be queued due to server recovery, service request processing, and other reasons. Therefore, we define effective shuffle intervals ${\iota }_m^{\prime }$ and effective decoy update intervals ${\iota }_d^{\prime }$.

3.2.1. Effective Shuffle Interval

The shuffle frequency of each selected server is:

$$f_m^{\prime }={\displaystyle \frac{n\ast f_m}{C}}\ast \left(1-R_d\right)$$

(16)

We can obtain the effective transformation interval through ${\iota }_m^{\prime }={\displaystyle \frac{1}{f_m^{\prime }}}$:

$${\iota }_m^{\prime }={\displaystyle \frac{C\ast {\iota }_m}{n\ast \left(1-R_d\right)}}$$

(17)

3.2.2. Effective Decoy Update Frequency

The effective update frequency for each decoy server is:

$$f_d^{\prime }=f_d\ast \left(1-R_d\right)$$

(18)

Similarly, we can obtain the effective decoy update interval:

$${\iota }_d^{\prime }={\displaystyle \frac{{\iota }_d}{\left(1-R_d\right)}}$$

(19)

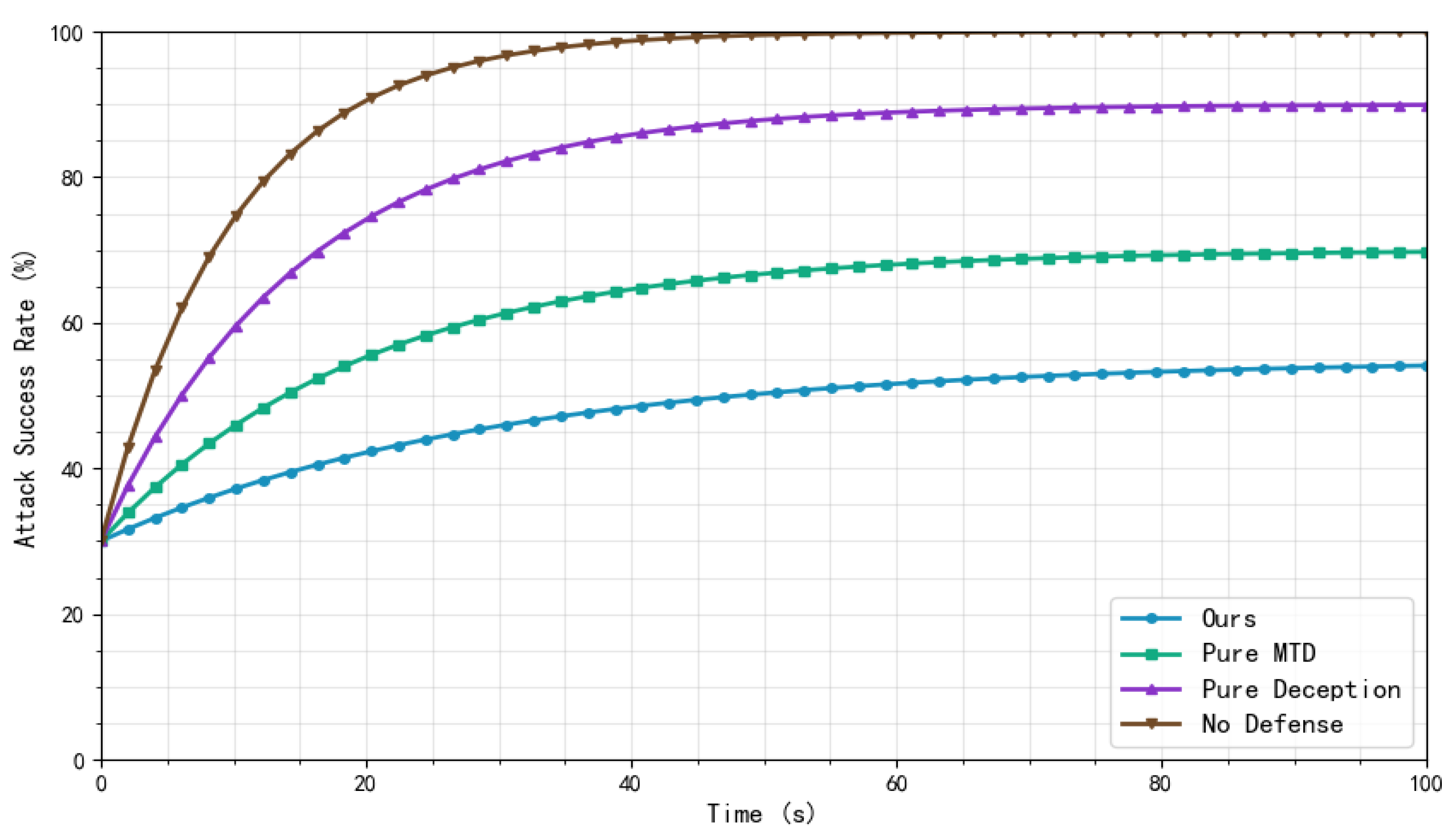
3.3. Analysis of Safety

We identify two types of attacks based on research on existing attack behaviours. The first involves continuous high-intensity attacks by the attacker on all potential targets until the system is paralyzed. The second type is a more covert approach, where the attacker conducts prolonged reconnaissance to identify vulnerabilities in specific targets, then executes targeted attacks while adjusting the strategy based on ongoing reconnaissance. From this analysis, we assume two different attack behaviours: fixed strategy attacks and variable strategy attacks.

• Static strategy attacks: In this attack type, the attacker continuously attacks until all targets are compromised. The base attack success rate increases linearly over time [30].
• Changing strategy attacks: In this case, the attacker constantly gathers information and adjusts the attack strategy to target specific vulnerabilities more precisely. The base attack success rate grows exponentially [31].

MTD works by frequently changing attributes such as addresses and ports, disrupting the attack chain and slowing down the attack rate. The higher the frequency, the more significant the slowdown. Cyber deception, through bait and its updates, diverts the attacker’s attention and resets their perception, causing the success rate to decrease periodically, although the overall growth pattern remains the same. When combined, MTD and deception create a “slowdown + suppression” effect: MTD provides long-term slowdown, while deception offers periodic suppression. We assume that the attacker’s initial success rate is $P_0$. From this, we can derive the attack success rate functions for static strategy attacks $P_s\left(t\right)$, and changing strategy attacks $P_c\left(t\right)$.

$$P_s\left(t\right)=P_0+\left(1-r\ast \gamma \left(t\right)\right)\ast {\displaystyle \frac{k_0}{f_m^{\prime }}}\ast t$$

(20)

$$P_c\left(t\right)=P_0+\left(1-r\ast \gamma \left(t\right)\right)\ast \left(1-e^{-a\ast t\ast {\displaystyle \frac{1}{f_m^{\prime }}}}\right)$$

(21)

Among them, $k_0$ is the success rate growth parameter of the static attack strategy, $a>0$ is the attacker’s knowledge accumulation rate parameter of the changing attack strategy, and both equations satisfy $P_s\left(0\right)=P_c\left(0\right)=P_0$.

3.4. Analysis of Defense Cost

Defense requests consume server capacity and reduce the processing available for legitimate services. We account for three effects: (i) service capacity is shared across request types in proportion to their arrival rates; (ii) decoys occupy part of the servers; and (iii) servers executing an MTD reconfiguration are unavailable during their recovery window. The effective service rate for legitimate traffic is:

$${\mu }_e=\mu \ast {\displaystyle \frac{{\lambda }_l}{{\lambda }_{total}}}\ast \left(1-{\displaystyle \frac{r+\left(\frac{t_R}{t_A}\ast n\ast f_m^{\prime }\right)}{C}}\right)$$

(22)

Among them, $\mu$ represents the average service rate of each server; ${\displaystyle \frac{{\lambda }_1}{{\lambda }_{total}}}$ represents the service opportunities obtained by regular services according to the arrival ratio; and the decrease of the effective available servers caused by the number of decoys r and MTD recovery occupation ${\displaystyle \frac{t_R}{t_A}}\ast n\ast f_m^{\prime }$. The feasibility constraint is:

$$0<r+\left({\displaystyle \frac{t_R}{t_A}}\ast n\ast f_m^{\prime }\right)<C,{\mu }_e>0$$

(23)

On this basis, the effective utilization ${\rho }_e$ and payload $a_e$ of normal services are:

$${\rho }_e={\displaystyle \frac{{\lambda }_l}{C\ast {\mu }_e}}$$

(24)

$$a_e={\displaystyle \frac{{\lambda }_l}{{\mu }_e}}$$

(25)

Moreover, it must meet the ${\rho }_e<1$ stability condition. It can be seen that increasing the MTD frequency or increasing the number of decoys will monotonically decrease ${\mu }_e$, thereby increasing ${\rho }_e$ and queuing pressure; reducing the recovery time $t_R$ or improving unit service efficiency (reducing $t_A$) can alleviate this impact.

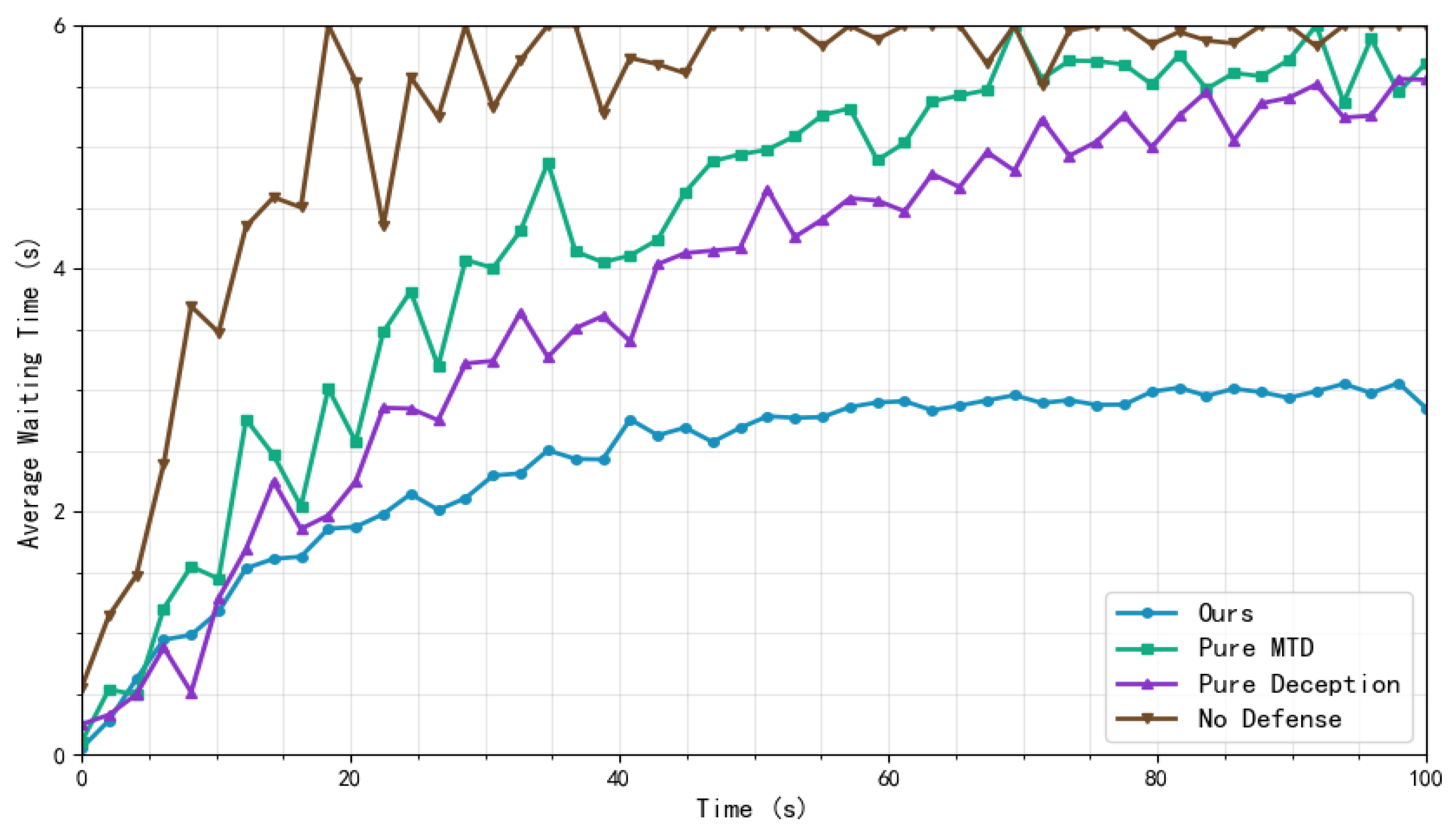
3.5. Analysis of Reliability

We evaluate reliability using the average waiting time for requests and the request drop rate. Based on the system analysis above, the legitimate service queue can be approximated by an M/M/C model with parameters $\left({\lambda }_l,{\mu }_e,C\right)$. Let the Erlang-C (delay) probability:

$$ErlC\left(a_e,C\right)={\displaystyle \frac{\frac{a_e^C}{C!\left(1-{\rho }_e\right)}}{{\sum }_{k=0}^{C-1}\frac{a_e^k}{k!}+\frac{a_e^C}{C!\left(1-{\rho }_e\right)}}}$$

(26)

The average waiting time for requests is:

$$\overline{W_q}={\displaystyle \frac{ErlC\left(a_e,C\right)}{C\ast {\mu }_e-{\lambda }_l}}$$

(27)

The system adopts the strategy of “drop when exceeding the threshold” (waiting time threshold $W_0$), and its dropout rate is equal to the probability of waiting time exceeding $W_0$:

$$\begin{array}{cc}\hfill R_d& =\mathrm{Pr}\{W_q>W_0\}\hfill \\ \hfill & =\mathrm{ErlC}\left(a_e,C\right)exp\left(-\left(C{\mu }_e-{\lambda }_{\ell }\right)W_0\right)\hfill \end{array}$$

(28)

So, when $R_d>R_0$, it is determined that the system is unavailable.

3.6. Evolutionary Game of MTD and Cyber Deception

We consider the defender’s MTD and cyber deception strategies as competitive strategies and construct an evolutionary game model. The system state comes from a queuing model. We build a payoff function that balances security gain, reliability, and cost, set up the optimization problem, and then use replicator dynamics to update strategy probabilities until they converge to optimal trigger and update rates.

$N=\left\{N_m,N_d\right\}$ represents the game participants, where $N_m$ is MTD strategy, $N_d$ is cyber deception strategy.

$\Theta =\left\{W,R_d,{\mu }_e\right\}$ represents a set of the system status. W represents the average service request waiting time. $R_d$ represents the average drop rate of service requests. ${\mu }_e$ represents the effective service rate.

$S=\left\{S_m,S_d\right\}$ represents a set of defender strategy, where $S_m,S_d$ denotes the defender adopt MTD strategy and deception strategy. Among them, $S_m=\left\{f_{m1},f_{m2},\dots ,F_m\right\}$ represent the set of the frequency of sending MTD shuffle requests, $S_d=\left\{f_{d1},f_{d2},\dots ,F_d\right\}$ represents the set of the frequency of sending decoy update requests. $F_m$ and $F_d$ are the maximum MTD shuffle and decoy update frequencies.

$Q=\left\{q\left(f_{mi},f_{dj}\right)\right\}$ represents the probability function, where $q\left(f_{mi},f_{dj}\right)>0$ denotes the probability of defender adopt frequency $f_{mi}$ to execute MTD shuffle and frequency $f_{dj}$ to update decoy.

$U=\left\{U_s,U_c\right\}$ indicates the payoff function. $U_s\left(f_m,f_d\right)$ represents the defender’s payoff when the attacker adopts a fixed strategy. $U_c\left(f_m,f_d\right)$ represents the defender’s payoff when the attacker adopts a variable strategy. The payoff consists of three parts: (1) the effect of reducing the success rate of attacks; (2) the benefit brought by reliability; (3) the defence cost penalty composition. Under the mixed strategy $\left(f_{mi},f_{dj}\right)$:

$$\begin{array}{ccc}\hfill U_s\left(q\left(f_{mi},f_{dj}\right)\right)& =& \left(1-\left(1-r\gamma \left(t\right)\right){\displaystyle \frac{k_0}{f_{mi}^{\prime }}}t\right)\hfill \\ & & +\left(1-{\displaystyle \frac{W_l}{W_0}}-{\displaystyle \frac{R_d}{R_0}}\right)\hfill \\ & & -\left({\displaystyle \frac{f_{mi}^{\prime }}{F_m}}+{\displaystyle \frac{f_{dj}^{\prime }}{F_d}}\right)\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill U_c\left(q\left(f_{mi},f_{dj}\right)\right)& =& \left(1-\left(1-r\gamma \left(t\right)\right)\left(1-e^{-at{\displaystyle \frac{1}{f_{mi}^{\prime }}}}\right)\right)\hfill \\ & & +\left(1-{\displaystyle \frac{W_l}{W_0}}-{\displaystyle \frac{R_d}{R_0}}\right)\hfill \\ & & -\left({\displaystyle \frac{f_{mi}^{\prime }}{F_m}}+{\displaystyle \frac{f_{dj}^{\prime }}{F_d}}\right)\hfill \end{array}$$

(30)

To facilitate evolutionary updates, the comprehensive payoff is defined as:

$$U*=U_s+U_c$$

(31)

The replicator dynamic equation gives the evolution of mixed strategy probability over time t:

$$\begin{array}{cc}\hfill {\displaystyle \frac{dq(f_{mi},f_{dj})}{dt}}& =q(f_{mi},f_{dj})(U*\left(f_{mi},f_{dj}\mid \Theta (Q)\right)\hfill \\ \hfill & -\sum _{k=0}^{F_m}\sum _{l=0}^{F_d}q(f_{mk},f_{dl})U*\left(f_{mk},f_{dl}\mid \Theta (Q)\right))\hfill \end{array}$$

(32)

3.7. Optimization Problem

According to the evaluation game, the defender should maximize the payoff to ensure security, reliability and cost. At the same time, ensure the packet loss rate and service waiting time are within an acceptable range. Thus, the problem can be expressed as:

$$\begin{array}{cc}\hfill \mathbf{Problem}:& \underset{f_{mi},f_{dj}}{max}{U}_s\left(q\left(f_{mi},f_{dj}\right)\right)+U_c\left(q\left(f_{mi},f_{dj}\right)\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\overline{W_q}<W_0\hfill \\ \hfill & R_d<R_0\hfill \end{array}$$

(33)

3.8. MTD and Cyber Deception Collaborative Optimization Selection Algorithm

The Algorithm 1 discretises the MTD and decoy update frequencies into a strategy grid. Each strategy pair first uses queueing theory to calculate the effective service rate and reliability for regular services. Then, it incorporates an attack behaviour model to assess the attack success rate, creating an overall payoff matrix. Next, replicator dynamic equations are applied to the strategy grid, continuously shifting probability mass toward higher-reward frequency combinations until it converges to an equilibrium, resulting in the optimal MTD and Cyber deception frequency configuration.

Algorithm 1 MTD and Cyber Deception Collaborative Optimization Selection Algorithm

Input: Constraint thresholds $R_0$ (max drop rate), $W_0$ (max waiting time); system parameters $C,n,r,\mu ,{\lambda }_l,t_R,t_A,a,k_0,{\gamma }_0,R_0,W_0$; strategy sets $S_m=\{f_{m1},\dots ,f_{mM}\}$ and $S_d=\{f_{d1},\dots ,f_{dD}\}$

Output: $f_m^{*}$ (optimal MTD transform frequency), $f_d^{*}$ (optimal deception update frequency)

1: Step 1: Initialize system parameters and strategy space   2: Initialize system parameters: $C,n,r,\mu ,{\lambda }_l,t_R,t_A,a,k_0,{\gamma }_0,R_0,W_0$;   3: Initialize define strategy spaces: $S_m=f_{m}1, f_{m}2,\dots , F_m$, $S_d=f_{d}1, f_{d}2,\dots , F_d$;

4: Step 2: Calculate system state and attack success probability   5: For each strategy pair $(f_{mi}, f_{dj})$:   6: Compute parameters ${\lambda }_{\mathrm{total}},P(C,a),W,R_d,{\mu }_e,{\iota }_m^{\prime },{\iota }_d^{\prime }$   7: $P_{\mathrm{attack}}=P_s+P_c$

8: Step 3: Construct payoff matrix   9: For each strategy pair $(f_{mi}, f_{dj})$: 10: $U_{\mathrm{security}}=1-P_{\mathrm{attack}}$. 11: if  $W_l\le W_0$ and $R_d\le R_0$ then 12: $\hspace{1em}\hspace{1em}{U}_{\mathrm{service}}\leftarrow 1-W_l/W_{max}-R_d/R_0$. 13: else 14: $\hspace{1em}\hspace{1em}{U}_{\mathrm{service}}\leftarrow -100$. 15: end if 16: $U_{\cos \mathrm{t}}=f_{mi}/F_m+f_{dj}/F_d$. 17: $U_{\mathrm{total}}=U_{\mathrm{security}}+U_{\mathrm{service}}-U_{\mathrm{cost}}$. 18: $A[i,j]\leftarrow U_{\mathrm{total}}$.

19: Step 4: Replicator dynamics on $S_m\times S_d$ 20: function REPLICATORDYNAMICS(Q, A) 21: $\hspace{1em}\hspace{1em}{U}_{\mathrm{avg}}={\sum }_{i=1}^M{\sum }_{j=1}^D{q}_{ij}A[i,j]$. 22:   For each strategy pair $(f_{mi},f_{dj})$: 23: $\hspace{1em}\hspace{1em}dQdt[i,j]=q_{ij}\left(A[i,j]-U_{\mathrm{avg}}\right)$. 24:    return $dQdt$ 25: end function

26: Step 5: Evolution to equilibrium and selection 27: Initialize $Q=Q_0$ with $q_{ij}\ge 0$ and ${\sum }_{i,j}{q}_{ij}=1$; set $\Delta t,T,\epsilon$, and $t=0$. 28: repeat 29: $\hspace{1em}\hspace{1em}{Q}_{\mathrm{old}}=Q$. 30: $\hspace{1em}\hspace{1em}dQdt\leftarrow {\mathrm{R}}_{\mathrm{EPLICATOR}}{\mathrm{D}}_{\mathrm{YNAMICS}}(Q_{\mathrm{old}},A)$. 31: $\hspace{1em}\hspace{1em}{Q}_{\mathrm{new}}=Q_{\mathrm{old}}+\Delta t·dQdt$. 32:    Project to simplex: set each $q_{ij}=max(q_{ij},0)$, then renormalize so ${\sum }_{i,j}{q}_{ij}=1$. 33: $\hspace{1em}\hspace{1em}{\Delta }_Q={\sum }_{i=1}^M{\sum }_{j=1}^D|Q_{\mathrm{new}}[i,j]-Q_{\mathrm{old}}[i,j]|$. 34: $\hspace{1em}\hspace{1em}t\leftarrow t+\Delta t$; $Q\leftarrow Q_{\mathrm{new}}$. 35: until ${\Delta }_Q\le \epsilon$ or $t\ge T$ 36: Find indices $(i*,j*)$ such that $Q[i*,j*]$ is maximal. 37: return $f_m^{*}\leftarrow f_{mi*}$, $f_d^{*}\leftarrow f_{dj*}$.

4. Experiment

4.1. Experimental Setup

We implemented the experiments using SimPy4.11, a Python-based (version 3.8), process-oriented discrete-event engine. We used SimPy4.11 on a dedicated control node to co-schedule workload arrivals, resource reconfiguration, and decoy rotation. A real XenServer8 virtualization environment executes scripted operations on the backend VM pool to enact the reconfigurations and decoy updates. Service requests are emulated by throughput-oriented TCP flows generated with iPerf3, while Nmap and hping3 synthesize active scanning and flooding/probing traffic. Attack intensity and risk thresholds are annotated with reference to public vulnerability databases and Common Vulnerability Scoring System (CVSS) scores. The controller hosts a built-in monitoring process that periodically records metrics such as queueing delay and packet loss rate.

We set the constant parameters in the model as follows. The number of servers C is 20. The maximum waiting time for a request W₀ is 6 s. The server recovery wait time $t_R$ is 3 s. The average processing time for a service request $t_A$ is 2 s. The other constants are $a=1.1$ and $k_0=2$.

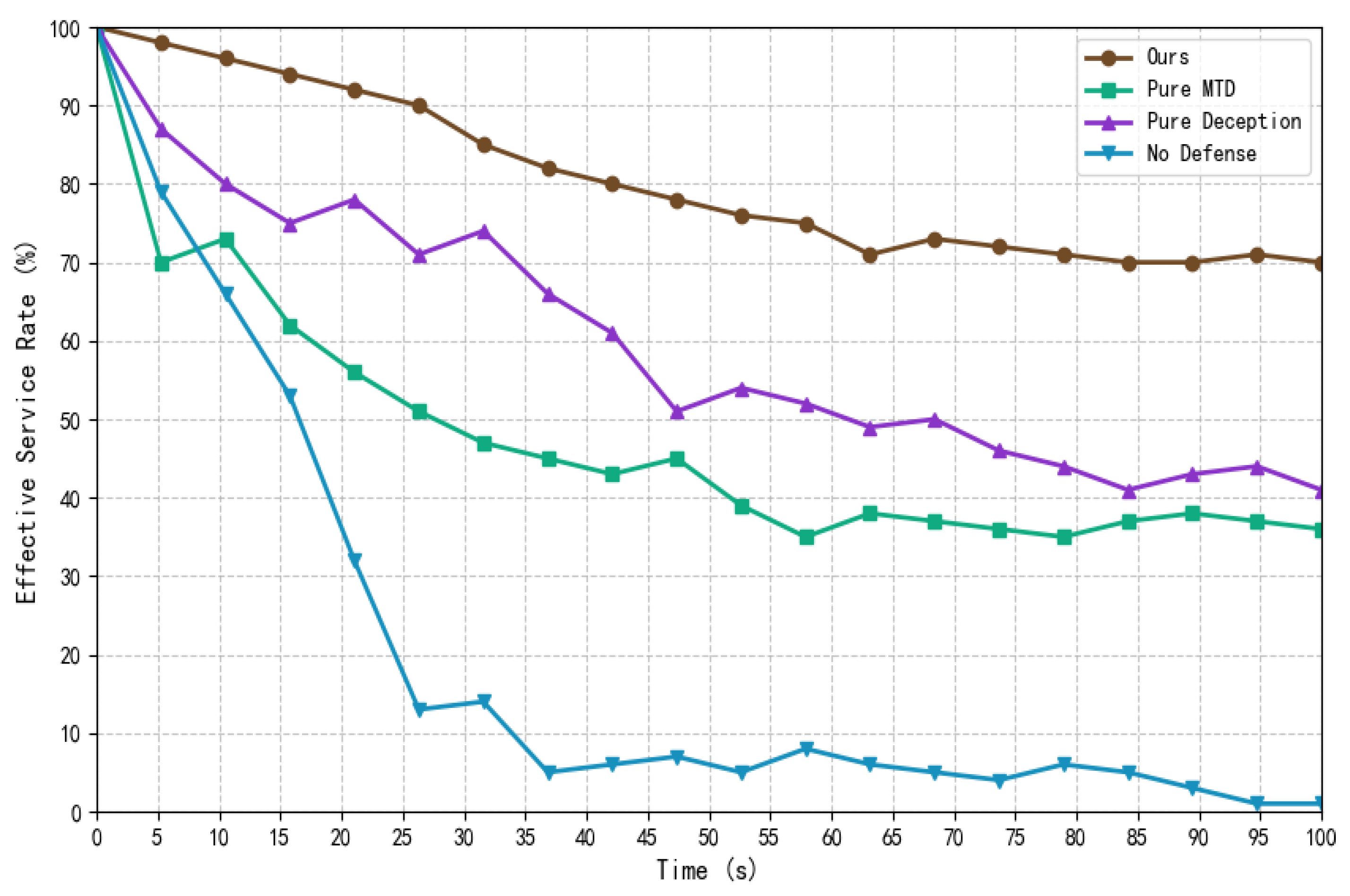
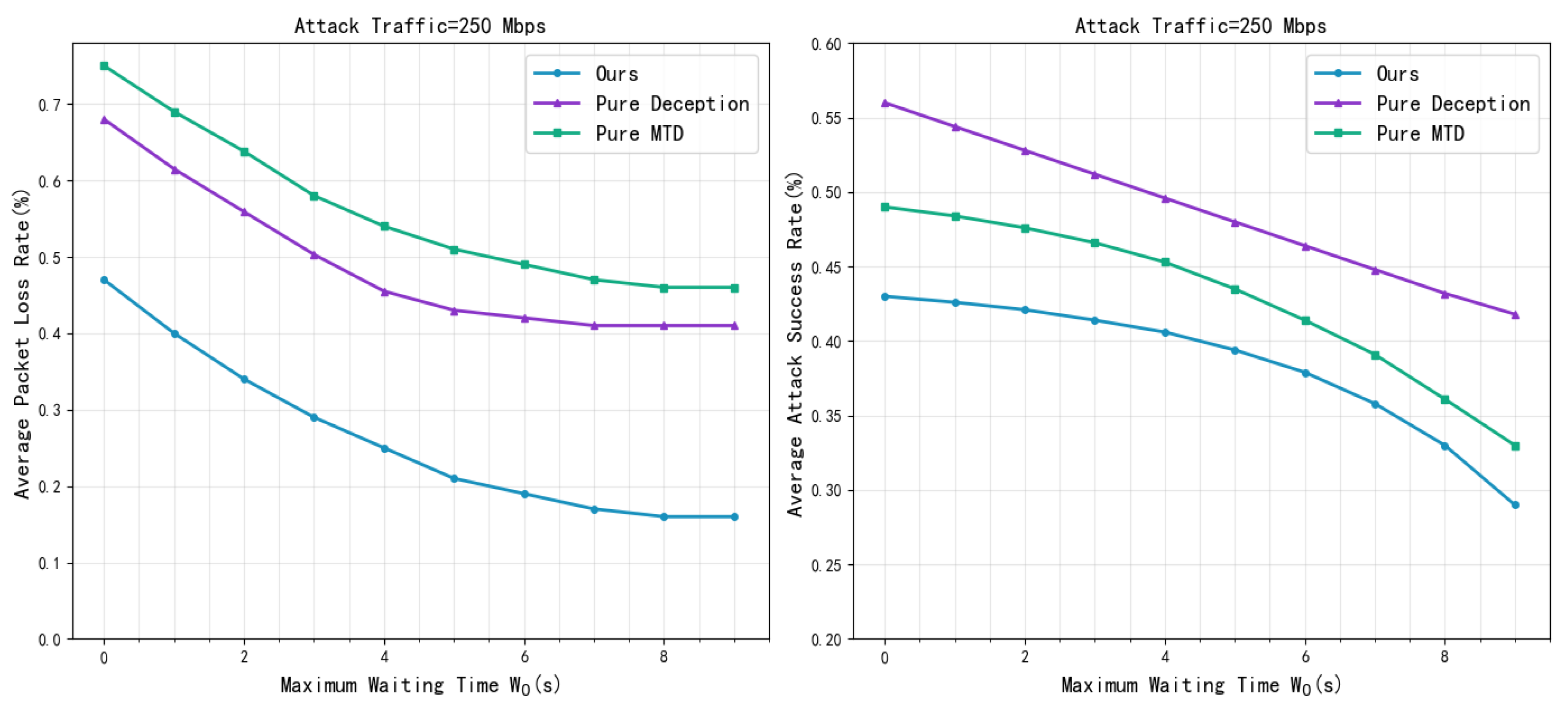
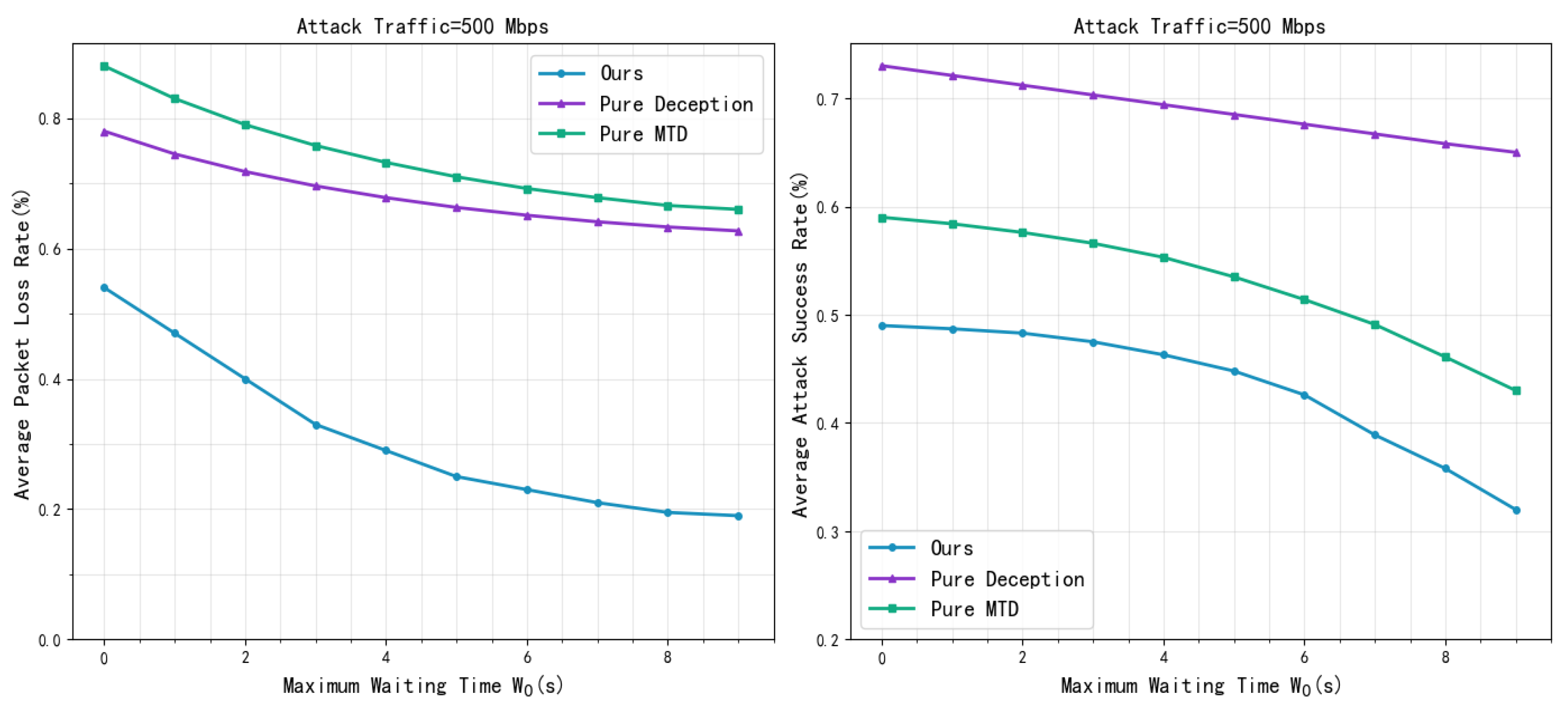
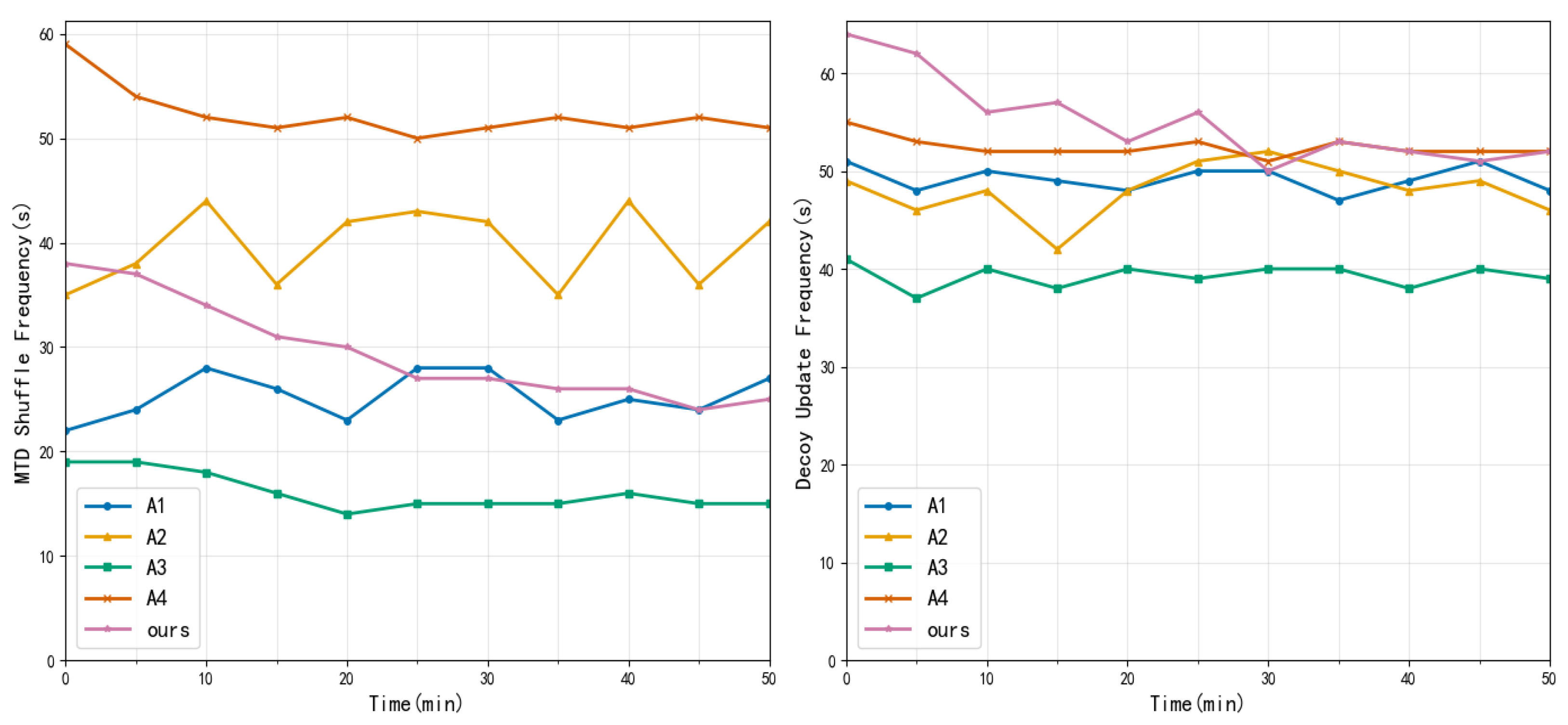
4.2. Experimental Results

First, we adjusted the input parameters and evaluated the framework from a security, resource overhead, and availability perspective. We tested under different basic attack success rates. We analyzed how the defense strategy affects the packet loss rate, the average request waiting time, and the effective service rate. We also compared our method with three baseline strategies: no defense, the pure MTD strategy, and the pure deception strategy. The pure MTD indicated that the defender only deployed the shuffle-based MTD technique, and the pure deception strategy indicated that the defender only deployed the decoy.

We set the basic attack success rate at $P_0=30\%$ and evaluate how the attacker’s success rate changes over time, as shown in Figure 2. The curve representing the non-defense strategy illustrates the change in attack success rate over time. Due to the attacker’s ability to detect decoys, the success rate of attacks under a pure deception strategy is approximately 90%. Although the pure MTD strategy can effectively mitigate attacks, its restrictions on reliability prevent it from achieving optimal effects. Our method stabilizes at approximately 55%, effectively limiting further growth. This proves that hybrid defense methods can effectively ensure the system’s security compared to pure MTD and deception methods.

Figure 3 presents the change in request waiting time during the attack. Many servers are compromised, and the system cannot process requests effectively without defences. Our method enforces a bound on waiting time and converges to about 3 s. For the other strategies, the average waiting time rises and approaches the maximum limit. Figure 4 compares the average packet loss rate with and without attacks. In the absence of attacks, our method has a slightly higher packet loss rate than no defense and is close to the pure cyber deception strategy. Under attack, the packet loss rates of the pure MTD and pure cyber deception strategies increase rapidly and reach up to 50%. Our method effectively constrained the packet loss rate. This proves that hybrid defense methods can effectively ensure the system’s reliability compared to pure MTD and deception methods.

Figure 5 shows the effective service rate during the attack. As the attack continues, a system without defense suffers server failures and its effective service rate drops sharply. The pure MTD strategy also declines quickly due to the frequent MTD requests. The pure cyber deception strategy updates less often, so its effective service rate decreases slowly. Our method shows a similar downward trend to deception and, with resource overhead constrained, it stabilizes at about 70%. This proves hybrid defense methods can effectively reduce defense costs compared to pure MTD and deception methods.

Then, we varied the attack intensity to evaluate how security, resource overhead, and availability relate under different attack levels. We first adjusted the maximum waiting time limit $W_0$ to get the relationship between attack success rate and average packet loss rate. Figure 6 and Figure 7 show that when attack traffic is 250 Mbps, lowering the maximum waiting time limit reduces the average packet loss rate. In this case, both the deception method and our method keep the attack success rate low while maintaining service availability. The MTD strategy can suppress the attack success rate, but it cannot sustain normal availability. When attack traffic rises to 500 Mbps, the attack success rate under the cyber deception method increases significantly. In contrast, our method continues to reduce the attack success rate and keeps the system available.

We also present the optimal MTD shuffle frequency and decoy update frequency under different constraints on the maximum waiting time $W_0$ and maximum packet loss rate $R_0$ to serve as the basis for the preceding experiments; the results are shown in

Table 2. The optimal triggering interval(s) under different constraints of maximum packet loss rate $R_0$ and maximum waiting time $W_0$.

Metric	${\mathit{R}}_0$			${\mathit{W}}_0$
	20%	25%	30%	3 s	4 s	5 s	6 s
MTD shuffle frequency	41.5 s	33.4 s	25 s	41.5 s	33.4 s	28.7 s	25 s
Decoy update frequency	68 s	51.7 s	42.6 s	68 s	60.5 s	54 s	42.6 s

.

Finally, we assessed the performance of the hybrid MTD and deception framework across several evaluation metrics in other studies, including attack success rate, average packet loss rate, average service waiting time, and effective service rate, as shown in

Table 3. Performance of Hybrid Defense Framework under Different Metrics Constraints.

	Attack Success Rate	Average Packet Loss Rate (${\mathit{R}}_0=30$%)	Average Waiting Time (${\mathit{W}}_0=6$ s)	Average Effective Service Rate
A1	37.61%	26.42%	3.06 s	55.67%
A2	35.56%	58.16%	4.04 s	71.36%
A3	29.07%	69.70%	4.52 s	48.31%
A4	43.55%	53.12%	3.97 s	72.43%
Ours	38.20%	22.01%	2.97 s	79.66%

. The settings are as follows. A1 is committed to selecting the MTD strategy schedule that can achieve the desired levels of security for the system [21]. A2 focuses on enhancing the security of hybrid MTD technology against multi-phased cyber-attacks and, to some extent, mitigating the performance degradation caused by MTD triggering [19]. A3 has conducted a more comprehensive evaluation of security through several security metrics [9]. A4 evaluates MTD in smart grid, aiming to maximize the generation-cost benefits [32].

The results of the performance show that A1 focuses on considerations of security and reliability, neglecting the costs associated with defense deployment. A2 neglected the consideration of reliability, resulting in an average waiting time that exceeds the standard. A3 achieves the lowest attack success rate but fails to strike a balance between service effectiveness and cost. A4 focuses on benefits and reliability, which can lead to a lack of safety assurance. The framework meets system requirements, and only three criteria are satisfied.

We also measure the change in defense strategies over time. As shown in Figure 8, A1 can balance security and reliability, but raising the MTD shuffle frequency and the decoy update frequency consumes the processing capacity needed for regular services. A2 supports more precise defense deployment, yet lowering the defense frequency leaves security insufficiently protected. A3 seeks to reduce the attack success rate by issuing many MTD shuffle and decoy update requests, but it cannot maintain system reliability or control defense overhead. A4 seeks to ensure the system’s reliability by reducing the defense deployment, but sacrificing security does not improve reliability. Our method has a slightly higher attack success rate than A3 but effectively preserves reliability and keeps defense overhead in check.

5. Conclusions

We propose a performance evaluation method combining queuing and evolutionary game theory in a single framework for hybrid defense with MTD and cyber deception. The method uses an M/M/C queue to model system reliability and defense cost, and uses static and adaptive attack models to describe attack propagation. With evolutionary game theory, we treat MTD and cyber deception as competing strategies and optimize the MTD trigger frequency and the decoy update frequency through replicator dynamics. This creates an integrated analysis and simulation workflow for strategy selection and parameter tuning. Experiments show that the method balances security, availability, and cost under multiple criteria. It provides quantitative guidance for configuring trigger and deployment strategies, reducing attack success rates while limiting unnecessary resource use and maintaining QoS.