Social Distancing in Indoor Spaces: An Intelligent Guide Based on the Internet of Things: COVID-19 as a Case Study

Abstract

Using Internet of Things (IoT) solutions is a promising way to ensure that social distancing is respected, especially in common indoor spaces. This paper proposes a system of placement and relocation of people within an indoor space, using an intelligent method based on two optimizers (ant colony and particle swarm) to find the optimal relocation of a set of people equipped with IoT devices to control their locations and movements. As a real-world test, an amphitheater with students was used, and the algorithms guided students toward correct, safe positions. Two evolutionary algorithms are proposed to resolve the studied problem, ant colony optimization and particle swarm optimization. Then, a comparative analysis was performed between these two algorithms and a genetic algorithm, using different evaluation metrics to assess the behavior of the proposed system. The results show the efficiency of the proposed intelligent IoT system.

1. Introduction

Faced with the crisis of the COVID-19 pandemic, which has caused considerable economic and health problems, an important issue has arisen, i.e. how to organize, position, and reposition people, especially in indoor spaces, while maintaining the minimum recommended social distance. Such spaces can be stadiums, university lecture halls, supermarkets, or even party halls or means of public transport. Knowing how to manage people and how to guarantee social distance can greatly contribute to the fight against COVID-19. A minimum of two meters is advised as a minimum safe social distance by the World Health Organization (WHO) [1].

Several countries are racing against time to find a reliable vaccine for COVID-19; however, even with this anticipated vaccine, several biological scientific studies [2] claim that similar crises may easily occur soon given the huge number of undiscovered viruses in wild animals that can be transmitted to the global population.

This possibility has prompted researchers to find other solutions to fight against future pandemics. Technological solutions are both the best suited to and the most promising for the situation. In this regard, several applications have been proposed in several countries for contact tracing in order to record a person’s visited places and alert them afterwards if a person who later tests positive for COVID-19 visited one of these places in the same period or a short time after the person using the contact tracing application. Although the designers of these applications claim that user data backup occurs locally in their smartphones and that the data are transferred anonymously only if the person is infected, there are several doubts about the privacy of the data. We present another technological solution, i.e., deploying and locating Internet of Things (IoT) devices in order to create a social IoT network limited to a specific indoor space. This network is made up of connected objects; each object has a unique identifier and is capable of automatically interacting with and transferring data to another IoT object or a server. The communication protocols that are used generally rely on 802.15.4 or Bluetooth due to their low power consumption. Our goal is to find ideal, socially distanced locations within a given space while keeping devices, and therefore students, away from each other.

Indeed, in different networking applications, thousands of sensors using limited batteries are deployed. Depleted batteries can cause network disconnection and failure in achieving the mission for which the network was designed. This implies that when designing wireless networks, the placement of objects must be carefully designed.

The goal of methods aimed at finding solutions for placing and relocating IoT objects is to find the ideal locations for these objects while meeting the purposes for which the network was designed. Depending on the application needs and the accessibility of the region of interest (RoI), the object’s placement plan, namely the RoI coverage, can be either random or deterministic. In general, random coverage is not efficient, because it requires a large number of sensors and the distribution density of these sensors is not uniform over the entire RoI. This has allowed the emergence of different methods to control the placement of sensors in order to build reliable network topology.

In addition, another factor affecting network performance is that it is very sensitive to the way in which sensors are placed. This factor is the localization of the nodes. Indeed, in order to be able to collect the data, sensors should have the capability of locating themselves efficiently. This is related firstly to their locations. Poor localization accuracy can cause several problems in the network. The different paradigms, discussed in Section 2, suggest efficient schemes for the placement, relocation, and localization of sensors.

This problem is NP-hard [3] even for a small number of IoT devices. Indeed, the complexity analysis defines the proportional dependency between the size of the population and the execution time. Table 1 shows the complexity of different algorithms resolving the relocation problem. Each algorithm uses a population composed of n individuals in which n is the size of the problem and M is the number of objectives considered by the optimization algorithm.

Table 1. Comparison of the complexity of optimization algorithms resolving the relocation problem.

	ACO	PSO	GA
Best Case	O(logn*M*n)	O(logn*M*n)	O(Mn2)
Worst Case	O(Mn2)	O(Mn2)	O(Mn2)

Table 1 shows that ant colony optimization (ACO) and particle swarm optimization (PSO) have better complexity than the genetic algorithm (GA) when resolving the relocation problem.

Hence, this study uses an approximative resolution approach based on metaheuristics and evolutionary optimization algorithms such as PSO [4] and ACO [5].

The main contributions of this study are summarized as follows:

• Two optimizers (PSO and ACO) were adapted to the problem of indoor placement of IoT devices to maintain social distance between people in order to reduce the propagation of COVID-19.
• The behavior of each algorithm was evaluated in a real-world environment using prototyping on different parameters, different network metrics (such as the average distance between students and the rate of transferred data between nodes), and different optimization metrics (such as convergence time and quality of the solution). The results were then interpreted and discussed.
• Contrary to contact tracing applications, privacy is preserved, and the security of the user’s data is guaranteed by the proposed system (optimizers and IoT network prototyping).
• The use of the proposed system may be easily extended for use in other indoor places, such as stadiums, cinema rooms, malls, and public transport vehicles.

The next sections focus on the following: In Section 2, we investigate recent studies regarding the PSO and ACO resolutions for indoor placement; in Section 3, we illustrate the proposed PSO and ACO algorithms for the placement problem; in Section 4, we present and discuss the numerical and experimental tests evaluating the suggested algorithms; and in Section 5, we discuss the conclusion and future research directions.

2. Related Works

In this section, recent studies proposing indoor IoT placement and relocation using optimization algorithms such as PSO and ACO are investigated and discussed.

The study in [6] suggested a PSO algorithm combined with a fuzzy clustering method (FCM) to minimize interruptions in the network. The PSO-FCM method was compared to standard FCM, PSO, and the GA. The hybrid PSO-FCM algorithm was repeatedly executed until the optimal topology of the sensor was determined. Simulations demonstrated that the proposed system enhanced the connection rate and energy consumption better than the GA or PSO alone.

In [7], a PSO method was suggested to achieve coverage in random static wireless networks. The proposed approach divided the network into a set of grids, and then computed the coverage degree of each grid. This method enhanced consumed energy and coverage as compared with the standard PSO. However, some real constraints were not taken into consideration, such as the existence of obstacles in the RoI.

The authors in [8] suggested the use of AcNSGA-III, which combined ACO and NSGA-III to find better solutions for the indoor placement of devices in IoT networks. The assessment of the behavior of AcNSGA-III, achieved using simulations and prototyping, showed its advantage over ACO and NSGA-III.

In [9], an ant colony optimization and local search (ACO-LS) algorithm was used to optimize the placement of nodes with minimum reliability cost to the network. The results indicated the efficiency of ACO-LS as compared with greedier algorithms.

Another hybrid ACO algorithm, named ACO-MCC3D, was developed in [10] to find optimal solutions for the three-dimensional (3D) GCLC problem. The framework of the algorithm was composed of a first phase that used a modified ACO to determine locations sparsely while the two-ants-based second phase discarded redundant sensors. The simulation indicated a reduction in the number of nodes and the time needed for computation. However, there was no comparative analysis with other paradigms and only the number of iterations and the execution time were used as a metric to evaluate the proposed method.

The study in [11] suggested a 3D indoor placement of IoT devices using two optimizers (NSGA-III [12] and MOEA/D [13]) to enhance four objectives, i.e., energy consumption, coverage, number of nodes, and localization. One of the main drawbacks of this study was that the comparison of the two methods relied only on simulations.

In [14], the coverage achievement of the void-hole problem in underwater wireless networks was investigated using a hybrid PSO and virtual force (VF) method. Indeed, VF on the centroid of the node guided the PSO. The suggested hybridization overcame the issue of fast premature PSO and fell into local optima. The simulations confirmed the performance of the found coverage and convergence speed, but this method did not model the transmission of data between nodes and did not prove the scalability of the algorithm.

In [15], a hybrid ACO and PSO was implemented to enhance the moving paths of mobile agents in wireless networks. Although the simulations indicated the efficiency of the proposed algorithm in achieving better data gathering and energy consumption, there were no real-world experiments or comparisons with other algorithms. Moreover, only network metrics were evaluated, i.e., overflowing data, path length, and energy consumption. Algorithmic and optimization metrics were not used to assess the behavior of the tested hybrid algorithm.

In [16], the authors suggested a recent metaheuristic named the “Mendelian evolutionary theory optimization (METO) algorithm”, which imitated the Mendel rule of heredity in plant genetics and deployed a multispecies binary-coded algorithm. Despite the limitation of METO on plate-shaped, bowl-shaped problems, it may be applied on different types of problems such as the relocation of nodes in sensor networks. Other recent research studies have investigated the optimization of IoT devices in different engineering fields, such as agriculture machinery fault diagnosis. In [17], the authors used artificial intelligence (AI) to enhance the structure and the complexity of IoT end devices used on agriculture end points. Moreover, in [18], the authors suggested using an AI strategy that relied on an economic data analytic on IoT edge devices in order to optimize the health monitoring of agriculture machines.

In order to enhance the quality of the suggested solutions for relocation, some methods of noise reduction in data can be applied. One of the most interesting noise-removing strategies is the Savitzky–Golay filter combined with wavelet decomposition.

3. Proposed PSO and ACO for Student Positioning

The first possible solution to the problem of distributing a set of people over an entire indoor space while maximizing the social distance between them is to propose a mathematical function of uniform distribution, which automatically orders people. This solution is not applicable in our case, in which a group of students progressively enter the room or amphitheater. The entry of several groups of students requires a dynamic distribution for which we must add new IoT devices (people) each time and restart the existing devices while minimizing the number of movements of the old devices and maximizing the distances between all devices in the space. Since this problem has been proven to be NP-hard, we resorted to approximative heuristic algorithms. Two algorithms, ACO and PSO, were used to solve the student positioning problem.

3.1. The Proposed PSO Algorithm for IoT Indoor Positioning

PSO is a random global search approach and is introduced in [4]. It imitates the behavior of animals swarming (e.g., birds or fish) when searching and foraging for food. In PSO, the animal is called the ”individual”. Each individual in the swarm should match the velocity of its neighbors and avoid collision with them. A possible solution for the optimization problem in PSO is an individual (or particle) in the search space. In the problem of indoor student positioning, a student (particle) has a set of possible locations in the amphitheater that satisfy both the maximum distance between students and the minimum required movements of the existing students. Each particle has a fitness value, which is identified by the optimized function, i.e., a speed that controls its distance and direction. While moving in the solution space, particles follow the best particle. Figure 1 presents the steps of the standard version of PSO.

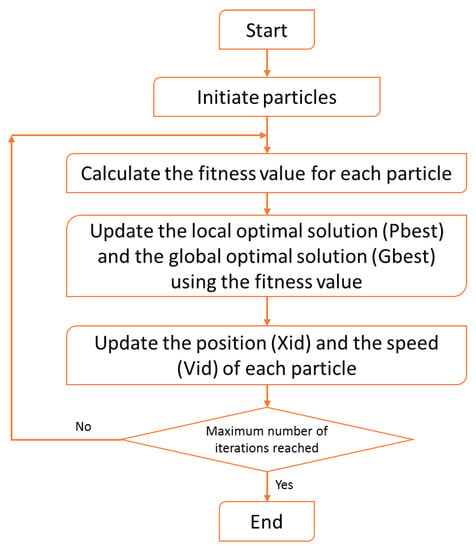
Figure 1. The particle swarm optimization (PSO) algorithm.

The position of each particle (Xid) is updated by Equation (1). The velocity of each particle (Vid) is updated by Equation (2):

V_id = ω V_id + C₁ random (0,1)(PBest_i − X_id) + C₂ random (0,1)(GBest_i − X_id)

(1)

X_id = X_id + V_id

(2)

The parameters used in Equations (1) and (2) are as follows: Gbest represents the optimal global location (optimal local solution) of all particles in the swarm and Pbest represents the optimal location (optimal local solution) of a specific particle, i. C1 and C2 are two acceleration constants, C1 represents the particle’s learning factor, and C2 is the particle’s collective learning factor; ω is a positive inertia factor that is dependent on global optimization and inversely dependent on the local optimization ability.

3.2. The Proposed ACO Algorithm for IoT Indoor Positioning

The ACO algorithm relies on a set of artificial ants that imitate the behavior of real-world ants by releasing an evaporated chemical substance called a pheromone to identify the shortest path between the nest and the food. The ants follow the path that has a higher pheromone concentration. The ACO, illustrated in Figure 2, is characterized by easy implementation and a strong global optimal ability, which makes it highly suitable for hybridization with other optimizers.

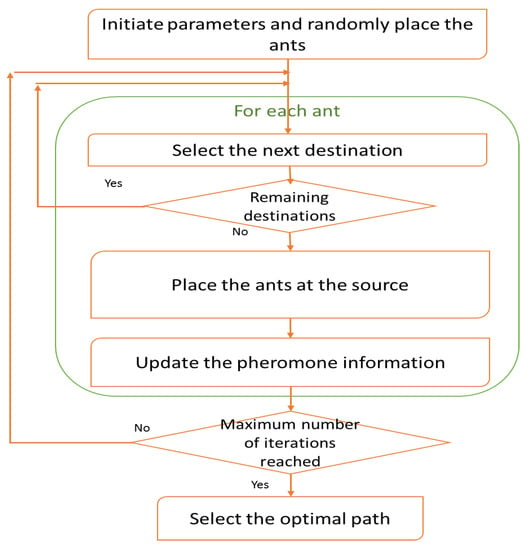
Figure 2. The ant colony optimization (ACO) algorithm.

4. Results

In this section, the node and algorithm settings are identified, the experimental scenario determined, and a set of metrics are computed to evaluate the performance of the ACO and PSO and their contributions are compared with the random distribution of nodes. Then, there is a discussion section and findings are illustrated.

4.1. Parameters and Scenario of IoT Prototyping in Classes of Students

4.1.1. Parameters of Nodes

Figure 3 illustrates the Mini IoT ESP32 M5StickC nodes used [19], and Table 2 lists their technical specifications.

Figure 3. Photographs of the Mini IoT ESP32 M5StickC nodes.

Table 2. Parameters of the Mini IoT ESP32 M5StickC nodes.

Parameter	Value
RoI (m)	90 × 30
Number of IoT devices	23
Range of IoT devices (m)	20 to 25
Initial energy Eo (J)	1
Data packet length (bit)	4500
Ratio of data generation	1 bits/s
Average consumption of energy (Eelec)	40 nJ/bit
Transmission	Wi-Fi/BLE
Frequency	2.4 GHz
Transmission power (mW)	100
Memory (Mb)	4
Antenna	ESP32 transceiver

The RoI is taken as 90 × 30 m according to a typical area of a lecture hall in a university. The number of IoT devices is set to 23 to model a medium-sized lecture hall with 23 students. The rest of the parameters are specific to the type of nodes used, i.e., the Mini IoT M5StickC nodes.

4.1.2. Scenario of IoT Prototyping

When students are free to choose their places in the amphitheater, they often choose places nearest the entry point or they gather in groups. The suggested approach seeks a new distribution of student placement. An amphitheater that measures 150 × 240 m with 300 seats was used. The students were equipped with a node each and randomly entered the amphitheater. The best configuration for placement was computed; then, the new locations were sent to the nodes as a message that indicated the number of the suggested seat. Students were instructed to move toward the suggested position if they were not already there. If a new group of students entered, a new calculation of the positions was achieved using the optimization algorithms while maintaining maximum spacing between the students and a minimum number of displacements of the students already in the room. Hence, the aim was to guarantee a maximum distance between each couple of nodes (therefore between each couple of students) and to guarantee a minimum number of movements of people toward the RoI in order to minimize the contact between them. An average of 20 executions was performed for each experiment to overcome the probabilistic nature of the optimization algorithms.

4.2. ACO and PSO Parameters

The ACO parameters of α, β, and ρ are important parameters that affect the performance of the ACO. After several empirical simulations and prototyping tests, the best configuration of these parameters was found to be 2, 1, and 0.5 for α, β, and ρ, respectively.

The PSO parameters of η, c1, and c2 are also relevant parameters that affect the search process of PSO. After testing several combinations, the best configuration of values for the indicated parameters was found to be 0.8, 0.4, and 0.6 for η, c1, and c2, respectively.

In order to ensure realistic results, the PSO and ACO algorithm results were finalized after several empirical tests and in relation to previous prototyping studies.

4.3. Comparing the Average Distance between Students

As per the results shown in Table 3, both the PSO and ACO are better than the random distribution of students in the RoI. They are both also better than the GA. On the basis of a comparison of ACO and PSO, we concluded that ACO is better than PSO for a small number of students (10 to 20), but PSO becomes more efficient as the number of students increases. Hence, PSO is more appropriate for dynamic contexts where the number of students is high and variant.

Table 3. Average distance between students.

Number of Students	Random Distribution of Students	PSO	ACO	GA
10 (in real prototyping)	5.73	7.92	8.34	6.38
20 (in real prototyping)	4.81	7.68	7.89	4.20
40 (in simulations)	2.01	6.26	5.65	3.94
100 (in simulations)	1.92	3.65	2.92	2.68
250 (in simulations)	0.74	2.04	1.98	1.49

4.4. Comparing the Amount of Transmitted Data

Table 4 illustrates the average amount of data, in Mbit, generated by the transmitted packages between the nodes and between the nodes and the base station. This result provides an idea of the degree of network interactivity.

Table 4. Average amount of transmitted data.

	Random Distribution of Nodes	ACO	PSO	GA
Average amount of transmitted data (Mbit)	77.35	178.93	163.64	124.6

It can be concluded from Table 3 that ACO and PSO are better than both the GA and the random distribution of nodes.

4.5. Comparing the Convergence Time of PSO and ACO

Figure 4 identifies the convergence time of PSO, ACO, and the GA according to the number of students (used IoT devices).

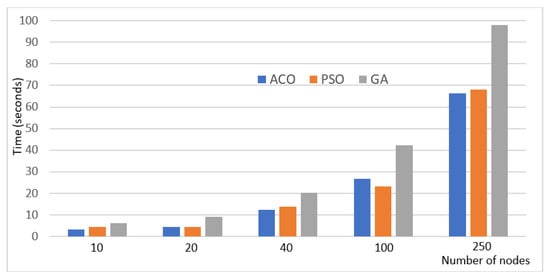
Figure 4. Convergence time of PSO, ACO, and the genetic algorithm (GA).

This figure shows the superior performance of ACO and PSO again as compared with the GA; however, the convergence time of ACO and PSO is similar.

4.6. Comparing the Quality of Solutions of PSO and ACO

Table 5 compares the quality of the solutions found by the optimizers, using average and standard deviation performance measures.

Table 5. Comparing the quality of the solutions.

Measure		Algorithm
	ACO	PSO	GA
Average	0.03243096	0.03391269	0.17198354
Standard deviation	0.01304763	0.01872561	0.19478108

Table 5 demonstrates that ACO is a better-quality solution than PSO and the GA.

4.7. Discussion and Findings

The deduced results rely on experimental prototyping on testbeds and enhance the accuracy and realism of the deductions. The analysis of these results shows the following different findings:

• In addition to computing a configuration for the manner of distributing the nodes in the region, the proposed approach computes the frequency of contacts between nodes and measures the duration, time, and distances that separate the nodes during these contacts.
• In terms of the average distance separating the students, the amount of transmitted data, convergence time, and the quality of solutions, both PSO and ACO are more efficient than random distribution and the GA.
• In terms of the amount of transmitted data and the quality of solutions, ACO is better than PSO, whereas with regard to the high number of students, PSO is better than ACO. The two algorithms have comparable performance in terms of convergence time.
• The achieved real-world experiments highlight the contribution and efficiency of evolutionary optimizers for resolving complex engineering problems [20].
• Contrary to the contact tracing applications currently in use via smartphones, the problems of user data and COVID-19 infection status privacy are not a concern when using our suggested IoT indoor placement system.

5. Conclusions

In this study, a system of placement and replacement of people within an indoor space was developed. The aim was to maintain the recommended social distance between people while minimizing, if needed, the displacement of people who were already present in the area. The approach relies on two evolutionary algorithms, namely ACO and PSO. Their behaviors and performances were compared with the random placement of nodes and with another optimizer, namely a GA. The results show the efficiency of ACO and PSO in terms of different metrics and measures and highlight the practical nature of such methods for preserving social distance during the COVID-19 pandemic and future anticipated health crises. Future research should explore the constraint of existing obstacles in the region of interest, and the proposed system should be tested on other common indoor spaces, such as public transport, restaurants, and cinema rooms to assess its performance in different contexts. Moreover, some new optimizers such as TATS [19] have been recently proposed. TATS may be adapted to our problem of node relocation. Hence, the aim of future works is to test the efficiency of recent advances on optimization algorithms such as METO [16] or TATS [19] on the problem of the relocation of nodes in sensor networks.