Development of a Test-Bench for Evaluating the Embedded Implementation of the Improved Elephant Herding Optimization Algorithm Applied to Energy-Based Acoustic Localization
Abstract
1. Introduction
2. Related Work
3. Theoretical Background
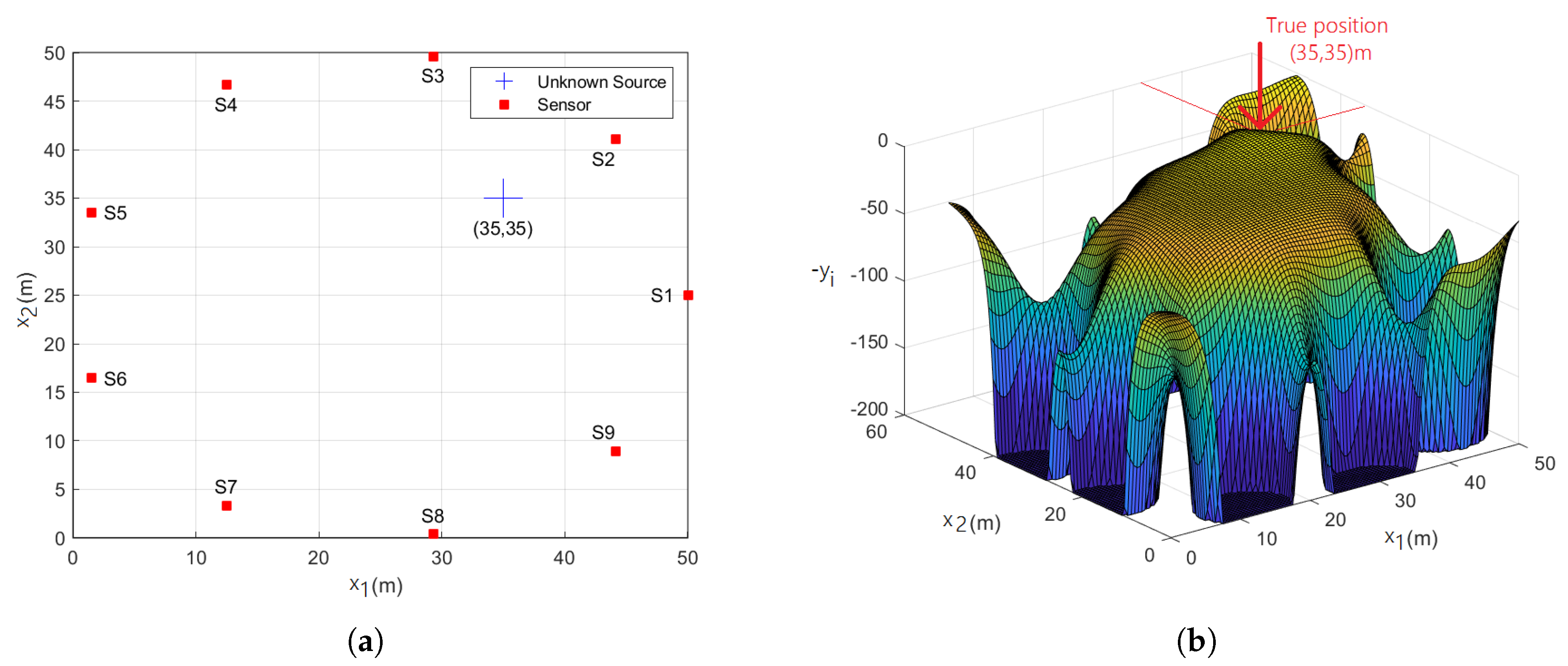
3.1. Acoustic Problem Formulation
3.2. Swarm Optimization
4. Methodology and Experimental Setup
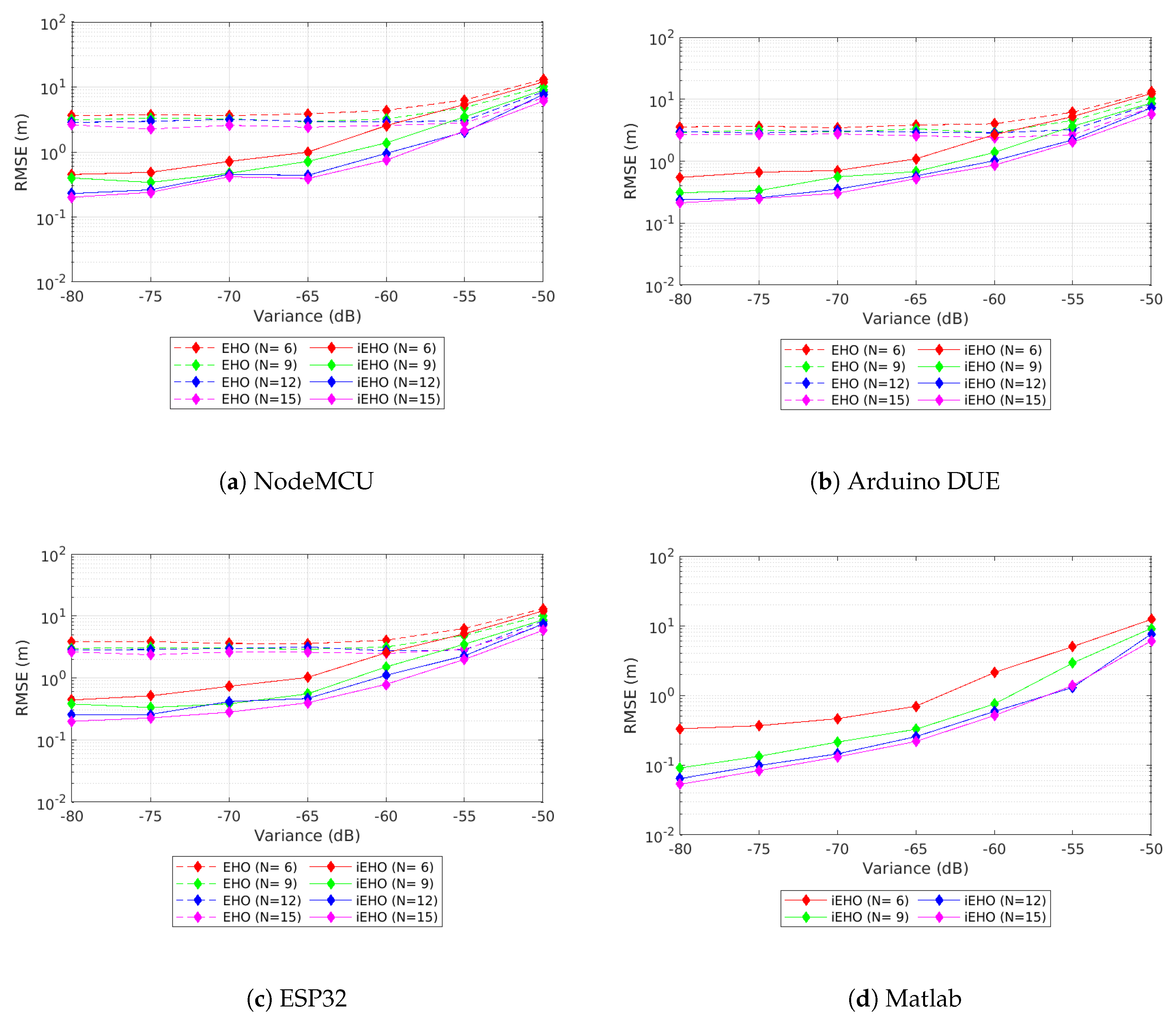
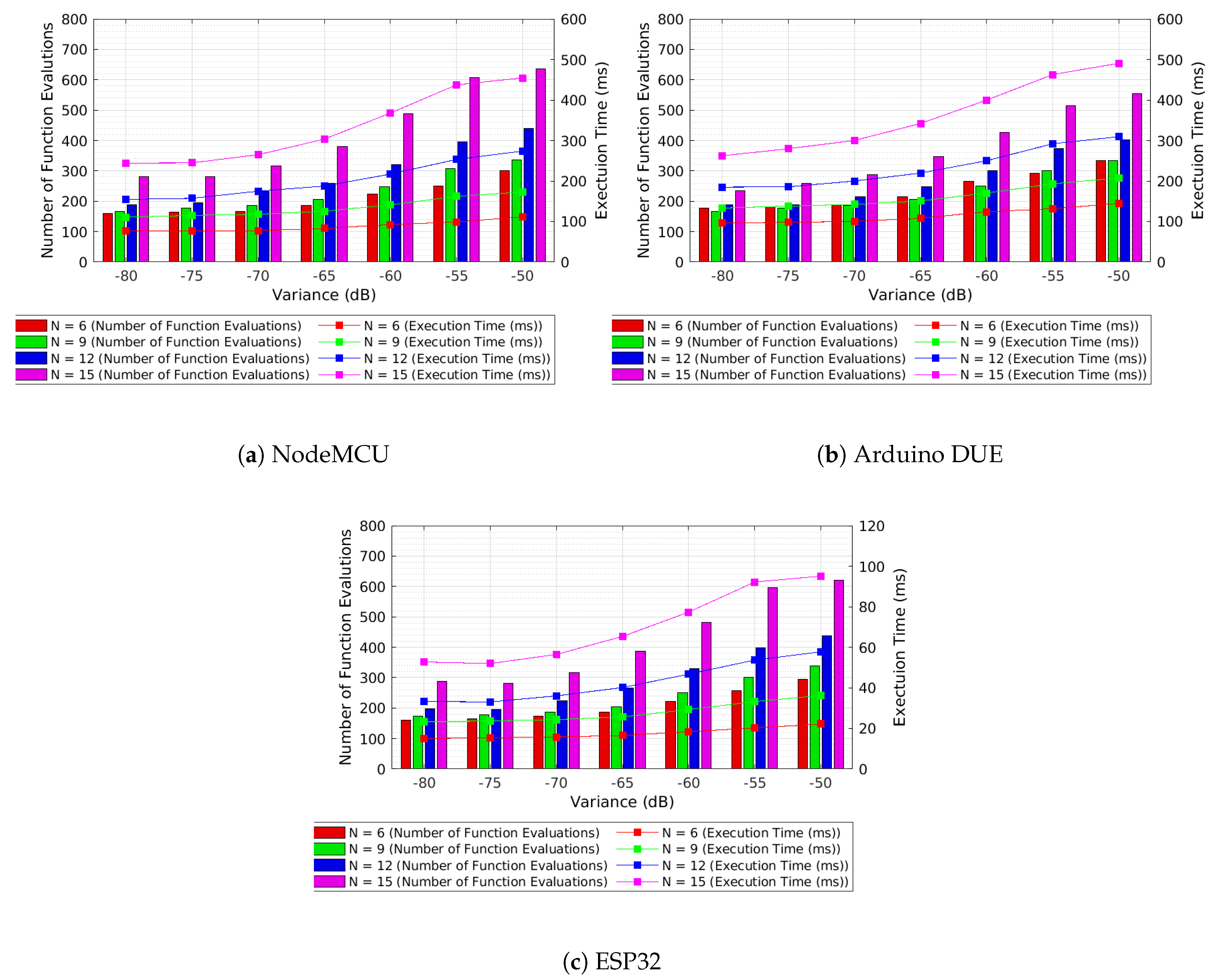
5. Results and Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Hac, A. Embedded systems and sensors in wireless networks. In Proceedings of the IEEE 2005 International Conference on Wireless Networks, Communications and Mobile Computing, Maui, HI, USA, 13–16 June 2005; Volume 1, pp. 330–335. [Google Scholar] [CrossRef]
- Kopetz, H. Internet of Things. In Real-Time Systems Design Principles for Distributed Embedded Applications; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2011; pp. 1–28. ISBN 978-1-4419-8236-0. [Google Scholar]
- Sangiovanni-Vincentelli, A.; Di Natale, M. Embedded System Design for Automotive Applications. Computer 2007, 40, 42–51. [Google Scholar] [CrossRef]
- Kovatsch, M.; Weiss, M.; Guinard, D. Embedding internet technology for home automation. In Proceedings of the 15th IEEE Conference on Emerging Technologies & Factory Automation, Bilbao, Spain, 13–16 September 2010. [Google Scholar] [CrossRef]
- Pinheiro, E.M.; Correia, S.D. Software Model for a Low-Cost, IoT oriented Energy Monitoring Platform. Int. J. Comput. Sci. Eng. 2018, 7, 1–5. [Google Scholar] [CrossRef]
- Pinheiro, E.M.; Correia, S.D. Hardware Architecture of a Low-Cost Scalable Energy Monitor System. Int. J. Eng. Trends Technol. 2018, 61, 1–5. [Google Scholar] [CrossRef]
- Pinheiro, E.M.; Correia, S.D. Analog Input Expansion Board Based on I2C Communication with Plug-and-Play Feature, Applied to Current Measurements. Int. J. Electron. Commun. Eng. 2018, 2, 1–5. [Google Scholar] [CrossRef]
- Alsina-Pagès, R.; Hernandez-Jayo, U.; Alías, F.; Angulo, I. Design of a Mobile Low-Cost Sensor Network Using Urban Buses for Real-Time Ubiquitous Noise Monitoring. Sensors 2016, 17, 57. [Google Scholar] [CrossRef]
- Noriega-Linares, J.; Ruiz, J.N. On the Application of the Raspberry Pi as an Advanced Acoustic Sensor Network for Noise Monitoring. Electronics 2016, 4, 74. [Google Scholar] [CrossRef]
- Dezan, C.; Zermani, S.; Hireche, C. Embedded Bayesian Network Contribution for a Safe Mission Planning of Autonomous Vehicles. Algorithms 2020, 7, 155. [Google Scholar] [CrossRef]
- Baras, N.; Nantzios, G.; Ziouzios, D.; Dasygenis, M. Autonomous Obstacle Avoidance Vehicle Using LIDAR and an Embedded System. In Proceedings of the 2019 8th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 13–15 May 2019; pp. 1–4. [Google Scholar] [CrossRef]
- White, E. Making Embedded Systems, 1st ed.; O’Reilly Media, Inc.: Sevastopol, CA, USA, 2011; ISBN 978-1449302146. [Google Scholar]
- Heath, S. Embedded Systems Design, 2nd ed.; Butterworth-Heinemann: Waltham, MA, USA, 2002. [Google Scholar]
- Luo, G.; Guo, B.; Shen, Y.; Liao, H.; Ren, L. Analysis and Optimization of Embedded Software Energy Consumption on the Source Code and Algorithm Level. In Proceedings of the 2009 Fourth International Conference on Embedded and Multimedia Computing, Jeju, Korea, 10–12 December 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Engin, M. Energy Efficiency of Embedded Controllers. In Proceedings of the 8th Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 10–14 June 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. A survey on sensor networks. IEEE Commun. Mag. 2002, 40, 2–114. [Google Scholar] [CrossRef]
- Yılmaz, M.; Günel, B. Investigation of Acoustic Source Localization algorithm performances for Gunshot Localization on helicopters. In Proceedings of the 2016 24th Signal Processing and Communication Application Conference (SIU), Zonguldak, Turkey, 16–19 May 2016; pp. 1885–1888. [Google Scholar] [CrossRef]
- Kotus, J.; Lopatka, K.; Czyzewski, A. Detection and localization of selected acoustic events in acoustic field for smart surveillance applications. Multimed. Tools Appl. 2014, 68, 5–21. [Google Scholar] [CrossRef]
- Colliera, T.C.; Kirschel, A.N.G.; Taylor, C.E. Acoustic localization of antbirds in a Mexican rainforest using a wireless sensor network. J. Acoust. Soc. Am. 2010, 128, 182–189. [Google Scholar] [CrossRef] [PubMed]
- Mumolo, E.; Nolich, M.; Vercelli, G. Algorithms for acoustic localization based on microphone array in service robotics. Robot. Auton. Syst. 2003, 42, 69–88. [Google Scholar] [CrossRef]
- Alsina-Pagès, R.M.; Alías, F.; Socoró, J.C.; Orga, F. Detection of Anomalous Noise Events on Low-Capacity Acoustic Nodes for Dynamic Road Traffic Noise Mapping within an Hybrid WASN. Sensors 2018, 18, 1272. [Google Scholar] [CrossRef]
- Hollosi, D.; Nagy, G.; Rodigast, R.; Goetze, S.; Cousin, P. Enhancing Wireless Sensor Networks with Acoustic Sensing Technology: Use Cases, Applications and Experiments. In Proceedings of the IEEE International Conference on Green Computing and Communications and IEEE Internet of Things and IEEE Cyber, Physical and Social Computing, Beijing, China, 20–23 August 2013; pp. 335–342. [Google Scholar] [CrossRef]
- Quintana-Suárez, M.A.; Sánchez-Rodríguez, D.; Alonso-González, I.; Alonso-Hernández, J.B. A Low Cost Wireless Acoustic Sensor for Ambient Assisted Living Systems. Appl. Sci. 2017, 7, 877. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Optimization Algorithms; Elsevier Inc.: Amsterdam, The Netherlands, 2020; 300p, ISBN 978-0-12-416743-8. [Google Scholar]
- Zhang, Y.; Wang, S.; Ji, G. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications. Math. Probl. Eng. 2015, 2015, 38. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Wang, G.; Deb, S.; Gao, X.; Coelho, L.S. A new metaheuristic optimisation algorithm motivated by elephant herding behavior. Int. J. Bio-Inspir. Comput. 2017, 8, 394–409. [Google Scholar] [CrossRef]
- Correia, S.D.; Beko, M.; Cruz, L.A.S.; Tomic, S. Elephant Herding Optimization for Energy-Based Localization. Sensors 2018, 18, 2849. [Google Scholar] [CrossRef]
- Correia, S.D.; Beko, M.; Tomic, M.; Da Silva Cruz, L.A. Energy-Based Acoustic Localization by Improved Elephant Herding Optimization. IEEE Access 2020, 8, 28548–28559. [Google Scholar] [CrossRef]
- Mishra, S.; Singh, N.K.; Rousseau, V. Debug Interfaces. In System on Chip Interfaces for Low Power Design; Morgan Kaufmann: Burlington, MA, USA, 2016; Chapter 12; pp. 359–366. ISBN 9780128016305. [Google Scholar] [CrossRef]
- Broekman, B.; Notenboom, E. Testing Embedded Software; Addison-Wesley: Boston, MA, USA; Sogeti Nederland: Vianen, The Netherlands, 2003. [Google Scholar]
- IEEE. Standard Test Access Port and Boundary-scan Architecture; IEEE std 1149.1-2001; IEEE: Piscataway, NJ, USA, 2001. [Google Scholar]
- Whetsel, L. A High Speed Reduced Pin Count JTAG Interface. In Proceedings of the 2006 IEEE International Test Conference, Santa Clara, CA, USA, 22–27 October 2006; pp. 1–10. [Google Scholar] [CrossRef]
- Singh, B.; Patil, S. Single Wire Debug Interface. In Proceedings of the 2020 IEEE 63rd International Midwest Symposium on Circuits and Systems (MWSCAS), Springfield, MA, USA, 9–12 August 2020; pp. 814–817. [Google Scholar] [CrossRef]
- Gialelis, J.; Fokaeos, M.; Theodorou, G.; Paparizos, C.; Tsafas, N. A Low Cost Energy Efficient IoT Node Utilized in the Agricultural Field. In Proceedings of the 2020 9th Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 8–11 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Huang, F. A Platform with JTAG Debugging of SoC Based on System Level Verification. In Proceedings of the 2019 IEEE International Conference on Electron Devices and Solid-State Circuits (EDSSC), Xián, China, 12–14 June 2019; pp. 1–2. [Google Scholar] [CrossRef]
- Park, H.; Xu, J.; Park, J.; Ji, J.-H.; Woo, G. Design of On-Chip Debug System for embedded processor. In Proceedings of the 2008 International SoC Design Conference, Busan, Korea, 24–25 November 2008; pp. 11–12. [Google Scholar] [CrossRef]
- Hansen, M.T. Multi-purpose passive debugging for embedded wireless. In Proceedings of the 10th ACM/IEEE International Conference on Information Processing in Sensor Networks, Chicago, IL, USA, 12–14 April 2011; pp. 155–156. [Google Scholar]
- Shen, C.; Herman, H.; Charbiwala, Z.; Srivastava, C.; Shen, H.; Herman, Z.C.; Srivastava, M.B. Demo abstract: MiDebug: Microcontroller integrated development and debugging environment. In Proceedings of the 2012 ACM/IEEE 11th International Conference on Information Processing in Sensor Networks (IPSN), Beijing, China, 16–19 April 2012; pp. 133–134. [Google Scholar] [CrossRef]
- Capella, J.V.; Campelo, J.C.; Bonastre, A.; Ors, R. A Reference Model for Monitoring IoT WSN-Based Applications. Sensors 2016, 16, 1816. [Google Scholar] [CrossRef]
- Guerrero-Rodríguez, J.M.; Cobos-Sánchez, C.; González-de-la-Rosa, J.J.; Sales-Lérida, D. An Embedded Sensor Node for the Surveillance of Power Quality. Energies 2019, 12, 1561. [Google Scholar] [CrossRef]
- Ferracuti, F.; Freddi, A.; Monteriú, A.; Prist, M. An Integrated Simulation Module for Cyber-Physical Automation Systems. Sensors 2016, 16, 645. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Choi, K.Y.; Lee, J.W. Fault Localization Method by Partitioning Memory Using Memory Map and the Stack for Automotive ECU Software Testing. Appl. Sci. 2016, 6, 266. [Google Scholar] [CrossRef]
- Li, D.; Hu, Y.H. Energy Based Collaborative Source Localization Using Acoustic Micro-Sensor Array. Appl. Signal Process 2003, 321–337. [Google Scholar] [CrossRef]
- Sheng, X.; Hu, Y.H. Maximum likelihood multiple-source localization using acoustic energy measurements with wireless sensor networks. IEEE Trans. Signal Process 2005, 53, 44–53. [Google Scholar] [CrossRef]
- Sun, G.; Chen, J.; Guo, W.; Liu, K.J.R. Signal processing techniques in network-aided positioning: A survey of state-of-the-art positioning designs. IEEE Signal Process. Mag. 2005, 22, 12–23. [Google Scholar] [CrossRef]
- Ho, K.C.; Sun, M. An accurate algebraic closed-form solution for energy-based source localization. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 2542–2550. [Google Scholar] [CrossRef]
- Beck, A.; Stoica, P.; Li, J. Exact and Approximate Solutions of Source Localization Problems. IEEE Trans. Signal Process 2008, 56, 1770–1778. [Google Scholar] [CrossRef]
- Meesookho, C.; Mitra, U.; Narayanan, S. On energy-based acoustic source localization for sensor networks. IEEE Trans. Signal Process. 2008, 56, 365–377. [Google Scholar] [CrossRef]
- Wang, G.; Yang, K. A Semidefinite Relaxation Method for Energy-based Source Localization in Sensor Networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 15 April 2011; pp. 2257–2260. [Google Scholar] [CrossRef]
- Beko, M. Energy-based localization in wireless sensor networks using semidefinite relaxation. In Proceedings of the IEEE Wireless Communications and Networking Conference, Cancun, Mexico, 28–31 March 2011; pp. 1552–1556. [Google Scholar] [CrossRef]
- Beko, M. Energy-Based Localization in Wireless Sensor Networks Using Second-Order Cone Programming Relaxation. Wirel. Pers. Commun. 2014, 77, 1847–1857. [Google Scholar] [CrossRef]
- Correia, S.D.; Beko, M.; Cruz, L.A.S.; Tomic, S. Implementation and Validation of Elephant Herding Optimization Algorithm for Acoustic Localization. In Proceedings of the 26th Telecommunications Forum (TELFOR), Belgrade, Serbia, 20–21 November 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Kim, C.T.; Choi, T.Y.; Choi, B.; Lee, J.J. Robust estimation of sound direction for robot interface. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 3475–3480. [Google Scholar] [CrossRef]
- Badali, A.; Valin, J.M.; Michaud, F.; Aarabi, P. Evaluating real-time audio localization algorithms for artificial audition in robotics. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 2033–2038. [Google Scholar] [CrossRef]
- Hilsenbeck, B.; Kirchner, N. Listening for people: Exploiting the spectral structure of speech to robustly perceive the presence of people. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 2903–2909. [Google Scholar] [CrossRef]
- Deng, F.; Guan, S.; Yue, X.; Gu, X.; Chen, J.; Lv, J.; Li, J. Energy-Based Sound Source Localization with Low Power Consumption in Wireless Sensor Networks. IEEE Trans. Ind. Electron. 2017, 64, 4894–4902. [Google Scholar] [CrossRef]
- Faraji, M.M.; Shouraki, M.M.; Iranmehr, E. Fuzzy based algorithm for acoustic source localization using array of microphones. In Proceedings of the 2017 Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 2–4 May 2017; pp. 2102–2105. [Google Scholar] [CrossRef]
- Wang, T.; Choy, Y. An approach for sound sources localization and characterization using array of microphones. In Proceedings of the 2015 International Conference on Noise and Fluctuations (ICNF), Xian, China, 2–6 June 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Vikhar, P.A. Evolutionary algorithms: A critical review and its future prospects. In Proceedings of the 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, India, 22–24 December 2016; pp. 261–265. [Google Scholar] [CrossRef]
- Strumberger, I.; Bacanin, N.; Tomic, S.; Beko, M.; Tuba, M. Static drone placement by elephant herding optimization algorithm. In Proceedings of the 25th Telecommunication Forum (TELFOR), Belgrade, Serbia, 21–22 November 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Alihodzic, A.; Tuba, E.; Capor-Hrosik, R.; Dolicanin, E.; Tuba, M. Unmanned aerial vehicle path planning problem by adjusted elephant herding optimization. In Proceedings of the 25th Telecommunication Forum (TELFOR), Belgrade, Serbia, 21–22 November 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Bentouati, B.; Chettih, S.; El Sehiemy, R.; Wang, G.G. Elephant herding optimization for solving non-convex optimal power flow problem. J. Electr. Electron. Eng. 2017, 10, 31–36. [Google Scholar]
- Shankar, K.; Elhoseny, M.; Perumal, E.; Ilayaraja, M.; Sathesh Kumar, K. An Efficient Image Encryption Scheme Based on Signcryption Technique with Adaptive Elephant Herding Optimization. In Cybersecurity and Secure Information Systems; Hassanien, A., Elhoseny, M., Eds.; Advanced Sciences and Technologies for Security Applications; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Sambariya, D.K.; Fagna, R. A robust PID controller for load frequency control of single area re-heat thermal power plant using elephant herding optimization techniques. In Proceedings of the International Conference on Information, Communication, Instrumentation and Control (ICICIC), Indore, India, 17–19 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Sambariya, D.K.; Fagna, R. A novel Elephant Herding Optimization based PID controller design for Load frequency control in power system. In Proceedings of the International Conference on Computer, Communications and Electronics (Comptelix), Jaipur, India, 1–2 July 2017; pp. 595–600. [Google Scholar] [CrossRef]
- Strumberger, I.; Beko, M.; Tuba, M.; Minovic, M.; Bacanin, N. Elephant Herding Optimization Algorithm for Wireless Sensor Network Localization Problem. In Technological Innovation for Resilient Systems; Camarinha-Matos, L., Adu-Kankam, K., Julashokri, M., Eds.; DoCEIS 2018; IFIP Advances in Information and Communication Technology; Springer: Cham, Switzerland, 2018; Volume 521. [Google Scholar] [CrossRef]
- Strumberger, I.; Minovic, M.; Tuba, M.; Bacanin, N. Performance of Elephant Herding Optimization and Tree Growth Algorithm Adapted for Node Localization. Sensors 2019, 19, 2515. [Google Scholar] [CrossRef]
- Cohen, R.; Davy, G.; Féron, E.; Garoche, P. Formal Verification for Embedded Implementation of Convex Optimization Algorithms. IFAC-PapersOnLine 2017, 50, 5867–5874. [Google Scholar] [CrossRef]
- Diamond, S.; Boyd, S. CVXPY: A Python-Embedded Modeling Language for Convex Optimization. J. Mach. Learn. Res. 2016, 17, 1–5. [Google Scholar]






| Specifications | NodeMCU (ESP8266) | Arduino DUE | ESP32 |
|---|---|---|---|
 |  |  | |
| Microcontroller | ESP8266 | AT91SAM3X8E | ESP32-WROOM-32 |
| CPU Core | Tensilica Xtensa LX106 | ARM Cortex-M3 | Tensilica Xtensa LX6 |
| Clock Speed | 80 MHz | 84 MHz | 160 MHz |
| Flash Memory | 128 KB | 512 KB | 4 MB |
| SRAM | 4 MB | 96 KB | 520 KB |
| Digital I/O Pins | 16 | 54 | 32 |
| Analog Input Pins | 1× 10-bit ADC | 12× 12-bit ADC | 18× 12-bit ADC |
| Analog Output Pins | - | 2× 12-bit DAC | 2× 8-bit DAC |
| IEEE 802.11 b/g/n | Native USB | 802.11 b/g/n | |
| Connectivity | FTDI USB UART | FTDI USB UART | Bluetooth v4.2 BR/EDR and BLE |
| FTDI USB UART |
| Model and Test Parameters | Algorithm Parameters | ||
|---|---|---|---|
| Search Space | (from [28]) | 0.7 | |
| P | 5 | (from [28]) | 0.1 |
| 1 () | L (from [29]) | 3 | |
| 2 | |||
| 1000 | Number of Clans | 4 | |
| Variance Noise | −80 dB dB | Population Size | 120 |
| Sensor Number | Maximum Evaluations | 3000 | |
| N | Execution Time Test-Bench Data | |||||||
|---|---|---|---|---|---|---|---|---|
| 6 | Var(dB) | −80 | −75 | −70 | −65 | −60 | −55 | −50 |
| EHO (ms) | 818.34 | 818.36 | 818.43 | 818.32 | 818.47 | 818.49 | 818.25 | |
| iEHO (ms) | 76.20 | 76.93 | 77.43 | 82.73 | 92.23 | 98.71 | 111.54 | |
| F(%) | 9.31% | 9.40% | 9.46% | 10.11% | 11.27% | 12.06% | 13.63% | |
| 9 | Var(dB) | −80 | −75 | −70 | −65 | −60 | −55 | −50 |
| EHO (ms) | 1183.2 | 1183.2 | 1183.2 | 1183.2 | 1183.2 | 1183.0 | 1182.7 | |
| iEHO (ms) | 110.5 | 115.1 | 117.9 | 125.3 | 140.9 | 162.0 | 172.8 | |
| F(%) | 9.34% | 9.72% | 9.96% | 10.59% | 11.91% | 13.70% | 14.61% | |
| 12 | Var(dB) | −80 | −75 | −70 | −65 | −60 | -55 | −50 |
| EHO (ms) | 1545.59 | 1545.65 | 1545.61 | 1545.62 | 1545.56 | 1545.31 | 1544.83 | |
| iEHO (ms) | 154.44 | 157.20 | 174.85 | 187.47 | 217.06 | 253.24 | 273.80 | |
| F(%) | 9.99% | 10.17% | 11.31% | 12.13% | 14.04% | 16.39% | 17.72% | |
| 15 | Var(dB) | −80 | −75 | −70 | −65 | −60 | −55 | −50 |
| EHO (ms) | 1912.87 | 1912.80 | 1912.89 | 1912.76 | 1912.74 | 1912.50 | 1912.08 | |
| iEHO (ms) | 244.31 | 244.73 | 264.92 | 303.40 | 367.66 | 43740 | 454.54 | |
| F(%) | 12.77% | 12.79% | 13.85% | 15.86% | 19.22% | 22.87% | 23.77% | |
| N | Execution Time Test-Bench Data | |||||||
|---|---|---|---|---|---|---|---|---|
| 6 | Var(dB) | −80 | −75 | −70 | −65 | −60 | −55 | −50 |
| EHO (ms) | 1002.25 | 1002.32 | 1002.30 | 1002.20 | 1002.50 | 1002.57 | 1002.44 | |
| iEHO (ms) | 96.75 | 97.82 | 100.30 | 108.09 | 123.93 | 131.63 | 144.72 | |
| F(%) | 9.65 | 9.76 | 10.01 | 10.78 | 12.36 | 13.13 | 14.44 | |
| 9 | Var(dB) | −80 | −75 | −70 | −65 | −60 | −55 | −50 |
| EHO (ms) | 1444.84 | 1444.83 | 1444.76 | 1444.80 | 1444.61 | 1444.55 | 1444.15 | |
| iEHO (ms) | 133.16 | 138.01 | 142.31 | 150.65 | 170.22 | 193.09 | 207.42 | |
| F(%) | 9.22 | 9.55 | 9.85 | 10.43 | 11.78 | 13.37 | 14.36 | |
| 12 | Var(dB) | −80 | −75 | −70 | −65 | −60 | −55 | −50 |
| EHO (ms) | 1881.47 | 1881.58 | 1881.68 | 1881.62 | 1881.58 | 1881.24 | 1880.41 | |
| iEHO (ms) | 184.88 | 185.52 | 199.90 | 219.50 | 250.08 | 292.01 | 309.36 | |
| F(%) | 9.83 | 9.86 | 10.62 | 11.67 | 13.29 | 15.52 | 16.45 | |
| 15 | Var(dB) | −80 | −75 | −70 | −65 | −60 | −55 | −50 |
| EHO (ms) | 2323.59 | 2323.50 | 2323.52 | 2323.29 | 2323.37 | 2323.19 | 2322.74 | |
| iEHO (ms) | 262.21 | 279.68 | 300.02 | 342.04 | 399.72 | 462.74 | 490.71 | |
| F(%) | 11.28 | 12.04 | 12.91 | 14.72 | 17.20 | 19.92 | 21.13 | |
| N | Execution Time Test-Bench Data | |||||||
|---|---|---|---|---|---|---|---|---|
| 6 | Var(dB) | −80 | −75 | −70 | −65 | −60 | −55 | −50 |
| EHO (ms) | 171.71 | 171.72 | 171.73 | 171.70 | 171.73 | 171.77 | 171.77 | |
| iEHO (ms) | 15.08 | 15.39 | 15.81 | 16.55 | 18.40 | 20.26 | 22.19 | |
| F(%) | 8.78 | 8.96 | 9.21 | 9.64 | 10.71 | 11.80 | 12.92 | |
| 9 | Var(dB) | −80 | −75 | −70 | −65 | −60 | −55 | −50 |
| EHO (ms) | 252.35 | 252.37 | 252.37 | 252.37 | 252.36 | 252.35 | 252.34 | |
| iEHO (ms) | 23.15 | 23.61 | 24.23 | 25.58 | 29.19 | 33.12 | 36.13 | |
| F(%) | 9.17 | 9.36 | 9.60 | 10.13 | 11.57 | 13.12 | 14.32 | |
| 12 | Var(dB) | −80 | −75 | −70 | −65 | −60 | −55 | −50 |
| EHO (ms) | 332.82 | 332.85 | 332.84 | 332.84 | 332.83 | 332.80 | 332.75 | |
| iEHO (ms) | 33.19 | 32.95 | 35.93 | 40.06 | 46.67 | 53.63 | 57.68 | |
| F(%) | 9.97 | 9.90 | 10.79 | 12.03 | 14.02 | 16.12 | 17.33 | |
| 15 | Var(dB) | −80 | −75 | −70 | −65 | −60 | −55 | −50 |
| EHO (ms) | 413.30 | 413.29 | 413.29 | 413.27 | 413.26 | 413.24 | 413.20 | |
| iEHO (ms) | 52.70 | 51.90 | 56.42 | 65.28 | 77.31 | 92.16 | 95.10 | |
| F(%) | 12.75 | 12.56 | 13.65 | 15.80 | 18.71 | 22.30 | 23.01 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Correia, S.D.; Fé, J.; Tomic, S.; Beko, M. Development of a Test-Bench for Evaluating the Embedded Implementation of the Improved Elephant Herding Optimization Algorithm Applied to Energy-Based Acoustic Localization. Computers 2020, 9, 87. https://doi.org/10.3390/computers9040087
Correia SD, Fé J, Tomic S, Beko M. Development of a Test-Bench for Evaluating the Embedded Implementation of the Improved Elephant Herding Optimization Algorithm Applied to Energy-Based Acoustic Localization. Computers. 2020; 9(4):87. https://doi.org/10.3390/computers9040087
Chicago/Turabian StyleCorreia, Sérgio D., João Fé, Slavisa Tomic, and Marko Beko. 2020. "Development of a Test-Bench for Evaluating the Embedded Implementation of the Improved Elephant Herding Optimization Algorithm Applied to Energy-Based Acoustic Localization" Computers 9, no. 4: 87. https://doi.org/10.3390/computers9040087
APA StyleCorreia, S. D., Fé, J., Tomic, S., & Beko, M. (2020). Development of a Test-Bench for Evaluating the Embedded Implementation of the Improved Elephant Herding Optimization Algorithm Applied to Energy-Based Acoustic Localization. Computers, 9(4), 87. https://doi.org/10.3390/computers9040087








