1. Introduction
Estimating geometric relations between images is to find a transformation to associate images of the same scene but taken at different viewpoints [
1]. The estimation of the epipolar geometry, which is the intrinsic projective geometry between two views, can be found from different experimental setups. For instance, when a moving camera captures a static scene, or when a static camera views a moving object, or even in the case when multiple cameras capture the same scene from different viewpoints.
The importance of finding geometric relations becomes evident considering that it is a necessary task for many computer vision applications. For instance, geometric relations are needed for stitching together a series of images to generate a panorama image [
2,
3,
4]. Other applications that require the estimation of geometric relations are associated to camera calibration, where each camera pose and focal length are computed with their associated correspondences [
5,
6,
7,
8]; to 3D reconstruction systems, where incremental structure from motion is applied using geometric entities given by the epipolar geometry [
9,
10]; to the removal of camera movements, when the motion of an object is studied in a video [
11,
12]; to the process of digitizing the appearance and geometry of objects in 3D, when textures are used [
13]; to the control of robots, where homographies are used [
14,
15]; to topological mapping, where visual information is used [
16]; to the reconstruction of 3D flame with color temperature, where they perform an epipolar plane matching and epipolar line equalization [
17]; to the reality augmentation of buildings, where accurate homographies are needed [
18], among others [
19,
20,
21,
22].
Most of the approaches for computing geometrical relations encoded in the fundamental matrix and the homography are very complex and sometimes inefficient. The reason is that classical optimization techniques are used. For instance, different conventional methods to geometrical solutions have been proposed in the literature [
23,
24,
25,
26,
27]. However, despite their popularity, these conventional methods present a great weakness. The methods are very sensitive to the initial solution. If the initialization is far from the optimum, it is difficult for those approaches to converge to an optimal solution. Therefore, those classical optimization methods also have more chance of being entrapped in a local minimum.
To avoid the drawbacks of the aforementioned methods, yet preserving accuracy, heuristic approaches have been proposed. The most popular of such approaches is the Random Sample Consensus (RANSAC) [
28]. In the RANSAC algorithm, a minimum number of samples of experimental data are randomly taken. Then, for each sample, a model is proposed and evaluated according to a distance error to determine how well each model fits the data. This process is repeated until a number of iterations are completed. Finally, the model with the lower error (maximum number of inliers) is taken. Even considering that RANSAC is a robust and simple algorithm, it has some disadvantages [
29].
The RANSAC algorithm experiences troubles with a noisy dataset for a high multi-modality problem. For a better estimation under such circumstances, the RANSAC algorithm needs to be set appropriately. Two different parameters should be tuned: The threshold error
, and the number of samples
. However, tuning these parameters is not an easy task. The tuning should be done by taking into account the relationships between the model and the number of outliers. Usually, this error relationship is assumed to be Gaussian [
1]. If the assumptions fail, the RANSAC algorithm performs poorly, and two problems arises. A low
value may increase the accuracy of the model but it makes the algorithm sensitive to noisy data; while a high
value can improve the noise tolerance, but at the cost of false detections. On the other hand, a small sample set (
) can lead to a faster search, but to more inaccuracies; while a larger
may enhance accuracy, but at a higher computational cost.
Given the two main problems with RANSAC described above, explorations with recent approaches utilized to solve engineering problems that usually are ill-posed and complex can be done. These approaches applied modern optimization methods such as swarm and evolutionary algorithms, which have delivered better solutions in comparison with classical methods. The use of metaheuristics for estimating multiple view relations has been reported using the Harmony Search algorithm (HS) [
30,
31], and the Clonal Selection Algorithm (CSA) [
29]. Unfortunately, many parameters still need to be tuned using these metaheuristics. For instance, the CSA needs the tuning of the clonal size and the mutation rate along with the length of the antibody and others. HS, on the other hand, requires the pitch adjusting and harmony memory consideration rates, along with the number of improvisations.
Differently from previous metaheuristic approaches, in this work we propose the utilization of a metaheuristic called the Teaching and Learning Based Optimization algorithm (TLBO). By using the TLBO algorithm, we provide the method with a better-guided search while keeping the parameter tuning to a minimum. The TLBO algorithm only needs the number of iterations and the size of the population. Thus, the proposed TLBO-based estimator does not require the tunning of other algorithm-specific parameters. Further, since the proposed method accumulates information of the problem at each iteration it achieves better results than the purely random selection performed by the RANSAC algorithm. Experimental results validate the efficiency of the resultant method in terms of accuracy, and robustness.
The order of the remainder of the paper is as follows. The next section,
Section 2, describes the epipolar-geometry elements that the proposed algorithm estimates. Then,
Section 3, describes the TLBO algorithm as implemented in this work.
Section 4 depicts the proposed method.
Section 5 exposes the results; and finally,
Section 6 states the conclusions and future work.
2. Epipolar Geometry
In this work, we tackle the problem of estimating geometric relations from point correspondences. These relations are given by the fundamental matrix, , and the homography, . In this section, we first describe the operations to compute point matching, and then we show how to compute the fundamental matrix and the homography using the Teaching Learning-Based Optimization algorithm.
2.1. Feature Matching
The feature correspondence task aims to find the pixel coordinates in two different images I and that refer eventually to the same point in the world. The image-matching process consists of three main operations: (i) feature detection; (ii) feature description; and (iii) feature matching.
In the detection operation, we must find stable matching primitives. Choosing special points when matching images and performing a local analysis on these ones instead of looking at the image as a whole has the advantage of reducing the computational cost. There are many feature points detectors, some of these are: Harris Corners [
32], Scale Invariant Feature Transform (SIFT) [
33], Speeded Up Robust Features (SURF) [
34], Features from Accelerated Segment Test (FAST) [
35], Binary Robust Independent Elementary Features (BRIEF) [
36], Oriented FAST and Rotated BRIEF (ORB) [
37] and others. In this work, the SURF method has been employed, since its complexity is
, and the method is invariant to illumination, scale, and rotation. The SURF detector has been demonstrated to be effective for both, high- and low-resolution images [
38].
In the second operation, feature description, the previously detected features in I and are described with a compress structure. The descriptors of the image features can be computed with some algorithms including SIFT, SURF, BRIEF along with others. In this work, the SURF descriptor is employed. The SURF algorithm computes a 64-element descriptor vector to characterize each feature point. When the SURF detector and descriptor are applied to the images I and , two sets of feature points described by its own vector are obtained, and , respectively.
In the final operation, feature matching, the descriptor of each feature within the first set is compared with all other descriptors in the second set using some distance calculation. In this work, the Euclidean distance is used to compare descriptor vectors from the first image with descriptors from the second image to build pairs of corresponding points; the match is selected as the one with the shortest distance. After these three operations, N point matches are found, and a set with matches is generated. For this process, an erroneous estimation of matched points may emerge on different sections of the images. This is because the process does not discriminate with complete certainty one point from another.
The noisy dataset U obtained with the above process is the input of the algorithm to compute either the fundamental matrix or the homography. We now describe these geometric relations to later explain how the TLBO-based method computes them considering the epipolar geometry.
2.2. Geometric Entities of the Epipolar Geometry
Given a set of matched projected points, geometric relations can be estimated. In this work, we estimate the fundamental matrix and homography that encapsulate the intrinsic projective geometry between two views.
2.2.1. Fundamental Matrix
Let there be a set of
N matched points
between two images
I and
. The 2D image positions of these points are denoted in homogeneous coordinates as
in the
I image, and
in the
image. These positions are related by the epipolar geometry as follows:
where
is the fundamental matrix, and can be computed with a set of eight good matches as described in [
1,
39]. The epipolar geometry represents the intrinsic geometry between two-views. It is independent of the scene structure and only depends on the camera’s internal parameters and relative localization between the cameras
. The fundamental matrix
is the algebraic representation of this intrinsic geometry, called epipolar geometry.
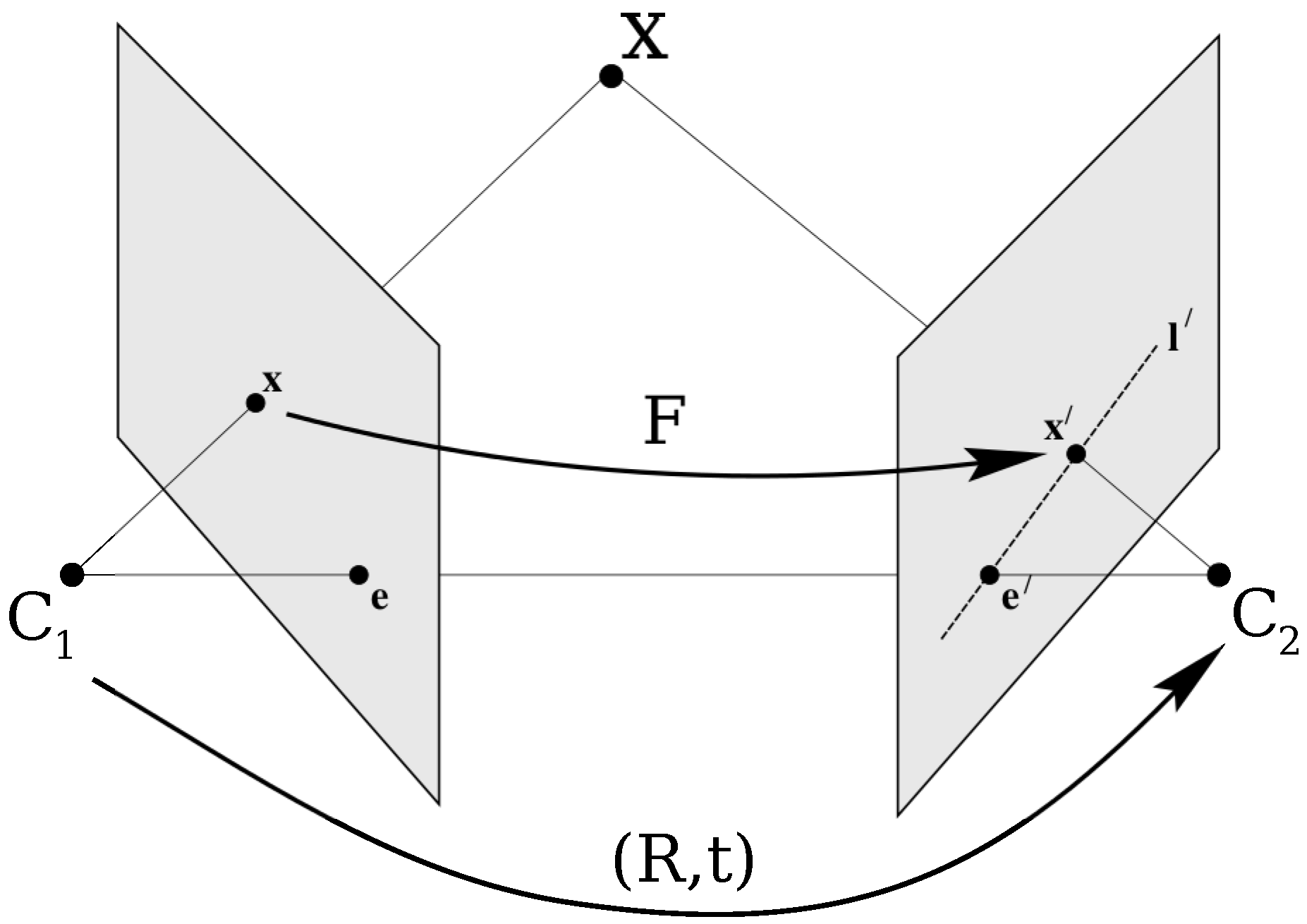
The epipolar geometry can be used to validate the match
, since it constrains the position of the points
and
. As shown in
Figure 1, the epipolar line at the point
, in the second image, is the intersection of the epipolar plane passing through the optical centers
and
and the point
within the plane of the second image. If the matrix
and the point
in the first image are known, the epipolar line in the second image where the point
is restricted to be, is given by
. Similarly,
specifies the epipolar line in the first image that corresponds to the point
in the second image. This epipolar constraint that restrict the positions of
and
is used in the proposed method to evaluate candidate solutions by their mapping accuracy.
Given a matrix
computed from noisy point correspondences, the quality of the estimated fundamental matrix is evaluated using the epipolar lines. This is done by considering the distance between the points and the epipolar lines to which they must belong. Considering the notation
, the distance
between the point
and the line
can be computed as follows:
Likewise, denoting
, the other corresponding distance can be calculated as:
To evaluate
, a mismatch error
produced by the
i-correspondence
is defined by the sum of squared distances from the points to their corresponding epipolar lines as follows:
2.2.2. Homography
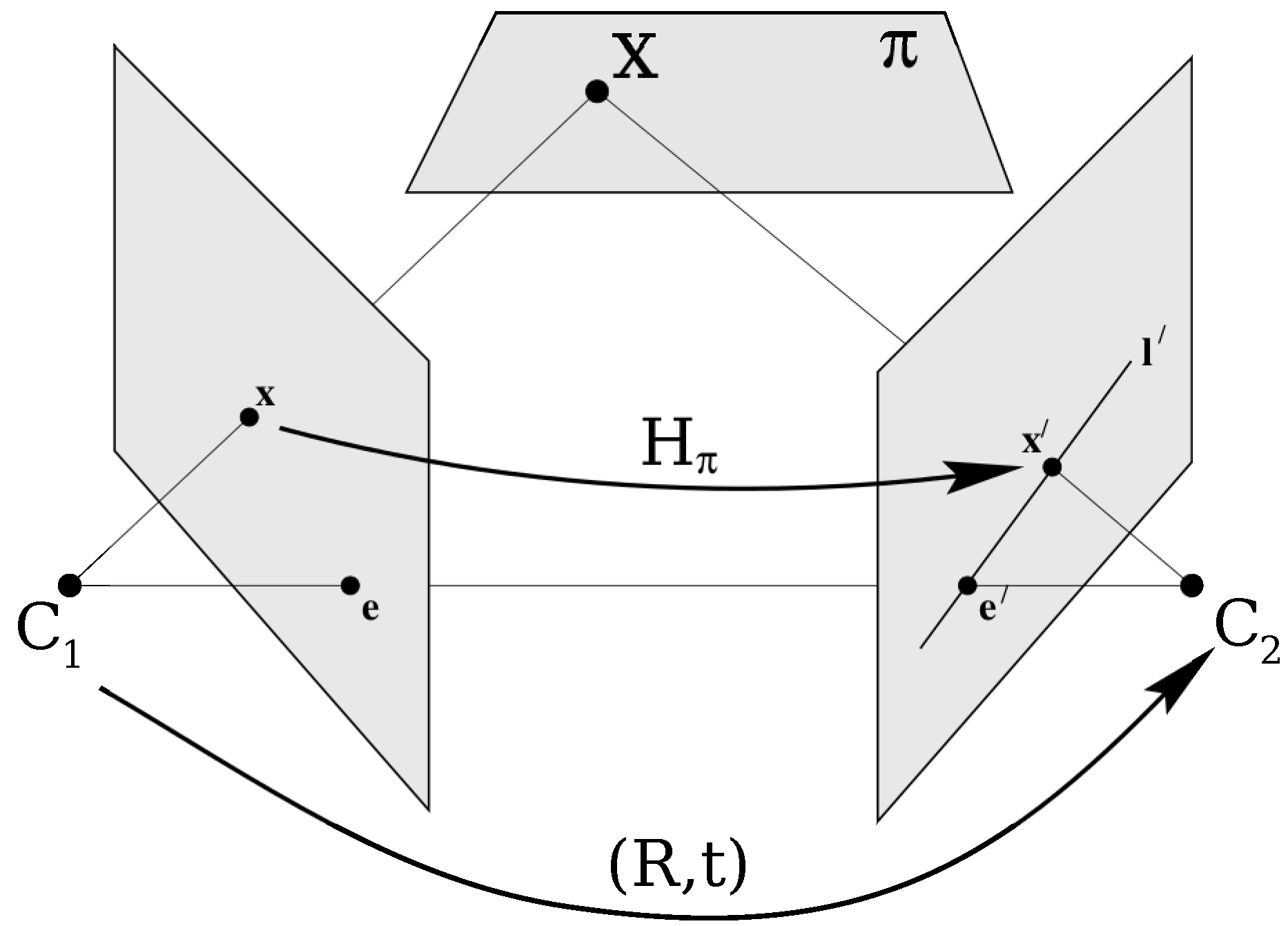
If the match points are said to be in a plane
, a homography can be computed. As shown in
Figure 2, two perspective images can be geometrically linked through a plane
of the scene by a homography
. The homography
is a projective transformation, and it relates matching or corresponding points belonging to the plane
that is projected into two images by
or
. To find the homography given by two different views, a linear equation system can be generated from a set of four different corresponding points (matches). Then the system can be solved analytically [
1].
The computed homography can be evaluated to obtain an accuracy measure. This quality measure can be computed by considering the distance (usually the Euclidean distance) between the position of the point found with the
matrix and the actual position of the projection of the observed 3D point. Thereby, the
i-correspondence
will produce a mismatch error
. This error is computed using the sum of squared distances from the estimated point positions to their actual location as stated in following equation
Having described the epipolar geometry, and how a candidate fundamental matrix and homography can be evaluated, we now depict the TLBO algorithm as implemented in the proposed approach.
3. Teaching and Learning Based Optimization Algorithm
The procedure of the TLBO algorithm is based on the metaphor of the teaching and learning processes. First, a population of M students or solutions, S is randomly initialized within the search space. Thus, the initial population is . Each individual , is a real-valued vector with D elements. In the metaphor, D represents the number of assigned subjects a student has, therefore D is the dimension of the problem.
Once the population is initialized the algorithm proceeds to execute the teaching and learning stages. The aim of these two consecutive stages is to enhance the population by modifying individuals. Within the teaching stage, the TLBO algorithm attempts to increase the knowledge (quality) of the population by helping students individually. In the learning stage, on the other hand, the interaction between students is promoted to enhance the quality of the students. The algorithm is carried out until a certain number of iterations.
In the teaching stage, the knowledge transfer is performed by the teacher. Hence within this stage, the individual with the highest fitness value is appointed as the teacher . The TLBO algorithm aims to enhance every other student by moving its position in the teacher direction.
This is done by using the mean value of current population. The locus of student
is updated by:
In the above equation, is a real random number, and the teaching factor, is also randomly decided. If has a better quality, i.e., a better fitness value, is replaced by in the population.
As stated by Equation (
6), the improvement of the student is affected by both the comparison with the teacher knowledge and the mean quality of all students. The TLBO capabilities of exploration and exploitation are granted by the factors
r and
. For instance, for the settings of
and
r near to 1, individuals tend to approximate the teacher. This contributes to the exploitation of the search space surrounding the teacher. Conversely, more exploration in proportion with the
r value is performed when
.
Finally, during the learner stage, a student
tries to improve its fitness value (knowledge) by interacting with an arbitrary student
. If
is better than
,
is moved towards
accordant with:
If
is not better than
,
is moved away from
accordant with:
Similar to the teacher stage, if has a better fitness value, is replaced by in the population.
The TLBO algorithm is a powerful metaheuristic. It solves complex optimization problems yet remaining simple and easy to implement. Therefore, several engineering and scientific applications using this metaheuristic have been published [
40,
41,
42,
43]. Differently from the previous work in [
44,
45,
46], this paper proposes a novel application for the TLBO algorithm. Instead of searching for image patterns like the work in [
44,
45] or detecting vanishing points [
46], in this work the TLBO algorithm is implemented for the novel task of estimating the fundamental matrix and homography. The work in [
46] deals with the problem of vanishing points detection. While this work tackles the problem of geometric relations encoded in homographies or the fundamental matrix. Although these two problems are different, they can be solved by sampling-based methods such as RANSAC. RANSAC-like methods find models by randomly sampling the search space. Vanishing points can be found by modeling Manhattan frame rotations using sampled image lines. Quite different, the homograpy or fundamental matrix is modeled using RANSAC by sampling candidate matched points. Metaheuristics like the TLBO algorithm also sample the search space, although this sample is not blind but guided by the objective function. In this paper we demonstrate the benefits of metaheuristics over pure random procedures such as RANSAC.
Algorithm 1 depicts the simplest procedure for the process described in this section, which is used in this work for the optimization task of estimating the fundamental matrix and homography as now explained.
| Algorithm 1: Simplest form of the Teaching–Learning-Based Optimization (TLBO) algorithm. |
![Computers 09 00101 i001 Computers 09 00101 i001]() |
4. Epipolar Geometry Estimation Using Tlbo
In this section, we depict the utilization of the TLBO algorithm to find multiple view relations, which is a novel task for this metaheuristic. For a metaheuristic to work properly, three different components must be defined: The search space organization, the individual representation, and the objective-function definition. We now describe these elements.
4.1. Search Space
To generate the search space where the TLBO algorithm optimizes, two gray-scale images are processed to find key-features with its corresponding descriptors as described in
Section 2. Then, the descriptors are matched using the Euclidean distance in order to find matching pair points
. Finally, every pair is added in a set
, where
M is the number of matches found. For the proposed algorithm to work, it is assumed that the tentative matches in
U are consistent with at least one geometric relation model, i.e., a fundamental matrix or a homography. In other words, the two input images are supposed to view the same scene from different viewpoints.
4.2. Individual Representation
In the TLBO-based estimation process, each candidate student
S encodes either a homography
, or a fundamental matrix
. In order to construct a candidate solution or individual
that encodes a homography, four indexes are selected from the set of correspondences
U. Likewise, in the case of the fundamental matrix, eight indexes are selected from
U. A transformation from indexes to either
or
is done according to Ref. [
1].
4.3. Objective Function
In this work, the problem to solve consists in finding the parameters of or through a set of M different noisy correspondences. To find a solution using the TLBO algorithm, this problem is treated as an optimization procedure.
The proposed method implements the TLBO to generate samples or candidate solutions based on information about their quality, rather than randomness as in the case of RANSAC-like algorithms. In the traditional RANSAC method, the classical objective function evaluates only to the number of inliers. Distinctively, we improve results by using a different objective function to accurately evaluate the quality of a candidate model.
The objective function proposed for the TLBO-based estimator uses not only the number of inliers, but also the residual error. Both values are combined into a simple quotient by the following expression:
where
represents the quadratic errors
or
(see
Section 2) produced by the
jth correspondence considering the candidate transformation
or
, whereas
is defined as follows:
Therefore, the maximization of implies to obtain the candidate solution S having both the highest number of inliers and the lowest residual error, simultaneously. The threshold allows us to assign a number of inliers to a particular candidate solution. When a candidate solution does not map points correctly, the overall quadratic error increases, and the number of outliers must increase as well. Within this work, we have chosen empirically.
The objective function evaluates the quality of a candidate transformation. Guided by the values of this objective function, the set of encoded candidate solutions are modified by using the TLBO process so that they can improve their quality as the optimization process evolves. We now describe the whole process proposed in this work.
4.4. Tlbo for Epipolar Geometry Estimation
The presented approach can be summarized as shown in
Figure 3. First, a preprocessing step is carried out to construct the search space. Then, within the initialization procedure of the TLBO algorithm, candidate solutions are randomly generated. After that, the teaching and learning processes of the TLBO algorithm are iteratively executed to improve the quality of the population. Finally, at the end of the predefined number of iterations, the best individual (
) is selected as the final solution. This solution is used to filter out false matches, i.e., matches not respecting the epipolar restriction. Then, the fundamental-matrix or homography is estimated using all the points in the subset of inliers.
5. Experimental Results
In this section, results of the proposed TLBO-based estimator are reported. A comparison with other approaches is also carried out. The experiments are performed on real images, and the comparisons with the following five different methods: RANSAC as the most recent implementation in OpenCV, MLESAC as implemented in the last version of the Matlab vision toolbox, CSA-RANSAC as implemented in [
29] with the same proposed parameters, and an implementation using a Genetic Algorithm (GA), and the Differential Evolution approach (DE) with the same search space and objective function as the TLBO-based estimator.
Images for experimentation are shown in
Figure 4,
Figure 5,
Figure 6 and
Figure 7 and 12. Room_1 (640 × 480) and Room_2 (640 × 480) belong to the CIMAT-NAO-A dataset, which was acquired with a NAO humanoid robot. The dataset contains 399 different images with blur effects and low textures. Street_1 (1241 × 376) belongs to the Kitty dataset which is usually used for autonomous driving experiments [
47]. Street_2 (1348 × 374), on its part, is taken from the work in [
48]. Calibration_rig (690 × 470), Park (720 × 450), and Corridor (370 × 490) are taken from a repository of free images. Finally, Book_1 (671 × 503) and Book_2 (671 × 503) were capture by a generic cellphone camera. The whole set of experiments were carried out on a 2.80 GHz Intel Core i7-7700HQ CPU. The TLBO-based estimator was implemented in C++. Image preparation tasks such as Key-point detection and description were performed by the OpenCV library.
The parameter setup for the metaheuristic approaches, i.e., the TLBO, GA and DE were chosen empirically as usual for metaheuristic methods. The setups are shown in
Table 1,
Table 2 and
Table 3. To perform a fair comparison all metaheuristics were set to execute the same number of objective function evaluations. This particular setting forces the metaheuristics to sample the search space to the same extent. This allows a fair comparison. On the contrary, if a metaheuristic executes more objective function evaluations it gathers more information about the problem, thus having more chances to find a better solution. To compute the objective function, the
parameter was empirically determined to 5. All parameters were fixed for the whole set of experiments.
The parameters for the non-metaheuristic methods, i.e., RANSAC and MLESAC were set as follows. Both algorithms need a maximum distance from a point to an epipolar line, and the number of sampling attempts. For the two approaches, the maximum distance was set to 5 pixels similarly to the objective function proposed in Equation (
10), and the number of samples equal to the number of objective function evaluations for the metaheuristics estimators.
To show the capabilities of the proposed method for the task of estimating the fundamental matrix
, we present
Figure 4 and
Figure 5. The proposed method also estimates the homography
, as shown by the results of
Figure 6.
To quantitatively test all methods and compare results, three values are studied: the inlier number , the error , and the residual error, . We first describe the number and the error. Then, results for the residual error are presented.
5.1. Number of Inliers and error
As described in [
29,
31], the inlier number
is used to express the number of detected inliers that are stored in the set
. The
error, on the other hand, is used to provide a quantitative measure for the quality of the candidate geometric relation.
is assessed from the standard deviation of only the inliers. Thus, the error
is computed as follows:
where
is the quadratic error produced by the
i-th inlier. The term
corresponds to
or
as described in
Section 2, and represent the errors produced by the
ith inlier considering the final fundamental matrix
or homography
, respectively.
In three out of four experiments, the TLBO algorithm achieved the smallest error in comparison to the other methods. It was only in the case of the Room_1 image that the GA-based estimator outperformed slightly the TLBO algorithm in terms of the error by 0.01. However, The TLBO algorithm found a greater number of inliers, i.e., matched points within 5 pixels distant from its corresponding epipolar line.
The different performance of each method is linked with its approach to solve the problem. The RANSAC and MLESAC perform a random sampling within the search space, while the metaheuristic-based estimators carried out a guided search. RANSAC-like methods try many different random subsets of the corresponding point matches, and estimate the model using this subset to solve the system. Finally, the best subset is then used to produce the final model that will filter out wrong matches. To achieve this, RANSAC-based methods perform a model computation from point correspondences, and compute an error to rank and compare subsets. The TLBO algorithm, on the other hand, leverages of this error computation to guide the search in order to perform a better space search.
In the experiments, all the methods start with the same set of point correspondences. This set contains both good and bad matches. The non-metaheuristic methods are constrained to sample the search space an equal number of times as the metaheuristic approaches. Given that the former methods are purely random, the less they sample the space, the greater the probability of giving a wrong model. In the case of the metaheuristic approaches, the capability of finding an accurate model resides in the exploration and exploitation capacities of the method. Each metaheuristic can be tuned to modify the exploration and exploitation of the search space. The advantage of the TLBO algorithm resides in that it has fewer parameters to tune, still keeping its accurate performance.
To further show the performance of the proposed method as compared to other approaches, the residual error is computed for the fundamental matrix estimation, and a comparison of correct matched points using the homography is perform.
5.2. Residual Error
Accurate estimation of epipolar entities is important for multiple applications. For instance, camera calibration and 3D reconstruction rely on a nonlinear cost function defined from the relationship between the projection matrices and fundamental matrices. Vision-based control of robots and global motion compensation depend on homography transformations between consecutive frames. Since epipolar correlations are determined from the matched points, these applications strive when only a few points are available. Lack of data is present when there are appearance ambiguities, multi-plane scenes, and dominant dynamic features instead of static features. To show the capabilities of the proposed approach to accurately estimate epipolar entities with few data, we compute the residual error,
:
where
is the distance in pixels between point
and line
. The error is the squared distance between an epipolar line and the matching point in the other image, average over all
N matches. This particular error is not minimized directly by any of the algorithms.
For the experimental procedure, each pair of images is preprocessed as in
Section 4 to found a set of noisy matched points
U. Then, a number
n of matched points are chosen randomly from
U. Finally, the fundamental matrix is estimated, and the residual error computed. The residual error is evaluated over all
N matched points, and not just the
n matches used to compute
. The set of images for experimentation is shown in
Figure 7.
The aforementioned procedure was repeated 100 times for each value of
n and each pair of images. The average residual error is plotted against
n in
Figure 8,
Figure 9,
Figure 10 and
Figure 11. Likewise, this values are shown in
Table 6,
Table 7,
Table 8 and
Table 9. This gives an idea of how the different algorithms behave as the number of points increases.
As shown in
Figure 8, the error for the Calibration rig is the smallest over the whole set of experiments. This is because the matched points were known precisely. As indicated in
Table 6, however, the TLBO algorithm attained a better error in more cases than the rest of the methods. From these results, it can be said that for this experiment a metaheuristic approach guided by the objective function performs better than a purely random procedure.
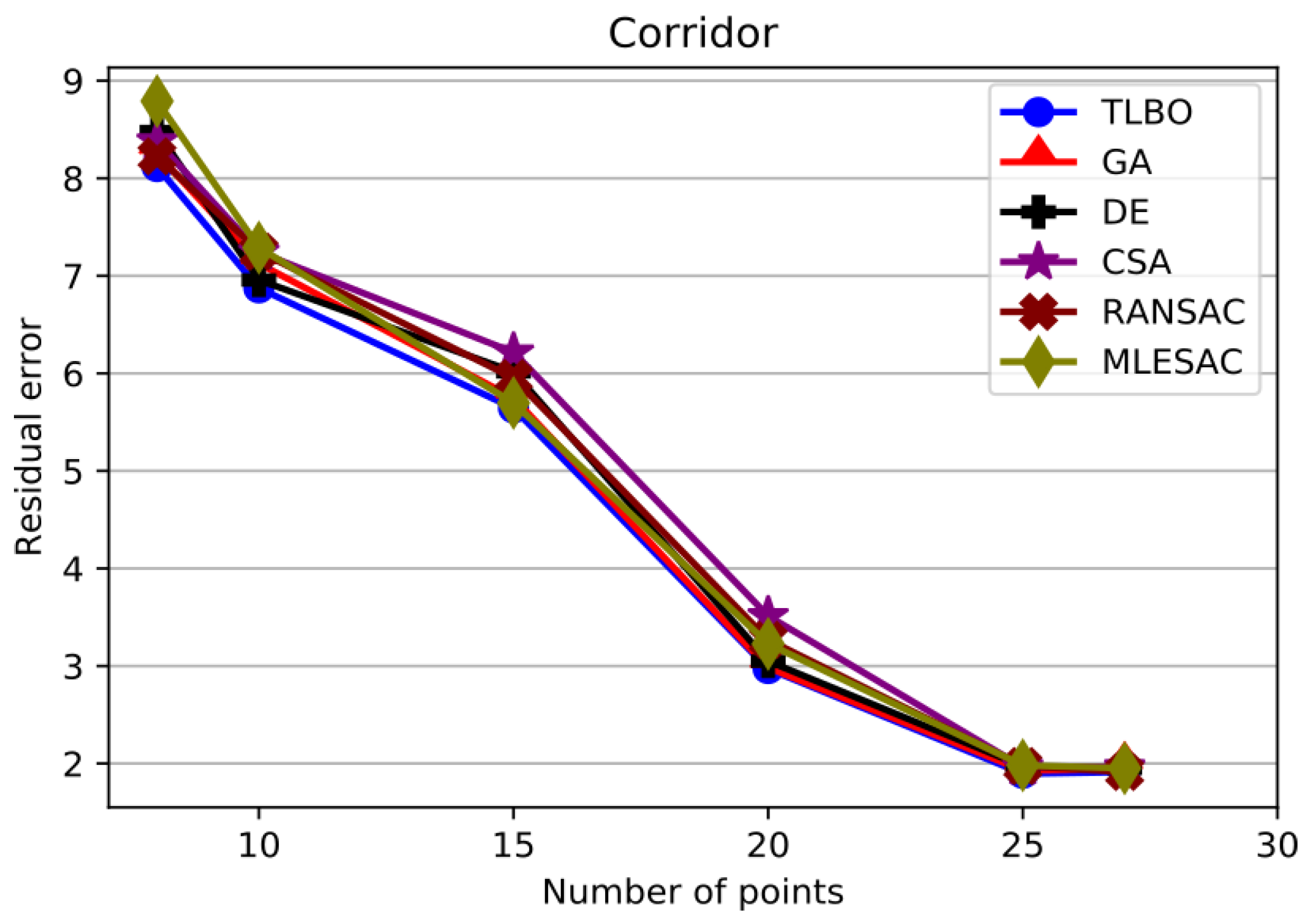
When images get more complicated, the TLBO algorithm outstands from the rest of the methods. For the Park image shown in
Figure 9, for instance, the proposed method excels with a smaller error for each value of
n. The same is the case for the Corridor image as shown in
Figure 10.
Results from the Book image are depicted in
Figure 11. In this case, the TLBO algorithm attained a better error overall. Only for
n = 15 it was outperformed slightly by the GA-based estimator by 0.007. The cause for the different performance is the searching procedure each algorithm performs. RANSAC, and its variation MLESAC, sample the data randomly to choose the model with the most votes. The TLBO algorithm, on the other hand, guides the search by minimizing an objective function and performing particular operations in the candidate solutions to move them towards the best solution. This permits the TLBO algorithm to achieve a smaller error with less sampling executions.
An accurate estimation of a fundamental matrix or homography is also used to filter out false matches. Regarding the homography estimation,
Figure 12 depicts results for the computation of the homography. As shown in the figure, the TLBO algorithm found 103 true positive matched points, while the other methods found either less true points or more false positives. As can be concluded by the experiments, the TLBO algorithm is and efficient metaheuristic for estimating epipolar entities.
The comparison experiments with the whole set of methods involved the task of finding the smallest error given the same threshold (maximum distance in pixels for a point to be considered an inlier), and the same possibility of space search. Feature detection was performed to sub-pixel accuracy, which allowed us to compare in this scale. As shown from the results, the TLBO-based estimator outperformed the rest of the methods overall. The reason for this outcome lies in the capabilities of the TLBO. The proposed method does not require many sampling executions because it explores and exploits the search space in a metaheuristic fashion. It also optimizes over the search space guided by a detailed objective function.
Since we constrained the number of samples every method can perform, the RANSAC-like methods performed poorly. This is because, ideally, the threshold should be computed assuming the measurement error Gaussian with zero mean, and the number of samples according to the proportion of outliers. Even when the MLESAC algorithm differs from RANSAC in the error definition, it adopts the same sampling strategy as RANSAC to generate putative solutions, thus it suffers if the number of samples is set to low.
Another reason for the proposed method to outperform the RANSAC-like methods is the definition of the objective function. RANSAC chooses the solution that maximizes the number of inliers, and MLESAC chooses the solution that maximizes the likelihood. The proposed method, on the other hand, is guided by an accurate objective function that takes into account both the number of inliers and the residual of the quadratic error.
Regarding the other metaheuristics, the TLBO algorithm performed better in comparison to the DE and CSA methods. The GA-based estimator outperformed slightly the TLBO algorithm in 3 different cases. However, given that the objective of this work is to present a method that accurately estimates epipolar entities without the need to adjust various parameters for different kinds of images, the proposed approach achieved this task better than the other metaheuristic methods. Differently from the other metaheuristic-based estimators, the TLBO algorithm does not need the tuning of any algorithm-specific parameters.
6. Conclusions
This work tackles the problem of computing the fundamental matrix and homography using the TLBO algorithm. The task of finding multiple view geometric relations is a novel application of the TLBO metaheuristic. The proposed approach is a robust method for estimating the epipolar geometry in spite of poorly matched points. The TLBO-based solution computes the best model for the homography or fundamental matrix, and at the same time it filters out wrong point correspondences. Instead of being purely random as RANSAC-like methods, the proposed approach improves the computed solution by performing a metaheuristic search by using the TLBO algorithm.
Differently from the pure random strategy that the RANSAC algorithm performs, the proposed approach, guided by the TLBO algorithm, builds iteratively new potential solutions considering previously generated candidate individuals. The method takes into consideration the quality of these solutions. Furthermore, the proposed method uses a better objective function.
To certainly evaluate the quality of a candidate model (solution), the used objective function uses both the number of inliers and the residual error. As a result of this approach, a considerable reduction of the number of iterations in comparison with RANSAC is achieved, still maintaining the robustness capability of RANSAC. Future work can be directed towards the metaheuristic solution of the non-linear cases of the epipolar geometry.