Abstract
In the pedagogical process, a serious game acts as a method of teaching and upbringing, the transfer of accumulated experience and knowledge. In this paper, we describe an interactive serious programming game based on game-based learning for teaching JavaScript programming in an introductory course at university. The game was developed by adopting the gamification pattern-based approach. The game is based on visualizations of different types of algorithms, which are interpreted in the context of city life. The game encourages interactivity and pursues deeper learning of programming concepts. The results of the evaluation of the game using pre-test and post-test knowledge assessment, the Technology Acceptance Model (TAM), and the Technology-Enhanced Training Effectiveness Model (TETEM) are presented.
1. Introduction
Ubiquitous learning is an emerging educational paradigm that is based on digital content, mobile devices, smart environments, and wireless communication to provide teaching–learning experiences to learners at anytime, anywhere, and in any way [1]. Ubiquitous learning allows students to break beyond the traditional classroom-based setting of formal education and to interact with different computing devices and digital technologies in a blended way. An important enabler of ubiquitous learning is serious games, i.e., games whose primary purpose transcends pure entertainment [2]. Specifically, educational serious games primarily aim at education rather than entertainment [3]. They have been shown to promote critical thinking and strategic and logical skills in computer-supported learning environments [4].
In pedagogy, serious games are used as an attractive way to transfer experience and knowledge to a learner [5]. The implementation of serious games as a part of teaching curricula leads to the gamification of education and instruction, which is considered to be appealing and engaging among the learners [6,7]. Gamification is designed to make the necessary routine fascinating, whether it is the study of a large amount of information, but at the same time leaving the person in his/her reality, by himself/herself, allowing him/her to improve the skills necessary for this particular subject. The game and game technologies in pedagogical practice depend on the creation of certain conditions for achieving goals, the modeling of a special game reality with its internal laws (role-playing games, business games, organizational activity games, etc.). Games complement traditional forms of education and contribute to the activation of the learning process and the successful implementation of collaboration-based learning [8] in practice. Unlike in traditional teaching resources and digital media, educational games provide a virtual space for learners, in which learners can practice and actively engage in the subject of learning without being subject to the stress typically associated with formal learning [9].
Games have a strong emotional impact on students and can help form many skills and abilities: first of all, communication skills, the ability to work in a group, to make decisions, and to take responsibility for oneself. Serious games combined with other educational technologies increase the effectiveness of programming education. Recent studies claim that learning outcomes and learner engagement are improved when using digital game-based learning versus traditional teaching methods [10]. In contrast to entertainment-only games in general, pedagogy-oriented games have an essential feature—a clearly defined goal of teaching and corresponding pedagogical results that can be substantiated, singled out in an explicit form, and are characterized by an educational and cognitive orientation [11]. The reasons why students love computer games can be summarized as follows:
- computer games represent fantasy and follow a simple principle: win or lose with instant results [12];
- games use aesthetic modeling and recognizable features to grab the learner’s attention with visual feedback [13];
- games are an interactive environment and provide complete immersion in it [14];
- games open up different ways to solve problems [15].
The multi-aspectual nature of computer games creates an opportunity to develop creativity, technical skills, and collaborative work experience [16]. Moreover, they have been demonstrated to positively affect students’ learning outcomes [17,18].
Several studies claim that students usually prefer playing a serious game over traditional pedagogical methods in several areas of science, technology, engineering, and mathematics (STEM) education (see, e.g., [19] for a comprehensive case study for mathematics). Certain qualities of educational games can help increase student interest: a challenge that encourages the learner to explore a specific topic and bring knowledge and skills to perfection because only in this case can one go to the next level. In particular, programming education for non-STEM students should use enjoyable game-based tools to overcome their anxiety, increase their engagement and motivation [20,21], and support computational thinking [22]. There is no single definition of serious games. The disagreements and discrepancies among definitions of serious games lead educators, tutors, and mentors into confusion when they try to figure out which games should be used for effective teaching. The general point of view is that:
- a learning model is built into such games;
- they have content that the process of playing the game teaches;
- learning assessment can occur within the gameplay itself or outside it.
Educational serious games provide educational materials, by choosing which, the student himself/herself chooses the pace of learning. In most educational serious games, the cognitive and visual load of students is realized through the computer (or smartphone) screen. The game is an interface in which one or more loads are constantly increasing, each time increasing the level of difficulty and thus keeping the participants in suspense. In some games, there are high cognitive loads, since during the game the student must understand how the storyline develops and analyze the situation [23]. Such examples of mobile app-based serious games for education include math games [24], musical games for preschool children [25], digital games for teaching young children about programming [26], a gamified informatics course [27], improving children’s procedural abstraction thinking skills in Scratch [28], a collaborative gamified quiz [29], game for fighting child obesity [30], or a serious game for carers of dementia patients [31]. For a systematic review of open educational games, see [32,33]. Each game is characterized primarily by a specific game context (the inner “world” of the game), which is built and maintained using special means, and assumes the presence of a set of positions and roles of the participants and, therefore, a controlled communication system, as well as special mechanisms that allow for generating game actions.
Our goal is to design, implement and launch an application designed for mobile devices, which will simultaneously visualize: the course of action of an algorithm (input data, change of data state, output data) and the source code responsible for these changes. The contribution of this paper is as follows: (1) providing a design of a mobile app implementing a serious game aimed at teaching how to solve common algorithmic problems in the JavaScript programming language, and (2) the evaluation of the game using the Technology Acceptance Model (TAM) and Technology-Enhanced Training Effectiveness Model (TETEM).
The organization of the remaining sections of this paper is as follows. Section 2 discusses the pedagogical and methodological backgrounds. Section 3 describes the game scenario, the design of gamification, and the implementation of the app. Section 4 presents the evaluation results. Section 5 presents the discussion. Finally, Section 6 presents conclusions and discusses future work.
2. Pedagogical and Methodological Backgrounds
In the traditional model of teaching programming at university [34], the leading role in the lecture belongs to the teacher. From him/her is required not only good knowledge of the training material but also the ability to put it to the audience: to present it in an interesting, figurative, and clear way. The most common way to visualize lectures is to prepare demonstration materials (presentations in MS PowerPoint). Using MS PowerPoint presentation materials allows for visually presenting the studied material in the form of static text or graphic information. Interest in the subject increases if, along with the systematic presentation of the material, including in the discipline program, the lecturer shows his understanding of the perspective on the development of the subject, shares the experience of his scientific developments, and can refer to the history and reasons that prompted the study of this or a different phenomenon.
The methodological backgrounds for the application of serious games for education are Game-Based Learning (GBL) [35,36], simulation gaming [37], and mobile microlearning [38]. Here, mobile microlearning means that the educational content is created for the small screens of smartphones, and is structured in small, self-contained bits of knowledge, which can be assimilated by students in no more than five minutes. The digitalization of information directly affects and modifies human mental activity in the process of education. The problem of the influence of a computer on human mental activity can be considered based on three main approaches established in psychology [39]: substitution theory, complement theory, and transformation theory. Substitution theory identifies the work of a computer program with the process of human mental activity. Complement theory is based on the theory of thinking, according to which a computer significantly increases a person’s ability to process and perceive information. Transformation theory claims that the computer transforms human mental activity, and contributes to the emergence of new forms of mediation. The interactivity of a program is its ability to conduct a “dialogue” with the user, i.e., to respond to user-entered requests or commands. A feature of human–machine interaction is its belonging to a special type of communication called interaction. Interaction involves not only the exchange of information between the participants in the communication but also their joint activity. The system immediately reacts to commands and user requests (feedback), and allows the latter to determine and, if necessary, adjust their further actions.
Current approaches to enriching the traditional lecture with elements of entertainment and games include embedding computation in physical objects like cubes, etc. [40], developing tangible interfaces for teaching children about robot programming [41], or gamified quizzes and puzzles [42]. However, these games usually focus on young school children and teens, whereas they are considered as too simplistic by young adults such as university students. Our novelty is the development of a serious game for mobile devices, which is aimed at teaching university students how to solve common algorithmic problems in the JavaScript programming language, while simultaneously visualizing: the course of action of an algorithm (input data, change of data state, output data) and the source code responsible for these changes.
3. Materials and Methods
3.1. Pedagogical Models
In this paper, we have adopted a model of game-based learning from [43] (see Figure 1). When developing an interactive game, we followed the guidelines for integrating gamified learning in the classroom [44] as follows. First, we clearly define the pedagogical objectives, which are to acquaint the students with introductory concepts in programming. Next, we determine the technological competency of our target students. Finally, we identify the content to teach.
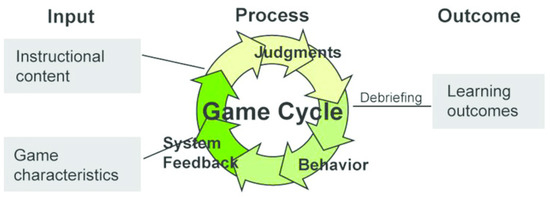
Figure 1.
Model of game-based learning (adapted from [34]).
Our pedagogical model of the learning process based on the serious game (Figure 2) is based on 5 key elements, which interact in achieving a sustainable serious outcome while keeping the students engaged and motivated. The model starts with the element representing the pedagogical aims, i.e., the learning of the JavaScript (JS) programming language. Other elements such as adaptive learning [45] are used to support the achievement of this aim. Adaptive learning ensures the adaptiveness of learning through feedback, which constructs an individual learning path for each learner. As a result, gaps in knowledge are closed and the difficult topics are encouraged to be repeated for rooting the acquired knowledge. At the same time, adaptive learning ensures that the well-understood topics can be covered faster and without unnecessary repetition. Game mechanics are used to support such reinforcement of desired learning behavior in an engaging and motivating way. The effectiveness of the pedagogical process is evaluated using the TAM and TETEM, which allow for evaluating the effectiveness of the game-based learning process. Finally, in line with the current trends for interdisciplinarity and woke pedagogy [46], the digital game is placed within the context of ecology and sustainability issues, which promotes and encourages green thinking [47] to raise awareness of societal issues and provide diversity in education that transcends the direct needs of the programmer profession. Furthermore, the game, which can be played remotely and anytime on a smart user device (smartphone), fits well into the concept of 21st century online education [48], which is going to dominate the landscape of education in the post-COVID-19 world.
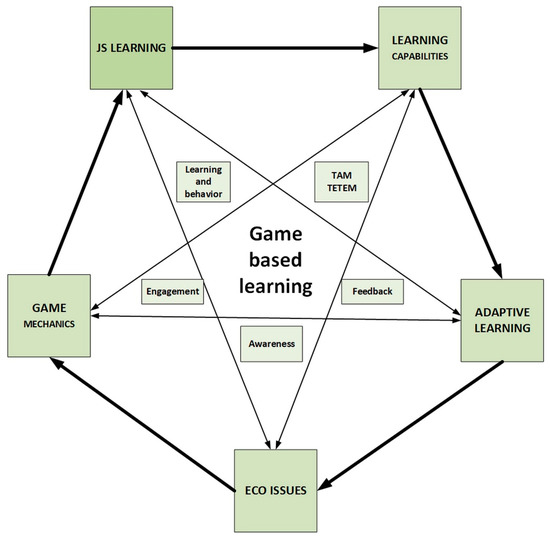
Figure 2.
The pedagogical model of the learning process-based on serious game. TAM is Technology Acceptance Model. TETEM is Technology-Enhanced Training Effectiveness Model.
3.2. Design of Game Scenarios and Game Implementation
The game was developed by adopting the gamification pattern-based approach [49]. The designed interactive game has four major structural blocks: an authorization block (entering the game, choosing a topic), a game mechanics block (instructions, game rules), a learning block (user interface), and a game situation assessment block (analysis and evaluation). A schematic representation of the game flow is given in Figure 3.
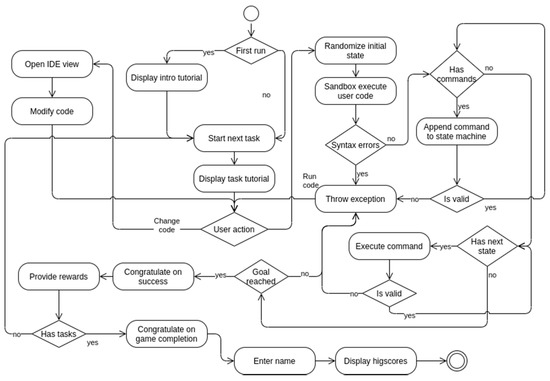
Figure 3.
Schematic representation of the game flow. ◯ is the start of the game. ◎ is the end of the game.
The story of the game is based on environmental awareness of ecological problems occurring in everyday life, while the direct (not-serious) aim is the prevention of city pollution in daily activities. The user acts as a commercial advisor having to solve puzzles to build an industrial quarter for the city to start generating income while avoiding excessive pollution, which decreases the game score. Successful implementation of programming-related tasks allows for increasing city revenue and the game score. The game is available online at http://algo-js.usz.edu.pl/.
3.3. Gamification of Programming Algorithms
Many studies [50,51] claim that problems in programming education arise due to the complexity of abstractions and concepts of programming such as variables, arrays, functions, or loops. To overcome this barrier for learning programming, the principles of visual programming, which focus on the use of visual abstractions corresponding to programming abstractions [52], are adopted. The selection of topics follows the list of suggested topics of an undergraduate computer science course by ACM Computing Curricula [53].
The concepts that our system supports are common programming algorithms: linear algorithms, branching (conditional) algorithms, iterative algorithms, search and sorting algorithms, recursion, tree traversal, and graph algorithms. We describe the gamification of these algorithms in more detail in the following subsections.
3.3.1. Linear Algorithm
Linear algorithms are algorithms which do not involve branching, i.e., there are no conditional statements. Examples of such algorithms are recipes, which describe how to complete a task by executing several steps. The case for such an algorithm is finding an exit through a maze of streets in a city. The idea is represented by the following image from the game’s interface (Figure 4). Each command is evaluated and visualized in a loop. The algorithm finishes the execution if: the client is found (or the exit is reached), or the car object makes an invalid move. The visualization includes showing the truck position with a rotation related to the last command. Each step of a truck should be visualized as well. Several levels could be implemented. The difficulty of the task is managed through the maze complexity. The introductory level includes only one command and a very simple maze. Additional levels include using an increasing number of commands. In the highest levels, a maze is generated randomly, so that a student has to make a correct algorithm in one go.
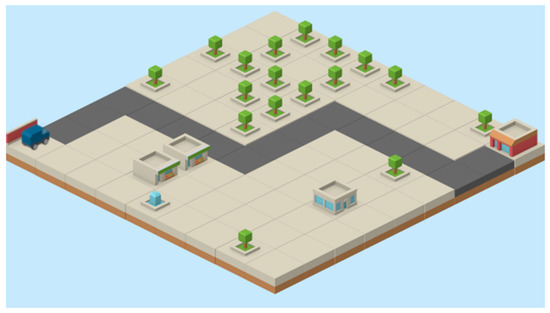
Figure 4.
Illustration of a linear style algorithm by finding an exit through a maze of streets in a city.
3.3.2. Branching (Conditional) Algorithms
Branching refers to conditional statements, conditional expressions, and conditional constructs, which are dedicated to performing some computations or actions depending on the evaluation of the programmer-specified Boolean condition. To solve the task, a student has to write conditional statements including equals, not equals, less than, more than, less than or equal, and more than or equal, which are visualized as turning decisions at each city intersection (Figure 5). To reach the aim, the branching conditions must be written correctly.
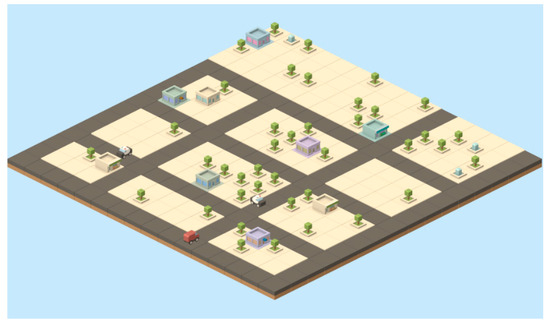
Figure 5.
Illustration of a conditional algorithm—finding a correct route in the city streets.
A student will have to implement a function that will be tested with several sets of input data. Each command except the conditional statement is evaluated and visualized in a loop. The algorithm finishes if all test cases were successfully executed, or there was a mistake in a test case. There are three containers of different sizes and the task is to sort out several types of color-coded waste (green—bio, blue—plastic, red—construction waste, etc.) trucks to the appropriate waste dumps. Visualization includes moving a person to a container and dropping an item. Each step of a person’s movement is visualized as well.
3.3.3. Iterative Sum Algorithm
A simple summation task which does not include arrays could be formulated like this: given a number n, find the sum of digits in all numbers from 1 to n. The sum algorithm normally involves a variable where the sum is accumulated (sometimes called an accumulator) and a loop that iterates within a given interval. The general case for such an algorithm is has an increasing number of objects which are moved to a container of a specific type and the sum of the objects in the container is displayed. The narrative of this case is that there are several parking places and the parking place number denotes how many cars it can contain. The task is to calculate the sum of the cars which could be placed in a given number of parking places.
Each command is evaluated and visualized in a loop. If the sum variable is equal to the previous sum plus the expected number of trucks, then the animation should start moving trucks to the big waste depot. The algorithm finishes if all trucks are moved to the empty waste deposit place, or there is a mistake and the sum variable is not equal to any possible combination. Visualization includes moving trucks to the waste deposit lot and showing the value of the sum variable.
3.3.4. Iterative Search Algorithm
The simple search task is to find a specific value of a specific item in a given range of values. In this case, we could use the waste truck scenario. Given the array of random truck numbers assigned to waste deposit places, we need to find a maximum (or a minimum) number of trucks in a waste depot (Figure 6). A student will have to implement the minimum or maximum finding functions. That function receives an array of numbers called trucks which has to be investigated and the minimum or the maximum number of cars is found.
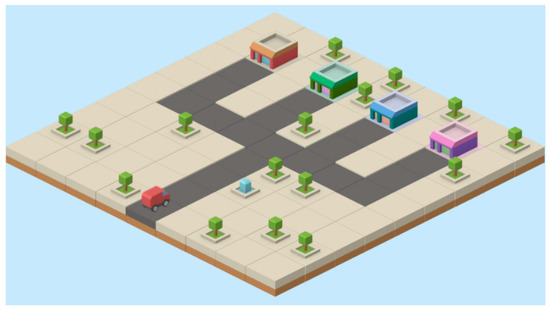
Figure 6.
Illustration of an iterative search algorithm—finding the correct waste deposit lot.
Each command is evaluated and visualized in a loop. Each item from the cars array is evaluated against the current min or max variable. The algorithm finishes if the loop finishes successfully and the min/max value is found, or there is a mistake in the provided solution and the min/max value is not found. The visualization includes comparing the current state of the truck array to the minimum or maximum value found before that iteration.
3.3.5. Iterative Sorting Algorithm
Sorting consists of ordering a list of objects according to the value of a specified property. We start familiarizing the student with this concept from the simplest (and less efficient) algorithm called bubble sort. In this case, we could use the building scenario. Given a set of city buildings, we need to sort them according to their heights (number of floors) as larger buildings pollute more.
A student will have to implement the building sorting function. That function receives an array of heights called buildings which have to be sorted in increasing order (see Figure 7). Each command is evaluated and visualized in a nested loop. The users’ data array is investigated in each iteration, and if there is a change in an array, then the animation of swapping two players starts. The algorithm finishes if the loop finishes successfully and the data are sorted in increasing order, or there is a mistake and the returned data do not match the sorted data. Variations of the implemented algorithm may include changing the sorting direction.
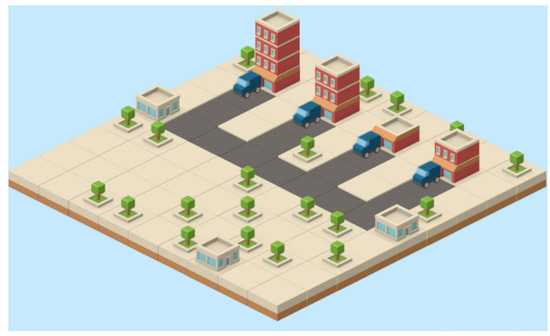
Figure 7.
Illustration of sorting algorithm using the building ordering scenario (the higher building is a more polluting building).
3.3.6. Recursion
The recursion is implemented by using functions that call themselves from within their code. The Fibonacci recursive algorithm, which generates the Fibonacci number sequence, is used to visualize the recursion. The task for this scenario is to implement a function that takes one parameter (n) and returns the corresponding Fibonacci number. The scenario narrative includes trucks and waste deposit places. The idea is that every newly built waste depot should be able to contain the waste trucks from the waste deposit places built before. A student has to implement the Fibonacci sequence calculation function. The calls to the Fibonacci function are visualized as a call stack. Numbers are visualized as trucks that appear after the result of the function call is returned. The algorithm finishes if all test cases were successfully executed, or there was a mistake in a test case.
3.3.7. Tree Traversal Algorithms
Traversal is visiting all the nodes of a tree data structure and executing the associated actions. Generally, we traverse a tree to find and access an item stored in the tree data structure. To visualize tree traversal algorithms, we use the city maze scenario. The maze is organized as a tree that has several levels. Given the picture, the student will have to create a tree data structure and to implement the chosen tree traversal algorithm. Thus, the picture needs to be transformed into a tree. The city maze root node is a maze itself. It has two children—greenery and structures. Greenery contains parks, lakes, and fields. Structures contain buildings, roads, and parking places. Each node has a title, coordinates, and children. A student needs to create a tree data structure and construct the specific tree of a given city maze. Initially, the game app shows a semi-hidden maze (a semi-transparent layer is shown over the maze). According to the data structure and the tree construction code created by a student, the app opens specified tiles. The task will be completed if all tiles are opened.
3.3.8. Graphs—Shortest Pathfinding Algorithm
A graph is an abstract data type used to model a set of connections. To find the shortest path, the city maze needs to be transformed into a weighted graph with the weights corresponding to the distance between intersections. The most important/well known algorithm to find the shortest path in a weighted graph is Dijkstra’s algorithm. The task is to find an exit through the maze of streets in a city. That image needs to be transformed into a graph. The game narrative is a truck driving through the city to get some building materials or to pick up waste. To solve this task, a student needs to create a graph structure. For that purpose, the street intersections need to be named and visualized in a city street maze. According to the graph created by a student, the game visualizes the connections as lines and numbers assigned to these connections as weights. The connections are drawn in a green color if the connections exist in the reference graph. Otherwise, the student graph connections will be drawn in red. The app draws the weights in a green color if the weights are accurate compared to the reference graph. Otherwise, the student graph weights will be drawn in red.
3.4. Evaluation Measures
To assess the effectiveness of the game in teaching the introductory concepts and the construct of programming logic and thinking, a pre-test and the post-test were performed and analyzed. All tests were created by computer science teachers. Each test (pre-test and post-test) included the same topics of programming and covered the same content of materials and degree of complexity.
The pre-test assessment was done before the start of the course to find the knowledge of programming constructs and abstractions among students before the course, while the post-test was taken by the students after the course. Each group was given 10 exercises to solve within a time limit of 90 min. After the end of the course, the students were given a post-test, which was delivered in the same way as the pre-test. Finally, the overall assessment was done by comparing the evaluation scores obtained during the pre-test and post-test to find the improvement in the student knowledge.
To validate the developed game, a survey was conducted using the Technology Acceptance Model (TAM) [54]. The TAM was already used for evaluating the use of gamification for serious purposes [55]. The questionnaire had 10 questions that address five elements (two questions per each element of the TAM) to validate: perceived usefulness (PU), perceived ease of use (PEU), attitude towards use (ATU), intention to use (IU), and perceived enjoyment (PE) as an external factor. PU evaluates how useful gamification is for improving professional competencies. PEU is an indicator that measures users’ behavioral attitudes towards the ease of technology use. ATU is the degree to which a student perceived desirable feelings related to the use of a serious game for learning. IU measures the intention to use a serious game for learning. PE evaluates the hedonic enjoyment of students while using the serious game. Each item is assessed with a 7-point Likert-type scale from 1 (strongly disagree) to 7 (strongly agree). For the evaluation of the internal consistency of survey results, we use Cronbach’s alpha, which verifies the reliability of the measurement scale used.
We also adopted the Technology-Enhanced Training Effectiveness Model (TETEM), which was created to analyze the adoption of virtual worlds in organizational training [56], but later adopted to evaluate the effects of gamification [57]. The model evaluates experience with videogames (EVG), attitudes toward game-based learning (AGBL), control valence (CV), and gamified valence (GV), and can be used to assess the relationship between gamification and training. EGV refers to the amount of time spent playing different games, and identification with gaming culture. Valence refers to the anticipation of gain from learning, which in turn influences student reactions, outcomes, and the degree of knowledge transfer. Each item is assessed with a 5-point Likert-type scale from 1 (strongly disagree) to 5 (strongly agree).
The results of the survey are evaluated using statistical testing (Shapiro–Wilk normality test, Mann–Whitney U test) and correlation analysis (Pearson correlation coefficient). The Shapiro–Wilk normality test is used to test the hypothesis that the data are normally distributed. The Mann–Whitney U test is a nonparametric test commonly used to compare outcomes between two independent groups.
Pearson correlation is a statistical measure that assesses the linear correlation between two variables. We used it to check the relationship between the elements of the TAM and TETEM.
4. Results
4.1. Participants and Educational Setting
The participants consisted of 54 undergraduate students at Kaunas University of Technology (Lithuania). The sample was 83.4% male and 16.6% female (mean age = 19.43, SD = 1.17). The survey was approved by the Institutional Review Board at the Faculty of Informatics, Kaunas University of Technology. All participants voluntarily agreed to take part in the survey. Answers were fully anonymous, and no personal data were collected, while only aggregate information was later used.
Based on the prior academic results, the participants were randomly split into two groups (game group and control group) to maintain academic balance. Both groups attended a traditionally delivered (with PowerPoint-based lectures) programming course, but the game group was introduced to the game and encouraged to play it.
For the TAM survey, we used the original TAM questionnaire as in [58]. For the TETEM survey, we used the questionnaire presented in [59], in which we only replaced “video games” with “computer games”, and “work training” with “programming training”.
4.2. Results of Performance Evaluation
The results of the pre-test evaluation were explored using skewness and kurtosis values, which satisfied the normality requirement, suggesting that any diversity in the students’ background knowledge originated from a normally distributed population. To support this assumption, a Shapiro–Wilk normality test was performed to examine the distribution of scores achieved by students. The results indicated that the scores may have been normally distributed (W = 0.9263, p-value = 0.2158; W = 0.9366, p-value = 0.2267, for both groups, respectively).
In our case, the Mann–Whitney U test was used to compare the background knowledge between students from both groups, showing that there was not a statistically significant difference (p = 0.08) between students from the game group (M = 6.56, SD = 1.24) and the control group (M = 6.65, SD = 1.38) in the pre-test evaluation. The control group achieved slightly better results than the game group in the pre-test evaluation. In the post-test, there was a statistically significant (p < 0.001) difference between students from the experimental (M = 8.41, SD = 1.29) and control (M = 7.62, SD = 1.16) groups according to the Mann–Whitney U test (Figure 8).
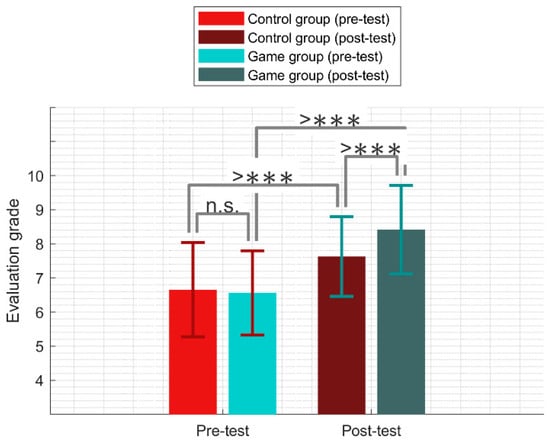
Figure 8.
Summary of pre-test and post-test evaluation of game group and control group. ***—statistically significant (p < 0.001). n.s.—not significant (p > 0.5).
Moreover, the game group has a learning gain (MD = 1.855) greater than the control group (MD = 0.969) between the two evaluations, while the statistical significance of this difference was confirmed by the Mann–Whitney U test (p < 0.001). The results are summarized visually in Figure 9.
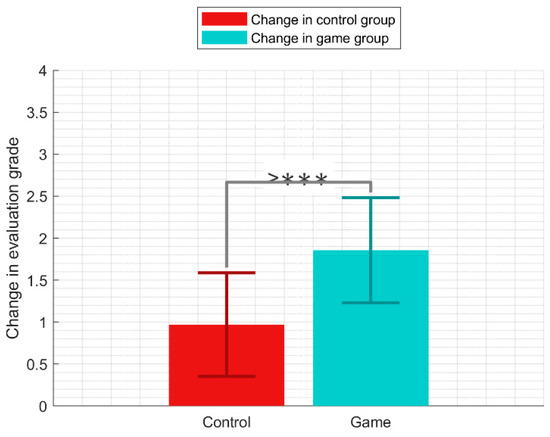
Figure 9.
Change in evaluation scores of the game group and control group between pre-test and post-test. ***—statistically significant (p < 0.001).
4.3. TAM
For the evaluation of the internal consistency of TAM responses, we use Cronbach’s α, which is equal to 0.89. Note that α ≥ 0.80 is considered good.
Pearson correlation was calculated to check the relationship between the analyzed TAM elements (see Figure 10). A positive correlation was observed between PEU and PU (R = 0.516, p < 0.001), between PU and ATU (R = 0.798, p < 0.001), between PU and IU (R = 0.417, p < 0.01), and between ATU and IU (R = 0.446, p < 0.01).
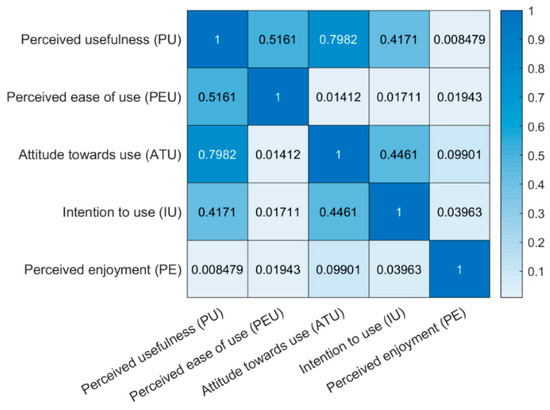
Figure 10.
Pearson correlations between the elements of the TAM.
4.4. TETEM
For the evaluation of the internal consistency of TETEM responses, we use Cronbach’s alpha. The result is α = 0.96. Note that α ≥ 0.80 is considered good.
Pearson correlation was calculated to check the relationship between the analyzed TETEM elements (see Figure 11). The statistically significant correlation was noticed between EVG and GV (R = 0.60; p < 0.001), and AGBL and GV (R = −0.38, p < 0.01). The results of the survey support the claim that a gamified learning experience leads to higher valence, which provides for a causal relationship between the use of gamification and the learning outcomes.
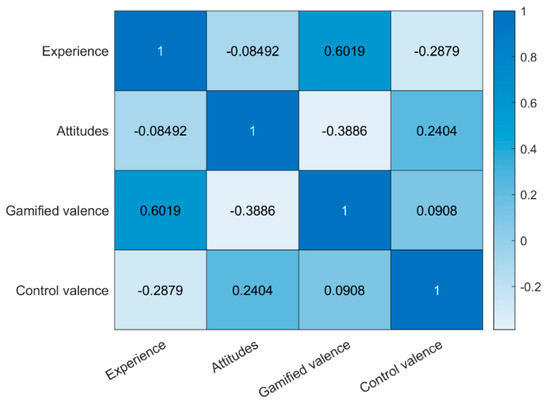
Figure 11.
Pearson correlation between the elements of the TETEM.
5. Discussion
Game-based learning is a process both unpredictable and difficult to manage. Its course is affected by some factors, which are very difficult to calculate, and even more so to assess their mutual influences. However, the systematic and purposeful use of game methods can give certain results, both in changing the basic qualities of a person and in the effectiveness of educational activities. So, we can discuss gamification as a new way of organizing training, which has a huge pedagogical potential. Inherent mechanics of gamification allow you to run the very highest level activity, which is the root cause, the source of the child’s activity, which has a creative character [59], with how to stimulate subjective activity, but does not remove a learner from the reality.
Elements of gamification make the standard university course more interesting. For example, game mechanics can motivate a student to do homework and solve tests, and if the topic is too complex, then simple programming examples with gamification will help to better understand and learn the material for the future. A large programming course, in which students risk getting lost, can be supplemented with a serious game—such a tool provides an incentive for the student to complete the course. Incentive badges or points for different actions when completing practical programming tasks will motivate the student to pass the course on time. Among other things, game mechanics make the learning activities themselves more attractive, which was confirmed by the results of the TETEM survey (item “gamification valence”). This study is the first study that had adopted the TETEM questionnaire for evaluating a serious game for teaching programming.
On the other hand, the TAM model is well known and has been used for evaluating games several times. Wang et al. [60] used the TAM to evaluate a mobile game, which supported students in learning color mixing in design education. They found a significant correlation between PEU and PU, between PU and ATU, and between ATU and IU. Onashoga et al. [61] developed a 3D game-based learning approach for increasing awareness of phishing attacks. The study has found that all relationships between PEU, PU, ATU, and actual usage of the system (AUOS) were significant and positive. Giannakoulas and Xinogalos [62] developed an educational game for teaching simple programming concepts to primary school children. They used the TAM to evaluate the game but did not perform an analysis of relationships between the TAM concepts. Therefore, our results of evaluating the developed game using the TAM model are largely in agreement with the results achieved by other studies.
Thus, the main principle of gamification is to ensure that constant, measurable feedback from the student is received, which provides the possibility of dynamic adjustment of his/her learning behavior to achieve adaptive learning, and, as a result, the rapid development of all the functionalities of the serious game application and the gradual mastering of educational material. The latter aspect is especially relevant in the era of COVID-19 lockdowns, which have disrupted the usual flow of teaching in schools and universities, while current modes of remote learning, which were hastily enacted, lack feedback mechanisms to monitor the learning process effectively, raising new challenges for educators and serious game designers [63,64]. The mobile game, such as the one presented in this paper, can be used to sustain student–student and student–teacher ties in the learning process by putting the student in the learning-oriented gaming community. The emergence of educational serious games also changes the pedagogical position of the teacher and creates conditions for the development of new modes of remote education for the COVID-19 world. These new modes based on mobile applications, including mobile games, can be used to bridge the digital divide in teaching information technologies [65]. However, the usefulness of a serious game for improving the learning performance among disenfranchised groups of learners still requires further research.
The adoption of serious games also has limitations. Our approach is limited to a single course in the programming study curriculum at the university level. Developing games for a different study course (especially for a course attended by non-technologically oriented students) may require adopting a different set of solutions. Designing a game for school or high school students also may require adjustment of the pedagogical model. Finally, when evaluating our game, we followed a closed-world assumption, as the students did not use any games for learning in other courses. If a serious game-based learning approach were adopted more widely, for example, at the study program level, and the students would use the games in many courses, and the attractiveness of a serious game as an educational tool per se may decrease.
Following our experience of using the game in the teaching process, we outline the following limitations of the application of serious games in education as follows. External rewards, such as points, are certainly necessary, but the internal motivation of students to study is more important [66]. The student must clearly understand that it is the educational achievements for which the awards (badges, points, etc.) are given. There is a risk that gamification can undermine behavior psychologically as some students may focus solely on receiving awards rather than on the educational process itself.
6. Conclusions
In this paper, we described the use of our developed interactive mobile application as a serious game for learning how to solve common algorithmic problems in the JavaScript programming language. The game was validated using the TAM and TETEM. The results of the TETEM survey supported our assumption that gamified learning experience leads to higher valence, which supports the positive relationship between the use of gamification and the learning outcomes. On the other hand, the TAM survey revealed positive relationships between perceived usefulness (PU) and perceived ease of use (PEU), as well as between attitude towards use (ATU) and intention to use (IU), which support the use of gamification as a tool for improving professional competencies, and the student intention to use the developed serious game for learning.
Future work will focus on the repurposing of our approach for other fields of education beyond programming and computer science.
Author Contributions
Conceptualization, J.S. and R.M.; methodology, J.S., R.M., T.B., and R.D.; software, A.K.; validation, J.S., R.M., T.B., and R.D.; formal analysis, J.S., R.M., and R.D.; investigation, J.S., R.M., A.K., T.B., and R.D.; resources, J.S., R.M., and T.B.; writing—original draft preparation, J.S., R.M., T.B., and R.D.; writing—review and editing, R.M. and R.D.; visualization, R.M. and A.K.; supervision, J.S. and R.M.; project administration, J.S. and R.M.; funding acquisition, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
Supported by a grant from the Cooperation Fund Foundation within the “Paths of cooperation—support for entities implementing international cooperation” project co-financed from the European Social Fund under the Operational Programme Knowledge Education Development.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cárdenas-Robledo, L.A.; Peña-Ayala, A. Ubiquitous learning: A systematic review. Telemat. Inform. 2018, 35, 1097–1132. [Google Scholar] [CrossRef]
- Connolly, T.M.; Boyle, E.A.; MacArthur, E.; Hainey, T.; Boyle, J.M. A systematic literature review of empirical evidence on computer games and serious games. Comput. Educ. 2012, 59, 661–686. [Google Scholar] [CrossRef]
- Girard, C.; Ecalle, J.; Magnan, A. Serious games as new educational tools: How effective are they? A meta-analysis of recent studies. J. Comput. Assist. Learn. 2013, 29, 207–219. [Google Scholar] [CrossRef]
- Bonanno, P.; Kommers, P.A.M. Exploring the influence of gender and gaming competence on attitudes towards using instructional games. Br. J. Educ. Technol. 2007, 39, 97–109. [Google Scholar] [CrossRef]
- Damaševičius, R. Towards Empirical Modelling of Knowledge Transfer in Teaching/Learning Process. In Cyberspace Data and Intelligence, and Cyber-Living, Syndrome, and Health; Springer Science and Business Media LLC: Larkspur, CA, USA, 2014; Volume 465, pp. 359–372. [Google Scholar]
- Subhash, S.; Cudney, E.A. Gamified learning in higher education: A systematic review of the literature. Comput. Hum. Behav. 2018, 87, 192–206. [Google Scholar] [CrossRef]
- Zainuddin, Z.; Chu, S.K.W.; Shujahat, M.; Perera, C.J. The impact of gamification on learning and instruction: A systematic review of empirical evidence. Educ. Res. Rev. 2020, 30, 100326. [Google Scholar] [CrossRef]
- Plauska, I.; Damaševičius, R. Educational Robots for Internet-of-Things Supported Collaborative Learning. In Cyberspace Data and Intelligence, and Cyber-Living, Syndrome, and Health; Springer Science and Business Media LLC: Larkspur, CA, USA, 2014; Volume 465, pp. 346–358. [Google Scholar]
- Zeng, J.; Parks, S.; Shang, J. To learn scientifically, effectively, and enjoyably: A review of educational games. Hum. Behav. Emerg. Technol. 2020, 2, 186–195. [Google Scholar] [CrossRef]
- Bawa, P. Game On! Int. J. Game-Based Learn. 2020, 10, 16–46. [Google Scholar] [CrossRef]
- Askarova, U.; Jabborova, D. The Use of Game Technologies in Primary Education. Am. J. Soc. Sci. Educ. Innov. 2020, 2, 478–485. [Google Scholar] [CrossRef]
- Granic, I.; Lobel, A.; Engels, R.C.M.E. The benefits of playing video games. Am. Psychol. 2014, 69, 66–78. [Google Scholar] [CrossRef]
- Ravyse, W.S.; Blignaut, A.S.; Leendertz, V.; Woolner, A. Success factors for serious games to enhance learning: A systematic review. Virtual Real. 2017, 21, 31–58. [Google Scholar] [CrossRef]
- Cheng, M.; She, H.-C.; Annetta, L. Game immersion experience: Its hierarchical structure and impact on game-based science learning. J. Comput. Assist. Learn. 2014, 31, 232–253. [Google Scholar] [CrossRef]
- Hamlen, K.R. General Problem-Solving Styles and Problem-Solving Approaches in Video Games. J. Educ. Comput. Res. 2017, 56, 467–484. [Google Scholar] [CrossRef]
- Swacha, J.; Skrzyszewski, A.; Syslo, W.A. Computer Game Design Classes: The Students’ and Professionals’ Perspectives. Inform. Educ. 2010, 9, 249–260. [Google Scholar] [CrossRef]
- Huang, R.; Ritzhaupt, A.D.; Sommer, M.; Zhu, J.; Stephen, A.; Valle, N.; Hampton, J.; Li, J. The impact of gamification in educational settings on student learning outcomes: A meta-analysis. Educ. Technol. Res. Dev. 2020, 68, 1875–1901. [Google Scholar] [CrossRef]
- Ibanez, M.-B.; Di-Serio, A.; Delgado-Kloos, C. Gamification for Engaging Computer Science Students in Learning Activities: A Case Study. IEEE Trans. Learn. Technol. 2014, 7, 291–301. [Google Scholar] [CrossRef]
- Garneli, V.; Giannakos, M.; Chorianopoulos, K. Serious games as a malleable learning medium: The effects of narrative, gameplay, and making on students’ performance and attitudes. Br. J. Educ. Technol. 2017, 48, 842–859. [Google Scholar] [CrossRef]
- Kurkovsky, S. Mobile game development: Improving student engagement and motivation in introductory computing courses. Comput. Sci. Educ. 2013, 23, 138–157. [Google Scholar] [CrossRef]
- Woo, J.-C. Digital game-based learning supports student motivation, cognitive success, and performance outcomes. Educ. Technol. Soc. 2014, 17, 291–307. [Google Scholar]
- Yallihep, M.; Kutlu, B. Mobile serious games: Effects on students’ understanding of programming concepts and attitudes towards information technology. Educ. Inf. Technol. 2020, 25, 1237–1254. [Google Scholar] [CrossRef]
- Kalyuga, S.; Plass, J.L. Evaluating and Managing Cognitive Load in Games. In Handbook of Research on Effective Electronic Gaming in Education; IGI Global: Hershey, PA, USA, 2009; pp. 719–737. [Google Scholar]
- Oyesiku, D.; Adewumi, A.; Misra, S.; Ahuja, R.; Damasevicius, R.; Maskeliunas, R. An Educational Math Game for High School Students in Sub-Saharan Africa. In Cyberspace Data and Intelligence, and Cyber-Living, Syndrome, and Health; Springer Science and Business Media LLC: Larkspur, CA, USA, 2018; Volume 942, pp. 228–238. [Google Scholar]
- Raziunaite, P.; Miliunaite, A.; Maskeliunas, R.; Damasevicius, R.; Sidekerskiene, T.; Narkeviciene, B. Designing an educational music game for digital game based learning: A Lithuanian case study. In Proceedings of the 2018 41st International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 21–25 May 2018; pp. 800–805. [Google Scholar]
- Gomes, T.C.S.; Falcão, T.P.; Tedesco, P.C.D.A.R. Exploring an approach based on digital games for teaching programming concepts to young children. Int. J. Child-Comput. Interact. 2018, 16, 77–84. [Google Scholar] [CrossRef]
- Davis, K.; Sridharan, H.; Koepke, L.; Singh, S.; Boiko, R. Learning and engagement in a gamified course: Investigating the effects of student characteristics. J. Comput. Assist. Learn. 2018, 34, 492–503. [Google Scholar] [CrossRef]
- Rose, S.P.; Habgood, M.P.J.; Jay, T. Designing a Programming Game to Improve Children’s Procedural Abstraction Skills in Scratch. J. Educ. Comput. Res. 2020, 58, 1372–1411. [Google Scholar] [CrossRef]
- Garcia-Sanjuan, F.; Jurdi, S.; Jaen, J.; Nacher, V. Evaluating a tactile and a tangible multi-tablet gamified quiz system for collaborative learning in primary education. Comput. Educ. 2018, 123, 65–84. [Google Scholar] [CrossRef]
- Timotijevic, L.; Acuna-Rivera, M.; Gemen, R.; Kugelberg, S.; McBarron, K.; Raats, M.M.; Zolotonosa, M. Adolescents’ perspectives on personal and societal responsibility for childhood obesity-the study of beliefs through ‘serious’ game (PlayDecide). Child. Soc. 2018, 32, 405–416. [Google Scholar] [CrossRef]
- Maskeliunas, R.; Damaševičius, R.; Lethin, C.; Paulauskas, A.; Esposito, A.M.; Catena, M.; Aschettino, V. Serious Game iDO: Towards Better Education in Dementia Care. Information 2019, 10, 355. [Google Scholar] [CrossRef]
- Da Silva, J.P.; Silveira, I.F. A Systematic Review on Open Educational Games for Programming Learning and Teaching. Int. J. Emerg. Technol. Learn. 2020, 15, 156–172. [Google Scholar] [CrossRef]
- Limantara, N.; Meyliana, H.A.N.; Prabowo, H. The elements of gamification learning in higher education: A systematic literature review. Int. J. Mech. Eng. Technol. 2019, 10, 982–991. [Google Scholar]
- French, S.; Kennedy, G. Reassessing the value of university lectures. Teach. High. Educ. 2017, 22, 639–654. [Google Scholar] [CrossRef]
- Plass, J.L.; Homer, B.D.; Kinzer, C.K. Foundations of Game-Based Learning. Educ. Psychol. 2015, 50, 258–283. [Google Scholar] [CrossRef]
- Qian, M.; Clark, K.R. Game-based Learning and 21st century skills: A review of recent research. Comput. Hum. Behav. 2016, 63, 50–58. [Google Scholar] [CrossRef]
- Crookall, D. Serious Games, Debriefing, and Simulation/Gaming as a Discipline. Simul. Gaming 2010, 41, 898–920. [Google Scholar] [CrossRef]
- Jahnke, I.; Lee, Y.-M.; Pham, M.; He, H.; Austin, L. Unpacking the Inherent Design Principles of Mobile Microlearning. Technol. Knowl. Learn. 2019, 25, 585–619. [Google Scholar] [CrossRef]
- McInerney, D.M. Educational Psychology—Theory, Research, and Teaching: A 25-year retrospective. Educ. Psychol. 2005, 25, 585–599. [Google Scholar] [CrossRef]
- Wang, D.; Wang, T.; Liu, Z. A Tangible Programming Tool for Children to Cultivate Computational Thinking. Sci. World J. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Sapounidis, T.; Demetriadis, S.N.; Papadopoulos, P.M.; Stamovlasis, D. Tangible and graphical programming with experienced children: A mixed methods analysis. Int. J. Child-Comput. Interact. 2019, 19, 67–78. [Google Scholar] [CrossRef]
- Yassine, A.; Berrada, M.; Tahiri, A.; Chenouni, D. A Serious Game for Teaching Python Programming Language. In Advances in Intelligent Systems and Computing; Springer Science and Business Media LLC: Larkspur, CA, USA, 2020; Volume 1076, pp. 389–397. [Google Scholar]
- Garris, R.; Ahlers, R.; Driskell, J.E. Games, Motivation, and Learning: A Research and Practice Model. Simul. Gaming 2002, 33, 441–467. [Google Scholar] [CrossRef]
- Brunvand, S.; Hill, D. Gamifying your Teaching: Guidelines for Integrating Gameful Learning in the Classroom. Coll. Teach. 2018, 67, 58–69. [Google Scholar] [CrossRef]
- Benbow, C. Peabody Journal of Education. Peabody J. Educ. 2018, 95, 160–172. [Google Scholar] [CrossRef]
- Caldera, A. Woke Pedagogy: A Framework for Teaching and Learning. Divers. Soc. Justice Educ. Lead. 2018, 2, 1. [Google Scholar]
- Selby, D. A Darker Shade of Green: The Importance of Ecological Thinking in Global Education and School Reform. Theory Pract. 2000, 39, 88–96. [Google Scholar] [CrossRef]
- Wogu, I.A.P.; Misra, S.; Assibong, P.A.; Olu-Owolabi, E.F.; Maskeliūnas, R.; Damasevicius, R. Artificial Intelligence, Smart Classrooms and Online Education in the 21st Century. J. Cases Inf. Technol. 2019, 21, 66–79. [Google Scholar] [CrossRef]
- Ašeriškis, D.; Damaševičius, R. Gamification Patterns for Gamification Applications. Procedia Comput. Sci. 2014, 39, 83–90. [Google Scholar] [CrossRef]
- Topalli, D.; Cagiltay, N.E. Improving programming skills in engineering education through problem-based game projects with Scratch. Comput. Educ. 2018, 120, 64–74. [Google Scholar] [CrossRef]
- Swidan, A.; Hermans, F.; Smit, M. Programming Misconceptions for School Students. In Proceedings of the 2018 ACM Conference on International Computing Education Research—ICER ’18, Espoo, Finland, 13–15 August 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 151–159. [Google Scholar]
- Yurin, A.Y.; Dorodnykh, N.O. Personal knowledge base designer: Software for expert systems prototyping. SoftwareX 2020, 11, 100411. [Google Scholar] [CrossRef]
- The Joint Task Force on Computing Curricula; Association for Computing Machinery (ACM); IEEE Computer Society. Computer Science Curricula 2013: Curriculum Guidelines for Undergraduate Degree Programs in Computer Science; Association for Computing Machinery (ACM): New York, NY, USA, 2013. [Google Scholar]
- Marangunić, N.; Granić, A. Technology acceptance model: A literature review from 1986 to 2013. Univers. Access Inf. Soc. 2015, 14, 81–95. [Google Scholar] [CrossRef]
- Vanduhe, V.Z.; Nat, M.; Hasan, H.F. Continuance Intentions to Use Gamification for Training in Higher Education: Integrating the Technology Acceptance Model (TAM), Social Motivation, and Task Technology Fit (TTF). IEEE Access 2020, 8, 21473–21484. [Google Scholar] [CrossRef]
- Landers, R.N.; Callan, R.C. Training Evaluation in Virtual Worlds: Development of a Model. J. Virtual Worlds Res. 2012, 5, 1–20. [Google Scholar] [CrossRef]
- Landers, R.N.; Armstrong, M.B. Enhancing instructional outcomes with gamification: An empirical test of the Technology-Enhanced Training Effectiveness Model. Comput. Hum. Behav. 2017, 71, 499–507. [Google Scholar] [CrossRef]
- Davis, F.D. Perceived Usefulness, Perceived Ease of Use, and User Acceptance of Information Technology. MIS Q. 1989, 13, 319–340. [Google Scholar] [CrossRef]
- Co-Creativity through Play and Game Design Thinking. Electron. J. E-Learn. 2019, 17. [CrossRef]
- Wang, C.-S.; Huang, Y.-M.; Hsu, K.-S. Developing a mobile game to support students in learning color mixing in design education. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Onashoga, A.S.; Ojo, O.E.; Soyombo, O.O. Securix: A 3D game-based learning approach for phishing attack awareness. J. Cyber Secur. Technol. 2019, 3, 108–124. [Google Scholar] [CrossRef]
- Giannakoulas, A.; Xinogalos, S. A pilot study on the effectiveness and acceptance of an educational game for teaching programming concepts to primary school students. Educ. Inf. Technol. 2018, 23, 2029–2052. [Google Scholar] [CrossRef]
- Fabricatore, C.; Gyaurov, D.; Lopez, X. Rethinking Serious Games Design in the Age of COVID-19: Setting the Focus on Wicked Problems. In Computer Vision ECCV 2020; Springer Science and Business Media LLC: Larkspur, CA, USA, 2020; pp. 243–259. [Google Scholar]
- Kriz, W.C. Gaming in the Time of COVID-19. Simul. Gaming 2020, 51, 403–410. [Google Scholar] [CrossRef]
- Chatterjee, S.; Majumdar, D.; Misra, S.; Damaševičius, R. Adoption of mobile applications for teaching-learning process in rural girls’ schools in India: An empirical study. Educ. Inf. Technol. 2020, 25, 4057–4076. [Google Scholar] [CrossRef]
- Ašeriškis, D.; Damaševičius, R. Computational evaluation of effects of motivation reinforcement on player retention. J. Univers. Comput. Sci. 2017, 23, 432–453. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).