1. Introduction
Breakthroughs in electronics and telecommunications fields have made Internet of Things (IoT) a reality, with an every day growing number of sensors and devices around us. Nowadays, diverse critical services, such as smart-grid, e-health, agricultural or industrial automation, depend on an IoT infrastructure. At any rate, as the services around IoT grow dramatically, so do the security risks [
1,
2].
Low-cost IoT devices, currently characterized by their resource constraints in processing power, memory, size and energy consumption, are also recognizable by their minimal or non-existent security. Combining this lack of security with their network dependability, they become the perfect target as a gateway to the whole network [
3]. There are already some attacks where a vulnerable IoT sensor was used to gain control over the whole system (in [
4], wireless sensors are used to gain access to an automotive system).
This is the reason why general research [
5], 5G-related research [
6] or specific calls such as that of NIST for lightweight cryptography primitives [
7], are addressing this concerning topic. Although different protocols of communication and orchestration are being proposed [
8], lightweight cryptography in general and stream ciphers in particular are the stepping stones on which such protocols are built to guarantee both device and network security.
Currently, linear feedback shift registers (LFSRs) are key components in stream ciphers, often used as pseudo-random number generators (PRNG). A representative example of LFSR-based practical design is the J3Gen, a pseudo-random number generator for low-cost passive radio frequency identification (RFID) tags. Such a generator has been analyzed and revised in [
9,
10], respectively.
In addition, we present the generalized self-shrinking generator, a family of ciphers suitable for cryptography [
11]. This generator remains strong against different algorithms that analyze the cryptographic strength (e.g., linear complexity) of its sequences. Such algorithms can be enumerated as follows: (1) the well-known Berlekamp–Massey algorithm [
12], (2) the sequence decomposition algorithm developed by Cardell et al. in [
13] and (3) the folding sequence decomposition algorithm introduced in this paper. To our knowledge, no other algorithms to calculate the parameter linear complexity of binary sequences are described in the literature.
The study of the generalized self-shrinking generator is not a random choice. Indeed, it produces not only sequences that are difficult to be analyzed by the Berlekamp–Massey algorithm, but also it has been implemented in hardware [
14] along on RFID devices [
15]. Studying the robustness of these sequences could prevent vulnerabilities on the IoT devices and the services built on them.
The paper is organized as follows.
Section 2 includes a succinct revision of LFSRs and sequence generators based on irregular decimation, a wide type of generators including the generalized self-shrinking generator.
Section 3 describes the characteristics and generalities of the binomial sequences (BS), binary sequences that constitute the foundations of the two last algorithms mentioned above. The main contributions of this work are in
Section 4, where we analyze three algorithms to calculate the linear complexity of binary sequences: (a) the standard Berlekamp–Massey algorithm, (b) the basic binomial sequence decomposition (b-BSD) algorithm, an improved version of the algorithm developed in [
13], that analyzes different properties of the binary sequences and (c) the folding binomial sequence decomposition (f-BSD) algorithm, the novel proposal based on the symmetry of the binomial sequences.
Section 5 includes the discussion and comparison among the three previous algorithms. Finally, conclusions and possible future research lines in
Section 6 end the paper.
2. Sequence Generators Based on Linear Feedback Shift Registers
Linear feedback shift registers (LFSRs) [
16] are linear structures currently used in the generation of pseudo-random sequences. The LFSRs are electronic devices included in the majority of sequence generators described in the literature. The main reasons for such a generalized use of LFSRs are: these devices provide high performance when used for sequence generation, they are particularly well-suited to hardware implementations, and such registers can be easily analyzed by means of basic algebraic techniques.
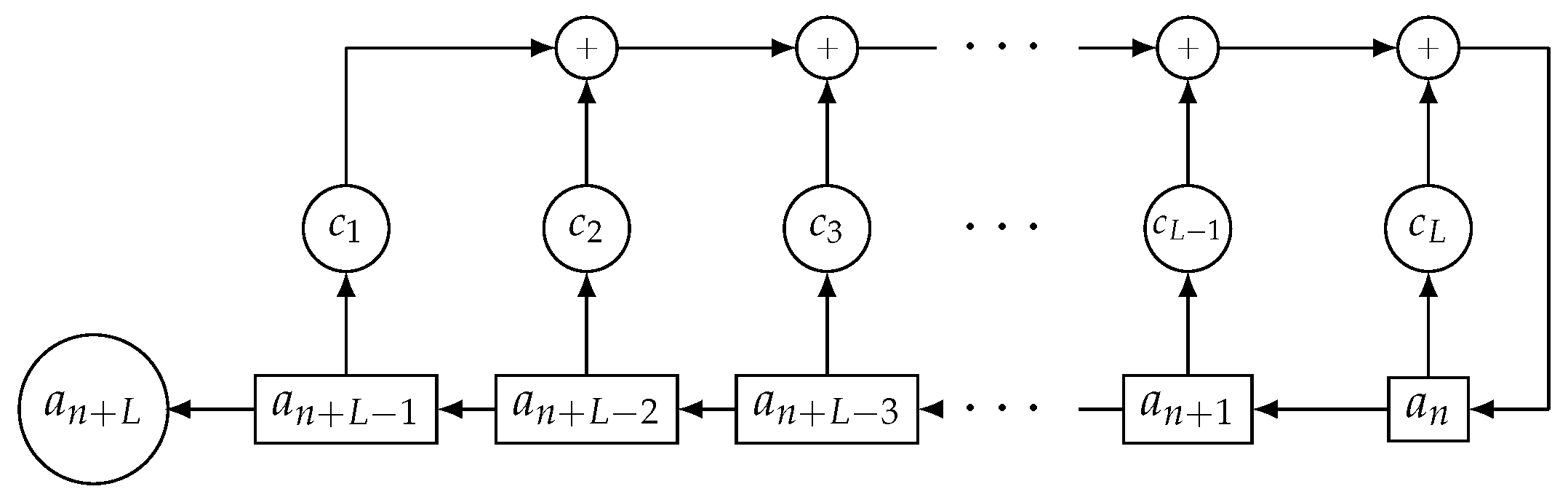
According to
Figure 1, a LFSR consists of: (a)
L interconnected stages numbered from left to right
where each of them stores one bit, (b) the feedback polynomial
of degree
L notated
with binary coefficients
and (c) the initial state or stage contents at the initial time. LFSRs generate sequences by means of shifts of the stage contents and linear feedback to the last stage.
The output of an LFSR with nonzero initial state is a binary sequence denoted by
. If the polynomial
is primitive [
16], then the output sequence is called PN-sequence (or pseudo-noise sequence). In addition, the period of a PN-sequence is
bits with
ones and
zeros.
The linear complexity of a sequence, notated , quantifies the number of bits necessary to reconstruct the whole sequence. For particular applications of binary sequences, e.g., cryptographic applications (stream ciphers), must be as large as possible. Moreover, the linear complexity is a parameter closely related to the concept of LFSR. In fact, the linear complexity of a sequence is defined as the length of the shortest LFSR that generates such a sequence.
Although an LFSR in itself is an excellent generator of pseudo-random sequence, in practice it has undesirable linearity properties which reduce the security of its use. Due to these linearities, LFSRs exhibit a very low
of value just
L. Consequently, in the process of generation of the pseudo-random sequence, any type of nonlinearity must be introduced. The irregular decimation of PN-sequences is one of the most popular techniques to destroy the inherent linearity of the LFSRs [
17,
18]. In brief, this procedure is based on the fact of removing some bits of a PN-sequence according to the bits of another one.
Inside the type of irregularly decimated generators, we can enumerate: (a) the shrinking generator introduced in [
19] that includes two LFSRs, (b) the self-shrinking generator [
20] that involves just one LFSR and (c) the generalized self-shrinking generator proposed in [
21] that is considered as a simplification of the shrinking generator as well as a generalization of the self-shrinking generator. In this work, we focus on the last type of generator, that is, the generalized self-shrinking generator.
The Generalized Self-Shrinking Generator (GSSG)
The generalized self-shrinking generator can be described as follows:
It makes use of two PN-sequences: a PN-sequence produced by an LFSR with L stages and a shifted version of such a sequence denoted by . In fact, , thus corresponds to the own sequence rotated cyclically p positions to the left with .
In order to generate the output sequence, it relates both sequences by means of a simple decimation rule.
For
, the decimation rule is defined as follows:
Thus, for each value of
p, an output sequence
is generated. Such a sequence is called the
p generalized self-shrunken sequence (GSS-sequence) or simply generalized sequence associated with the shift
p. Recall that
remains fixed while
is the sliding sequence or left-shifted version of
. If
p ranges in the interval
, then we obtain the
members of the family of generalized sequences based on the PN-sequence
. Since the PN-sequence has
ones, the period of any generalized sequence will be
or divisors of this number, in any case, a power of 2. In addition, the
of every GSS-sequence is upper-bounded by
[
22] (Theorem 2). Next, an illustrative example of a family of GSS-sequences is introduced.
Example 1. For an LFSR with primitive polynomial and initial state , we generate the generalized sequences depicted in Table 1. The bits in bold in the different sequences are the digits of the corresponding GSS-sequence associated to the corresponding shift p. The PN-sequence with period is written at the bottom of the table in columns 2 and 5. There are two particular facts that differentiate the GSS-sequences from the PN-sequences generated by LFSRs:
3. Binomial Sequences: Characteristics and Generalities
In this section, we introduce the binomial sequences as a new representation of the binary sequences whose period is a power of 2. Next, the close relationship between binomial sequences and Sierpinski’s triangle is also considered.
3.1. Concepts and Fundamentals of the Binomial Sequences
The binomial number is the coefficient of the i-th power in the polynomial expansion of . For every non-negative integer n, it is a well-known fact that , as well as for all .
The concept of binomial sequence is defined in terms of the binomial coefficients reduced modulo 2.
Definition 1. Given an integer , the sequence is called the i-th binomial sequence if its elements are binomial coefficients reduced modulo 2, that is .
Binomial sequences are currently notated and the integer i is the index of the binomial sequence. When n takes successive values, the binomial coefficients modulo 2 define the terms of a binary sequence with its corresponding period and linear complexity.
Table 2 shows the eight first binomial sequences
,
, see [
24], where
and
denote period and linear complexity, respectively.
Next, fundamental properties of the binomial sequences that will be used throughout the work are introduced.
Given the binomial sequence
, with
and
r being a non-negative integer, we have that [
13] (Proposition 3):
- (a)
This binomial sequence has period .
- (b)
The period of such a binomial sequence has the following structure:
Every binary sequence whose period is a power of 2 can be written as a linear combination of a finite number of binomial sequences [
13] (Theorem 2). Such a combination is called the binomial sequence decomposition (BSD) of the sequence under consideration.
The linear complexity of the binomial sequence
with
is
, see [
13] (Theorem 13).
Given a sequence with BSD
, where
are integer indexes, then its linear complexity is given by
, see [
13] (Corollary 14).
Given a sequence with BSD
, where
are integer indexes, then its period
T is that of the binomial sequence
, see [
24] (Theorem 1).
According to the previous properties, two important remarks are derived:
Remark 1. The period T of the binomial sequences () can be quantified as follows:
binomial sequences with period .
binomial sequences with period .
binomial sequences with period .
…and so on.
In general, binomial sequences with period with .
On the other hand, the linear complexity of the binomial sequences is different for each binomial sequence and takes the value .
Remark 2. The generalized sequences are binary sequences whose period is a power of 2. Consequently, they can be written in terms of binomial sequences satisfying all the previous properties.
3.2. The Sierpinski’s Triangle
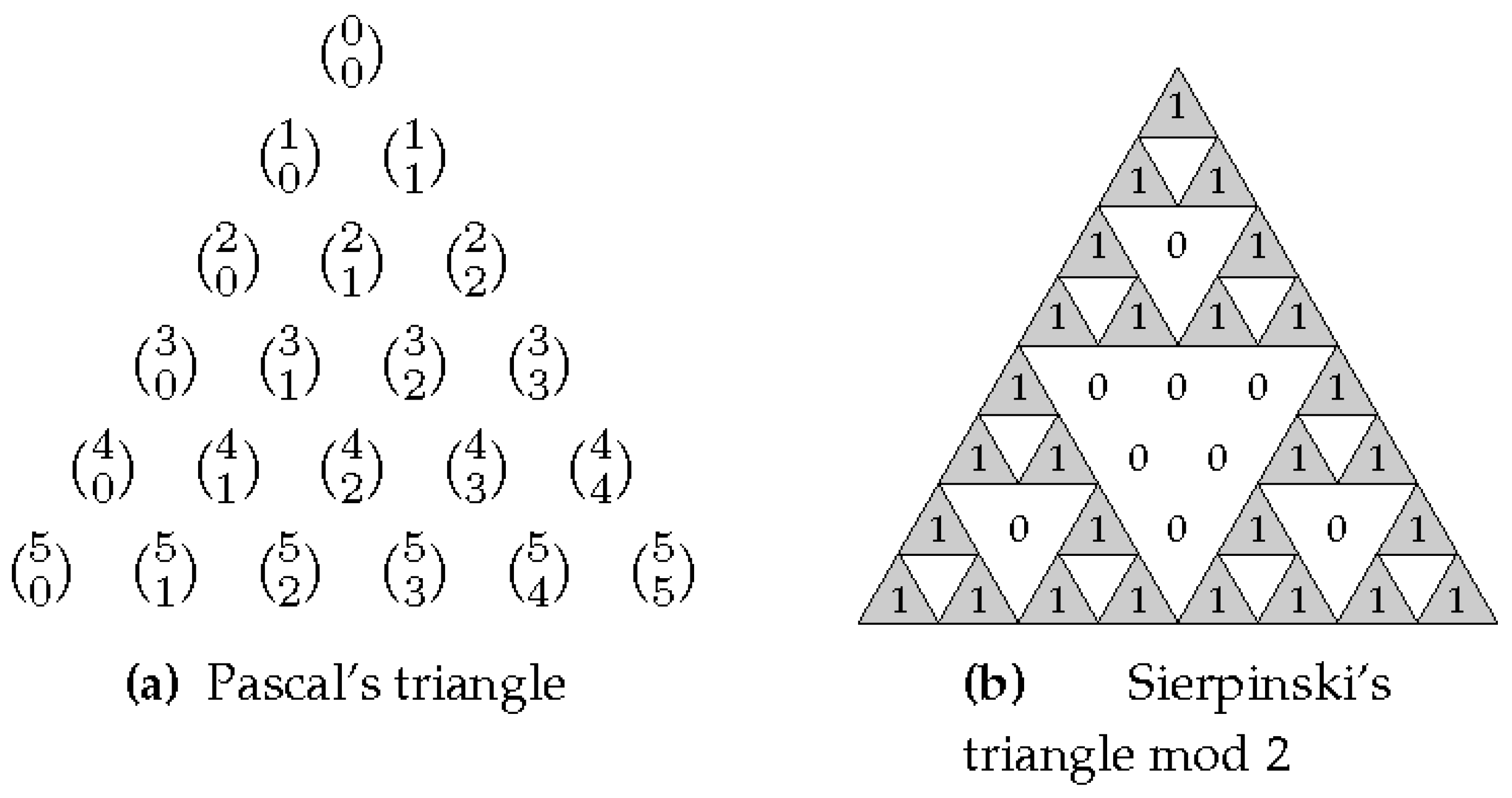
When the binomial coefficients are arranged into rows for the successive values of
(a row for each value of
n), then the generated structure is the well-known Pascal’s triangle depicted in
Figure 2a. If we color the odd numbers and shade the even ones in such a triangle, then we get the Sierpinski’s triangle whose version reduced mod 2 is depicted in
Figure 2b.
Recall that the successive diagonals of the Sierpinski’s triangle in
Figure 2b correspond to the successive binomial sequences
,
with
. That is, each diagonal of the triangle starts at the first 1 of the corresponding binomial sequence. Consequently, the binomial sequences can be found inside the Sierpinski’s triangle mod 2, as well as they can also be found inside certain linear cellular automata, e.g., cellular automata with rules 102 and 60 in Wolfram’s notation. See [
13] for more details.
4. Algorithms to Calculate the Linear Complexity
In this section, we describe and develop different algorithms to calculate the linear complexity of binary sequences. Except for the first algorithm (Berlekamp–Massey algorithm), the remaining may be applied exclusively to sequences whose length (period) is a power of 2. They are based on the characteristics and properties of the binomial sequences.
Once the Berlekamp–Massey algorithm has been considered, this section introduces in detail the basic binomial sequence decomposition algorithm (b-BSD) and possible improvements to its implementation.
Next, a new approach to the binomial sequence decomposition is developed, giving rise to the folding binomial sequence decomposition algorithm (f-BSD). Such an algorithm improves the throughput of previous methods thanks to the symmetry of the binomial sequences.
A comparison among Berlekamp–Massey, b-BSD and f-BSD algorithms will be presented in the next section of this work.
Previously to the algorithms, we introduce a particular notation to be used systematically in the sequel.
NOTATION: For the sake of simplicity, in the successive algorithms of this section, the binomial coefficient will denote the corresponding k-th binomial sequence. Then, the term stands for the binary sub-sequence of between the bits i and j, while denotes the j first bits of the binomial sequence .
4.1. Berlekamp–Massey Algorithm
Traditionally, the general method of calculating the linear complexity of a sequence is the Berlekamp–Massey algorithm [
12]. It can be applied to sequences of any length, not necessarily a power of 2. Consequently, it is the most general among the algorithms that calculate the linear complexity of a sequence.
Given a binary sequence, this algorithm provides one with a general solution to the problem of synthesizing the shortest LFSR that generates such a sequence. At each step, the algorithm incrementally adjusts the length of the LFSR and the feedback polynomial to generate the sub-sequence analyzed to that point. The algorithm terminates when the whole sequence has been generated.
In order to work, this algorithm needs to process
bits of the sequence with a computational complexity of
[
25].
4.2. Basic Binomial Sequence Decomposition (b-BSD)
Based on the mathematical results provided in the previous section, a basic binomial sequence decomposition algorithm (b-BSD) can be designed in order to calculate the of a given sequence. In particular, two facts are used:
A sequence of length
l can be decomposed in
binomial sequences (item 2. in
Section 3.1):
The linear complexity of a sequence can be calculated from the binomial sequence of maximum index in its BSD (item 3. in
Section 3.1). Since the binomial sequences are written in increasing order, then
satisfies the following expression:
The resulting algorithm can be seen in Algorithm 1. It takes the sequence to be analyzed as input and checks for every bit equal to 1. When is equal to 1, it sums the sequence with the corresponding binomial sequence (), stopping when all the binomial sequences have been already found. In that case, the resulting sequence is the identically null sequence.
Once the BSD has been obtained, the binomial sequence
allows us, via the Equation (
1), to calculate
. A step-by-step example of the algorithm decomposing a sequence
of length
can be seen in
Table 3.
| Algorithm 1 Basic Binomial Sequence Decomposition (b-BSD). |
Require:: intercepted bits for ++ do if then end if end for return : Binomial decomposition of the intercepted bits
|
Thus, the b-BSD algorithm is able to calculate , as the Berlekamp–Massey algorithm does, but after having processed only bits of the sequence instead of . The complexity of b-BSD algorithm, which performs the sum of two sequences of l bits (l additions) for every binomial sequence, is , t being the number of binomial sequences in which the main sequence is decomposed with .
Moreover, the logic of the algorithm can be improved by avoiding the sum of the sub-sequences that are zero. On the one hand, thanks to item 1 (b) in
Section 3.1, we know that
. On the other hand, at each step of the b-BSD algorithm, the sequence begins with zeros. That is, at step
i, the
first terms of the sequence are zeros.
If these two facts are combined, then the number of operations performed by the algorithm can be reduced. When the algorithm detects the first 1 in the i-th position of , instead of performing the sum of two sequences of l bits (), it just sums both sequences between the i-th and -th bits (), as the beginning of both sequences (from bit 0 up to bit ) are made up of zeros.
Compared with
, the number of operations is reduced as follows:
In addition, for sequences whose
is upper bounded, we do not need to perform the sum of any binomial sequence after the binomial of maximum index is attained. This is the case for every GSS-sequence produced by the generalized self-shrinking generator. Since the linear complexity of this family of sequences satisfies the inequality:
and its maximum length is
(
L being the number of stages in the LFSR that generates the GSS-sequences), then
Therefore, the maximum index
in the BSD of these sequences is:
and the final number of operations in the algorithm will be:
Thus, at each algorithm step, the number of operations is incrementally reduced.
To upgrade the code in Algorithm 1, only the summation limits must be changed, which will now be
, with
given in Equation (
2).
In brief, the b-BSD algorithm will require at most () bits of the sequence to calculate the with a complexity less than .
4.3. Folding Binomial Sequence Decomposition (f-BSD): Theoretical Foundations
Despite the improvement in both complexity and length requirements between b-BSD and Berlekamp–Massey, there is still room for enhancing the decomposition mechanism.
In the next subsection, a new algorithm design is explained, improving the results of the b-BSD algorithm by taking advantage of the symmetry of the binomial sequences.
In this subsection, we develop new properties of the binomial sequences, particularly symmetric properties, on which the f-BSD algorithm is based.
First of all, a result that relates the index k of a binomial sequence with the period of such a sequence is introduced.
Theorem 1. For every binomial sequence with , there exists an integer , such that is the period of the binomial sequence, as well as the index k satisfying the inequality: Proof. In fact, any integer
can be written in the range
, where
and
are two consecutive powers of 2 and
. In this case,
j being an integer in the interval
. Thus, the binomial sequence can be written as:
and, according to item 1. (b) in
Section 3.1, its period will be
. □
Therefore, the index
k determines the period of the binomial sequence
. Moreover, recall that in Equation (
3)
if , then k takes the minimum value ,
if , then k takes the maximum value .
Thus, k ranges in the interval and the next corollary follows directly:
Corollary 1. The number of different binomial sequences with the same period () is .
Symmetry of ()
There are different properties regarding the symmetric structure of the binomial sequences and their relation to the powers of 2 that are explained in the following.
Every binomial sequence
with length
(
) can be divided into two sub-sequences of length
as follows:
On the other hand, recall that the binomial sequence
starts with
k zeros. Therefore, if
, then such a sequence can be divided in the following way:
where
represents the sub-sequence identically null of length
.
In fact, this is a simplification of a stronger result, defined in the next theorem.
Theorem 2. Every binomial sequence can be divided into two sequences of length as follows:
Proof. Since
, it can be written as
with
. Then,
Since
, it can be written as
with
, where
i and
j are integers as well as
. The binomial sequence
has length
, that is a power of 2, as well as
. Thus, the first and second sub-sequences in Equation (
4) are equal.
□
In
Table 4, where the binomial decomposition of
is represented with
, the condition 1 of the Theorem 2 is observable on the binomial sequences
and
. In contrast, the binomial sequences
and
satisfy the condition 2, where the eight first bits repeat themselves.
Putting together the facts regarding the symmetry of the binomial sequences, they can be classified in two groups depending on the value of their index. This fact is explained in Algorithm 2.
| Algorithm 2 Binomial Sequences Classification. |
For a given sequence : ifthen else end if
|
If the binomial sequences are divided as seen in Algorithm 2, then the binomial representation of a sequence results in a block matrix
, that is, a matrix representation of the BSD, as follows:
Three important characteristics about the matrix representation shown in (
5) are the core of the folding BSD algorithm.
.
.
As the length of the sequence is of the form , the matrix representation can be extended in a recursive way, taking and repeating the same process until it cannot be divided anymore (length = 1).
The following expression (
7) is an example of the matrix representation of the sequence decomposition of
Table 4.
In order to calculate the
of the given sequence, only the highest binomial sequence of its decomposition is needed. Thus, the f-BSD algorithm will benefit from the symmetry of the binomial sequences, by reducing recursively the length of the sequence to analyze, as depicted in the matrix expression (
6).
4.4. Folding Binomial Sequence Decomposition Algorithm
The previous subsection described all the elements needed by the f-BSD algorithm. In fact, the algorithm locates the maximum binomial sequence to calculate . At every step, it sums the first half of the sequence with the second half. If the result is different from zero, then it continues with the resulting sequence. Otherwise, it continues with half the previous sequence. The procedure ends when only one bit is left.
At every step, the folding mechanism reduces the length of the studied sequence by 2. It performs a bit sum of the successive halves of the sequence, with a total of
steps. Given a sequence
with length
l, the number of operations of the algorithm can be calculated as follows:
The final pseudo-code of the algorithm, for a given binary sequence of length
l (although we can reduce it to (
), as explained in
Section 4.2) and complexity O(
l), can be found in Algorithm 3. The way that this algorithm searches for the maximum binomial sequence is similar to that of the binary search algorithm. The difference results in the binary search only performing one comparison in each step, while our algorithms need to perform
operations per step.
Let us see how it works with an example.
Example 2. Take the same sequence as before .
Step 1: As = , then = = and k = 8.
Step 2: As , then .
Step 3: As , then and .
Step 4: As , then .
End: the maximum binomial sequence is .
A representation of the algorithm workflow can be seen in
Figure 3.
| Algorithm 3 Folding Binomial Sequences Classification. |
Require:: intercepted bits while do aux = + if then else end if end while return k: maximum binomial sequence
|
5. Algorithm Discussion
The three algorithms for linear complexity calculation we have visited in our work have different properties and capabilities. Thus, it is worth discussing all of them. In
Table 5, there is a simple comparison between the sequence length required and the computational complexity in each one of these algorithms.
The Berlekamp–Massey algorithm is the classic algorithm to calculate the linear complexity of any sequence. Nevertheless, for sequences whose is near their length, e.g., the GSS-sequences, it needs twice the length l of the sequence and its computational complexity is O(). When it is applied to LFSR-based sequences, this result can become impractical, particularly when these sequences may exhibit a length of bits, for instance, the GSS-sequences in cryptographic applications.
Concerning the basic binomial sequence decomposition algorithm (b-BSD), it allows an improvement in the amount of sequence required regarding the Berlekamp–Massey algorithm. Nevertheless, its computational complexity can be tricky to assess, because it depends on the number t of binomial sequences that appear in the BSD of the sequence under consideration.
5.1. Number of Sequences in the Decomposition
The number of sequences in the binomial decomposition, t, has not been studied previously in the literature. This is one of the facts that makes it difficult to measure the actual improvement of the b-BSD algorithm, whose computational complexity depends on this specific parameter.
In order to study the behavior of t and its dependency on the original sequence, some experiments were carried out.
In our experiments, all the employed sequences were the GSS-sequences coming from LFSRs with polynomials of degrees between five and ten. As a result, we observed on average a number of binomial sequences given by
,
n being the degree of the LFSR polynomials
. The plots corresponding to the number of binomial sequences in the decomposition of all these GSS-sequences are depicted in the
Figure 4.
The distribution of the number of sequences in a binomial decomposition seems to be close to a normal distribution, although a thin tail on the left can be noticed, which means that for a few sequences, the number of binomial sequences will be lower. In those particular cases, this algorithm will perform better than in the general case.
At any rate, recall that this result is backed up by experimental results and no mathematical proof exists regarding the t parameter behavior.
5.2. f-BSD Performance
On the other hand, the folding binomial sequence decomposition algorithm (f-BSD) has a set of characteristics that improves its performance when compared with both Berlekamp–Massey and b-BSD algorithms. In fact, it requires the same length as that of the b-BSD algorithm and improves considerably this requirement when it is compared with the Berlekamp–Massey algorithm. Another interesting characteristic is that its computational complexity does not depend on the number t of binomial sequences as the b-BSD algorithm does, which introduces a penalty factor of about in the b-BSD algorithm performance.
The reason for its improvement is that, at each step of the algorithm, the length of the resulting sequence is divided by two, as can be seen in
Figure 3. Consequently, the number of operations to be performed and the memory needed are progressively reduced.
Although the final purpose of this work is not the implementation of the different algorithms, it is worth pointing out that the f-BSD algorithm can be transformed into a concurrent algorithm for the linear complexity calculation. This fact theoretically improves its performance when the f-BSD algorithm is implemented in an environment with concurrent computation capabilities, as opposed to the b-BSD algorithm, which performs its calculations in a sequential way and cannot operate in a concurrent fashion.
Finally, a comparison of our work and previous works [
26,
27] can be summarized in
Table 6.
In such a table, we point out the main contributions of our current work compared to past works: the introduction of the f-BSD algorithm, the complexity analysis of b-BSD (already introduced in [
13]), backed up by our experiments on the number of sequences in the BSD, and the complexity analysis of f-BSD, which in the end shows how the f-BSD outperforms the previous algorithms.
6. Conclusions
In this work, a new algorithm, the folding BSD algorithm, has been introduced and developed. It exhibits a better performance than similar algorithms to compute the lineal complexity of a binary sequence, especially on sequences that are particularly difficult to be decomposed by the Berlekamp–Massey algorithm. This is a big step in the study of the binary sequences with period a power of two, and makes it easier to detect flaws in this kind of sequences. Detecting such vulnerabilities in a cipher implemented in practical applications could compromise the corresponding IoT devices and the services behind them.
Moreover, the binomial decomposition of sequences as a way to extract information from a given sequence is an innovative but powerful tool, and it is left for future work its application to other kinds of binary sequences.
An experimental approximation to the complexity of the b-BSD algorithm based on the density of binomial sequences has been introduced, but this topic requires further research to find hard proof on the number of sequences that appear in a binomial decomposition.
In regard to the f-BSD algorithm presented in this article, it shows better theoretical characteristics in both complexity and length of the sequence required. Future works may study the algorithm performance in real world scenarios by applying it to different binary sequences and taking advantage of the algorithm parallel capabilities.
To compare the performance of the novel f-BSD algorithm with b-BSD, we carried out experiments to analyze the number of decomposed sequences, as this parameter deeply affects the performance of the b-BSD algorithm. As a result of our experiments, we were able to approximate the value of the parameter and the performance of b-BSD, which helps to show how the new algorithm f-BSD improves its performance when the length of the sequence starts to grow.
Author Contributions
Conceptualization, J.L.M.-N. and A.F.-S.; methodology, J.L.M.-N. and A.F.-S.; software, J.L.M.-N.; validation, A.F.-S.; formal analysis, A.F.-S.; investigation, J.L.M.-N.; resources, A.F.-S.; data curation, J.L.M.-N. and A.F.-S.; writing—original draft preparation, A.F.-S.; writing—review and editing, J.L.M.-N. and A.F.-S.; visualization, J.L.M.-N.; supervision, A.F.-S.; project administration, A.F.-S.; funding acquisition, J.L.M.-N. and A.F.-S. All authors have read and agreed to the published version of the manuscript.
Funding
Research partially supported by Ministerio de Economía, Industria y Competitividad, Agencia Estatal de Investigación, and Fondo Europeo de Desarrollo Regional (FEDER, UE) under project COPCIS (TIN2017-84844-C2-1-R) and by Comunidad de Madrid (Spain) under project CYNAMON (P2018/TCS-4566), also co-funded by European Union FEDER funds.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Chin, W.L.; Li, W.; Chen, H.H. Energy big data security threats in IoT-based smart grid communications. IEEE Commun. Mag. 2017, 55, 70–75. [Google Scholar] [CrossRef]
- Meyer, D.; Haase, J.; Eckert, M.; Klauer, B. New attack vectors for building automation and IoT. In Proceedings of the IECON 2017 43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 8126–8131. [Google Scholar]
- Gallegos-Segovia, P.L.; Bravo-Torres, J.F.; Argudo-Parra, J.J.; Sacoto-Cabrera, E.J.; Larios-Rosillo, V.M. Internet of things as an attack vector to critical infrastructures of cities. In Proceedings of the 2017 International Caribbean Conference on Devices, Circuits and Systems (ICCDCS), Cozumel, Mexico, 5–7 June 2017; pp. 117–120. [Google Scholar]
- Rouf, I.; Miller, R.D.; Mustafa, H.A.; Taylor, T.; Oh, S.; Xu, W.; Gruteser, M.; Trappe, W.; Seskar, I. Security and Privacy Vulnerabilities of In-Car Wireless Networks: A Tire Pressure Monitoring System Case Study. In Proceedings of the USENIX Security Symposium, Washington, DC, USA, 11–13 August 2010. [Google Scholar]
- Cynthia, J.; Sultana, H.P.; Saroja, M.; Senthil, J. Security protocols for IoT. In Ubiquitous Computing and Computing Security of IoT; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–28. [Google Scholar]
- Mavromoustakis, C.X.; Mastorakis, G.; Batalla, J.M. Internet of Things (IoT) in 5G Mobile Technologies; Springer: Berlin/Heidelberg, Germany, 2016; Volume 8. [Google Scholar]
- NIST Lightweight Cryptography Project. Available online: https://csrc.nist.gov/Projects/Lightweight-Cryptography (accessed on 30 March 2020).
- McGinthy, J.M. Solutions for Internet of Things Security Challenges: Trust and Authentication. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2019. [Google Scholar]
- Peinado, A.; Munilla, J.; Fúster-Sabater, A. EPCGen2 Pseudorandom Number Generators: Analysis of J3Gen. Sensors 2014, 14, 6500–6515. [Google Scholar] [CrossRef] [PubMed]
- Peinado, A.; Munilla, J.; Fúster-Sabater, A. Revision of J3Gen and Validity of the Attacks by Peinado et al. Sensors 2015, 15, 11988–11992. [Google Scholar] [CrossRef] [PubMed]
- Cardell, S.D.; Requena, V.; Fúster-Sabater, A.; Orúe, A.B. Randomness Analysis for the Generalized Self-Shrinking Sequences. Symmetry 2019, 11, 1460. [Google Scholar] [CrossRef]
- Massey, J. Shift-register synthesis and BCH decoding. IEEE Trans. Inf. Theory 1969, 15, 122–127. [Google Scholar] [CrossRef]
- Cardell, S.D.; Fúster-Sabater, A. Binomial Representation of Cryptographic Binary Sequences and Its Relation to Cellular Automata. Complexity 2019, 2019, 2108014. [Google Scholar] [CrossRef]
- Chang, K.Y.; Lee, M.K.; Lee, H.R.; Do Won, H.O.N.G.; Kang, J.S.; Cho, H.S.; Chung, K.I. Method and Apparatus for Generating Keystream. U.S. Patent 7,587,046, 8 September 2009. [Google Scholar]
- Kang, Y.S.; Kim, H.W.; Chung, K.I. Apparatus and Method for Protecting RFID Data. U.S. Patent 8,386,794, 26 February 2013. [Google Scholar]
- Golomb, S.W. Shift Register Sequences; Aegean Park Press: Laguna Hills, CA, USA, 1967. [Google Scholar]
- Cardell, S.D.; Fúster-Sabater, A. The t-Modified self-shrinking generator. In Proceedings of the International Conference on Computational Science, Krakow, Poland, 16–18 June 2021; Springer: Berlin/Heidelberg, Germany, 2018; pp. 653–663. [Google Scholar]
- Cardell, S.D.; Fúster-Sabater, A. Cryptography with Shrinking Generators: Fundamentals and Applications of Keystream Sequence Generators Based on Irregular Decimation; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Coppersmith, D.; Krawczyk, H.; Mansour, Y. The shrinking generator. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 22–26 August 1993; Springer: Berlin/Heidelberg, Germany, 1993; pp. 22–39. [Google Scholar]
- Meier, W.; Staffelbach, O. The self-shrinking generator. In Communications and Cryptography; Springer: Berlin/Heidelberg, Germany, 1994; pp. 287–295. [Google Scholar]
- Hu, Y.; Xiao, G. Generalized self-shrinking generator. IEEE Trans. Inf. Theory 2004, 50, 714–719. [Google Scholar] [CrossRef]
- Fúster-Sabater, A.; Cardell, S.D. Linear complexity of generalized sequences by comparison of PN-sequences. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A Matemáticas 2020, 114, 79. [Google Scholar] [CrossRef]
- Cardell, S.D.; Climent, J.J.; Fúster-Sabater, A.; Requena, V. Representations of Generalized Self-Shrunken Sequences. Mathematics 2020, 6, 1006. [Google Scholar] [CrossRef]
- Fúster-Sabater, A. Generation of cryptographic sequences by means of difference equations. Appl. Math. Inf. Sci. 2014, 8, 475. [Google Scholar] [CrossRef]
- Cusick, T.W.; Stanica, P. Cryptographic Boolean Functions and Applications; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Martin-Navarro, J.L.; Fúster-Sabater, A. Folding-BSD Algorithm for Binary Sequence Decomposition. In Proceedings of the International Conference on Computational Science and Its Applications, Santa Barbara, CA, USA, 22–26 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 345–359. [Google Scholar]
- Martín-Navarro, J.L.; Fúster-Sabater, A.; Cardell, S.D. An Innovative Linear Complexity Computation for Cryptographic Sequences. In Proceedings of the Conference on Complex, Intelligent, and Software Intensive Systems, Loze, Poland, 1–3 July 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 339–349. [Google Scholar]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).