Inertial Sensor Based Solution for Finger Motion Tracking
Abstract
1. Introduction
1.1. Motivation
- Top level (map level),
- Object level,
- Source level.
1.2. Tracking Approaches
1.2.1. Related Works
- Solutions that use magnetometers cannot operate correctly in a significantly non-homogeneous magnetic field; otherwise, they require a complex calibration procedure,
- Methods that use only 6D data do not provide absolute yaw information, or require a resetting procedure, and suffer from drift,
- Most existing solutions include three inertial sensors on a finger to independently track the orientation of each phalange and, thus, do not take into account some important details of finger movement,
- Mixed solutions can include all limitations listed above or combine some.
1.2.2. Proposed Approach
2. Materials and Methods
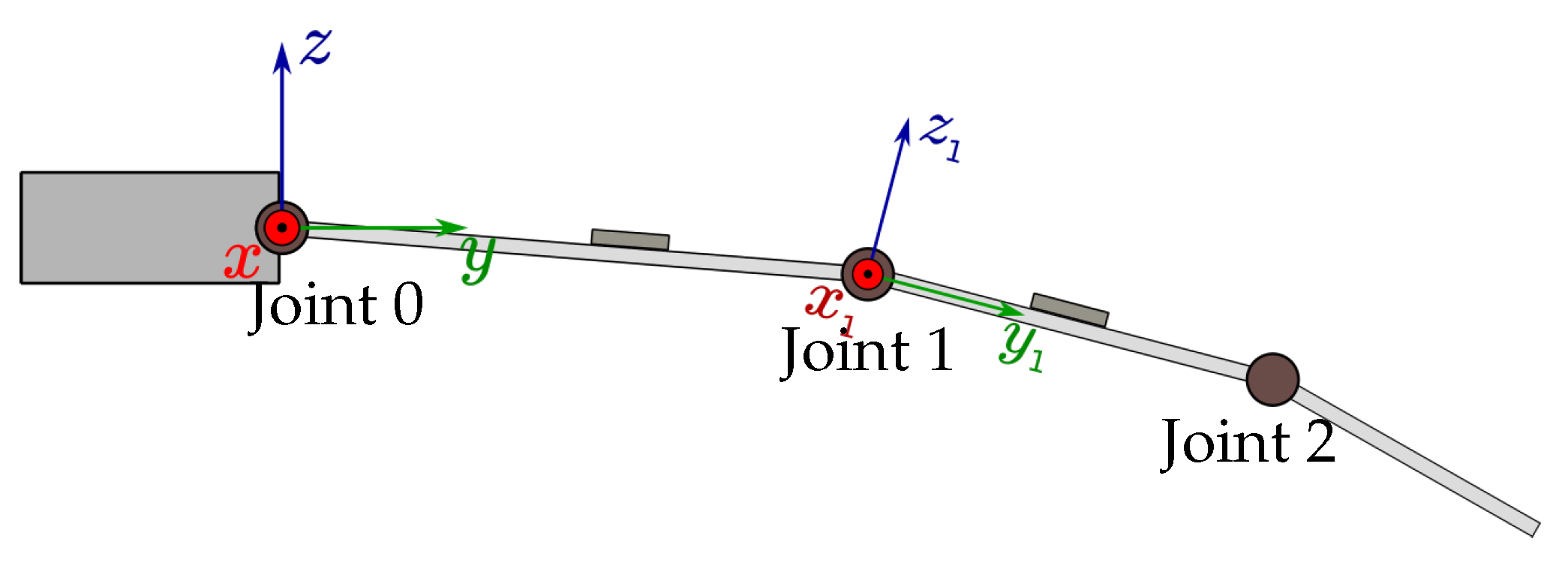
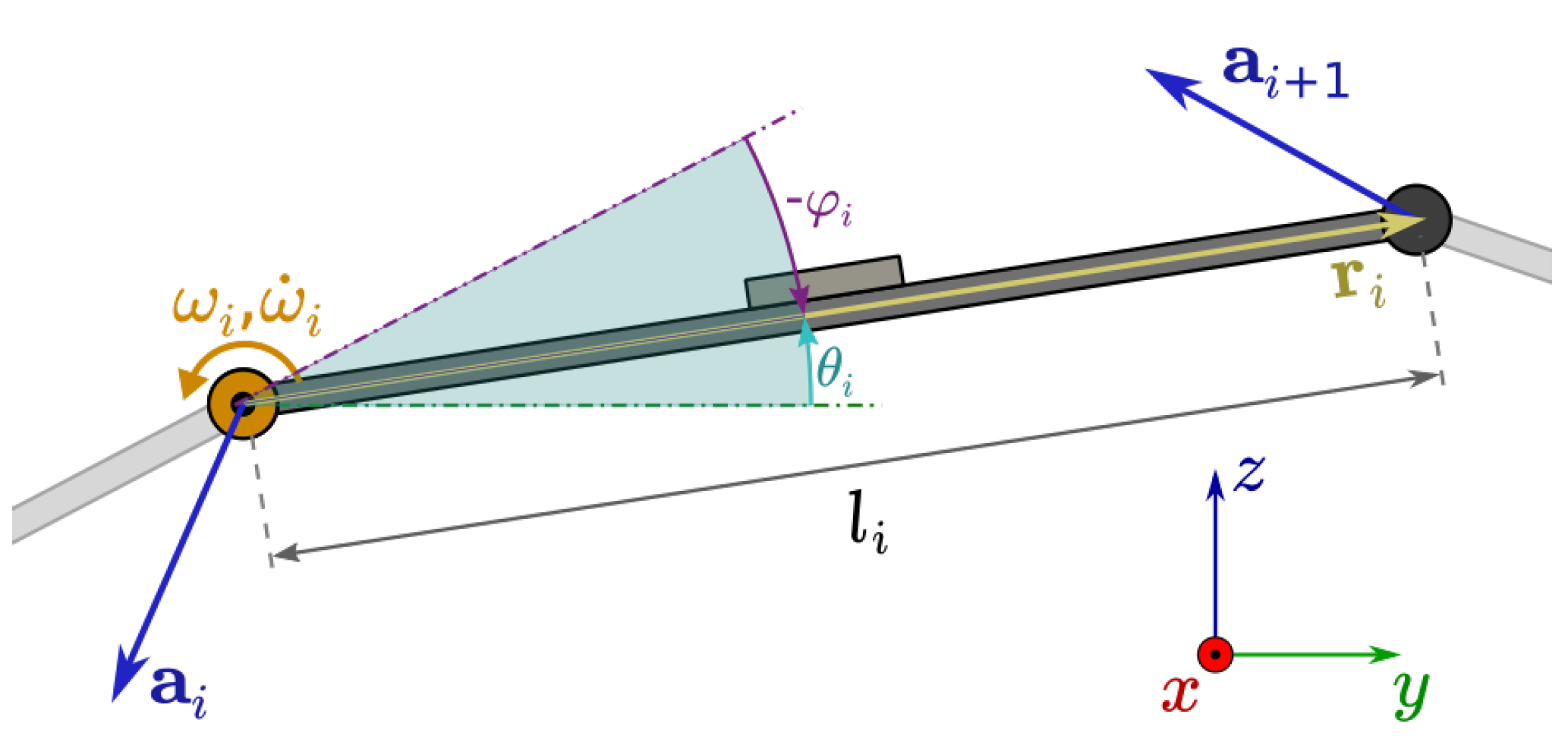
2.1. Finger Model
2.2. Simple Switching Tracking Algorithm
2.2.1. Algorithm of The Position Estimation of The Single Phalange
2.2.2. Slow Motion Estimation
2.2.3. Fast Movement Estimation
2.2.4. Errors in The Estimation Algorithms for Slow and Fast Motion
2.2.5. Switching Algorithm
- 1.
- receive sensor readings ;
- 2.
- calculate and ;
- 3.
- choose the estimation mode:
- if currently in fast motion mode and , then switch to slow motion mode, and assign ;
- if currently in slow motion mode and , then switch to fast motion mode, taking as the initial estimate, and assign .
- 4.
- Calculate a new orientation estimate using the currently selected estimation algorithm.
2.3. Madgwick Filter Modification
2.3.1. Finger Rotation Estimation
2.3.2. Combining Filter Algorithm
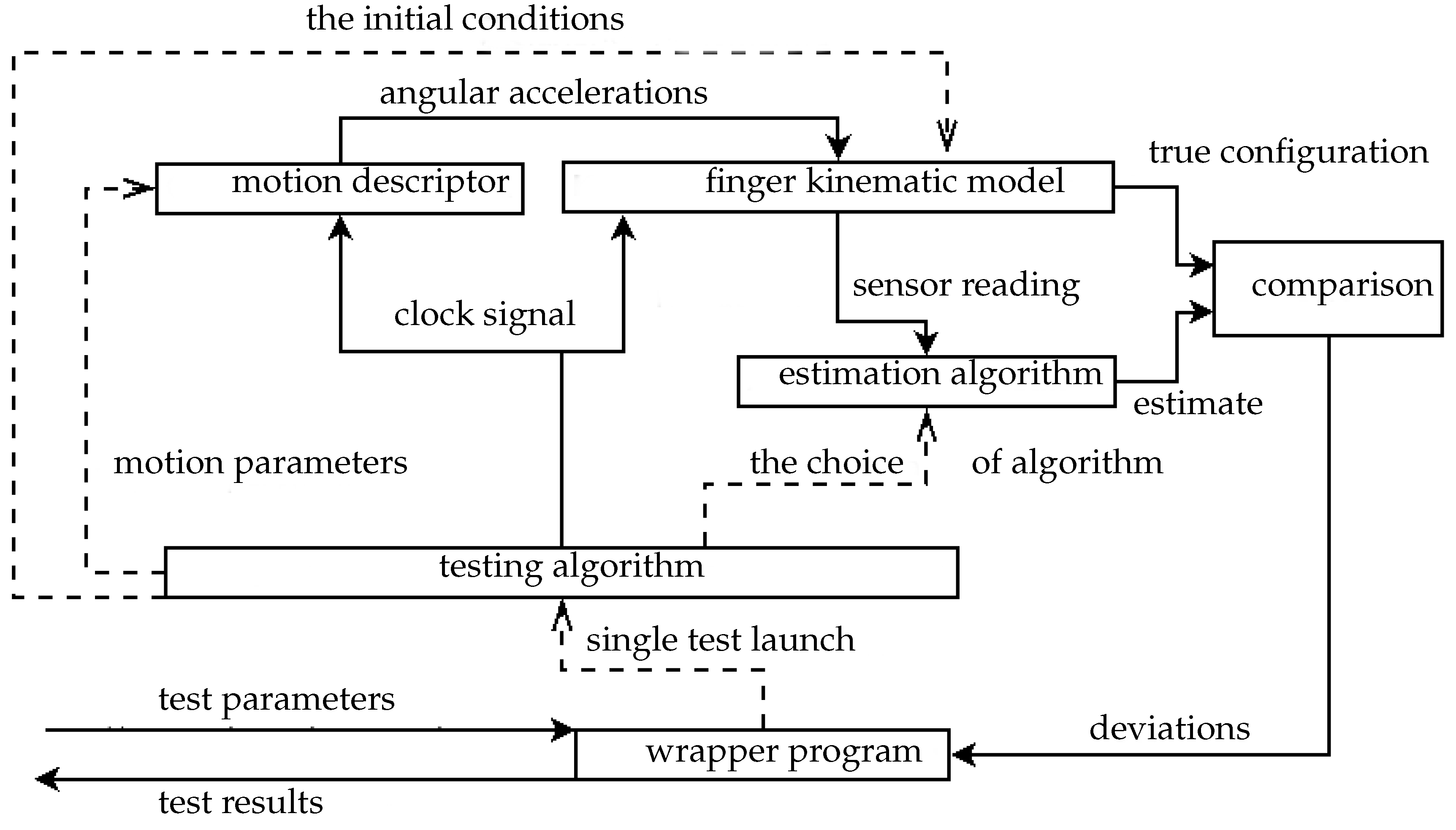
3. Verification of Algorithms Using Numerical Model Data
- a model of a moving finger equipped with inertial sensors,
- a set of parametric descriptors for some groups of finger movements,
- implementations of the simple switching algorithm and the modified Madgwick filter,
- a wrapper program applying logic to conducting tests of estimation algorithms on generated model data.
- A static interval lasting ;
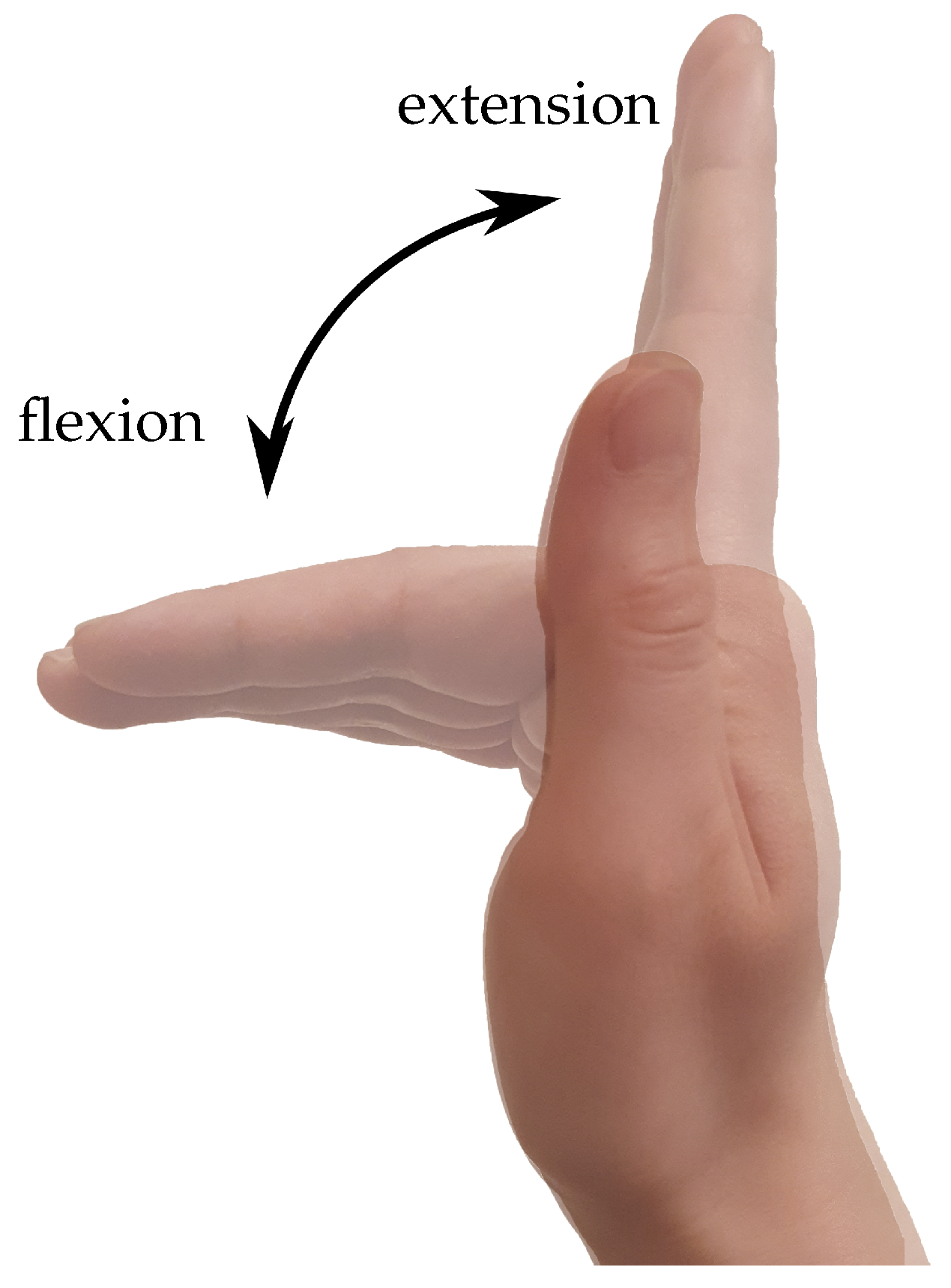
- The extension of a straight finger in the MCPjoint (Joint 0) to a angle lasting ;
- Simultaneous flexion of the finger in Joint 0 to and in the interphalangeal (1 and 2) joints to an angle of lasting .
- Initial conditions for the kinematic model of the finger were specified. This position was considered as the known accurate initial estimate.
- The motion and its parameters were specified.
- The modeling of a given movement was performed, during which we collected data with a given sampling rate:
- -
- the readings of virtual sensors were calculated and transferred to the evaluation algorithm with the addition of sensor errors;
- -
- the current true configuration (phase coordinates and speeds) of the finger model and the configuration estimate by the algorithm were recorded.
- After the simulation was completed, a measure of the deviation of the estimate from the actual configuration was calculated.
- with white noise;
- with a zero offset;
- with errors of both kinds.
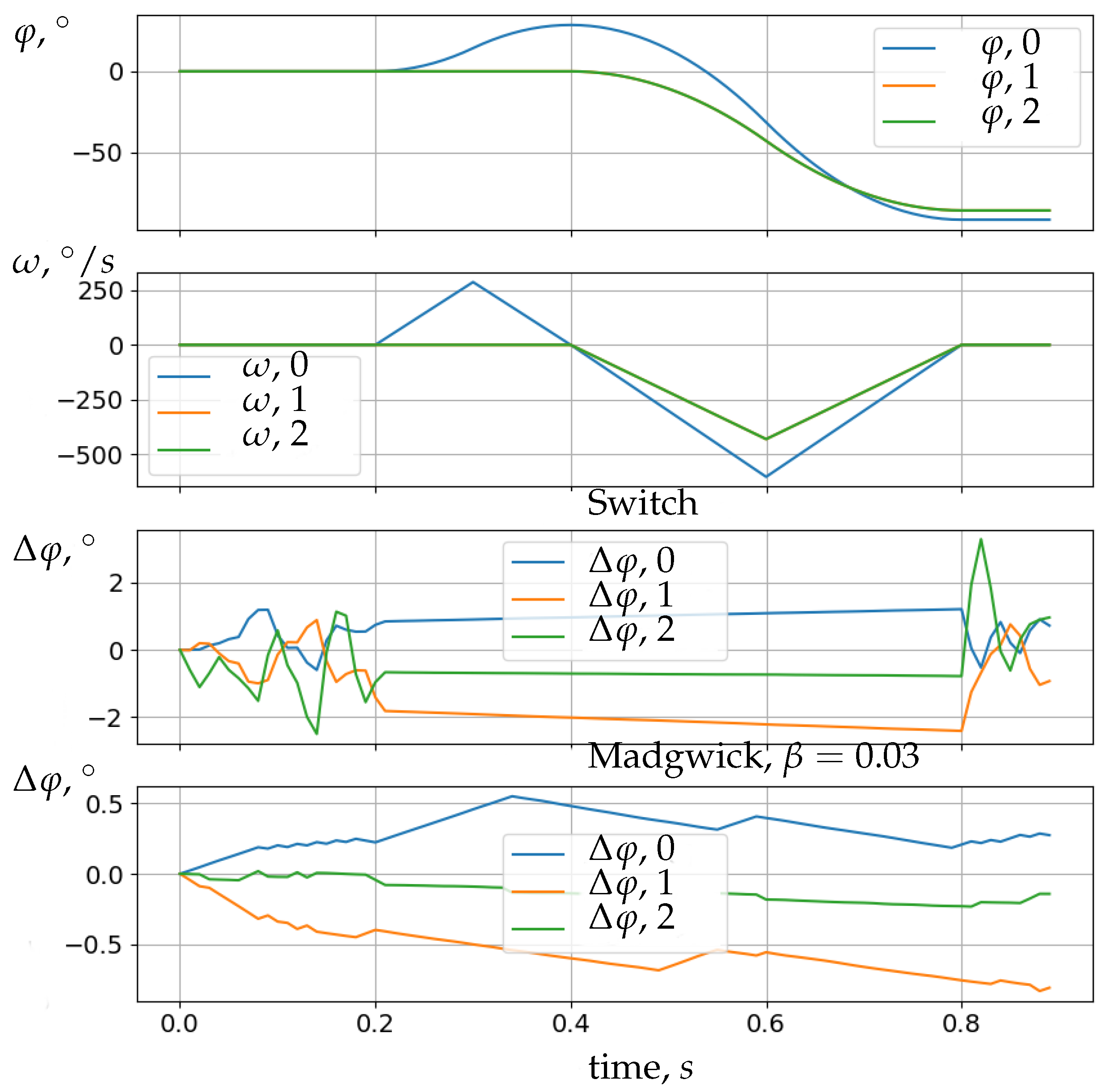
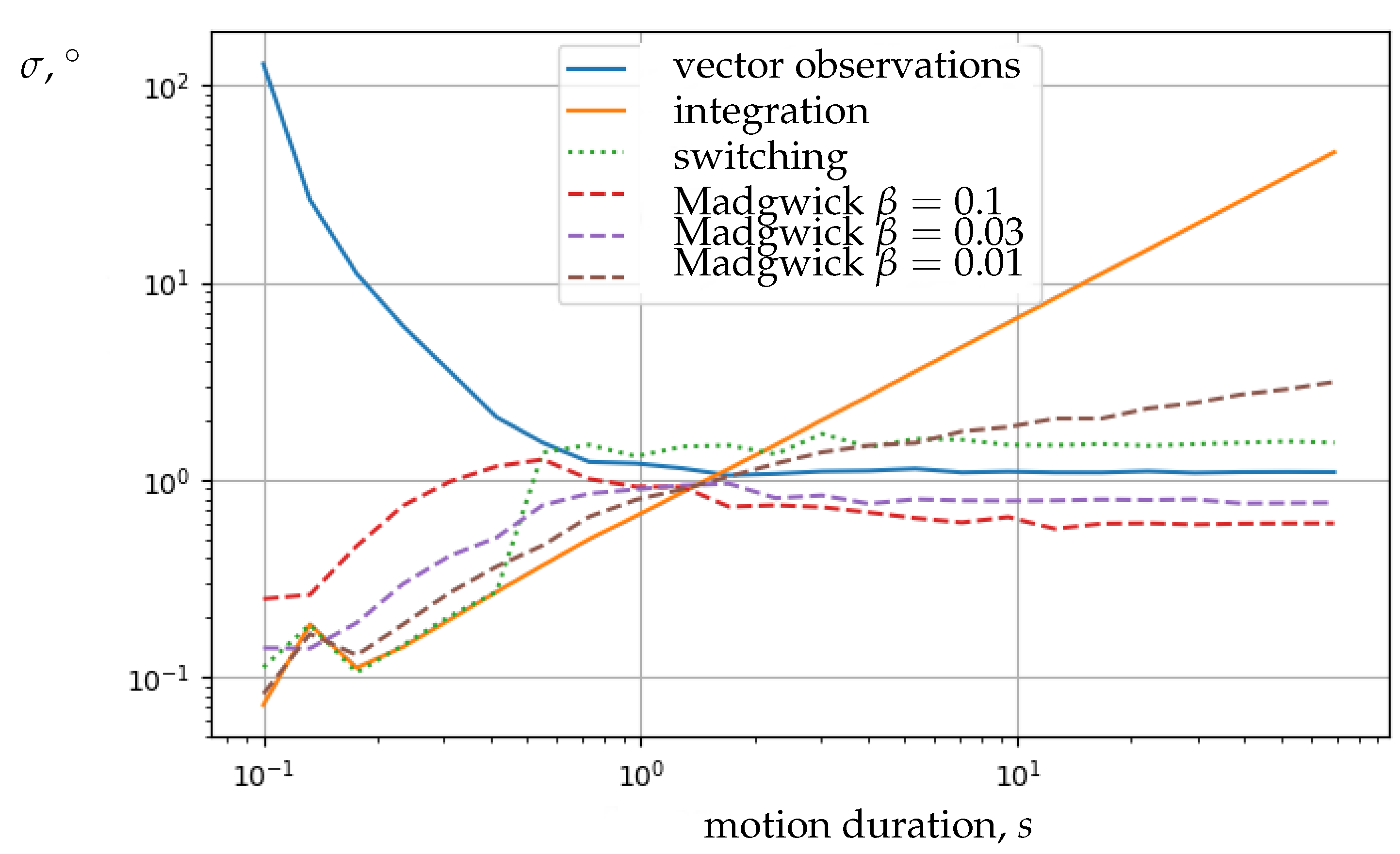
Test Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| IMU | Inertial Measurement Unit |
| AVS | Angular Velocity Sensor |
| INS | Inertial Navigation System |
| RMS | Root-Mean-Square |
| VR | Virtual Reality |
References
- Lemak, S.; Chertopolokhov, V.; Kruchinina, A.; Belousova, M.; Borodkin, L.; Mironenko, M. O zadache optimizatsii raspolozheniya elementov interfeysa v virtual’noy real’nosti (v kontekste sozdaniya virtual’noy rekonstruktsii istoricheskogo rel’yefa Belogo goroda). Istor. Inform. 2020, 67–76. [Google Scholar] [CrossRef]
- Borodkin, L.; Mironenko, M.; Chertopolokhov, V.; Belousova, M.; Khlopikov, V. Tekhnologii virtual’noy i dopolnennoy real’nosti (vr/ar) v zadachakh rekonstruktsii istoricheskoy gorodskoy zastroyki (na primere moskovskogo Strastnogo monastyrya). Istor. Inform. 2018, 76–88. [Google Scholar] [CrossRef]
- Figueiredo, L.; Rodrigues, E.; Teixeira, J.; Teichrieb, V. A comparative evaluation of direct hand and wand interactions on consumer devices. Comput. Graph. 2018, 77, 108–121. [Google Scholar] [CrossRef]
- Wachs, J.; Stern, H.; Edan, Y.; Gillam, M.; Feied, C.; Smith, M.; Handler, J. A Real-Time Hand Gesture Interface for Medical Visualization Applications. In Applications of Soft Computing; Tiwari, A., Roy, R., Knowles, J., Avineri, E., Dahal, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 153–162. [Google Scholar]
- Tamura, H.; Liu, J.; Luo, Y.; Ju, Z. An Interactive Astronaut-Robot System with Gesture Control. Comput. Intell. Neurosci. 2016. [Google Scholar] [CrossRef]
- Yang, L.; Jin, H.; Feng, T.; Hong-An, W.; Guo-Zhong, D. Gesture interaction in virtual reality. Virtual Real. Intell. Hardw. 2019, 1, 84–112. [Google Scholar] [CrossRef]
- Bugrov, D.; Lebedev, A.; Chertopolokhov, V. Estimation of the angular rotation velocity of a body using a tracking system. Mosc. Univ. Mech. Bull. 2014, 69, 25–27. [Google Scholar] [CrossRef]
- Colyer, S.; Evans, M.; Cosker, D.; Salo, A. A Review of the Evolution of Vision-Based Motion Analysis and the Integration of Advanced Computer Vision Methods Towards Developing a Markerless System. Sports Med. Open 2018, 4, 24. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Meydan, T.; Williams, P. A Two-Axis Goniometric Sensor for Tracking Finger Motion. Sensors 2017, 17, 770. [Google Scholar] [CrossRef]
- Zhang, Z. The Design and Analysis of Electromagnetic Tracking System. J. Electromagn. Anal. Appl. 2013, 5, 85–89. [Google Scholar] [CrossRef][Green Version]
- Paperno, E.; Sasada, I.; Leonovich, E. A new method for magnetic position and orientation tracking. Magn. IEEE Trans. 2001, 37, 1938–1940. [Google Scholar] [CrossRef]
- Raab, F.; Blood, E.; Steiner, T.; Jones, H.R. Magnetic position and orientation tracking system. IEEE Trans. Aerosp. Electron. Syst. 1979, 15, 709–718. [Google Scholar] [CrossRef]
- Vavilova, N.B.; Golovan, A.A.; Parusnikov, N.A. Problem of information equivalent functional schemes in aided inertial navigation systems. Mech. Solids 2008, 43, 391–399. [Google Scholar] [CrossRef]
- Choi, Y.; Yoo, K.; Kang, S.; Seo, B.; Kim, S.K. Development of a low-cost wearable sensing glove with multiple inertial sensors and a light and fast orientation estimation algorithm. J. Supercomput. 2016, 74. [Google Scholar] [CrossRef]
- Lin, B.S.; Lee, I.J.; Yang, S.Y.; Lo, Y.C.; Lee, J.; Chen, J.L. Design of an Inertial-Sensor-Based Data Glove for Hand Function Evaluation. Sensors 2018, 18, 1545. [Google Scholar] [CrossRef]
- Salchow-Hömmen, C.; Callies, L.; Laidig, D.; Valtin, M.; Schauer, T.; Seel, T. A Tangible Solution for Hand Motion Tracking in Clinical Applications. Sensors 2019, 19, 208. [Google Scholar] [CrossRef]
- Bellitti, P.; Bona, M.; Borghetti, M.; Sardini, E.; Serpelloni, M. Sensor Analysis for a Modular Wearable Finger 3D Motion Tracking System. Proceedings 2018, 2, 1051. [Google Scholar] [CrossRef]
- Bellitti, P.; Angelis, A.; Dionigi, M.; Sardini, E.; Serpelloni, M.; Moschitta, A.; Carbone, P. A Wearable and Wirelessly Powered System for Multiple Finger Tracking. IEEE Trans. Instrum. Meas. 2020, 69, 2542–2551. [Google Scholar] [CrossRef]
- Maereg, A.; Secco, E.; Agidew, T.; Reid, D.; Nagar, A. A Low-Cost, Wearable Opto-Inertial 6-DOF Hand Pose Tracking System for VR. Technologies 2017, 5, 49. [Google Scholar] [CrossRef]
- Madgwick, S.; Harrison, A.; Vaidyanathan, R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In Proceedings of the International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; p. 5975346. [Google Scholar] [CrossRef]
- Lin, B.S.; Lee, I.J.; Chiang, P.Y.; Huang, S.Y.; Peng, C.W. A Modular Data Glove System for Finger and Hand Motion Capture Based on Inertial Sensors. J. Med. Biol. Eng. 2019, 39, 532–540. [Google Scholar] [CrossRef]
- Laidig, D.; Lehmann, D.; Bégin, M.A.; Seel, T. Magnetometer-free Realtime Inertial Motion Tracking by Exploitation of Kinematic Constraints in 2-DoF Joints. In Proceedings of the 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; Volume 2019, pp. 1233–1238. [Google Scholar] [CrossRef]
- Hulst, F.; Schätzle, S.; Preusche, C.; Schiele, A. A functional anatomy based kinematic human hand model with simple size adaptation. In Proceedings of the IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–19 May 2012; pp. 5123–5129. [Google Scholar] [CrossRef]
- Buchholz, B.; Armstrong, T. A kinematic model of the human hand to evaluate its prehensile capabilities. J. Biomech. 1992, 25, 149–162. [Google Scholar] [CrossRef]
- Cobos, S.; Ferre, M.; Uran, M.; Ortego, J.; Peña Cortés, C. Efficient Human Hand Kinematics for Manipulation Tasks. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 2246–2251. [Google Scholar] [CrossRef]
- Chen, F.; Appendino, S.; Battezzato, A.; Favetto, A.; Mousavi, M.; Pescarmona, F. Constraint Study for a Hand Exoskeleton: Human Hand Kinematics and Dynamics. J. Robot. 2013, 2013. [Google Scholar] [CrossRef]
- Chao, E.Y.S.; An, K.N.; Cooney, W.P.; Linscheid, R.L. Normative Model of Human Hand; World Scientific: Singapore, 1989. [Google Scholar]
- Lenarčič, J.; Bajd, T.; Stanišić, M. Kinematic Model of the Human Hand. In Robot Mechanisms; Springer: Berlin, Germany, 2013; pp. 313–326. [Google Scholar]
- Stillfried, G. Kinematic Modelling of the Human Hand for Robotics. Ph.D. Thesis, Technische Universitat Munchen, Munchen, Germany, 2015. [Google Scholar]
- van Beers, R.; Sittig, A.; van der Gon, J. Integration of proprioceptive and visual position-information: An experimentally supported model. J. Neurophysiol. 1999, 81, 1355–1364. [Google Scholar] [CrossRef] [PubMed]
- Bokov, T.; Suchalkina, A.; Yakusheva, E.; Yakushev, A. Mathematical modelling of vestibular nystagmus. Part I. The statistical model. Russian J. Biomech. 2014, 18, 40–56. [Google Scholar]
- DEXMART. Kinematic Modelling of the Human Hand; Technical Report; Dexmart Deliverable D1.1: Napoli, Italy, 2009. [Google Scholar]
- Hazewinkel, M. Encyclopedia of Mathematics; Springer Science+Business Media B.V.; Kluwer Academic Publishers: Berlin, Germany, 1994. [Google Scholar]
- InvenSense, I. MPU-9250 Product Specification; Revision 1.1; InvenSense Inc.: San Hosem CA, USA, 2014. [Google Scholar]
- Fahn, C.S.; Sun, H. Development of a Fingertip Glove Equipped with Magnetic Tracking Sensors. Sensors 2010, 10, 1119–1140. [Google Scholar] [CrossRef]
- Borodkin, L.I.; Valetov, T.Y.; ZHerebyat’ev, D.I.; Mironenko, M.S.; Moor, V.V. Reprezentaciya i vizualizaciya v onlajne rezul’tatov virtual’noj rekonstrukcii. Istor. Inform. 2015, 3–4, 3–18. [Google Scholar]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lemak, S.; Chertopolokhov, V.; Uvarov, I.; Kruchinina, A.; Belousova, M.; Borodkin, L.; Mironenko, M. Inertial Sensor Based Solution for Finger Motion Tracking. Computers 2020, 9, 40. https://doi.org/10.3390/computers9020040
Lemak S, Chertopolokhov V, Uvarov I, Kruchinina A, Belousova M, Borodkin L, Mironenko M. Inertial Sensor Based Solution for Finger Motion Tracking. Computers. 2020; 9(2):40. https://doi.org/10.3390/computers9020040
Chicago/Turabian StyleLemak, Stepan, Viktor Chertopolokhov, Ivan Uvarov, Anna Kruchinina, Margarita Belousova, Leonid Borodkin, and Maxim Mironenko. 2020. "Inertial Sensor Based Solution for Finger Motion Tracking" Computers 9, no. 2: 40. https://doi.org/10.3390/computers9020040
APA StyleLemak, S., Chertopolokhov, V., Uvarov, I., Kruchinina, A., Belousova, M., Borodkin, L., & Mironenko, M. (2020). Inertial Sensor Based Solution for Finger Motion Tracking. Computers, 9(2), 40. https://doi.org/10.3390/computers9020040




