Evaluation of a Cyber-Physical Computing System with Migration of Virtual Machines during Continuous Computing

Abstract

The Markov model of reliability of a failover cluster performing calculations in a cyber-physical system is considered. The continuity of the cluster computing process in the event of a failure of the physical resources of the servers is provided on the basis of virtualization technology and is associated with the migration of virtual machines. The difference in the proposed model is that it considers the restrictions on the allowable time of interruption of the computational process during cluster recovery. This limitation is due to the fact that, if two physical servers fail, then object management is lost, which is unacceptable. Failure occurs if their recovery time is longer than the maximum allowable time of interruption of the computing process. The modes of operation of the cluster with and without system recovery in the event of a failure of part of the system resources that do not lead to loss of continuity of the computing process are considered. The results of the article are aimed at the possibility of assessing the probability of cluster operability while supporting the continuity of computations and its running to failure, leading to the interruption of the computational (control) process beyond the maximum permissible time. As a result of the calculation example for the presented models, it was shown that the mean time to failure during recovery under conditions of supporting the continuity of the computing process increases by more than two orders of magnitude.

1. Introduction

Cyber-physical systems are characterized by a direct interaction between computational processes in computer systems and physical processes in the real world. A cyber-physical system is a complex system of computing and physical elements, that receives arrays of data from the environment and uses them to make decisions on managing objects. Currently, such systems are complex and diverse and they pass the stage of rapid development. Cyber-physical systems are one of the results of global progress in the field of industry and technology.

Cyber-physical systems are connected to the physical world through sensors, with the help of which they receive information processed inside such a system and convert them into decisions and actions on real objects. The growth in the number of devices with built-in processors and storage means has made cyber-physical systems the most relevant in the modern world. Cyber-physical systems are many times superior to human ability to control physical objects, which is precisely why such systems are increasingly fulfilling roles intended only for humans in the past.

The scopes of cyber-physical systems are as follows:

• Cyber-physical systems can improve production processes by providing real-time information exchange between agents in the production chain.
• Cyber-physical systems can monitor indicators of the human body.
• In “smart” cities, houses, and devices, cyber-physical systems can optimize the use of resources for the most efficient existence of this environment.
• In the transport infrastructure, such systems can optimize traffic by processing traffic information, repairs, and other information.
• In the information space of the Internet, cyber-physical systems can improve the interaction of applications with users.

The functioning of cyber-physical systems is associated with a number of problems. The main requirements for such systems in the fields of transport, healthcare, and critical computing are reliability and safety. In the case of failures, measures should be considered to eliminate and minimize the negative consequences. The probability of failures and malfunctions in such systems should be minimized. The influence of such systems on the surrounding physical world should be closely controled and monitored, because failure to perform actions or their incorrect execution can lead to long-term damage.

The following information and communication tools can be distinguished as part of cyber-physical systems by physical location:

• Embedded computers are directly connected and located in the construct of the physical system; as a rule, they implement real-time monitoring and control functions. Classic embedded systems are implemented on the basis of controllers that perform control functions. With the limited computing capabilities of the controllers, they implement the lower level of control, often based on a simplified view of the physical object and the environment. Modern cyber-physical systems can exist and make decisions in the real modern world; accordingly, the security and accuracy of the decisions of such systems have increased.
• Cluster computer systems: A cluster is a related summation of several computing systems, working together to perform a common task. In the event of failure of cluster nodes, their functions are redistributed among other devices. The cluster implements the functions of the upper level control of the cyber-physical system.
• Distributed computer systems: A distributed system is a system in which the processing of information is concentrated not on one computer, but distributed among several computers.
• Networks: They are designed to interconnect computer systems.

Based on the above systems, modern cyber-physical systems have appeared and are developing.

For cluster computing cyber-physical systems, especially in real-time, the key is to ensure reliability and fault tolerance while maintaining the continuity of the computing process. The achievement of high and stable performance indicators, reliability, fault tolerance [1,2,3], and security of computer systems is facilitated by the use of technologies for consolidation of clustering and virtualization resources, accompanied by replication and migration of virtual machines between physical servers. Migration and replication of virtual machines speed up the reconfiguration process after failures of physical resources and contribute to support the continuity of the computing process required for managing cyber-physical systems and real-time technological processes [4,5,6].

One of the effective ways to achieve fault tolerance of computing systems and processes is the migration of virtual resources between the physical nodes of a computing system of a cluster architecture. In a cluster with replication of VM (Virtual machines) on different physical nodes, they can migrate between cluster nodes in the event of failure of physical resources without stopping calculations on servers [7,8].

Virtualization allows optimizing the use of computing resources, increases the scalability, fault tolerance, and extensibility of the infrastructure, due to the rapid redistribution of the virtual resource [9,10,11].

Fault tolerance provides continuity of the computing process in the cluster. In Random Access Memory (RAM), two copies of the VM (Virtual machines) are located on different physical servers. Thus, after the failure of one of the physical servers, the calculations continue on the second. In this case, the virtual disk images of the VM should be stored on a dedicated or distributed data storage with synchronous data replication [12,13,14].

In the well-known works [7,8,9,10,11,12,13,14] related to ensuring the reliability of cluster systems based on the migration of virtual machines, issues of ensuring the reliability of real-time cluster systems are not discussed, for which strict requirements are imposed on the continuity of the computing process, including when the recovery time after failures of redundant resources may exceed the maximum allowable time of interruption of the computing process. In such systems, resource failures that provide computation during recovery of failed resources are critical. To analyze the reliability of cluster systems with fault tolerance based on the migration of virtual machines, Markov models are known [15,16,17,18,19], but they do not take into account the considered features of real-time cluster systems associated with the possibility of disruption in the continuity of the computing process. The importance of these studies is associated with the criticality of the security of cyber-physical systems to possible violations of the continuity of the computing process.

The purpose of the work is to increase the functional reliability of a computer cluster with real-time virtual machine migration, for which the maximum allowable time for the interruption of the computing process due to failures is less than the system recovery time after failures.

A feature of the considered approach to assessing functional reliability is that the system failure conditions are associated not only with structural failures of the system nodes, but also with possible violations of the continuity of the computing process for a time longer than the maximum permissible.

By functional reliability, we mean the ability of systems to perform the required functions, taking into account the operability of the resources involved and ensuring the conditions for their implementation, including computational delays and ensuring the continuity of processing and data transfer processes. Thus, the requirements for ensuring the continuity of the computational process can be put forward as working conditions in the case of inadmissibility of interruptions in the operation of the redundant system in the process of its restoration or reconfiguration.

To achieve this goal, this article assumes the following:

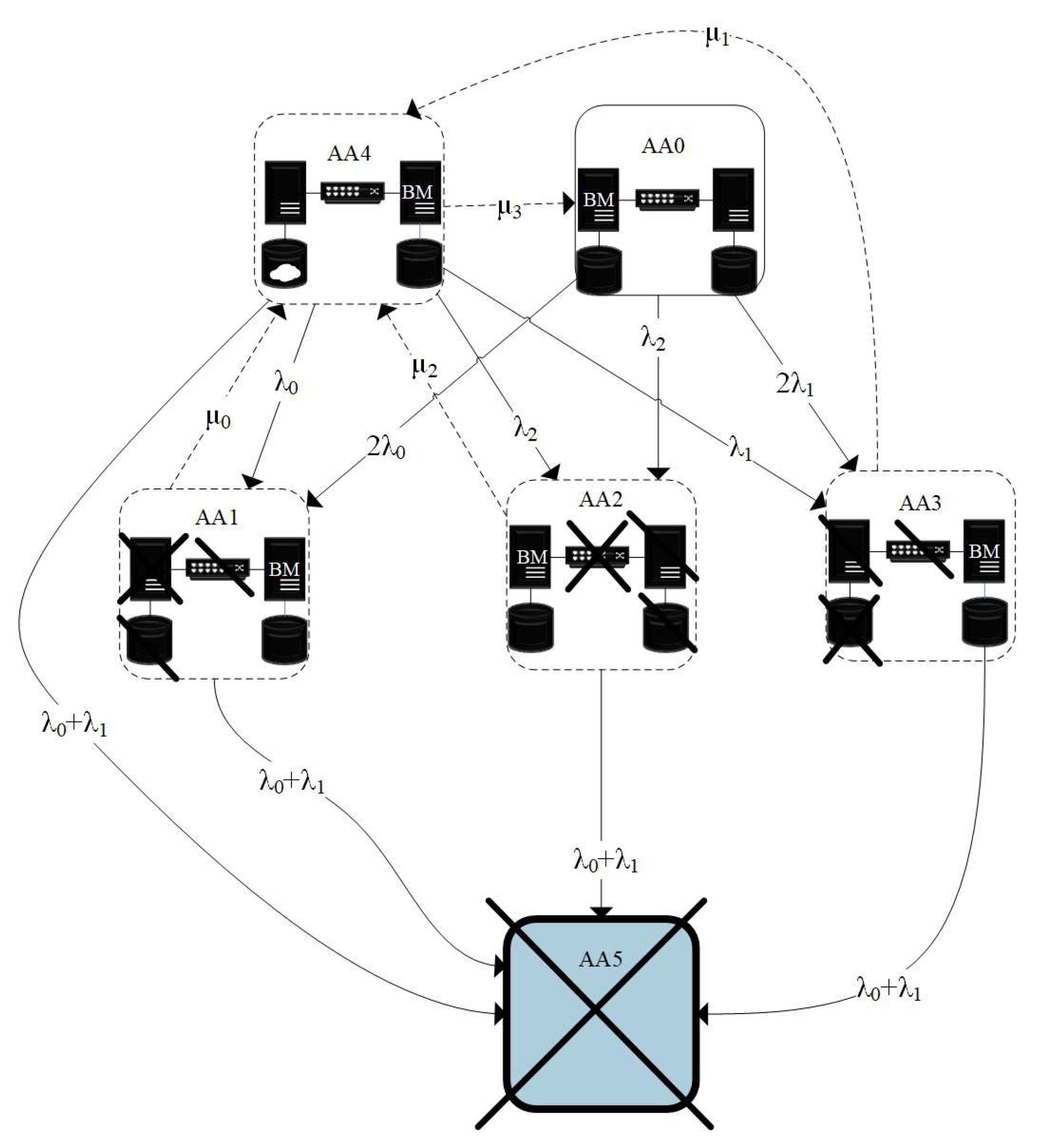
• A Markov model reflecting the restrictions on the maximum permissible interruption of the computing process and the danger of violations of these restrictions during the implementation of calculations in the recovery period of failed computing resources is constructed (Markov model of a system with the migration of virtual machines while ensuring the continuity of the computing process).
• The model is modified with the modes of functioning of the cluster without restoring the system in the case of failure of part of the system resources that do not lead to loss of continuity of the computing process (Markov model of a system with the migration of virtual machines while ensuring the continuity of the computing process).
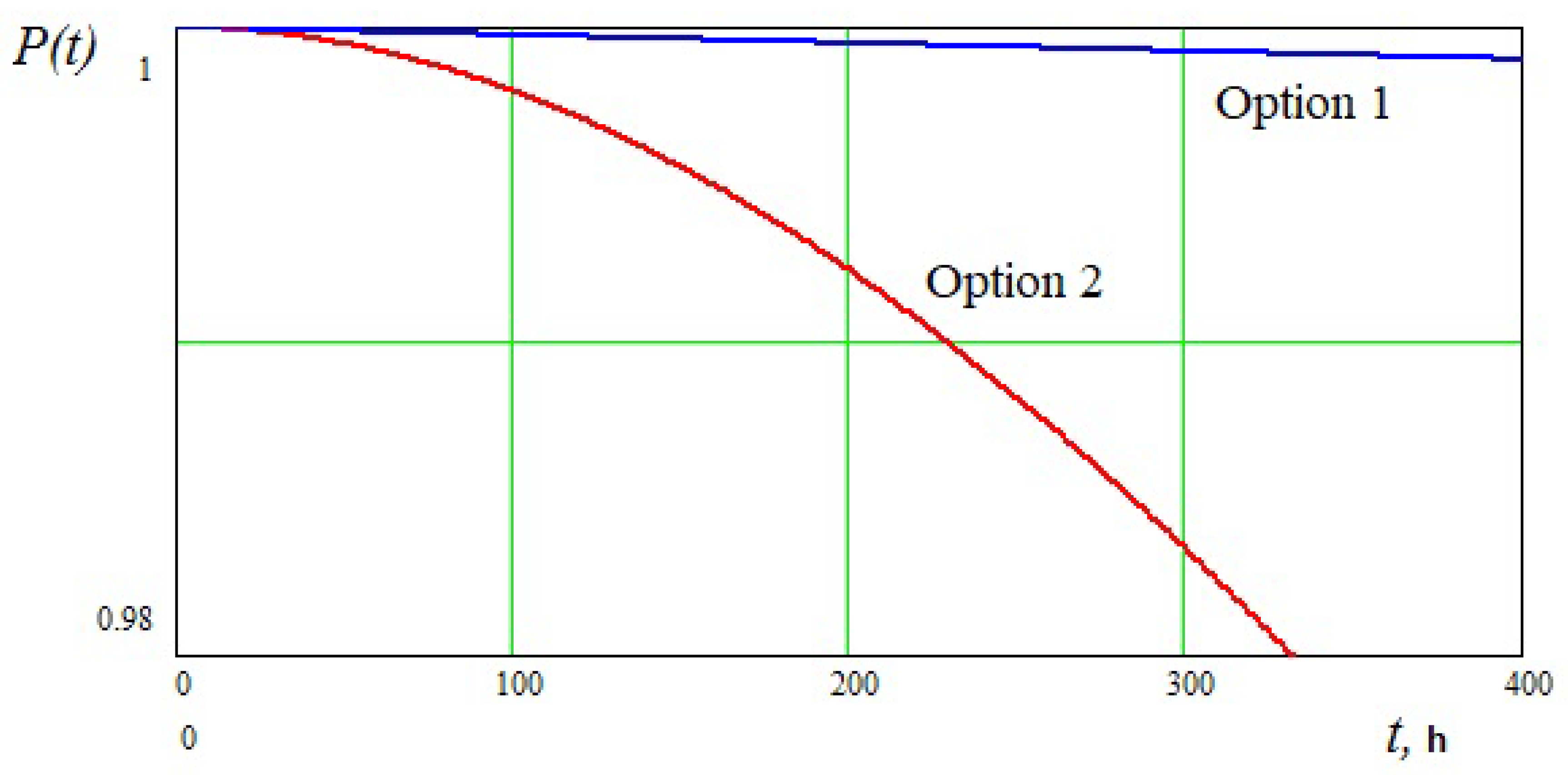
• The probability of system operability while ensuring continuity of calculations is assessed (calculation of the probability of operability of duplicated systems)
• The time to failure, leading to the interruption of the computational (control) process in excess of the maximum permissible time, is estimated (calculation of the probability of operability of duplicated systems)

This cluster architecture computer system contains servers (Figure 1). Each server is connected directly to one local storage device. In the system for providing automatic reconfiguration, aimed at supporting the continuity of computing processes in the cluster, pairs of physical servers of the primary and backup are allocated. The main server performs the required tasks critical to the continuity of the computing process. The backup server is designed to perform dynamic reconfiguration with ensuring the continuity of the computing process in case of possible failures of the primary server. The backup server, in addition to implementing dynamic system reconfiguration, performs some background tasks that are not critical to the continuity of the computational process and to the time of query execution.

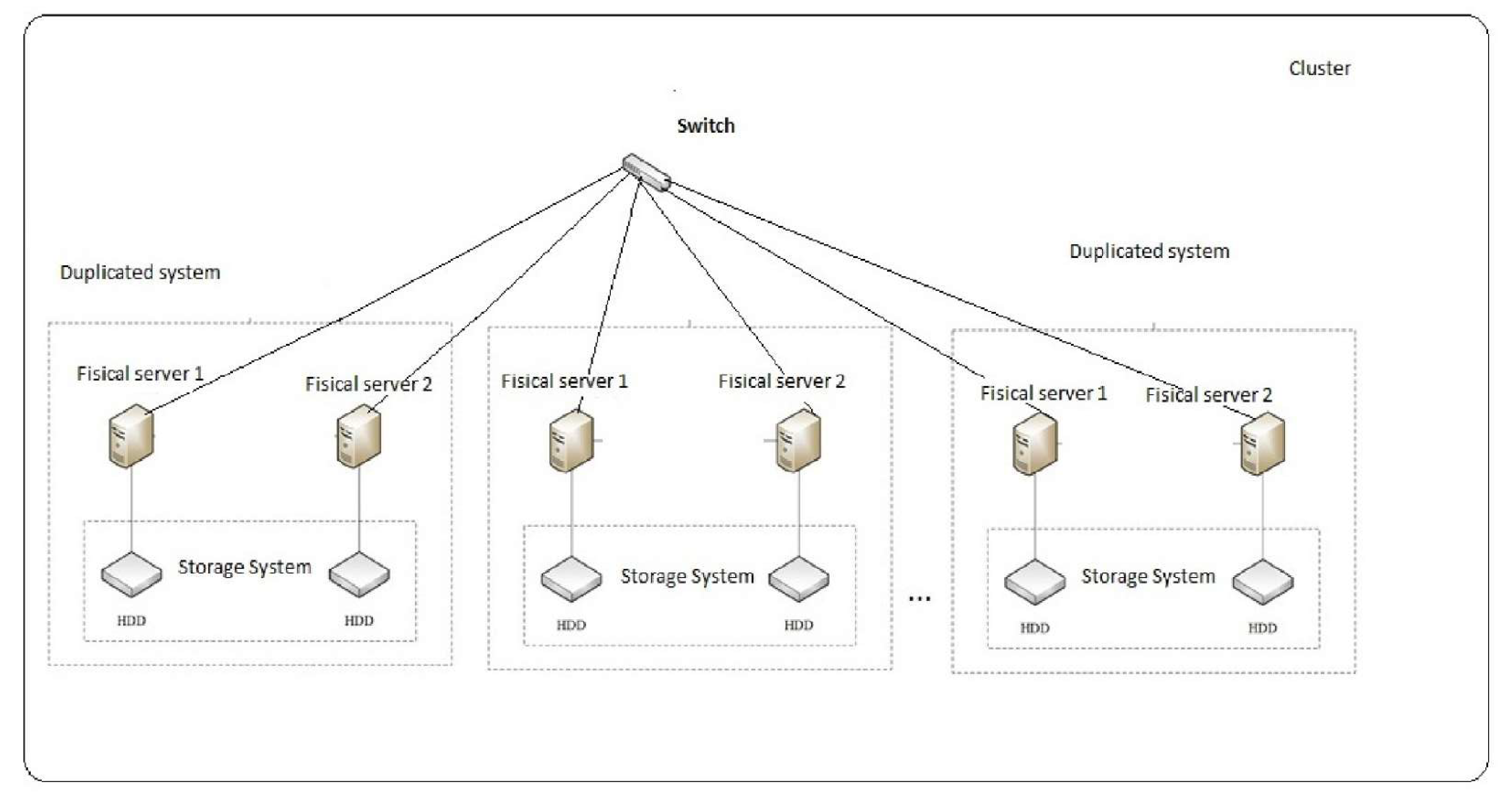
2. Cluster Organization and Options for Its Recovery

Consider the options for the discipline of maintaining systems with fault tolerance based on virtual machines:

• Option A provides for system recovery, provided there is no disruption to the continuity of the computing process.
• Option B does not involve system recovery.

Option B is possible with limited system maintenance, for example due to its autonomous operation.

A situation of disruption of the computational process continuity with Option A is possible, for example, when nodes supporting computations fail during the recovery of failed resources. In this case, the reserve has been exhausted, and the time of their recovery of the cluster exceeds the maximum permissible time of disruption of the continuity of the computing process.

For the considered options for servicing the transition to the state of failure with the inability to implement the required functions for a time exceeding the specified maximum permissible value, it entails the transition to the state of unrecoverable failure.

3. Markov Model of a System with the Migration of Virtual Machines While Ensuring the Continuity of the Computing Process

We construct a Markov model of the reliability of a real-time computer cluster with the migration of virtual machines, for which the condition for operability is the inadmissibility of interruption of the computing process.

We assume that a violation of the continuity of the computing process occurs when, during the recovery of failed nodes, the resources involved in performing functional tasks fail, when their reserve in the cluster is exhausted, and the recovery time exceeds the allowable interruption time of the computing process.

To emphasize the model on the study of the influence of disruptions in the computational process on cluster reliability, we consider the simplest case of pairwise integration of physical servers to ensure the fault tolerance of such pairs during migration of virtual machines.

For each pair of physical servers allocated in the cluster that interact to support dynamic reconfiguration, state diagrams and transitions of the Markov model for organization variants A and B are shown in Figure 2 and Figure 3 The diagram shows the failure and recovery rates of the server ${\lambda }_0$ and ${\mu }_0$; disk ${\lambda }_1$, ${\mu }_1$; and commutator ${\lambda }_2$, ${\mu }_2$. The actual data replica is loaded onto the recovered disk (synchronization of the distributed storage system) with an intensity of ${\mu }_3$. The VM startup time on the backup server and the user application loading on it are negligibly small in comparison with the loading of the current data replica; therefore, in this study, an instant switch between servers is assumed.

In the initial state (AA0 and B0 for service Options A and B, respectively), all resources of the system under consideration are operational.

Depending on which element failed, the system goes into one of three states. For a model with organization Option A, when a computer fails, the system goes into state AA1, switch AA2, and hard drive AA3. If the system has the ability to recover, then, after repair, it goes into state AA4 with working elements. In state AA4, data are replicated between hard drives. If during replication some element fails, then the system will again go into the corresponding failure state (AA1, AA2, and AA3). If replication is completed and all the elements are functional, the system goes to its initial state (AA0 and B0). If during the repair an element of the backup computer fails, the system goes into complete failure mode.

The system of differential equations in accordance with the state diagram and transitions in Figure 2 for Option A has this form:

$$P_0^{\prime }\left(t\right)=-(2{\lambda }_0+{\lambda }_2+2{\lambda }_1)P_0\left(t\right)+{\mu }_3{P}_4\left(t\right),$$

$$P_1^{\prime }\left(t\right)=-({\lambda }_1+{\lambda }_0+{\mu }_0)P_1\left(t\right)+2{\lambda }_0{P}_0\left(t\right)+{\lambda }_0{P}_4\left(t\right),$$

$$P_2^{\prime }\left(t\right)=-({\lambda }_1+{\lambda }_0+{\mu }_2)P_2\left(t\right)+{\lambda }_2{P}_0\left(t\right)+{\lambda }_2{P}_4\left(t\right),$$

$$P_3^{\prime }\left(t\right)=-({\lambda }_1+{\lambda }_0+{\mu }_1)P_3\left(t\right)+{\lambda }_1{P}_4\left(t\right)+2{\lambda }_1{P}_0\left(t\right),$$

$$P_4^{\prime }\left(t\right)=-(2{\lambda }_0+{\lambda }_2+2{\lambda }_1+{\mu }_3)P_4\left(t\right)+{\mu }_1{P}_3\left(t\right)+{\mu }_0{P}_1\left(t\right)+{\mu }_2{P}_2\left(t\right),$$

$$P_5^{\prime }\left(t\right)=-({\lambda }_1+{\lambda }_0)(P_1\left(t\right)+P_2\left(t\right)+P_3\left(t\right)+P_4\left(t\right)).$$

For Option B in Figure 3, it has the form:

$$P_0^{\prime }\left(t\right)=-(2{\lambda }_0+{\lambda }_2+2{\lambda }_1)P_0\left(t\right),$$

$$P_1^{\prime }\left(t\right)=-({\lambda }_1+{\lambda }_0)P_1\left(t\right)+2{\lambda }_0{P}_0\left(t\right),$$

$$P_2^{\prime }\left(t\right)=-({\lambda }_1+{\lambda }_0)P_2\left(t\right)+{\lambda }_2{P}_0\left(t\right),$$

$$P_3^{\prime }\left(t\right)=-({\lambda }_1+{\lambda }_0)P_3\left(t\right)+2{\lambda }_1{P}_0\left(t\right),$$

$$P_4^{\prime }\left(t\right)=-({\lambda }_1+{\lambda }_0)(P_1\left(t\right)+P_2\left(t\right)+P_3\left(t\right)).$$

The presented systems of differential equations make it possible to determine the dependence of the probabilities of all states of the system from time.

The probability of a system working under the condition of maintaining the continuity of the computing process for Options A is defined as:

$$P\left(t\right)=\sum _{i=0}^4{P}_i\left(t\right),$$

and for Option B is defined as:

$$P\left(t\right)=\sum _{i=0}^3{P}_i\left(t\right).$$

It is of interest to expand the proposed Markov models in the case of combining physical servers into larger groups with the migration of virtual machines in them, provided that the computational process is preserved, as well as taking into account the possibility of increasing the probability of timely service in clusters based on their replication [20]. The presented Markov models suggest the ideal control. In this regard, the development of models is of interest, allowing to take into account the influence of control [21] on the reliability of the clusters of the organization under consideration. It is also of interest to study the criticality of the influence of these mechanisms on the potentially attainable level of reliability of cluster systems.

4. Calculation of the Probability of Operability of Duplicated Systems, Provided that the Computational Process Is Continuous

The results of calculating the probability of duplicated computer systems’ operability of the maintaining process’ organization, provided that the computing process is continuous for Options A and B, are presented in Figure 4.

The calculations were performed with the failure rates ${\lambda }_0=1.115·{10}^{-5}(1/h)$, ${\lambda }_1=3.425·{10}^{-6}(1/h)$, and ${\lambda }_2=2.3·{10}^{-6}(1/h)$ and recovery rates ${\mu }_0=0.33(1/h)$, ${\mu }_1=0.17(1/h)$, ${\mu }_2=0.33(1/h)$, and ${\mu }_3=1(1/h)$.

The presented dependences make it possible to assess the influence on the probability of maintaining the operability of a duplicated system of a restriction on the inadmissibility of interruption of the computing process for the considered options for systems with service Options A and B.

5. Calculation of the Probability of Operability of Duplicated Systems

Having determined the probability $P\left(t\right)$ of maintaining the system’s operability under the condition of ensuring the continuity of the computing process using the well-known relation:

$$T=\underset{0}{\overset{\infty }{\int }}P\left(t\right)dt,$$

the mean time between failures caused by a violation of the continuity of the computing process is found.

The mean time to failure can be obtained by integrating the system of differential equations for a model with an absorbing state, the initial conditions $P_1\left(0\right)=1,\dots P_k\left(0\right)=0,P_n\left(0\right)=0$ for a model with n states.

For the systems under study, the left and right sides of the systems of equations for the models under consideration are integrated. Given that, in the presence of an absorbing state, $P_i(\infty )=0$, for the organizing system of Option A, we have [22,23]:

$$-(2{\lambda }_0+{\lambda }_2+2{\lambda }_1)T_0+{\mu }_3{T}_4=-1,$$

$$-({\lambda }_1+{\lambda }_0+{\mu }_0)T_1+2{\lambda }_0{T}_0+{\lambda }_0{T}_4=0,$$

$$-({\lambda }_1+{\lambda }_0+{\mu }_2)T_2+{\lambda }_2{T}_0+{\lambda }_2{T}_4=0,$$

$$-({\lambda }_1+{\lambda }_0+{\mu }_1)T_3+{\lambda }_1{T}_4+2{\lambda }_1{T}_0=0,$$

$$-(2{\lambda }_0+{\lambda }_2+2{\lambda }_1+{\mu }_3)T_4+{\mu }_1{T}_3+{\mu }_0{T}_1+{\mu }_2{T}_2=0,$$

$$-({\lambda }_1+{\lambda }_0)(T_1+T_2+T_3+T_4)=0.$$

For that of Option B, we have:

$$-(2{\lambda }_0+{\lambda }_2+2{\lambda }_1)T_0=-1,$$

$$-({\lambda }_1+{\lambda }_0)T_1+2{\lambda }_0{T}_0=0,$$

$$-({\lambda }_1+{\lambda }_0)T_2+{\lambda }_2{T}_0=0,$$

$$-({\lambda }_1+{\lambda }_0)T_3+2{\lambda }_1{T}_0=0,$$

$$-({\lambda }_1+{\lambda }_0)(T_1+T_2+T_3)=0.$$

where $T_i$ is the average time spent in working condition i when starting work from an operable state. Mean time to failure is determined by summing $T_i$, for all operational states [23]:

$$T=\sum T_i.$$

For the system under consideration, the time to failure with service discipline Option A is $T_1=3.891\times {10}^5$ h, and with Option B is $T_2=3.277\times {10}^3$ h.

Thus, as a result of calculations for the presented example, it is shown that the mean time to failure during recovery in the case of supporting the continuity of the computing process increases by more than two orders of magnitude. This confirms the significance of the impact of the considered service disciplines on the reliability of cluster systems with the migration of virtual machines.

6. Conclusions

A Markov model is proposed for the reliability of a real-time computer cluster with the migration of virtual machines, for which the condition for the system to work is not to allow the interruption of the computing process.

The proposed model allows considering disciplines with and without recovery of the system by operators, provided that the computational process continues after failures.

Based on the proposed cluster models with the migration of virtual machines, the probability of maintaining the system’s operability is estimated provided that the computing process is continuous and the mean time to failure leading to disruption of the computing process is continuous.

In the future, it is planned to investigate more complex cluster systems that provide for the migration of virtual machines between physical servers, united in groups. It is supposed to investigate the influence of control and redundant request servicing on the reliability of cluster systems and on the probability of timely servicing of queries in them and maintaining the continuity of the computing process.