To Adapt or Not to Adapt: A Quantification Technique for Measuring an Expected Degree of Self-Adaptation †
Abstract
1. Introduction
- How can we quantify the observed adaptation effort within a large-scale SASO system consisting of a possibly large set of autonomous entities or subsystems?
- How can we derive statements about the stability of configurations if self-adaptation of the individual entities/subsystems are continuously happening and desired?
- How can we determine an expected degree of self-adaptation of this overall SASO system according to a given environmental context (or a ’situation’)?
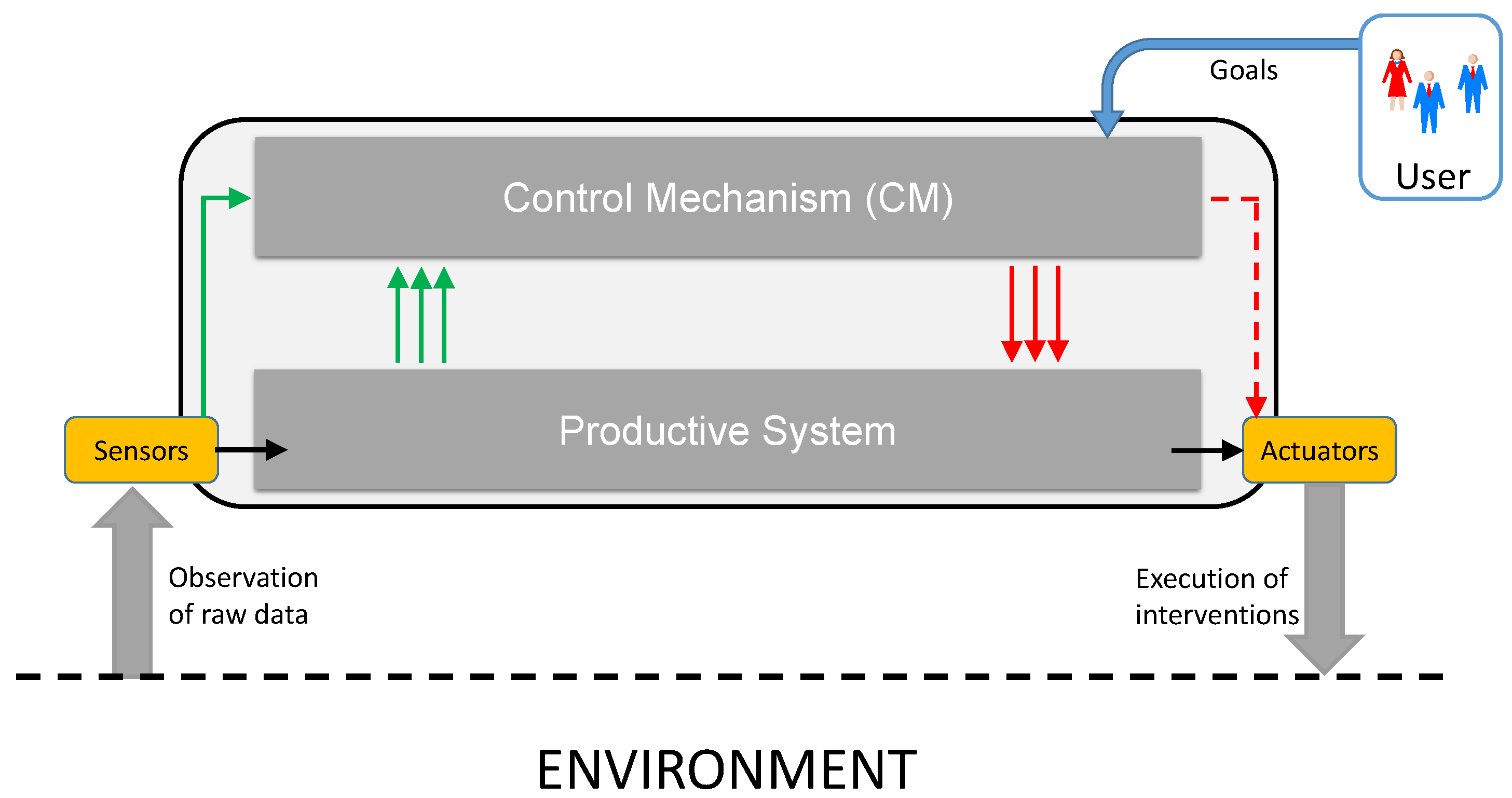
2. System Model
3. State of the Art
4. Quantification of Expected Self-Adaptation
4.1. Challenges for Defining a Measurement Framework
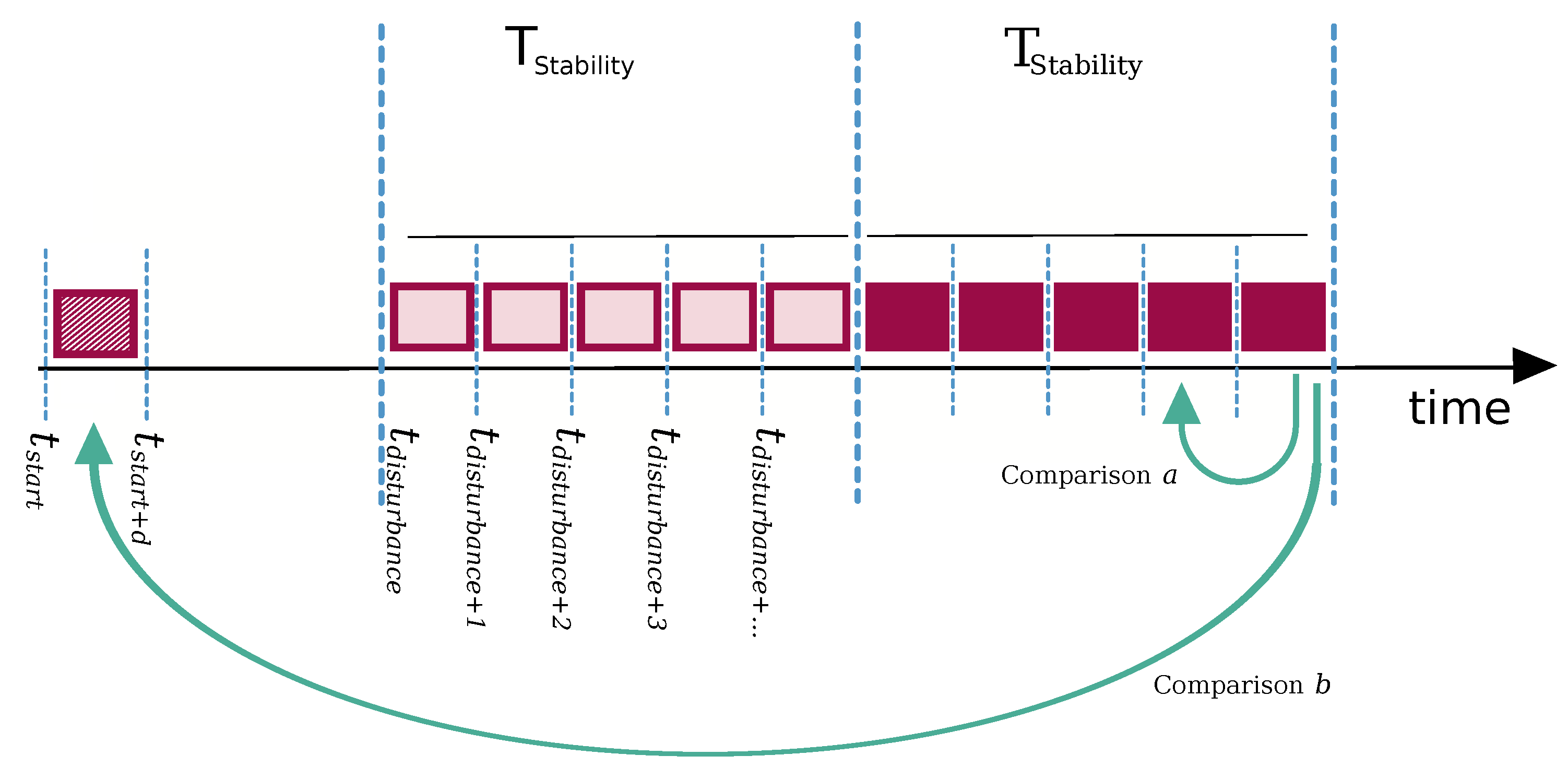
4.2. Measuring a Degree of Adaptation Based on Generative Probabilistic Models
- In comparison to approaches following the concept of measuring autonomy as outlined, e.g., in [26], our method does not rely on a static encoding of possible configurations pre-defined in number of bits.
- In comparison to approaches using the discrete entropy (e.g., outlined for measuring emergence in [34]), it is continuous and does not rely on binning (which introduces more parameters and a certain bias).
- It is independent of the notion of other concepts such as self-organization or emergence.
- Although it makes use of measurement period (windows), it is continuously applied. It does not need a trigger (e.g., the detection of a disturbance as used [27], for instance).
- It does not require a model of the internal decision processes of the autonomous subsystems , since it just considers the externally visible configuration settings.
- It can easily be applied to, e.g., hierarchical structures of SASO systems in terms of considering only those subsystems that belong to a certain authority.
- It is zero if both distributions (i.e., derived from the reference and the current observation period) are identical. This means that the same configurations are observed. Theoretically, there may be switches between different agents running the configuration of the other one and vice versa, but in general this is a reliable approximation for constant behavior.
- In turn, high values of KL indicate strong changes in the configurations of the contained subsystems. This indicates a high degree of self-adaptation.
- A major issue in this context is that the values of KL highly depend on the considered feature vector (i.e., the number, the type, and the resolution of the configuration parameters) as well as the frequency in which adaptations are done. These values are highly application-dependent. However, the comparison is always made within the domain—meaning that the ordering is correct, but the individual actual value does not much about the severity of the change. This can be defined in relation to a set of observations, i.e., based on experiences with the application under investigation. This leaves the question open how to determine a real ’level’ out of the KL values.
5. Use Cases and Evaluation
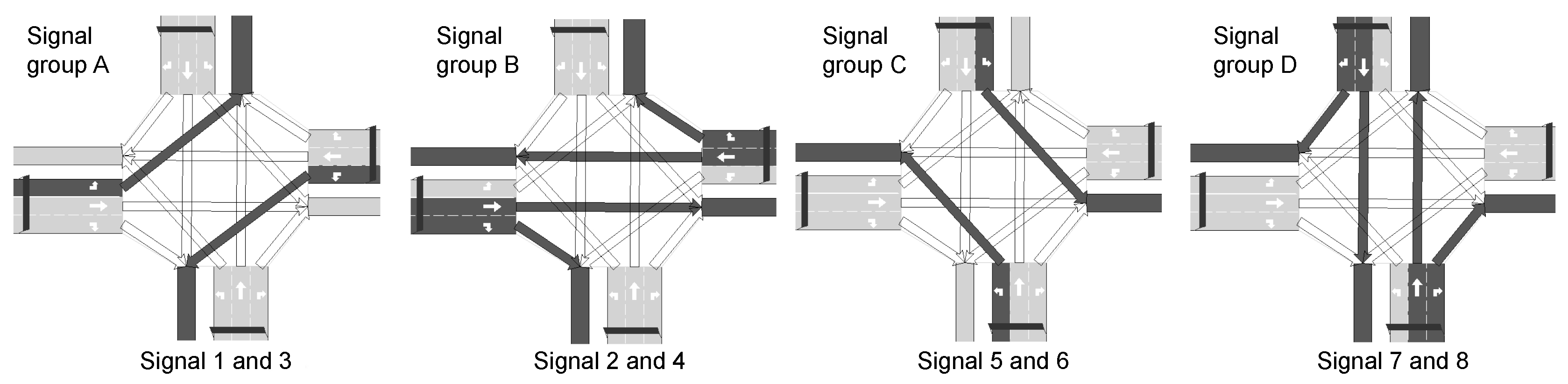
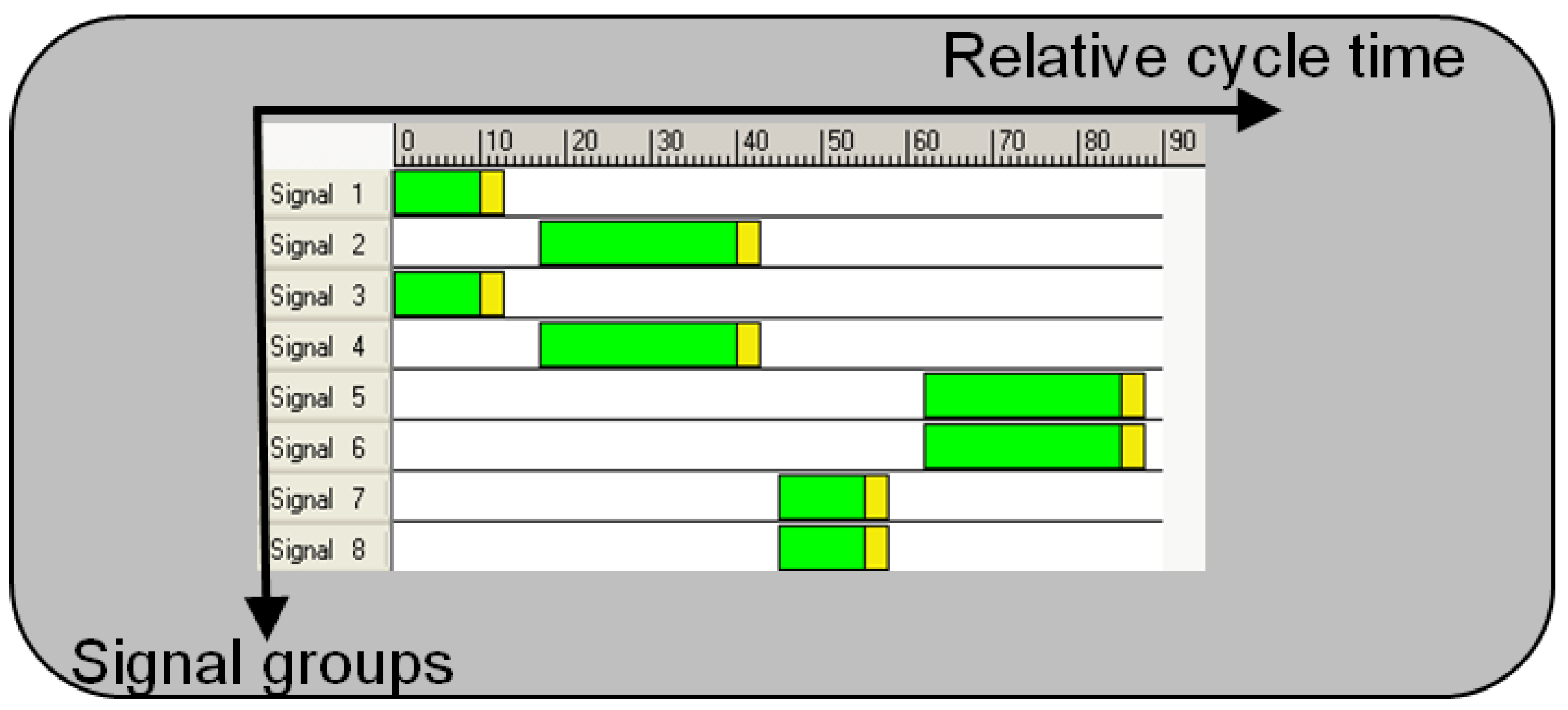
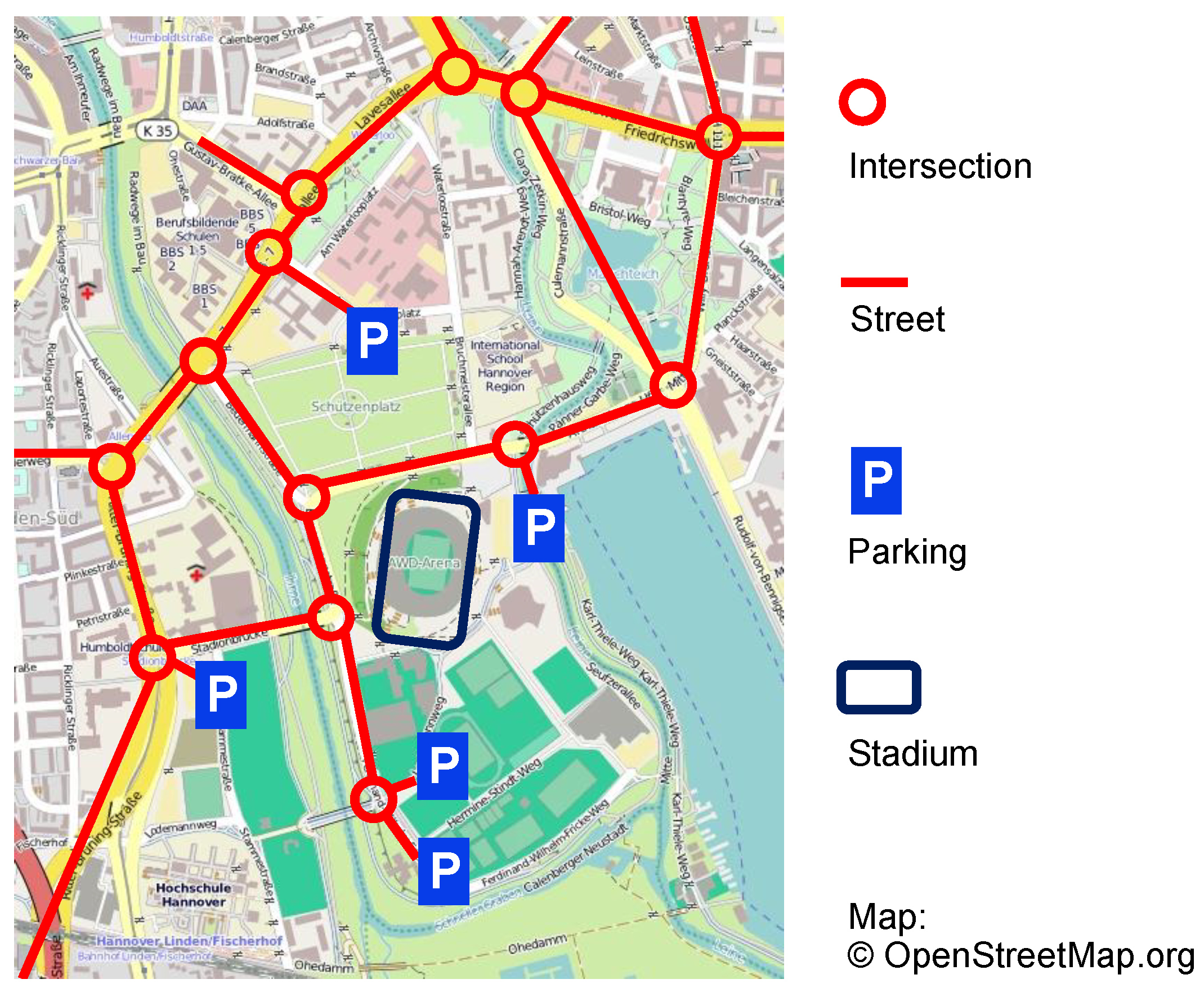
5.1. Application 1: Traffic Control
5.1.1. Parameters
5.1.2. Experimental Setup
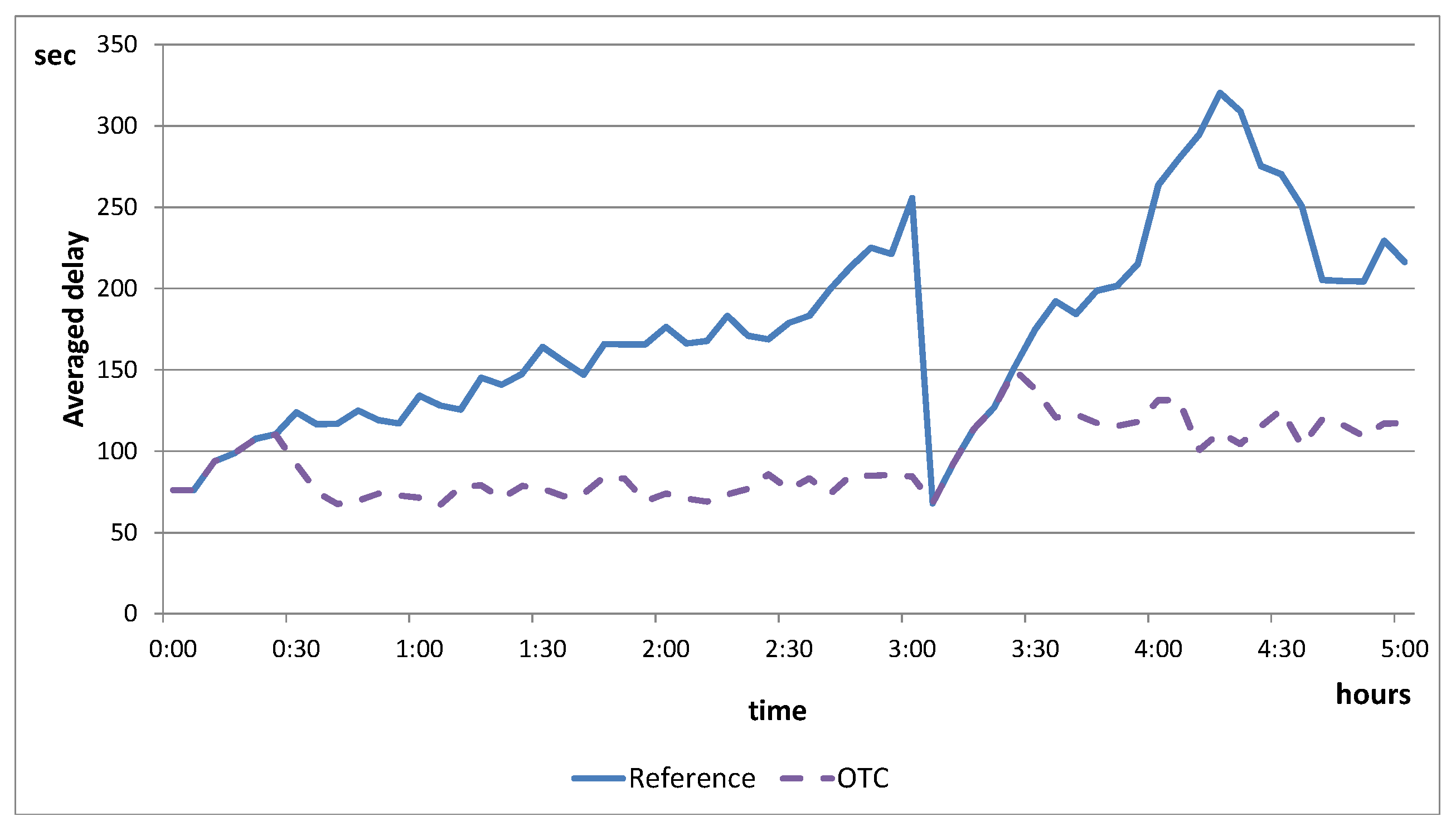
5.1.3. Evaluation
5.2. Application 2: Swidden Farming Model
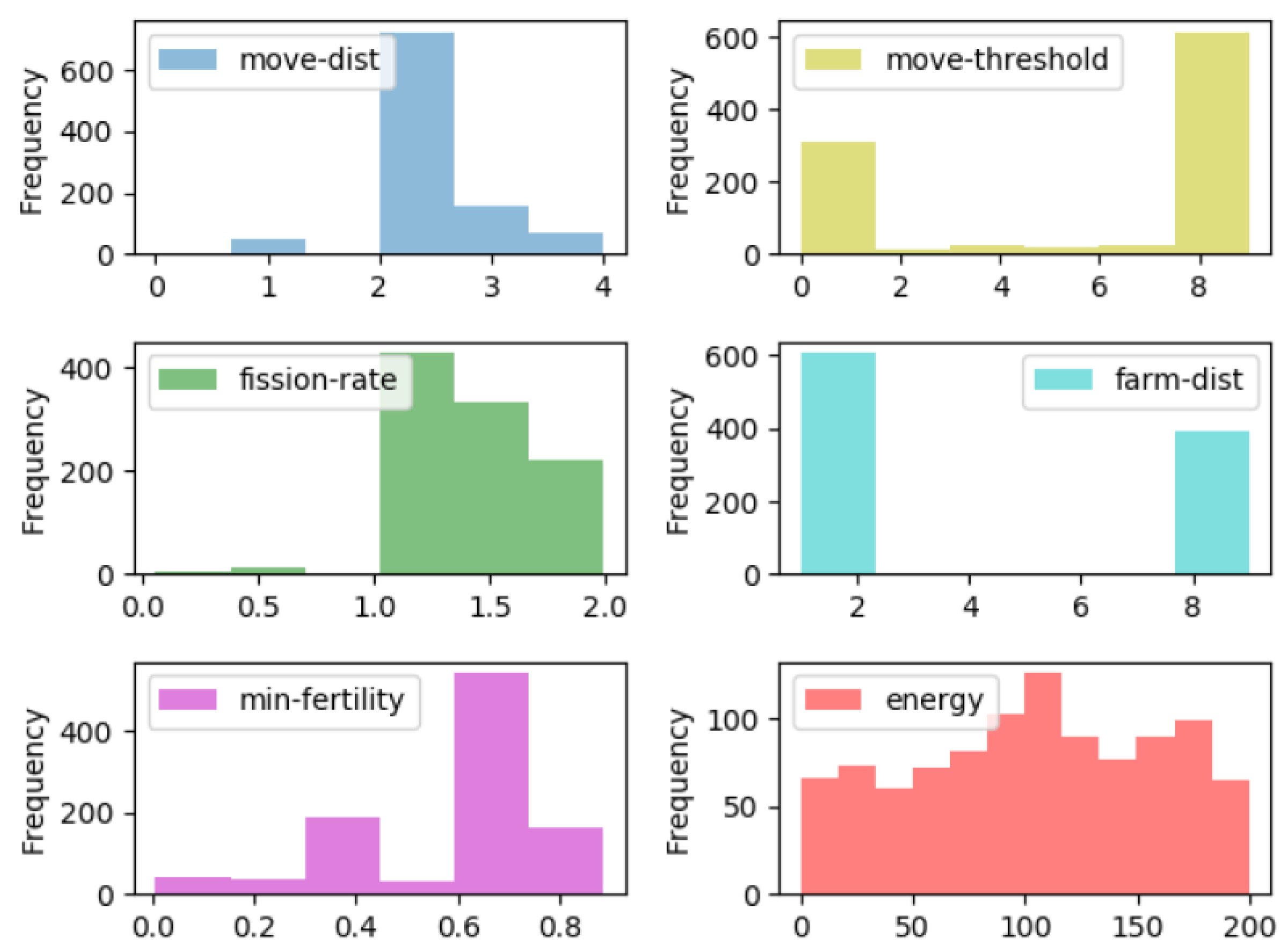
5.2.1. Parameters
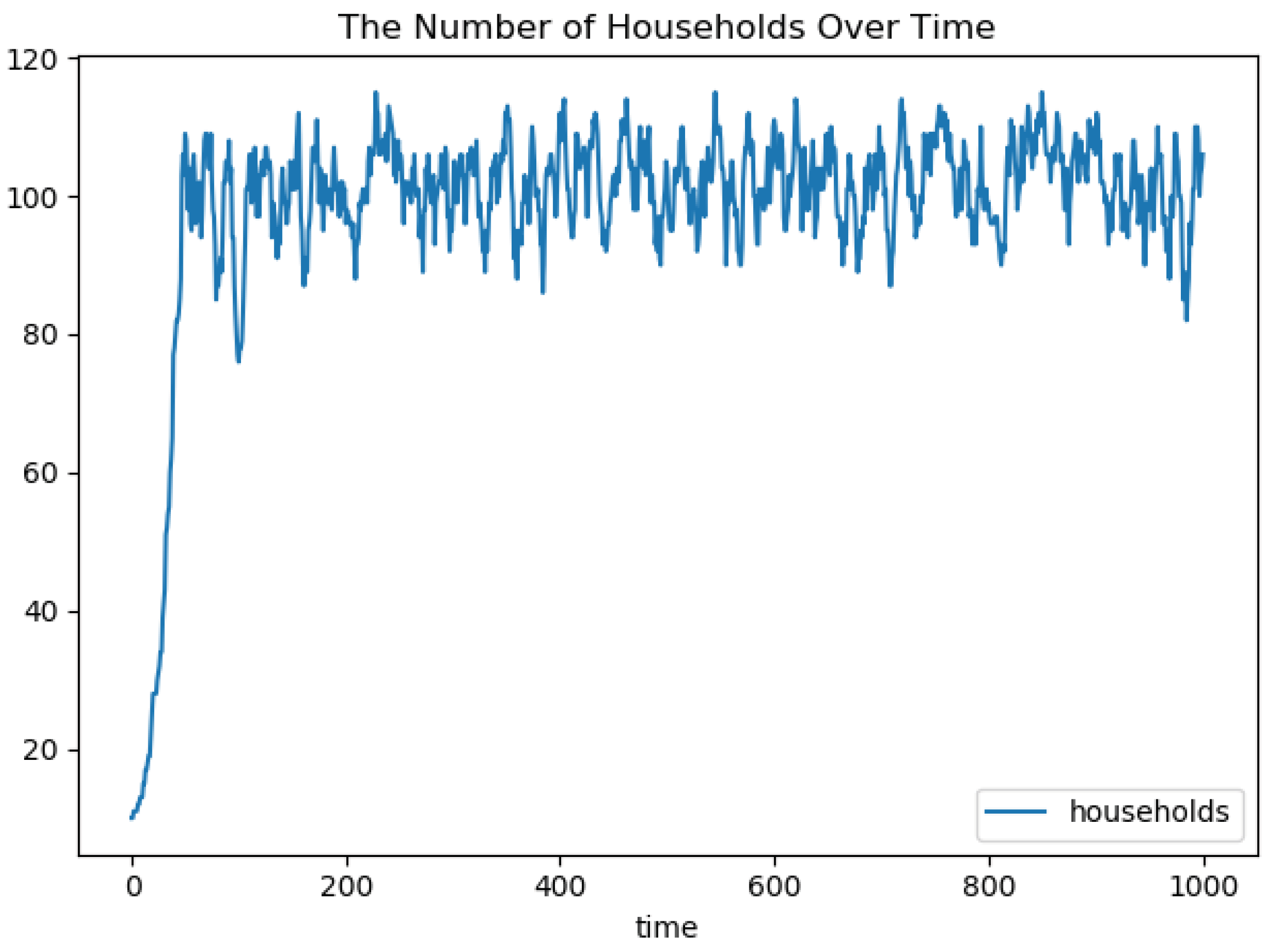
5.2.2. Experimental Setup
5.2.3. Evaluation
5.3. Application 3: Organic Network Control
5.3.1. Parameters
5.3.2. Experimental Setup
5.3.3. Evaluation
5.4. Discussion and Threats to the Approach
- Considering the absolute values given in Table 4 and Table 1 we can see that the values themselves come without meaning. We cannot make any statement about the relation between the changes. In particular, the differences just show that there is a change or a stronger/smaller change, but statements such as “X is twice as strong as Y” are not possible.
- A better approach than should come up with values that can be normalized to the standard interval , since this allows for better comparability.
- In turn, simply counting configurations and providing frequencies as done in Figure 10 describes just a small part of the truth, since it completely neglects the actual changes including the differences between two subsequent configurations.
- We can further see that the measurement is independent of changes in the number of participating subsystems, since it just collects samples of configuration vectors no matter how many in a certain time period. This is especially important in the context of open systems, where subsystems are free to join and leave at any time (e.g., in the context of Interwoven System, see [5,60]). However, each new subsystem has a severe impact on the measure.
- The values of KL highly depend on the considered feature vector (i.e., the number, the type, and the resolution of the configuration parameters) as well as the frequency in which adaptations are done. These values are highly application-dependent. For a generalized applicability, more studies and a systematic analysis of the search space are required.
- The absolute value of KL cannot be mapped directly to a ’degree of self-adaptation’—it just gives an ordering. It remains subject to future work how this can be done (e.g., by sampling more values of KL and estimating the range of values or synthetically generating strongly deviating distributions based on the specifications of the feature space).
- The changes in the adaptation behavior are quantified as difference between distributions of configurations within measurement cycles. Considering this as novel process or abnormal behavior suggests to augment the approach with mechanisms for anomaly detection (e.g., using approaches for self-adaptive systems as outlined in [61]).
- The considered cases all come with a feasible number of parameters. It remains open how the measurement behaves in high-dimensional spaces (i.e., how the dimensionality problem manifests in this context). However, in such high-dimensional scenarios, the self-adaptation mechanism itself may reach its limits.
- The measure is meant as an approach to analyzing and observing the system behavior at runtime. The determined values will be used as indicators later—which in turn may serve as basis for steering the self-adaptation behavior later (e.g., based on identifying an appropriate level of adaptation).
- The question is still if there can be something like an ’optimal’ degree of self-adaptation. We assume that such a value will not be based on quality attributes only, i.e., those that are already considered in the utility function or in the decision mechanism. In contrast, we user acceptance or stability of the solutions are candidates to consider in such an assessment.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moore, G.E. Cramming more components onto integrated circuits. Electron. Mag. 1965, 38, 114–117. [Google Scholar] [CrossRef]
- Glass, R.L. Facts and Fallacies of Software Engineering; Agile Software Development, Addison Wesley: Boston, MA, USA, 2002. [Google Scholar]
- Müller-Schloer, C.; Tomforde, S. Organic Computing—Technical Systems for Survival in the Real World; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Kephart, J.; Chess, D. The Vision of Autonomic Computing. IEEE Comp. 2003, 36, 41–50. [Google Scholar] [CrossRef]
- Tomforde, S.; Hähner, J.; Sick, B. Interwoven Systems. Informatik-Spektrum 2014, 37, 483–487. [Google Scholar] [CrossRef]
- Kounev, S.; Lewis, P.; Bellman, K.L.; Bencomo, N.; Camara, J.; Diaconescu, A.; Esterle, L.; Geihs, K.; Giese, H.; Götz, S.; et al. The Notion of Self-aware Computing. In Self-Aware Computing Systems; Springer International Publishing: Cham, Switzerland, 2017; pp. 3–16. [Google Scholar]
- Shaw, M.; Objects, B. Software design paradigm based on process control. ACM Softw. Eng. Notes 1995, 20, 27–39. [Google Scholar] [CrossRef]
- Prothmann, H.; Tomforde, S.; Branke, J.; Hähner, J.; Müller-Schloer, C.; Schmeck, H. Organic Traffic Control. In Organic Computing—A Paradigm Shift for Complex Systems; Birkhäuser Verlag: Basel, Switzerland, 2011; pp. 431–446. [Google Scholar]
- Krupitzer, C.; Roth, F.M.; VanSyckel, S.; Schiele, G.; Becker, C. A survey on engineering approaches for self-adaptive systems. Pervasive Mobile Comput. 2015, 17, 184–206. [Google Scholar] [CrossRef]
- Rudolph, S.; Tomforde, S.; Sick, B.; Hähner, J. A mutual influence detection algorithm for systems with local performance measurement. In Proceedings of the 2015 IEEE 9th International Conference on Self-Adaptive and Self-Organizing Systems, Cambridge, MA, USA, 21–25 September 2015; pp. 144–149. [Google Scholar]
- Tomforde, S. From “Normal” to “Abnormal”: A Concept for Determining Expected Self-Adaptation Behaviour. In Proceedings of the 2019 IEEE 4th International Workshops on Foundations and Applications of Self* Systems (FAS*W), Umea, Sweden, 16–20 June 2019; pp. 1–6. [Google Scholar]
- Tomforde, S.; Prothmann, H.; Branke, J.; Hähner, J.; Mnif, M.; Müller-Schloer, C.; Richter, U.; Schmeck, H. Observation and Control of Organic Systems. In Organic Computing—A Paradigm Shift for Complex Systems; Birkhäuser: Basel, Switzerland, 2011; pp. 325–338. [Google Scholar]
- Kantert, J.; Edenhofer, S.; Tomforde, S.; Hähner, J.; Müller-Schloer, C. Normative Control—Controlling Open Distributed Systems with Autonomous Entities. In Trustworthy Open Self-Organising Systems; Birkäuser: Basel, Switzerland, 2016; pp. 89–126. [Google Scholar]
- Chan, W. Interaction Metric of Emergent Behaviours in Agent Simulations. In Proceedings of the 2011 Winter Simulation Conference (WSC), Phoenix, AZ, USA, 11–14 December 2011; pp. 357–368. [Google Scholar]
- Eberhardinger, B.; Anders, G.; Seebach, H.; Siefert, F.; Reif, W. A research overview and evaluation of performance metrics for self-organization algorithms. In Proceedings of the Self-Adaptive and Self-Organizing Systems Works (SASO-W’15), Cambridge, MA, USA, 21–25 September 2015; pp. 122–127. [Google Scholar]
- Kaddoum, E.; Raibulet, C.; Georgé, J.P.; Picard, G.; Gleizes, M.P. Criteria for the Evaluation of Self-* Systems. In Proceedings of the ICSE Workshop on Software Engineering for Adaptive and Self-Managing Systems, Cape Town, South Africa, 3–4 May 2010; pp. 29–38. [Google Scholar]
- Cámara, J.; Correia, P.; de Lemos, R.; Vieira, M. Empirical resilience evaluation of an architecture-based self-adaptive software system. In Proceedings of the ACM Sigsoft Conference on Quality of Software Architectures, Lille, France, 30 June– 4 July 2014; pp. 63–72. [Google Scholar]
- Gronau, N. Determinants of an Appropriate Degree of Autonomy in a Cyber-physical Production System. Procedia CIRP 2016, 52, 1–5. [Google Scholar] [CrossRef][Green Version]
- Brown, D.; Goodrich, M. Limited bandwidth recognition of collective behaviours in bio-inspired swarms. In Proceedings of the International Conference on Autonomous Agents and Multi-Agent Systems, Paris, France, 5–9 May 2014; pp. 405–412. [Google Scholar]
- O’Toole, E.; Nallur, V.; Clarke, S. Towards Decentralised Detection of Emergence in Complex Adaptive Systems. In Proceedings of the of IEEE International Conference on Self-Adaptive and Self-Organizing Systems (SASO’14), London, UK, 8–12 September 2014; pp. 60–69. [Google Scholar]
- Deaton, J.; Allen, R. Development and application of system complexity measures for use in modeling and simulation. In Proceedings of the Conference on Summer Computer Simulation, Chicago, IL, USA, 26–29 July 2015; pp. 1–6. [Google Scholar]
- Shalizi, C.R.; Shalizi, K.L. Quantifying Self-Organization in Cyclic Cellular Automata. In Proceedings of the SPIE Noise in Complex Systems and Stochastic Dynamics, Bellingham, WA, USA, 7 May 2003; pp. 108–117. [Google Scholar]
- Heylighen, F. The Science of Self-Organization and Adaptivity. In Knowledge Management, Organizational Intelligence and Learning, and Complexity; Encyclopedia of Life Support Systems: Oxford, UK, 1999; pp. 253–280. [Google Scholar]
- Wright, W.; Smith, R.E.; Danek, M.; Greenway, P. A Generalisable Measure of Self-Organisation and Emergence. In Proceedings of the International Conference on Artificial Neural Networks (ICANN’01), Vienna, Austria, 21–25 August 2001; Springer: Cham, Switzerland, 2001; pp. 857–864. [Google Scholar]
- Gershenson, C.; Fernandez, N. Complexity and Information: Measuring Emergence, Self-organization, and Homeostasis at Multiple Scales. Complexity 2012, 18, 29–44. [Google Scholar] [CrossRef]
- Schmeck, H.; Müller-Schloer, C.; Çakar, E.; Mnif, M.; Richter, U. Adaptivity and Self-organization in Organic Computing Systems. ACM Trans. Auton. Adapt. Syst. 2010, 5, 1–32. [Google Scholar] [CrossRef]
- Kantert, J.; Tomforde, S.; Müller-Schloer, C. Measuring Self-Organisation in Distributed Systems by External Observation. In Proceedings of the 28th GI/ITG International Conference on Architecture of Computing Systems—ARCS Workshop on Self-Optimisation in Organic and Autonomic Computing Systems (SAOS15), Porto, Portugal, 24–27 March 2015; pp. 1–8. [Google Scholar]
- Rudolph, S.; Kantert, J.; Jänen, U.; Tomforde, S.; Hähner, J.; Müller-Schloer, C. Measuring Self-Organisation Processes in Smart Camera Networks. In Proceedings of the 29th International Conference on Architecture of Computing Systems (ARCS 2016); Varbanescu, A.L., Ed.; VDE Verlag GmbH: Nuremberg, Germany, 2016; Chapter 14; pp. 1–6. [Google Scholar]
- Tomforde, S.; Kantert, J.; Sick, B. Measuring Self-organisation at Runtime—A Quantification Method Based on Divergence Measures. In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), Porto, Portugal, 24–26 February 2017; Volume 1, pp. 96–106. [Google Scholar]
- Filieri, A.; Maggio, M.; Angelopoulos, K.; D’ippolito, N.; Gerostathopoulos, I.; Hempel, A.B.; Hoffmann, H.; Jamshidi, P.; Kalyvianaki, E.; Klein, C.; et al. Control Strategies for Self-Adaptive Software Systems. ACM Trans. Auton. Adapt. Syst. 2017, 11, 24:1–24:31. [Google Scholar] [CrossRef]
- Shalizi, C.R. Causal Architecture, Complexity and Self-Organization in the Time Series and Cellular Automata. Ph.D. Thesis, University of Wisconsin–Madison, Madison, WI, USA, 2001. [Google Scholar]
- Prokopenko, M.; Boschetti, F.; Ryan, A.J. An information-theoretic primer on complexity, self-organisation and emergence. Complexity 2007, 15, 11–28. [Google Scholar] [CrossRef]
- Holzer, R.; de Meer, H. Methods for Approximations of Quantitative Measures in Self-Organizing Systems. In Proceedings of the 5th International Works on Self-Organizing Systems (IWSOS’11), Karlsruhe, Germany, 23–24 February 2011; pp. 1–15. [Google Scholar]
- Mnif, M.; Müller-Schloer, C. Quantitative emergence. In Organic Computing—A Paradigm Shift for Complex Systems; Springer: Cham, Switzerland, 2011; pp. 39–52. [Google Scholar]
- Fisch, D.; Janicke, M.; Sick, B.; Muller-Schloer, C. Quantitative Emergence—A Refined Approach Based on Divergence Measures. In Proceedings of the 2010 Fourth IEEE International Conference on Self-Adaptive and Self-Organizing Systems, Budapest, Hungary, 27 September–1 October 2010; pp. 94–103. [Google Scholar]
- Chen, T.; Bahsoon, R.; Wang, S.; Yao, X. To adapt or not to adapt? Technical debt and learning driven self-adaptation for managing runtime performance. In Proceedings of the 2018 ACM/SPEC International Conference on Performance Engineering, Berlin, Germany, 9–13 April 2018; pp. 48–55. [Google Scholar]
- Bishop, C. Pattern Recognition and Machine Learning, 2nd ed.; Information Science and Statistics; Springer: Cham, Switzerland, 2011. [Google Scholar]
- Tomforde, S.; Kantert, J.; Müller-Schloer, C.; Bödelt, S.; Sick, B. Comparing the Effects of Disturbances in Self-adaptive Systems—A Generalised Approach for the Quantification of Robustness. Trans. Comput. Collect. Intell. 2018, 28, 193–220. [Google Scholar]
- Rudolph, S.; Tomforde, S.; Hähner, J. A Mutual Influence-based Learning Algorithm. In Proceedings of the International Conference on Agents and Artificial Intelligence (ICAART16), Porto, Portugal, 24–26 February 2016; pp. 181–189. [Google Scholar]
- Rudolph, S.; Tomforde, S.; Hähner, J. Mutual Influence-aware Runtime Learning of Self-adaptation Behavior. TAAS 2019, 14, 4:1–4:37. [Google Scholar] [CrossRef]
- Prothmann, H.; Branke, J.; Schmeck, H.; Tomforde, S.; Rochner, F.; Hähner, J.; Müller-Schloer, C. Organic traffic light control for urban road networks. IJAACS 2009, 2, 203–225. [Google Scholar] [CrossRef]
- Prothmann, H.; Rochner, F.; Tomforde, S.; Branke, J.; Müller-Schloer, C.; Schmeck, H. Organic Control of Traffic Lights. In Proceedings of the 5th International Conference on Autonomic and Trusted Computing (ATC-08), Oslo, Norway, 23–25 June 2008; Rong, C., Ed.; Springer: Cham, Switzerland, 2008; Volume 5060, pp. 219–233. [Google Scholar]
- Tomforde, S.; Prothmann, H.; Rochner, F.; Branke, J.; Hähner, J.; Müller-Schloer, C.; Schmeck, H. Decentralised Progressive Signal Systems for Organic Traffic Control. In Proceedings of the 2nd IEEE International Conference on Self-Adaption and Self-Organization (SASO’08), Venice, Italy, 20–24 October 2008; pp. 413–422. [Google Scholar]
- Sommer, M.; Tomforde, S.; Hähner, J. An Organic Computing Approach to Resilient Traffic Management. In Autonomic Road Transport Support Systems, Autonomic Systems ed.; McCluskey, T.L., Kotsialos, A., Müller, J.P., Klügl, F., Rana, O., Schumann, R., Eds.; Birkhäuser Verlag: Basel, Switzerland, 2016; pp. 113–130. [Google Scholar]
- Barceló, J.; Casas, J. Dynamic network simulation with AIMSUN. In Simulation Approaches in Transportation Analysis; Springer: Cham, Switzerland, 2005; pp. 57–98. [Google Scholar]
- Gabbard, J. Car-Following Models, Concise Encyclopedia of Traffic and Transportation Systems; Papageorgiou, M., Ed.; Pergamon Press: Oxford, UK, 1991. [Google Scholar]
- Barton, C.M. Complexity, social complexity, and modeling. J. Archaeol. Method Theory 2014, 21, 306–324. [Google Scholar] [CrossRef]
- Wilensky, U.; Rand, W. An Introduction to Agent-Based Modeling: Modeling Natural, Social, and Engineered Complex Systems with NetLogo; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Tomforde, S.; Cakar, E.; Hähner, J. Dynamic Control of Network Protocols—A new vision for future self-organised networks. In Proceedings of the 6th International Conference on Informatics in Control, Automation, and Robotics (ICINCO’09), Milan, Italy, 2–5 July 2009; Filipe, J., Cetto, J.A., Ferrier, J.L., Eds.; INSTICC: Milan, Italy, 2009; pp. 285–290. [Google Scholar]
- Tomforde, S.; Steffen, M.; Hähner, J.; Müller-Schloer, C. Towards an Organic Network Control System. In Proceedings of the 6th International Conference on Autonomic and Trusted Computing (ATC’09), Brisbane, Australia, 7–10 July 2009; Springer: Cham, Switzerland, 2009; pp. 2–16. [Google Scholar]
- Tomforde, S.; Hurling, B.; Hähner, J. Distributed Network Protocol Parameter Adaptation in Mobile Ad-Hoc Networks. In Informatics in Control, Automation and Robotics; Springer: Berlin/Heidelberg, Germany, 2011; Volume 89, pp. 91–104. [Google Scholar]
- Tomforde, S.; Hurling, B.; Hähner, J. Adapting parameters of mobile ad-hoc network protocols to changing environments. In Informatics in Control, Automation and Robotics—Selected Papers from the International Conference on Informatics in Control, Automation and Robotics 2010; Andrade-Cetto, J., Ferrier, J.L., Filipe, J., Eds.; Lecture Notes in Electrical Engineering Series Number 81; Springer: Berlin/Heidelberg, Germany, 2011; pp. 91–104. [Google Scholar]
- Tomforde, S.; Ostrovsky, A.; Hähner, J. Load-Aware Reconfiguration of LTE Antennas—Dynamic Cell-Phone Network Adapta-tion Using Organic Network Control. In Proceedings of the 11th International Conference on Informatics in Control, Automation, and Robotics (ICINCO’14), Vienna, Austria, 2–4 September 2014; pp. 243–263. [Google Scholar]
- Hähner, J.; Streit, K.; Tomforde, S. Cellular traffic offloading through network-assisted ad-hoc routing in cellular networks. In Proceedings of the 2016 IEEE Symposium on Computers and Communication (ISCC), Messina, Italy, 27–30 June 2016; pp. 469–476. [Google Scholar]
- Tomforde, S.; Gruhl, C.; Haehner, J. A Concept for Self-adapting and Self-learning Traffic Offloading in Cellular Networks. In Proceedings of the 30th International Conference on Architecture of Computing Systems (ARCS 2017), Vienna, Austria, 4–6 April 2017; pp. 1–8. [Google Scholar]
- Tomforde, S.; Kantert, J.; von Mammen, S.; Hähner, J. Cooperative Self-Optimisation of Network Protocol Parameters at Runtime. In Proceedings of the ICINCO’15, Madeira, Portugal, 21–23 July 2015; pp. 123–130. [Google Scholar]
- Kunz, T. Reliable Multicasting in MANETs. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, 2003. [Google Scholar]
- Luke, S.; Cioffi-Revilla, C.; Panait, L.; Sullivan, K. MASON: A New Multi-Agent Simulation Toolkit. In Proceedings of the 2004 Swarmfest Workshop, Budapest, Hungary, 10–15 May 2004. [Google Scholar]
- Fall, K. Network Emulation in the Vint/NS Simulator. In Proceedings of the 4th IEEE Symposium on Computers and Communications (ISCC’99), Red Sea, Egypt, 6–8 July 1999; p. 244. [Google Scholar]
- Bellman, K.L.; Gruhl, C.; Landauer, C.; Tomforde, S. Self-Improving System Integration—On a Definition and Characteristics of the Challenge. In Proceedings of the IEEE 4th International Workshops on Foundations and Applications of Self* Systems (FAS*W@SASO/ICCAC 2019), Umea, Sweden, 16–20 June 2019; pp. 1–3. [Google Scholar]
- Gruhl, C.; Sick, B.; Wacker, A.; Tomforde, S.; Hähner, J. A building block for awareness in technical systems: Online novelty detection and reaction with an application in intrusion detection. In Proceedings of the 2015 IEEE 7th International Conference on Awareness Science and Technology (iCAST), Qinhuangdao, China, 22–24 September 2015; pp. 194–200. [Google Scholar]


| ID | Parameter Name | Description | Parameter Range |
|---|---|---|---|
| 1 | move-dist | The distance an agent moves if it must find a new | [1;5] |
| location for its farmstead. | |||
| 2 | move-threshold | The households moves to a new unoccupied area if | [0;1] |
| its energy level drops below this threshold. | |||
| 3 | fission-rate | Amount of energy needed to reproduce a new household | [1;2] |
| Defined about the initial household energy. | |||
| 4 | farm-dist | Maximum distance an agent will travel to a farm | [1;20] |
| Radius of area a farmstead claims ownership, if | |||
| this is not already occupied by another farmstead | |||
| 5 | min-fertility | Minimum fertility of a patch for being considered | [0;1] |
| as next farmstead location. |
| Distribution | Reference Distributions | Current Distribution | |
|---|---|---|---|
| Distribution | Reference Distributions | Current Distribution | |
|---|---|---|---|
| Parameter | Standard Configuration |
|---|---|
| Delay | |
| AllowedHelloLoss | |
| HelloInterval | |
| HelloInterval | |
| Packet count | |
| Minimum difference | |
| NACK timeout | |
| NACK retries |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomforde, S.; Goller, M. To Adapt or Not to Adapt: A Quantification Technique for Measuring an Expected Degree of Self-Adaptation. Computers 2020, 9, 21. https://doi.org/10.3390/computers9010021
Tomforde S, Goller M. To Adapt or Not to Adapt: A Quantification Technique for Measuring an Expected Degree of Self-Adaptation. Computers. 2020; 9(1):21. https://doi.org/10.3390/computers9010021
Chicago/Turabian StyleTomforde, Sven, and Martin Goller. 2020. "To Adapt or Not to Adapt: A Quantification Technique for Measuring an Expected Degree of Self-Adaptation" Computers 9, no. 1: 21. https://doi.org/10.3390/computers9010021
APA StyleTomforde, S., & Goller, M. (2020). To Adapt or Not to Adapt: A Quantification Technique for Measuring an Expected Degree of Self-Adaptation. Computers, 9(1), 21. https://doi.org/10.3390/computers9010021





