J48SS: A Novel Decision Tree Approach for the Handling of Sequential and Time Series Data †
Abstract
1. Introduction
- categorical attributes, with information about the gender or the smoking habits;
- numerical attributes, with information about age and weight;
- time series data, tracking the blood pressure over several days, and
- discrete sequences, describing which symptoms the patient has experienced and which medications have been administered.
2. Background
2.1. The Decision Tree Learner J48 (C4.5)
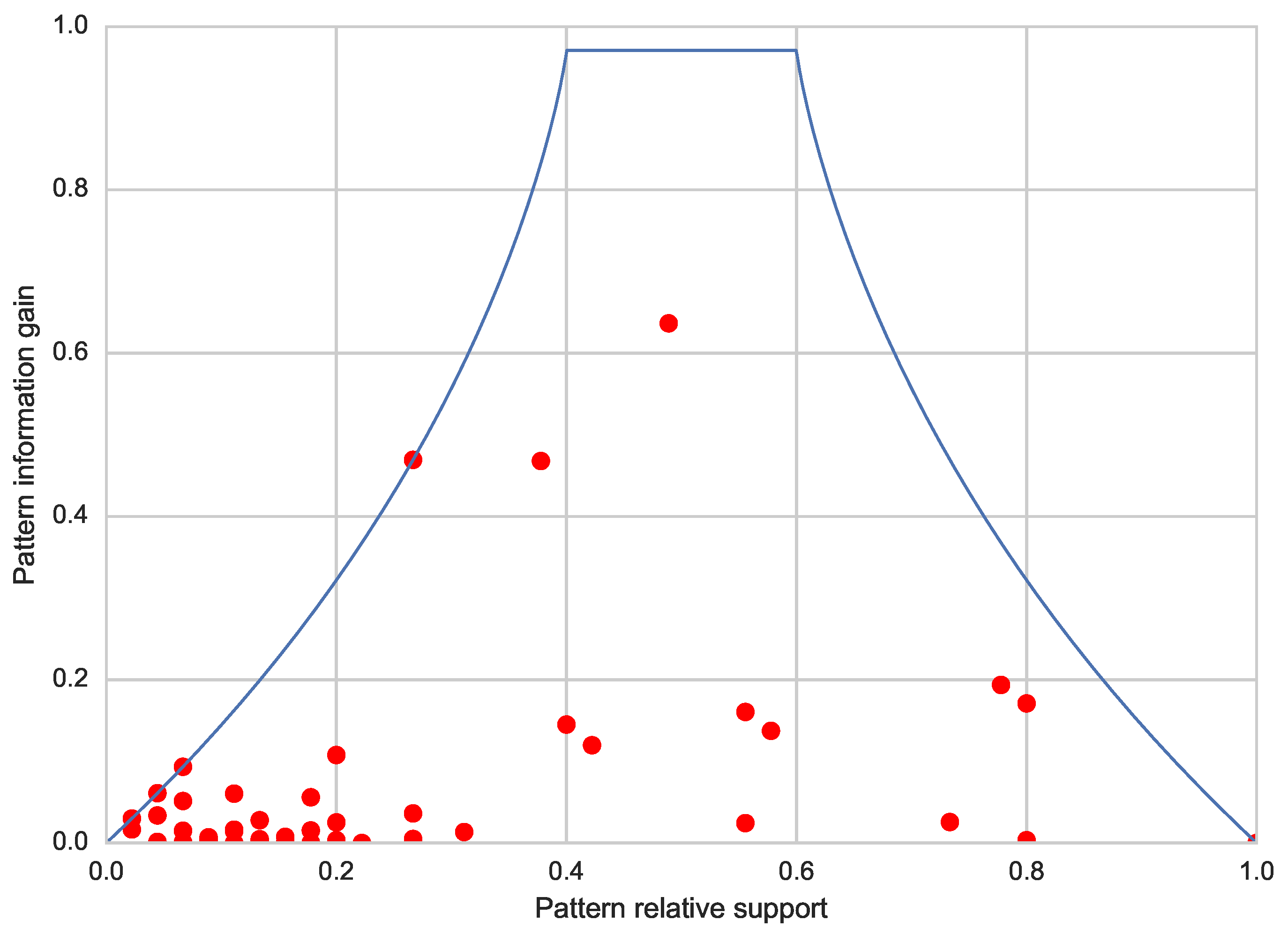
2.2. Sequential Pattern Mining
- it makes it difficult for a user to read and understand the output, and to rely on the patterns for subsequent data analysis tasks, and
- an overly large result set may require a too high resource consumption and too long computation time to be produced.
2.3. Evolutionary Algorithms
- there exists no such that improves for some i, with , and
- for all j, with and , does not improve .
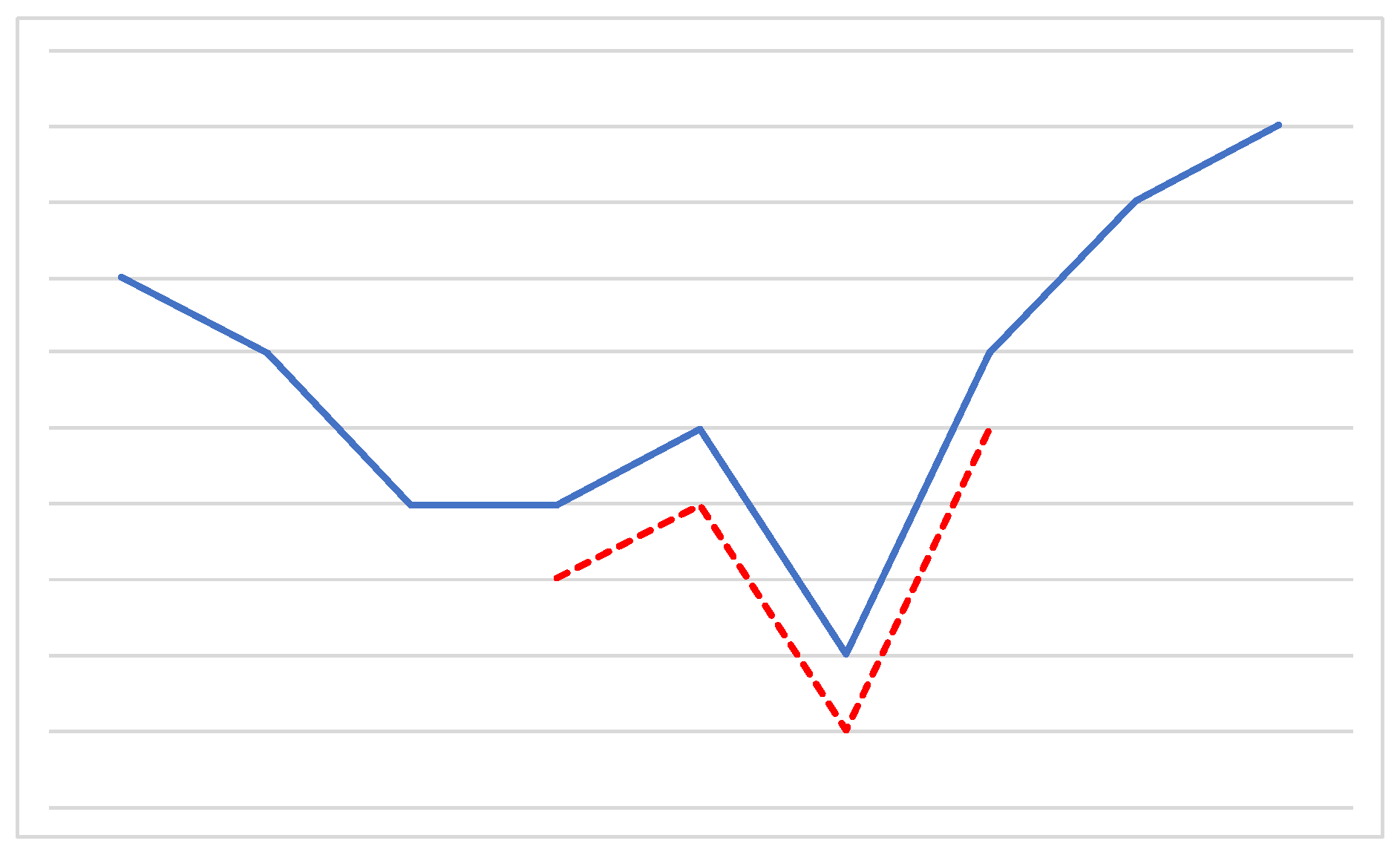
2.4. Time Series Shapelets
3. Materials and Methods
3.1. Handling of Sequential Data
3.1.1. Adapting VGEN
3.1.2. Adapting J48 to Handle Sequential Data
- we rely on a well-established and performing algorithm, such as J48, instead of designing a new one;
- we are able of mixing the usage of sequential and classical (categorical or numerical) data in the same execution cycle;
- our implementation allows the tuning of the abstraction level of the extracted patterns.
- the weight W, in order to control the abstraction level of the extracted pattern, and
- the normalized gain of the best attribute found so far, which, as previously described, can be used to prune the pattern search space.
3.2. Handling of Time Series Data
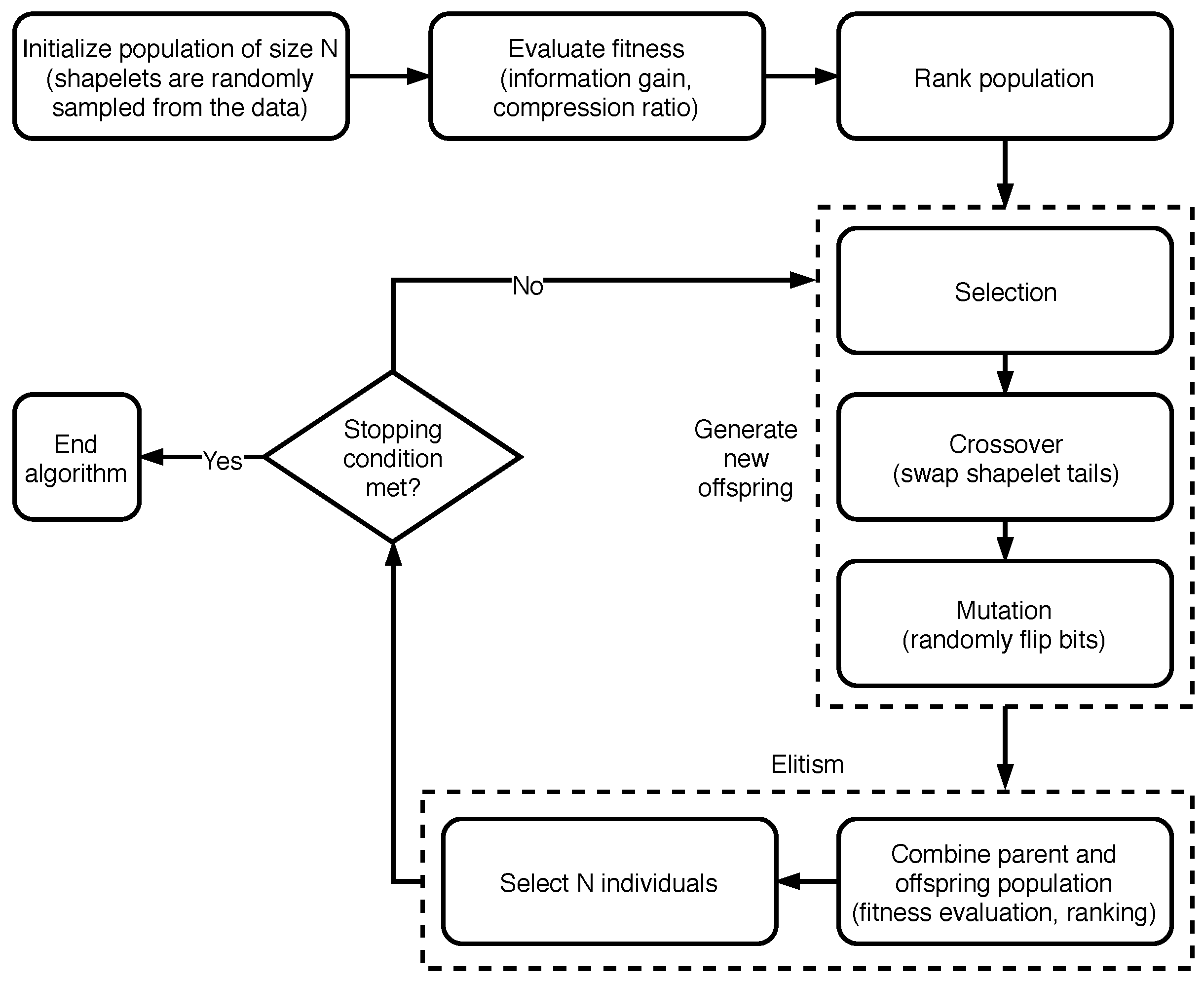
3.2.1. Using NSGA-II to Extract Time Series Shapelets
- how the population (i.e., potential solutions) is represented and how it is initialized;
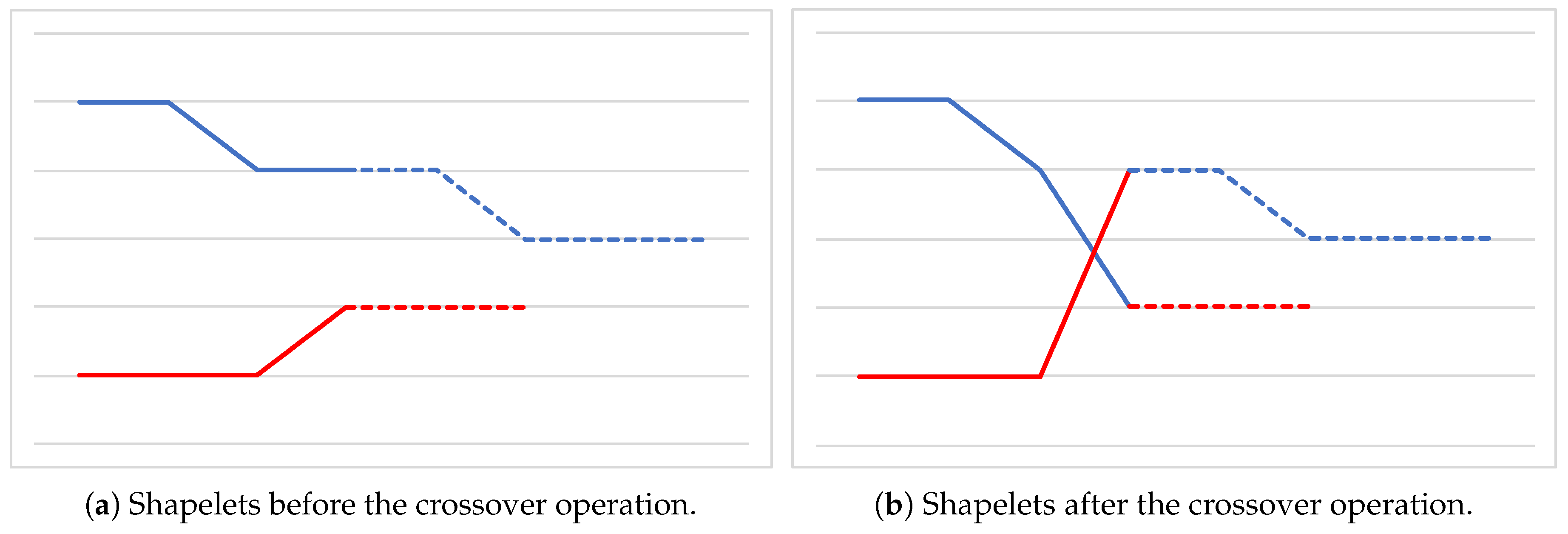
- how the crossover and mutation operators are defined;
- which fitness function and constraints are used;
- which decision method is followed to select a single solution from the resulting front, given that, as we shall see, we are considering a multi-objective setting.
- an early-stopping strategy inspired by the separate-set evaluation presented in [34]. We first partition the training instances into two equally-sized datasets. Then, we train the evolutionary algorithm on the first subset, with a single-objective fitness function aimed at maximizing the information gain of the solutions. We use the other dataset to determine a second information gain value for each solution. During the execution of the algorithm, we keep track of the best performing individual according to the separated set, and we stop the computation after k non improving evolutionary steps. Finally, we return the best individual according to the separated set;
- a bootstrap strategy inspired by the work of [33]. The evolutionary algorithm evaluates each individual on 100 different datasets, built through a random sampling (with replacement) of the original dataset. Two objectives are considered: the first one is that of maximizing the average information gain of the shapelet, as calculated along the 100 datasets, while the second one tries to minimize its standard deviation, in an attempt to search for shapelets that are good in general.
3.2.2. Adapting J48 to Handle Time Series Data
| Algorithm 1 Node splitting procedure |
|
- crossoverP determines the probability of combining two individuals of the population;
- mutationP determines the probability of an element to undergo a random mutation;
- popSize determines the population size, i.e., the number of individuals;
- numEvals establishes the number of evaluations that are going to be carried out in the optimization process.
4. Experimental Tasks
4.1. Call Conversation Transcript Tagging Task
4.1.1. Domain and Problem Description
4.1.2. Experimental Setting
- age: the agent asked the interviewed person his/her age;
- call_permission: the agent asked the called person for the permission to conduct the survey;
- duration_info: the agent gave the called person information about the duration of the survey;
- family_unit: the agent asked the called person information about his/her family unit members;
- greeting_initial: the agent introduced himself/herself at the beginning of the phone call;
- greeting_final: the agent pronounced the scripted goodbye phrases;
- person_identity: the agent asked the called person for a confirmation of his/her identity;
- privacy: the agent informed the called person about the privacy implications of the phone call;
- profession: the agent asked the interviewed person information about his/her job;
- question_1: the agent pronounced the first question of the survey;
- question_2: the agent pronounced the second question of the survey;
- question_3: the agent pronounced the third question of the survey.
4.1.3. Data Preparation and Training of the Model
4.2. UCR Time Series Classification Task
- the original time series, represented by a string;
- the original time series minimum, maximum, average, and variance numerical values;
- the slope time series, derived from the original one and represented by a string;
- the slope time series minimum, maximum, average, and variance numerical values;
5. Results
5.1. Results on Call Conversation Tagging
- accuracy, which is the fraction of times when a tag has been correctly identified in a chunk as present or absent;
- precision, that is, the fraction of chunks in which a specific tag has been identified as present by the method, and in which the tag is indeed present;
- recall, which shows the proportion of chunks presenting the specific tag, that have been in fact identified as such;
- true negative rate (TNR), that reports the proportion of chunks not presenting the specific tag, that have been classified as negative by the method.
IF the current instance contains neither the terms ‘recontact’ and ‘inform’, nor the term ‘thank’ followed by the term ‘cooperation’, THEN label such an instance with class ‘0’.
- the considered datasets may just not be large enough to justify the use of bigrams and trigrams, or
- tag recognition in calls generated in the context of the considered service may not be a difficult concept to learn, so unigrams are enough for the task.
5.2. Results on UCR Datasets Classification
5.2.1. Results of Single J48SS Models
5.2.2. Results of Ensembles of J48SS Models
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann: San Francisco, CA, USA, 1993. [Google Scholar]
- Brunello, A.; Marzano, E.; Montanari, A.; Sciavicco, G. J48S: A Sequence Classification Approach to Text Analysis Based on Decision Trees. In Proceedings of the International Conference on Information and Software Technologies, Vilnius, Lithuania, 4–6 October 2018; Springer: Berlin, Germany, 2018; pp. 240–256. [Google Scholar]
- Brunello, A.; Marzano, E.; Montanari, A.; Sciavicco, G. A Novel Decision Tree Approach for the Handling of Time Series. In Proceedings of the International Conference on Mining Intelligence and Knowledge Exploration, Cluj-Napoca, Romania, 20–22 December 2018; Springer: Berlin, Germany, 2018; pp. 351–368. [Google Scholar]
- Saberi, M.; Khadeer Hussain, O.; Chang, E. Past, present and future of contact centers: A literature review. Bus. Process Manag. J. 2017, 23, 574–597. [Google Scholar] [CrossRef]
- Cailliau, F.; Cavet, A. Mining Automatic Speech Transcripts for the Retrieval of Problematic Calls. In Proceedings of the Thirteenth International Conference on Intelligent Text Processing and Computational Linguistics (CICLing 2013), Samos, Greece, 24–30 March 2013; pp. 83–95. [Google Scholar] [CrossRef]
- Garnier-Rizet, M.; Adda, G.; Cailliau, F.; Gauvain, J.L.; Guillemin-Lanne, S.; Lamel, L.; Vanni, S.; Waast-Richard, C. CallSurf: Automatic Transcription, Indexing and Structuration of Call Center Conversational Speech for Knowledge Extraction and Query by Content. In Proceedings of the Sixth International Conference on Language Resources and Evaluation (LREC 2008), Marrakech, Morocco, 26 May–1 June 2008; pp. 2623–2628. [Google Scholar]
- Nerlove, M.; Grether, D.M.; Carvalho, J.L. Analysis of Economic Time Series: A Synthesis; Academic Press: New York, NY, USA, 2014. [Google Scholar]
- Wei, L.Y.; Huang, D.Y.; Ho, S.C.; Lin, J.S.; Chueh, H.E.; Liu, C.S.; Ho, T.H.H. A hybrid time series model based on AR-EMD and volatility for medical data forecasting: A case study in the emergency department. Int. J. Manag. Econ. Soc. Sci. (IJMESS) 2017, 6, 166–184. [Google Scholar]
- Ramesh, N.; Cane, M.A.; Seager, R.; Lee, D.E. Predictability and prediction of persistent cool states of the tropical pacific ocean. Clim. Dyn. 2017, 49, 2291–2307. [Google Scholar] [CrossRef]
- Chen, Y.; Keogh, E.; Hu, B.; Begum, N.; Bagnall, A.; Mueen, A.; Batista, G. The UCR Time Series Classification Archive. Available online: www.cs.ucr.edu/eamonn/timeseriesdata. (accessed on 27 Februray 2019).
- Kampouraki, A.; Manis, G.; Nikou, C. Heartbeat time series classification with support vector machines. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 512–518. [Google Scholar] [CrossRef] [PubMed]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM fully convolutional networks for time series classification. arXiv, 2018; arXiv:1709.05206. [Google Scholar] [CrossRef]
- Adesuyi, A.S.; Munch, Z. Using time-series NDVI to model land cover change: A case study in the Berg river catchment area, Western Cape, South Africa. Int. J. Environ. Chem. Ecol. Geol. Geophys. Eng. 2015, 9, 537–542. [Google Scholar]
- Schäfer, P.; Leser, U. Fast and Accurate Time Series Classification with WEASEL. In Proceedings of the Proceedings of the 2017 ACM Conference on Information and Knowledge Management (CIKM 2017), Singapore, 6–10 November 2017; ACM: New York, NY, USA, 2017; pp. 637–646. [Google Scholar]
- Frank, E.; Hall, M.A.; Witten, I.H. The WEKA Workbench. Online Appendix for “Data Mining: Practical Machine Learning Tools and Techniques”, 4th ed.; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2016. [Google Scholar]
- Esposito, F.; Malerba, D.; Semeraro, G. A comparative analysis of methods for pruning decision trees. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 476–491. [Google Scholar] [CrossRef]
- Fournier-Viger, P.; Lin, J.C.W.; Kiran, R.U.; Koh, Y.S.; Thomas, R. A survey of sequential pattern mining. Data Sci. Pattern Recognit. 2017, 1, 54–77. [Google Scholar]
- Agrawal, R.; Srikant, R. Mining Sequential Patterns. In Proceedings of the Eleventh IEEE International Conference on Data Engineering (ICDE 1995), Taipei, Taiwan, 6–10 March 1995; pp. 3–14. [Google Scholar]
- Pei, J.; Han, J.; Mortazavi-Asl, B.; Wang, J.; Pinto, H.; Chen, Q.; Dayal, U.; Hsu, M.C. Mining sequential patterns by pattern-growth: The prefixspan approach. IEEE Trans. Knowl. Data Eng. 2004, 16, 1424–1440. [Google Scholar] [CrossRef]
- Zaki, M.J. SPADE: An efficient algorithm for mining frequent sequences. Mach. Learn. 2001, 42, 31–60. [Google Scholar] [CrossRef]
- Ayres, J.; Flannick, J.; Gehrke, J.; Yiu, T. Sequential Pattern Mining Using a Bitmap Representation. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2002), Edmonton, AB, USA, 23–26 July 2002; pp. 429–435. [Google Scholar] [CrossRef]
- Yan, X.; Han, J.; Afshar, R. CloSpan: Mining Closed Sequential Patterns in Large Datasets. In Proceedings of the 2003 SIAM International Conference on Data Mining (SIAM 2003), San Francisco, CA, USA, 1–3 May 2003; pp. 166–177. [Google Scholar] [CrossRef]
- Wang, J.; Han, J. BIDE: Efficient Mining of Frequent Closed Sequences. In Proceedings of the Twentieth IEEE International Conference on Data Engineering (ICDE 2004), Boston, MA, USA, 30 March–2 April 2004; pp. 79–90. [Google Scholar] [CrossRef]
- Gomariz, A.; Campos, M.; Marin, R.; Goethals, B. ClaSP: An Efficient Algorithm for Mining Frequent Closed Sequences. In Proceedings of the Seventeenth Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD 2013), Gold Coast, Australia, 14–17 April 2013; pp. 50–61. [Google Scholar] [CrossRef]
- Fournier-Viger, P.; Gomariz, A.; Campos, M.; Thomas, R. Fast Vertical Mining of Sequential Patterns Using Co-Occurrence Information. In Proceedings of the Eighteenth Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD 2014), Tainan, Taiwan, 13–16 May 2014; pp. 40–52. [Google Scholar]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Lo, D.; Khoo, S.C.; Li, J. Mining and Ranking Generators of Sequential Patterns. In Proceedings of the 2008 SIAM International Conference on Data Mining (SIAM 2008), Atlanta, GA, USA, 24–26 April 2008; pp. 553–564. [Google Scholar] [CrossRef]
- Fournier-Viger, P.; Gomariz, A.; Šebek, M.; Hlosta, M. VGEN: Fast Vertical Mining of Sequential Generator Patterns. In Proceedings of the Sixteenth International Conference on Data Warehousing and Knowledge Discovery (DaWaK 2014), Munich, Germany, 1–5 September 2014; pp. 476–488. [Google Scholar]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing; Springer: New York, NY, USA, 2003. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Gonçalves, I.; Silva, S. Balancing Learning and Overfitting in Genetic Programming with Interleaved Sampling of Training Data. In Proceedings of the European Conference on Genetic Programming (EuroGP 2013), Vienna, Austria, 3–5 April 2013; pp. 73–84. [Google Scholar]
- Dabhi, V.K.; Chaudhary, S. A survey on techniques of improving generalization ability of genetic programming solutions. arXiv, 2012; arXiv:1211.1119. [Google Scholar]
- Fitzgerald, J.; Azad, R.M.A.; Ryan, C. A Bootstrapping Approach to Reduce Over-fitting in Genetic Programming. In Proceedings of the Proceedings of the Fifteenth Annual Conference Companion on Genetic and Evolutionary Computation (GECCO 2013), Amsterdam, The Netherlands, 6–10 July 2013; ACM: New York, NY, USA, 2013; pp. 1113–1120. [Google Scholar]
- Gagné, C.; Schoenauer, M.; Parizeau, M.; Tomassini, M. Genetic Programming, Validation Sets, and Parsimony Pressure. In Proceedings of the European Conference on Genetic Programming (EuroGP 2006), Budapest, Hungary, 10–12 April 2006; Springer: Berlin, Germany, 2006; pp. 109–120. [Google Scholar]
- Vanneschi, L.; Castelli, M.; Silva, S. Measuring Bloat, Overfitting and Functional Complexity in Genetic Programming. In Proceedings of the Twelfth Annual Conference on Genetic and Evolutionary Computation (GECCO 2010), Portland, OR, USA, 7–11 July 2010; ACM: New York, NY, USA, 2010; pp. 877–884. [Google Scholar]
- Lin, J.; Keogh, E.; Lonardi, S.; Chiu, B. A Symbolic Representation of Time Series, With Implications for Streaming Algorithms. In Proceedings of the Eight ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery (SIGMOD 2003), San Diego, CA, USA, 13 June 2003; ACM: New York, NY, USA, 2003; pp. 2–11. [Google Scholar]
- Moskovitch, R.; Shahar, Y. Classification-driven temporal discretization of multivariate time series. Data Min. Knowl. Discov. 2015, 29, 871–913. [Google Scholar] [CrossRef]
- Zhao, J.; Papapetrou, P.; Asker, L.; Boström, H. Learning from heterogeneous temporal data in electronic health records. J. Biomed. Inform. 2017, 65, 105–119. [Google Scholar] [CrossRef] [PubMed]
- Ye, L.; Keogh, E. Time Series Shapelets: A New Primitive for Data Mining. In Proceedings of the Fifteenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2009), Paris, France, 28 June–1 July 2009; ACM: New York, NY, USA, 2009; pp. 947–956. [Google Scholar]
- Grabocka, J.; Schilling, N.; Wistuba, M.; Schmidt-Thieme, L. Learning Time-series Shapelets. In Proceedings of the Twentieth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2014), New York, NY, USA, 24–27 August 2014; ACM: New York, NY, USA, 2014; pp. 392–401. [Google Scholar]
- Grabocka, J.; Wistuba, M.; Schmidt-Thieme, L. Scalable discovery of time-series shapelets. arXiv, 2015; arXiv:1503.03238. [Google Scholar]
- Hou, L.; Kwok, J.T.; Zurada, J.M. Efficient Learning of Timeseries Shapelets. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence (AAAI 2016), Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Karlsson, I.; Papapetrou, P.; Boström, H. Generalized random shapelet forests. Data Min. Knowl. Discov. 2016, 30, 1053–1085. [Google Scholar] [CrossRef]
- Rakthanmanon, T.; Keogh, E. Fast Shapelets: A Scalable Algorithm for Discovering Time Series Shapelets. In Proceedings of the 2013 SIAM International Conference on Data Mining (SIAM 2013), Austin, TX, USA, 2–4 May 2013; pp. 668–676. [Google Scholar]
- Renard, X.; Rifqi, M.; Erray, W.; Detyniecki, M. Random-Shapelet: An Algorithm for Fast Shapelet Discovery. In Proceedings of the 2015 IEEE International Conference on Data Science and Advanced Analytics (DSAA 2015), Paris, France, 19–21 October 2015; pp. 1–10. [Google Scholar]
- Wistuba, M.; Grabocka, J.; Schmidt-Thieme, L. Ultra-fast shapelets for time series classification. arXiv, 2015; arXiv:1503.05018. [Google Scholar]
- Shah, M.; Grabocka, J.; Schilling, N.; Wistuba, M.; Schmidt-Thieme, L. Learning DTW-shapelets for Time-series Classification. In Proceedings of the Third IKDD Conference on Data Science (CODS 2016), Pune, India, 13–16 March 2016; ACM: New York, NY, USA, 2016; p. 3. [Google Scholar]
- Arathi, M.; Govardhan, A. Effect of Mahalanobis Distance on Time Series Classification Using Shapelets. In Proceedings of the Forty-Ninth Annual Convention of the Computer Society of India (CSI 2015), Ghaziabad, India, 8–9 September 2015; Springer: Berlin, Germany, 2015; Volume 2, pp. 525–535. [Google Scholar]
- Cheng, H.; Yan, X.; Han, J.; Hsu, C.W. Discriminative Frequent Pattern Analysis for Effective Classification. In Proceedings of the Twenty-Third IEEE International Conference on Data Engineering (ICDE 2007), Istanbul, Turkey, 15–20 April 2007; pp. 716–725. [Google Scholar] [CrossRef]
- Fan, W.; Zhang, K.; Cheng, H.; Gao, J.; Yan, X.; Han, J.; Yu, P.; Verscheure, O. Direct Mining of Discriminative and Essential Frequent Patterns via Model-Based Search Tree. In Proceedings of the Fourteenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2008), Las Vegas, NV, USA, 24–27 August 2008; pp. 230–238. [Google Scholar] [CrossRef]
- Jun, B.H.; Kim, C.S.; Song, H.Y.; Kim, J. A new criterion in selection and discretization of attributes for the generation of decision trees. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 1371–1375. [Google Scholar] [CrossRef]
- Barros, R.C.; Freitas, A.A. A survey of evolutionary algorithms for decision-tree induction. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2012, 42, 291–312. [Google Scholar] [CrossRef]
- Durillo, J.J.; Nebro, A.J.; Alba, E. The jMetal Framework for Multi-Objective Optimization: Design and Architecture. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC 2010), Barcelona, Spain, 18–23 July 2010; pp. 4138–4325. [Google Scholar]
- Welch, T.A. A technique for high-performance data compression. Computer 1984, 17, 8–19. [Google Scholar] [CrossRef]
- Gans, N.; Koole, G.; Mandelbaum, A. Telephone call centers: Tutorial, review, and research prospects. Manuf. Serv. Oper. Manag. 2003, 5, 79–141. [Google Scholar] [CrossRef]
- Povey, D.; Ghoshal, A.; Boulianne, G.; Burget, L.; Glembek, O.; Goel, N.; Hannemann, M.; Motlicek, P.; Qian, Y.; Schwarz, P.; et al. The Kaldi Speech Recognition Toolkit. In Proceedings of the IEEE 2011 Workshop on Automatic Speech Recognition and Understanding (ASRU 2011), Honolulu, HI, USA, 11–15 December 2011; pp. 1–4. [Google Scholar]
- Hall, M.A. Correlation-Based Feature Selection For Machine Learning. Ph.D. Thesis, The University of Waikato, Hamilton, New Zealand, 1999. [Google Scholar]
- Shanmugam, R.; Chattamvelli, R. Statistics for Scientists and Engineers; Wiley-Blackwell: Hoboken, NJ, USA, 2016; Chapter 4; pp. 89–110. [Google Scholar]
- Ho, T.K. The Random Subspace Method for Constructing Decision Forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Boström, H. Concurrent Learning of Large-Scale Random Forests. In Frontiers in Artificial Intelligence and Applications; IOS Press: Amsterdam, The Netherlands, 2011; Volume 227, pp. 20–29. [Google Scholar]



| Parameter Name | Default | Description |
|---|---|---|
| maxGap | 2 | maximum gap allowance between itemsets (1 = contiguous) |
| maxPatternLength | 20 | maximum length of a pattern, in number of items |
| maxTime | 30 | maximum allowed running time of the algorithm, per call |
| minSupport | 0.5 | minimum support of a pattern |
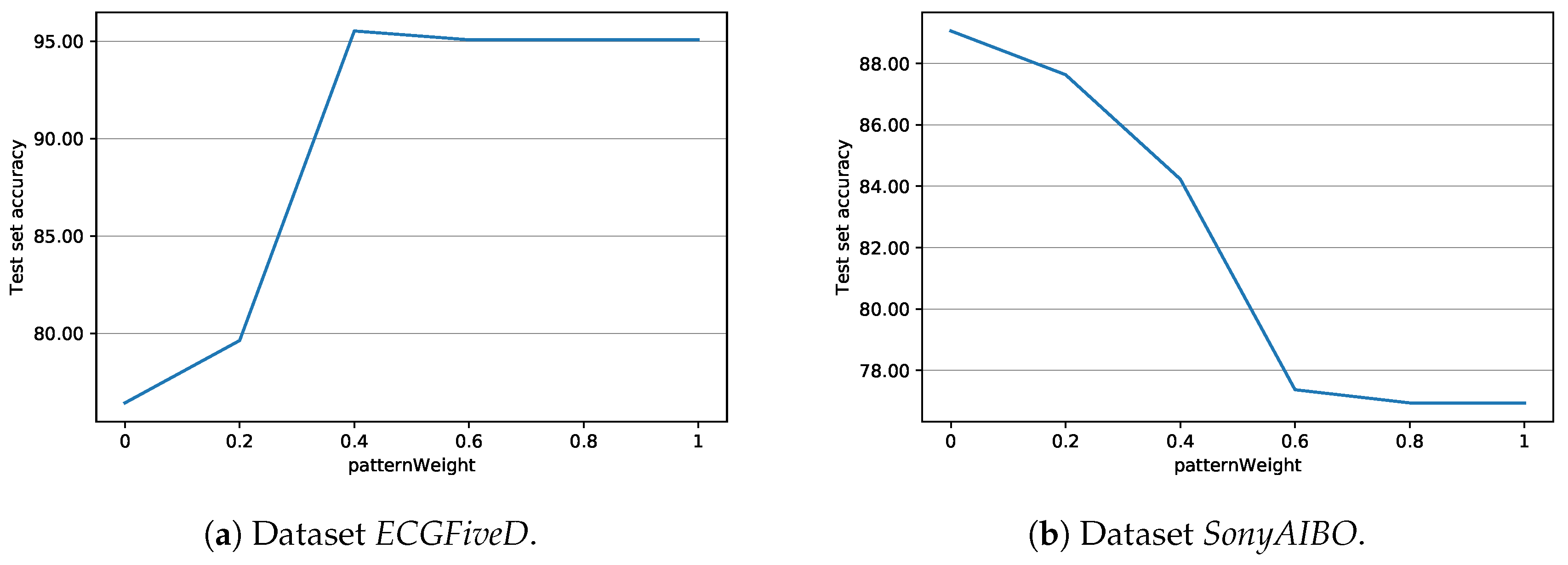
| patternWeight | 0.5 | weight used in VGEN for the extraction of the result |
| useIGPruning | True | use information gain pruning of the pattern search space |
| Parameter Name | Default | Description |
|---|---|---|
| crossoverP | 0.8 | crossover probability to be used in the evolutionary algorithm |
| mutationP | 0.1 | mutation probability to be used in the evolutionary algorithm |
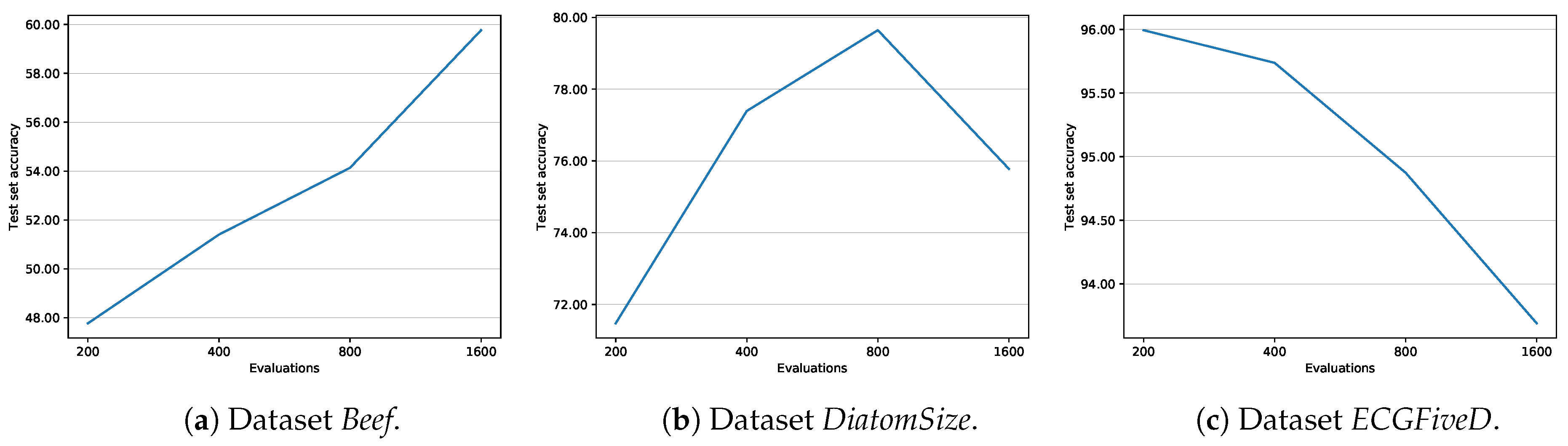
| numEvals | 500 | number of evaluations to be carried out by the evolutionary algorithm |
| patternWeight | 0.75 | weight used for the extraction of the final shapelet |
| popSize | 100 | population size to be used in the evolutionary algorithm |
| Phrase (Italian) | Phrase (English) | Tags |
|---|---|---|
| Si pronto buongiorno sono X dalla X di X, parlo con la signora X? | Hello, my name is X and I am calling from X of X, am I talking with Mrs X? | greeting_initial, person_identity |
| Lei è pensionato. Ultima domanda, senta, a livello statistico la data solo di nascita… millenovecento…? | You are retired. Last question, listen, statistically, the birth date only… nineteen hundred…? | age, profession |
| Ho capito. Posso chiederle il nome di battesimo? | Understood. May I ask you for your first name? | person_identity |
| Mi permette? Trenta secondi, tre domande velocissime… | May I? Thirty seconds, three quick questions… | duration_info |
| Tag Name | #Positive | %Positive | #Negative | %Negative |
|---|---|---|---|---|
| age | 638 | 13.1 | 4246 | 86.9 |
| call_permission | 565 | 11.6 | 4319 | 88.4 |
| duration_info | 491 | 10.1 | 4393 | 89.9 |
| family_unit | 506 | 10.4 | 4378 | 89.6 |
| greeting_initial | 560 | 11.5 | 4324 | 88.5 |
| greeting_final | 453 | 9.3 | 4431 | 90.7 |
| person_identity | 600 | 12.3 | 4284 | 87.7 |
| privacy | 440 | 9.0 | 4444 | 91.0 |
| profession | 391 | 8.0 | 4493 | 92.0 |
| question_1 | 516 | 10.6 | 4368 | 89.4 |
| question_2 | 496 | 10.2 | 4388 | 89.8 |
| question_3 | 500 | 10.2 | 4384 | 89.8 |
| Dataset | Domain | ∣Train∣ | ∣Test∣ | TS Length | patternWeight | numEvals |
|---|---|---|---|---|---|---|
| Adiac | Biology | 390 | 391 | 176 | 0.4 | 800 |
| Beef | Food quality | 30 | 30 | 470 | 0.5 | 800 |
| ChlorineC | Health | 467 | 3840 | 166 | 0.9 | 800 |
| Coffee | Food quality | 28 | 28 | 286 | 0.0 | 800 |
| DiatomSize | Biology | 16 | 306 | 345 | 0.0 | 400 |
| ECGFiveD | Health | 23 | 861 | 136 | 0.4 | 200 |
| FaceFour | Image recognition | 24 | 88 | 350 | 0.5 | 200 |
| GunPoint | Motion detection | 50 | 150 | 150 | 0.8 | 800 |
| ItalyPower | Energy consumption | 67 | 1029 | 24 | 0.6 | 800 |
| Lighting7 | Weather prediction | 70 | 73 | 319 | 0.9 | 800 |
| MedicalIm | Health | 381 | 760 | 99 | 0.2 | 400 |
| MoteStrain | Signal discrimination | 20 | 1252 | 84 | 0.9 | 200 |
| SonyAIBO | Robotics | 20 | 601 | 70 | 0.2 | 200 |
| Symbols | Health | 25 | 995 | 398 | 1.0 | 800 |
| Trace | Nuclear energy safety | 100 | 100 | 275 | 0.5 | 400 |
| TwoLead | Health | 23 | 1139 | 82 | 0.7 | 200 |
| Tag Name | Accuracy | Precision | Recall | TNR |
|---|---|---|---|---|
| age | 0.9655 | 0.9241 | 0.8171 | 0.9893 |
| call_permission | 0.9167 | 0.6500 | 0.6454 | 0.9532 |
| duration_info | 0.9739 | 0.9008 | 0.8516 | 0.9887 |
| family_unit | 0.9722 | 0.8779 | 0.8712 | 0.9848 |
| greeting_initial | 0.9739 | 0.9397 | 0.8195 | 0.9934 |
| greeting_final | 0.9916 | 0.9823 | 0.9328 | 0.9981 |
| person_identity | 0.9428 | 0.7851 | 0.6934 | 0.9753 |
| privacy | 0.9916 | 0.9550 | 0.9550 | 0.9554 |
| profession | 0.9840 | 0.8969 | 0.9063 | 0.9908 |
| question_1 | 0.9857 | 0.9688 | 0.9051 | 0.9962 |
| question_2 | 0.9815 | 0.9153 | 0.9000 | 0.9906 |
| question_3 | 0.9798 | 0.9237 | 0.8790 | 0.9915 |
| Macro average | 0.9716 | 0.8933 | 0.8480 | 0.9839 |
| Keyword Name | Accuracy | Precision | Recall | TNR |
|---|---|---|---|---|
| age | 0.9663 | 0.8974 | 0.8537 | 0.9844 |
| call_permission | 0.9310 | 0.7980 | 0.5603 | 0.9809 |
| duration_info | 0.9672 | 0.9083 | 0.7734 | 0.9906 |
| family_unit | 0.9630 | 0.8929 | 0.7576 | 0.9886 |
| greeting_initial | 0.9773 | 0.9206 | 0.8722 | 0.9905 |
| greeting_final | 0.9941 | 0.9912 | 0.9496 | 0.9991 |
| person_identity | 0.9369 | 0.7500 | 0.6788 | 0.9705 |
| privacy | 0.9907 | 0.9545 | 0.9459 | 0.9954 |
| profession | 0.9874 | 0.8932 | 0.9583 | 0.9899 |
| question_1 | 0.9840 | 0.9683 | 0.8905 | 0.9962 |
| question_2 | 0.9840 | 0.9244 | 0.9167 | 0.9916 |
| question_3 | 0.9848 | 0.9417 | 0.9113 | 0.9934 |
| Macro average | 0.9722 | 0.9033 | 0.8390 | 0.9893 |
| Dataset | Random Shapelet | J48SS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.10 | 0.20 | 0.50 | 1.00 | 2.00 | 10.00 | 20.00 | 25.00 | 33.33 | 50.00 | ||
| Adiac | 45.4 | 47.7 | 49.6 | 50.6 | 51.9 | 51.6 | 51.3 | 51.7 | 50.3 | 51.8 | 60.5 |
| Beef | 40.0 | 39.3 | 36.8 | 35.5 | 33.6 | 32.4 | 31.6 | 32.0 | 31.8 | 31.2 | 55.4 |
| ChlorineC | 54.2 | 54.8 | 55.7 | 55.9 | 56.0 | 57.2 | 57.2 | 55.5 | 58.1 | * | 61.4 |
| Coffee | 69.0 | 70.3 | 73.1 | 74.1 | 76.4 | 76.9 | 78.1 | 78.3 | 78.3 | 78.3 | 100.0 |
| DiatomSize | 83.6 | 85.4 | 82.5 | 80.5 | 78.6 | 77.4 | 79.5 | 79.8 | 79.9 | 79.7 | 82.7 |
| ECGFiveD | 94.2 | 96.2 | 96.7 | 97.2 | 97.3 | 97.7 | 97.3 | 97.0 | 96.7 | 96.1 | 96.2 |
| FaceFour | 72.1 | 71.6 | 73.8 | 72.9 | 72.8 | 74.2 | 74.6 | 75.0 | 75.5 | 74.4 | 84.5 |
| GunPoint | 89.3 | 88.3 | 87.9 | 87.3 | 87.3 | 84.4 | 82.9 | 82.7 | 82.8 | 82.9 | 91.8 |
| ItalyPower | 87.1 | 87.8 | 90.0 | 90.4 | 90.8 | 92.4 | 93.0 | 93.0 | 93.1 | 93.2 | 92.7 |
| Lighting7 | 61.9 | 61.0 | 58.1 | 56.9 | 56.9 | 63.50 | 63.5 | 63.9 | 64.9 | 63.0 | 66.0 |
| MedicalIm | 58.3 | 58.5 | 58.8 | 58.9 | 58.8 | 59.2 | 59.6 | 59.8 | 59.7 | 60.6 | 65.8 |
| MoteStrain | 78.4 | 78.9 | 79.2 | 79.2 | 79.2 | 81.5 | 81.8 | 82.3 | 82.2 | 82.0 | 81.5 |
| SonyAIBO | 83.8 | 84.9 | 85.5 | 86.9 | 86.3 | 86.8 | 87.2 | 87.9 | 88.6 | 89.8 | 89.2 |
| Symbols | 78.0 | 76.1 | 76.0 | 75.2 | 76.8 | 79.5 | 80.6 | 80.8 | 80.7 | 80.6 | 77.6 |
| Trace | 94.4 | 94.5 | 95.0 | 95.0 | 94.6 | 93.4 | 93.1 | 93.1 | 93.0 | 93.0 | 95.0 |
| TwoLead | 82.2 | 85.6 | 87.4 | 89.5 | 90.2 | 91.4 | 92.1 | 92.1 | 92.1 | 92.0 | 90.6 |
| Average | 73.2 | 73.8 | 74.1 | 74.1 | 74.2 | 75.0 | 75.2 | 75.3 | 75.5 | N/A | 80.7 |
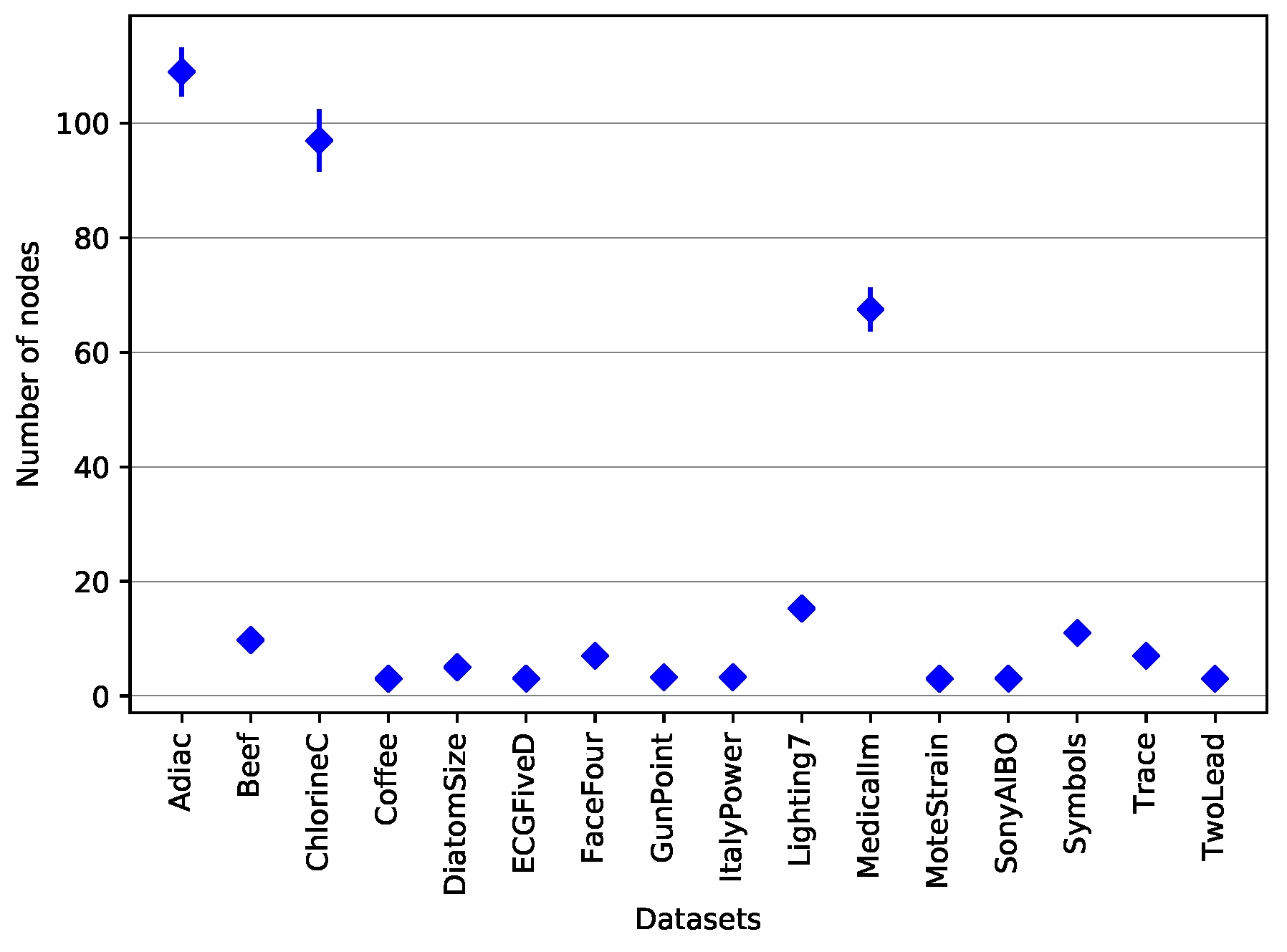
| Dataset | 200 Evals | 400 Evals | 800 Evals | 1600 Evals |
|---|---|---|---|---|
| Adiac | 14.1 | 20.8 | 37.8 | 98.9 |
| Beef | 3.7 | 5.2 | 7.72 | 14.8 |
| ChlorineC | 24.5 | 30.1 | 44.2 | 86.4 |
| Coffee | 1.1 | 1.4 | 2.0 | 4.0 |
| DiatomSize | 1.9 | 2.5 | 4.1 | 10.9 |
| ECGFiveD | 0.8 | 1.1 | 1.4 | 2.2 |
| FaceFour | 2.1 | 2.8 | 4.3 | 8.2 |
| GunPoint | 1.3 | 1.5 | 1.9 | 2.6 |
| ItalyPower | 0.8 | 0.9 | 1.3 | 2.4 |
| Lighting7 | 4.6 | 6.6 | 10.2 | 18.6 |
| MedicalIm | 8.3 | 11.0 | 17.4 | 38.4 |
| MoteStrain | 0.6 | 0.7 | 0.9 | 1.3 |
| SonyAIBO | 0.6 | 0.8 | 1.0 | 1.9 |
| Symbols | 2.7 | 3.9 | 6.3 | 14.5 |
| Trace | 2.2 | 3.0 | 4.6 | 9.5 |
| TwoLead | 0.5 | 0.7 | 0.9 | 1.5 |
| Dataset | gRSF Accuracy | EJ48SS Accuracy | EJ48SS Training Time (s) |
|---|---|---|---|
| Adiac | 74.2 | 78.1 | 2196.8 |
| Beef | 80.0 | 67.5 | 269.1 |
| ChlorineC | 67.3 | 72.2 | 2230.9 |
| Coffee | 100.0 | 100.0 | 49.0 |
| DiatomSize | 96.4 | 86.8 | 57.6 |
| ECGFiveD | 100.0 | 100.0 | 6.2 |
| FaceFour | 100.0 | 92.8 | 36.8 |
| GunPoint | 100.0 | 98.0 | 40.2 |
| ItalyPower | 94.0 | 95.6 | 19.3 |
| Lighting7 | 69.9 | 73.1 | 410.5 |
| MedicalIm | 73.3 | 75.5 | 392.2 |
| MoteStrain | 92.1 | 92.6 | 6.5 |
| SonyAIBO | 92.5 | 90.4 | 6.4 |
| Symbols | 96.8 | 76.1 | 215.2 |
| Trace | 100.0 | 99.1 | 61.5 |
| TwoLead | 100.0 | 97.1 | 5.8 |
| Average | 89.8 | 87.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brunello, A.; Marzano, E.; Montanari, A.; Sciavicco, G. J48SS: A Novel Decision Tree Approach for the Handling of Sequential and Time Series Data. Computers 2019, 8, 21. https://doi.org/10.3390/computers8010021
Brunello A, Marzano E, Montanari A, Sciavicco G. J48SS: A Novel Decision Tree Approach for the Handling of Sequential and Time Series Data. Computers. 2019; 8(1):21. https://doi.org/10.3390/computers8010021
Chicago/Turabian StyleBrunello, Andrea, Enrico Marzano, Angelo Montanari, and Guido Sciavicco. 2019. "J48SS: A Novel Decision Tree Approach for the Handling of Sequential and Time Series Data" Computers 8, no. 1: 21. https://doi.org/10.3390/computers8010021
APA StyleBrunello, A., Marzano, E., Montanari, A., & Sciavicco, G. (2019). J48SS: A Novel Decision Tree Approach for the Handling of Sequential and Time Series Data. Computers, 8(1), 21. https://doi.org/10.3390/computers8010021







