Generalized Majority Voter Design Method for N-Modular Redundant Systems Used in Mission- and Safety-Critical Applications
Abstract
:1. Introduction
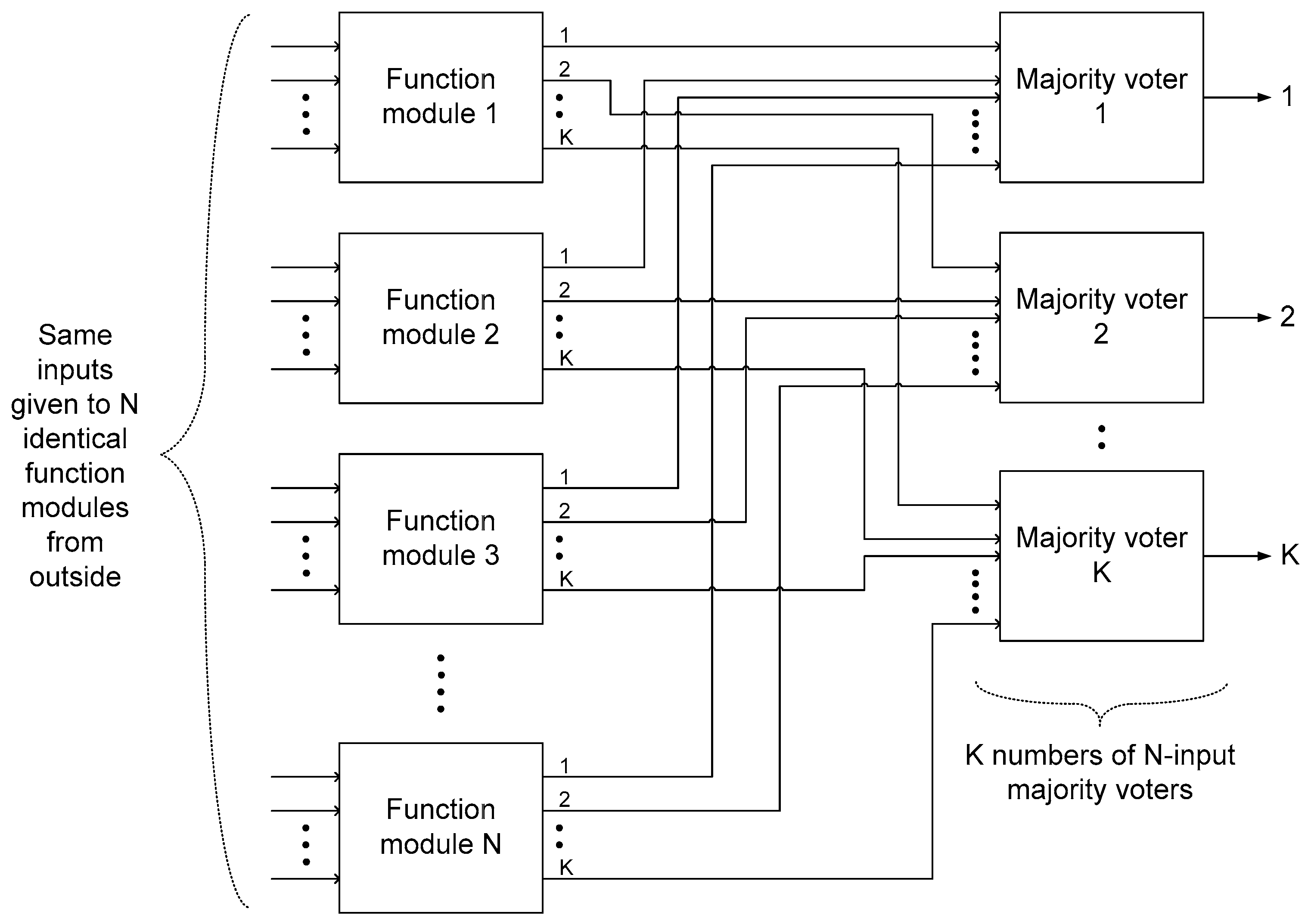
2. Methods
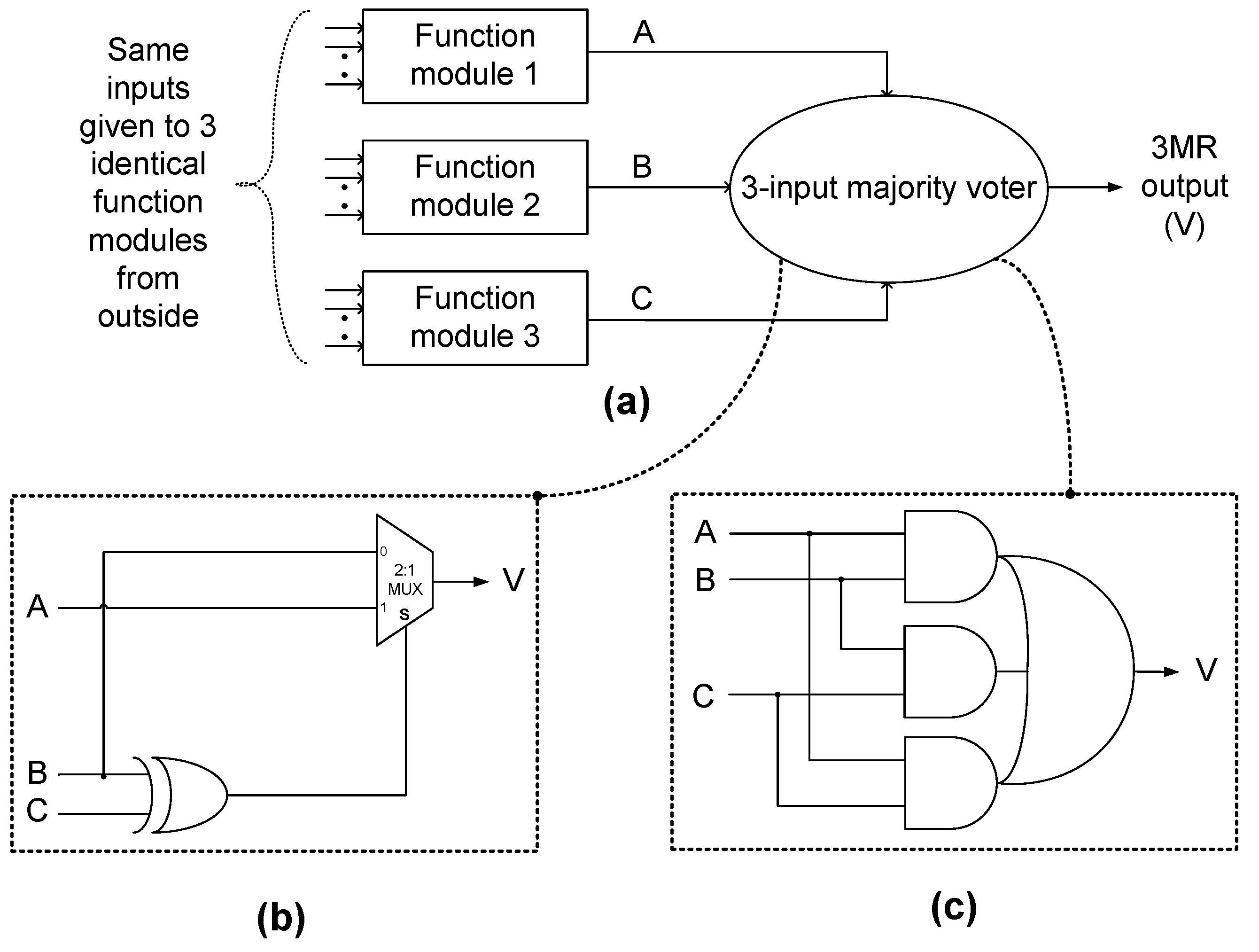
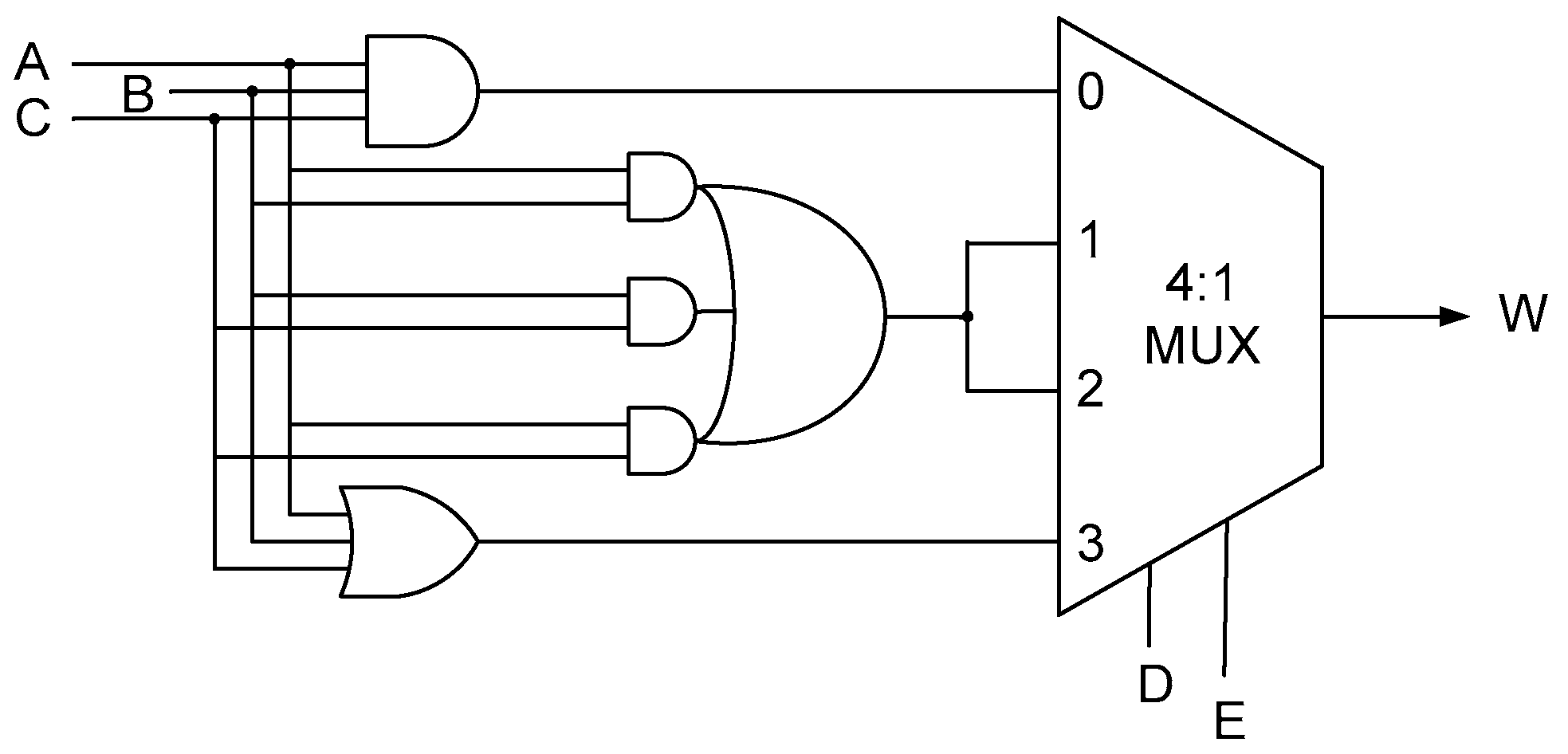
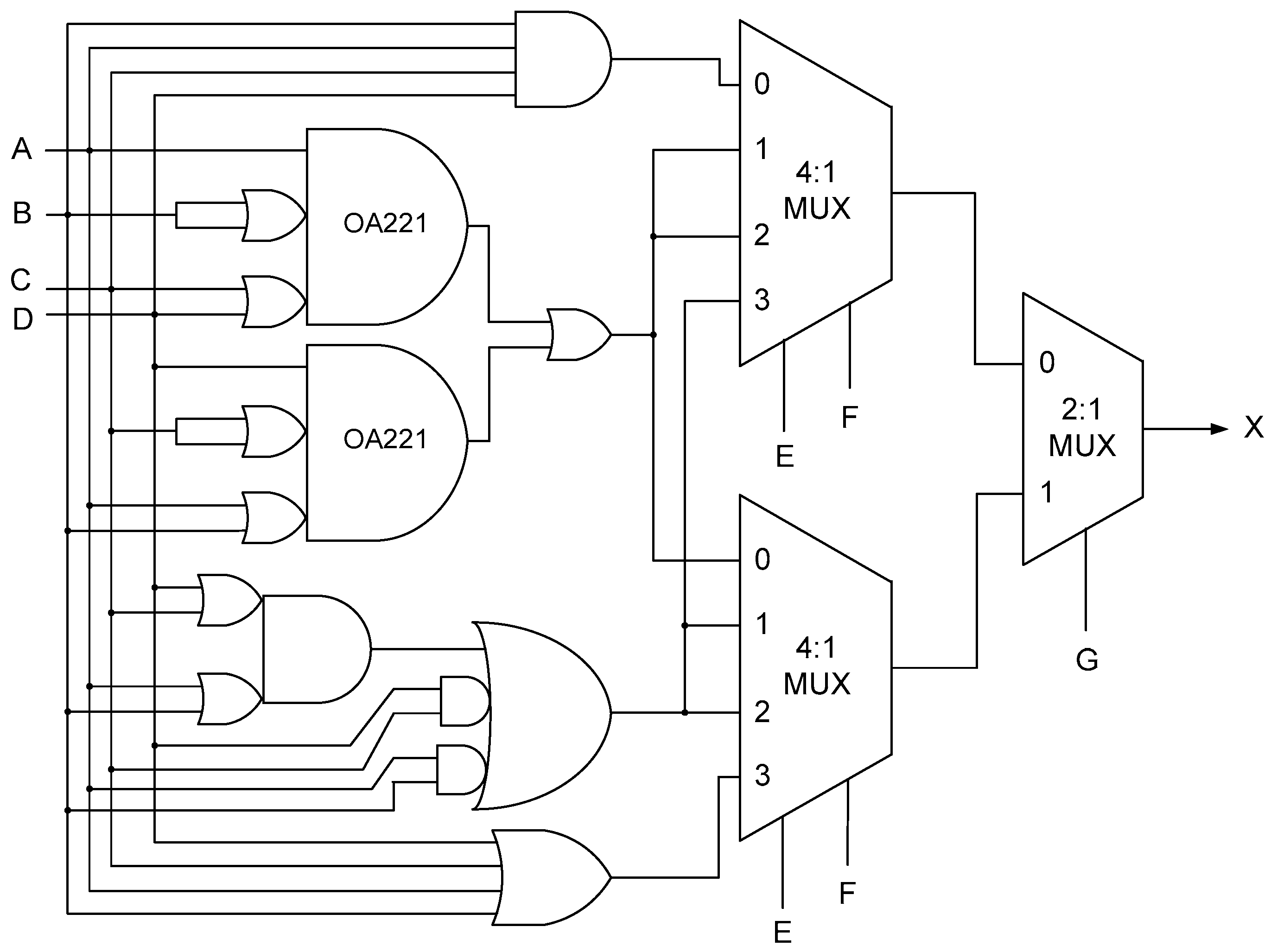
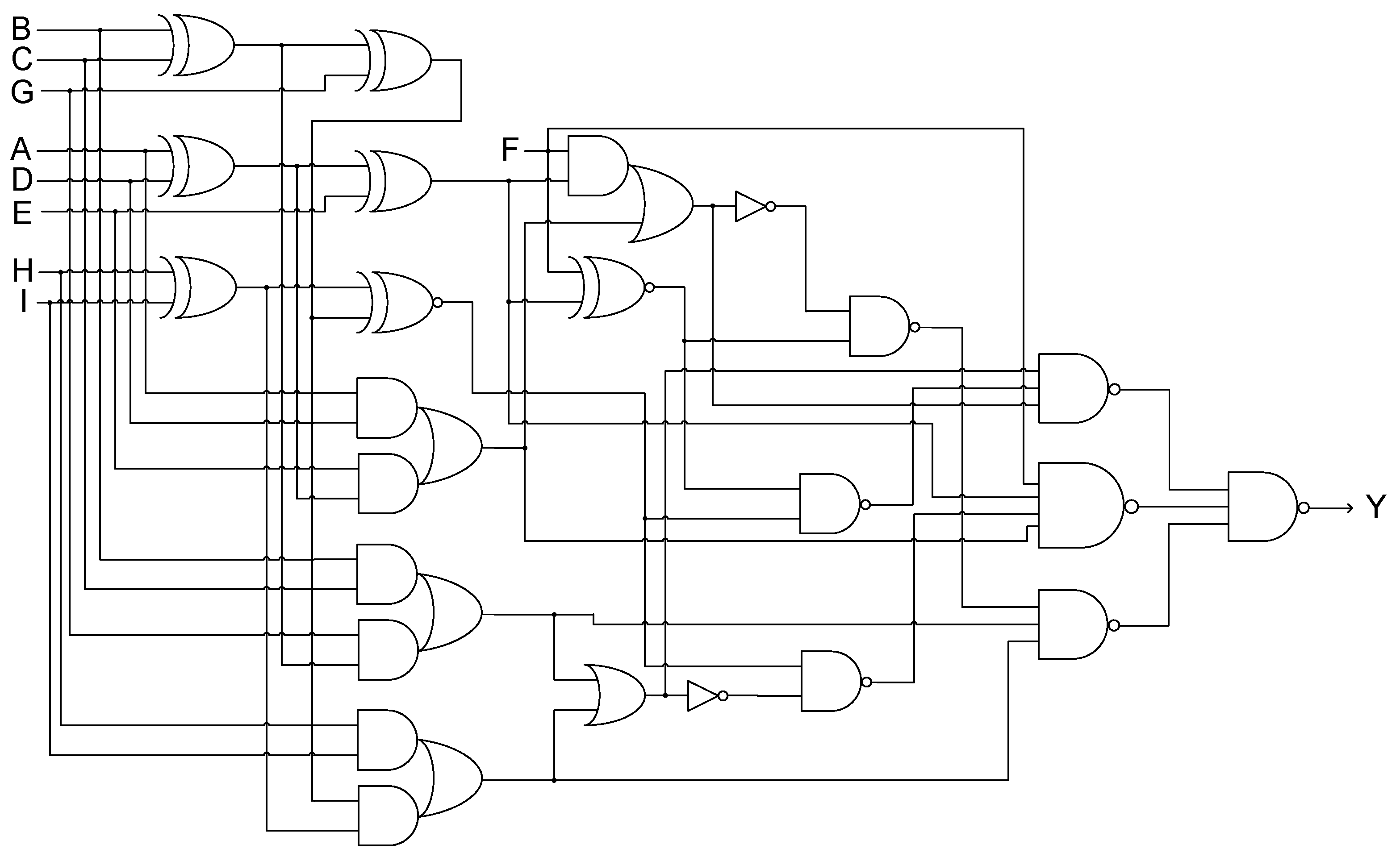
2.1. MUX-Based Design of Majority Voters
AD + BC + BD + CD)(E’FG + EF’G + EFG’) + (A + B + C + D)EFG
+ F’GH’I’ + FG’H’I’) + (ABC + ABD + ABE + ACD + ACE + ADE + BCD + BCE
+ BDE + CDE)(F’G’HI + F’GH’I + F’GHI’ + FG’H’I + FG’HI’ + FGH’I’) + (AB +
AC + AD + AE + BC + BD + BE + CD + CE + DE)(F’GHI + FG’HI + FGH’I +
FGHI’) + (A + B + C + D + E)FGHI
2.2. Direct Synthesis of Majority Voters
3. Proposed Design Method for Majority Voters
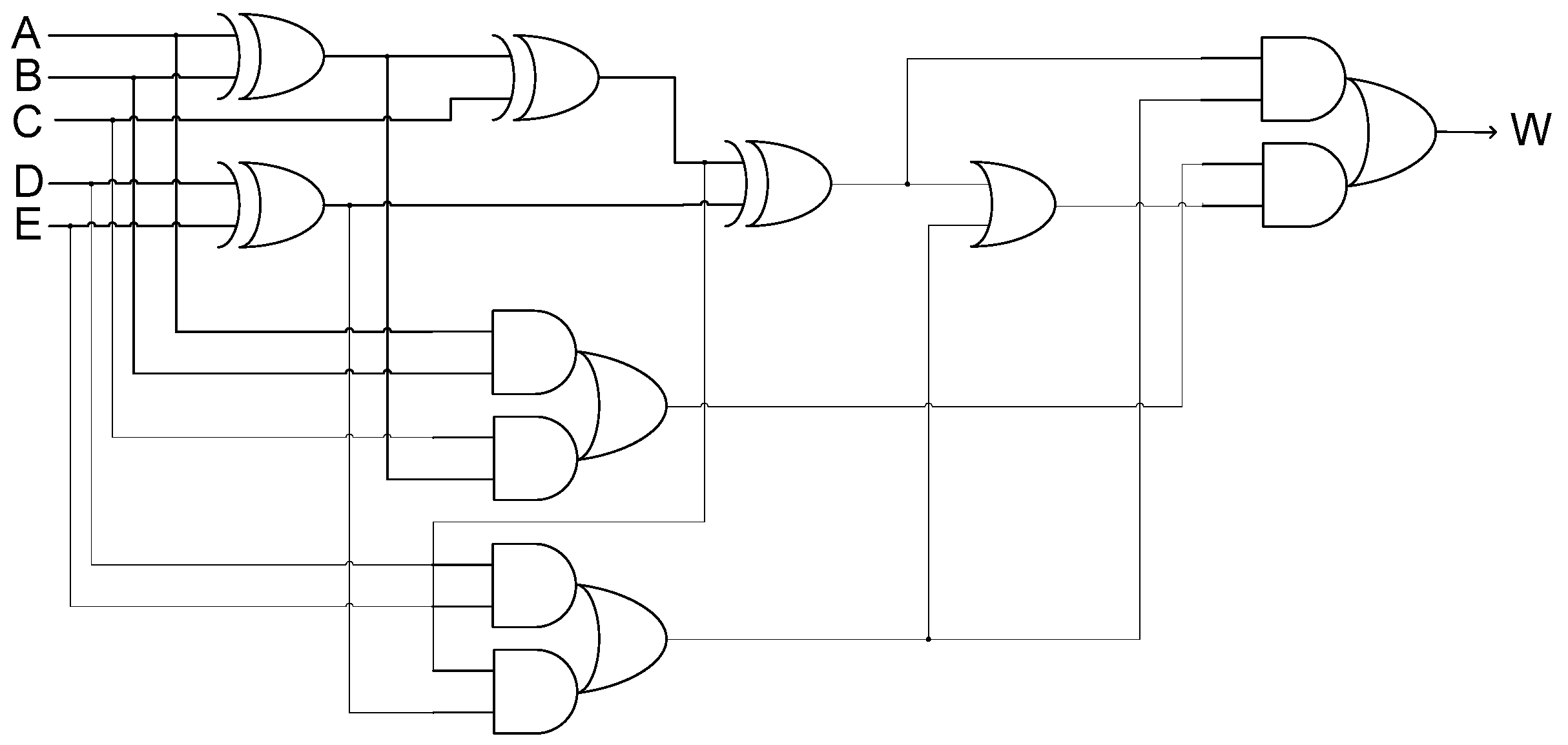
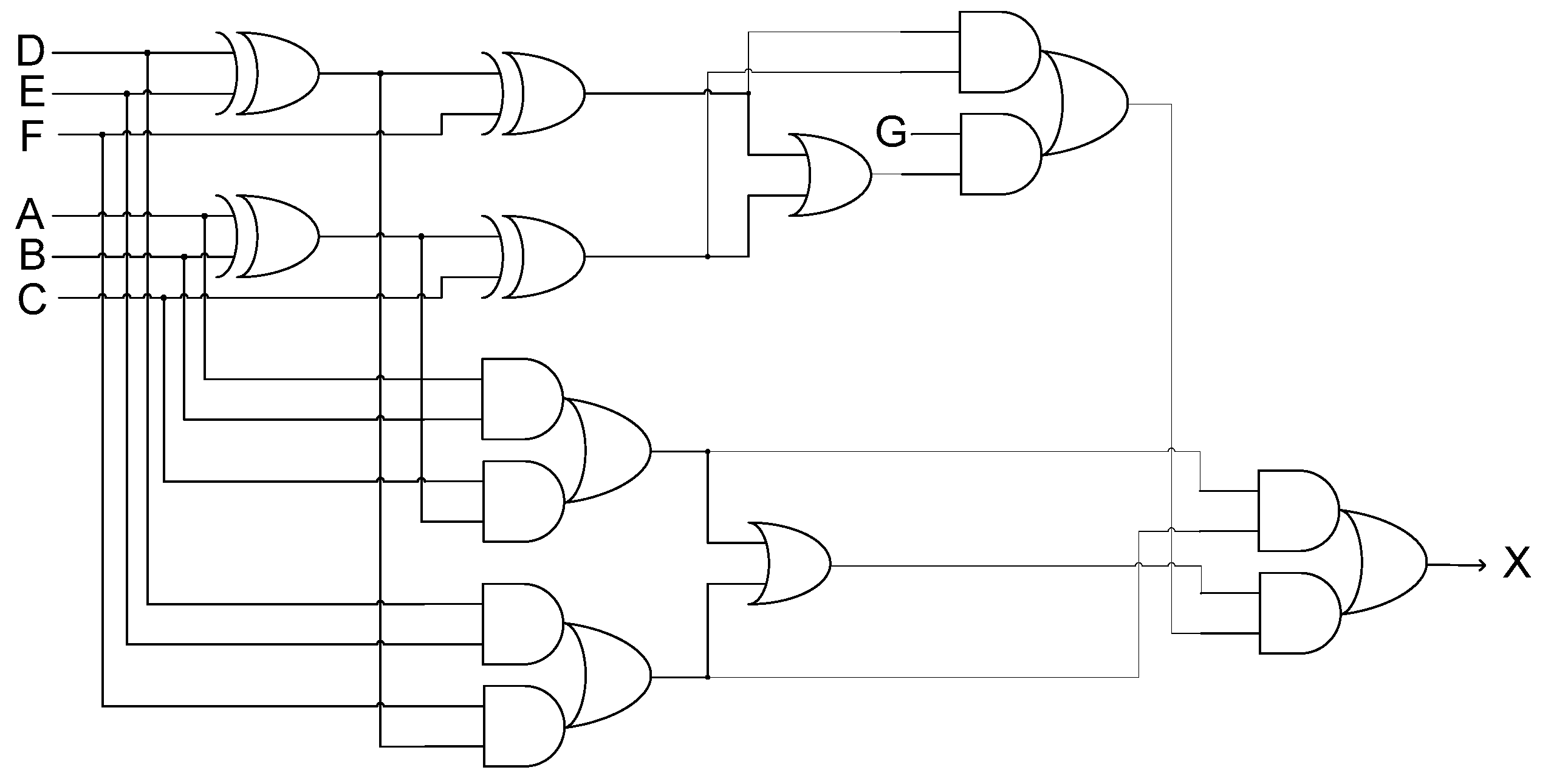
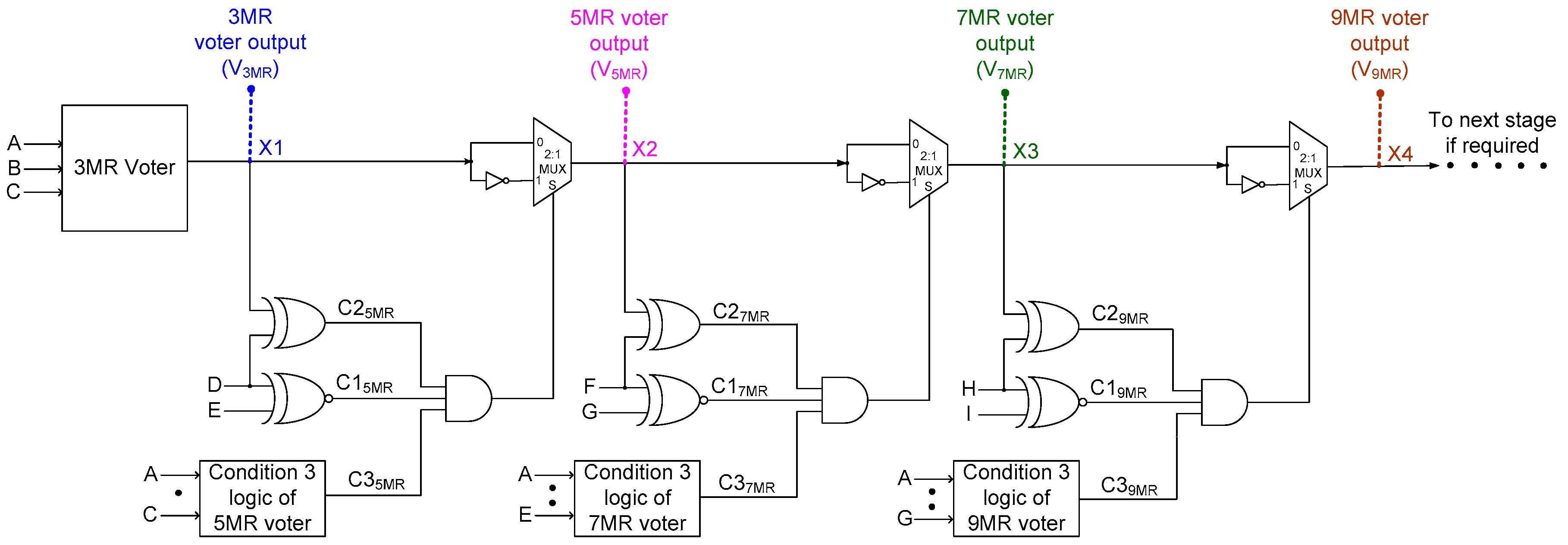
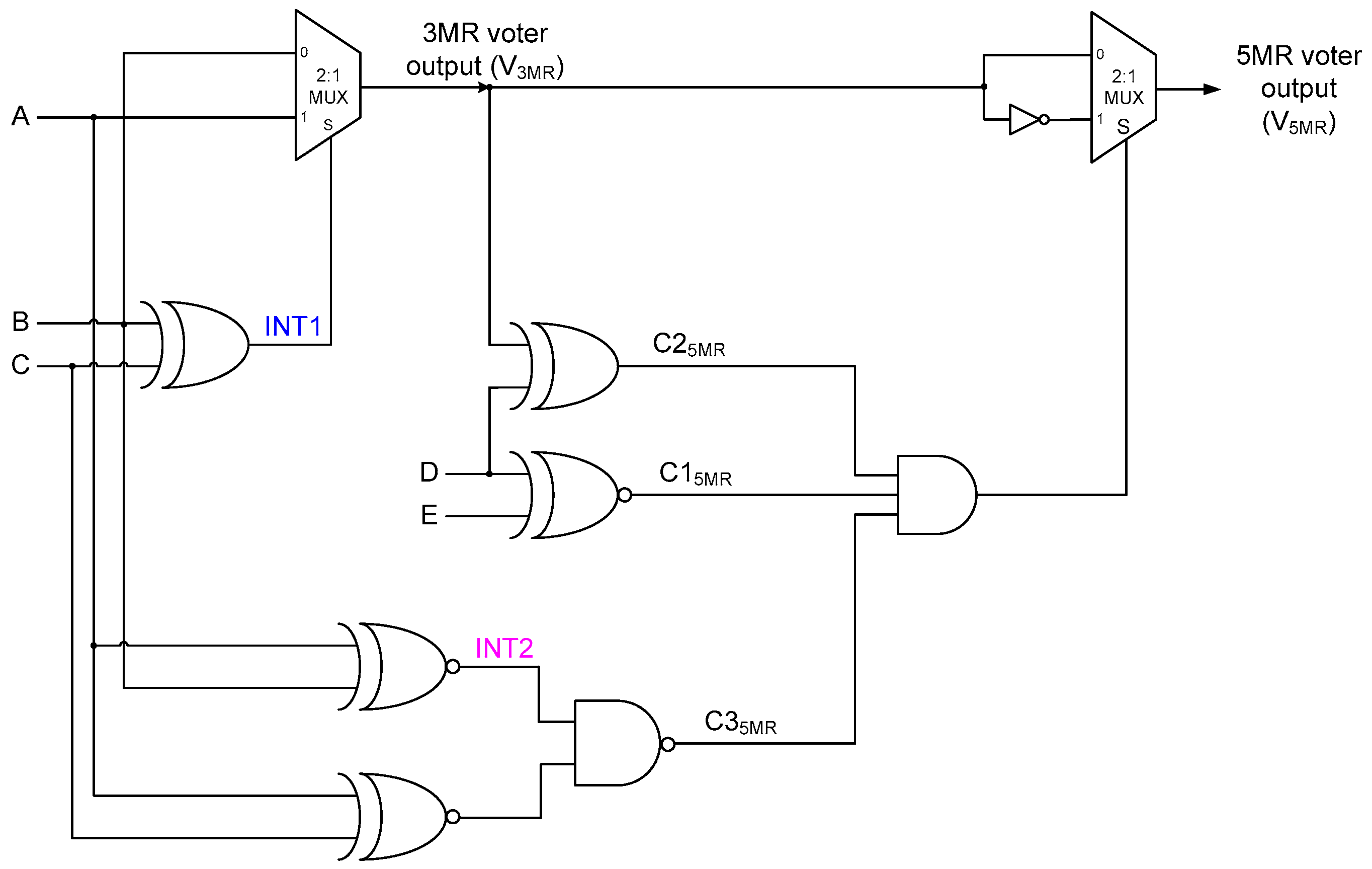
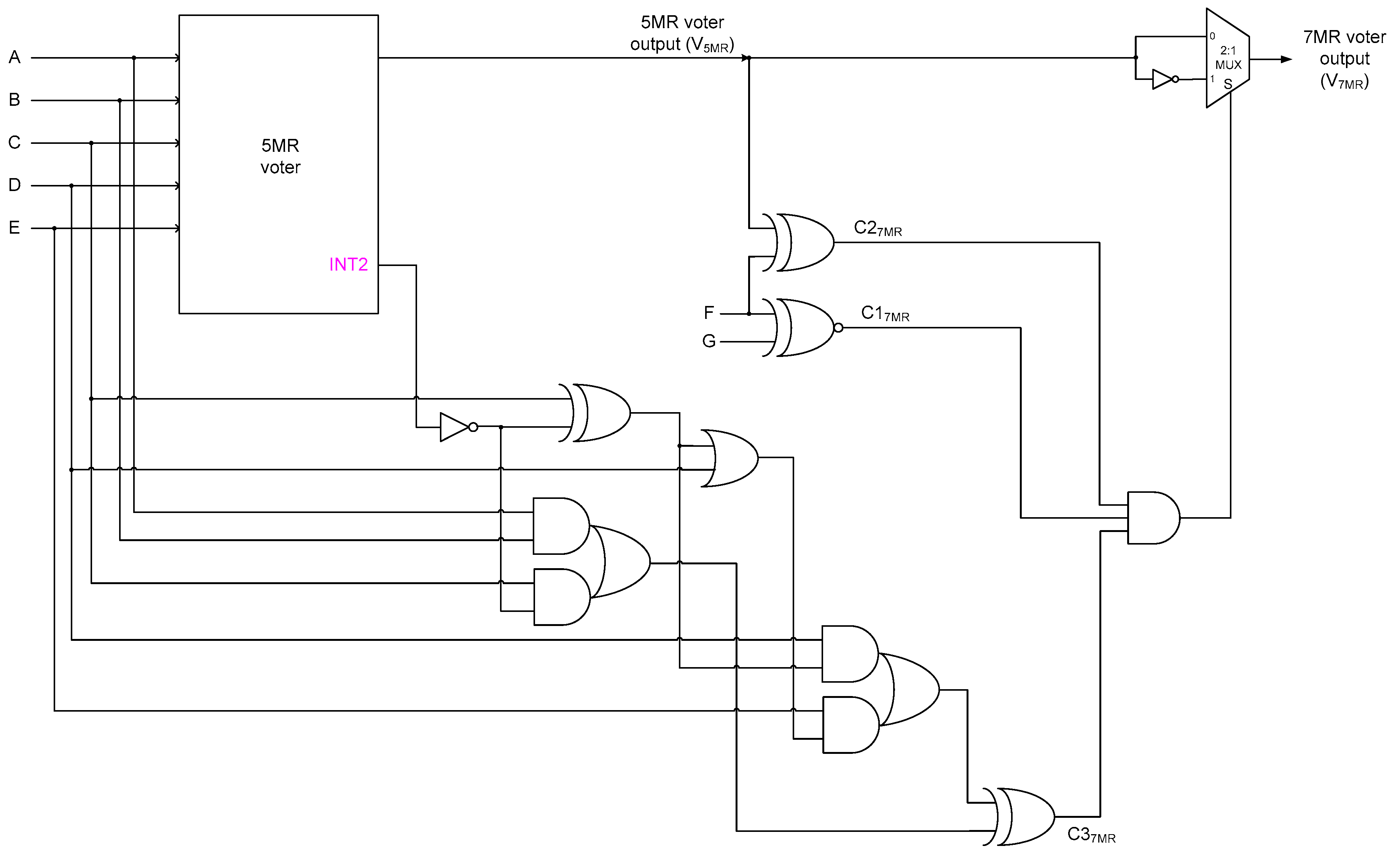
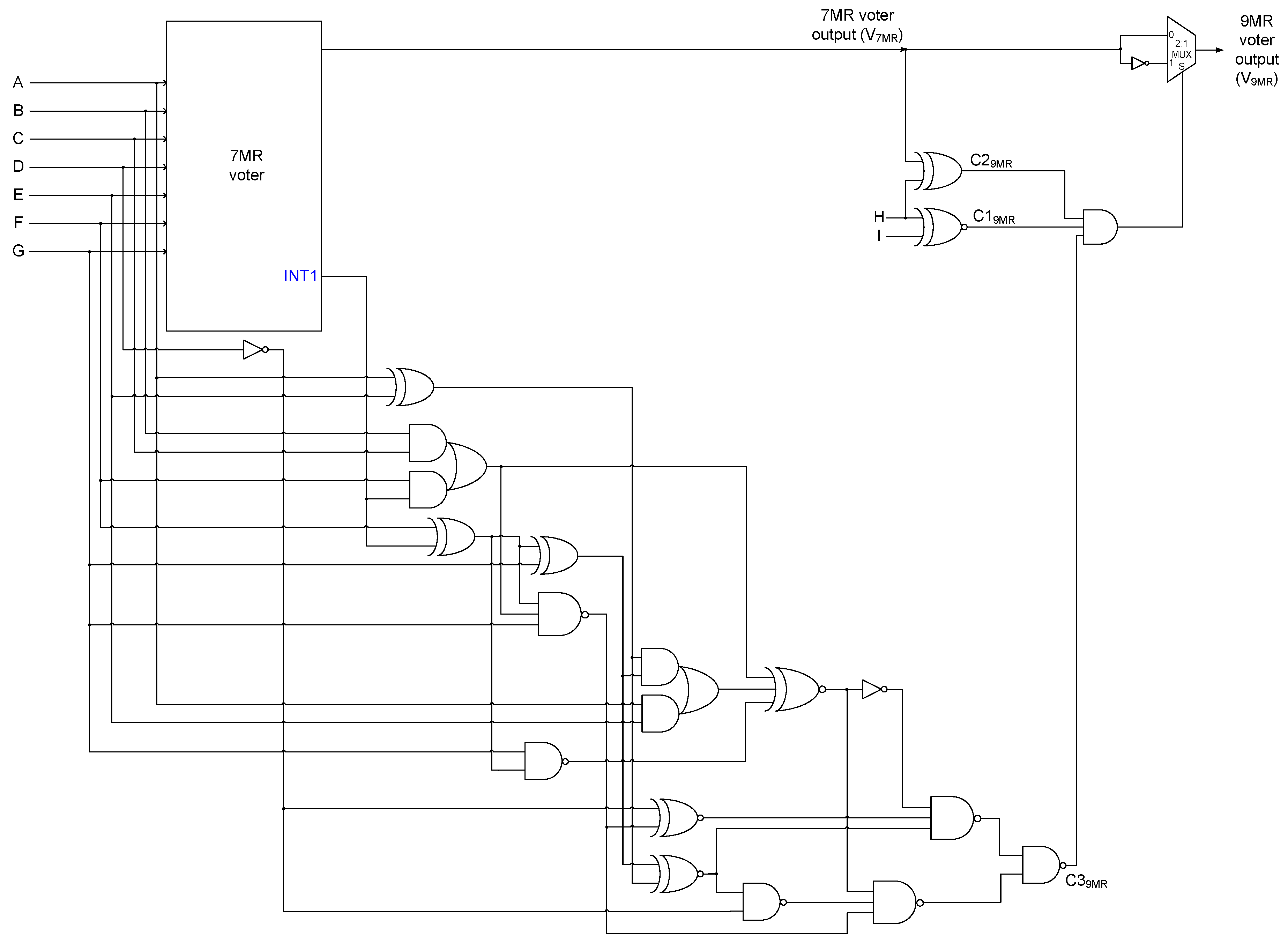
- Condition 1: Represents the XNOR-ing of the two extra inputs (X and Y) present in an NMR majority voter. If X and Y are equal, then C1 would assume 1, otherwise it would assume 0.
- Condition 2: Represents the XOR-ing of one of the extra inputs (say, X) with the (N − 2)MR majority voter output. C2 would assume 1 if the extra input considered is complementary to the (N − 2)MR majority voter output, otherwise it would assume 0.
- Condition 3: If C1 or C2 or both C1 and C2 would assume 0, the output of the 3-input AND gate would be 0 i.e., S = 0, which implies that the NMR voter output would be the same as the (N − 2)MR voter output. The logic used to realize Condition 3 is quite sophisticated and considers those input clauses for which an (N − 2)MR voter would output 0 or 1 due to only (N − 1)/2 inputs being 0 or 1 respectively, and consequently an NMR voter output may become contrary to the (N − 2)MR voter output. In conjunction with the logic used to realize Conditions 1 and 2, Condition 3 is used to either forward the (N − 2)MR voter output as the NMR voter output or complement the former and forward that as the NMR voter output. This is achieved by determining whether a 0 is produced by an (N − 2)MR majority voter due to all the (N − 2) inputs being 0 or only (N − 1)/2 inputs are 0, and similarly whether a 1 is produced by an (N − 2)MR majority voter due to all the (N − 2) inputs being 1 or only (N − 1)/2 inputs are 1.
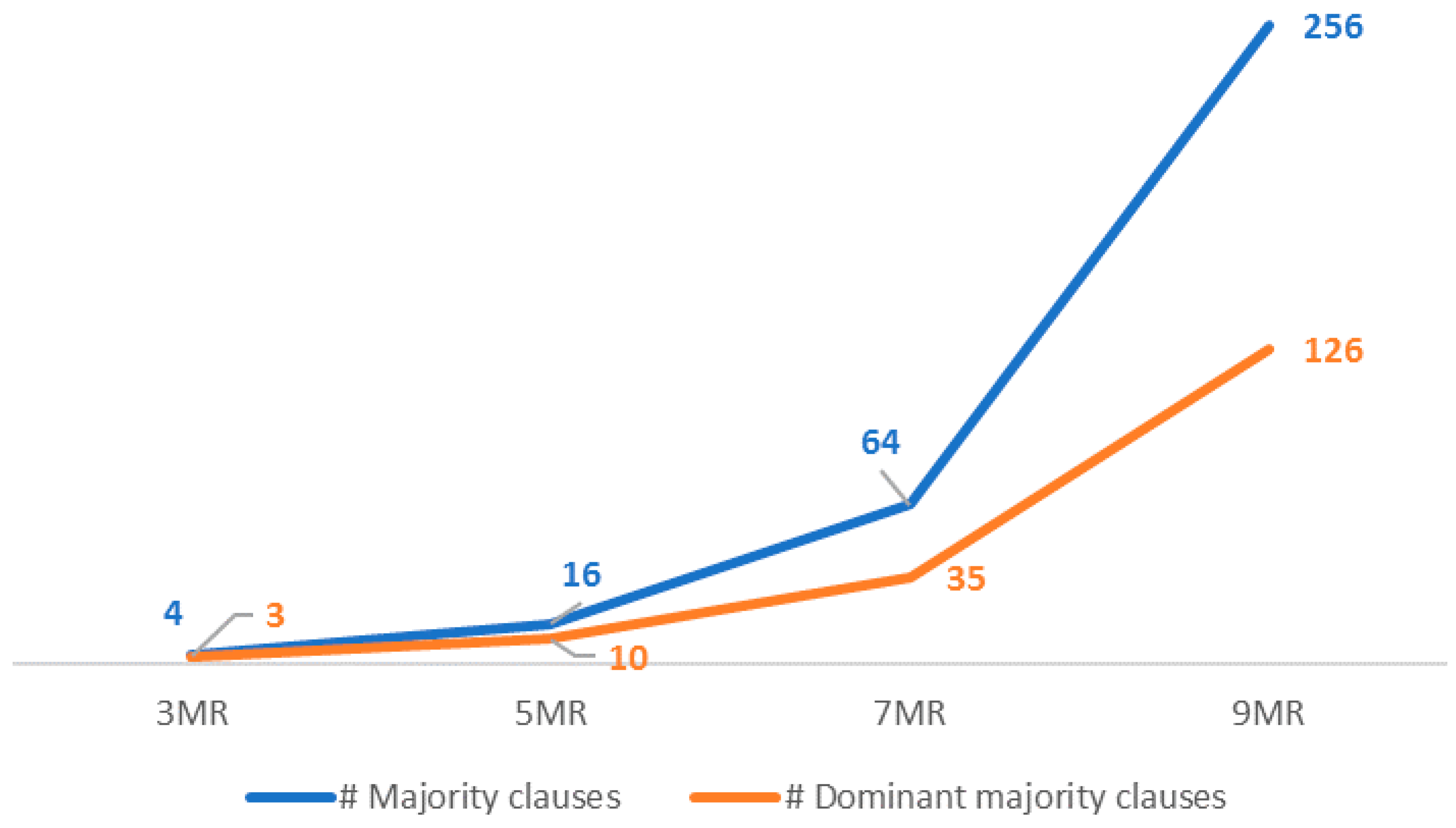
3.1. Proposed 5MR Majority Voter
3.2. Proposed 7MR Majority Voter
+ A’BC)(D’E + DE’) + (A’B’C’ + AB’C’ + A’BC’ + A’B’C)DE
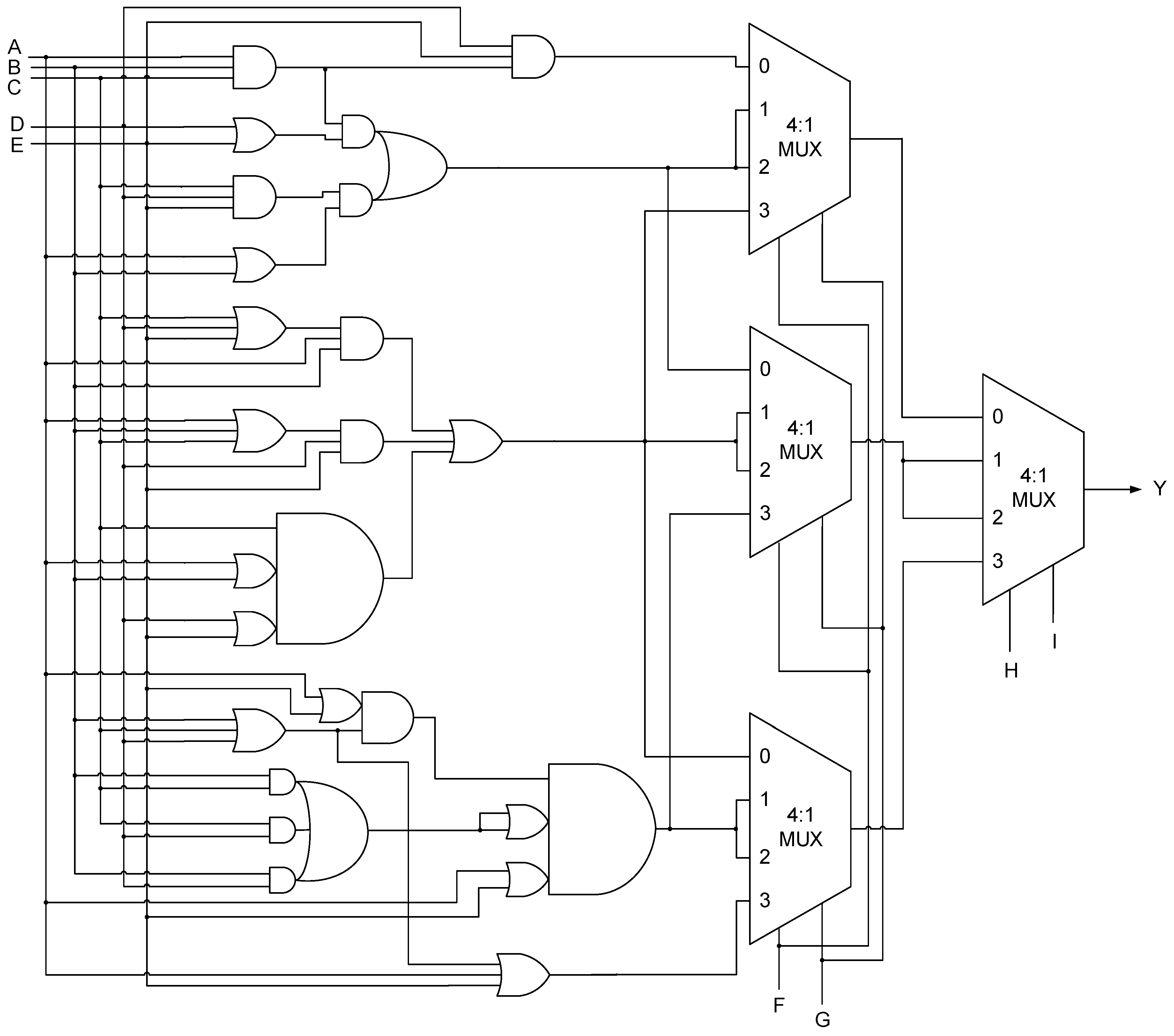
3.3. Proposed 9MR Majority Voter
AB’C’D + A’BCD’ + A’BC’D + ABCD’ + ABC’D + A’BCD + AB’CD + A’B’CD)(E’F’G
+ E’FG’ + EF’G’) + (AB’C’D’ + A’BC’D’ + A’B’CD’ + A’B’C’D + ABC’D’ + A’BCD’ +
A’BC’D + A’B’CD + AB’C’D + AB’CD’)(E’FG + EFG’ + EF’G) + (A’B’C’D’ + A’BC’D’
+ A’B’CD’ + A’B’C’D + AB’C’D’)EFG
4. Results and Discussion
4.1. Example NMR System Implementations with Single Redundancy
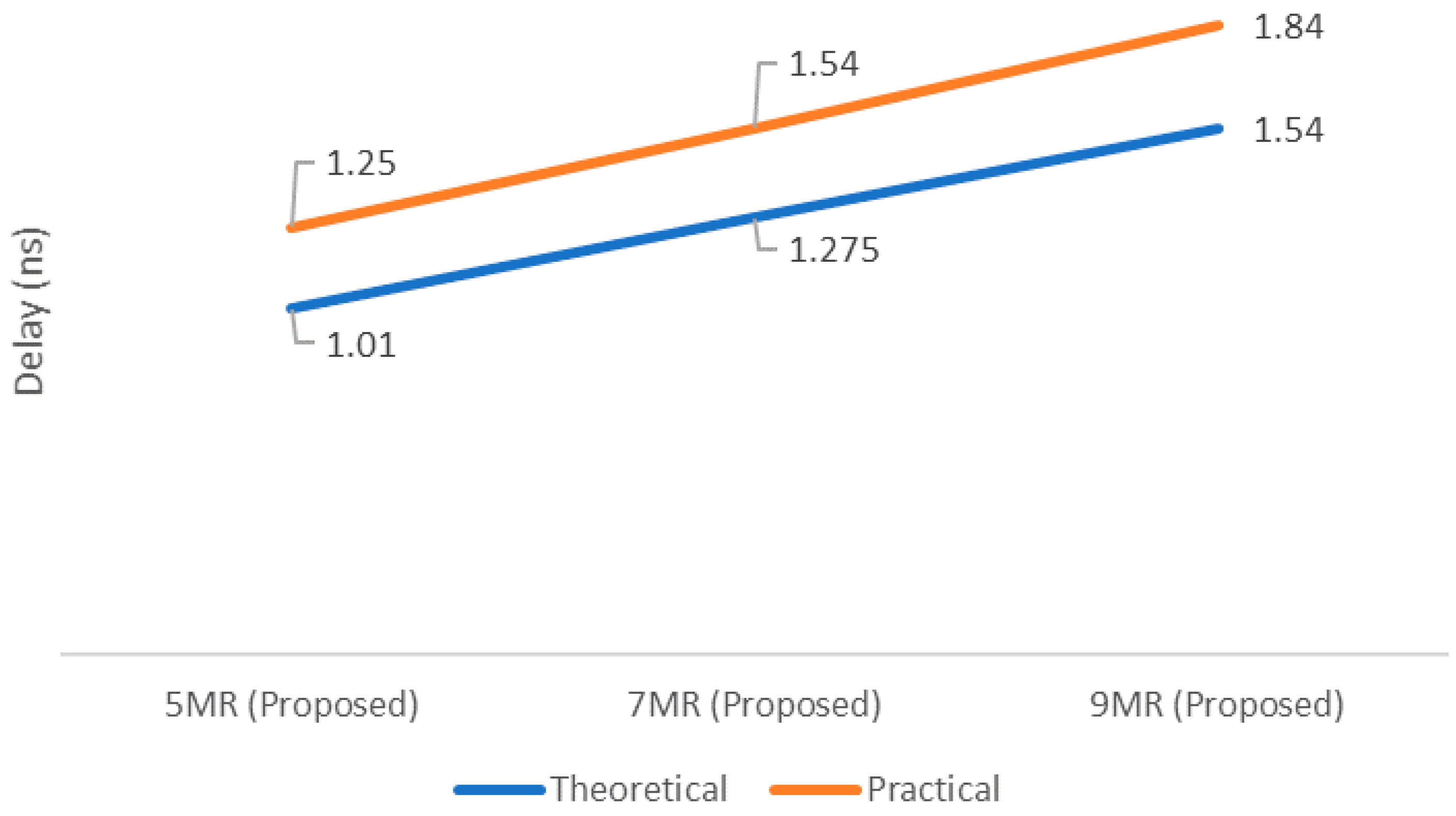
(N − 3)/2(TXOR2 + TAND3 + TMUX21)
4.2. Example NMR System Implementations with Multiple Redundancies
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Johnson, B.W. Design and Analysis of Fault-Tolerant Digital Systems; Addison-Wesley Publishing Company: Boston, MA, USA, 1989; ISBN 978-0201075700. [Google Scholar]
- Hardekopf, B.; Kwiat, K.; Upadhyaya, S. Secure and fault-tolerant voting in distributed systems. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 10–17 March 2001. [Google Scholar]
- Koren, I.; Mani Krishna, C. Fault-Tolerant Systems; Morgan Kaufmann Publishers: Burlington, MA, USA, 2007; ISBN 978-0120885251. [Google Scholar]
- Dubrova, E. Fault-Tolerant Design; Springer: New York, NY, USA, 2013; ISBN 978-1461421139. [Google Scholar]
- Franco, D.T.; Naviner, J.-F.; Naviner, L. Yield and reliability issues in nanotechnologies. Ann. Télécommun. 2006, 61, 1422–1457. [Google Scholar] [CrossRef]
- International Technology Roadmap for Semiconductors (ITRS) Design Report. Available online: http://itrs2.net (accessed on 10 December 2017).
- Miskov-Zivanov, N.; Marculescu, D. Multiple transient faults in combinational and sequential circuits: A systematic approach. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2010, 29, 1614–1627. [Google Scholar] [CrossRef]
- Quinn, H.; Graham, P.; Krone, J.; Caffrey, M.; Rezgui, S. Radiation-induced multi-bit upsets in SRAM-based FPGAs. IEEE Trans. Nucl. Sci. 2005, 52, 2455–2461. [Google Scholar] [CrossRef]
- Ban, T.; Naviner, L. Progressive module redundancy for fault-tolerant designs in nano-electronics. Microelectron. Reliab. 2011, 51, 1489–1492. [Google Scholar] [CrossRef]
- Ostler, P.S.; Caffrey, M.P.; Gibelyou, D.S.; Graham, P.S.; Morgan, K.S.; Pratt, B.H.; Quinn, H.M.; Wirthlin, M.J. SRAM FPGA reliability analysis for harsh radiation environments. IEEE Trans. Nucl. Sci. 2009, 56, 3519–3526. [Google Scholar] [CrossRef]
- Clark, L.T.; Patterson, D.W.; Ramamurthy, C.; Holbert, K.E. An embedded microprocessor radiation hardened by microarchitecture and circuits. IEEE Trans. Comput. 2016, 65, 382–395. [Google Scholar] [CrossRef]
- Pratt, B.; Caffrey, M.; Carroll, J.F.; Graham, P.; Morgan, K.; Wirthlin, M. Fine-grain SEU mitigation for FPGAs using partial TMR. IEEE Trans. Nucl. Sci. 2008, 55, 2274–2280. [Google Scholar] [CrossRef]
- Ruano, O.; Maestro, J.A.; Reviriego, P. A methodology for automatic insertion of selective TMR in digital circuits affected by SEUs. IEEE Trans. Nucl. Sci. 2009, 56, 2091–2102. [Google Scholar] [CrossRef]
- She, X.; Li, N. Reducing critical configuration bits via partial TMR for SEU mitigation in FPGAs. IEEE Trans. Nucl. Sci. 2017, 64, 2626–2632. [Google Scholar] [CrossRef]
- Haifley, T.; Bhatt, A. Fault-tolerant ICs: The reliability of TMR yield-enhanced ICs. IEEE Trans. Reliab. 1987, R-36, 224–226. [Google Scholar] [CrossRef]
- Vial, J.; Virazel, A.; Bosio, A.; Girard, P.; Landrault, C.; Pravossoudovitch, S. Is triple modular redundancy suitable for yield improvement? IET Comput. Digit. Tech. 2009, 3, 581–592. [Google Scholar] [CrossRef]
- Ban, T.; Naviner, L.A.B. A simple fault-tolerant digital voter circuit in TMR nanoarchitectures. In Proceedings of the 8th IEEE International NEWCAS Conference, Montreal, QC, Canada, 20–23 June 2010. [Google Scholar]
- Balasubramanian, P.; Mastorakis, N.E. Power, delay and area comparisons of majority voters relevant to TMR architectures. In Recent Advances in Circuits, Systems, Signal Processing and Communications; Mladenov, V., Ed.; WSEAS Press: Athens, Greece, 2016; pp. 110–117. ISBN 978-1618043665. [Google Scholar]
- Parhami, B. Voting networks. IEEE Trans. Reliab. 1991, 40, 380–394. [Google Scholar] [CrossRef]
- Balasubramanian, P.; Maskell, D.L. A distributed minority and majority voting based redundancy scheme. Microelectron. Reliab. 2015, 55, 1373–1378. [Google Scholar] [CrossRef]
- Synopsys SAED_CORE32/28_Databook, Revision 1.0.0. 2012. Available online: https://www.synopsys.com/community/university-program/teaching-resources.html (accessed on 10 August 2018).

| (N − 2)MR Majority Voter Output | Extra Inputs | Internal Outputs | MUX Select Input | NMR Majority Voter Output | |||
|---|---|---|---|---|---|---|---|
| X | Y | C1 | C2 | C3 | S | ||
| 0 | 0 | 0 | 0 | 1 | – | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | – | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | – | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0/1 | 0/1 | 0/1 |
| 1 | 0 | 0 | 1 | 1 | 0/1 | 0/1 | 0/1 |
| 1 | 0 | 1 | 1 | 0 | – | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | – | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | – | 0 | 1 |
| NMR System Type | Power (μW) | Delay (ns) | Area (μm2) |
|---|---|---|---|
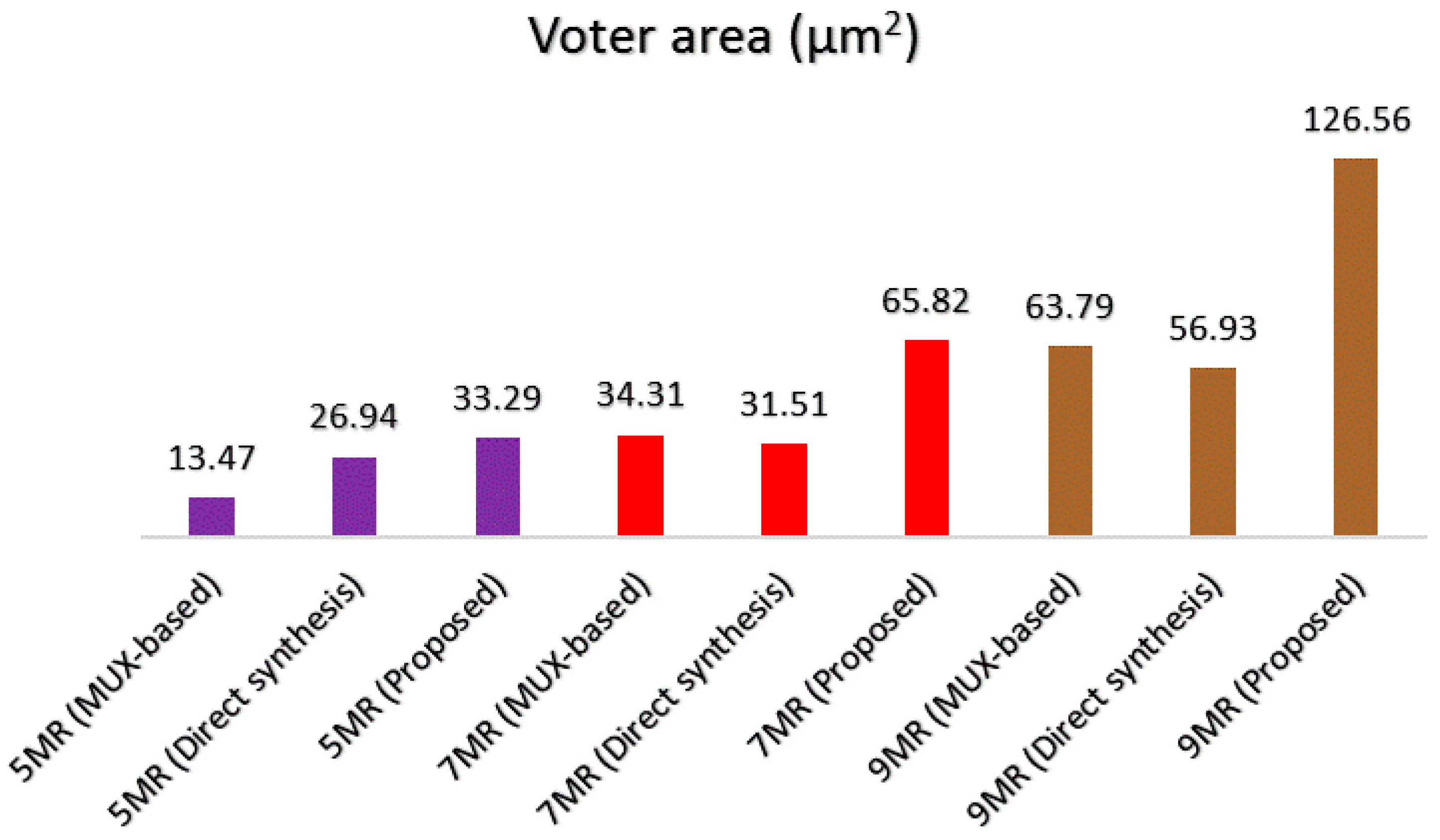
| 5MR (MUX-based design) | 120.7 | 0.98 | 529.64 |
| 5MR (Direct synthesis) | 134.9 | 1.25 | 637.39 |
| 5MR (Proposed) | 131.0 | 1.25 | 688.22 |
| 7MR (MUX-based design) | 191.3 | 1.12 | 865.11 |
| 7MR (Direct synthesis) | 181.7 | 1.19 | 842.74 |
| 7MR (Proposed) | 214.3 | 1.54 | 1117.22 |
| 9MR (MUX-based design) | 278.5 | 1.23 | 1269.7 |
| 9MR (Direct synthesis) | 250.0 | 1.33 | 1214.81 |
| 9MR (Proposed) | 334.9 | 1.84 | 1771.89 |
| Multiple NMR System Type | Power (μW) | Delay (ns) | Area (μm2) |
|---|---|---|---|
| 5MR-3MR (MUX-based design) | 128.7 | 0.98 | 590.63 |
| 5MR-3MR (Direct synthesis) | 142.9 | 1.25 | 698.39 |
| 5MR-3MR (Proposed) | 131.0 | 1.25 | 688.22 |
| 7MR-5MR-3MR (MUX-based design) | 221.0 | 1.14 | 1033.86 |
| 7MR-5MR-3MR (Direct synthesis) | 226.5 | 1.26 | 1119.25 |
| 7MR-5MR-3MR (Proposed) | 214.3 | 1.54 | 1117.22 |
| 9MR-7MR-5MR-3MR (MUX-based design) | 361.6 | 1.28 | 1712.93 |
| 9MR-7MR-5MR-3MR (Direct synthesis) | 339.6 | 1.35 | 1743.43 |
| 9MR-7MR-5MR-3MR (Proposed) | 334.9 | 1.84 | 1771.89 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choudhary, J.; Balasubramanian, P.; Varghese, D.M.; Singh, D.P.; Maskell, D. Generalized Majority Voter Design Method for N-Modular Redundant Systems Used in Mission- and Safety-Critical Applications. Computers 2019, 8, 10. https://doi.org/10.3390/computers8010010
Choudhary J, Balasubramanian P, Varghese DM, Singh DP, Maskell D. Generalized Majority Voter Design Method for N-Modular Redundant Systems Used in Mission- and Safety-Critical Applications. Computers. 2019; 8(1):10. https://doi.org/10.3390/computers8010010
Chicago/Turabian StyleChoudhary, Jaytrilok, Padmanabhan Balasubramanian, Danny M. Varghese, Dhirendra Pratap Singh, and Douglas Maskell. 2019. "Generalized Majority Voter Design Method for N-Modular Redundant Systems Used in Mission- and Safety-Critical Applications" Computers 8, no. 1: 10. https://doi.org/10.3390/computers8010010
APA StyleChoudhary, J., Balasubramanian, P., Varghese, D. M., Singh, D. P., & Maskell, D. (2019). Generalized Majority Voter Design Method for N-Modular Redundant Systems Used in Mission- and Safety-Critical Applications. Computers, 8(1), 10. https://doi.org/10.3390/computers8010010






