Deep Validation of Spatial Temporal Features of Synthetic Mobility Models

Abstract

This paper analyzes the most relevant spatial-temporal stochastic properties of benchmark synthetic mobility models. Each pattern suffers from various mobility flaws, as will be shown by the models’ validation. A set of metrics is used to describe mobility features, such as the speed decay problem, the density wave phenomenon, the spatial node distribution, and the average neighbor percentage. These metrics have already been validated for the random waypoint mobility model (RWPMM), but they have not yet been verified for other mobility patterns that are most frequently used. For this reason, this investigation attempts to deeply validate those metrics for other mobility models, namely the Manhattan Grid mobility, the Reference Point Group mobility, the Nomadic Community mobility, the Self-Similar Least Action Walk, and SMOOTH models. Moreover, we propose a novel mobility metric named the “node neighbors range”. The relevance of this new metric is that it proves at once the set of outcomes of previous metrics. It offers a global view of the overall range of mobile neighbors during the experimental time. The current research aims to more rigorously understand mobility features in order to conduct a precise assessment of each mobility flaw, given that this fact further impacts the performance of the whole network. These validations aim to summarize several parameters into 18,126 different scenarios with an average of 486 validated files. An exhaustive analysis with details like those found in this paper leads to a good understanding of the accurate behaviors of mobility models by displaying the ability of every pattern to deal with certain topology changes, as well as to ensure network performances. Validation results confirm the effectiveness and robustness of our novel metric.

1. Introduction

Mobility models (MMs) are aimed at describing the movement patterns of mobile users (nodes) and how their mobility parameters (position, speed, and acceleration) change during the observation period. Hence, mobility models attempt to emulate displacement patterns in real-life environments with high accuracy. They are relevant in view of the fact that they are applied to measure the performance of network protocols. Thus, mobility modeling represents a thriving field of research for mobile networks given throughput improvements, which can be achieved by using accurate models. So far, several synthetic mobility models which are mainly based on mathematical equations have been proposed. In other cases, they are described by physical motion laws. This category always attracts interest among the researcher community because these synthetic MMs can deploy an arbitrary number of nodes over a large simulation field in order to mimic a specific movement behavior in the presence of many network constraints. Recently, this category has shown magnificent progress, especially for sociality/human-based mobility models. Indeed, numerous synthetic patterns are presented to represent movements under diverse situations of mobile networks, for example military operations, disaster relief systems, and rescue events. Mobility management in ad hoc wireless networks faces many challenges. It represents the set of mechanisms providing a time-varying mapping between the identifier of a mobile node and its location with respect to the network structure [1]. Mobility constantly causes the network topology to change. In order to keep accurate routes, the routing protocols must dynamically readjust to such changes. Thus, routing update traffic overhead is significantly high. Different mobility patterns have in general different impacts on specific network protocols or applications [2]. The performance of mobile networks is remarkably impacted by several factors that further govern network performances: the packet delivery ratio, the average end-to-end delay, and throughput [3]. The mobility model represents one of these influential factors which shape the adopted motion strategy. A set of metrics is used to quantify the mobility features. Each inaccuracy of the model produces one or several mobility problems that indicate serious flaws, such as imbalance in the average speed during simulation, a non-uniform distribution of mobile nodes within a defined field, or unacceptable fluctuation in the number of neighbors. These model validations have already been verified for the random waypoint mobility model (RWPMM), for example:

• the speed decay problem, described by Yoon et al. [4] and then in [5],
• spatial node distribution, introduced by Bettstetter et al. [6], later discussed in [7] for random networks and in [8] for the outage probability in wireless networks,
• the density wave phenomenon, reported by Royer et al. [9] and later in [10,11], for wireless networks.
• the average neighbor percentage, investigated by Camp et al. [12] and then in [13].

Based on those stochastic properties, it is possible to perform a precise analysis and simulation of a mobility model and the issues that can affect performances without needing to implement it on a real mobile wireless network. Network analysis is mainly done to verify the entire simulation process using appropriate performance metrics that only display a general perspective. Furthermore, a proper mobility validation can accurately detect the causes of network deterioration without needing to implement a mobility pattern to analyze the performances of the real mobile network. For these reasons, in this paper, we first validate the previously suggested mobility metrics for some popular synthetic mobility models that have not been verified until now. Then, we propose a novel mobility metric called the “node neighbors range,” which reveals the imbalance of mobility models during the simulation.

The remainder of this paper is organized as follows. Firstly, we introduce some features related to mobility models. Secondly, we validate the mobility metrics of some synthetic mobility models. Thirdly, we propose a novel mobility metric. Fourthly, we summarize the detailed features of the validated mobility metrics. We then discuss the relation of mobility metrics and resource management. Finally, the results are discussed and the main conclusions are presented.

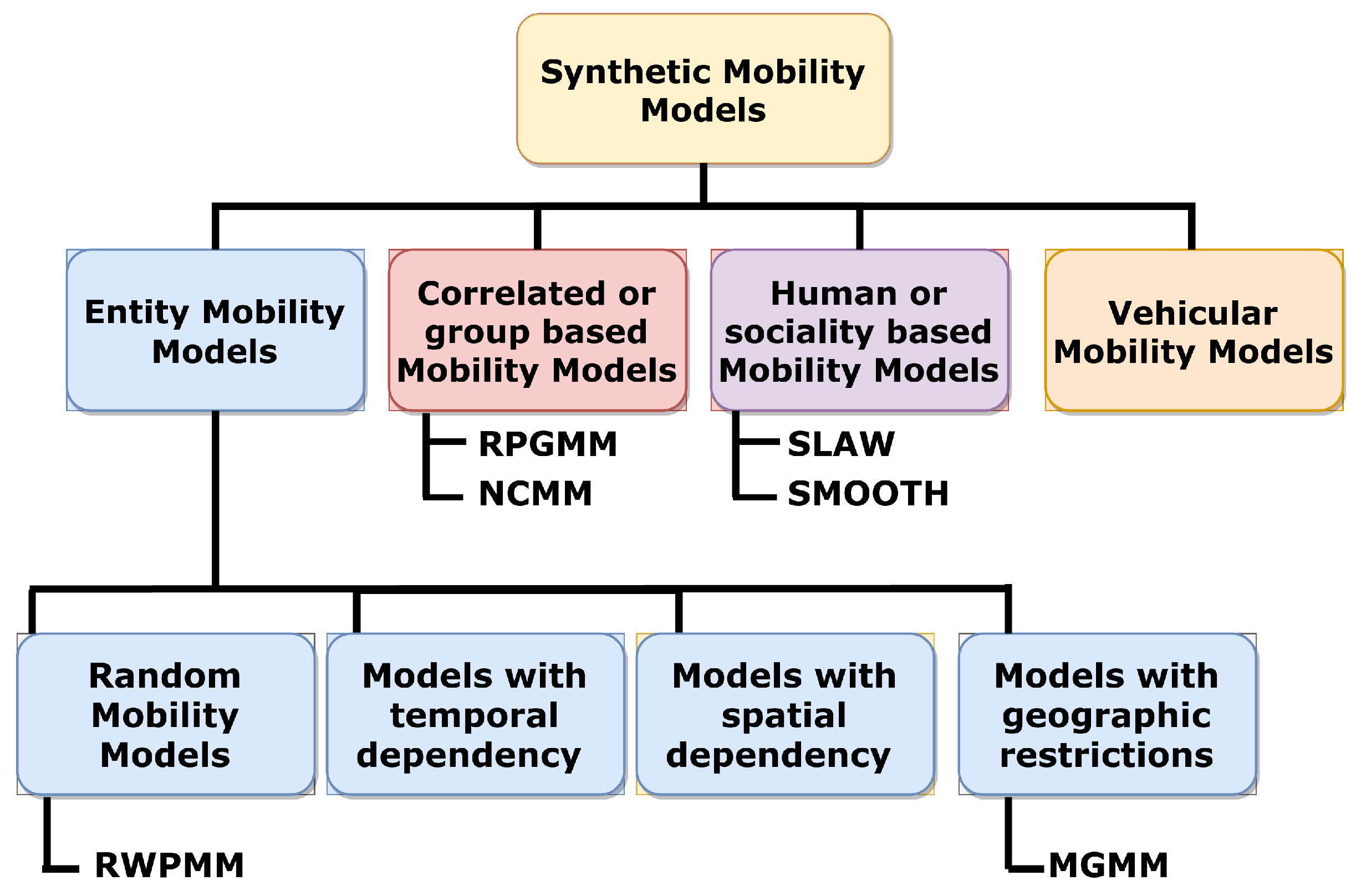
2. Preliminaries

Researchers are constantly eager to understand realistic mobility motions of mobile networks. Several traces are previously implemented to model real-life movements. In [14], the authors propose a new procedure aimed at collecting traces, while deployment phase failures are avoided, which improves the reliability of data. The introduced procedure makes possible the complete generation of traces with a minimum of damages without the need to recover mobile devices or losing them. Based on detecting and correcting all accidental issues in real-time, Morocco traces offer a set of relevant information about the vehicle status that was collected over seven months. The proposed procedure could be applied to generate vehicular traces. Likewise, it is suitable to record/generate human and animal traces. In [15], the authors studied data transfer opportunities between wireless devices carried by humans. They observed that the distribution of the intercontact time may be well approximated by a power law over the range [10 min; 1 day]. This observation is confirmed using eight distinct experimental data sets. In [16], pocket switched networks (PSNs) make use of both human mobility and local/global connectivity in order to transfer data between mobile users’ devices. This falls under the delay tolerant networking (DTN) space, focusing on the use of opportunistic networking. One key problem in PSNs is in designing forwarding algorithms that cope with human mobility patterns. The authors present an experiment measuring the mobility of 41 individuals at the Infocom 2005 conference. The results exhibit a power-law distrbution for the time between node contacts. They then discuss the implications of these results on the design of forwarding algorithms for PSN. In [17], the authors define a methodology composed of three steps. First, the positions of 700 humans, spread over a metropolitan area, were anonymously traced during a special gathering event. Then, with a multi-disciplinary approach, they inferred the contact events from the these traces. Finally, they assessed the effectiveness of an ad hoc network established by the mobile phones to disseminate emergency information to the population in a timely fashion. The results reveal that human mobility can effectively enable emergency communications among a significant subset of mobile phones, although the connectivity of the network strictly depends on the number of cooperating devices and on the maximum allowed delay. In [18], the authors anonymously collected the positions of almost 2000 mobile phone users, spread over a metropolitan area greater than 200 ${\mathrm{km}}^2$ for roughly one month. Then, with a multi-disciplinary approach, they estimated the mobility patterns from the collected data and, assuming Wi-Fi connectivity, inferred the contact events among the devices to evaluate the connectivity properties of a human-mobility-enabled wireless network.

Until now, several synthetic mobility models have been suggested and are sometimes inspired from these mobility traces with the aim of investigating diverse mobility management in wireless sensor networks (WSNs). In this section, we will briefly introduce and discuss the role and main features of a synthetic mobility model before performing the validation of some models which belong to these classes. We then specify the main movement context of each pattern, which helps us to analyze the metrics’ outcomes, which may display the mobility flaws of each model. Figure 1 shows a classification of mobility models that are grouped into four main classes.

• Entity MMs [19]: In this class, each mobile node is autonomous, moving in the network independently of other nodes. This class may be further divided into four subclasses: random mobility models, models with temporal dependencies, models with spatial dependencies, and models with geographic restrictions.
• Correlated or group-based MMs [20]: In this class, the motion of nodes is correlated and related to the movement of other nodes. The whole network is split into many groups of nodes, where each group is governed by one leader. This may be a logical leader in the network or a pre-defined node, for example, the Reference Point Group Mobility (RPGM) model [21] or the Nomadic Community Mobility Model (NCMM) [22].
• Human or sociality-based MMs [23]: In this class of models, the nodes somehow follow human socializing behaviors, such as the Self-Similar Least Action Walk Mobility Model [24].
• Vehicular MMs [25]: In this class, the nodes imitate the movement of a real vehicle by taking into consideration stops at traffic signals, speed variation, and queuing along highways [26]. This category shows remarkable superior performance due to vehicular communications of intelligent transport systems which are applied in smart cities [27]. This family is not the focus of the validation performed in this paper.

Regarding the first three classes, six different mobility models have been assessed and validated in order to inspect motion flaws in each category; that is, two entity MMs, two correlated MMs, and two human MMs have been considered. The most relevant properties of these patterns are as follows:

• The first experimental pattern is that of the RWPMM, which belongs to the random subclass of entity MMs. It was first defined by Johnson and Maltz [28] and then became a benchmark for mobility modeling of mobile ad-hoc networks. Using this pattern, nodes choose a new speed that is uniformly distributed within an established range to move toward the next waypoint during a given period. The node stops at the destination for a specific pause time and then repeats the whole process until the experimental time has elapsed. This model takes into consideration neither previous mobility decisions nor the relation between time, speed, and distance [29]. This memoryless property leads to an unrealistic motion as a consequence of the abrupt stops and sharp turns [30].
• The second validated pattern is the Manhattan Grid Mobility Model (MGMM) [31]. This is an entity synthetic mobility model with geographic restrictions. It represents a variation of the pathway/city section mobility model [32]. In this case, mobile nodes move not randomly but according to existing roads and paths. The MGMM attempts to imitate the motion motif of mobile nodes on streets defined on maps. It uses a grid-road-based topology and a probabilistic method to generate node movements where a node can turn either left or right with the same probability of 0.25 or maintain a straight movement with a probability of 0.5 [33].
• The third validated mobility pattern is the RPGM model [21]. This model belongs to the class of correlated or group-based mobility models where nodes behave in a co-operative manner and move in groups. Each group follows a reference point considered as the group leader, namely a node which may be a pre-defined leader or a center node. The motion of the entire group depends on the leader’s movement, including its speed and direction. This model successfully mimics diverse mobility behaviors, such as battlefield movements and disaster relief.
• The fourth verified mobility pattern is the Nomadic Community Mobility Model (NCMM) [22]. This model belongs to the class of correlated or group-based mobility models, which represent movement scenarios of a group where several nodes move together based on a single reference point. The whole group moves randomly from a given position to another one according to the mobility decisions of the leader. This mobility pattern is applied in mobile communications such as military applications, conferences, and museum visits by classes of students.
• The fifth pattern is the Self-Similar Least Action Walk (SLAW) [34]. This model belongs to the Human class. It considers that people are usually attracted and confined to popular places that are often rare. These places have high popularity and are clustered close together. On the other hand, less popular locations are numerous and far from each other. This is recognized as a fractal distribution of waypoints. This model integrates five major characteristics of human mobility:

  -

  self-similar dispersion of destinations;

  -

  truncated power-law inter-contact times;

  -

  heavy-tail flight and pause-time distribution;

  -

  least-action trip planning (LATP);

  -

  heterogeneously bounded mobility areas of individuals.

• The last pattern is SMOOTH [32], which belongs to the Human class. This model incorporates two major mobility features: pause time and truncated power-law distribution of flight length. The whole simulation field is split into a number of landmarks which represent communities, with clusters where each node is initially located randomly inside a cluster. In addition, the pause time follows the truncated power-law distribution, and nodes’ velocities are proportional to the flight length.

The previously presented models represent mobility modeling benchmarks that are commonly used to conduct performance analysis of wireless networks.

Table 1. Qualitative features of mobility models; Y: Yes, N: No, A: Ambiguous.

Mobility Models	Realistic	Scalable	Possibility of a	Uses
			Mathematical Representation	Geographic Map
RWMM	N	Y	Y	N
MGMM	N	Y	N	N
RPGMM	N	Y	A	N
NMM	N	Y	N	N
SLAW	Y	N	A	Y
SMOOTH	N	Y	N	Y

summarizes and highlights the reasons behind the robustness of MzMM, where Y means Yes, N means No, and A means Ambiguous. This may be a curse and a blessing for network communications if they suffer from mobility flaws that affect performances of the whole mobile network.

3. Validation of Mobility Models

In this section, we describe the first attempt to validate the movement steadiness of some benchmark mobility models. Such validation was previously only carried out only for the RWPMM. It is based on a number of mobility metrics in order to construct and deduce a precise assessment of each mobility imbalance. The motion test depicts rigorous features that have serious impacts on global network performances. The experimental settings are shown in

Table 2. Validation parameters.

Parameters	Values
Number of nodes	50
Speed	5 m/s
Pause time (s)	0
Mobility models	RWPMM, MGMM (Entity models)
	RPGMM, NCMM (Correlated MMs)
	SLAW, SMOOTH (Human MMs)
Mobility metrics	Speed decay problem
	Spatial node distribution
	Density wave phenomenon
	Average node neighbor percentage
Area	1030 m × 1030 m
Simulation time	1000 s
Iterations	20 times
Implementation tool	MATLAB

. The analyzed validation is carried out based on the following parameters:

• The four validated mobility metrics are the speed decay problem, spatial node distribution, density wave phenomenon, and average neighbor percentage.
• The six verified mobility models are distributed as follows: there are two entity models, the RWPMM and the MGMM, two correlated models, the RPGMM and the NCMM, and two human models: SLAW and SMOOTH.
• A spread out field of 1030 × 1030 m is considered as a very prominent mobility pattern.
• One hundred twenty different scenarios are examined with trials of 20 iterations per model over 1000 s and an average speed of 5 m/s.

The aforementioned experimental parameters are combined to evaluate all possible scenarios with the aim of obtaining the most accurate and complete knowledge of mobility problems. Using MATLAB implementation tool, the simulation results are depicted and discussed in Figure 2, Figure 3, Figure 4 and Figure 5 in the next sub-sections. These figures must endorse the movement strategy adopted by the analyzed models that were introduced in the previous section. Some important model features are described in

Table 3. Mobility models. C: Constant, HB: History Based, UD: Uniformly Distributed, PD: Probabilistically Distributed, P: Periodic, PL: Truncated Power Law, NA: Not Applicable.

Mobility Models	Model Class	Speed	Direction	Acceleration/Deceleration	Pause Time	Flight	Return Time and
						Length	Visiting Frequency
RWPMM	Random	UD	NA	NA	C/UD	NA	NA
	(Entity)
MGMM	Geographic	C/UD	UD on set	NA	C/UD	NA	NA
	restrictions (Entity)		of waypoints
RPGMM	Correlated/	Based on	Based on	NA	C/UD	NA	NA
	Group based	reference point	reference point
NCMM	Correlated/	NA	Around the	NA	NA	NA	NA
	Group based		reference point
SLAW	Human	NA	PD on set	NA	TPL	TPL	P
			destinations
SMOOTH	Human	NA	PD on set	NA	TPL	TPL	P
			destinations

, based on model conceptions. However, we will make sure that they are correct through these validations.

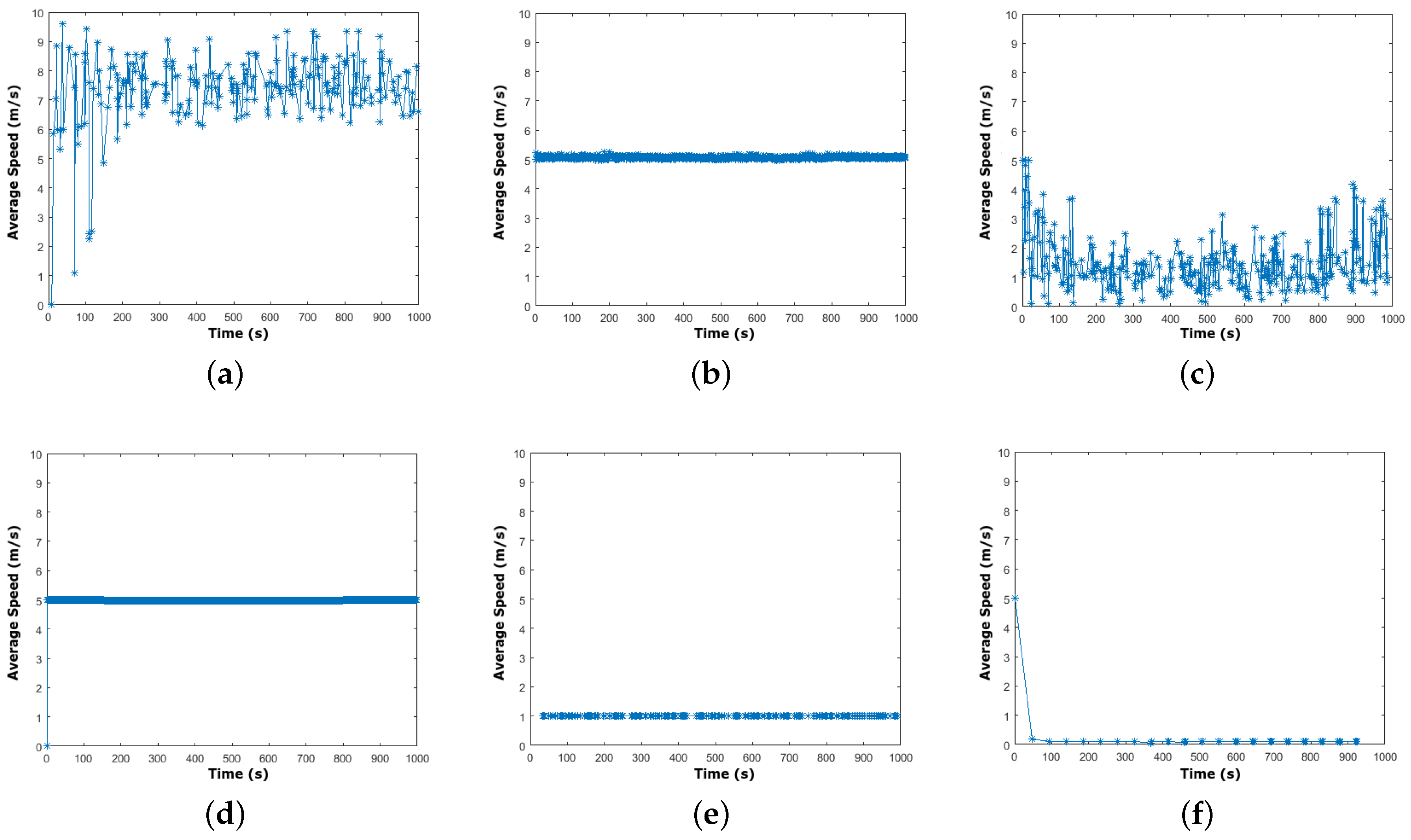
3.1. Speed Decay Problem

This property represents the degree of respecting the attributed speed that is allowed before generating the mobility model. Speed decay problem represents one of the most widely affronted issues. A mobility model suffers from speed decay when the average nodal speed decays to a steady-state level that falls below the initial average nodal speed. Such speed decay can have a dramatic influence on the measured performance and overhead. Consequently, one cannot present time-averaged metrics during this period of decay, as the underlying process is not stationary. This metric was introduced by Yoon et al. [4] for the RWPMM. Randomness contradicts the famous RWPMM assumption that the same average speed is maintained throughout the simulation, which is adequately tested in Figure 2a. We observe that the velocity suffers strong fluctuations when the experiment begins. It then adjusts to approach the attributed speed, showing scattered fluctuations before the simulation ends.

Meanwhile, Figure 2 shows the average speed fluctuation of other synthetic mobility models during the simulation. We observe the following:

• From Figure 2e,f, we conclude that human models suffer heavily from the speed decay problem and show the worst average speed. Even in the case where a specific speed is fixed, it will not be deployed by these models because it is lower than 5 m/s during the whole simulation period. This problem mainly relates to the non-attributed speed, acceleration, and deceleration in these models, as strictly reported by the settings of these models in Table 3.
• Figure 2c shows that the RPGMM presents a speed that fluctuates with time, starting from the specified speed and then oscillating between 0 and 5 m/s. This is due to the correlated strategy of mobile nodes. The nodes form several groups and each group has a leader that takes all mobility decisions. Sometimes, a node changes group and follows another group leader with a different speed. Table 3 also highlights that speed is based on reference points, while this validation metric precisely indicates that speed is uniformly distributed according to the reference points.
• In Figure 2b, the MGMM represents a nearly stable speed during the entire simulation. MGMM fluctuates in an acceptable margin between 5 and 5.25 m/s. This allows it to be steadier due to the adopted movement strategy, which is based on a uniform division of the simulation field with a constant or uniform speed, as depicted in Table 3.
• According to Figure 2d, we remark that the NCMM presents the best average speed out of all the validated models that keep the same speed during the simulation. This result mainly does not agree with the principal methodology of using the non-attributed speed, acceleration, and deceleration as shown in Table 3. Therefore, a relevant outcome of this research and this validation is that the NCMM showed a constant speed during the experiment since all MNs belong to a single leader.

As a conclusion, we can state that in order to avoid the speed decay problem, a stable mobility model must remain steady within an acceptable speed range, as for the MGMM and the NCMM. Consequently, it must respect motion laws in every mobility decision by taking into consideration the relation between time, speed, and distance while moving.

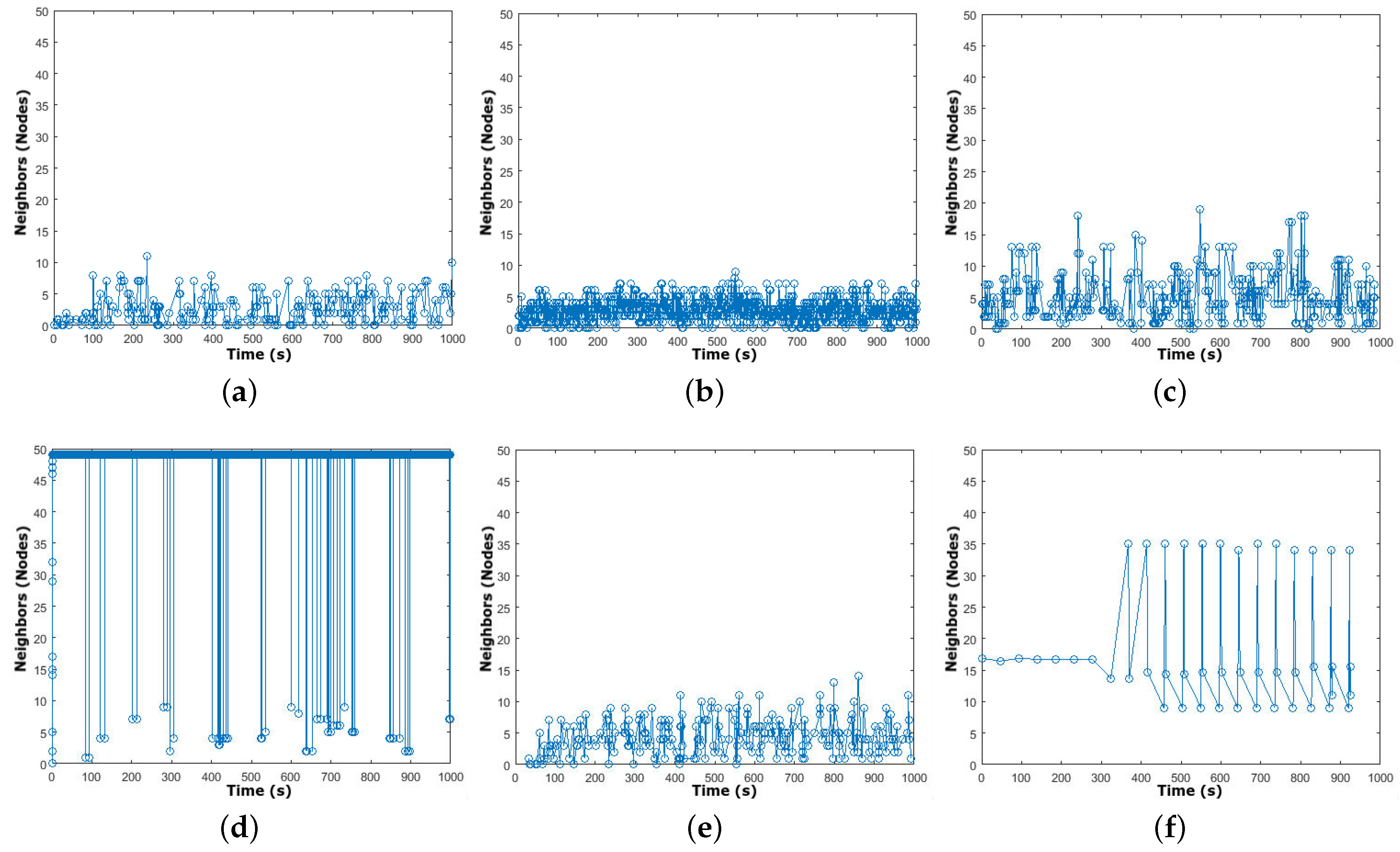
3.2. Density Wave Phenomenon

This mobility metric represents the average number of mobile neighbors of a definite mobile node at a specific time instant during the experiment. Density wave phenomenonrepresents the average number of neighbors that belong to each node and that fluctuate during the simulation, where nodes located in specific zones of the simulation area can have many more neighbors than others, i.e., their density changes. Royer, Melliar-Smith, and Moser [9] noticed that, in random waypoint models, the density recurrently fluctuates with time, as depicted in Figure 3a, with a moderate fluctuation between 0 and 11 nodes. However, this issue at most affects the performance of other models [3]. This feature shows the independent mobility of mobile nodes. According to Figure 3, it is worth remarking that.

• Entity models show, in Figure 3a,b, the worst density wave behavior when they are limited between 0 and 11 and between 0 and 9 for the RWPMM and the MGMM, respectively. Due to their independent selection of destination positions, nodes move independently without taking into consideration other nodes’ mobility decisions, with regard to directions and destinations.
• In Figure 3e, the SLAW oscillates moderately between 0 and 14 with certain moments in which the node has no neighbor due to the probabilistic distribution of nodes.
• However, the correlated RPGMM and NCMM show the best outcomes when considering only the effect of this issue. The output of these models fluctuate in a satisfactory range with fewer time instants without any neighbor, as shown in Figure 3c,d. These sub-figuresrefer to group-based movement where a mobile node always belongs to a specific group with the attached nodes.
• SMOOTH outperforms the other models when considering this property in the range of 8 to 35, as shown in Figure 3f. We can remark that the mobile node had at least eight neighbors during the simulation, which shows the best packet delivery ratio.

We conclude that most of the validated mobility models suffer from the density wave phenomenon except for SMOOTH and the correlated models. The NCMM shows the best robustness against this problem given that it offers a wide neighbor range of [0 to 49]. This is due to its method of operation of assigning one leader to all mobile nodes. The packet delivery rate of a given experimental simulation is noticeably affected in the presence of this issue [35]. To avoid this mobility flaw, mobile nodes must adopt a mobility strategy that allows them to move in a group with several nodes or they must be uniformly distributed within the simulation region. In addition, in order to ensure having at least one neighbor, they must move at the same speed when following rotational movements. This condition is not met by all mobile nodes.

3.3. Average Neighbor Percentage

This metric describes the cumulative percentage of the total number of neighboring nodes. That is the percentage of total MNs’ neighbors during the whole validation time. Low values of this metric reflect the degree of model instability in attaining neighbors, which further leads to worse network performances [12]. To strongly verify the results shown in Figure 3, we validate the average neighbor percentage during the simulation. Figure 4 shows the results of this feature. We can highlight the following.

• According to Figure 4a, the RWPMM presents the worst outcomes, where it fluctuates in a range of 0–16% with many detected time instants without any neighbors. At these moments, if a mobile node sends a packet, it finds no receiver to which these data can be forwarded. This behavior further increases the number of lost packets, and decreases the PDR of the RWPMM.
• From Figure 4b, the MGMM shows small fluctuations in the range of 4–9%, and more than two neighbors from the total of 49 nodes are always present. This allows this model to perform better than the RWPMM, but it stays enough to offer best performances.
• From Figure 4c,e, SLAW and the RPGMM show better results than the RWPMM and the MGMM. These models fluctuate in the ranges 0–18% and 0–25%, respectively, with fewer time instants are without any neighbors.
• However, from Figure 4d,f, SMOOTH and the NCMM have ranges of 18–70% and 8–98%, respectively. They both provide the best results, having more than four neighbors during the entire simulation. This feature allows them to outperform other models in mobile networks as they can deliver all the packets [36]. These models are more stable than other models.

This metric gives a general view of the density wave phenomenon via the average percentage within the validation period. These results strongly endorse the outcomes depicted in Figure 3, as summarized in

Table 4. Mobility metrics strengths and weaknesses; * Proposed metric.

	Mobility Models
Mobility Metrics	Entity		Correlated		Human
	RWPMM	MGMM	RPGMM	NCMM	SLAW	SMOOTH
Speed decay problem	3	2	4	1	5	6
Density wave phenomenon	5	6	3	2	4	1
Average neighbor percentage	6	5	4	1	3	2
Spatial node distribution	6	5	3	1	4	2
* Mobile neighbors range	6	5	3	1	4	2

.

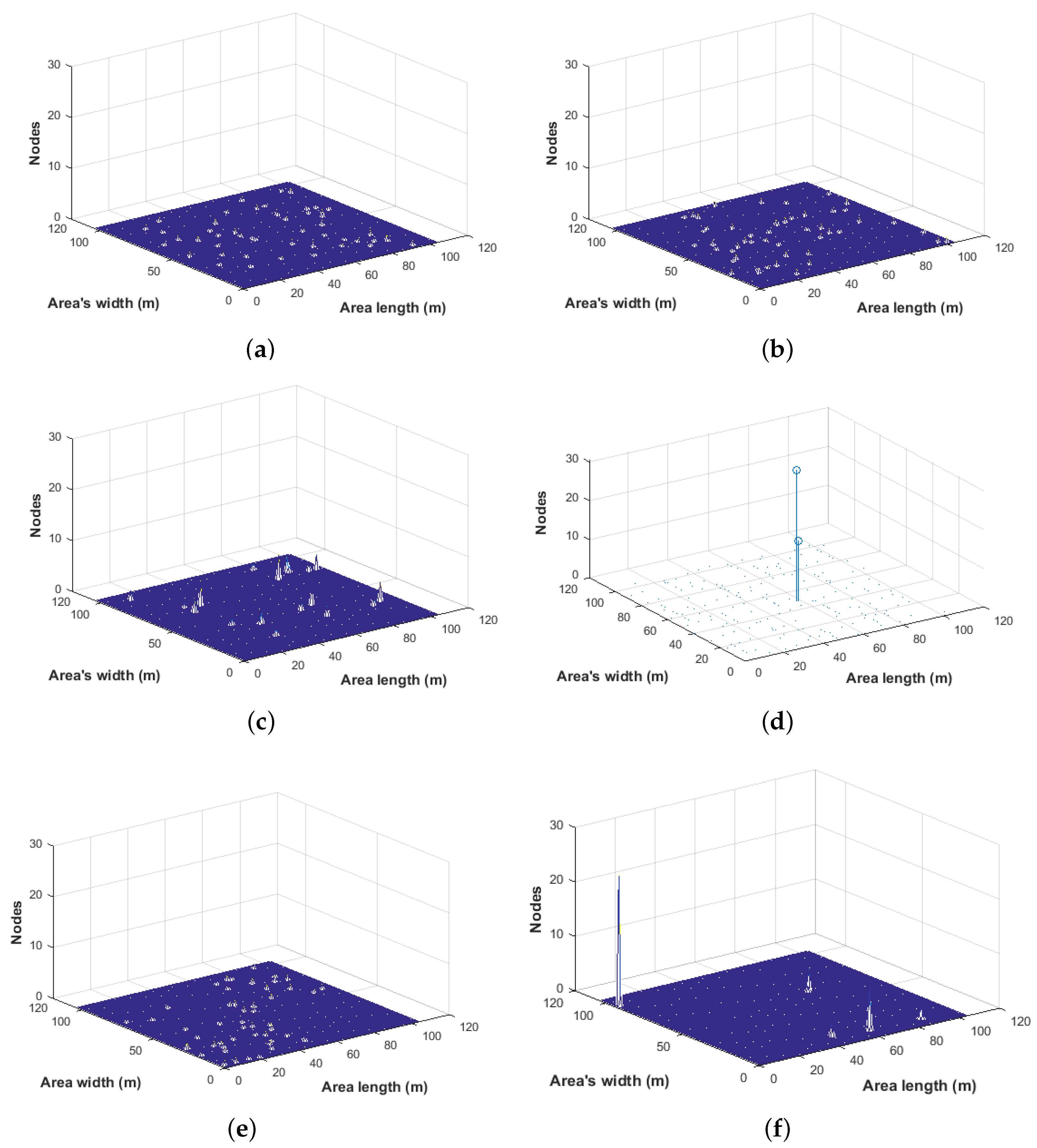
3.4. Spatial Node Distribution

This property describes how mobile nodes are spatially localized within the simulation field. It is mainly related to the fact that the initial positioning of the nodes is typically taken from what is established based on a uniform distribution; the mobility model may change this distribution during the simulation. This behavior usually occurs if the simulation area has borders. If we are not aware of how the used mobility model changes the node distribution, simulation results may be misinterpreted. Bettstetter et al. [6] validated this metric for the RWPMM. They recognized a non-uniform spatial distribution of this mobility model. When it reaches the steady state, mobile nodes gather at the center and move away from the boundaries, as observed in Figure 5a. In our validation, we choose to verify the final state (at t = 1000 s) of this property. From Figure 5, we can interpret the results obtained for the last two metrics, and it is worth remarking the following:

• Figure 5c,f provide insufficient results due to nodes gathering near the leaders in the RPGMM or in populated locations in SMOOTH. If the groups are sparsely located, the mobility model will show the worst performance if any intermediate neighbor is reached during transmission. This results in a more fragile network that is highly partitioned with many free simulation spaces.
• Based on Figure 5b,e, we remark that SLAW and the MGMM are slightly more distributed in the simulation field compared to the RWPMM, SMOOTH, and the RPGMM. Due to the area division in the MGMM, the mobile nodes are located at the boundaries with few empty spaces compared to the RWPMM in Figure 5a. This later represents the worst spatial distribution, being mainly based on totally random movement decisions.
• Figure 5d shows the best results, with all mobile nodes being located within one area which is governed by a nomadic leader while moving. This proves that all the nodes belong to just one reference point. The outcome of Figure 4d is exemplary with nearly 98% of nodes gathering together due to the concentrated spatial distribution of all nomadic nodes in one specific area.

We conclude that, if a mobility model shows a non-uniform spatial node distribution during the simulation, then nodes will also suffer from an unstable density wave phenomenon and a disturbed average neighbor percentage, as depicted in Figure 3 and Figure 4, respectively. These three mobility flaws are mainly related to each other.

Given the limitations of these metrics, a novel synthetic mobility metric is proposed to overcome such problems. This metric, which has several validated parameters with few limitations, is called the “mobile neighbors range” and is described in the next section.

4. The Proposed Metric: The Mobile Neighbors Range

In this section, in order to overcome the limitations shown by other metrics, we suggest a novel metric that offers multiple advantages to represent an accurate behavior of mobility model steadiness for all simulated nodes during the test time. Whatever the expected node and the targeted instant, we can easily depict the range of neighbors for each mobility model. The validation of this property is effective at all simulation instants. At the same time, this metric highlights the strengths and weaknesses of each mobility issue, which has been verified previously.

• Principle: We assess a set of synthetic mobility models of each pattern in order to define the range of the number of neighbors for all mobile nodes within the simulation. We generate all mobility models with a propagation range of 150 m. For this reason, a threshold setting (150 m) is present in our new metric to exactly reflect the correct outcomes. Then, we remove the lowest and highest values of the total number of neighbors recorded. Therefore, this metric makes it possible to inspect a total predefined propagation range based on all the mobility parameters, whatever the inspected node, the targeted model, and the time instant are. This property is calculated using the following Algorithm 1.
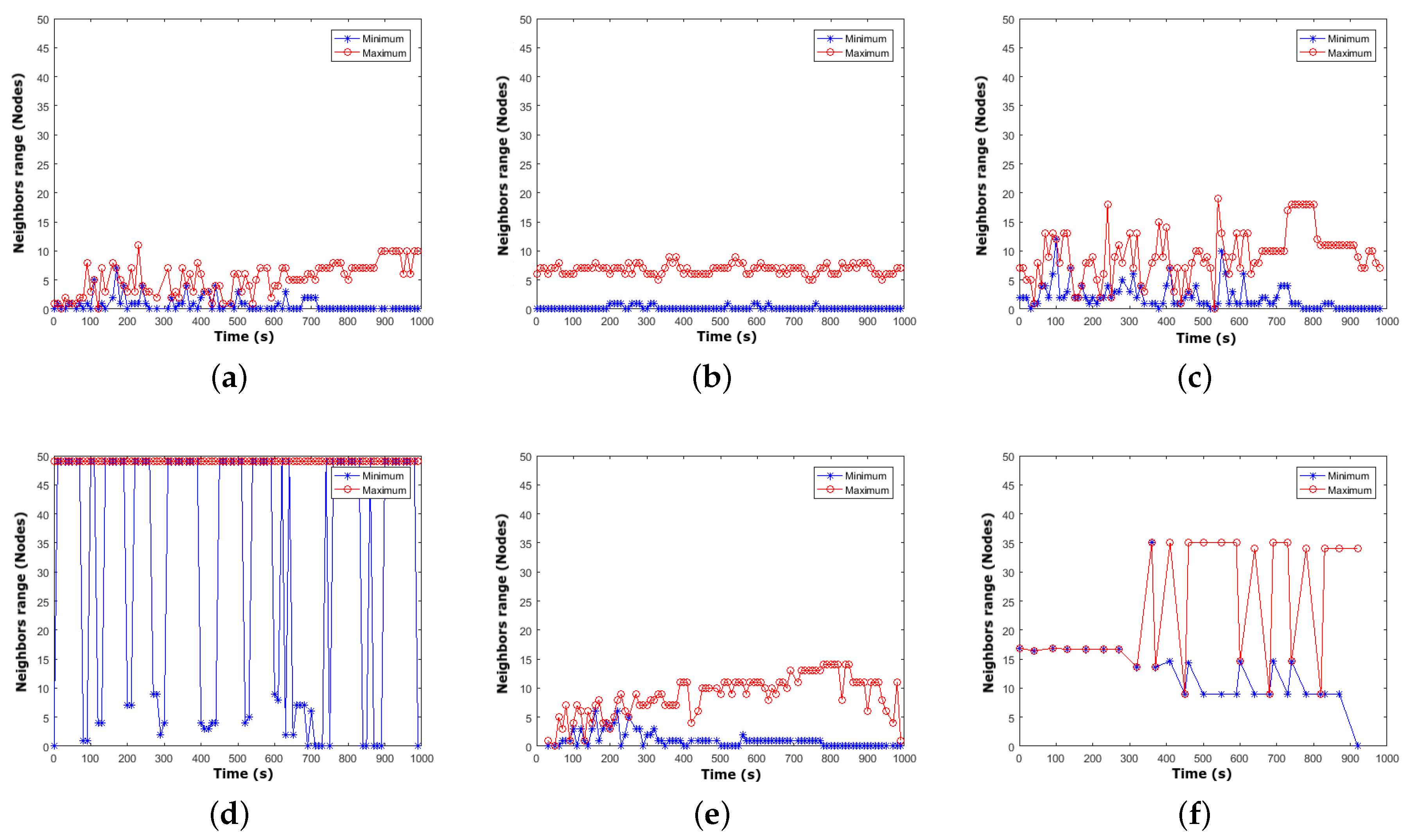
• Validation and results: The validation results are depicted in Figure 6. We observe that:

  -

  Based on Figure 6a,b, the RWPMM and the MGMM represent the worst mobility models according to this property, as they suffer dramatically from variation in the number of neighbors with time. However, the MGMM shows convenient oscillatory fluctuations of 0–9 with an obvious and regular gap, but with many instants in which there are no neighbors. This is in strong agreement with the results of previous metrics, such as the density wave phenomenon.

  -

  SLAW and the RPGMM show average performances with ranges of [0,14] and [0,19], respectively, according to Figure 6e,c. The RWPMM shows an irregular gap during the simulation within a moderate range. Some acceptable instants with no neighbors were recorded.

  -

  Figure 6d,f show that the NCMM and SMOOTH have few instants with no neighbors, and the range promptly converges to benefit the most possible from all deployed nodes. The NCMM peaks at 49 neighbors, which means it is the best model due to the correlated strategy of belonging to a single group with one leader for all mobile nodes (49 + the leader = 50 applied nodes (Table 2).

• Interpretations: After carrying out 600 trials for the mobile neighbor’s range, the following was found:

  -

  At instants with 0 at the minimum line (blue chart), one or several deployed nodes have no detected neighbors.

  -

  Moreover, the line maximum is too far away from the total number of mobile nodes deployed. This leads to a worse mobility model with an irregular gap in the mobile neighbors range with unsteadiness within experimental time.

  -

  Conversely, when the obtained lines have acceptable or big margin fluctuations, the minimum does not equal 0 and the maximum comes closer to the total number of nodes. This reflects the fact that the validated mobility model is more stable and steady with time that will lead to satisfactory outcomes in the performance analysis [3].

According to the features of the proposed metric, we deduce that it shows an obvious and effective neighborhood. It strongly endorses the results obtained by other existing metrics, such as the spatial node distribution, density wave phenomenon, and average neighbor percentage. From

Table 5. Mobility metrics comparison, + favor, − flaw, * Proposed metric.

Mobility Metrics	Validation Features
	Parameters Inspected	Precision Level	Limitations
	+All nodes	Low (speed only)	Nodes’ neighboring
Speed decay problem	+Whole Time
	+Average models
	−One node		Other nodes
Density wave phenomenon	+Whole time	Medium	+
	+Average models		Speed
	−One node		Other nodes
Average neighbor number	+Whole time	Medium	+
	+Average models		Speed
	+All nodes		Other models
Spatial node distribution	−Specific time	Low	+Time
	−Specific model		+Speed
	+All node
* Mobile neighbors range	+Whole time	High	Speed
	+Average models

, the suggested novel metric provides a high precision compared to the others. This result inspects all the deployed nodes that change with time to show us more apparent movement behaviors of all mobility patterns. We deduce that mobile neighbors range remedies the defects of all previously proposed metrics by curing their weaknesses via verifying all nodes of all mobility models during the whole simulation.

5. Mobility Metrics Global Intention

Based on these mobility metrics, we can predict the performance of the mobility models without the need to implement a real wireless mobile network as most of the tests do to carry out performance analyses. These validations aim to summarize several parameters into 18,126 different scenarios with an average of 486 validated files corresponding to the six mobility models. The validation details are displayed in

Table 6. Validation details; * Proposed metric.

Mobility Metrics	Mobility Models						Total Validations
	RWPMM	MGMM	RPGMM	NCMM	SLAW	SMOOTH
Speed decay problem	50 nodes	50 nodes	50 nodes	50 nodes	50 nodes	50 nodes	6000
	* 20 times	* 20 times	* 20 times	* 20 times	* 20 times	* 20 times
Density wave phenomenon	20 times	20 times	20 times	20 times	20 times	20 times	120
Average neighbor percentage	50 nodes	50 nodes	50 nodes	50 nodes	50 nodes	50 nodes	6000
	* 20 times	* 20 times	* 20 times	* 20 times	* 20 times	* 20 times
Spatial node distribution	1	1	1	1	1	1	6
* Mobile neighbors range	50 nodes	50 nodes	50 nodes	50 nodes	50 nodes	50 nodes	6000
	* 20 times	* 20 times	* 20 times	* 20 times	* 20 times	* 20 times
							18,120 files

.

An exhaustive analysis with the details in this paper leads to a good understanding of the accurate behaviors of mobility models by displaying the ability of every pattern to deal with certain topology changes and to ensure network performances. We conclude that they can be classified according to their results as summarized in Table 4. The best outcomes are shown by 1 and 2 cells, acceptable shifts are shown by 3 and 4 cells, and the worst results are shown by 5 and 6 cells.

According to the previously discussed validated metrics, we deduce the following:

• The density wave phenomenon is only obtained for a unique node during the simulation. It inspects one node to only reflect the fluctuation of the number of neighbors of the validated node. Verifying this property for all mobile nodes used in the simulation would be a worthless task.
• The average number of mobile nodes denotes the average number of neighbors of a specific node during the simulation. This metric is inaccurate in the cases in which it is lower or higher than the number of neighbors of all mobile nodes at a given time instant. This feature makes this metric inaccurate in reflecting exact changes in neighbor variability.
• The spatial node distribution must be validated at a concrete time instant because it cannot show all location changes over a continuous period.
• The speed decay problem only produces speed variation per time instant without taking into consideration the exact spatial locations of nodes.

Table 5 illustrates the comparative study of all the aforementioned properties that have been validated in this paper. We conclude that all the mobility metrics show complementary features that are aimed at accurately assessing mobility flaws and this finally allows the model flaws that have the greatest effect on the performance of the whole mobile network to be revealed. Choosing the wrong mobility model can have undesirable consequences due to the appearance of many network flaws.

6. Mobility Metrics and Resources Management Overview

Among the different resources whose usage must be optimized in WSNs, we can highlight energy consumption and bandwidth. Energy consumption is a critical parameter in mobile networks, where long battery life is required to guarantee operation, maintaining the performance and the QoS over an acceptable period of time. Bandwidth is another critical resource to be considered as most of the IoT devices (nodes) operate in the ISM band, interfering with each other and affecting both the performance and the QoS. In this paper, we have revisited a metric that has been used already, and a novel one is proposed. Density wave phenomenon represents the average number of neighbors that belong to each node that fluctuates during operation. Nodes located in specific zones of the considered area can have many more neighbors than others, and this fact can be taken into account to optimize the overall performance and resource optimization. The average neighbor percentage metric describes the cumulative percentage of the total number of neighboring nodes. The appropriate usage of energy and bandwidth resources could improve the results of this metric. In the novel approach introduced in this paper, the proposed node neighbor range metric reveals the imbalance of mobility models during the simulation. This concept can be linked with node clustering, which impacts the overall network performance, and with a node’s battery life. The metric can be combined with resource allocation optimization techniques in order to reveal the inefficiencies in energy and bandwidth usage. In the next paragraphs, we introduce techniques that can be adopted to improve the network performance based on the metric results.

Several works have been developed aiming at the optimization of network performance. Among the ideas to improve resource usage in the proposed metric, we can consider the results in [37], the authors of which proposed a multi-cluster, multi-hop packet radio network architecture for wireless adaptive mobile information systems, allowing spatial reuse of time slots and codes and guaranteeing bandwidth for real time traffic.

In [38], the authors describe a self-organizing, multihop, mobile radio network that relies on a code division access scheme for multimedia support, which offers spatial reuse of the frequencies, bandwidth sharing, and robustness against topological changes caused by node motion, a case considered in this paper.

The authors in [39] propose heuristic routing schemes for clustered multihop, mobile wireless networks that improve packet delay and consider the effect of channel fading.

There are interesting results obtained by other researchers that could be applied to the proposed approach in order to improve network efficiency. In [40], the problem of interest, energy-aware and physically aware coalition formation, and resource management in smart IoT applications is studied. A distributed resource management mechanism is proposed for determining the optimal transmission power of each M2M device in order to fulfill its QoS prerequisites. This concept can be amalgamated with the proposed metric in order to optimize energy-saving given that it introduces a holistic utility-based transmission power allocation approach to optimize a mobile node’s battery life, through a novel formulation of the power control problem as a distributed non-cooperative game among devices. Applying this idea, it is feasible to extend the battery-life extension of the M2M devices by an efficient clustering strategy and by adopting wireless powered communication techniques.

In [41], the authors introduce the concept of a joint consideration of interest, physically and energy-related properties in the clustering, and resource management processes in M2M communication networks supporting various IoT applications. Initially, a joint interest and physically aware and energy-aware cluster formation mechanism is proposed. This concept can be combined with the proposed metric to define a new one that further improves the properties of the node neighbors’ range metric.

In considering the neighboring issue used in the metric, the concept introduced in [42], where the authors face the problem of socio-physical and mobility-aware coalition formation among the trapped users and the first responders in public safety networks in order to guarantee connectivity, stability, and energy-efficient communicate, can be considered as well. In the proposed approach, each user is associated with socially, physically, and mobility-related characteristics and attributes in a public safety network, forming nodes clusters that can be considered by the node neighbors’ range metric to improve its properties.

7. Conclusions

In this investigation, we have shown the first attempt to validate some mobility models in networks taking into consideration the most relevant mobility metrics, namely the speed decay problem, the density wave phenomenon, spatial node distribution, and the average neighbor percentage. These validations aim to summarize several parameters into 18,126 different scenarios with an average of 486 validated files.

Based on the various experiments conducted, we conclude that entity models show the worst performance due to their independent movement model and the total randomness of the RWPMM. In a second step, a better performance is shown by the RPGMM and SLAW, as demonstrated in the previously depicted results. Nevertheless, it is worth noting that the NCMM and SMOOTH represent the mobility pattern with the best performance. In accordance with this result, we have proposed a new mobility metric called the “mobile neighbors range”, which proves the set of outcomes of previous metrics and can be substituted for those metrics. This novel metric shows an effective behavior neighbor changes in mobility patterns, showing accurate results for all mobile nodes during the implementation of the experiment. The proposed metric merges the strengths and weaknesses of all of the stochastic properties that have been previously discussed. An exhaustive analysis of the details in this paper leads to a good understanding of the accurate behaviors of mobility models by displaying the ability of every pattern to deal with some topology changes and to ensure network performance. Mobility management in ad hoc wireless networks faces many challenges. Mobility constantly causes the network topology to change. In order to maintain accurate routes, the routing protocols must dynamically readjust to such changes. Thus, routing update traffic overhead is significantly high. Different mobility patterns have in general a different impact on a specific network protocol or application. As future work, we will discuss in detail the consequences of each mobility model on the resource management and respectively on the networks’ resource savings. Toward this direction, we will aim to combine the nodes’ mobility characteristics to their information exchange interest in order to improve the resource savings within the overall network. In addition to application scenarios of each mobility model (e.g., ultra-dense networks, heterogeneous networks, and public safety networks), we will engage in, among other things, a complexity analysis for the implementation of each mobility model as well as a discussion of its real-time applicability and the implementation cost of each mobility model with respect to the real-world applications.