1. Introduction
The
Hotline Miami series of games [
1,
2] involves a set of psychopathic killers who wear various animal masks during their attacks. It stylistically takes inspirations from movies like
Drive and other neo-noir films with 1980s bright neon visuals and a synthesizer europop soundtrack. The storyline has been compared to the movies of David Lynch. The game is a top-down view of what looks like an architecture diagram of the building where a player has perfect knowledge of the space. Game play is fast paced, meeting with the idea of a psychopathic murder’s spree, and the player is killed with a single hit by an enemy; upon death, the player is immediately re-spawned into the level at the start in order to play through the level again. This makes the design of such levels decidedly different from the majority of game genres investigated for implementing Procedural Content Generators (PCG) for level design, see [
3].
Hotline Miami levels are best examined, like for example top down dungeon crawlers and non-digital games such as
Dungeons & Dragons [
4,
5,
6,
7,
8]. Action based Role Playing Games (ARPGS) such as
Diablo are close to the feel of
Hotline Miami, however, the level size is much larger in
Diablo, and considerations of line of sight are not as pressing in a hack and slash world with a character able to take a number of hits, compared to the immediate death and re-spawn mechanic of
Hotline Miami. See
Figure 1 for examples of the levels.
Many representations were introduced that allow the designer control over the type of mazes that are generated, e.g., caverns, rooms, and etc. Ashlock et al.’s studies [
6,
7] use a checkpoint-based genetic algorithm that optimizes the fitness function toward creating mazes with user-defined characteristics. McGuinness and Ashlock [
5] showed that the resulting mazes generated in the previous work could be tiled in order to create larger, more complex mazes. This technique could be extended to include other generation types, e.g., terrain, in order to create large maps. Valtchanov and Brown [
8] use a genetic programming approach to create
Diablo style levels via the placement of pre-generated tiles. The tile method follows a number of current industry practices of the creation of random levels with game elements. The fitness functions used include a placement of ‘event rooms’ which could contain boss battles or treasure rooms. Aslam et al. [
9] uses Genetic Algorithms as a placement method for title in a serious game, and demonstrate that they outperform humans on relatively simple placement tasks compared with an objective measure of fitness.
There have also been a number of PCG generations for the design of the interiors of buildings, primarily for architectural design problems such as those in [
10,
11,
12]. However, their evaluations are based on optimizations of floor plans for realistic buildings and look to architectural requirements as their constraints. These methods primarily assume the external structures are fixed and are akin to layout and packing problems which have additional restrictions on the flow between the named areas, or restrictions based on use of the rooms, e.g., placing bathroom beside the master bedroom.
However, in all of these methods little integration to real games has been presented. In this paper, looking at
Hotline Miami it was necessary to reverse engineer the level files in order to place the developed levels into a commercially playable game, rather than acting as a simple technical demo. We present a Genetic Algorithm (GA) approach, first seen in [
13], to create the layout for levels using the reverse engineered level files, and examine a set of fitness functions for their suitability to create level layouts which meet with the constraints of player movement and with creating a connected tight space for players to act within. This is then extended looking at the placement of objects within the space via Petri nets, and the placement of enemies with a second GA.
Small example games have shown how PCG integration can be used to create an entire game. Cook and Colton [
14] build an entire arcade game using various PCG techniques as presented above for a framework known as ANGELINA. The system creates what the authors call a
multi-faceted evolution which procedurally generates a map, a layout defined as the player and NPC positions, and a rule-set for the game. Yet, very few academic generative methods have been applied with much success to current games and methods in the industry, in part due to trade secrets employed by developers. Noteworthy examples of PCG for commercially available games include: Ropossum levels [
15],
Mario Levels [
16], a generator for
Zelda levels [
17], and
Spelunky generation [
18]. However, none of these examples are using the commercial game’s own engine as part of the tool chain and instead require a complete reimplementation of the game. Due to the reverse engineering of the file format for the available level editor, the generations upon
Hotline Miami demonstrated in this paper can be used in the working commercial game, and the file format is described allowing for others to also demonstrate other techniques in this game. The method chosen allows for a level of control in generation via the use of a series of fitness evaluators which examine the generations for mechanical issues in game play, as well as for aspects in the connections, room size, and movement within the level. The generator produces levels ready for further development by a human to ensure aspects such as game difficulty which are currently beyond the scope of this work.
The development of PCG for Hotline Miami will progress in two stages. The first stage is the development of the level layout, and the second stage is placement of objects, enemies, and power-ups. We will examine the first of these two stages in detail, and give directions for the placement of objects and enemies.
2. Methodology
Evolutionary Algorithms (EA) use principles from Darwinian evolutionary theory, specifically a fitness biased selection method, in order to solve problems in diverse field such as optimization and planning, see [
19] for a general overview. We are interested in its ability to work as a design tool, which allows for a diversity of solutions, as well as optimization against a set of requirements. Genetic Algorithms (GA) are EAs developed first by Holland [
20] which have populations of candidate solutions to the problem called
chromosomes. Chromosomes are tested for their ability to solve a problem via a
fitness evaluation which produces a fitness score. The fitness score informs a fitness biased
selection which decides on the chromosomes which undergo
variation operators. GAs use the notion of a genetic breeding between pairs of chromosomes, a
crossover, and small changes to a single chromosome,
mutation, as variation operators.
2.1. Representation and Translation
2.1.1. Representation
The representation used in this study is similar to the
indirect positive method used by Ashlock et al. [
6] which defines rooms using an integer representation of the areas they take up. We do not utilize a mapping function nor is placement relative to previous rooms such as in [
8], but instead expressly place rooms into the space.
Rooms are defined as a five-tuple where:
x is the starting x-coordinate of a room
y is the starting y-coordinate of a room
l is the length of the room
w is the width of the room
t is the placement type of a room, if it places on-top of (O) or under (U) previously placed rooms.
Chromosomes are sequences of rooms which will be placed in order. The first room is placed into the space. In order to ensure connectivity, a new room is only placed into the layout when it overlaps with a currently existing room. This allows for the algorithm to create levels with a number of rooms less or equal to the length of the chromosome. Doorways are important within Hotline Miami as they block line of sight for enemies, and doorways can be used to attack enemies by knocking them down, which stuns them for a coup de grâce by the player. The potential doorways are defined by adjacent borders of rooms. Doorways are placed at the random location in each adjacent wall. In an O type room, the wall of the newly placed room defines the potential doors, a U type room defines the walls of the previously placed rooms as being the locations of potential doors.
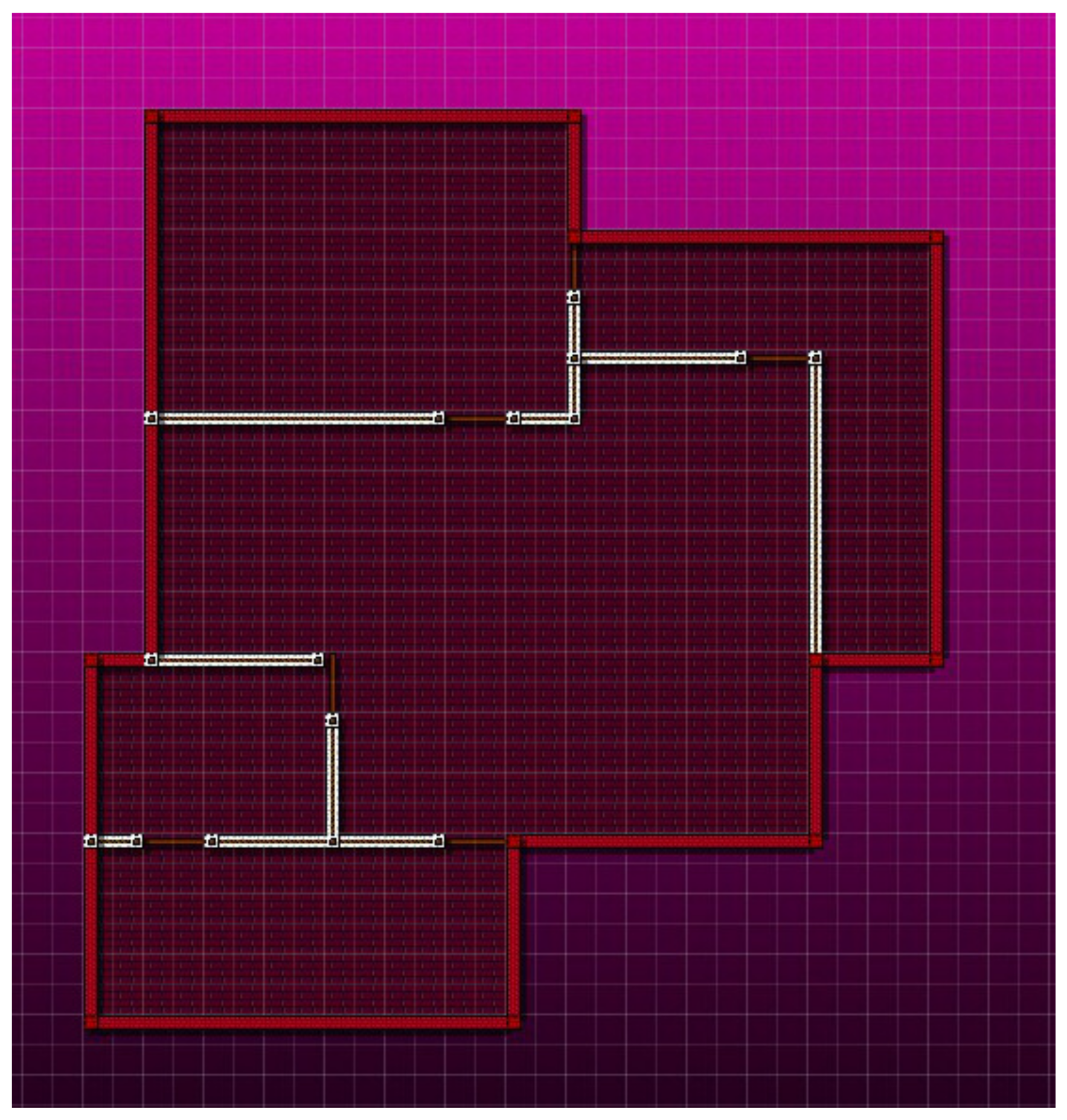
Figure 2 displays the generated level rendered by the in game development render for the chromosome in
Figure 3.
2.1.2. Translation
The translation step changes the chromosome into a full working level for the game. A level editor for Hotline Miami 2: Wrong Number was released in beta, and via an exploratory process the level files were reverse engineered.
A Hotline Miami level is described by a set of plain text files, described below, with each line encoding a single value.
level.hlm ‘Hotline Miami level’ file.
Holds meta information about the level such as name of the level, name of the author, and size of the level. See
Table 1 for the breakdown of the attributes. The level of Hotline Miami is organized in square tiles each having the size of 16 px by 16 px. Maximum allowed size of the level is 1088 px by 768 px.
level.ver ‘version’ file.
Contains a single integer, which represents version of the editor. At the moment of writing the value was ‘2’.
level0.obj ‘objects’ file.
Holds information about the player character, player’s car, doors, enemies and decoration objects. Each entity is described by its object ID, coordinates
, sprite ID, rotation in degrees of the sprite, behaviour type for AIs(static, patrol, idle), index of the frame for the sprite of this object. This index allows the game to select the current image from the sprite sheet allowing the game to make animations. See
Table 2 for a breakdown of the attributes.
level0.tls ‘tiles’ file.
Describes the floor tiles. Each tile is a square of size 16 px × 16 px. See
Table 3 for a breakdown of the attributes.
level0.wll ‘wall’ file.
Contains descriptions of wall segments. Each wall is assumed to be 2 tiles or 32 px wide. See
Table 4 for a breakdown of the attributes.
level0.play ‘play’ file.
This file contains all game entities. On level launch, every entity from other files is transferred here. Level editor works without this file, but the game will not launch.
This was a major undertaking to decode the files to allow for a new level to be input into the system and demonstrates that developers who have explicitly provided level editors can prevent ease of use of their systems for the modding and academic communities by not using a human readable format.
2.2. The Algorithm
2.2.1. Internal Representation
Walls in Hotline Miami span two tiles, so to be properly translated into Hotline level format we used ’Wall Segment’ class which holds block of 2 × 2 tiles. For each segment there is a corresponding number describing to which room this segment belongs.
2.2.2. Level Building
The core of the algorithm is the level building step, see
Figure 4, which takes a chromosome and subsequently adds each rectangle to the level. During that process a room is created and assigned a list of segments that belong to the room. If overlapping rooms split another room into two sections, then they will not be placed. After all chromosomes have been added, the algorithm places a door between adjacent rooms.
2.3. Variation Operations
The evolution progresses for 100 generations, rounds of fitness evaluation followed by crossover/mutation, with a randomly initialized population subject to the following operations:
2.3.1. Crossover
The crossover utilized is a uniform order method with a probability of 0.5 for taking a room from each of the parents. See
Figure 5 for an example.
2.3.2. Mutation
The mutation operation selects a random room and replaces it with a randomly generated one. See
Figure 6 for an example.
2.4. Selection
The population in this study is set to 20 chromosome levels of size 10, which are evaluated via the fitness function. The crossover of the two fittest individuals is copied over the entire population, and the children are then subjected to the application of a mutation.
2.5. Fitness Evaluations
In order to demonstrate the method, and to show control over the level of development, a number of fitness evaluations were proposed to discover a setting which will create levels with properties beneficial to the game experience. At first, evaluation was set to encourage maximum amount (10) of rooms. However, in this case, rooms were disconnected from each other. To fix that, a new constraint was introduced: only overlapped or connected rooms are used in fitness calculation. With these conditions, other fitness functions were implemented:
2.5.1. Maximize Rooms
This evaluator increases fitness value for each connected room.
This provides levels with larger amounts of rooms that are connected. Note that as non-connected rooms are removed from the final translation of a chromosome into a layout, the evolution has an indirect control on the number of rooms placed.
2.5.2. Maximize Total Rooms Area
This evaluator increases fitness value for each tile inside building. One tile is a unit of area.
This provides levels with large rooms and/or many rooms.
2.5.3. Minimize Total Rooms Area
This evaluator decreases fitness value for each tile and has maximizing number of rooms in priority, to prevent one small room in the output of the generator.
This fitness attempts to provide small rooms and also to cause rooms to not be utilized in the chromosome.
2.6. Graph Based Fitnesses
The following fitnesses assume that the reader has some familiarity with graph theory, see [
21] for a review. A
Simple Graph is a non-empty set
V of vertexes or nodes and a set
E of unordered pairs of elements of
V, called edges. Two distinct nodes,
and
, are said to be
neighbours if
. The number of edges in
E which contain a vertex is called the
degree of the vertex. The
diameter of a graph is the largest number of edges in any shortest path between any two of the vertices.
2.6.1. Maximize Degree
For the given chromosome, a graph is constructed, where every room defines a vertex, and each adjacent wall defines connection between two rooms. The fitness evaluator returns cardinality of edge set.
This fitness function should create levels with many connections between rooms.
2.6.2. Maximize Diameter
For the given graph, this evaluator calculates the diameter and returns the sum of rooms quantity and diameter.
where
is the number of rooms.
This fitness function should encourage long paths between any pair of rooms.
2.6.3. Minimize Diameter
For the given graph, this evaluator calculates the diameter and returns the difference of rooms quantity and diameter.
This fitness function should encourage short paths between any pair of rooms.
2.7. Fitnesses with Corridor Penalty
2.7.1. Corridor Penalty
In all the aforementioned cases, fitness functions created narrow rooms in which a character could not move. This fitness function penalizes the gene for each tile in a narrow corridor and for one tile rooms.
where
is the number of narrow rooms (with width or height equals to 1 tile) and
is the number of one tiled rooms.
2.7.2. Complex Fitness
This evaluator was developed to create interesting and realistic buildings. This fitness function aims to maximize the number of rooms, the diameter of graph, and keep the average degree close to two. It also penalizes each tile in a narrow corridor and one tile rooms.
where
.
The goal of the evaluation of all these fitness functions is to demonstrate that the fitness function can provide a control to the designer on generation to create a room with the required characteristics.
3. Generated Level Examples
In order to show this control to be effective, a number of levels were generated of each type and compared statistically to demonstrate the effect of the control from the fitness functions above. The evaluated feature set includes the: Number of rooms placed in the final level, the total area taken by the map, the minimum room area, the maximum room area, the number of one tile corridors, the diameter of the graph formed by the connections between doors and the average degree of the graph formed by the connected rooms. The one tile corridors value is important, as a player character cannot move though such corridors, and should be minimized. The fitnesses expressed in
Section 2.5 are examined on the average of 30 runs of the generator and means and
confidence intervals are shown in
Table 5, in order to show the expression of the levels based on the selected fitness function.
The statistics from the developed levels demonstrate that the generator responds well to control via a fitness function.
The maximize rooms fitness method was able to utilize all rooms in all cases; other fitness methods which provided the same outcome were the minimize area and the two diameter controls. Total Area and Min/Max Room Area in maximization of rooms fitness was not that different from the diameter fitness cases. One tile corridors were reduced in the minimization of diameter. Respectively, the Minimize and Maximize Diameter both were significantly different from Maximize Rooms in both diameter and degree. The Maximize Rooms fitness has no controls over area, diameter, or degree, and thus provided a baseline assessment of the generated room layouts.
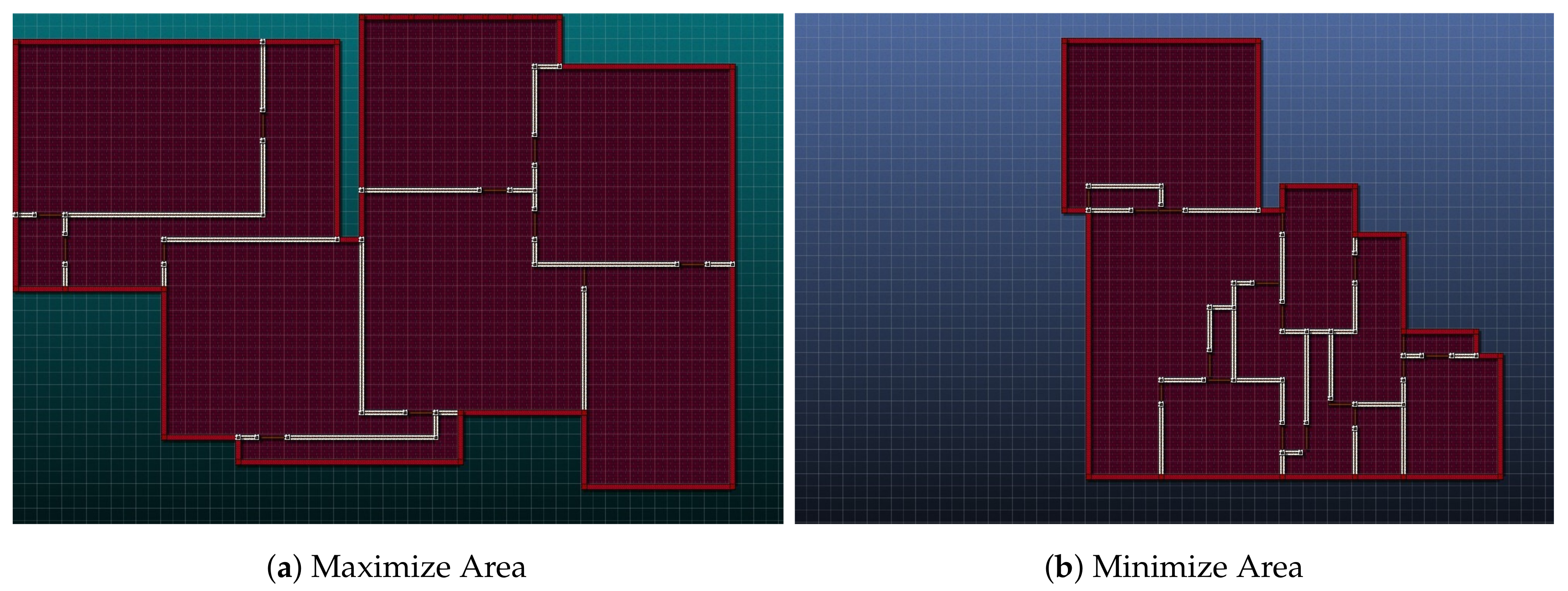
There is a statistically significant increase/decrease in the room size for the Maximize/Minimize Area while maintaining similar degree and diameter of the graph, as seen in
Figure 7. The levels visually demonstrate a common connective look, but the space is compressed or expanded.
Similarly, changes to the Min/Max Diameter of the graph do not significantly change other parameters, however, levels with low diameter have higher degree of about one more. This is expected as reduction of diameter is an outcome that results in higher connectivity between rooms. The GA can successfully see this trade. The maximization of the degree reduced the diameter compared to the Maximization Diameter fitness function, and even was significantly higher from minimization of diameter, accomplished most likely by small trade-offs on the number of rooms utilized.
The Corridor Penalty in its own fitness check removes the one tile rooms completely as part of the fitness. The Complex fitness levels share this removal of tight corridors as they also penalize the smaller rooms. Via removal of these small corridors, there is a significant increase, about five units, except for Maximize Areas where it is only two, in the minimum room area against all fitness functions which do not apply this penalty.
The Complex fitness function provided for levels which are close to some of those seen in the game, such as in
Figure 8. The generated examples met with our original requirements of a compact construction of rooms with many connected doors which closely resembles a building layout as seen from above. Interestingly, this fitness function provided for statistically significant less rooms than any of the other methods, and was smaller in terms of total area, while keeping the minimum room area relatively high. Degree was kept within a tight distance to exactly two, only deviating upwards by 0.08. The diameter was also the second highest value. Other than the number of rooms, the generated levels were well within our requirements of this fitness function, most likely this is due to the fitness function in a way expecting too much and the lacking room penalization not being high enough to provide selection pressures away from increasing the other values by losing rooms.
4. Placement Problems in Generated Layouts
The layout of the level is only one factor in a fully featured generation. After the layout is developed, objects and enemies should populate the levels in order to both complete the mechanical requirement, that a player needs to defeat all the enemies in a level, as well as the narrative or thematic believability of a space as being lived in, rooms are not just empty in buildings as they have purpose for their construction and roles for their use.
The system first constructs the placing of objects into the rooms and then placing enemies. Objects can interfere mechanically with the player and with enemies’ movements which can make substantive changes to the outcome of the difficulty of a level based on blocked lines of movement.
4.1. Object Placement
Objects are placed in rooms using the Petri net method examined by Taylor and Parberry [
22]. A Petri net is a directed bipartite graph with a set of tokens. The nodes in first partition are called places and the nodes in another partition are called transitions. Tokens are put on places of Petri net and transitions describe how they can move around the graph. If all of the places which connected by incoming edges with the transition contain at least one token then the transition is called live. At each step, one live transition is randomly chosen to fire, one token from each incoming place is removed and one token is added to each outgoing place.
Taylor and Parberry proposed to use anchor points of room as tokens in Petri net. Anchor points are some precomputed places in the room where objects can be set. In our case this is the tiles near walls, corner tiles and tiles in the center of the room excluding points near the doorways to prevent them from blocking.
For each incoming edge user can specify which type of tokens are allowed. Each incoming edge can create an object at the anchor point represented by the token. The tokens are fed to starting places of Petri net at the start of the program and after that live transitions execute randomly.
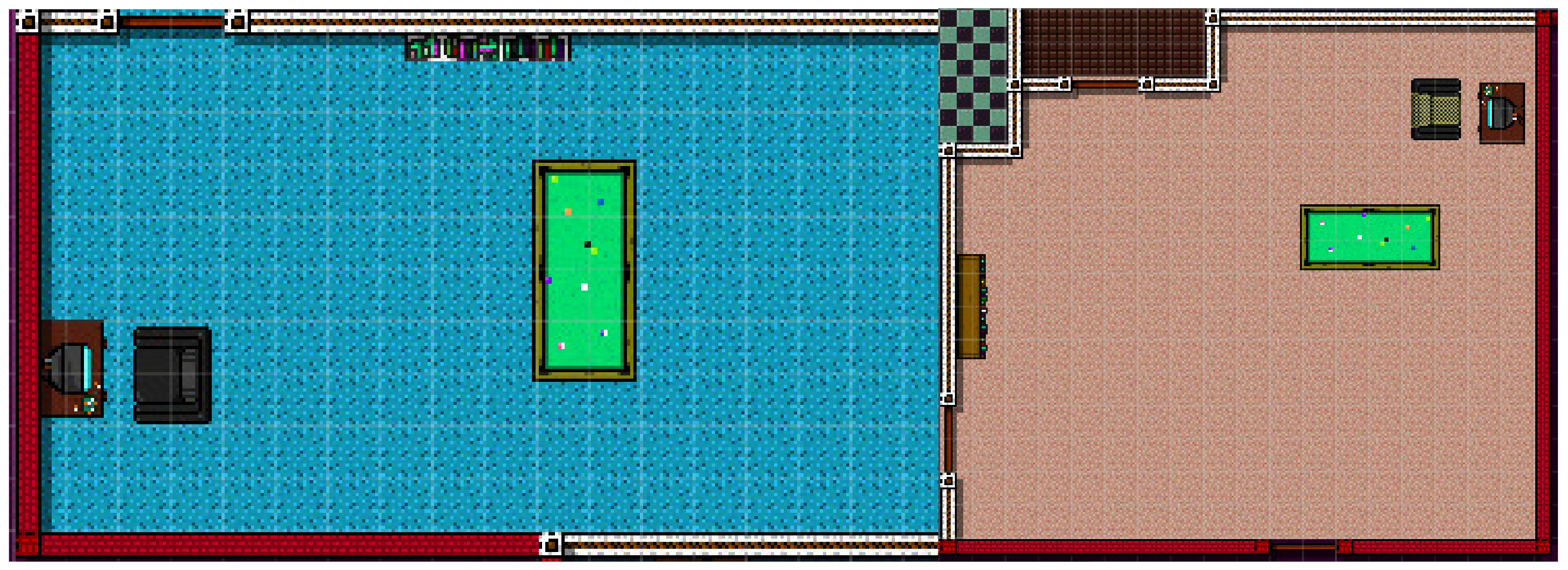
The objects within these rooms were limited to placement of a television, a bookshelf, and a billiards table into the room, to create something narratively described as a rec-room.
Figure 9 displays an example output. However, the definition of these assets is rather general, and hence, themes for the rooms can be implemented.
4.2. Enemy Placement
We examine an early development of the enemy placement. Enemies are generated using a second Genetic Algorithm. The enemy placement algorithm is based on the previously generated room layout, decor objects, and placed level entrance. Each generated room has a list of tiles. Each decor object occupies some tiles. The graph of the generated rooms is used to calculate the indexes for the rooms in the chromosomes. First, the center of each room is calculated by calculating the center of all tiles of the room. This allows us to assign edges of the graph weights equal to distances between these centers. Then the distance from the entrance room to all the other rooms is calculated. Using the list of distances, the rooms are ordered and assigned indexes starting from 0.
A chromosome is represented by a list of enemies in one of the generated rooms and the generated index of that room. Tiles are represented by their absolute coordinates on the level plane. Available tiles are the tiles of the room less the tiles occupied by the decor objects. An enemy is represented by the tile it occupies and its type—an integer that corresponds to the type of the enemy in the game is described in detail later.
Generation of a chromosome is done by selecting a random amount of tiles from the available tiles of the room and placing enemies with random types in these tiles.
A desired difficulty is set for the level. Fitness of the generated gene (list of all chromosomes representing generated enemies) is calculated by a comparison of the desired difficulty of each room to the evaluated difficulty of the generated chromosomes.
This fitness function is defined to ensure four goals:
Set a desired level of difficulty for the whole level.
Adjust the types of enemies in the level by changing their difficulty.
Make the level progressively more difficult until the end
Add more enemies to the large rooms, and less to the smaller rooms
Each enemy type is assigned a difficulty value for a player. The list of the difficulty of types of enemies in descending order are: boss—100 points, dodger—80 points, dogs—40 points, uzi—30, shotgun—30, 9 mm—20 points, melee—10 points. The uzi, shotgun, 9 mm, and melee enemies can be set to a static position, or a patrol/random route. If they are set to have a patrol/random route they are worth an extra five points.
Fitness evaluation of the gene is done in the following steps: First the desired difficulty of each room is calculated based upon a developer assigned difficulty level:
where
The minimum and maximum sizes of a room are the settings of the generator of the level above. Then the difficulty of the generated enemies in each room are calculated by taking the square of the number of enemies in the room plus the sum of the point values of those enemies.
This value is then compared to the desired difficulty of the room to give the final fitness value of a room:
The sum of these differences for the rooms is then minimized by the GA.
For our example, see
Figure 10 we used the settings of a desired difficulty of 80. It was run for 100 iterations with a population of 20. The top two results repeatedly breed to fill out the remainder of the population. We use a uniform crossover point crossover and a mutation which changes the enemies in a single room.
6. Conclusions
As stated above the goal of this project is to fully automate the development of levels for
Hotline Miami in two stages: development of the level space and the placement of enemies and power-ups. This study fully examined the development of levels and the representation. We have shown a quantitative analysis of the effects of changing the fitness function, in order to allow for different characteristics to be shown in the developed levels. This set of fitness functions, much like those shown in [
6,
8], demonstrates an effective control on the features seen in a level under this framework. Controls can be placed on individual features, in this case size and graph measures, to prevent the level generation from demonstrating poor behaviours, i.e., small corridors, or combined into a composite function to provide entire levels meeting with a description of the space.
In future work we aim to include the further development of the placement of the enemies into this framework. In terms of the Petri nets we have only looked at the development of the level layout in terms of the mechanical properties and have not examined the aesthetics of the rooms—such as placing items to show a room to be a kitchen or an office building.
Play Testing
The design process for a game should always include a requirement of play testing of the levels in order to determine suitability for the players at all skill levels and ensure the game is
fun. This requirement should not be removed by the use of a PCG method, see [
24] for a good example of PCG with player feedback. In fact, it is even more necessary as the generator is creating levels solely on the objective basis of the fitness function, which while meeting with constraints of the system may not meet with the subjective requirements of players. The game should be presented to a number of human players of various skill levels and qualitative and quantitative responses should be gathered about the levels. This would allow for a refinement of fitness functions.
Further, the levels generated could be compared to human developed methods in order to allow for a test on the human competitive ability of the process. One method would be to run a Turing test between human and generative methods [
25]. Though many human developed levels will not meet with the principles of game design which most developers aspire towards, we believe a better test would be to look at the scores by a human play test group in terms of the
playability or
fun, when compared to a set of levels from the game itself and a set of player created levels. Otherwise, a test would be to release levels created by the generator via the Steam Workshop framework and look at user feedback, while not framing the level as a computer generated method.