1. Introduction
Designing a system that meets optimization goals (e.g., performance, energy, energy-delay product (EDP), etc.), is becoming a major goal for system designers in all computing device domains, from high-performance servers to embedded systems. Since hardware requirements, such as the cache memory size, processor speed, front bus speed, number arithmetic logic units, etc., differ for each application, an optimized system for one application is not necessarily an optimized system for another application.
System optimization can be achieved using configurable hardware, which has configurable/tunable parameters [
1,
2,
3,
4] that can be tuned during runtime to adhere to optimization goals. A set of parameter values constitutes a configuration and all possible configurations compose the complete design space. The configuration that most closely adheres to the application’s requirements while achieving optimization goals constitutes the application’s best configuration.
Tuning is the process of exploring the design space to determine the best configuration. Many prior tuning methods [
5,
6,
7] executed applications on different configurations during runtime, measured execution characteristics, such as the cache miss-rate, cycles per instruction, using hardware counters, and then selected the best configuration. However, these methods incurred significant tuning overhead, including energy and performance overheads expended while executing the application in non-best configurations. To reduce the tuning overhead, other methods [
8,
9] measured the application’s execution characteristics and used analytical models to predict the best configuration based on these characteristics. However, these methods required complex computations and lengthy calculation processing time [
8], or high application persistency to amortize the tuning overhead [
9].
To eliminate the runtime tuning overhead and complex computations, Wang et al. [
10] tuned the configurable hardware offline, prior to system runtime, stored the application’s best configurations in a lookup table, and used the information during runtime to tune the hardware to the best configuration. However, offline tuning required a priori knowledge of applications and a lengthy simulation time for large design spaces.
Since one of the major challenges with configurable hardware is efficiently and effectively searching a large design space, prior work [
11] empirically determined that the complete design space was not necessary to achieve optimization goals. The authors observed that many configurations provided similar optimization potential, such that the design space contains many near-best configurations. Near-best configurations are configurations that adhere to optimization goals nearly as well as the best configuration and therefore, the design space does not need to contain all configurations to adhere to the optimization goals. Runtime tuning overhead and lengthy simulation time of offline tuning can be reduced if the complete design space is pruned into a subset of configurations containing near-best configurations.
However, since applications have disparate hardware requirements, the near-best configurations are application-specific. Given a general purpose system, the subset must be large enough to contain best or near-best configurations for all applications that are expected to run on the system in order to adhere to optimization goals for every application. A major challenge in selecting this subset is ensuring that the subset is large enough to meet all disparate application requirements, but not so large that the design space exploration time remains long. Therefore, the best tradeoff between the subset size and adherence to optimization goals requires an exhaustive exploration of all subset sizes and subset configuration combinations [
11].
To determine the best subset size and configurations, designers must evaluate all of the applications’ optimization goal adherence for every combination of subset size and configurations, and then select the highest quality subset. High-quality subsets are subsets that contain a combination of configurations that most closely adhere to optimization goals as compared to the complete design space. Although prior work [
11] used a heuristic [
12] to speed up the high-quality subset determination, the heuristic still required a priori knowledge of all expected applications in order to evaluate the subset quality, which limited the usage of configuration subsetting in general purpose systems.
The challenge is then, during design time, to determine the subsets that contain best or near-best configurations with very low or no a priori knowledge of the applications. However, since applications are typically required to evaluate the configurations’ qualities and select the best subset, varying the a priori knowledge of the application will affect the subset’s quality. Furthermore, since configuration/subset quality evaluations require executing the applications, the number of applications evaluated impacts the evaluation time. However, the extent of this impact is not linear, since application execution times vary based on the nature of the application (i.e., using half of the applications does not necessarily result in a 2X speedup in the design space exploration times). To gain an insight into the performance-quality tradeoff, it is imperative to determine the minimum number of applications required to select high-quality subsets.
In this paper, we evaluated and quantified the extent to which a priori knowledge of all anticipated applications affects subset quality and determined that a small training set of applications provides sufficiently high-quality subsets. This observation significantly broadens the usability of the heuristic [
12] by alleviating the requirement of a priori knowledge of all applications. We used training application sets to determine the configuration subsets and evaluated the quality of the configuration subsets using a disjoint testing application sets. To evaluate the subset quality, we compared the adherence to the design optimization goals using the subset’s configurations as compared to using the complete design space.
Based on these results, we conjectured that if there is a basic knowledge of the anticipated applications’ hardware requirements (e.g., a large cache size, deep pipeline, fast clock frequency, etc.), a test set containing applications with similar hardware requirements would improve the subset quality. To test this correlation, we used three methods to select our training application sets: a random method which required no a priori knowledge of anticipated applications, and two classification methods. The first classification method is a basic classification method that classified applications based on the general hardware requirements of the anticipated applications. To gain insights on the classification method’s impact on selecting a subset, the second classification method hierarchically classified applications based on the similarity of the applications’ hardware requirements.
Additionally, to quantify the impact of a priori knowledge on the speedup of the heuristic [
12] to select a high-quality subset, we compared the execution time of our algorithms to prior work [
11]. We compared the execution time that our random method required to select a subset using training applications as compared to using the complete application set. Furthermore, since training applications differ for different classes, we compared the execution time of our classification methods to determine the subsets as compared to our random method.
Our results revealed that a priori knowledge of all anticipated applications is not required to obtain high-quality subsets, and rather, a fraction of training applications is sufficient to obtain a configuration subset of high-quality (i.e., a subset with 22.2% of the complete design space achieves an average energy savings within 17.7% of the complete design space). These results suggest that subsets alleviate design efforts for general purpose computing while closely adhering to optimization goals. Our results also showed that the subset quality can be improved with a basic knowledge of the anticipated applications’ hardware requirements, by as much as 10.4% on average. Thus, designers can determine application-domain-specific subsets and reuse the subset for any application that belongs to that domain. However, using a domain-specific subset for an application not of that domain greatly depreciated that application’s energy savings. Our hierarchical classification revealed that this degradation in energy saving is alleviated if applications are classified using the application’s hardware requirements.
Our speedup results showed that the training application set had the most impact on subset design space exploration time, and a basic knowledge of the anticipated applications reduced the subset design space exploration time by up to 6.6X. Additionally, our results revealed that hierarchical classification performed slower than basic classification since hierarchical classification iteratively classified applications based on the applications’ hardware requirements.
The remainder of this paper is organized as follows.
Section 2 discusses the foundational related work that makes our contributions possible. Since the cache memory hierarchy has a significant impact on the system’s performance and energy,
Section 3 discusses our cache configurations design space.
Section 4 introduces design space exploration as a data mining algorithm, and the heuristic we evaluated in this work.
Section 5 describes our training application selection methodologies used in this paper.
Section 6 provides our experiment setup environment, and
Section 7 and
Section 8 discuss the results and analysis of the subset quality and speedup, respectively.
6. Experimental Setup
To provide a fair comparison, we modeled our experimental setup similarly to prior work [
11]. We evaluated 34 embedded system applications: sixteen from the EEMBC automotive application suite [
33], six from Mediabench I [
34], and twelve from Motorola’s Powerstone applications [
3].
Table 1 depicts our configuration design space where
c18 is the base configuration (
Section 3.1). We used Algorithm 1 to select subsets
S with |
S| = 4 [
11] for random training set sizes 1–10, 17, and 34 (
Section 5.1) and the basic and hierarchical classification training sets containing three applications (
Section 5.2.1). For the hierarchical classification, we used Algorithm 2,
M as 2-D (34 applications, average miss-rate),
R = 3, and
I = “Euclidean”. We set the training set size to 3 (
Section 5.2.2) for each class in
Z.
To evaluate the subsets’ qualities of the random training sets, we compared ᴪ for each application to the application’s cb ϵ C and to the base configuration c18 by normalizing ᴪ to cb and c18, respectively. For the basic classification training sets, we compared the test set’s Qi’s applications’ energy consumptions for sb ϵ S—selected using TBC,3—to the energy consumptions of Qi for sb ϵ S—selected using T3. We compared these energy consumptions by normalizing the energy consumption of Qi for sb ϵ S—selected using TBC,3—to cb ϵ C. To compare the subset quality between hierarchical and basic classification, we normalized the energy consumption of the test applications using sb ϵ S—selected using THC,3—to sb ϵ S (selected using TBC). To quantify the tradeoff between energy savings and hardware requirements (i.e., the number of configurations), we normalized the energy consumption of Qi for sb ϵ S—selected using TBC,3—to the energy consumption of Qi for sb ϵ S (selected using THC,3).
Furthermore, to evaluate the design-time overhead tradeoff, we use the execution time of Algorithm 1 to determine S for random, basic classification, and hierarchical classification. We note that the execution time for Algorithm 2 is negligible compared to that of Algorithm 1 and thus, we exclude this comparison from our analysis.
Figure 3 depicts our cache hierarchy energy model used for the instruction and data caches, which considered the dynamic and static energies [
11]. We obtained the dynamic energy using CACTI [
35] for 0.18-micron technology, estimated the static energy as 10% of the dynamic energy (a valid approximation for 0.18-micron technology [
9]), and calculated the CPU stall energy to be approximately 20% of the active energy [
9]. Since our modeled system did not have a shared level two cache, and thus no dependencies between the instruction and data cache behavior, we evaluated separately the private level one instruction and data caches and used SimpleScalar [
36] in order to obtain the cache accesses/hits/misses for each configuration for each application. We obtained off-chip access energy from a standard low-power Samsung memory, estimated that a fetch from main memory took forty times longer than a level one cache fetch, and the memory bandwidth was 50% of the miss penalty (44 cycles) [
9].
7. Subset Quality Results and Analysis
We extensively evaluated the random, basic, and hierarchical classification training sets subsets’ qualities, and quantified the criticality of a priori knowledge of the anticipated applications by comparing these training sets subsets’ qualities. We compared the subsets selected using T3 (created using random training sets) and TBC,3 (created using basic classification training sets) and compared the subsets’ qualities by normalizing the associated test set’s Qi, applications’ energy consumptions for using sb ϵ S–selected using T3–to the energy consumptions for using sb ϵ S (selected using TBC,3). Similarly, we analyzed the classification method’s impact on selecting subsets by comparing the subsets selected using TBC,3 to the subsets selected using THC,3.
7.1. Random Method Subset Quality
Figure 4a,b depict the instruction and data cache energy consumptions averaged over all test applications for the random application training sets of varying sizes and a subset size of four normalized to the best configuration in the complete design space and the base configuration, respectively. For brevity, each bar corresponds to the average (instead of per-application) energy consumption using
sb ϵ
S for all
Qi applications for a given
Ti, however, we discuss and evaluate the per-application energy consumption. In
Figure 4a, 1.0 corresponds to the baseline energy consumption for the best configuration
cb ϵ
C and subsets with normalized energy consumptions closer to 1.0 represent higher quality subsets. In
Figure 4b, 1.0 corresponds to the baseline energy for the base configuration
c18 ϵ C.
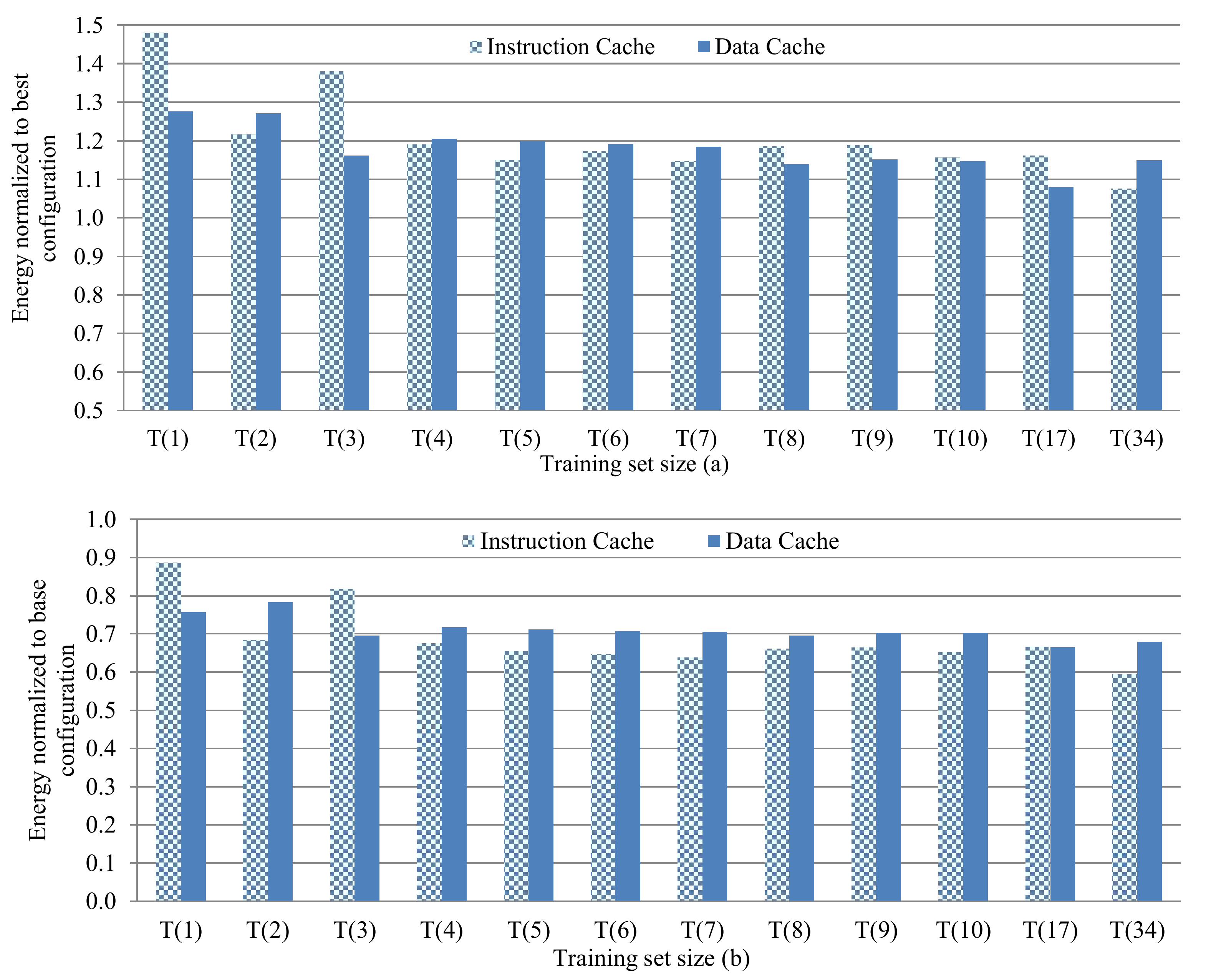
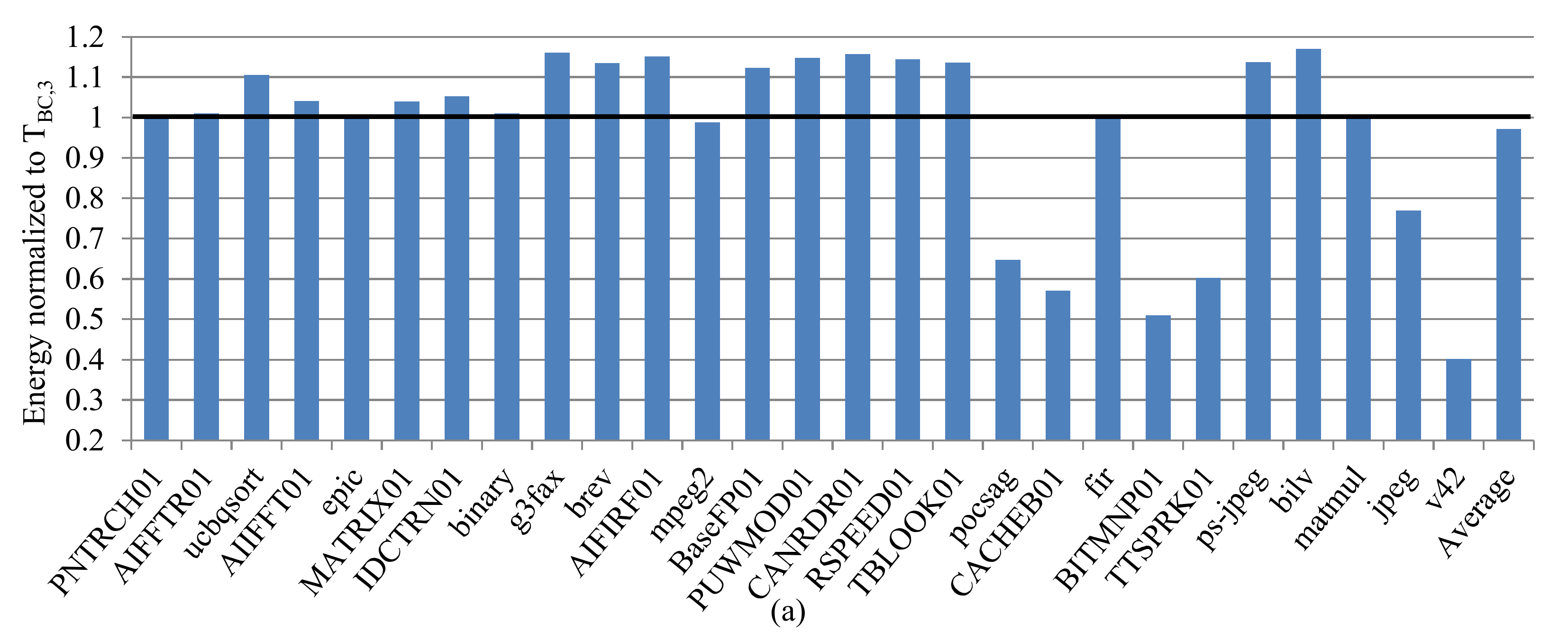
The instruction and data caches showed similar energy consumption trends as the training set size increased. However, since these training sets contained randomly-selected applications, on a per-application basis for the instruction cache, larger training sets did not necessarily equate to higher quality subsets, even though the moving average of the energy increase over all applications decreased as the training set size increased. For example, T3 provided energy consumption within 16.2% of the complete design space for the instruction cache, while T4 increased the energy to 20.4%. The instruction cache results showed that the largest training set T34 produced the highest quality subsets (the smallest average energy increase was 7.5%), while for the data cache, T17 produced the highest quality subsets (the smallest average energy increase was 8.0%). These results suggest that, since the data caches generally exhibit lower inherent spatial and temporal locality and thus, a greater miss-rate and cache-requirement variation, it is more challenging to capture enough cache parameter variation in a small subset created from randomly-selected training applications.
Figure 4b reveals that the random training sets’ subsets always resulted in energy savings as compared to the base configuration, with a general increase in savings as the training set size increased. Even the smallest training set
T1 yielded average energy savings of 11.3% and 24.2% as compared to the base configuration for the instruction and data caches, respectively. Per-application analysis revealed that
T3 was the smallest training set size where 94.1% of the test applications in
Q3 had lower energy consumption, on average, as compared to the base configuration. For
T3, the best-case application’s instruction cache had energy savings of 57.5% and 57.6%, compared to the base configuration, which was only a 3.18% and 3.8% energy increase compared to the best configuration in the complete design space, for the instruction and data caches, respectively. On average, for the instruction and data caches, the energy increase with respect to the complete design space was 19.8% and 17.7%, respectively, and the average energy savings with respect to the base configuration was 31.3% and 29.0%, respectively.
Analysis of training set size versus energy savings with respect to the base configuration revealed that T3 and T8 had the highest average energy savings of 30.3% and 30.5%, respectively. Although T8’s energy savings was 0.5% more than T3, T8 required a priori knowledge of eight applications, instead of three, which imposes significantly more design-time effort due to a 3034X increase in the subset design space. Thus, T3 provided the best tradeoff between training set size and energy savings.
7.2. Criticality of A Priori Knowledge of Applications
7.2.1. Basic Knowledge Criticality
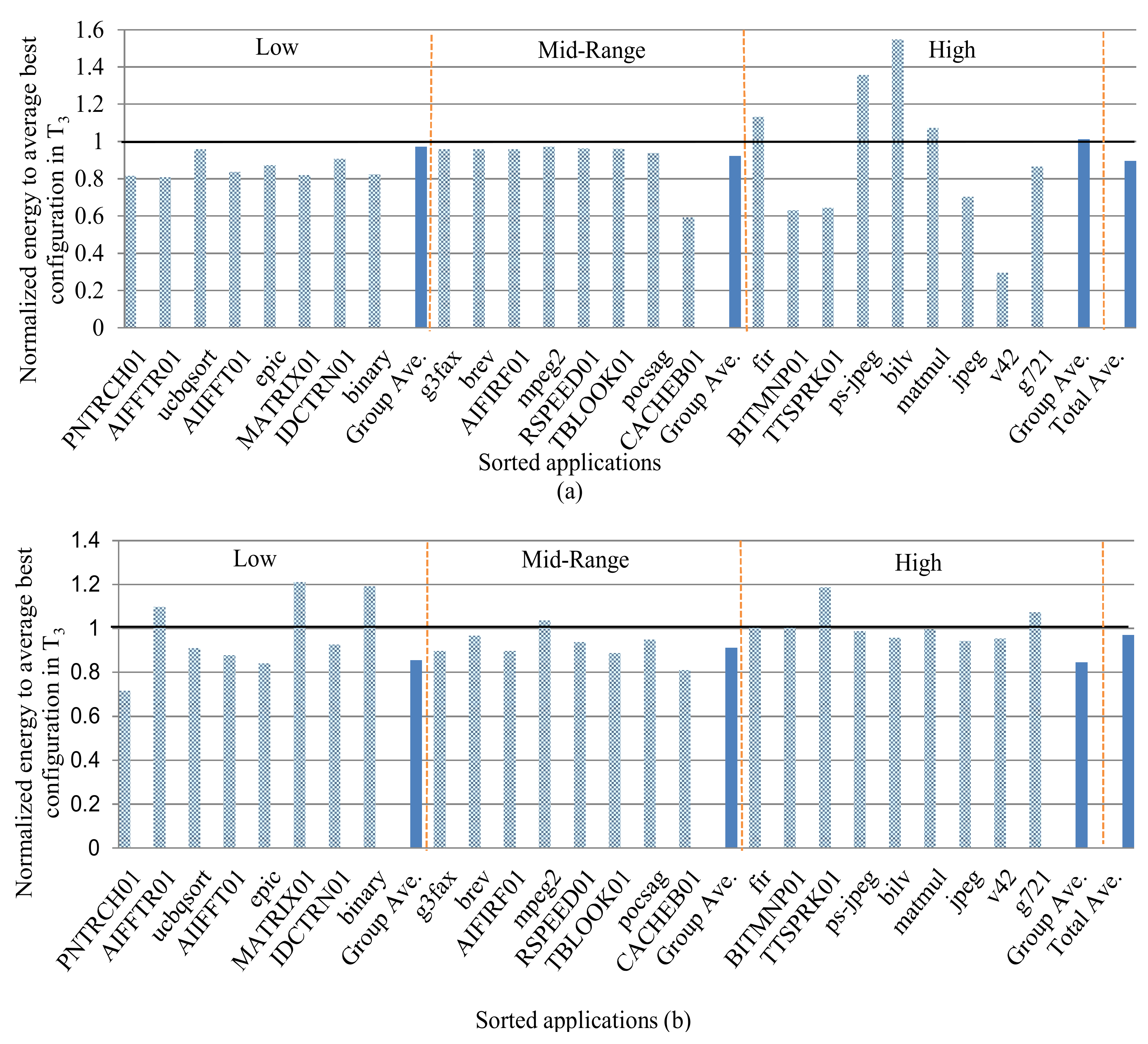
Figure 5a,b depict the instruction and data cache energy consumptions, respectively, for test set applications for the low, mid-range, and high miss-rate groups (ordered similarly to
Figure 1) normalized to
ᴪ, which is the average of all of the applications’ energies using
sb ϵ
S–selected using
T3–for all subset combinations for
T3. 1.0 denotes
T3’s baseline, where normalized energies below 1.0 represent an energy improvement (i.e., an increased subset quality) as compared to
T3. On average over all miss-rate groups, the basic classification-based training sets increased the energy savings by 10.4% and 3.1% compared to
T3 for the instruction and data caches, respectively. Analyzing the instruction and data caches’ normalized energy consumption variances revealed that the instruction cache energy consumption had a higher variance than the data cache, 0.058 and 0.013, respectively.
The data cache’s lower variance is expected since applications with similar data cache miss-rates indicate similar cache requirements. Thus, grouping anticipated applications into basic classification-based groups yields less varied energy savings.
We extended the analysis of
Figure 5 to determine the subset quality if the subsets and test set applications belonged to different miss-rate groups. Using similar normalization as in
Figure 5, we analyzed the quality of a subset selected using applications from one miss-rate group and tested it with applications from a different miss-rate group. The data cache results revealed significant increases in energy consumption for the test set applications as compared to
T3. For example, executing high miss-rate test applications using a subset selected using low and mid-range miss-rate training applications
increased the energy consumption by as much as 640% and 190%, respectively, as compared to
T3, while executing high miss-rate test applications with a subset selected using high miss-rate training applications
reduced energy consumption by 20% as compared to
T3. The instruction cache results revealed a smaller increase in energy consumption. For example, executing high miss-rate test applications with a subset selected using low and mid-range miss-rate training applications increased the energy consumption by as much as 290% and 130%, respectively, as compared to
T3.
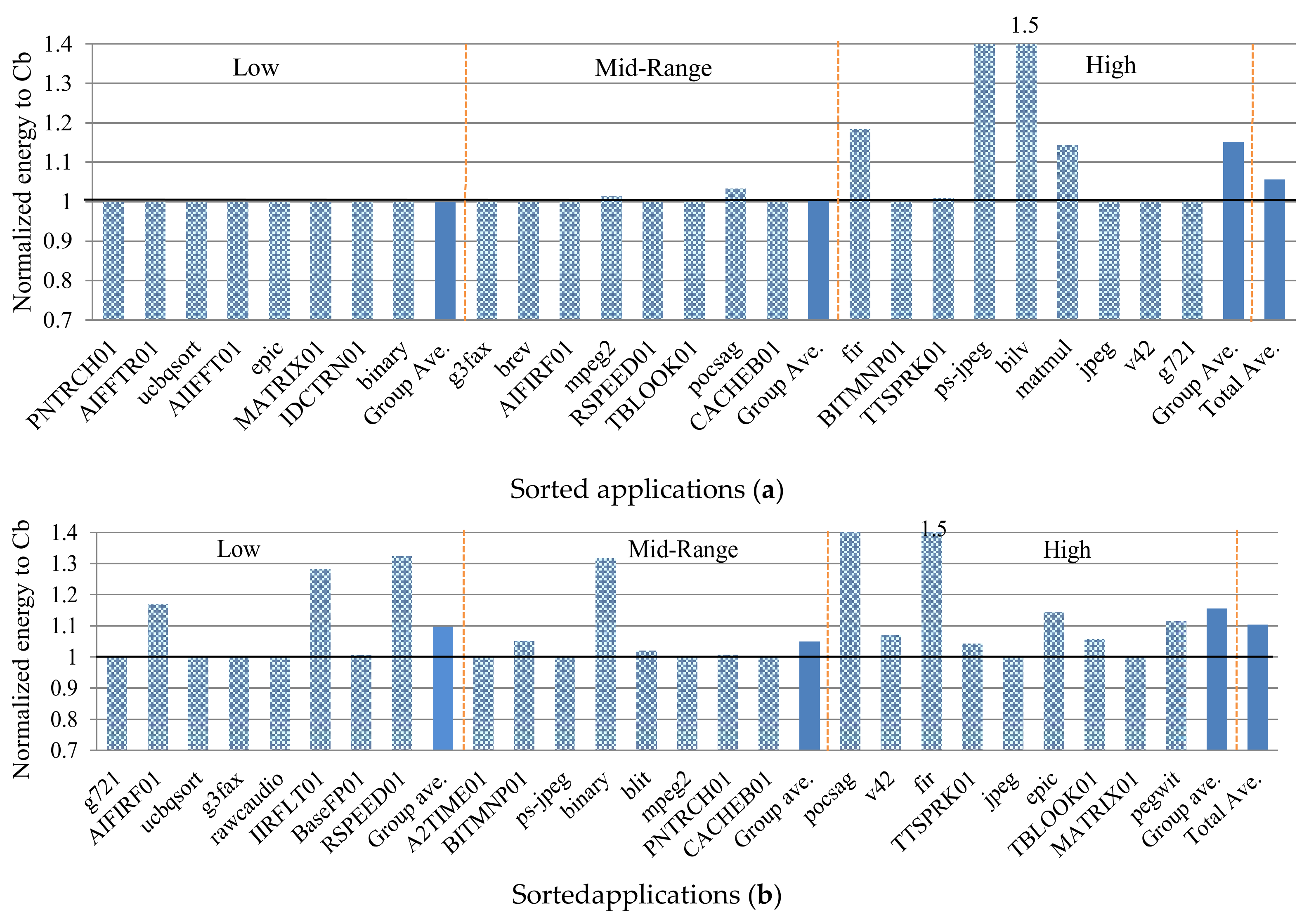
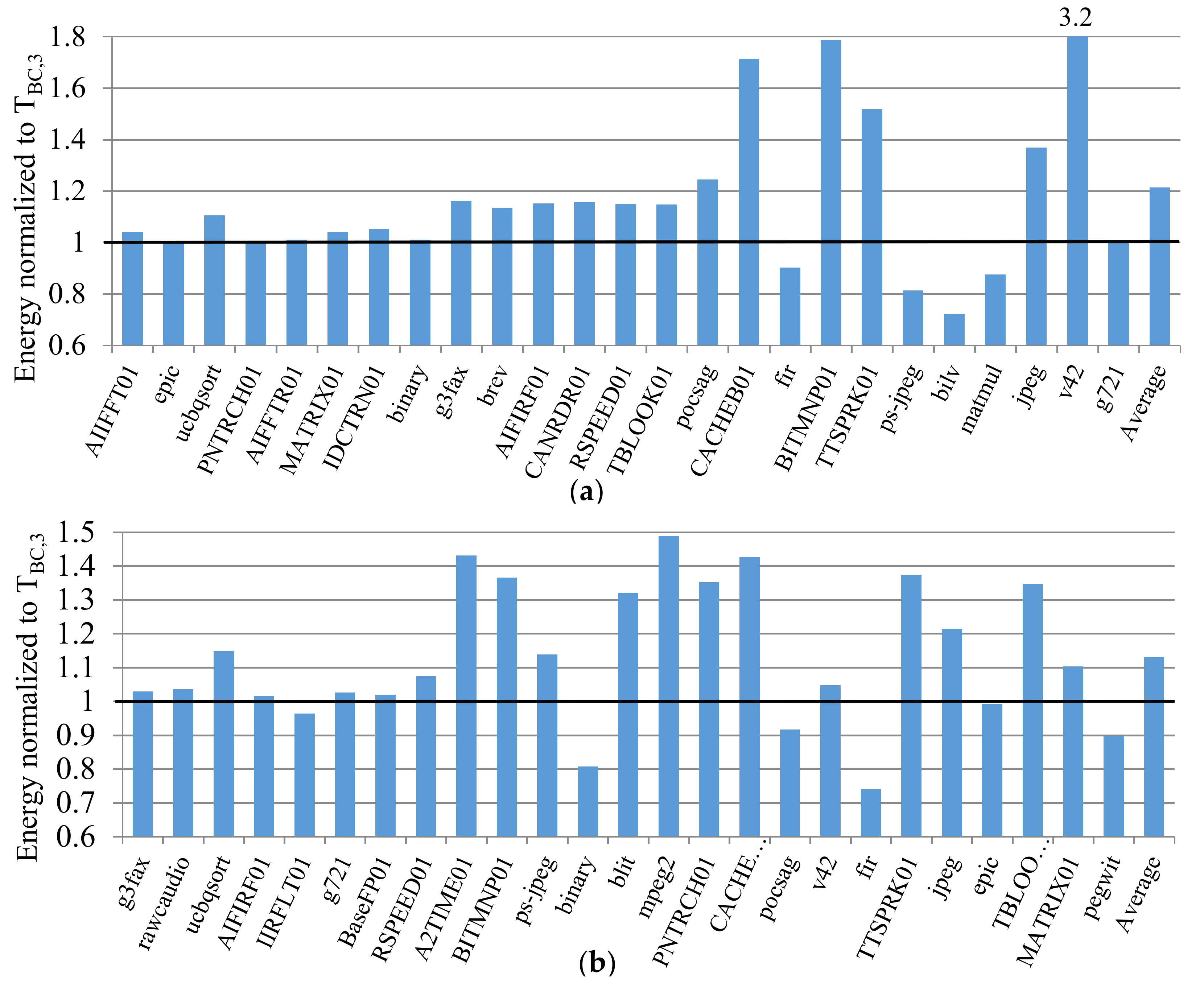
Figure 6 depicts the applications’ energy consumptions using
sb ϵ
S–selected using
TBC,3–and normalized to
cb ϵ
C with the baseline at 1.0. The applications are sorted in ascending cache miss-rate order from left to right with demarcations showing the low, mid-range, and high miss-rate groups. The averages are shown for each group (group average) and across all groups (total average). A normalized energy over 1.0 is an increase in energy consumption as compared to the best configuration. For the low and mid-range miss-rate groups, the average energy increases were similar, 0% and 0.05%, respectively, but the energy increase was much higher for the high miss-rate group, 14.8%. The data cache high miss-rate group’s average was similar, 15%, but the low and mid-range miss-rate groups’ averages were much higher, 9.7% and 4.9%, respectively. Although the total average energy increase for the instruction cache was smaller than for the data cache—5.6% and 10.2%, respectively—the instruction cache’s average energy range was 11% higher than the data cache’s energy range: 0–62% versus 0–51%, respectively.
Additionally, we compared the average energy increases with subsets selected using TBC,3 and T3 as compared to cb ϵ C. The analysis revealed that, on average, the subsets selected using TBC,3 revealed 32.5% and 6.5% more energy savings when compared to the subsets selected using T3, for the instruction and data caches, respectively.
7.2.2. Classification Method Impact
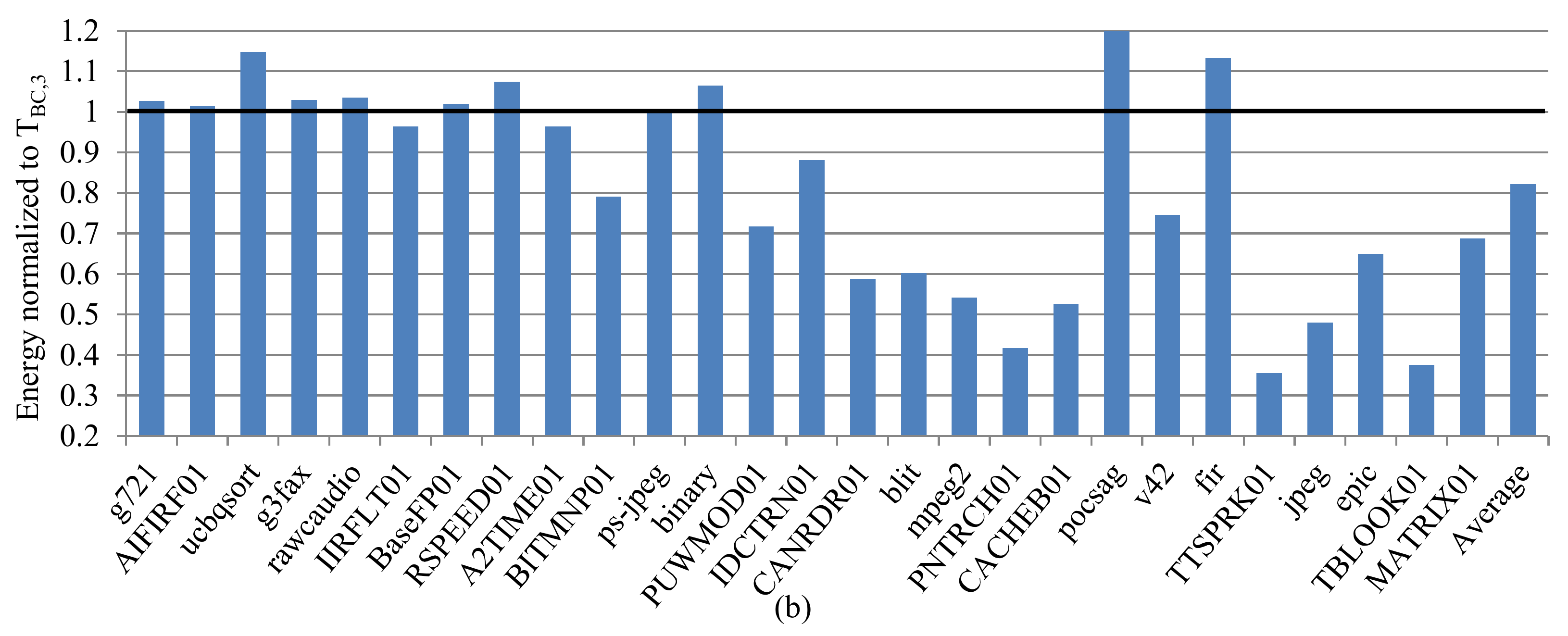
Since we used three classes in hierarchical classification to provide a fair comparison with basic classification, we compared the subset quality for each method using the subsets from these classes.
Figure 7a,b depict the average energy consumption of the test applications
Qi using
sb ϵ
S–selected using
THC,3–and normalized to the energy consumption of the test applications using
sb ϵ
S–selected using
TBC,3–for the instruction and data caches, respectively. A value of 1.0 denotes the baseline for
TBC,3, where normalized energy below 1.0 represents an energy improvement as compared to
TBC,3.
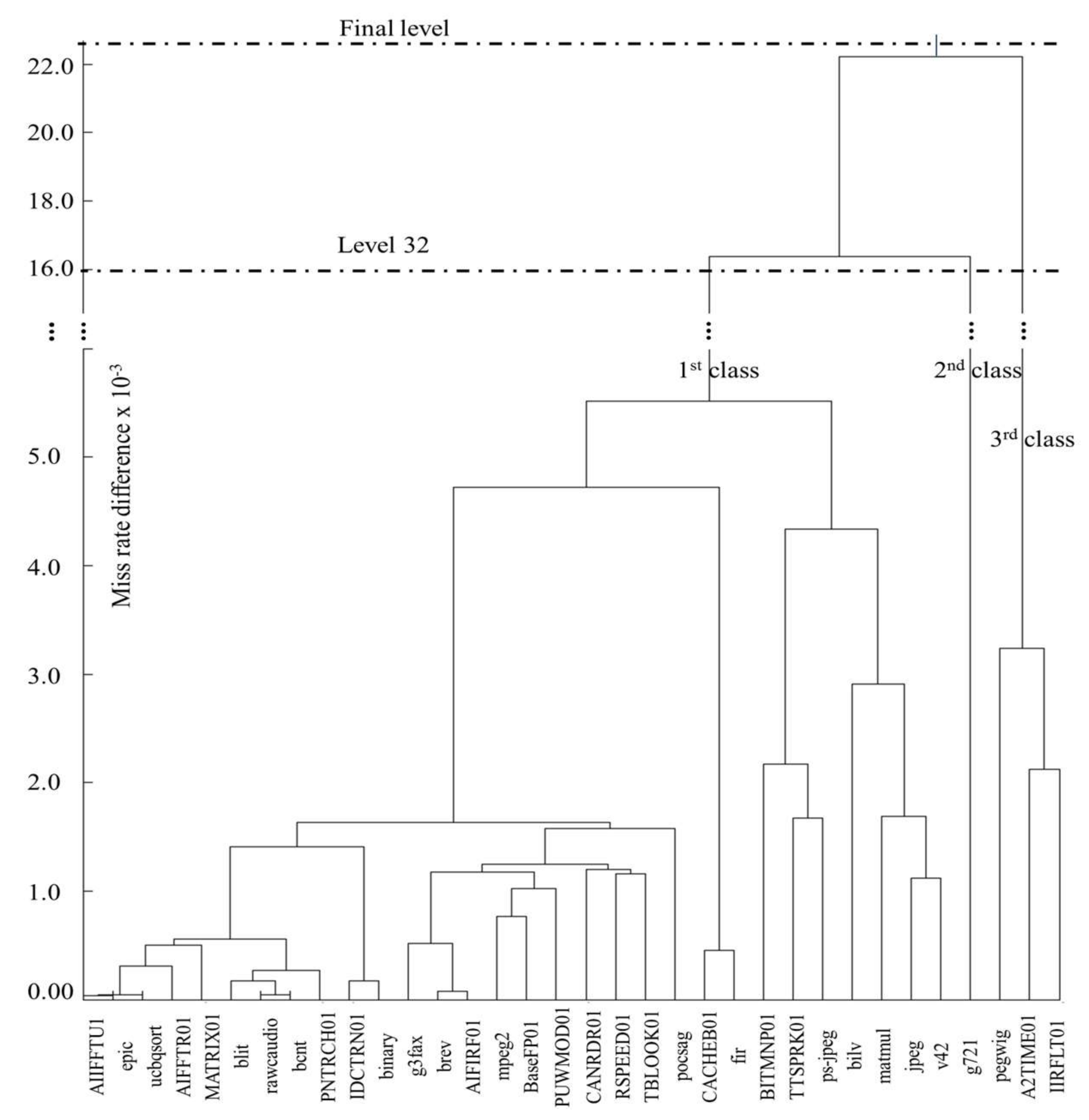
The hierarchical classification’s subsets both improved and degraded the energy consumption across different applications. However, on average, the energy consumption degraded by 21.3% and 13.1% for the instruction and data caches, respectively. For the three-class level in the dendrogram in
Figure 2, the hierarchical clustering classified thirty applications in one class compared to the basic classification, which classified eleven of these applications in the low miss-rate class, eleven in the mid-range miss-rate class, and the remaining eight in the high miss-rate class. Hierarchical clustering resulted in one subset adhering to thirty applications’ disparate hardware requirements, while the basic classification resulted in three subsets to achieve similar adherence.
To validate the class size’s impact on subset quality, we evaluated the quality of a subset of a small class using disjoint applications from a larger class. We evaluated the subset
S—selected using
TBC,3—for the low miss-rate class using disjoint test applications from the 1st class of
THC,3 (i.e., the 27 disjoint applications).
Figure 8a,b depict the instruction and data cache’s energy consumption, respectively, for these test applications using
sb ϵ
S–selected using
THC,3–and normalized to the energy consumption of
sb ϵ
S–selected using
TBC,3–for the low-range class. On average, the hierarchical classification subset resulted in a 2.9% and 17.9% improvement in the energy consumption for the instruction and data caches, respectively. Since the basic classification used only three training applications to determine the
S–selected using
TBC,3–for the low miss-rate class, the quality of this subset is high only for the test application from the low miss-rate class.
Additionally, comparing this analysis to our analysis in
Section 7.1, we observe that the subset quality does not necessarily deteriorate when used for larger application classes. A specific training set (e.g., the three training applications when using basic classification) resulted in a high-quality subset for test applications
Qi of the same class, but in very low quality subsets for test applications
Qi from other classes (e.g., the mid-range or high miss-rate classes). However, a subset determined by hierarchical classification for the 1st class was of higher quality for a larger number of applications (30 applications). This is due to the hierarchical classification’s intrinsic of grouping applications with similar hardware requirements (i.e., ‘
single distance’). Thus, the classification method that dictates the similarity of application hardware requirements, rather than the class size, has a higher impact on subset quality. Basic classification results in high-quality subsets per class, for small classes (e.g., the ten-application class). However, hierarchical classification produced a higher quality subset for a larger class (e.g., the thirty-application class), compared to the basic classification.
8. Speedup Results and Analysis
To quantify the design-time effort, we evaluated the speedup of our subset selection algorithm, as compared to prior work (T34), the impact of the subset size on the performance of our algorithms, the overhead associated with our classification algorithms, and the subset quality-speedup tradeoff. We performed our speedup analysis of our algorithms for the data and instruction caches. However, we obtained identical results, since the execution times of our algorithms are dependent on the training application set size and not the type of cache (instruction or data). For brevity, we discuss the results of our algorithm’s speedup analysis of the data cache.
8.1. Subset Selection Speedup
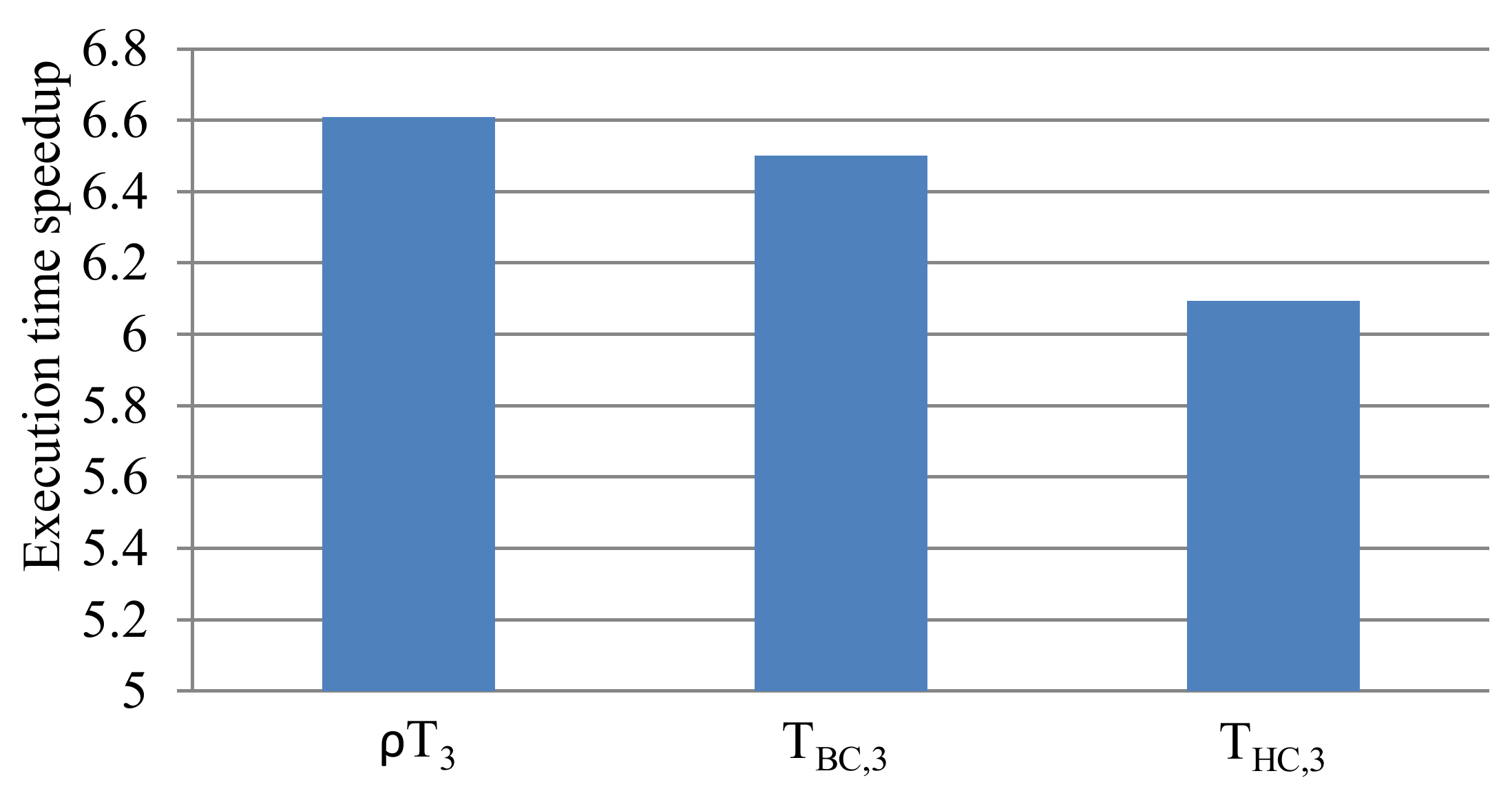
Since
T3 provided the best tradeoff between the training set size and energy savings, we performed our speedup analysis on subsets of the size 3:
ρT3,
TBC,3, and
THC,3. To compare the performance of Algorithm 1 to prior work, we used the execution time of Algorithm 1 to obtain the configuration subsets for
ρT3,
TBC,3, and
THC,3 and normalized the values to the execution time of prior work.
Figure 9 depicts the normalized results, where a value of 1.0 denotes the baseline execution time and the normalized execution times above 1.0 represent a speedup, compared to prior work. The results revealed that using Algorithm 1 explored the subset design space and determined a subset as much as 6.6, 6.5, and 6.1X faster for
ρT3, TBC,3, and
THC,3, respectively, compared to prior work. Since Algorithm 1 used an application-configuration energy matrix as an input and calculated the average energy increase
µΔ for all applications in that matrix, the number of training applications evaluated had a large impact on Algorithm 1’s execution time.
Furthermore, to evaluate the performance variations of Algorithm 1 for ρT3, TBC,3, and THC,3, we normalized the execution times of Algorithm 1 for TBC,3 and THC,3 to the execution time of Algorithm 1 for ρT3. The results revealed that Algorithm 1 explored the subset design space 1.69% and 8.47% slower for TBC,3 and THC,3, respectively, compared to ρT3. Our code instrumentation accounted the discrepancies to the overhead required by Algorithm 1 to navigate the application-configuration energy matrix to select the training set applications. Although Algorithm 1 needed three applications for each execution, randomly selecting three training applications required less time than specified applications in a given class/group. We emphasize that these variations are negligible compared to the speedup obtained, as compared to prior work.
To further evaluate the training set size impact on the speedup, we analyzed the execution time of Algorithm 1 to select subsets of various sizes. Since the speedups of ρT3, TBC,3, and THC,3 are similar, analyzing the speedup of all ρT(i), where i ϵ [1–10, 17] also provides insight into the speedup for TBC,i and THC,i. We normalized the execution times of Algorithm 1 with ρT(i) for i ϵ [1–10, 17] to prior work and evaluated the correlation between the training application set size and speed up.
Figure 10 depicts the speedups for Algorithm 1, using varying training set sizes normalized to the execution time of prior work. For sets with one application (
T1 and 2nd class in
THC,3), Algorithm 1 used one application and explored the design space 7.8X faster as compared to using the complete application set
A. Alternatively, for sets with 17 applications, Algorithm 1 explored the subset design space and determined a subset as much as 1.5X faster, compared to using the complete application set
A. Furthermore, the correlation analysis revealed a −0.90 correlation factor between the set size and the speedup; the smaller the size, the higher the speedup; and that the correlation is not perfectly linear and saturates for training sets with sizes above 17. This result suggests that for a potentially very large design space, a significant speedup can be obtained for training sets that are less than half the size of the entire application set. However, using a very small training set size can result in lower quality configuration subsets (
Section 7.2).
8.2. Classification Algorithm Speedup
Since prior work did not do any classification, we juxtaposed the time it required for our basic and hierarchical (Algorithm 2) classification algorithms to execute and classify the applications.
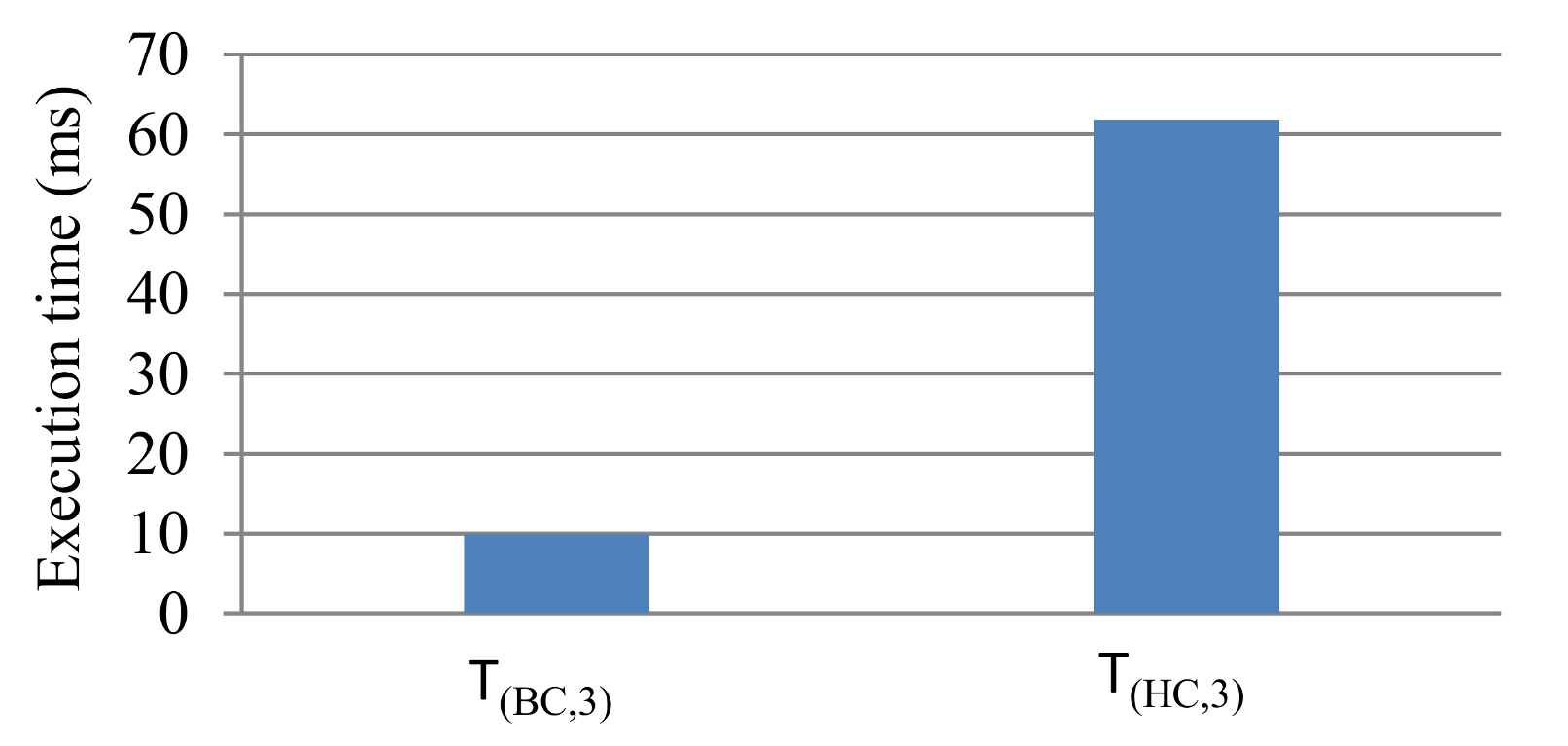
Figure 11 depicts the raw average execution times in milliseconds for the basic classification and hierarchical classification to select three training applications that are used in Algorithm 1 as the training application. We used a machine with an x86 core that ran with a clock speed of 1.2 GHz and performed the measurement ten times and calculated the average execution time. The results revealed that, on average, Algorithm 2 required 62 ms to execute while the basic classification required 10 ms. Comparatively, hierarchical classification is 6.2X slower than basic classification. Although both algorithms select 3 applications out of 34, the basic classification algorithm required a shorter execution time since basic classification only sorts the applications once, while Algorithm 2 iteratively merges applications into classes of the closest Euclidean distance.
This result suggested that the distance/classification metric (Euclidean, city-block, Chebychev, etc.) had an impact on Algorithm 2. Subsequently, Algorithm 2 is likely to execute slower for a design space with higher dimensions (application performance, code density, compatibility, etc.) that require a high-dimension distance metric.
8.3. Classification Methods Speedup versus Subset Quality
Our experiments also proved that a design space subset can be characteristically determined, rather than application-specifically determined, thus, easing subset selection based on generalized characteristics rather than application specifics. Alternatively, hierarchical clustering required the application miss-rates in order to calculate the distance between application hardware requirements and subsequently classify the applications. However, hierarchical classification can determine the cutoff miss-rate for each class using application traces, mini-applications, kernel applications, etc. and thus, no a priori knowledge of exact applications is required.
These basic classification training set results illustrate that a priori knowledge of the general application domain’s miss-rate characteristics can significantly enhance subset quality. We emphasize that exact miss-rate analysis is not required and a simple miss-rate range classification (i.e., low, mid-range, high) shows appreciable subset quality improvements with greater improvement potential if the designer has more anticipated application characteristic information. Algorithm 2, for instance, demonstrated a higher subset quality, with an average of 17.9% (
Figure 8), at the cost of a slower execution time, as much as 6.2X (
Figure 11), as compared to the basic classification algorithm.
Since classification metrics have the largest impact on Algorithm 2 (
Section 8.2), Algorithm 2 will require a longer execution time for design spaces with high dimensions, compared to the basic classification algorithm. However, high dimensional design spaces represent more disparate hardware requirements that could not be realized with the basic classification algorithm and hierarchical classification produced a higher quality subset for a large set of applications that had disparate hardware requirements compared to the basic classification (
Section 7.2.2). The subset-quality-execution time tradeoff provides the designer with options to meet the required design constraints.
9. Conclusions and Future Work
Configurable caches enable the cache hierarchy to adapt to varying application-specific requirements to reduce energy consumption. However, highly configurable caches which provide a myriad of cache configurations for highly disparate application requirements, require potentially prohibitive design space exploration time. To reduce the design space exploration time, we evaluated cache configuration design space subsetting using a set of training applications and evaluated the subsets’ qualities in terms of energy savings potential using a disjoint test set rather than the complete, unsubsetted design space. Our results showed that randomly-selected application training sets can significantly reduce the design space to small, high-quality configuration subsets, and using basic classification-based training sets can increase the subsets’ qualities. These analyses enable designers to harness the large energy savings potential of configurable caches for both general and domain-specific application requirements, with minimal design-time effort and only a general knowledge of the anticipated applications.
Our results also revealed that hierarchical classification (Algorithm 2) requires longer execution time. However, it is favorable when hardware resources are scarce; one subset can adhere to more application’s hardware requirements, compared to the basic classification. Whereas both classification methods require application miss-rates to determine the application’s class, both algorithms alleviate the necessity of profiling new, unknown applications for all configurations in the design space; a simple profiling on a base configuration, for instance, provides a basic knowledge of the application’s hardware requirements, and thus the application’s class.
Future work includes investigating different classification methods that consider application behavior, such as computation and data movements (linear, n-body simulation, spectral methods, and so on) and additional application statistics, such as static code analysis, instruction count, clock cycles, and so on. Since the order of which the algorithm traverses the design space dictates the pruned configurations, using these additional statistics in a multidimensional space (i.e., statistic per dimension space), we plan to investigate the impact of design space exploration algorithms in determining Pareto optimal subsets.