A Comprehensive Approach to Instruction Tuning for Qwen2.5: Data Selection, Domain Interaction, and Training Protocols

Abstract

Instruction tuning plays a pivotal role in aligning large language models with diverse tasks, yet its effectiveness hinges on the interplay of data quality, domain composition, and training strategies. This study moves beyond qualitative assessment to systematically quantify these factors through extensive experiments on data selection, data mixture, and training protocols. By quantifying performance trade-offs, we demonstrate that the implicit method SuperFiltering achieves an optimal balance, whereas explicit filters can induce capability conflicts. A fine-grained analysis of cross-domain interactions quantifies a near-linear competition between code and math, while showing that tool use data exhibits minimal interference. To mitigate these measured conflicts, we compare multi-task, sequential, and multi-stage training strategies, revealing that multi-stage training significantly reduces Conflict Rates while preserving domain expertise. Our findings culminate in a unified framework for optimizing instruction tuning, offering actionable, data-driven guidelines for balancing multi-domain performance and enhancing model generalization, thus advancing the field by providing a methodology to move from intuition to systematic optimization.

1. Introduction

Supervised fine-tuning (SFT) has driven remarkable improvements for large language models (LLMs) in tasks like mathematical reasoning, code generation, and instruction following. While the concept of aligning models with curated examples is well-established, the efficacy of this process hinges on more than just the volume of data. Foundational work, such as Zhou et al. [1], has demonstrated that high performance is achievable with surprisingly small, high-quality datasets. This highlights a critical insight: the success of SFT is not merely a matter of scale, but a complex optimization problem governed by the interplay of three fundamental pillars: data selection [2], data mixture [3], and the training protocol [4]. Achieving peak model performance requires a systematic and coordinated optimization of these factors, yet their intricate interactions remain insufficiently explored.

Existing approaches to data selection diverge across multiple dimensions. While many methods have explored quality optimization from various perspectives—including diversity selection [5], data complexity selection [6], and instruction-following difficulty selection [7]—a comprehensive analysis and comparison of these approaches from the perspectives of data volume, domain composition, and model parameters remains scarce. Recent work by Dong et al. [3] systematically quantifies code-math conflicts in SFT, yet their analysis focuses on pairwise interactions rather than multi-domain synergies. Furthermore, while Gu et al. [8] establishes critical mixture ratios (CMRs) for continual pre-training, similar principles have not been validated in instruction tuning scenarios. The community still lacks systematic analysis on interactions within specialized domains themselves, particularly regarding dynamic trade-offs between conflicting capabilities.

To address these gaps, we investigate three core research questions through controlled experiments:

RQ1: Can different data selection methods result in different LLM model performances?

RQ2: How does scaling general and domain specific data (e.g., code vs. math) affect cross-domain performance?

RQ3: How can different training protocols mitigate multi-domain conflicts?

Our methodology builds on three research frontiers: (1) selection method compatibility, where we systematically compare the effects of Instag [5], Deita [6], and SuperFiltering [7]—along with four combination strategies—on both holistic and domain-specific performance; (2) domain mixture scaling, extending Gu et al.’s CMR framework [4,8] to quantify cross-domain impacts through dynamic interaction coefficients; (3) training protocol optimization, developing conflict mitigation strategies inspired by Dong et al.’s capability interference analysis [3]. Using the state-of-the-art Qwen2.5 model family as a representative case study, we systematically evaluate three data selection methods (Instag, SuperFiltering, Deita) and their four combination variants, four domain mixtures (general knowledge, mathematics, code, and tool use), and three training protocols (multi-task, sequential, multi-stage) across six capability dimensions: knowledge, mathematical reasoning, code generation, tool use, complex reasoning, and instruction following. We further quantify performance conflicts through two metrics: Cross-Impact Coefficients (CICs) for pairwise domain interactions, and Conflict Rate and Forgetting Rate for multi-domain trade-offs, formally defined in Methodology.

Key findings reveal fundamental trade-offs and optimization strategies: First, data selection methods exhibit domain-specific biases, with SuperFiltering achieving optimal balance by perplexity and instruction-following difficulty (IFD) score, while explicit selection methods, such as Instag for mathematics and Deita for code, induce higher capability conflicts exceeding 1.18%. Second, cross-domain analysis demonstrates near-linear competition between code and mathematics, with Cross-Impact Coefficients (CICs) ranging from 0.27 to 0.30 per 10 K data, while tool use data shows minimal interference (CIC < 0.05). Furthermore, multi-stage training—specialized data followed by general alignment—reduces Conflict Rates by 53% while preserving 96.8% of domain expertise. These findings establish a unified framework for optimizing instruction tuning across competing objectives, offering actionable guidelines for balancing multi-domain performance.

2. Related Works

Data Selection research focuses on optimizing instruction data quality through four paradigms: (1) metric-based systems combining linguistic features [9]; (2) self-supervised difficulty assessment [2]; (3) LLM-powered filtering via quality scoring [10] and complexity balancing [6]; and (4) hybrid frameworks integrating reward models [11]. While curated 5–15% data achieves GPT-4-level alignment [1], challenges remain in evaluation standardization [5] and computational efficiency [7], with emerging solutions proposing lightweight architectures [4].

Task Composition studies reveal task mixing’s dual effects: diversity enhances generalization [12,13] but induces conflicts through distribution discrepancies [3]. Mathematical reasoning shows synergistic improvements at small scales but degrades with excessive data [3], prompting dynamic selection methods via gradient similarity [14] and representation alignment [15]. While expert ensembles offer alternatives [16], unified models dominate due to efficiency advantages, necessitating systematic frameworks to balance capability trade-offs [17].

3. Methodology

We conduct full-parameter supervised fine-tuning on the Qwen2.5-3B/7B-base model to systematically investigate the impact of data selection, data mixture, and training protocol on model performance. The training data encompasses four domains: general domain, where there are 1.45 M samples from Infinity Instruct-Gen (0729) (https://huggingface.co/datasets/BAAI/Infinity-Instruct (accessed on 8 December 2024)), integrating open-source datasets like Alpaca (https://huggingface.co/datasets/tatsu-lab/alpaca (accessed on 8 December 2024)) and BELLE (https://huggingface.co/BelleGroup/BELLE-on-Open-Datasets (accessed on 8 December 2024)) for open-domain QA, multi-turn dialogue, and text summarization; code domain, which is 1 M code snippets in programming languages such as Python, Java, and JavaScript, sourced from the InfInstruct-7M-Code; math domain, which includes 800 K competition-level and daily math problems from MATH and GSM8K with multi-step reasoning annotations; and tool use domain, which contains 150 K structured API workflows from diverse sources including ToolACE, UltraTooland SealTools, etc. As a result, a mixed-domain corpus is constructed with 500 K general-domain samples and 450 K domain-specific data in which code, math, and tool data contributes 150 K equally.

Model evaluation employs the OpenCompass framework, spanning six capability dimensions: knowledge (MMLU and CMMLU), mathematical reasoning (MATH and GSM8K), code generation (HumanEval and MBPP), tool invocation (Teval), instruction compliance (IFEval), and complex reasoning (BBH).

3.1. Data Selection

We systematically investigate the impact of three data selection methods and their combinatorial variants on model capabilities. These methods were chosen as they represent three distinct and influential paradigms in data filtering: label diversity (Instag), instruction-following difficulty (SuperFiltering), and quality-complexity scoring (Deita). These three provide a foundational comparison of core selection philosophies, allowing us to analyze their fundamental trade-offs.

Core Data Selection Methods

Instag [5] employs a fine-grained tag system to prioritize samples that maximize label diversity, selecting data that introduces novel semantic intents. SuperFiltering [7] leverages the instruction-following difficulty (IFD) metric, calculated as the ratio between the conditional perplexity of generating a response given an instruction $P_{\theta }\left(A\right|Q)$ and the standalone response perplexity $P_{\theta }\left(A\right)$, to identify high-value training samples. Deita [6] utilizes a dual-criteria scoring model trained on LLaMA-13B, evaluating both instruction complexity (0–5 scale) and response quality (0–5 scale).

• Instag (Label Diversity Filtering)

The method leverages Infinity Instruct’s hierarchical tag system, focusing on fine-grained secondary tags (e.g., “multi-step equation solving”, “API parameter validation”). The workflow is as follows:

• Sort 500,000 data samples in descending order based on the number of tags per sample (higher tag counts indicate greater task complexity).
• Initialize an empty label set. Iterate through the sorted data.
• Retain a sample if its tags expand the current label set (i.e., introduce new tags). Skip samples whose tags are fully covered by the existing set (implying redundant or less complex tasks).
• Repeat until 50 K samples are selected.

• SuperFiltering (Instruction-Following Difficulty Filtering)

Samples are selected using the instruction-following difficulty (IFD) metric:

$$\mathrm{IFD}(Q,A)={\displaystyle \frac{P_{\theta }\left(A\right|Q)}{P_{\theta }\left(A\right)}},$$

where $P_{\theta }\left(A\right|Q)$ is the conditional perplexity of generating the response A given instruction Q, and $P_{\theta }\left(A\right)$ is the standalone perplexity of A. To address distributional biases across languages and dialogue turns,

• Partition data into four categories: Chinese single-turn, Chinese multi-turn, English single-turn, and English multi-turn;
• Rank samples by IFD within each category and perform stratified sampling to retain the original distribution;
• Select 50 K samples in total.

• Deita (Complexity–Quality Dual Scoring)

Utilizes Deita’s pre-trained scoring model (based on LLaMA-13B) to evaluate instruction complexity ($S_{\mathrm{complex}}$) and response quality ($S_{\mathrm{quality}}$) on a 0–5 scale:

• Compute the average score $S_{\mathrm{avg}}={\displaystyle \frac{S_{\mathrm{complex}}+S_{\mathrm{quality}}}{2}}$.
• Partition data into four categories (language and turn count) to mitigate distribution shifts.
• Select the top 40 K high-score samples from each category and randomly sample 10 K samples from the remainder to balance simple-task performance.
• Combine results to form the final 50 K dataset.

3.2. Integrated Data Selection Methods

Apart from the above three single data selection methods, we also evaluate four integrated strategies, including Instag+Deita, Instag+SuperFiltering, Deita+SuperFiltering, and a full hybrid approach. All filtering strategies selected 50 K samples from a 500,000 general-domain data pool, with a control group using random sampling.

• Instag+Deita (Label-Score Hybrid)
  • Normalize Instag’s tag counts ($N_{\mathrm{tags}}$) and Deita’s average scores ($S_{\mathrm{avg}}$) separately using min–max scaling.
  • Calculate fused scores: $S_{\mathrm{fusion}}=0.5\times {\tilde{N}}_{\mathrm{tags}}+0.5\times {\tilde{S}}_{\mathrm{avg}}$.
  • Sort data by $S_{\mathrm{fusion}}$ in descending order and apply Instag’s label set expansion strategy to select 50 K samples.

• Instag+SuperFiltering (Label-Perplexity Hybrid)
  • Normalize Instag’s tag counts ($N_{\mathrm{tags}}$) and SuperFiltering’s IFD values.
  • Calculate fused scores: $S_{\mathrm{fusion}}=0.5\times {\tilde{N}}_{\mathrm{tags}}+0.5\times \widetilde{\mathrm{IFD}}$.
  • Sort data by $S_{\mathrm{fusion}}$ in descending order and filter using Instag’s label set expansion.

• Deita+SuperFiltering (Score-Perplexity Hybrid)
  • Rank samples by Deita’s $S_{\mathrm{avg}}$ and SuperFiltering’s IFD in descending order, obtaining percentile ranks ${\mathrm{Rank}}_{\mathrm{deita}}$ and ${\mathrm{Rank}}_{\mathrm{super}}$.
  • Calculate combined ranks: ${\mathrm{Rank}}_{\mathrm{fusion}}={\displaystyle \frac{{\mathrm{Rank}}_{\mathrm{deita}}+{\mathrm{Rank}}_{\mathrm{super}}}{2}}$.
  • Select the top 50 K samples by ascending ${\mathrm{Rank}}_{\mathrm{fusion}}$.

• Instag+Deita+SuperFiltering (Full Hybrid)
  • Rank samples by Deita’s $S_{\mathrm{avg}}$ and SuperFiltering’s IFD separately.
  • Calculate average percentile ranks: ${\mathrm{Rank}}_{\mathrm{avg}}={\displaystyle \frac{{\mathrm{Rank}}_{\mathrm{deita}}+{\mathrm{Rank}}_{\mathrm{super}}}{2}}$.
  • Sort data by ascending ${\mathrm{Rank}}_{\mathrm{avg}}$ and apply Instag’s label set expansion to select 50 K samples.

• Note: All methods were applied to a 500 K general-domain pool, with fixed training parameters (Qwen2.5-3B-Base, 3 epochs, learning rate of 3 × 10⁻⁵).

Conflict Rate (CR) Metric

While methods such as gradient similarity analysis provide deep, white-box insights into capability conflicts, they are often computationally intensive and require access to model internals. To offer a practical, black-box alternative for high-level performance auditing, we define the Conflict Rate (CR) metric. It is designed to be a lightweight, output-based indicator that allows practitioners to rapidly quantify the trade-offs between different capabilities using only benchmark results. Building on the systematic evaluation of model performance across different data selection methods, we further define the Conflict Rate (CR) metric to quantify the impact of various filtering strategies on model capability conflicts:

$$\mathrm{CR}={\displaystyle \frac{{\sum }_{i\ne j}\frac{max(0,M_i^{\mathrm{base}}-M_i^{\mathrm{new}})}{M_i^{\mathrm{base}}}}{\frac{M_j^{\mathrm{new}}-M_j^{\mathrm{base}}}{M_j^{\mathrm{base}}}}}\times 100\%$$

(1)

where $M_j$ and $M_i$ are performance metrics for the target and non-target domains, respectively. CR > 100% indicates severe conflicts.

3.3. Data Mixture

We also investigate the impact of data mixture strategies for large language models through independent scaling experiments across four domains: general, code, mathematics, and tool use.

3.3.1. Scaling Strategy and Experimental Design

We vary the size of data from either general or specific domains. General domain experimental groups incrementally scale data size from 50 K to 200 K (step size: 50 K) while maintaining fixed code, math, and tool use data at 10 K each, with the total data size ranging from 80 K to 230 K. Domain-specific experimental groups independently scale code, math, or tool use data (0 K, 2 K, 5 K, 10 K, 15 K, 20 K) while fixing general data at 100 K and non-target domains at 10 K each. A control group (general 100 K + code 10 K + math 10 K + tool 10 K) serves as the baseline for fair comparison.

The scaling increments were chosen to balance experimental granularity with computational feasibility; these intervals are large enough to induce measurable changes in model performance while keeping the total number of experiments manageable.

3.3.2. Cross-Impact Coefficient (CIC)

Similarly, to provide an accessible, model-agnostic tool for quantifying domain interactions without needing gradient-level analysis, we introduce the Cross-Impact Coefficient (CIC). This metric operates directly on performance scores, making it a practical instrument for rapid, data-driven decisions in tuning pipelines. To systematically analyze the impact of different data scaling ratios on model capabilities, we define the Cross-Impact Coefficient (CIC):

$${\mathrm{CIC}}_{X\to Y}={\displaystyle \frac{\Delta Y/Y_{\mathrm{base}}}{\Delta X/X_{\mathrm{base}}}}$$

(2)

where $\Delta X$ and $\Delta Y$ are data increments and performance changes for domains X and Y, respectively. Positive CIC values indicate synergy, while negative values denote competition.

3.4. Training Protocols

We further compare three supervised fine-tuning protocols: multi-task training, sequential training, and multi-stage training, to investigate the impact of data organization on capability acquisition and conflict mitigation. These experiments are conducted on the Qwen2.5-7B-Base model using full fine-tuning with a fixed dataset of 130 K samples (100 K of general domain, 10 K of code, 10 K of math, and 10 K of tool use).

3.4.1. Multi-Task Training Protocol

The multi-task training strategy serves as the baseline, where all data are randomly shuffled and trained for one epoch to simulate conventional mixed training.

3.4.2. Sequential Training Protocols

For sequential training, three predefined data-ordering schemes are implemented: (1) Special Towards General: the first 30 K samples (10 K code, 10 K math, 10 K tool use) precede 100 K general-domain data; (2) Hybrid Initialization: the initial 40 K samples are mixed with 10 K general data and 30 K specialized data, followed by 90 K general data; (3) Progressive Supplementation: the first 34 K samples blend partial specialized and general data, while the remaining 96 K include general data and supplementary specialized samples.

3.4.3. Multi-Stage Training Protocol

The multi-stage training strategy further divides sequential training into two phases: Stage 1 trains on the initial segment of a sequential scheme for one epoch and saves the intermediate checkpoint, while Stage 2 continues training on the remaining data. All training protocols adopt identical hyperparameters to ensure fair comparison.

3.4.4. Output Forgetting Rate (OFR)

To further analyze the impact of training protocols on capability retention, we define the Forgetting Rate (OFR) metric:

$$\mathrm{OFR}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\displaystyle \frac{M_{i,\text{stage1}}-M_{i,\text{stage2}}}{M_{i,\text{stage1}}}}\times 100\%$$

(3)

where $M_{i,\text{stage1}}$ and $M_{i,\text{stage2}}$ are capability scores after stage 1 and stage 2 training, respectively. OFR < 0 indicates capability enhancement.

4. Experiments

4.1. Data Selection Result Analysis

• Comparison of Single Methods

Table 1. Performance comparison of single data selection methods.

Method	MMLU	CMMLU	GSM8K	HumanEval	BBH	CR (%)
Random	66.3	72.6	75.5	68.3	55.6	–
Instag	67.4	72.0	78.3	64.6	55.8	1.67
Deita	64.9	72.3	71.1	73.2	56.4	1.18
SuperFiltering	66.9	72.7	76.2	69.5	57.3	0

CR = Conflict Rate, Defined in (1).

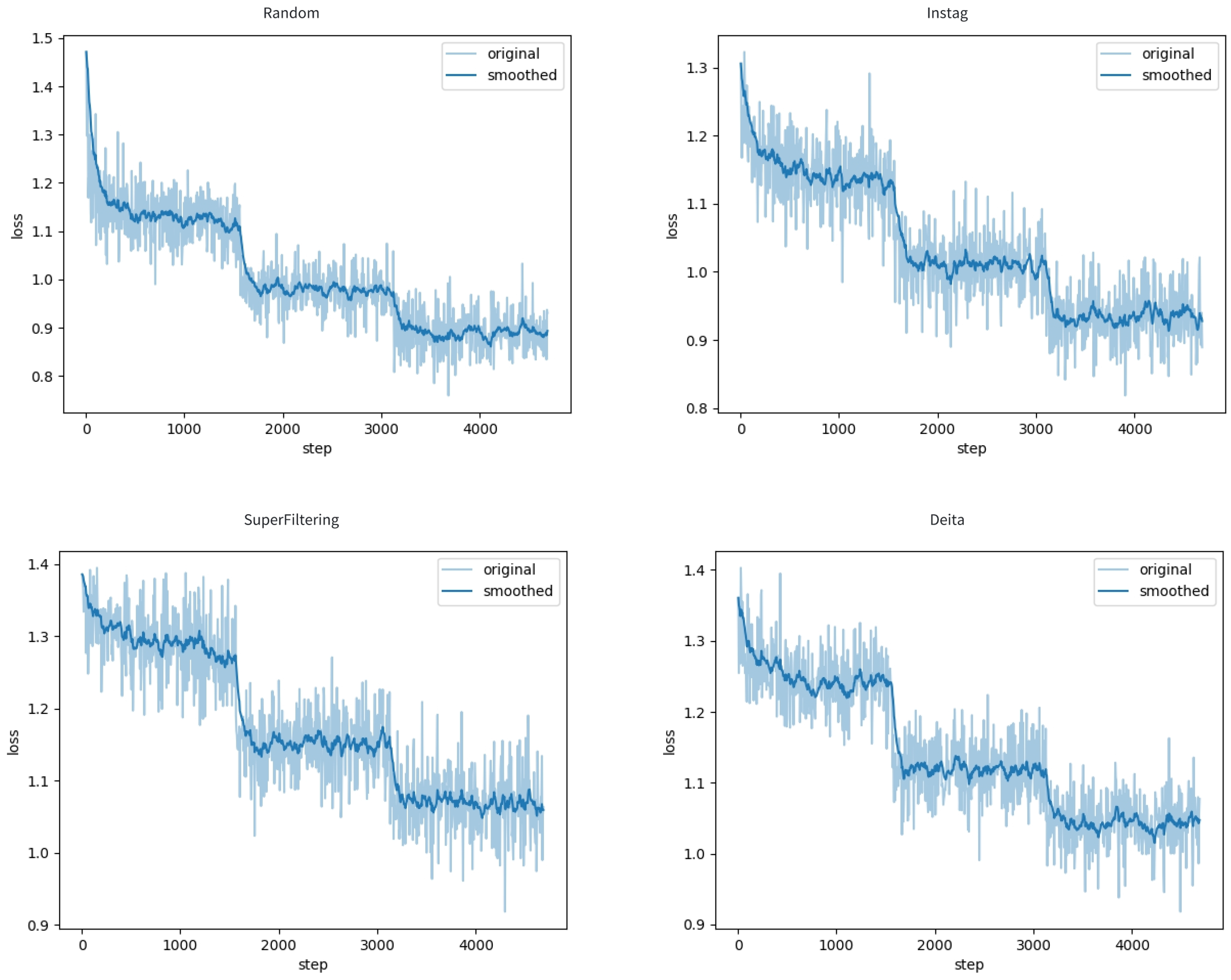
presents the performance comparison of individual selection methods across core capabilities. Figure 1 illustrates their respective training loss trajectories, while Figure 2 reveals fundamental selection biases through category distribution analysis.

As detailed in Table 1, all three methods—Instag, Deita, and SuperFiltering—demonstrate improved performance over random selection on specific benchmarks, albeit with distinct capability trade-offs. For example, Instag significantly enhances mathematical reasoning (GSM8K: +2.8 points), while Deita boosts code generation (HumanEval: +4.9 points) and SuperFiltering improves complex reasoning (BBH: +1.7 points).

Label distributions reveal paradoxes: Instag outperforms Random in mathematical reasoning despite fewer math-related labels, prioritizing task complexity over quantity. Conversely, Deita underperforms in mathematics despite comparable label counts, as its complexity scoring favors syntactic code features.

Training loss patterns reveal that SuperFiltering and Deita select more challenging samples, as evidenced by their higher initial and final losses compared to Random and Instag. As shown in Figure 1, all methods exhibit two abrupt loss drops indicating learning phase transitions, but only Random and Instag stabilize around 0.9, while SuperFiltering and Deita remain above 1.0, suggesting persistent difficulty in model convergence due to increased instruction-response complexity.

• Integrated Methods

Table 2. Performance comparison of hybrid data selection methods.

Method	MMLU	CMMLU	GSM8K	HumanEval	BBH	CR (%)
Random	66.3	72.6	75.5	68.3	55.6	—
Instag+Deita	66.9	72.3	74.2	64.6	55.9	9.1
Instag+SuperFiltering	68.1	72.1	75.5	69.5	55.9	0.26
Deita+SuperFiltering	67.2	73.0	76.2	69.5	55.5	0.14
Full Hybrid	67.7	72.7	73.4	67.1	55.9	2.19

CR = Conflict Rate, Defined in (1).

evaluates integrated selection strategies. Figure 3 compares their loss convergence patterns, and Figure 2 also reveals integrated methods’ fundamental selection biases through category distribution analysis.

Experimental results demonstrate that integrating Deita and Instag exacerbates domain conflicts, with the results underperforming in both individual methods. The inherent conflict arises from opposing selection criteria—Deita prioritizes code complexity while Instag emphasizes mathematical diversity. Combining SuperFiltering with either method partially mitigates this interference (Conflict Rate: 3.69→1.68), though at the cost of reduced domain specialization.

All integrated selection strategies fail to outperform individual methods, highlighting that naive combination of multiple selection criteria introduces conflicting optimization signals and compounded learning difficulty. As illustrated in Figure 3, hybrid methods consistently exhibit higher final losses and flatter descent curves, with the Deita and SuperFiltering combination reaching the highest terminal loss (1.1), indicating that merged selection logic preserves data complexity and hampers convergence.

4.2. Data Mixture Results Analysis

We analyze cross-domain interaction patterns through controlled scaling experiments across four domains (general, code, math, tool), and use Cross-Impact Coefficients (CICs) to quantify the conflict magnitude.

Table 3. General-domain scaling effects on core capabilities (Code/Math/Tool fixed at 10 K).

General (K)	MMLU	CMMLU	MATH	GSM8K	HumanEval	IFEval
50	74.50	80.40	47.42	80.74	78.66	59.35
100	74.49	80.23	46.92	80.97	80.49	56.37
150	74.41	79.96	47.40	83.32	78.05	58.34
200	74.15	79.87	47.14	81.05	75.61	58.93

shows the result when we only scale general domain data from 50 K to 200 K,

Table 4. Code-domain scaling effects (General = 100 K; Math/Tool = 10 K).

Code (K)	MMLU	GSM8K	MATH	HumanEval	MBPP	IFEval
0	74.54	82.64	48.74	73.78	63.60	57.60
2	74.72	82.79	48.72	78.66	61.60	58.03
5	74.57	82.49	47.86	79.27	61.00	57.95
10	74.49	80.97	46.92	80.49	62.40	56.37
15	74.76	81.05	46.90	78.66	62.00	50.00
20	74.35	78.92	46.04	81.10	59.20	57.61

CIC_code→math = 0.27/10 K; CIC_code→tool = 0.03.

,

Table 5. Math-domain scaling effects (General = 100 K; Code/Tool = 10 K).

Math (K)	MMLU	GSM8K	MATH	HumanEval	MBPP	IFEval
0	74.11	84.53	47.70	81.71	63.00	57.94
2	74.49	80.52	46.70	82.32	61.40	58.45
5	74.54	80.74	46.80	78.66	63.00	58.44
10	74.49	80.97	46.92	80.49	62.40	56.37
15	74.57	80.74	47.72	78.66	62.20	59.35
20	74.71	80.29	46.76	76.22	61.80	59.87

CIC_math→code = 0.25/10 K; CIC_math→tool < 0.05.

and

Table 6. Tool-domain scaling effects (General = 100 K; Code/Math = 10 K).

Tool (K)	Teval	MMLU	GSM8K	HumanEval	MBPP	IFEval
0	85.94	74.71	81.20	78.66	52.00	56.65
2	86.08	74.56	82.41	78.05	60.80	58.03
5	84.19	74.51	82.94	76.22	61.40	57.55
10	84.13	74.73	82.71	78.05	59.80	57.67
15	84.57	74.14	81.35	76.83	60.60	57.74
20	84.08	74.59	83.40	78.66	61.60	57.02

CIC_{tool→others} < 0.05 for all domains.

show the result when we only scale domain specific data, and Figure 4 shows the training loss curves.

• Analysis of General Data Scaling Effects

Experimental results demonstrate that scaling general-domain data has limited impact on knowledge retention, confirming foundational knowledge resides in pre-training. Code generation capability (HumanEval) peaks at 80.49 with 100 K general data, while mathematical reasoning (MATH) shows marginal fluctuations (±0.5), demonstrating general data’s role in complex instruction handling. Instruction-following capability (IFEval) exhibits near-linear improvement, confirming general data’s role in enhancing complex instruction handling.

• Cross-Domain Interference Patterns

The code and mathematics exhibit near-linear competition with asymmetric CIC values: code expansion reduces math performance (CIC = 0.27/10 K) more severely than vice versa (CIC = 0.55/10 K), reflecting their conflicting learning paradigms—syntactic pattern recognition versus symbolic reasoning. Tool data shows domain independence (CIC < 0.05) while improving tool invocation by 15.7%, attributed to structural simplicity and instruction compatibility. Mathematical performance plateaus beyond 15,000 samples, emphasizing data quality over quantity, whereas code generation benefits from scaled data despite interference effects.

• Training Dynamics Across Scaling Strategies

Training loss trajectories further highlight the contrasting effects of general versus domain-specific data scaling. As shown in Figure 4, increasing general-domain data leads to progressively higher stabilized loss, suggesting diminishing marginal utility and potential overfitting to redundant patterns. In contrast, scaling domain-specific data (code, math, tool) results in consistently lower final losses, indicating enhanced learning efficiency and better model convergence. These patterns reinforce the hypothesis that specialized data introduces more informative supervision, while excessive general data, defined in our experiments as quantities beyond 100 K samples, may dilute optimization signals, as evidenced by the performance degradation in code generation (HumanEval) when scaling from 100 K to 200 K samples (see Table 3).

4.3. Training Protocols Results Analysis

We compare three training protocols: multi-task, sequential, and multi-stage training.

Table 7. Performance comparison of training protocols. Conflict Rate (CR) quantifies non-target capability degradation per unit target improvement. Output Forgetting Rate (OFR) measures capability decay between stages.

Strategy and Order	MMLU	CMMLU	Math	GSM8K	HumanEval	MBPP	BBH	IFEval	Teval	CR (%)	OFR (%)
Multi-task	74.66	79.37	44.36	82.18	75.00	62.00	69.35	53.80	85.11	–	–
Seq: Spe→Gen	74.49	79.67	44.10	81.88	77.44	63.00	69.09	54.99	85.39	47.8	–
Multi-stage1: S→G	74.05	81.25	48.12	80.44	73.17	63.60	68.05	47.91	83.53	236.5	–
Multi-stage2: S→G	74.45	79.49	47.16	84.23	72.56	64.40	69.63	54.44	86.87	56.0	1.67
Seq: Hybrid Init	74.49	79.66	44.44	82.71	75.61	63.00	69.77	51.83	85.06	244.8	–
Multi-stage1: Hybrid	74.42	80.39	48.22	80.82	76.83	62.60	69.03	53.61	82.90	61.9	–
Multi-stage2: Hybrid	74.47	79.76	43.20	84.38	73.78	64.60	68.98	53.75	86.48	122.1	3.81
Seq: Prog. Supp	74.28	79.44	45.64	81.27	76.83	63.40	69.10	53.98	85.62	68.4	–
Multi-stage1: Prog.	74.51	80.23	47.80	79.30	78.66	63.20	69.38	53.22	84.65	68.6	–
Multi-stage2: Prog.	74.34	79.39	44.60	82.11	77.44	62.40	69.03	55.15	85.98	30.0	1.88

summarizes performance across eight dimensions with Conflict Rate (CR) and Forgetting Rate (OFR) metrics.

• Analysis of Training Protocols

Multi-stage training demonstrates superior capability balancing compared to other approaches. The Specific→General strategy achieves peak mathematical reasoning (GSM8K: 84.23) and code generation performance while reducing Conflict Rates by 76.3% compared to single-stage training. This validates the effectiveness of separating domain specialization and general alignment phases. Hybrid initialization strategies suffer from conflicting optimization signals, yielding 122.1% Conflict Rates due to premature mixing of general data. Progressive supplementation maintains parameter stability through controlled data reintroduction, limiting Forgetting Rates to 1.88% versus 3.81% in hybrid approaches.

• Analysis of Specific Capability

Distinct capability evolution patterns emerge during phased training. Mathematical reasoning shows improvement in basic arithmetic (GSM8K: +2.58) due to foundational math samples in general data, while complex problem-solving (MATH) declines, indicating forgetting of advanced mathematical skills. Code generation exhibits language-specific effects: Python tasks (MBPP) improve as general data predominantly contains Python samples, whereas multi-language synthesis (HumanEval) declines due to reduced exposure to diverse programming languages. These patterns highlight the selective impact of general data on different capability dimensions. Instruction compliance metrics (IFEval) and tool use (Teval) consistently benefit from general data integration, demonstrating +5.58 and +15.7% improvements, respectively. These patterns confirm the necessity of dynamic data ratio adjustments during different training phases.

5. Discussion

Our systematic investigation addresses three core research questions through controlled experiments, yielding actionable insights for instruction tuning optimization. While some of the high-level findings, such as the competition between code and math, may align with community intuition, the core contribution of this work lies not in the discovery of these phenomena, but in their systematic quantification and the establishment of an accessible, unified framework to manage them. By providing concrete metrics and protocols, we move beyond anecdotal evidence and provide practitioners with a structured methodology for balancing competing objectives.

Data Selection trade-offs (RQ1): Explicit selection methods (Instag, Deita) exhibit domain-specific biases due to their reliance on predefined criteria, with Instag favoring mathematics and Deita prioritizing code generation. SuperFiltering achieves optimal balance because its core metric—the ratio of conditional to unconditional perplexity (IFD)—is inherently domain-agnostic. Unlike methods that rely on explicit content tags or scoring models trained on specific data distributions, SuperFiltering identifies high-quality instructional data by measuring the pure informational value of an instruction for generating a response. Practical applications should align selection strategies with target domains: explicit methods suit specialized models, while implicit methods benefit multi-task balance. Combining multiple selections often induces metric conflicts, unless implemented in staged workflows.

Domain Interaction Dynamics (RQ2): Code and mathematics exhibit near-linear competition due to conflicting structural requirements—syntactic patterns versus symbolic reasoning. Tool data demonstrates minimal interference through structural simplicity and instruction compatibility. General data linearly enhances instruction following despite containing implicit domain conflicts. Practical mixtures should determine critical ratios for high-conflict domains through small-scale CIC analysis while freely expanding low-conflict domains like tool use.

Training Protocol Optimization (RQ3): Multi-stage training reduces the Conflict Rates by 53% through phased specialization–generalization. While the exact percentage reduction varies by data ordering, the trend of conflict mitigation was consistent across the tested scenarios. Initial domain-specific training establishes core capabilities, while subsequent general data integration enables synergy via parameter fine-tuning. Retaining 15% domain data during generalization phases preserves 96.8% specialized performance while enhancing instruction compliance. Strict phase separation proves crucial—even minimal cross-phase contamination triggers capability degradation. Progressive supplementation outperforms hybrid initialization by maintaining stable parameter updates through controlled data reintroduction.

These findings establish a three-pillar optimization framework: (1) target-aligned data selection, (2) CIC-driven domain mixing, and (3) phased training with conflict-aware scheduling. This approach balances specialization and generalization while revealing fundamental principles of capability interaction during instruction tuning.

6. Conclusions

This study establishes a systematic framework for optimizing instruction tuning by moving from intuition to quantification. Its key innovations are threefold. First, we introduce practical metrics—Conflict Rate and Cross-Impact Coefficient—to provide a quantitative language for capability trade-offs and domain interactions. Our analysis uses these metrics to precisely measure that (1) the implicit method SuperFiltering achieves optimal balance due to insensitivity to domain data, while explicit selection methods induce capability conflicts exceeding 1.18%; (2) code and mathematics exhibit near-linear competition, whereas tool data shows minimal interference; (3) multi-stage training reduces the Conflict Rates by 53% while preserving 96.8% domain expertise through phased optimization.

Based on these quantitative insights, we propose a three-step optimization protocol: (1) hierarchical data selection combining quality metrics and task criteria, (2) CIC-driven domain mixture ratios prioritizing low-conflict expansions, a practically beneficial approach that allows for efficient model improvement by enhancing a target capability with minimal risk of degrading other expensively acquired abilities, and (3) phased training isolating domain specialization before general alignment. This framework enables effective balancing of multi-domain performance while maintaining model generalization.

Future work should extend this framework to larger-scale models and advanced reasoning paradigms. These extensions will further advance both theoretical understanding and practical deployment of instruction-tuned LLMs.

7. Limitations

While this study provides valuable insights into SFT optimization, there are a few limitations: Scope of Experimental Validation: Our study is intentionally designed as a deep-dive case study on the Qwen2.5 model series (3B and 7B). This focused approach allows for a controlled and systematic analysis, isolating the effects of data and training protocols from architectural variables. However, we acknowledge that while the observed principles—such as the competition between code and math, and the benefits of multi-stage training—are likely tied to fundamental properties of transformer-based architectures, and the specific quantitative results may vary across different model families and larger scales (e.g., 70B+). Future work should validate whether the identified trade-offs and optimal ratios generalize to a wider range of models. Selection Method Coverage: Although we analyzed three representative data selection approaches, emerging techniques like reinforcement learning-based selection and LLM self-curation were not included. The combination strategies (e.g., weighted averaging) represent initial explorations rather than exhaustive optimizations of multi-criteria integration. Granularity of Mixture Analysis: The fixed 10 K-step scaling intervals in our data mixture experiments, while yielding statistically significant Cross-Interaction Coefficient (CIC) values ($0.22$–$0.30$), may obscure fine-grained interaction dynamics. We posit that a higher-resolution analysis, such as with 1 K-step increments, is necessary to resolve non-linear phase transitions (e.g., performance cliffs or plateaus). Identifying such inflection points is critical for optimizing data mixture ratios to maximize synergistic effects and pinpoint the onset of competitive interference. Theoretical Depth of Mechanisms: Our proposed metrics, Conflict Rate (CR) and Cross-Impact Coefficient (CIC), are designed as practical, output-based tools and are empirically effective. However, they are not intended to replace more theoretically grounded analyses like gradient similarity measurement or loss landscape visualization. While our metrics offer high accessibility and computational efficiency, a deeper theoretical investigation correlating these black-box indicators with the underlying white-box dynamics of parameter updates would be a valuable direction for future work.

These limitations highlight opportunities for future research while not diminishing the practical value of our findings. The established framework provides a robust foundation for subsequent investigations into scalable SFT optimization.