Enhancing Cryptographic Solutions for Resource-Constrained RFID Assistive Devices: Implementing a Resource-Efficient Field Montgomery Multiplier

Abstract

Radio Frequency Identification (RFID) assistive systems, which integrate RFID devices with IoT technologies, are vital for enhancing the independence, mobility, and safety of individuals with disabilities. These systems enable applications such as RFID navigation for blind users and RFID-enabled canes that provide real-time location data. Central to these systems are resource-constrained RFID devices that rely on RFID tags to collect and transmit data, but their limited computational capabilities make them vulnerable to cyberattacks, jeopardizing user safety and privacy. Implementing the Elliptic Curve Cryptography (ECC) algorithm is essential to mitigate these risks; however, its high computational complexity exceeds the capabilities of these devices. The fundamental operation of ECC is finite field multiplication, which is crucial for securing data. Optimizing this operation allows ECC computations to be executed without overloading the devices’ limited resources. Traditional multiplication designs are often unsuitable for such devices due to their excessive area and energy requirements. Therefore, this work tackles these challenges by proposing an efficient and compact field multiplier design optimized for the Montgomery multiplication algorithm, a widely used method in cryptographic applications. The proposed design significantly reduces both space and energy consumption while maintaining computational performance, making it well-suited for resource-constrained environments. ASIC synthesis results demonstrate substantial improvements in key metrics, including area, power consumption, Power-Delay Product (PDP), and Area-Delay Product (ADP), highlighting the multiplier’s efficiency and practicality. This innovation enables the implementation of ECC on RFID assistive devices, enhancing their security and reliability, thereby allowing individuals with disabilities to engage with assistive technologies more safely and confidently.

1. Introduction

The RFID assistive system represents a sophisticated integration of RFID technology and the IoT, aimed at enhancing the autonomy, safety, and quality of life for individuals with disabilities. For instance, an RFID navigation system is a key application that assists blind users in unfamiliar environments by providing vital orientation cues, thereby preventing accidents and promoting safe navigation [1,2]. These systems employ strategically placed RFID tags throughout public spaces, allowing visually impaired users to detect these tags using handheld or wearable RFID readers. This technology provides audible or tactile feedback, guiding users effectively while alerting them to potential hazards in real time. A notable innovation in this field is the RFID cane, which is equipped with a tag reader and antenna that emits radio waves to interact with nearby RFID tags, accurately pinpointing the user’s location [1]. This enhanced mobility aid not only helps users navigate their surroundings but also fosters a sense of security and confidence. Furthermore, the RFID cane can transmit information via Bluetooth or ZigBee, enabling users to save destination names as voice messages, thus streamlining their travel experience and enhancing their ability to explore new environments independently.

Wearable devices that monitor vital signs and transmit data to healthcare professionals play a crucial role in supporting individuals with disabilities by ensuring timely medical assistance tailored to their specific health needs. RFID technology can enhance these devices by enabling precise tracking of users’ health metrics in real time, allowing for immediate intervention when necessary and thereby enhancing the overall well-being of disabled individuals [3,4,5,6,7,8]. Similarly, smart home technologies significantly improve accessibility for disabled users by automating daily tasks and enabling control through voice commands or adaptive interfaces. Incorporating RFID systems into smart home environments can facilitate seamless interactions between users and devices, allowing for personalized settings and efficient management of their surroundings. These technologies empower individuals with disabilities to manage their environments more independently, facilitating activities that may have previously required assistance [1,9,10]. By leveraging RFID technology, these innovations not only empower individuals with disabilities to engage more fully in society by facilitating access to education, employment, and social activities but also streamline daily living, fostering a greater sense of autonomy and confidence that significantly enhances their overall quality of life.

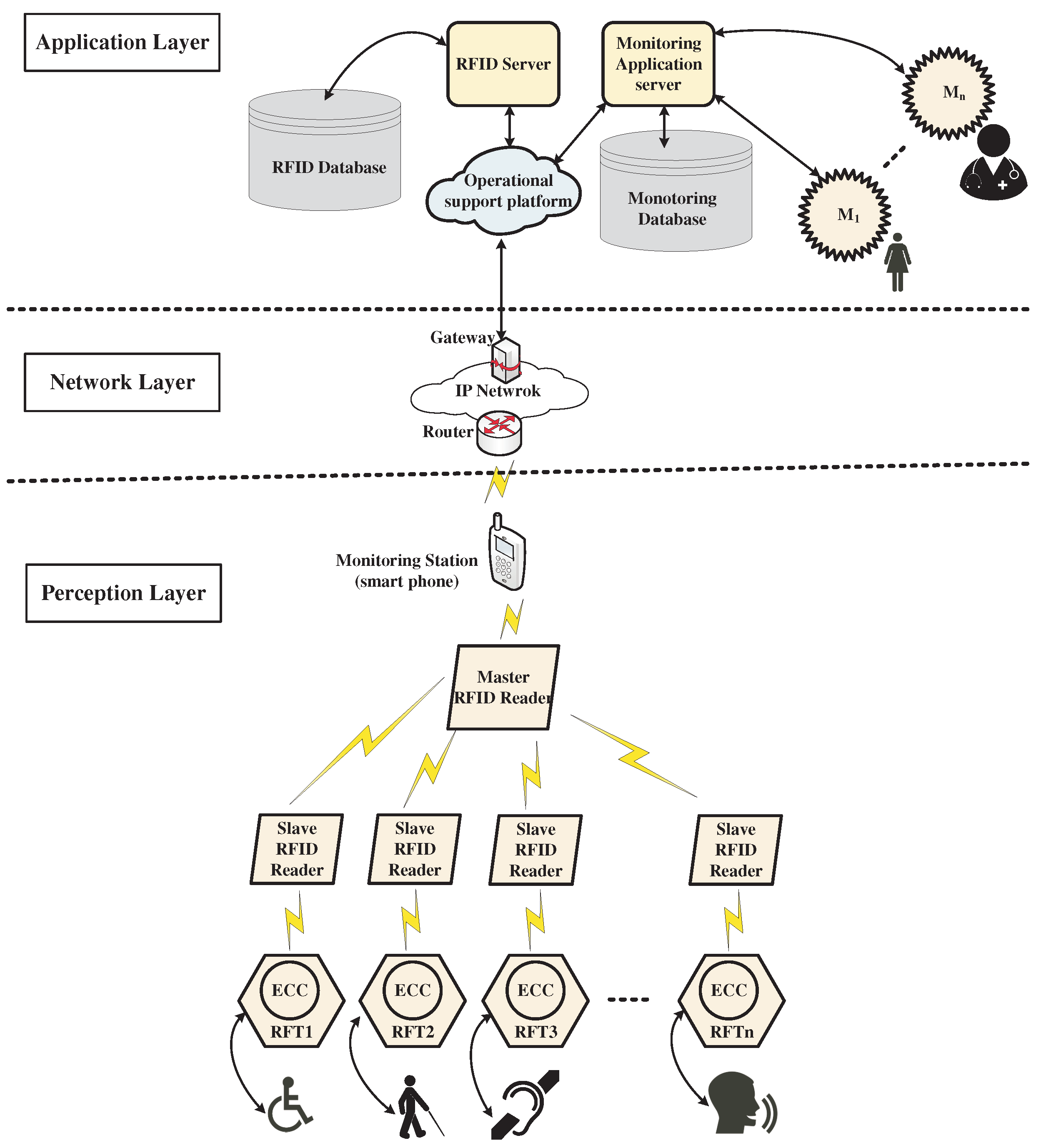
The RFID assistive system operates through a cohesive three-layer architecture that includes the perception layer, the network layer, and the application layer, as displayed in Figure 1. Each layer plays a critical role in ensuring the system’s functionality, security, and adaptability to the unique needs of its users. At the perception layer, multiple slave RFID readers are strategically placed throughout various environments—such as homes, workplaces, and public spaces—to continuously scan for RFID tags worn by disabled people or attached to nearby objects. Each RFID tag emits a unique identifier when it comes within proximity of a reader, allowing for precise tracking of the disabled individual’s location and interactions with their surroundings. The master RFID reader collects data from all slave readers, aggregating this information to ensure comprehensive coverage and accurate monitoring of the individual’s presence and interactions.

The data are captured and transmitted to the network layer, which comprises a router, an IP network, and a gateway. The router connects the master RFID reader to the IP network, facilitating seamless communication between the various components of the system. This network enables the flow of data from the RFID readers to the operational support platform. The gateway plays a critical role in linking the IP network to this platform, ensuring that the data processed by the readers can be effectively accessed and utilized for further analysis. The incorporation of IoT technology allows for enhanced data transmission and remote monitoring, enabling continuous updates and real-time insights.

In the application layer, the data stored in the RFID database plays a vital role in the overall functionality of the system. This database not only stores information about the RFID tags and their associated disabled individuals but also facilitates data retrieval and analysis to generate actionable insights. The data are transformed into relevant information through a monitoring application server, which hosts applications designed to provide tailored assistance based on the unique needs of each disabled individual. For example, the system can provide auditory alerts to people with visual impairments when they approach obstacles or important objects, helping them navigate their environment safely. For those with hearing impairments, visual indicators or vibrations can signal important notifications or alerts in their surroundings. Disabled individuals with mobility impairments can benefit from the system’s ability to automatically adjust the environment, such as opening doors or rearranging furniture, to facilitate easier access and movement. Additionally, the system can assist individuals with cognitive impairments by offering reminders or prompts through various devices, such as smartphones or tablets, to help with daily tasks and routines.

The RFID server serves as a critical component in the application layer, managing the communication between the RFID readers and the operational support platform. It processes incoming data from the readers, ensuring efficient data handling and storage while facilitating the integration of various system components, thereby enhancing overall system performance and reliability.

The monitoring application server connects not only to disabled individuals but also to doctors, nurses, and caregivers, allowing them to stay informed about those they support. These healthcare professionals can access real-time data, receive alerts about unusual activities, and monitor the health and safety of their patients through a user-friendly interface on smartphones or tablets. For instance, if a visually impaired individual approaches a specific object, the system can generate auditory alerts or provide contextual information about that object.

Through its connection with IoT, the RFID assistive system can also connect to other smart devices within the environment. This allows for automated responses, such as adjusting lighting or providing notifications to caregivers when specific conditions are met. Overall, the RFID assistive system represents a comprehensive solution designed to enhance the safety and autonomy of individuals with disabilities. Additionally, it fosters a supportive environment by ensuring that caregivers and healthcare professionals remain informed and engaged in the care process. Through the seamless integration of data collection, processing, and application, the system guarantees that disabled individuals receive timely assistance tailored to their specific needs. This approach not only promotes their independence but also significantly improves their overall quality of life.

The RFID assistive system, while offering significant benefits to individuals with disabilities, presents several privacy and security concerns at each layer of its architecture [11,12]. Understanding these vulnerabilities is critical to ensuring user safety and maintaining trust in the technology. At the perception layer, eavesdropping emerges as a prominent threat. Attackers can intercept communication between RFID tags and readers, thereby exposing sensitive information regarding an individual’s location and activities. For instance, a visually impaired user utilizing an RFID navigation system may be subjected to tracking by malicious actors, leading to potential harassment or exploitation. The ramifications of such breaches are severe, as they undermine users’ sense of safety and independence.

Relay attacks represent another significant issue within this layer. In this scenario, an attacker employs two devices to extend the communication range between an RFID tag and a reader, misleading the system into believing that the user is situated in a different location. This deception can enable unauthorized access to secure areas or generate false alarms, resulting in confusion and potential harm, particularly for users with cognitive impairments who may struggle to process unexpected situations. For individuals with mobility impairments, being inadvertently directed into restricted areas can result in hazardous situations, especially in unfamiliar environments.

Denial of Service (DoS) attacks can significantly disrupt the functionality of the RFID assistive system. By overwhelming communication channels, attackers can render the system inoperative, depriving users of the critical guidance they rely upon for navigation. For example, if a visually impaired individual’s navigation system fails due to a DoS attack, they may become disoriented and susceptible to accidents. This scenario underscores their reliance on technology for safety, highlighting how disruptions can significantly impact their ability to navigate effectively and maintain independence.

Spoofing represents another significant concern at the perception layer, wherein attackers impersonate legitimate RFID tags. This fraudulent activity can cause the system to provide inaccurate information, thereby exposing individuals with cognitive impairments to misleading alerts or directions. Such misrepresentation may place these individuals in precarious situations, undermining their safety and autonomy.

While the perception layer faces substantial risks, the network layer is also susceptible to security threats that can compromise the integrity and confidentiality of user data. Man-in-the-Middle (MitM) attacks can intercept and alter communications between RFID readers and the gateway, jeopardizing the accuracy of the information transmitted. For instance, if health data from a wearable device is tampered with during transmission, it could lead to inappropriate medical interventions, thereby endangering the health of individuals with chronic conditions. Furthermore, data tampering within the network layer can compromise the reliability of the system. Unauthorized modifications to transmitted data could result in erroneous system responses, such as failing to alert caregivers during emergencies. For disabled individuals, especially those with mobility impairments, such failures can have severe consequences, including delayed assistance in critical situations.

At the application layer, security vulnerabilities can lead to severe privacy violations. Data breaches may expose sensitive information about disabled individuals, encompassing their health data and daily routines. Such breaches not only compromise privacy but can also result in discrimination or exploitation. For caregivers and healthcare providers, unauthorized access to the RFID database can lead to misinformation, resulting in inappropriate care or neglect. Additionally, malware attacks targeting the application layer can disrupt the monitoring application server, impairing its functionality or facilitating the theft of sensitive data. This disruption can prevent caregivers from receiving critical alerts or accessing real-time information about their patients, further jeopardizing the health and safety of disabled individuals who rely on timely interventions.

While security issues at the network and application layers are crucial, this study refrains from addressing solutions for these areas, as the existing literature has already provided a thorough exploration of various security measures and a comprehensive understanding of the related threats and mitigations. Focusing on the perception layer is especially urgent due to its direct impact on user safety and the immediate threats faced by individuals with disabilities. By prioritizing this layer, we aim to improve the security and effectiveness of assistive technologies that are essential for their safety and independence.

To mitigate cyberattacks targeting the RFID assistive system at the perception layer, significant efforts have been made to develop tailored security solutions. Advanced authentication protocols, particularly those employing ECC, offer enhanced security by leveraging strong cryptographic properties. However, implementing ECC on low-cost RFID tags is challenging due to the associated high computational demands, which often exceed the limited processing power, memory, and battery life of these devices [8,13]. In response, lightweight protocols utilizing simpler encryption methods have been proposed, but these solutions often exhibit vulnerabilities, such as susceptibility to impersonation and eavesdropping [14,15,16,17]. Recent innovations, including group authentication protocols compliant with established standards and schemes based on permutation matrix encryption, aim to balance security and efficiency for low-cost RFID systems [18]. Despite these advancements, many solutions assume secure communication between servers and readers, which may not be feasible in mobile RFID contexts where communication channels are inherently less secure.

We have chosen to employ ECC in our RFID assistive system rather than adopting other recommended lightweight cryptographic standards such as ASCON and GIFT-COFB due to several compelling advantages [19,20]. ECC is recognized for its efficiency as a public-key cryptographic method that leverages the mathematical properties of elliptic curves over finite fields, providing robust security with smaller key sizes—typically 256 bits—equivalent to much larger keys in traditional algorithms like RSA. This not only enhances security but also reduces computational load, making ECC particularly suitable for resource-constrained environments where efficiency and power conservation are essential. Furthermore, ECC supports a comprehensive range of functionalities, including encryption, user and message authentication, digital signatures, and key distribution, which are critical for establishing trust and verifying identities in secure communications. In contrast, ASCON and GIFT-COFB are primarily symmetric algorithms focused solely on encryption and message authentication, lacking the versatility and broader application scope that ECC offers.

Table 1. Comparison of ECC with ASCON and GIFT-COFB.

Feature/Algorithm	ECC	ASCON	GIFT-COFB
Type	Public-Key Cryptography	Secret-Key Cryptography	Secret-Key Cryptography
Key Size	256 bits (common)	128 bits	128 bits
Cryptographic Functions	Comprehensive Suite	Authenticated Encryption	Authenticated Encryption
Security Basis	Elliptic Curve Discrete Log	Permutation and XOR	Lightweight Block Cipher
Finite Field Multiplication	Yes	No	No
Potential Vulnerabilities	Side-channel attacks	Collision attacks	Cryptanalysis attacks

presents a comparison of these algorithms to ECC; ASCON is an effective authenticated encryption algorithm that utilizes a permutation-based structure, while GIFT-COFB relies on a lightweight block cipher. While symmetric algorithms may provide speed advantages, they do not support the public-key functionalities essential for digital signature and secure key distribution. Moreover, every algorithm carries its own potential vulnerabilities: ECC may have potential vulnerability to side-channel-attacks if not implemented properly. Additionally, ASCON may be susceptible to collision attacks based on its hashing foundation, and GIFT-COFB may face challenges related to certain cryptanalysis techniques that its security are based on using light weight block cipher. Overall, the choice of ECC is driven by its superior efficiency, robust security, and ability to deliver a comprehensive suite of cryptographic functionalities essential for our RFID assistive system.

Implementing ECC-based authentication can significantly enhance the security of RFID assistive systems. However, deploying ECC on resource-constrained RFID tags presents several challenges. These tags typically have limited processing power, memory, and battery life, making it difficult to execute complex cryptographic operations efficiently. The computational overhead associated with ECC may lead to slow response times, increased energy consumption, and potential system failures, all of which are critical concerns for devices designed to support individuals with disabilities.

To address these challenges, a specialized hardware solution tailored for ECC can be developed. This solution would optimize the hardware architecture to accommodate the unique constraints of RFID tags while maintaining the integrity of cryptographic operations. The ECC algorithm primarily involves finite field arithmetic, with finite field multiplication serving as the foundational operation for various cryptographic functions, including field inversion and field division [21,22,23,24,25,26,27,28,29,30,31,32]. Therefore, finite field multiplication is a critical component of ECC, and its efficient implementation is essential for the overall performance and feasibility of cryptographic solutions on resource-constrained devices. Successfully implementing this operation on RFID tags is essential for the effective deployment of robust ECC cryptographic solutions. By optimizing this operation, it becomes feasible to execute ECC computations without overloading the limited resources of these tags. Traditional multiplication designs are often unsuitable for such devices due to their excessive area and energy requirements, which can hinder their practicality in low-cost, resource-constrained environments.

This work tackles these challenges by proposing an efficient and compact one-dimensional bit-parallel semi-systolic field multiplier optimized for the Montgomery multiplication algorithm, a widely used method in cryptographic applications. The proposed design significantly reduces both space and energy consumption while maintaining computational performance, making it well-suited for resource-constrained environments. By minimizing the area and power requirements of finite field multiplication, this solution enables the practical implementation of ECC on RFID tags, enhancing the overall security of the system. This strategy not only improves the security of RFID assistive systems but also ensures that individuals with disabilities can access reliable and effective assistive technology.

Based on the background provided, the remainder of this study will primarily focus on the design methodology used for implementing an efficient and compact finite field multiplier that supports the computational demands of the ECC algorithm. This makes it suitable for integration into resource-constrained RFID tags designed for individuals with disabilities. The ASIC implementation results presented at the conclusion of this study demonstrate significant improvements in key metrics, including area, power consumption, Power-Delay Product (PDP), and Area-Delay Product (ADP), ensuring compliance with the stringent requirements of low-cost RFID assistive devices while delivering robust security. This innovation has the potential to greatly enhance the safety and autonomy of individuals with disabilities, allowing them to benefit from secure and reliable assistive technologies in their everyday lives.

2. Literature Review

The effectiveness of finite field multiplications depends critically on the choice of base representations for the elements in GF($2^m$). The advantages of other basis representations, such as Polynomial Basis (PB), Normal Basis (NB), Dual Basis (DB), and Redundant Basis (RB), are clear [33]. When it comes to these representations, polynomial basis arithmetic stands out as a simple, reliable, and scalable method, especially for hardware implementation [34,35,36,37,38]. Polynomial basis arithmetic is commonly used in cryptographic protocols because it does not require basis conversion, unlike other representations. The effectiveness of finite field multipliers is greatly influenced by the irreducible polynomial chosen. All-Ones Polynomial (AOP), trinomials, and pentanomials are a few examples of irreducible polynomials that are employed in cryptographic techniques. Despite the fact that trinomial and pentanomial-based multipliers are more efficient, generic polynomial-based multipliers are still useful for a variety of applications. Although irreducible AOPs are not utilized as often as irreducible trinomials or pentanomials, they still have the potential to design efficient multipliers [39,40,41].

Different methods of implementation can lead to the creation of diverse multipliers with varying characteristics. Bit-serial multipliers are known for their space efficiency and significant power savings, albeit at the expense of slower operation, requiring m clock cycles to multiply two elements [22,42,43]. On the other hand, bit-parallel multipliers provide the advantage of producing results in a single clock cycle but come with higher hardware costs and power consumption [24,25,28,44,45,46,47,48,49]. In the framework of Very Large Scale Integration (VLSI) implementations, systolic/semi-systolic serial or concurrent multiplier topologies are chosen over traditional approaches. This is because they possess qualities such as regularity, modularity, local relatively homogeneous connectivity, and concurrency, which make them ideal for VLSI designs. Furthermore, systolic/semi-systolic arrays have underlying pipeline properties that allow for high clock frequencies irrespective of substantial resource use.

Numerous researchers have made significant efforts to devise effective implementations of systolic/semi-systolic multipliers for binary extension fields GF($2^m$). These studies primarily focus on constructing multiplier architectures using specific irreducible polynomials. For instance, Lee and Chiou introduced in their work an error-detecting semi-systolic array multiplier [22,50]. Huang proposed an efficient semi-systolic array multiplier aimed at reducing both time and space costs [23]. In their work, Choi and Lee addressed the need for a highly efficient systolic array architecture that performs unified multiplication and squaring operations with minimal hardware overhead [25]. They developed a serial and parallel systolic array that enables rapid modular exponentiation by concurrently executing multiplication and squaring operations. This architecture is designed to optimize performance while minimizing resource utilization. Moreover, the incorporation of LSB-first multiplication and exponentiation algorithms further enhances the efficiency of the systolic array, allowing for faster computation of modular exponentiation.

In a separate study, Chiou proposed a semi-systolic array multiplier that offers reduced time complexity [51]. By carefully designing the multiplier structure, they achieved significant improvements in computational efficiency. This reduction in time complexity is crucial for applications that require fast and efficient multiplication, such as cryptographic algorithms. Recent research by Lee introduced novel semi-systolic Montgomery modular multipliers that leverage two levels of systolic computation [52,53]. These multipliers demonstrate efficient area utilization and reduced delay, which are essential factors in VLSI implementations. The utilization of systolic computation allows for parallel processing and pipelining, enabling faster and more efficient modular multiplication operations.

Mathe and Boppana proposed a multiplier architecture that supports both parallel and serial inputs [54]. This architecture provides flexibility in handling different types of operands and allows for efficient multiplication and squaring operations. By accommodating various input configurations, the multiplier can adapt to different application requirements and optimize performance accordingly. Additionally, Ibrahim introduced efficient one-dimensional bit-serial and bit-parallel systolic array structures for multiplication and squaring operations over GF($2^m$) [32]. These structures are specifically designed for computations within the finite field GF($2^m$) and offer efficient utilization of hardware resources. The bit-serial and bit-parallel systolic arrays enable optimized processing of binary data, making them suitable for applications such as error correction codes and cryptography.

In recent research by Pillutla and Boppana, a novel GF($2^m$) polynomial basis systolic multiplier was introduced, specifically targeting field sizes m = 233 and m = 409 [36]. The proposed architecture incorporates suggested trinomials to enhance its performance. While GF($2^m$)-based multipliers have been created for a variety of applications, they frequently encounter difficulties owing to their high hardware complexity and large delay durations, especially in security-related applications. Therefore, it is crucial to conduct further investigations to explore multiplication architectures that can provide efficient performance while minimizing space and time requirements.

In the realm of bit-parallel systolic multipliers, a multiplier structure was initially proposed by Lee that utilized equally spaced and AOP polynomials as the foundation for its design [44,45]. However, in 2005, Lee introduced a mapping approach aimed at reducing the complexity of the AOP-based bit-parallel systolic multiplier [46]. The foundation of the multiplier was changed from AOP polynomials to trinomials as part of this mapping method. The multiplier architecture’s complexity was significantly reduced by using trinomials as the foundation, resulting in enhanced efficiency and performance.

In an effort to decrease the complexity of the Montgomery-based bit-parallel multiplier, Lee proposed a novel approach that involved utilizing the Toeplitz matrix-vector representation [47]. By employing this technique, the complexity associated with the multiplier was effectively reduced, resulting in a more efficient and practical design. The use of Toeplitz matrices in the representation of the multiplier allowed for efficient and streamlined computations, improving overall performance.

Sarmadi introduced a two-dimensional parallel systolic multiplier based on the Montgomery algorithm [48]. This innovative multiplier structure offered high performance capabilities while also minimizing space requirements. The parallel systolic design allowed for simultaneous and independent processing of multiple operations, leading to improved throughput and reduced computation time. By optimizing the space utilization, Sarmadi’s approach provided an efficient solution for applications that demand high-performance multiplication operations. Building upon these advancements, Mathe implemented a two-dimensional parallel systolic multiplier structure designed to minimize space overhead. The structure was based on an interleaving multiplication method over GF($2^m$) [49]. By utilizing interleaving techniques, Mathe achieved an efficient utilization of hardware resources while maintaining high-performance multiplication operations. The resulting multiplier architecture offered a balanced trade-off between space requirements and computational efficiency.

2.1. Paper Contribution

This work focuses on the development of a one-dimensional bit-parallel semi-systolic implementation of the field Montgomery multiplication algorithm, as suggested by Lee et al. [53]. The algorithm efficiently handles multiplication operations over GF($2^m$) by utilizing a general irreducible polynomial as its foundation. One notable advantage of the adopted Montgomery algorithm, in contrast to many other algorithms, is its ability to reduce latency. Furthermore, it offers the additional benefit of minimizing time and area overhead by employing the same architecture for executing both iterative parts of the algorithm [53]. However, previous works in the literature often rely on ad hoc approaches when extracting the hardware structure, without considering how the structure could be modified to optimize system performance factors such as latency, throughput, power, and area. Unlike ad hoc approaches, the proposed method takes into account the selection of appropriate scheduling and projection functions in order to extract an optimal architecture that is specifically tailored to meet the requirements of the target application. This mathematical approach offers several advantages, including the ability to systematically analyze the multiplier structure and optimize its performance characteristics. By adopting this mathematical approach, it becomes possible to enhance the overall efficiency of the systolic/semi-systolic implementation. The proposed methodology facilitates a more systematic and comprehensive exploration of the design space, enabling the identification of the most suitable architectural configuration for achieving optimal performance metrics. This, in turn, contributes to the overall improvement of system performance, including reduced latency, increased throughput, optimized power consumption, and minimized area overhead.

In order to facilitate the extraction of the Dependency Graph (DG) for the algorithm, the proposed multiplier structure is expressed in a bit-level format. This allows for easier visualization and analysis of the dependencies between different operations. The DG acts as a great tool for generating the recommended multiplier construction, assisting in its development and optimization, by carefully picking suitable time-scheduling and node-projection functions. One of the primary advantages of the suggested multiplier structure is its much lower area complexity when compared to previously identified bi-dimensional arrangements. While many known structures have an spatial complexity of order $\mathcal{O}\left(m^2\right)$, the proposed building has an spatial complexity of order $\mathcal{O}\left(m\right)$. This reduction in complexity results in significant reductions in physical space and energy consumption, making the construction more efficient and inexpensive. Despite the reduced area complexity, the performance of the recommended multiplier construction remains the same. It has the same temporal delays as bi-dimensional constructions, ensuring fast computing. This means that, while the structure provides considerable advantages in terms of decreased complexity and power consumption, it does not sacrifice performance. Furthermore, the suggested multiplier design’s modular form and local connectivity between the constituent Processing Elements (PEs) make it ideal for VLSI implementation. The local link between the PEs simplifies the overall construction and improves performance by reducing wire delays. This local connectivity not only enhances data transmission efficiency but also adds to the overall effectiveness of the suggested multiplier organization.

The significant savings in space, delay, and power provided by the proposed multiplier architecture make it a highly promising solution for implementing computationally demanding cryptographic protocols in small RFID sensor tags tailored for applications that support individuals with disabilities. This innovation paves the way for enhancing the security and efficiency of RFID-based assistive systems, ultimately improving the quality of life and safety of disabled individuals.

2.2. Paper Organization

An outline of the paper’s structure is provided as follows: in Section 3, the chosen Montgomery multiplication algorithm is mathematically modeled, providing a clear understanding of its underlying principles and operations. Additionally, the bit-level representation of the algorithm is presented, which serves as a crucial foundation for further analysis and design considerations. Moving forward, Section 4 delves into the detailed description of the DG associated with the adopted algorithm. This section explores the intricate relationships and dependencies between various operations within the algorithm. Section 5 focuses on outlining the process of obtaining the suggested one-dimensional bit-parallel semi-systolic multiplier layout. This section explains the step-by-step methodology employed in designing the multiplier structure, taking into account the insights derived from the DG and specific requirements of the algorithm. To thoroughly evaluate the proposed multiplier’s effectiveness, Section 6 conducts a comprehensive analysis of its complexity. This includes an examination of the space complexity, comparing it to existing effective multipliers to highlight potential space savings. Moreover, the time complexity is also analyzed and compared with relevant multiplier designs to assess its efficiency. Furthermore, the paper includes a thorough evaluation of the performance of the suggested multiplier design, providing a realistic assessment of its capabilities. This evaluation includes a comparison with other multiplier designs that have been synthesized using ASIC technology. Finally, Section 7 provides a concise summary of the paper’s key findings and contributions.

3. Montgomery Multiplication in GF($2^m$)

Table 2. Definition of the general notations used in the Mongomery multiplication algorithm in GF($2^m$).

Notation	Definition
m	Finite field size
$H\left(\lambda \right)$	Irreducible polynomial of degree m
$h_j$	jth coefficient of polynomial $H\left(\lambda \right)$
$h_{j-1}$	$(j-1)$th coefficient of polynomial $H\left(\lambda \right)$
$h_{m-j}$	$(m-j)$th coefficient of polynomial $H\left(\lambda \right)$
$\sigma$	Root of $H\left(\lambda \right)$
${\sigma }^{j-1}$	$(j-1)$th term of the root $\sigma$
${\sigma }^j$	$\left(j\right)$th term of the root $\sigma$
$\chi$ and $\tau$	Elements in the binary extension field GF($2^m$)
$\pi$	Montgomery unique factor equal to ${\sigma }^{(m-1)/2}$
C and D	Montgomery residues of $\chi$ and $\tau$, respectively
T	Output product of Montgomery multiplication
U and V	Polynomial T is represented as the sum of these two polynomials
$C^{\left(i\right)}$	Polynomial C when updated at iteration i.
$U^{\left(i\right)}$	Polynomial U when updated at iteration i.
$V^{\left(i\right)}$	Polynomial V when updated at iteration i.
$u_{j-1}$	$(j-1)$th coefficient of polynomial U
$v_{j-1}$	$(j-1)$th coefficient of polynomial V
$d_{j-1}$	$(j-1)$th coefficient of polynomial D
$c_j^{\left(i\right)}$	jth coefficient of polynomial C at iteration i.
$c_{j-1}^{(i-1)}$	$(j-1)$th coefficient of polynomial C at iteration $i-1$.
$c_0^{\left(i\right)}$	First coefficient of polynomial C at iteration i.
$c_0^{(i-1)}$	First coefficient of polynomial C at iteration $i-1$.
$c_{m-1}^{(i-1)}$	$(m-1)$th coefficient of polynomial C at iteration $i-1$.
$c_{m-1}^{\left(i\right)}$	$(m-1)$th coefficient of polynomial C at iteration i.
$c_{m-j-1}^{\left(i\right)}$	$(m-j-1)$th coefficient of polynomial C at iteration i.
$u_{j-1}^{\left(i\right)}$	$(j-1)$th coefficient of polynomial U at iteration i.
$u_{j-1}^{(i-1)}$	$(j-1)$th coefficient of polynomial U at iteration $i-1$.
$v_{m-j}^{\left(i\right)}$	$(m-j)$th coefficient of polynomial V at iteration i.
$v_{m-j}^{(i-1)}$	$(m-j)$th coefficient of polynomial V at iteration $i-1$.
$d_{(m+2i-3)/2}$	$\left(\right(m+2i-3)/2)$th coefficient of polynomial D at iteration i.
$d_{(m+2i-3)/2}$	$\left(\right(m-2i+1)/2)$th coefficient of polynomial D at iteration i.

summarizes the notations used in the Montgomery multiplication algorithm over GF($2^m$), along with their definitions. This serves as a reference to clarify the roles and significance of each term within the algorithm.

Assume that $H\left(\lambda \right)$ is an irreducible polynomial of degree m, with coefficients $h_m$ and $h_0$ both equivalent to 1, and that it is employed to create the finite field GF$\left(2^m\right)$. Considering that $\sigma$ is a root of $H\left(\lambda \right)$, this implies that $h_{\sigma }$ should be equivalent to 0. A polynomial of degree less than m over GF(2) should be used to define the elements in GF$\left(2^m\right)$. Bitwise exclusive-OR (XOR) is an efficient way to add two polynomials in GF($2^m$). In contrast, multiplying two polynomials in GF($2^m$) is somewhat challenging as the intermediate outcomes necessitates a further modular reduction by ${\sigma }^m={\sum }_{j=1}^m{h}_{j-1}{\sigma }^{j-1}$.

Presume that two of the GF($2^m$) elements to be multiplied are $\chi$ and $\tau$. Assume that $\pi$ is a unique factor meeting $gcd(\pi ,H)=1$ and that C and D are the Montgomery residues of $\chi$ and $\delta$, respectively. The Montgomery Modular Multiplication (MMM) of $C=\chi \pi modH={\sum }_{j=1}^m{c}_{j-1}{\sigma }^{j-1}$ and $D=\tau \pi modH={\sum }_{j=1}^m{d}_{j-1}{\sigma }^{j-1}$ is computed by $T=CD{\pi }^{-1}modH=\chi \tau \pi modH={\sum }_{j=0}^{m-1}{t}_j·{\sigma }^j$. Employing T and 1 as inputs, Montgomery multiplication is then applied to yield the final output $\psi$, which is calculated as follows: $\psi =T{\pi }^{-1}modH=\chi \tau modH$.

In numerous applications involving recurring multiplications, like inversion, exponentiation, and elliptic curve point multiplication, Montgomery multiplication is beneficial due to the necessity of pre- and post-transformation. Due to its greater efficiency in the execution of elliptic curve point multiplication, field size m is usually selected as an integer with an odd value in real-world applications. For instance, the five binary fields that the National Institute of Standards and Technology (NIST) recommends for use with ECC, ($m=163,233,283,409,571$), have the characteristic that m is odd. In this situation, we are able to select $\pi ={\sigma }^{(m-1)/2}$ to represent the Montgomery multiplication $T=CD{\pi }^{-1}modH$, as the sum of two separately calculating polynomials $U={\sum }_{j=1}^m{u}_{j-1}{\sigma }^{j-1}$ and $V={\sum }_{j=1}^m{v}_{j-1}{\sigma }^{j-1}$. The calculation of T can be given as [52,53]:

$$\begin{array}{cc}\hfill T& =(\sum _{j=1}^m{d}_{j-1}{\sigma }^{j-1})C{\sigma }^{-(m-1)/2}modH\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =\sum _{j=(m+1)/2}^m{d}_{j-1}C{\sigma }^{(2j-m-1)/2}modH\hfill \end{array}$$

(1a)

$$\begin{array}{cc}\hfill & +\sum _{j=(m-1)/2}^1{d}_{j-1}C{\sigma }^{(2j-m-1)/2}modH\hfill \end{array}$$

(1b)

We focus on Equation (1a), of the previous expression. Consider that $C^{\left(i\right)}=C^{(i-1)}\sigma modH$, where $C^{\left(i\right)}={\sum }_{j=1}^m{c}_{j-1}^i{\sigma }^{j-1}$ and $C^{\left(0\right)}=C$, denote the intermediary outcome at the $i^{th}$ iteration for $i\in [1,(m+1)/2]$ and $j\in [1,m]$. Using the expanded form, we are able to denote $C^{\left(i\right)}$ as follows:

$$\begin{array}{cc}\hfill C^{\left(i\right)}& =(\sum _{j=1}^m{c}_{j-1}^{(i-1)}{\sigma }^{j-1})\sigma modH\hfill \\ \hfill & =\sum _{j=1}^m{c}_{j-1}^{(i-1)}{\sigma }^{j}modH\hfill \\ \hfill & =c_{m-1}^{(i-1)}\sum _{j=1}^m{h}_{j-1}{\sigma }^{j-1}+\sum _{j=1}^{m-1}{c}_{j-1}^{(i-1)}{\sigma }^j\hfill \end{array}$$

(2)

It is quite obvious that Equation (2) is produced by moving the coefficients of $C^{(i-1)}$ by 1 to the left side, and then H is used to reduce the term $c_{m-1}^{(i-1)}{\sigma }^m$. As a result, we are left with the following $C^{\left(i\right)}$ coefficients:

$$\begin{array}{cc}\hfill c_j^{\left(i\right)}=& c_{j-1}^{(i-1)}+c_{m-1}^{(i-1)}{h}_j\hfill \end{array}$$

(3)

with $c_j^0=c_j$, $0\le j\le m-1$, and $c_{m-1}^{(i-1)}$ can be allocated to $c_0^i$ for $1\le i\le (m-1)/2$. Right now, we are able to formulate Equation (1a) as:

$$\begin{array}{c}\hfill U^{\left(i\right)}=U^{(i-1)}+d_{(m+2i-3)/2}{C}^{(i-1)}\end{array}$$

(4)

with $U^{\left(i\right)}={\sum }_{j=1}^m{u}_{j-1}^{\left(i\right)}{\sigma }^{j-1}$ defining the ith interim outcome. It is possible to rephrase $U^{\left(i\right)}$ as follows:

$$\begin{array}{cc}\hfill U^{\left(i\right)}& =(\sum _{j=1}^m{u}_{j-1}^{\left(i\right)}{\sigma }^{j-1})\hfill \\ \hfill & =\sum _{j=1}^i{d}_{(m+2j-3)/2}C{\sigma }^{j-1}\hfill \\ \hfill & =\sum _{j=1}^m{u}_{j-1}^{(i-1)}{\sigma }^{j-1}+d_{(m+2i-3)/2}C{\sigma }^{i-1}\hfill \\ \hfill & =\sum _{j=1}^m{u}_{j-1}^{(i-1)}{\sigma }^{j-1}+d_{(m+2i-3)/2}\sum _{j=1}^m{c}_{j-1}^{(i-1)}{\sigma }^{j-1}\hfill \end{array}$$

(5)

with $U^{\left(0\right)}=0$. Equation (5) can simply be produced by multiplication and accumulation (MAC) operations. The values of the coefficients of $U^{\left(i\right)}$ can be found using Equation (5) in the following manner:

$$\begin{array}{cc}\hfill u_{j-1}^{\left(i\right)}=& u_{j-1}^{(i-1)}+d_{(m+2i-3)/2}{c}_{j-1}^{(i-1)}\hfill \end{array}$$

(6)

with $u_j^0=0$ and $c_j^0=c_j$ for $0\le j\le m-1$. Additionally, $c_0^i=c_{m-1}^{(i-1)}$ for $1\le i\le (m-1)/2$. The outcome of $U^{(m+1)/2}$ becomes available after $(m+1)/2$ rounds. It should be noted that Equations (2) and (6), which share the same term $c_{j-1}^{(i-1)}$, are additionally independent of one another and can therefore be evaluated simultaneously.

Now, we will examine Equation (1b),

Assuming that $C^{\left(i\right)}=C^{(i-1)}{\sigma }^{-1}modH$, with $C^{\left(i\right)}={\sum }_{j=1}^m{c}_{j-1}^i{\sigma }^{j-1}$ denotes the interim outcome at the ith iteration and $C^{\left(0\right)}=C$, for $i\in [1,(m+1)/2]$ and $j\in [1,m]$.

Any irreducible polynomial should have the properties that $h_0=h_m=1$, and $\sigma$ is a root of H. We can generate ${\sigma }^{-1}={\sum }_{j=1}^m{h}_j{\sigma }^{j-1}$ by multiplying the two components of $H={\sum }_{j=1}^{m+1}{h}_{j-1}{\sigma }^{j-1}$ = 0 by ${\sigma }^{-1}$ and rearranging the terms. By applying ${\sigma }^{-1}$, $C^{\left(i\right)}$ could be constructed in the following way:

$$\begin{array}{cc}\hfill C^{\left(i\right)}& =(\sum _{j=1}^m{c}_{j-1}^{(i-1)}{\sigma }^{j-1}){\sigma }^{-1}modH\hfill \\ \hfill & =\sum _{j=1}^m{c}_{j-1}^{(i-1)}{\sigma }^{j-2}modH\hfill \\ \hfill & =c_0^{(i-1)}\sum _{j=1}^m{h}_j{\sigma }^{j-1}+\sum _{j=2}^m{c}_{j-1}^{(i-1)}{\sigma }^{j-2}\hfill \end{array}$$

(7)

It is quite obvious that Equation (7) is produced by moving the coefficients of $C^{(i-1)}$ by 1 to the right side, and then H is used to reduce the term $c_0^{(i-1)}{\sigma }^{-1}$. As a result, we are left with the following $C^{\left(i\right)}$ coefficients:

$$\begin{array}{cc}\hfill c_{m-j-1}^{\left(i\right)}=& c_{m-j}^{(i-1)}+c_0^{(i-1)}{h}_{m-j}\hfill \end{array}$$

(8)

with $c_j^0=c_j$, $0\le j\le m-1$, and $c_0^{(i-1)}$ can be allocated to $c_{m-1}^i$ for $1\le i\le (m-1)/2$. Right now, we are able to formulate Equation (1b) as:

$$\begin{array}{c}\hfill V^{\left(i\right)}=V^{(i-1)}+d_{(m-2i+1)/2}{C}^{(i-1)}\end{array}$$

(9)

with $V^{\left(i\right)}={\sum }_{j=1}^m{v}_{j-1}^{\left(i\right)}{\sigma }^{j-1}$ defining the ith interim outcome. It is possible to rephrase $V^{\left(i\right)}$ as follows:

$$\begin{array}{cc}\hfill V^{\left(i\right)}& =(\sum _{j=1}^m{v}_{j-1}^{\left(i\right)}{\sigma }^{j-1})\hfill \\ \hfill & =\sum _{j=1}^i{d}_{(m-2j+1)/2}C{\sigma }^{j-1}\hfill \\ \hfill & =\sum _{j=1}^m{v}_{j-1}^{(i-1)}{\sigma }^{j-1}+d_{(m-2i+1)/2}C{\sigma }^{j-1}\hfill \\ \hfill & =\sum _{j=1}^m{v}_{j-1}^{(i-1)}{\sigma }^{j-1}+d_{(m-2i+1)/2}\sum _{j=1}^m{c}_{j-1}^{(i-1)}{\sigma }^{j-1}\hfill \end{array}$$

(10)

with $V^{\left(0\right)}=0$. Equation (10) can simply be produced by multiplication and accumulation (MAC) operations. The values of the coefficients of $V^{\left(i\right)}$ can be found using Equation (10) in the following manner:

$$\begin{array}{cc}\hfill v_{m-j}^{\left(i\right)}=& v_{m-j}^{(i-1)}+d_{(m-2i+1)/2}{c}_{m-j}^{(i-1)}\hfill \end{array}$$

(11)

with $v_j^0=0$, $d_{(m-1)/2}=0$, and $c_j^0=c_j$ for $0\le j\le m-1$, $c_{m-1}^{\left(i\right)}=c_0^{(i-1)}$ for $1\le i\le (m-1)/2$. The outcome of $V^{(m+1)/2}$ becomes available after $(m+1)/2$ rounds. It should be noted that Equations (8) and (11), which share the same term $c_{m-j}^{(i-1)}$, are additionally independent of one another and can therefore be evaluated simultaneously.

Ultimately, $U^{(m+1)/2}$ and $V^{(m+1)/2}$ have to be combined by m 2-input XOR gates to produce the MMM result T as an output.

Algorithms 1 and 2 reflect the algorithmic framework of the already addressed equations. As we notice, Algorithm 2 is the bit-level version of Algorithm 1.

Algorithm 1 Efficient Montgomery Multiplication Algorithm over Binary Finite Fields

Input: C, D, π−1 = σ−(m−1)/2, and H

Output: T

Initialization:

U0 ← 0, V0 ← 0, C0 ← C

Algorithm:

1: for  $1\le i\le (m+1)/2$  do 2:     $C^i=C^{i-1}\sigma modH$ 3:     $U^i=U^{i-1}+d_{(m+2i-3)/2}{C}^{i-1}$ 4: end for 5: for  $1\le i\le (m+1)/2$  do 6:     $C^i=C^{i-1}{\sigma }^{-1}modH$ 7:     $V^i=V^{i-1}+d_{(m-2i+1)/2}{C}^{i-1}$ 8: end for 9: $T=U^{(m+1)/2}+V^{(m+1)/2}$

Algorithm 2 Bit-Level Implementation of the Montgomery Multiplication Algorithm

Input: C = (cm−1cm−2 ⋯ c0), D = (dm−1dm−1 ⋯ d0), H = (hmhm−1 ⋯ h0)

Output: T = (tm−1tm−2 ⋯ t0)

Initialization:

$U^0=(u_{m-1}^0{u}_{m-2}^0\cdots u_0^0)\leftarrow (00\cdots 0)$

$V^0=(v_{m-1}^0{v}_{m-2}^0\cdots v_0^0)\leftarrow (00\cdots 0)$

$C^0=(c_{m-1}^0{c}_{m-2}^0\cdots c_0^0)\leftarrow (c_{m-1}{c}_{m-2}\cdots c_0)$

Algorithm:

1: for  $1\le i\le (m+1)/2$  do 2:     $c_0^i=c_{m-1}^{i-1}$ 3:     for $1\le j\le m$ do 4:         $c_j^i=c_{j-1}^{i-1}+c_{m-1}^{i-1}{h}_j$ 5:         $u_{j-1}^i=u_{j-1}^{i-1}+d_{(m+2i-3)/2}{c}_{j-1}^{i-1}$ 6:     end for 7: end for 8: for  $1\le i\le (m+1)/2$  do 9:     $c_{m-1}^i=c_0^{i-1}$ 10:     for $1\le j\le m$ do 11:         $c_{m-j-1}^i=c_{m-j}^{i-1}+c_0^{i-1}{h}_{m-j}$ 12:         $v_{m-j}^i=v_{m-j}^{i-1}+d_{(m-2i+1)/2}{c}_{m-j}^{i-1}$ 13:     end for 14: end for 15: for  $1\le j\le m$  do 16:     $t_{j-1}=u_{j-1}^{(m+1)/2}+v_{j-1}^{(m+1)/2}$ 17: end for

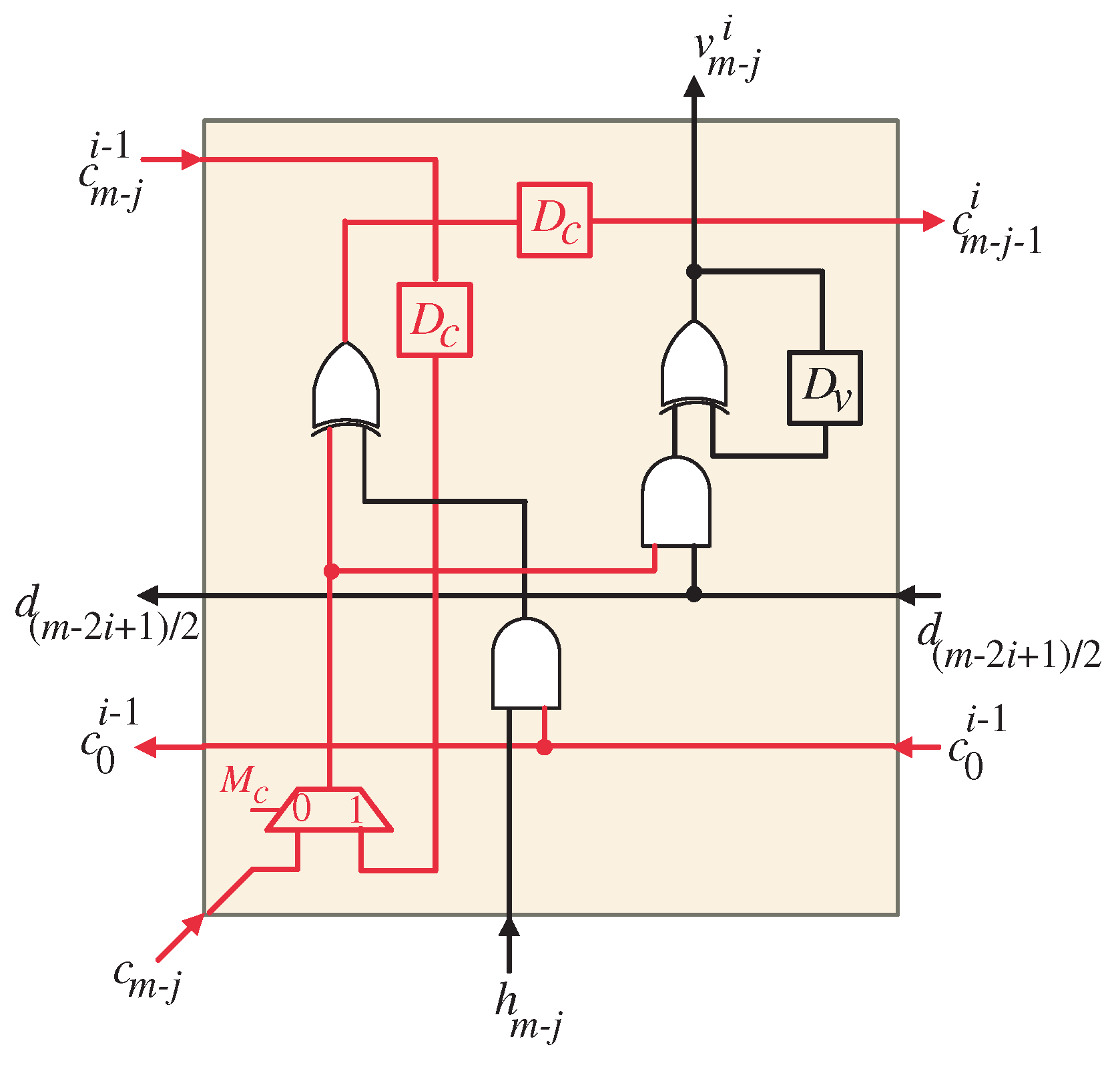
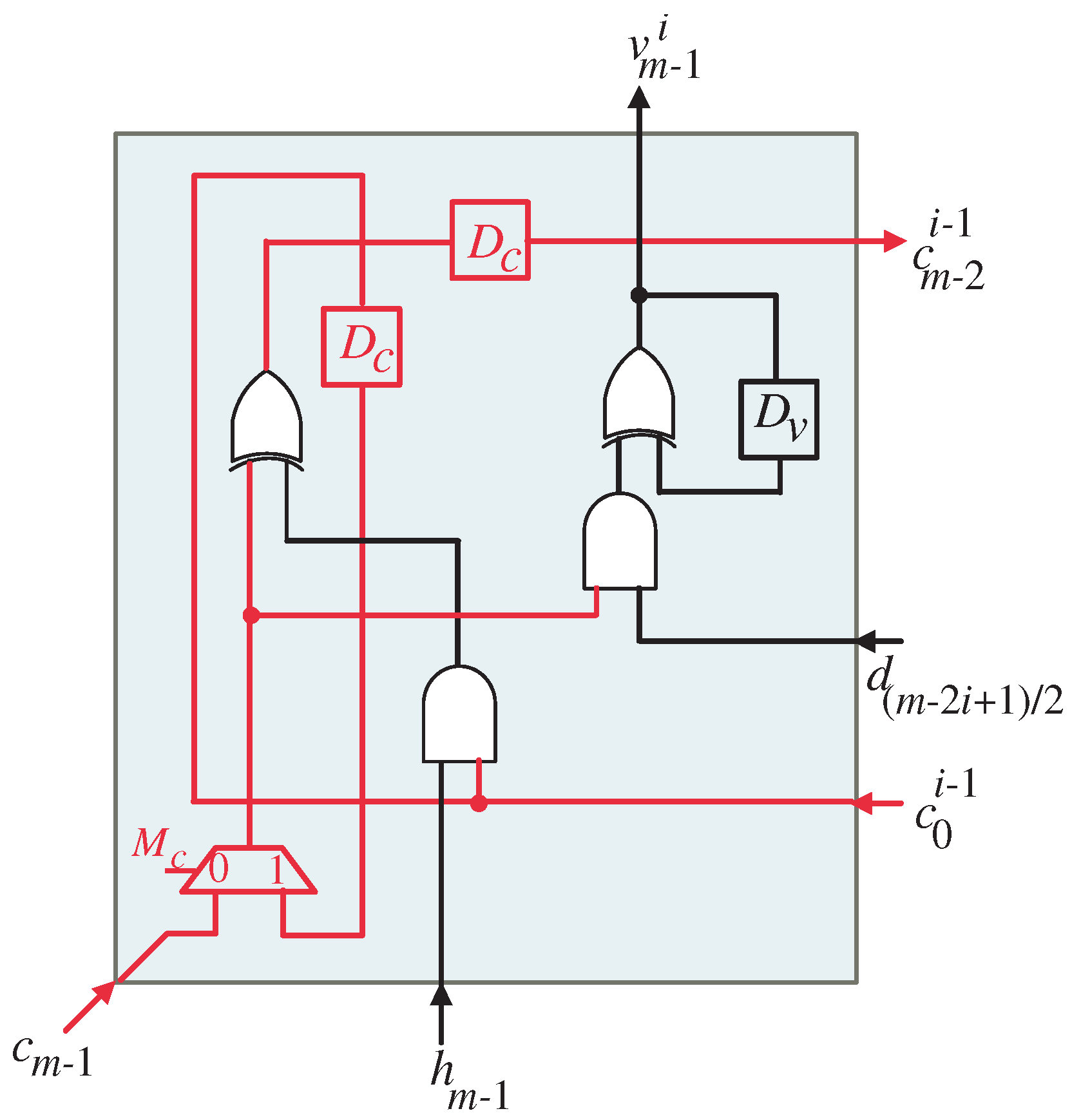
4. Dependency Graph

The iterative portion of the Montgomery multiplication algorithm involves recursive Equations (3), (6), (8) and (11) that describe the computation steps. These equations have a similar computation structure but differ in terms of their coordinate directions. To better understand the computational dependencies and patterns in the algorithm, we can represent them using DGs. These DGs provide a visual representation of the computations involved in the iterative portion of the algorithm. In this case, we have derived DGs for a specific field size of $m=5$, which are displayed in Figure 2 and Figure 3. These graphs are defined in a two-dimensional integer domain $\mathbb{D}$, with indices i and j indicating the nodes in the graph.

By analyzing the DGs, we can gain insights into the parallelism and coordination of the computations in the algorithm. Each node in the DG represents a computation step, and the edges between nodes indicate the dependencies between these steps. The iterative formulas of the algorithm are computed by these nodes, which can be organized and scheduled to exploit parallelism and optimize performance.

The DGs provide valuable information for designing efficient hardware architectures for the Montgomery multiplication algorithm. By understanding the dependencies and patterns in the iterative computations, it is possible to develop specialized structures that maximize parallelism, minimize resource usage, and optimize performance. These architectures can be particularly beneficial in the context of VLSI implementation, where efficient hardware utilization is crucial.

In Figure 2, the data entry points within the DG are organized along designated pathways to facilitate an orderly processing sequence. The following section outlines the various input pathways along with their associated signals:

• Left-to-Right pathway: This pathway serves to introduce the input signals $d_{(m+2i-3)/2}$, with $1\le i\le (m+1)/2$. These signals are fed into the DG from the left edge, ensuring a smooth integration into the processing sequence. The notation $(m+2i-3)/2$ indicates the specific indexing of the input signals based on the field size m.
• Top Entry Point: The top portion of the DG serves as the entry point for the input signals $h_j$ and the initial zero values of signals $u_{j-1}$, where $1\le j\le m$.
• Red Slanted Lines: The reddish angled lines at the rightmost spots of the entry points are for the insertion of the input signals $c_{j-1}$, where $1\le j\le m$.

Inside DG, each node computes the intermediate outputs of the coefficients associated with the variable U. Once calculated, these outputs are transmitted to the nodes located in the subsequent row, adhering to the pathways indicated by the arrows in the graph. This procedure persists until the final row of the DG is attained. At the bottom of the DG, the resulting coefficients of variable U are produced. These coefficients represent the final output of the computation process. By organizing the inputs and computations in this manner, the DG facilitates the calculation of intermediate partial products and the generation of the final output coefficients of variable U. The directional flow ensures that the computations are performed in the desired order and that the dependencies between the nodes are properly maintained.

In a similar fashion, the data entering the DG depicted in Figure 3 are strategically organized along specific pathways to enable the necessary calculations to occur. Let us take a closer look at these input paths and the various types of signals they convey:

• Right-to-Left pathway: The pathway moving from right to left serves to introduce the input signal $d_{(m-2i+1)/2}$, where i is constrained to be between 1 and $(m+1)/2$. These data points are fed into the DG from the lateral right edge.
• Bottom Entry Point: The lower section of the DG serves as the designated area for inserting the input signal $h_{m-j}$ alongside the starting values of zero for the signal $v_{m-j}$. This insertion takes place for indices satisfying the condition $1\le j\le m$.
• Red Slanted Lines: The red slanted lines depicted at the left corners of the input nodes are used to insert the input signals $c_{m-j}$, where $1\le j\le m$.

Within the DG, each node calculates the cumulative totals of the V data coefficients. These totals are then passed on to the nodes in the next row, following the paths indicated by the arrows in the diagram. This ensures that each node builds upon the information received from the previous row. This iterative process continues until the uppermost row of the DG is attained, providing a comprehensive overview of the data. At the top of the DG, the resulting coefficients of variable V are produced. These coefficients represent the final output of the computational process.

The final product T is obtained by summing the resulting coefficients of $U^{(m+1)/2}$ and $V^{(m+1)/2}$. To implement this summation, 2-input XOR gates can be utilized. Each corresponding bit of the coefficients is connected to an input of the XOR gate. The outputs of the XOR gates are then combined to obtain the final result T.

5. Development of the Semi-Systolic Multiplier Architecture

In this section, we utilize the previously outlined approach by the authors to develop a one-dimensional concurrent semi-systolic multiplier framework [55,56,57]. This method incorporates scheduling and node projection techniques, which are implemented within the Data Graphs (DGs) to create a high-performance parallel multiplier configuration derived from the selected Montgomery algorithm. We will apply this approach to the first DG illustrated in Figure 2. The second DG, depicted in Figure 3, features a similar configuration but differs in the orientation of its coordinates. Despite these directional variations, both structures will yield the same semi-systolic configuration, with signals directed oppositely.

5.1. Scheduling Function

In analyzing the structure of the DG shown in Figure 2, we consider the individual points (nodes) that are represented as coordinates. Each of these points is denoted as $\mathbf{p}(i,j)=\left[ij\right]$. To determine the execution sequence for each point, we utilize a scheduling vector $\mathbf{s}=\left[s_0{s}_1\right]$, along with a corresponding scheduling function. The scheduling function, represented as $L\left(\mathbf{p}\right)$, can be defined as:

$$L\left(\mathbf{p}\right)=\mathbf{s}\mathbf{p}-k=i{s}_0+j{s}_1-k$$

(12)

where $\mathbf{p}$ represents the position vector $\left[ij\right]$, which indicates the specific location within the DG, while k is a scalar value that may denote a constant or a specific parameter relevant to our calculations. The purpose of incorporating k is to ensure that only positive time values are assigned to the DG nodes. In this case, selecting $k\equiv 0$ guarantees that all nodes in the DG shown in Figure 2 are allocated positive time values.

The scheduling vector $\mathbf{s}=\left[s_0{s}_1\right]$ must adhere to specific constraints. One important constraint stipulates that nodes positioned at $\mathbf{p}=[i,j]$ should only begin execution after the completion of the nodes located at $\mathbf{p}=[i-1,j]$. This requirement ensures proper sequencing of operations and can be expressed as the inequality:

$$L(\mathbf{p}=[i,j\left]\right)>L(\mathbf{p}=[i-1,j\left]\right)$$

(13)

When considering the coordinate values of the scheduling vector $\mathbf{s}$, this inequality can be formulated as:

$$\begin{array}{ccc}\hfill i{s}_0+j{s}_1& >& (i-1)s_0+j{s}_1\hfill \\ \hfill s_0& >& 0\hfill \end{array}$$

(14)

The previously outlined condition on the timing vector $\mathbf{s}$ stipulates that the time value designated for a node at $\mathbf{p}=[i,j]$ must exceed the time value designated for the node at $\mathbf{p}=[i-1,j]$. This requirement is crucial for maintaining the correct order of execution, as it prevents any potential conflicts that could arise from overlapping operations. By following this constraint, the desired operational sequence of nodes within the DG can be effectively realized, ultimately leading to a more efficient processing of tasks and better resource management.

Based on the given iterations in Equations (3), (6), (8), and (11), we have an additional timing restriction. In particular, it is imperative that tasks assigned to points $\mathbf{p}=[i,j+1]$ are executed only after the completion of tasks associated with points $\mathbf{p}=[i-1,j]$. This sequential dependency is critical for maintaining the integrity of the operations, as it ensures that all prerequisite tasks are completed before proceeding to subsequent ones. This relationship can be formally expressed as:

$$L(\mathbf{p}=[i,j+1\left]\right)>L(\mathbf{p}=[i-1,j\left]\right)$$

(15)

Expanding the expressions using the coordinate values of $\mathbf{s}$, we have:

$$\begin{array}{ccc}\hfill i{s}_0+j{s}_1+s_1& >& i{s}_0-s_0+j{s}_1\hfill \\ \hfill s_1& >& -s_0\hfill \end{array}$$

(16)

This relational expression delineates the temporal constraint imposed on the scheduling vector $\mathbf{s}$. It verifies that the time indicator of a node situated at $\mathbf{p}=[i,j+1]$ must exceed the time indicator of the node positioned at $\mathbf{p}=[i-1,j]$. By enforcing this limitation, the intended sequence of operational execution within the DG is secured, thereby facilitating a more efficient and coherent workflow in task processing.

By examining the relational Expressions (14) and (16), we can identify appropriate scheduling vectors that satisfy the established constraints. These expressions provide a framework for analyzing the dependencies between tasks, enabling us to derive vectors that ensure the correct sequence of execution. A viable option for a compliant scheduling vector is:

$$\begin{array}{ccc}\hfill \mathbf{s}& =\hfill & \hfill \left[\begin{array}{cc}1& 0\end{array}\right]\end{array}$$

(17)

The timing arrangement of the nodes, following the implementation of this scheduling vector on the DGs, is visualized in Figure 4 and Figure 5. A review of these diagrams reveals that the incoming signals $c_{j-1}$, $c_{m-j}$, $h_j$, and $h_{m-j}$ are processed concurrently. Following $(m+1)/2$ clock cycles, the produced signals $u_{j-1}$ and $v_{m-j}$ (for values of j ranging from 1 to m) are produced simultaneously. This observation highlights the effectiveness of the scheduling vector in optimizing task execution within the DGs.

5.2. Projection Function

Based on the research performed by the second contributor, the projection function is essential for converting a multitude of DG nodes or locations, represented by $\mathbf{p}(i,j)$, into one unified processing element $\overline{\mathbf{p}}$ [55]. This transformation facilitates efficient data handling and processing within the system. Through the interconnection of these processing elements, a systolic or semi-systolic arrangement is formed, optimizing performance and resource utilization. The projection function can be represented as:

$$\overline{\mathbf{p}}=\mathbf{G}\mathbf{p}$$

(18)

In this formulation, $\mathbf{G}$ denotes the projection matrix. To establish this projection matrix, it is necessary to determine the null space associated with it, referred to as $\mathbf{E}$. As highlighted in [55], it is vital to apply a particular constraint on the projection vector $\mathbf{E}$ to guarantee both robustness and accuracy in the resulting projections. This constraint is instrumental in maintaining the fidelity of the data being processed, thereby enhancing the effective use of the projection matrix in a range of applications.

$$\mathbf{sE}\ne \mathbf{0}$$

(19)

This constraint ensures that each processing element carries out its specific tasks at varied times, which allows for enhanced efficiency in the utilization of the processing elements through multiplexing. By distributing the workload across different time intervals, the system can minimize idle time and maximize throughput.

By considering the constraint outlined in Equation (19), along with the specified scheduling vector $\mathbf{s}=\left[10\right]$, we can better understand the implications for system design. Furthermore, given the requirement for a bit-parallel semi-systolic architecture, the projection vector that fulfills these specific conditions can be articulated as follows:

$$\begin{array}{ccc}\hfill \mathbf{E}& =\hfill & \hfill \left[\begin{array}{cc}1& 0\end{array}\right]\end{array}$$

(20)

This particular projection vector guarantees that both the scheduling vector $\mathbf{s}$ and the projection vector $\mathbf{E}$ conform to the constraint specified in Equation (19). Consequently, this alignment not only facilitates the development of a bit-parallel semi-systolic structure but also ensures that it exhibits the required characteristics for optimal performance in practical applications, ultimately contributing to improved efficiency and reliability in system operations.

The projection matrix $\mathbf{G}$ can be derived based on the fact that $\mathbf{E}$ is the null space of $\mathbf{G}$. It can be expressed as:

$$\begin{array}{ccc}\hfill \mathbf{G}& =\hfill & \hfill \left[\begin{array}{cc}0& 1\end{array}\right]\end{array}$$

(21)

This matrix serves to illustrate the transformation from the primary set of Directed Graph (DG) nodes or points to a singular processing element. This mapping not only clarifies the relationships among the nodes but also enhances the efficiency of data management within the processing architecture, ensuring that each node is effectively integrated into the computational framework.

5.3. Exploring the Design of Semi-Systolic Multiplier Layout

The functions $L\left(\mathbf{p}\right)$ and $\overline{\mathbf{p}}\left(\mathbf{p}\right)$ corresponding to each node $\mathbf{p}[i,j]$ within the DG presented in Figure 2 can be formulated by incorporating the vectors $\mathbf{s}=\left[10\right]$ and $\mathbf{G}=\left[01\right]$ into the Expressions (12) and (18). This methodological integration facilitates a precise definition of the resulting functions, which are integral to the analysis of the graph’s structural properties and operational dynamics. The resultant functions can be delineated as follows:

$$\begin{array}{c}\hfill L\left(\mathbf{p}\right)=i\\ \hfill \overline{\mathbf{p}}\left(\mathbf{p}\right)=j\end{array}$$

(22)

Applying a similar procedure to each DG node $\mathbf{p}[i,m-j]$ in Figure 3, we can determine the functions $L\left(\mathbf{p}\right)$ and $\overline{\mathbf{p}}\left(\mathbf{p}\right)$ as follows:

$$\begin{array}{c}\hfill L\left(\mathbf{p}\right)=i\\ \hfill \overline{\mathbf{p}}\left(\mathbf{p}\right)=m-j\end{array}$$

(23)

By utilizing the derived functions $L\left(\mathbf{p}\right)=i$ and $\overline{\mathbf{p}}\left(\mathbf{p}\right)=m-j$ for the DG nodes of Figure 2 and Figure 3, we can construct a bit-parallel semi-systolic multiplier structure, which is a computational architecture commonly used for high-performance multiplication operations. The structure is depicted in Figure 6 and consists of two one-dimensional semi-systolic arrays. Each array is composed of m Processing Elements (PEs) arranged in a linear fashion.

The upper semi-systolic array is responsible for computing the coefficients of the polynomial U. The internal logic of the intermediate PE is illustrated in Figure 7. This PE performs the necessary computations to generate the coefficients of the polynomial U based on the inputs it receives. It is worth noting that the first and last PEs shown in Figure 8 and Figure 9, respectively, are simplified versions of the intermediate PE. These simplified PEs may have reduced functionality compared to the intermediate PE, as they are located at the boundaries of the upper semi-systolic array.

The lower semi-systolic array, depicted in Figure 6, is responsible for computing the coefficients of the polynomial V. Each PE within the lower semi-systolic array performs specific computations to generate the coefficients of V based on the inputs it receives. The internal logic of the intermediate PE in the lower semi-systolic array is illustrated in Figure 10. This PE incorporates the necessary operations and calculations to compute the coefficients of the polynomial V. It is worth mentioning that the first and last PEs shown in Figure 11 and Figure 12, respectively, are simplified versions of the intermediate PE. These simplified PEs are designed to accommodate the specific requirements and constraints at the boundaries of the lower semi-systolic array. Their simplified design may involve reduced functionality compared to the intermediate PE.

In Figure 6, it can be observed that the inputs $u_{j-1}^0$ and $v_{m-j}^0$ are both equal to zero. This observation allows for optimizations in terms of area and delay complexities by resetting the $D_u$ and $D_v$ flip-flops (shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12) at the appropriate time. By resetting these flip-flops, the required zero values can be directly presented at the input of the XOR gate, eliminating the need for additional logic to compute those values. Furthermore, in the last PE, ${\mathrm{PE}}_m$, there is no need to compute the updated values of $c_j^i$ and $c_{m-j-1}^i$. Therefore, the logic structure responsible for computing these variables can be removed from ${\mathrm{PE}}_m$, resulting in a simplified design as shown in Figure 9 and Figure 12, respectively. This modification significantly reduces the area overhead of the semi-systolic array.

In contrast to the regular PEs, the first PE, ${\mathrm{PE}}_1$, utilizes the signals $c_{m-1}^{i-1}$ and $c_0^{i-1}$ as inputs to the multiplexer $M_c$ instead of $c_{j-1}^{i-1}$ and $c_{m-j}^{i-1}$. This configuration allows for assigning the signals $c_{m-1}^{i-1}$ and $c_0^{i-1}$ to the corresponding signals $c_0^i$ and $c_{m-1}^i$, effectively implementing the rotate right operation required in the computation process. Overall, these modifications result in a more optimized and streamlined semi-systolic array, reducing the spatial footprint and improving operational effectiveness by eliminating extraneous computations and refining the logical framework.

The introduced semi-systolic multiplier represents a noteworthy advancement compared to previously documented bi-dimensional parallel systolic architectures in terms of spatial complexity. While conventional bi-dimensional parallel systolic architectures typically exhibit a spatial complexity of magnitude $\mathcal{O}\left(m^2\right)$, the proposed semi-systolic multiplier achieves a more favorable spatial complexity of magnitude $\mathcal{O}\left(m\right)$, thus enabling more effective resource allocation. Specifically, when assessed against the Montgomery bi-dimensional parallel semi-systolic configurations detailed in [52,53], the proposed multiplier configuration showcases a superior spatial footprint. This reduction in spatial complexity facilitates a more optimal arrangement of hardware resources, thereby establishing the introduced multiplier configuration as a leading option in spatial performance. Furthermore, in contrast to parallel multipliers based on established field multiplication techniques, such as those referenced in [23,24,48,49,51,58,59], the proposed multiplier configuration presents significant advantages in spatial footprint. The forthcoming results and performance metrics will be elaborated upon in the results section, highlighting the superiority of the introduced multiplier configuration regarding both spatial and power complexities.

The layout of the developed parallel semi-systolic multiplier, based on the information from Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, can be described as follows:

• Input Signals: The input signals $c_{j-1}$, $c_{m-j}$, $h_j$, and $h_{m-j}$, where $1\le j\le m$, are assigned to each PE within the layout.
• Zero Initialization: The initial values of the input signals $u_{j-1}$ and $v_{m-j}$, where $1\le j\le m$, are set to zero. As a result, the inputs near the left corners of the upper PEs and the inputs near the right corners of the lower PEs are assigned zero values.
• Sequential Input Signals: The input signals $d_{(m+2i-3)/2}$ and $d_{(m-2i+1)/2}$, where $1\le i\le (m+1)/2$, are fed sequentially and pass through all the PEs. These input signals propagate through the PEs in a regular sequence.
• Intermediate Signal Generation: Each PE generates intermediate signals $c_{m-j-1}^i$ and $c_j^i$, where $1\le i\le (m+1)/2$ and $1\le j\le m$. These intermediate signals are computed based on the inputs received by each PE. The intermediate signals are pipelined through $D_c$ latches (solid red box in Figure 7, Figure 9, Figure 10 and Figure 12) and passed to the next PE.
• Parallel Output: The resulting bits of $u_{j-1}^{(m+1)/2}$ and $v_{m-j}^{(m+1)/2}$, with j taking values from 1 to m, are available simultaneously at the outputs of all PEs after $(m+1)/2$ clock cycles. In the final product calculation stage, during clock cycle $(m+1)/2$, the final product bits $t_{j-1}$, corresponding to j from 1 to m, are obtained by executing XOR operations using 2-input XOR gates. The resulting bits from XORing the matching bits of $u_{j-1}^{(m+1)/2}$ and $v_{j-1}^{(m+1)/2}$ contribute to the formation of the final outcome, $t_{j-1}$.
• Final Product Calculation: The final product bits $t_{j-1}$, where $1\le j\le m$, are obtained at clock cycle $(m+1)/2$ by adding (using 2-input XOR gates) the bits of $u_{j-1}^{(m+1)/2}$ and $v_{j-1}^{(m+1)/2}$.

The studied bit-parallel semi-systolic multiplier structure’s operation can be described in the following sequence:

• Initialization: In the first clock period, the latches $D_u$ and $D_v$ are reset, causing the input bits $u_{j-1}$ and $v_{m-j}$ (where $1\le j\le m$) to be set to zero. Simultaneously, the control signal of MUX $M_c$ is deactivated, allowing the input signals $c_{j-1}$ and $c_{m-j}$ (where $1\le j\le m$) to be passed to the corresponding PEs within the layout.
• Computation: Starting from the second clock period until clock period $(m+1)/2$, the control signal of MUX $M_c$ is activated. This enables the intermediate signals $c_{j-1}^{i-1}$ and $c_{m-j}^{i-1}$ (where $1\le j\le m$) to be passed through the PEs for the computation of the intermediate values $c_j^i$, $c_{m-j-1}^{i-1}$, $u_{j-1}^i$, and $v_{m-j}^i$ (where $1\le j\le m$). Additionally, during these clock cycles, the input signals $d_{(m+2i-3)/2}$ and $d_{(m-2i+1)/2}$ are sequentially fed into the system.
• Parallel Output: At clock period $(m+1)/2$, the parallel output bits of the product T, denoted as $t_{j-1}$ (where $1\le j\le m$), are simultaneously produced at the outputs of the XOR gates depicted in Figure 6.

6. Results and Discussion

In this section, we will assess the recommended bit-parallel semi-systolic multiplier alongside a range of notable systolic and semi-systolic multiplier frameworks documented in the current literature [23,24,48,51,52,53,58]. This section is structured into two distinct subsections. In the first subsection, we will examine the spatial and time-related complexities of the recommended configuration in conjunction with those of competing architectures. By thoroughly investigating and contrasting these complexities, we aim to uncover valuable insights into the resource allocation and speed performance of our configuration when compared to rival designs. Transitioning to the second subsection, we will substantiate the findings from the complexity analysis through practical implementation. By realizing the recommended configuration in a real-world setting, we can effectively evaluate its actual performance and juxtapose it against the anticipated complexities. This hands-on implementation will ensure that our complexity analysis accurately reflects the operational behavior of the recommended multiplier in practical applications, validating the theoretical insights gained earlier.

6.1. Complexity Analysis

Upon closer examination of the provided semi-systolic architecture depicted in Figure 6, we can deduce that it consists of a total of $2m$ PEs. Each PE is composed of a varied set of components, including $4m-2$ AND gates, $4m-2$ XOR gates, $2m$ MUX selectors, and $6m-2$ storage latches. These essential components work cohesively to carry out the necessary calculations within each PE, thereby ensuring optimal processing efficiency and enhancing system performance.

To generate the output bits, represented specifically as $t_j$, an additional array of m XOR gates is effectively employed in the architecture. These particular XOR gates have the specific role of merging the corresponding bits of $u_{j-1}^{(m+1)/2}$ and $v_{m-j}^{(m+1)/2}$, where j takes on values from 1 up to m, thereby facilitating accurate computations. As a result, the total number of XOR gates required by this architectural design ultimately amounts to $5m-2$.

To accurately assess the operational speed of the newly introduced multiplier, it is essential to evaluate the Critical Path Delay (CPD), as this metric serves as a crucial measure of overall performance and efficiency in the system. The critical path refers to the longest path that determines the overall delay in the circuit. In this case, the critical path consists of a 2-to-1 MUX ($T_M$) and a 2-input XOR gate ($T_X$). By carefully analyzing the logic within the PEs, we can calculate the cumulative propagation delays of these components and determine the CPD.

Taking into account the operational characteristics of the framework, it is crucial to observe that the newly introduced multiplier generates its final results within $(m+1)/2$ clock intervals. This noteworthy aspect signifies that the complete computation, which begins with the initiation of the multiplication process and extends to the generation of the ultimate output bits, is finalized within $(m+1)/2$ clock cycles. Such information is invaluable as it enables us to thoroughly evaluate the overall effectiveness and speed of the multiplier in this context.

Table 3. Complexity investigations of the anticipated and existent multipliers with regard to space and time.

Design	AND	XOR	MUX	Latch	Latency	CPD	Area	Time
							Complexity	Complexity
Kim [24]	$2m^2+2m$	$2m^2+3m$	0	$3m^2+4m$	$\lfloor {\displaystyle \frac{m}{2}}\rfloor +1$	$T_A+T_X$	$\mathcal{O}\left(m^2\right)$	$\mathcal{O}\left(m\right)$
Sarmadi [48]	($m^2$) *	$1.5m^2+0.5m$	$1.5m^2-2.5m+3$	$1.5m^2+2m-1$	$m+2$	$T_N+T_X$	$\mathcal{O}\left(m^2\right)$	$\mathcal{O}\left(m\right)$
Huang [23]	$2m^2$	$2m^2$	0	$2m^2+m+1$	$m+1$	$T_A+T_X$	$\mathcal{O}\left(m^2\right)$	$\mathcal{O}\left(m\right)$
Chiou [51]	$m^2$	$3m^2+2m$	0	$3m^2+4m$	$m+1$	$T_A+3T_X$	$\mathcal{O}\left(m^2\right)$	$\mathcal{O}\left(m\right)$
Lee [52]	$m^2+m$	$m^2+2m$	0	$1.6m^2+4m$	$(m+7)/2$	$T_A+T_X$	$\mathcal{O}\left(m^2\right)$	$\mathcal{O}\left(m\right)$
Lee [53]	$m^2+m$	$m^2+(7m+1)/2$	0	$2.1m^2+6.5m$	$(m+7)/2$	$T_A+T_X$	$\mathcal{O}\left(m^2\right)$	$\mathcal{O}\left(m\right)$
Chiou [58]	$m^2$	$m^2+m$	m	$2m^2+3m$	$m+1$	$T_A+T_X+T_M$	$\mathcal{O}\left(m^2\right)$	$\mathcal{O}\left(m\right)$
Proposed	$4m-2$	$5m-2$	$2m$	$6m-2$	$(m+1)/2$	$T_M+T_X$	$\mathcal{O}\left(m\right)$	$\mathcal{O}\left(m\right)$

(*) 2-input NAND gates.

presents a comprehensive comparison between the suggested semi-systolic multiplier arrangement and several existing parallel systolic/semi-systolic multiplier constructions [23,24,48,51,52,53,58]. The comparison is based on three key aspects: the overall utilization of components (gates, MUXs, and latches), latency, and CPD. From the results presented in Table 3, it is evident that the spatial complexity of the multiplier layouts proposed in [23,24,48,51,52,53,58] exhibits an order of $\mathcal{O}\left(m^2\right)$. This indicates that the number of components required grows quadratically with the input size m. In contrast, the suggested semi-systolic multiplier arrangement demonstrates a spatial complexity of $\mathcal{O}\left(m\right)$, which signifies a significant reduction in resource utilization. This reduction in space complexity has practical implications, especially for RFID assistive devices where limited resources and area constraints are common. Additionally, the comparison in Table 3 reveals that all the considered designs exhibit a time complexity of $\mathcal{O}\left(m\right)$. This means that the proposed semi-systolic multiplier arrangement achieves comparable computational efficiency in terms of time complexity while utilizing significantly fewer resources. The ability to achieve similar performance with reduced resource utilization is a desirable characteristic for many practical applications.

The suggested semi-systolic multiplier layout offers several advantages that make it particularly suitable for RFID assistive devices. Firstly, its space-efficient design leads to reduced area requirements, enabling efficient utilization of available hardware resources. This reduction in space complexity has a direct impact on the Area-Delay Product (ADP) and Power-Delay Product (PDP) of the multiplier, resulting in improved overall performance and energy efficiency.

The superiority of the suggested multiplier arrangement is further supported by real implementation results provided in

Table 4. Examining the effectiveness of various multiplier constructions for $m=409$ and $m=571$.

Multiplier	m	Area	Delay	Power	ADP	PDP	Area Saving	Power Saving	ADP Saving	PDP Saving
		[Kgates]	[ns]	[mW]			(%)	(%)	(%)	(%)
Kim [24]	409	9120.3	6.8	304.3	62,018.0	2069.2	99.7	95.6	99.7	95.2
	571	18,058.2	9.5	578.2	171,552.8	5492.6	99.7	95.9	99.7	95.5
Sarmadi [48]	409	6250.7	11.9	234.3	74,383.3	2788.2	99.6	94.3	99.7	96.4
	571	12,376.4	16.6	444.6	205,448.0	7380.4	99.6	94.7	99.7	96.6
Huang [23]	409	7680.9	13.5	267.7	103,692.2	3613.9	99.7	95.0	99.8	97.2
	571	15,208.2	18.9	508.6	287,434.6	9612.5	99.7	95.4	99.8	97.4
Chiou [51]	409	8790.7	22.6	292.3	198,669.8	6605.9	99.7	95.4	99.9	98.5
	571	17,405.586	31.5	555.4	548,275.959	17,495.1	99.7	95.8	99.9	98.5
Lee [52]	409	3802.7	6.9	158.2	26,238.63	1091.6	99.4	91.6	99.3	90.9
	571	7529.3	9.5	300.6	71,528.8	2855.7	99.4	92.2	99.3	91.3
Lee [53]	409	5450.3	6.9	202.9	37,607.1	1400.0	99.5	93.4	99.5	92.9
	571	10,791.6	9.5	385.5	102,520.1	3662.3	99.5	93.9	99.5	93.2
Chiou [58]	409	4731.1	18.5	188.7	87,525.4	3490.9	99.5	93.0	99.8	97.1
	571	9367.6	25.7	358.5	240,746.8	9213.5	99.5	93.5	99.8	97.3
Proposed	409	22.5	7.5	13.2	150.8	88.4	-	-	-
	571	44.6	10.6	23.2	418.8	218.1	-	-	-

. These results validate the claims regarding reduced space complexity, improved ADP, and PDP. By reducing resource utilization while maintaining comparable performance, the suggested multiplier layout offers practical benefits for RFID-Based assistive devices where power consumption, area utilization, and overall efficiency are critical considerations.

6.2. Implementation Results

The suggested semi-systolic multiplier arrangement and the existing systolic/semi-systolic multiplier constructions [23,24,48,51,52,53,58] were thoroughly evaluated and compared using a comprehensive methodology. The VHDL programming language was employed to meticulously design and implement the various configurations of the multiplier. Additionally, the transformation phase was expertly carried out using the Synopsys Design Compiler, leveraging the Nangate library (15 nm, 0.8 V) for optimal results. This comprehensive setup allows for accurate and detailed evaluations of key performance metrics, including area footprint, latency, and power consumption, ensuring a thorough analysis at a highly detailed resolution. To ensure the correctness and functionality of the multiplier designs, thorough functional verification was conducted using ModelSim’s simulation tools. This verification process involved extensive testbench development and simulation runs to validate the correctness of the multiplier’s output for various input scenarios. Only after the functional verification process was successfully completed, the multiplier designs proceeded to synthesis. During the synthesis phase, the VHDL code for each specific multiplier layout underwent a careful transformation into a gate-level netlist utilizing the Synopsys Design Compiler. The Nangate library, which provides crucial technology-specific details such as gate dimensions, interconnect delays, and power characteristics, was integral to the synthesis process. The Design Compiler optimized the netlist according to defined constraints, such as area and power targets, ultimately producing a refined gate-level implementation for each distinct multiplier design. Once the synthesis process was completed, the area, delay, and power consumption metrics for each design were meticulously gathered from the resulting synthesized netlists. These vital metrics played a key role in enabling a thorough evaluation and comparison of the performance characteristics across the various multiplier layouts.

Table 4 presents a comprehensive overview of the synthesized results for the suggested semi-systolic multiplier architecture, which is analyzed in comparison with existing designs for field sizes $m=409$ and $m=571$ [23,24,48,51,52,53,58]. The key performance metrics of interest—namely, area, delay, power consumption, ADP, and PDP—were meticulously derived from the synthesis results obtained across the various implementations. This detailed analysis not only highlights the strengths and weaknesses of each design but also enables a more insightful evaluation of the performance differences among them.

By inspecting the eighth and ninth columns of Table 4, it is evident that the suggested semi-systolic multiplier arrangement achieves significant reductions in both spatial utilization and power consumption when contrasted with the current frameworks. The reduction in spatial usage ranges from 99.4% to 99.7% for both field sizes, indicating a substantial decrease in the required hardware resources, which is critical in applications where space is limited. Similarly, the power consumption reduction ranges from 91.6% to 95.9% for $m=409$ and 92.3% to 95.9% for $m=571$, reflecting a significant improvement in energy efficiency that is essential for prolonging the operational lifespan of battery-powered devices. Indeed, these results highlight that the suggested bit-parallel semi-systolic multiplier demonstrates significant space and power savings, making it highly suitable for deployment in resource-constrained RFID sensor tags tailored for disabled individuals, where minimizing hardware resources and power consumption is of utmost importance.

Upon analyzing the fourth column of Table 4, it is worth noting that the suggested design exhibits slightly higher delay compared to some of the existing designs. This is primarily due to the slightly increased CPD in the proposed layout. The CPD represents the longest delay path in the multiplier circuit and can affect the overall performance. Despite this slight increase in delay, the suggested design still offers comparable computational efficiency in terms of time complexity, making it suitable for RFID tags, where timely computations are essential for user experience. In assistive devices reliant on real-time data processing, even minor delays can adversely affect functionality and satisfaction. Moreover, the design’s efficiency in handling multiplication operations supports the used complex ECC cryptographic algorithm. Ultimately, the combination of space and power savings with a comparable delay underscores the viability of this design in enhancing the performance of RFID assistive system that require real-time processing.

In examining the last two columns of Table 4, it is crucial to emphasize that the proposed semi-systolic multiplier arrangement significantly outperforms existing designs in terms of ADP and PDP, achieving ADP reductions between 99.3% and 99.9% for both field sizes. This improvement is crucial for RFID tags tailored for individuals with disabilities, as lower ADP values facilitate compact integration into assistive devices without sacrificing performance. Moreover, the reductions in power-delay product (PDP)—ranging from 90.9% to 98.5% for $m=409$ and from 91.4% to 98.6% for $m=571$—underscore significant improvements in energy efficiency, which are crucial for battery-operated devices. Extended battery life can directly improve usability and reliability, allowing users to depend on these technologies throughout their daily activities. The design’s ability to maintain high performance while minimizing area and power usage aligns with the real-time data processing needs of assistive technologies. Improved energy management not only enhances user experience but also supports the development of sustainable solutions, ensuring that RFID systems provide critical support without imposing additional burdens on users. Ultimately, these results underscore the design’s potential to significantly enhance the performance and efficiency of RFID tags, making them more accessible and effective for individuals with disabilities.

Considering the aforementioned deign features, the proposed bit-parallel semi-systolic multiplier architecture presents significant advantages in terms of resource efficiency and energy conservation, thereby rendering it particularly suitable for deployment in RFID assistive devices characterized by limited computational resources. Optimizing energy consumption in such devices is crucial, as it can lead to extended operational lifetimes, reduced maintenance costs, and enhanced overall user satisfaction. Furthermore, the architecture’s capacity to deliver robust performance within a compact form factor facilitates seamless integration into assistive technologies, ultimately improving accessibility and enriching the user experience. By effectively balancing high performance with minimal resource consumption, this design addresses the challenges associated with real-time data processing while promoting the development of sustainable technological solutions. Additionally, the architecture significantly enhances the implementation of complex ECC algorithms on RFID tags, as it is central to ECC’s operational functionality. ECC has been recognized for its effectiveness in safeguarding sensitive data within assistive technologies, with empirical studies demonstrating that its adoption can substantially improve security levels, thereby ensuring greater reliability and trustworthiness for users.

In conclusion, the findings affirm the architecture’s potential as a transformative solution for RFID assistive systems, markedly enhancing security for disabled users who depend on these essential technologies. This architecture not only meets operational requirements but also aligns with broader objectives aimed at promoting secure accessibility for individuals with disabilities. Recent evaluations indicate that enhancing security features in assistive devices not only protects sensitive information but also bolsters user confidence, ultimately empowering users with disabilities and improving their overall quality of life.

7. Summary and Conclusions

This research work focused on enhancing cryptographic protocols in low-cost RFID assistive devices. To achieve this goal, we considered the implementation of the essential operation of these protocols, which is finite field multiplication. We developed a novel and highly efficient one-dimensional bit-parallel semi-systolic array layout for polynomial-basis Montgomery multiplication in GF($2^m$). The approach adopted in this work involves applying a conventional iterative algorithm represented by a DG. By assigning suitable scheduling and node projection functions to each node in the DG, a practical construction of a bit-parallel semi-systolic multiplier is achieved. This innovative design enables efficient and high-speed multiplication operations in GF($2^m$) using the Montgomery multiplication technique. The key advantage of the proposed one-dimensional parallel arrangement is its significantly reduced spatial complexity. Unlike previous parallel structures with a spatial complexity of $\mathcal{O}\left(m^2\right)$, the suggested layout exhibits a spatial complexity of $\mathcal{O}\left(m\right)$. This represents a substantial improvement in terms of resource utilization, making it highly suitable for VLSI implementation. The complexity analysis demonstrated that the suggested multiplier has a considerably smaller total area, further validating its efficiency and suitability for implementation. To evaluate the effectiveness of the recommended multiplier construction, both the proposed design and previously presented multiplier layouts were synthesized using the ASIC CMOS library. The findings from the synthesis process confirmed the substantial area and power reductions achieved by the proposed multiplier architecture. Additionally, important metrics such as PDP and ADP showed significant savings, reinforcing the efficiency gains of the suggested design. Based on these findings, it is evident that the proposed multiplier paradigm significantly enhances the implementation of complex ECC algorithm on low-cost RFID tags employed in assistive systems, ensuring greater reliability and trustworthiness for users.