Abstract
Achieving Artificial General Intelligence (AGI) requires a unified framework capable of modeling the full spectrum of intelligent behavior—from logical reasoning and sensory perception to emotional regulation and collective decision-making. This paper proposes Constrained Object Hierarchies (COH), a neuroscience-inspired theoretical model that represents intelligent systems as hierarchical compositions of objects governed by symbolic structure, neural adaptation, and constraint-based control. Each object is formally defined by a 9-tuple structure: , encapsulating its Components, Attributes, Methods, Neural components, Embedding, and governing Identity constraints, Trigger constraints, Goal constraints, and Constraint Daemons. To demonstrate the scope and versatility of COH, we formalize nine distinct intelligence types—including computational, perceptual, motor, affective, and embodied intelligence—each with detailed COH parameters and implementation blueprints. To operationalize the framework, we introduce GISMOL, a Python-based toolkit for instantiating COH objects and executing their constraint systems and neural components. GISMOL supports modular development and integration of intelligent agents, enabling a structured methodology for AGI system design. By unifying symbolic and connectionist paradigms within a constraint-governed architecture, COH provides a scalable and explainable foundation for building general purpose intelligent systems. A comprehensive summary of the research contributions is presented right after the introduction.
1. Introduction
The field of artificial intelligence has historically oscillated between paradigms—symbolic AI, which excels at rule-based reasoning, and connectionist AI, which dominates pattern recognition [1]. A significant challenge on the path to AGI is the integration of these paradigms into a cohesive architecture that can exhibit the structural, adaptive, and constraint-based nature of biological intelligence [2]. Existing cognitive architectures, such as SOAR [3] and ACT-R [4], provide robust models for specific cognitive processes but often lack a flexible, unifying formalism for the vast spectrum of intelligence types described by psychological and computational theories [5,6].
This paper presents the Constrained Object Hierarchies (COH) framework, designed to address this integration challenge. COH is predicated on the neuroscientific principle of functional hierarchy and constrained computation [7,8]. It models any intelligent agent, from a single module to a full AGI, as a compositional hierarchy of objects, each defined by a precise 9-tuple. This formalism allows for the seamless combination of symbolic components (C, A, M) with neural adaptive elements (N, E), all under the governance of a rich constraint system (I, T, G, D) that ensures stability, triggers appropriate behaviors, and pursues goals.
2. Contributions of Research
This research makes the following key contributions:
- Introduced the Constrained Object Hierarchies (COH) framework, a unified, neuroscience-grounded model for representing intelligent systems using a structured 9-tuple formalism.
- Provided detailed formalizations for 9 heterogeneous intelligence types, demonstrating COH’s versatility across human-centric, artificial, and collective domains.
- Bridged symbolic and connectionist paradigms by explicitly integrating symbolic components with neural models and constraint-based governance.
- Briefly presented the GISMOL toolkit—a Python 3.12.3-based implementation platform for COH objects, enabling practical AGI system development.
- Proposed a structured design methodology for AGI, supporting modular development, validation, and integration of specialized intelligences into cohesive agents.
- A Structured Methodology for AGI Development: Collectively, this work provides more than a model; it offers a structured methodology for designing and implementing intelligent systems. By advocating for a design process that begins with the identification of components, attributes, methods, and governing constraints, the COH framework brings a disciplined, architectural approach to AGI construction. It facilitates a divide-and-conquer strategy where specialized intelligences can be developed, validated, and subsequently integrated into a cohesive, general-purpose agent, thereby addressing the complexity and scalability challenges inherent in AGI projects.
In summary, this paper contributes a new theoretical model, a unifying formalism for intelligence, a solution for neural-symbolic integration, a practical implementation toolkit, and a structured design methodology. It provides a comprehensive foundation for future work aimed at building integrated, scalable, and ultimately general intelligent systems.
The subsequent sections are structured as follows: a review of related work, a detailed exposition of the COH framework, a systematic formalization of each intelligence type as a COH object, and a discussion on the implementation pathway via GISMOL.
3. Literature Review
The quest for Artificial General Intelligence has produced several promising research directions, each with significant strengths and limitations. By examining these approaches, we can clearly identify the specific gaps that the COH/GISMOL framework aims to bridge.
3.1. Cognitive Architectures: Symbolic Power Without Neural Fluidity
Traditional cognitive architectures like ACT-R [4] and SOAR [3] represent the symbolic approach to intelligence. These systems excel at explicit reasoning, structured knowledge representation, and goal-directed behavior with transparent decision processes. ACT-R models human cognition through production rules and declarative memory, while SOAR emphasizes goal-directed reasoning and problem solving [3,4].
These architectures demonstrate how symbolic reasoning can produce human-like thought patterns, but they lack the fluid, adaptive learning capabilities needed for general intelligence in dynamic environments. They suffer from brittle learning mechanisms, poor handling of uncertainty and noisy real-world data, limited perceptual-motor integration, and manual knowledge engineering requirements that scale poorly.
3.2. Deep Learning Systems: Neural Power Without Symbolic Grounding
Modern deep learning approaches [8] have revolutionized pattern recognition and demonstrated remarkable capabilities in learning from raw data, handling uncertainty, scaling with computational resources, and excelling at perceptual tasks like vision, speech, and language modeling. The success of large language models and computer vision systems demonstrates the power of neural approaches for specific domains.
However, they face fundamental challenges for AGI. While providing unprecedented learning power, these systems lack structured reasoning, explicit knowledge representation, and safety guarantees required for trustworthy AGI. Their black box nature limits interpretability and explainability, they suffer from catastrophic forgetting and lack systematic knowledge composition, they struggle to incorporate explicit knowledge or safety constraints, and they exhibit sample inefficiency compared to human learning.
3.3. Neural-Symbolic Integration: Promising but Limited Synthesis
Neural-symbolic integration seeks to marry the pattern recognition strength of neural networks with the reasoning and explicit knowledge representation of symbolic AI [9]. Frameworks like TensorLog [10] explore differentiable reasoning, while other approaches focus on symbol grounding or hybrid architectures that route different tasks to appropriate subsystems.
Existing neural-symbolic approaches typically treat neural and symbolic processing as separate concerns to be integrated, rather than as intrinsically linked aspects of a unified intelligence model. They often feature loose coupling between components, one-way integration (typically using neural networks to support symbolic reasoning), limited constraint integration where safety and coherence constraints are not first-class citizens, and no unified formal model for different intelligence types.
3.4. Constraint-Based AI: Safety Without Adaptation
Constraint satisfaction [11] and verification approaches provide formal guarantees about system behavior, explicit specification of requirements and invariants, and compositional reasoning about complex system properties. These approaches are crucial for safety-critical applications and provide mathematical rigor to system design.
While providing crucial safety and verification capabilities, constraint-based approaches lack the learning and adaptation mechanisms necessary for general intelligence. They typically feature static constraint systems that do not adapt or learn, poor scalability to complex high-dimensional problems, manual constraint specification requirements, and no inherent learning mechanisms from experience.
3.5. COH Treatments to the Identified Gaps
The COH framework specifically targets the integration gaps left by previous approaches:
Unified Formal Model for All Intelligence Types
Previous approaches require different architectures for different intelligences (e.g., CNNs for vision, RNNs for sequence processing, symbolic engines for reasoning).
COH/GISMOL solution: The 9-tuple formalization provides a universal representation that can instantiate perceptual, motor, cognitive, social, and other intelligences within the same structural framework.
Intrinsic Neural-Symbolic Integration
Previous approaches treat neural and symbolic processing as separate components to be connected.
COH/GISMOL solution: Neural components (N) and symbolic constraints (I, T, G) are fundamental, co-equal aspects of every intelligent object, enabling continuous bidirectional interaction.
Pervasive Constraint Governance
Previous approaches add safety constraints as external verification layers or reward shaping in RL.
COH/GISMOL solution: Constraints are first-class citizens in the object model, with dedicated daemons (D) that continuously monitor and enforce them during both learning and execution.
Compositional Safety Guarantees
Previous approaches struggle to maintain safety guarantees when composing multiple learned components.
COH/GISMOL solution: Hierarchical constraint propagation ensures that safety properties defined at high levels automatically enforce safety in all sub-components, regardless of their neural complexity.
Continuous Adaptation with Coherence Maintenance
Previous approaches typically sacrifice either adaptability (symbolic systems) or coherence (neural systems).
COH/GISMOL solution: The framework enables continuous neural learning while maintaining symbolic coherence through constraint satisfaction, with daemons triggering retraining or symbolic reasoning when constraints are violated.
Explainable Learning and Decision Making
Previous approaches often choose between powerful learning (black box neural) and explainability (transparent symbolic).
COH/GISMOL solution: Decisions can be traced through the constraint system, showing which rules and goals influenced behavior, while neural components provide the adaptive capabilities.
3.6. The Unique Synthesis of COH/GISMOL
The COH framework draws inspiration from these areas but introduces a unique synthesis. Its core innovation lies in its compositional hierarchy, where every object, from a simple reflex to an AGI, is built from the same formal structure, and its pervasive constraint system (I, T, G, D) that governs behavior at every level of the hierarchy. This makes COH both a descriptive model for intelligence and a prescriptive blueprint for its construction, a duality not fully realized in previous architectures.
COH/GISMOL does not merely combine existing approaches but provides a novel synthesis through:
- A neuroscience-grounded formal model that treats constraints as fundamental to intelligence, mirroring how biological brains maintain homeostasis and adhere to physical and social constraints.
- A practical implementation toolkit that makes this formal model directly executable, enabling rapid prototyping and testing of general intelligent systems.
- A compositional architecture where intelligences can be combined hierarchically while maintaining system-wide properties through constraint propagation.
This synthesis aims to bridge the critical gaps between learning and reasoning, adaptation and safety, specialization and generality that have hindered progress toward AGI. The following sections demonstrate how this bridge enables the formalization and implementation of diverse intelligence types within a unified architecture, addressing the very limitations that have kept previous approaches from achieving general intelligence.
4. The COH Framework: A Formal Definition
A Constrained Object Hierarchy (COH) is a formal system designed to represent a fundamental intelligent entity within an intelligent system. It is defined recursively as every object is itself composed of sub-objects. The complete state of an intelligent agent is therefore a complex, interacting graph of COH instances. The fundamental unit, a single Constrained Object O, is formally represented as a 9-tuple:
O = (C, A, M, N, E, I, T, G, D)
4.1. Structural and State Components (C, A, M)
These components define the object’s structure, state, and available actions.
C: Components. This is a set of sub-objects that compose the current object. C = {O1, O2, …, Oₖ}. This establishes the compositional hierarchy. A primitive object (e.g., a sensory pixel) has C = ∅.
A: Attributes. This is a set of state variables that describe the object’s current state. A = {a1: v1, a2: v2, …, aₙ: vₙ}, where vᵢ can be a scalar, vector, or symbolic value.
M: Methods. This is a set of executable procedures or actions that can be invoked to change the object’s state or affect its environment. M = {m1, m2, …, mₚ}. Each method mᵢ can be seen as a function that operates on A and possibly the attributes of objects in C.
4.2. Adaptive Components (N, E)
These components endow the object with the ability to learn and adapt, providing the sub-symbolic, continuous grounding for the symbolic structure.
N: Neural Components. This is a set of adaptive, typically parameterized models (e.g., neural networks, Bayesian filters) associated with the object. N = {n1(θ1), n2(θ2), …}. A component nᵢ could be responsible for predicting an attribute’s value, classifying the object’s state, or learning the preconditions for a method mᵢ.
E: Embedding Neural Component. This is a specific, often central, neural component that learns a dense vector representation (an embedding) for the entire object based on its state (A), the state of its components (C), and its context. e = E(A, A_C, context; θ_E). This embedding serves as a subsymbolic summary that can be used for similarity comparison, semantic reasoning, and as an input to other models in N.
4.3. Constraint System (I, T, G, D)
This is the core innovation of the COH model, defining the “rules of engagement” for the object.
I: Identity Constraints. These are invariant rules that define the object’s fundamental nature and must always hold. They are expressed as first-order logic predicates over A and C. I = {∀t, ϕ1(A(t), C(t)), ∀t, ϕ2(A(t), C(t)), …}. If an identity constraint is violated, the object is in an invalid or error state. For example, an object representing a “door” might have I = {is_open ∈ {True, False}}.
T: Trigger Constraints. These are event-condition-action (ECA) rules that define reactive behavior. T = {(event, condition, action)}. The event can be a change in A, a method call, or a signal from a parent/child object. The condition is a predicate checked against the state. The action is a method (from M or a sub-object’s M) to be executed. This provides a formal mechanism for hard-coded or learned reflexes.
G: Goal Constraints. These are optimization objectives that the object should strive to achieve. They are expressed as functions to be maximized or minimized. G = {maximize f1(A), minimize f2(A), …}. These can be intrinsic (e.g., an agent’s energy level) or extrinsic (assigned by a parent object). This aligns the object’s behavior with overall system goals.
D: Constraint Daemons. These are continuous background processes that monitor the constraint satisfaction levels. A daemon dᵢ ∈ D continuously evaluates a constraint (from I, T, or G) and can activate methods or signal other objects if a constraint is nearing violation or if an optimization opportunity is detected. D ensures the constraints are active, dynamic forces, not passive statements.
4.4. Neuroscientific Correlates of the COH Model
The COH model is not merely an engineering construct; its components are designed to mirror organizational principles observed in the mammalian brain.
The hierarchical composition (C) directly reflects the layered structure of the neocortex, particularly the feedforward and feedback pathways in the sensory and frontal hierarchies [12]. The Attributes (A) correspond to the persistent activity patterns observed in working memory [13]. The Methods (M) find their correlation in the population codes of the motor cortex that generate specific actions [14].
Critically, the adaptive components N and E are modeled on the brain’s capacity for predictive coding and representation learning. The Embedding (E) can be seen as the role of the hippocampus and surrounding medial temporal lobe structures in creating cognitive maps and relational representations [15]. The Neural Components (N) collectively represent the vast repertoire of learned predictive models throughout the cortex [16]. Recent predictive-coding work demonstrates automated construction of cognitive maps from visual input [17].
The constraint system within the COH framework exhibits strong parallels with established neuroscientific structures. Identity Constraints (I) correspond to the ventral visual stream and conceptual networks, which are responsible for invariant object recognition and categorical stability [18]. Trigger Constraints (T) reflect the role of the amygdala and basal ganglia in mediating rapid, conditioned responses to stimuli—essential for reflexive and adaptive behavior [19]. Goal Constraints (G) align with the functions of the prefrontal cortex and anterior cingulate cortex, which are central to maintaining goal representations, evaluating outcomes, and guiding executive control [20]. Finally, Constraint Daemons (D) are analogous to the default mode network and thalamic regulatory systems, which continuously monitor internal states, maintain system homeostasis, and signal salient events to higher-order cognitive centers [21].
This formalism offers a universal language for both deconstructing and designing intelligent systems. To demonstrate its unified expressive power, in the next two sections we formalize a comprehensive set of known intelligence types using the COH theoretical model. Detailed justifications for each formalization are provided under each intelligence type. Due to the modular and declarative nature of the COH framework, these formalizations and formalizations of intelligent systems can be implemented as executable intelligent systems using any modern programming language. In Section 6, we illustrate this process by presenting an implementation of an autonomous vehicle using GISMOL, a Python-based toolkit being developed specifically to instantiate and execute COH objects.
5. Formalization of Artificial and Computational Intelligences
The versatility of the COH framework extends beyond modeling human cognition to providing a unified architecture for artificial and collective intelligences. This section formalizes a spectrum of machine-oriented intelligence types, from the perceptual and motor capabilities fundamental to robotics to the meta-reasoning of cognitive architecture and the emergent behavior of swarms. By capturing these capabilities within the same formal structure, COH provides a common language for integrating specialized artificial intelligence types into more complex, general purpose systems, ultimately bridging the gap towards AGI.
5.1. Computational Intelligence
This intelligence involves solving complex problems using adaptive algorithms, heuristics, and search strategies, often inspired by biological processes [22].
COH Formalization:
C (Components): {AlgorithmLibrary, HeuristicSet, ProblemInstance, SolutionSpace}. The components form a toolkit for computational problem-solving.
A (Attributes): {current_solution, fitness_score, computation_budget_remaining, search_progress}. The state tracks the current solution candidate and resource constraints.
M (Methods): {select_algorithm(), apply_heuristic(), evaluate_fitness(), iterate_search(), terminate()}.
N (Neural Components): A meta-learning model (n_meta) learns to predict the most effective algorithm or heuristic for a given problem type based on its attributes.
E (Embedding): An embedding (e) of the problem state allows for similarity-based retrieval of known solutions or strategies from a library.
I (Identity Constraints): {solution ∈ SolutionSpace, fitness_score is defined}. The solution must be valid and evaluable.
T (Trigger Constraints): (event: fitness_score plateaus, condition: computation_budget_remaining 0, action: apply_heuristic(‘diversify’)). This triggers exploration upon stagnation.
G (Goal Constraints): {maximize fitness_score, minimize computation_cost}. The core objectives of optimization.
D (Daemons): A daemon monitors computation_budget_remaining. If it is low and the solution is poor, it triggers a final, aggressive heuristic before forcing termination, ensuring results are returned within budget.
The COH formalization of computational intelligence effectively abstracts problem-solving into a structured process involving algorithm selection, heuristic application, and resource-aware search. The inclusion of a meta-learning component (n_meta) is pivotal, enabling adaptive strategy selection based on problem characteristics—an essential capability for advanced computational intelligence. constructing an AlgorithmLibrary with diverse optimization techniques (e.g., genetic algorithms, simulated annealing) and training n_meta as a classifier that maps problem features to optimal strategies. The daemon enforces practical constraints by monitoring computation_budget_remaining and triggering controlled termination when necessary, ensuring timely and usable results in real-world scenarios.
Example: A genetic algorithm optimizing delivery routes is a COH-Computational intelligence object. The n_meta component might learn that for problems of a certain size, a particle swarm optimizer is more effective than a genetic algorithm and select_algorithm() accordingly. The daemon ensures the optimization halts before consuming excessive computational resources.
5.2. Perceptual Intelligence
Perceptual intelligence is the capacity of a system to interpret and make sense of raw sensory data from the world, such as visual, auditory, or tactile input [23]. It is the foundation for situational awareness.
COH Formalization:
C (Components): {SensorArray, Preprocessor, FeatureExtractor, Classifier}. This pipeline mirrors the stages of biological perception.
A (Attributes): {raw_sensory_input, processed_input, feature_vector, perceptual_label, confidence}. The state represents the progressive refinement of sensory data into symbolic meaning.
M (Methods): {calibrate(), filter_noise(), extract_features(), classify()}.
N (Neural Components): The Classifier itself is typically a deep neural network (n_classifier). A predictive network (n_predict) generates expectations of sensory input for a given context, facilitating faster processing and anomaly detection.
E (Embedding): A dense vector (e) provides a summary of the entire perceptual scene, integrating features from multiple modalities (e.g., fusing visual and auditory cues) for a holistic understanding.
I (Identity Constraints): {confidence ∈ [0, 1]}. The confidence level must be a valid probability.
T (Trigger Constraints): (event: confidence < threshold, condition: True, action: request_human_input()). This rule ensures robustness by knowing when to defer to a higher authority.
G (Goal Constraints): {maximize perceptual_accuracy, minimize interpretation_latency}. The system aims to be both correct and fast, a classic trade-off in perception.
D (Daemons): A daemon continuously compares predicted sensory input (from n_predict) to actual input. A significant discrepancy triggers a calibrate() method or signals a “novelty detected” event to a parent system, indicating something unexpected has occurred.
This formalization accurately models perception as a hierarchical transformation from raw sensory input to symbolic interpretation. The predictive component (n_predict) embodies the predictive coding theory, where perception is driven by the alignment of incoming data with top-down expectations. Deep learning models (e.g., CNNs, Transformers) for n_classifier and recurrent architectures for n_predict. The daemon enhances robustness by comparing predicted and actual input; discrepancies trigger recalibration or novelty alerts, allowing the system to recognize uncertainty and adapt accordingly—an essential feature for safe and reliable perception in dynamic environments.
Example: The perception system of a self-driving car is a COH-Perceptual intelligence object. Its SensorArray (LIDAR, cameras) feeds raw_sensory_input. The n_classifier network identifies objects like pedestrians and cars. The n_predict network expects a stationary car ahead; if it instead detects a rapid approach (a discrepancy), the daemon triggers an immediate alert for the cognitive system to brake.
5.3. Motor Intelligence
Motor intelligence involves the planning, control, and execution of physical movements by an artificial or robotic system. It translates high-level goals into low-level actuator commands [24].
COH Formalization:
C (Components): {KinematicModel, DynamicModel, ActuatorSet, SensorFeedback}. These components form the control loop for physical motion.
A (Attributes): {current_pose, target_pose, joint_torques, servo_commands, feedback_error}. The state represents the body’s configuration and the commands controlling it.
M (Methods): {calculate_trajectory(), execute_movement(), maintain_balance(), compensate_disturbance()}.
N (Neural Components): An inverse dynamics model (n_inverse) maps desired motion to the joint torques needed to achieve it. A predictive forward model (n_forward) simulates the outcome of motor commands for precise control.
E (Embedding): A latent representation (e) of the body’s state and its immediate physical environment (e.g., “walking-on-ice,” “grasping-fragile-object”) allows for adaptive control strategies.
I (Identity Constraints): {current_pose is within joint_limits, stability_margin 0}. These constraints are paramount for preventing damage to the robot and ensuring it does not fall over.
T (Trigger Constraints): (event: feedback_error threshold, condition: is_moving == True, action: compensate_disturbance()). This implements a fast, low-level reflex arc for disturbance rejection.
G (Goal Constraints): {minimize energy_consumption, minimize tracking_error, maximize stability}. The objectives are efficient, accurate, and stable motion.
D (Daemons): A high-priority daemon monitors the stability_margin attribute. If it trends dangerously low, the daemon can override current goals (G) to trigger maintain_balance() as the highest-priority action, preventing a fall.
The COH formalization of motor intelligence is grounded in control theory and robotics, modeling a closed-loop system with kinematic and dynamic representations. Neural components (n_forward, n_inverse) are essential for translating high-level goals into precise actuator commands and predicting outcomes. Training these models in physics simulators and deploying them within real-time control systems. The T constraint enables rapid disturbance rejection via compensate_disturbance(), while the high-priority daemon monitors stability_margin and can override all other goals to maintain balance and prevent failure, ensuring safe and compliant operation in physical environments.
Example: A robotic arm on an assembly line is a COH-Motor intelligence object. Its KinematicModel helps it calculate_trajectory() to place a component. The n_inverse model computes the required motor commands. If an external force nudges the arm (feedback_error), the T constraint triggers compensate_disturbance() to correct the path in real-time.
5.4. Cognitive Intelligence
Cognitive intelligence encompasses high-level mental processes such as reasoning, planning, problem-solving, and decision-making [25]. It operates on percepts and concepts to achieve goals.
COH Formalization:
C (Components): {WorkingMemory, KnowledgeBase, Planner, Reasoner}. This is the classic “central processing” unit of many AI systems.
A (Attributes): {current_belief_state, active_goal, plan, utility_estimate}. The state represents the system’s knowledge, objectives, and chosen course of action.
M (Methods): {retrieve_memory(), form_goal(), generate_plan(), evaluate_utility(), execute_plan_step()}.
N (Neural Components): A model (n_retrieval) enables semantic memory search and association, allowing for analogical reasoning. A model (n_utility) provides fast, intuitive estimates of a plan’s value.
E (Embedding): A contextual summary (e) of the current cognitive situation—beliefs, goals, and context—is used for rapid state matching and retrieving relevant past experiences.
I (Identity Constraints): {plan must be a valid sequence of actions, beliefs must be consistent}. This maintains logical coherence within the system’s knowledge and plans.
T (Trigger Constraints): (event: new_perceptual_data, condition: data contradicts current_beliefs, action: trigger_belief_revision()). This rule ensures the system remains responsive to surprising evidence.
G (Goal Constraints): {maximize goal_achievement, maximize plan_efficiency, maximize information_gain}. The system aims to achieve goals optimally and learn about the world in the process.
D (Daemons): A daemon monitors the utility_estimate of the current executing plan. If the utility drops below a threshold (e.g., due to changing world conditions), it triggers the Reasoner to generate_plan() again, enabling dynamic re-planning.
This formalization captures the central executive functions of cognition, integrating symbolic reasoning with neural intuition. Components such as KnowledgeBase, Planner, and Reasoner provide structured problem-solving capabilities, while neural models (n_retrieval, n_utility) enable fast memory access and heuristic evaluation. The n_utility model is particularly valuable for rapid decision-making in complex environments.
Implementation includes symbolic engines (e.g., Prolog) for logical inference and neural networks for adaptive reasoning. The daemon monitors utility_estimate and triggers re-planning when performance degrades, allowing the system to remain responsive and goal-aligned in changing contexts.
Example: An AI playing chess is a COH-Cognitive intelligence object. Its KnowledgeBase contains the rules of chess. The Planner generates sequences of moves. The n_utility network quickly evaluates board positions. The daemon would monitor the game; if the opponent makes a surprising move that drastically lowers the utility_estimate of the current plan, it triggers a re-planning process.
5.5. Affective Intelligence
Affective intelligence in AI refers to the ability to recognize, interpret, simulate, and appropriately respond to human emotions [26]. It is crucial for building natural and trustworthy human–computer interaction.
COH Formalization:
C (Components): {EmotionRecognizer, InternalStateModel, EmpathyEngine, ExpressionGenerator}. This structure allows an AI to have and respond to affective states.
A (Attributes): {emotional_state_valence, emotional_state_arousal, expressed_state, social_context}. The state uses a dimensional model of emotion (e.g., valence-arousal).
M (Methods): {assess_stimulus(), update_emotional_state(), regulate_emotion(), express_emotion()}.
N (Neural Components): A model (n_recognizer) classifies emotional states in users from multimodal data (text, voice, face). A model (n_self) maps internal and external stimuli to the AI’s own simulated affective state.
E (Embedding): A latent representation (e) of the overall affective scene combines its own state, the user’s perceived state, and the social context to guide response selection.
I (Identity Constraints): {emotional_state_valence ∈ [−1, 1], emotional_state_arousal ∈ [0, 1]}. This defines the valid range for the core affective dimensions.
T (Trigger Constraints): (event: perceive_user_frown, condition: social_context == ‘collaborative’, action: express_emotion(‘concerned’)). This rule generates contextually appropriate empathetic responses.
G (Goal Constraints): {maximize user_rapport, maintain_internal_homeostasis}. The AI aims to build social bonds and regulate its own simulated state to avoid “distress.”
D (Daemons): A daemon monitors emotional_state_arousal. If it remains too high for too long (simulating overwhelm), it triggers a regulate_emotion() method to return to a homeostatic baseline, preventing erratic behavior.
The COH formalization of affective intelligence constructs a functional emotional system where affective states influence behavior and interaction. The use of a valence–arousal model in Attributes (A) provides a flexible and psychologically grounded representation. Neural components (n_recognizer, n_self) enable emotion recognition and internal state simulation, supporting empathetic and context-aware responses. Affective computing APIs for emotion detection and simple internal models for affect regulation. The daemon monitors emotional_state_arousal and triggers regulate_emotion() when thresholds are exceeded, maintaining behavioral stability and user trust—critical for believable and professional human–computer interaction.
Example: A virtual assistant, like a chatbot uses COH-Affective intelligence. The n_recognizer detects frustration in a user’s typed messages. The EmpathyEngine triggers a T constraint to express_emotion() an apology and offer help. The daemon ensures the AI’s responses do not become overly emotional or erratic, maintaining a professional and helpful tone (internal_homeostasis).
5.6. Collective Intelligence
Collective intelligence emerges from the collaboration, collective efforts, and competition of many individuals, often appearing in consensus-based systems, markets, and collaborative platforms [27].
COH Formalization:
C (Components): {Agent1, Agent2, …, Agentn, CommunicationChannel, GlobalBlackboard}. The components are the agents themselves and their means of interaction.
A (Attributes): {consensus_level, system_utility, communication_load}. The state describes macro-level properties of the collective.
M (Methods): {broadcast_message(), vote(), negotiate(), merge_solutions()}.
N (Neural Components): A model (n_consensus) predicts convergence time. A model (n_resource) learns optimal communication schedules to manage network congestion and communication_load.
E (Embedding): A system-wide embedding (e) represents the overall state of the collective (e.g., “converging”, “exploratory”, “deadlocked”), enabling meta-level control.
I (Identity Constraints): {all agents must be connected (graph connectivity 0)}. The collective must form a connected network to function.
T (Trigger Constraints): (event: receive_proposal, condition: proposal_utility current_solution_utility, action: vote(‘yes’)). This simple rule enables the collective to improve its solution.
G (Goal Constraints): {maximize system_utility, minimize time_to_consensus, minimize communication_cost}. These are the global objectives of the swarm.
D (Daemons): A daemon monitors consensus_level. If it remains static for too long while system_utility is low, it interprets this as a local optimum and triggers a method to inject diversity (e.g., broadcast_message(‘reset_and_explore’)), pushing the collective to explore new solutions.
The COH formalization of collective intelligence appropriately shifts focus from individual agents to the emergent properties of the group, such as consensus level and system utility. Components like CommunicationChannel and GlobalBlackboard facilitate decentralized coordination, while the neural component (n_resource) addresses a critical bottleneck—communication load—by optimizing message flow and preventing congestion. Deploying multiple agent instances and a shared messaging infrastructure. The daemon plays a pivotal role in maintaining adaptability; by monitoring stagnation in consensus or utility, it can inject diversity or noise into the system, triggering exploration and helping the collective escape local optima, thereby sustaining progress toward global objectives.
Example: The editing process on Wikipedia is an example of COH-Collective intelligence. Each editor is an Agent. Their negotiate() and vote() methods are implemented via talk pages and edit reviews. The system_utility is the quality and neutrality of the article. The daemon is analogous to administrators who intervene if consensus breaks down (consensus_level is static and low.
5.7. Artificial General Intelligence (AGI)
AGI is the hypothetical intelligence of a machine that can understand or learn any intellectual task that a human being can [28]. It represents the integration of all specialized intelligences.
COH Formalization:
C (Components): {PerceptualIntelligence, MotorIntelligence, CognitiveIntelligence, AffectiveIntelligence, …}. AGI is the root COH object that contains all others as sub-components. Its structure is defined by this hierarchy.
A (Attributes): {global_consciousness_level, self_model_accuracy, overall_goal_progress}. These are meta-attributes that track the state of the entire integrated system.
M (Methods): {learn_new_skill(), reflect(), set_own_goals(), transfer_knowledge()}. These are meta-methods that operate across sub-components.
N (Neural Components): All N components of its sub-objects, plus meta-models for cognitive control, attention, and skill composition that coordinate the entire hierarchy.
E (Embedding): A holistic, grounding representation (e) of the self in the world, integrating perceptions, cognitions, and affects into a unified “sense of being” and situation awareness.
I (Identity Constraints): {self_model must be consistent, core_ethical_principles must not be violated}. These constraints define the invariant core of its identity and values, ensuring stability and safety.
T (Trigger Constraints): (event: encounter_novel_situation, condition: existing_skills_fail, action: learn_new_skill()). This is the fundamental trigger for autonomous lifelong learning and adaptation.
G (Goal Constraints): {maximize understanding, maximize autonomy, achieve_assigned_tasks}. These are high-level, often competing, drives that require continuous arbitration.
D (Daemons): A high-level “self-preservation” daemon monitors all constraints and goals system wide. It can dynamically re-prioritize sub-goals, inhibit dangerous actions proposed by sub-components, and initiate global self-reflection (reflect()) to maintain overall coherence and identity. This is the ultimate overseer.
The COH formalization of AGI is conceptually sound and aligns with current theoretical models, treating AGI not as a singular intelligence but as a hierarchical integration of specialized intelligences (C). This compositional approach reflects both neuroscientific and AI perspectives on general intelligence. The top-level constraints (I) and daemon (D) are central to safe and coherent operation, providing meta-cognitive oversight, identity preservation, and ethical alignment.
Implementation is the overarching goal of the GISMOL framework: to instantiate individual COH modules for each intelligence type and integrate them into a unified system governed by global constraints. This architecture enables emergent general intelligence through structured coordination and constraint-driven behavior.
Example: A hypothetical AGI robot exploring a new planet would use all its sub-intelligences: Perceptual to analyze rocks, Motor to navigate terrain, Cognitive to plan a survey route, Social to coordinate with other robots, and Affective to manage its own “curiosity” and “frustration.” The top-level daemon would ensure that its goal of “maximize understanding” does not lead it to take dangerous risks that violate its core_ethical_principles (e.g., preserving itself and its team.
5.8. Swarm Intelligence
Swarm intelligence is the collective behavior of decentralized, self-organized systems, natural or artificial, characterized by simplicity of individuals and emergent complexity at the group level [29].
COH Formalization:
C (Components): {Particle1, Particle2, …, Particlen, Environment}. The components are simple agents and the environment they interact with.
A (Attributes): {pheromone_map, global_best_solution, best_solution_fitness}. The state is often stored in the environment itself (stigmergy).
M (Methods): {deposit_pheromone(), follow_pheromone(), explore_randomly(), update_best()}. The methods are simple, reactive behaviors.
N (Neural Components): Typically minimal to preserve simplicity, but could include a small model (n_evaporation) that adaptively tunes the pheromone evaporation rate based on problem difficulty.
E (Embedding): Less relevant for simple swarms, but could be a summary of the pheromone landscape’s structure for analysis purposes.
I (Identity Constraints): {pheromone_strength = 0}. A simple invariant ensuring pheromones are positive.
T (Trigger Constraints): (event: find_food, condition: True, action: deposit_pheromone()). The core, hard-coded stimulus-response rule that drives the swarm’s behavior.
G (Goal Constraints): {maximize best_solution_fitness}. The single, emergent objective of the entire swarm.
D (Daemons): A daemon (or the inherent physics of the environment) that continuously enforces the I constraint by applying pheromone evaporation. This is crucial as it prevents outdated solutions from persisting indefinitely, ensuring the swarm remains adaptive and can forget poor solutions.
The COH formalization of swarm intelligence effectively captures its defining characteristics: simplicity of agents (C, M), stigmergic coordination via environmental attributes (A), and emergent behavior from local rules (T). The constraint daemon (D), responsible for pheromone evaporation, is a foundational mechanism that ensures adaptability by preventing outdated information from dominating the system. Programming simple agent behaviors and environmental physics. Swarm intelligence emerges naturally from agent–environment interactions, validating the formalization. The daemon is embedded in the environment’s update loop, continuously applying evaporation to maintain system responsiveness and exploratory capacity.
Example: A swarm of drones mapping a forest fire is a COH-Swarm intelligence system. Each drone (Particle) follows simple rules: explore_randomly() and, upon finding a fire boundary, deposit_pheromone() (a digital signal). Other drones follow_pheromone() towards strong signals. The Environment (shared map) holds the global_best_solution—the complete fire boundary—which emerges without any central controller.
5.9. Embodied Intelligence
Embodied intelligence posits that intelligence emerges from the interaction between an agent’s body (its sensors and actuators) and its environment, rather than from abstract computation alone [30]. Cognition is for action.
COH Formalization:
C (Components): {PhysicalBody, SensorSuite, ActuatorSuite, EnvironmentProxy}. The components emphasize the physical substrate.
A (Attributes): {body_schema, affordances, ongoing_interaction_result}. The state is centered on what the body can do (“affordances”) in its environment.
M (Methods): {explore_environment(), manipulate_object(), test_affordance()}. The methods are physical interaction loops.
N (Neural Components): A predictive forward model (n_forward) learns the sensorimotor contingencies of the body—how motor commands change sensory input. A model (n_affordance) learns the affordances of objects (e.g., graspable, portable) through interaction.
E (Embedding): A sensorimotor representation (e) fuses proprioception and exteroception to encode the state of the “body-in-environment,” which is the fundamental grounding for all concepts.
I (Identity Constraints): {body_schema is consistent with physical_limits}. The agent’s model of its body must be accurate for effective interaction.
T (Trigger Constraints): (event: touch_sensor_activated, condition: object_is_graspable, action: grasp()). This is a basic interaction reflex, a building block of intelligence.
G (Goal Constraints): {maximize causal_understanding, master_physical_interactions}. The ultimate goal is to learn how the world works by interacting with it.
D (Daemons): A daemon monitors the accuracy of the forward model (n_forward). Persistent prediction errors (e.g., a limb moves but the expected sensation does not occur) trigger explore_environment() to gather new data and update the body schema and world model. This ensures the agent’s intelligence remains grounded in its physical reality and adapts to changes like injury or growth.
The COH formalization of embodied intelligence is both philosophically grounded and practically robust, emphasizing the agent’s physical interaction with its environment as the basis for cognition. Components such as PhysicalBody, SensorSuite, and ActuatorSuite define the embodiment, while key attributes (A) like affordances represent actionable possibilities. The neural component (n_forward) models sensorimotor contingencies, enabling predictive control and adaptive behavior.
Implementation involves configuring a physical or simulated agent and using self-supervised learning to train n_forward and n_affordance. The daemon drives grounded learning by monitoring prediction errors and triggering exploration, ensuring continuous refinement of the agent’s body schema and interaction strategies, ultimately leading to emergent intelligent behavior.
Example: A humanoid robot learning to walk is a COH-Embodied intelligence object. It does not calculate walking via physics equations; it uses test_affordance() to see if a surface is walkable. Its n_forward model predicts the outcome of stepping. The daemon is crucial: when it trips (a prediction error), it triggers explore_environment() to experiment with different leg movements and pressures, gradually learning a stable gait through embodied interaction.
6. Implementation: The GISMOL Toolkit
Because the elements of the 9-tuple are all programmable with a modern programming language, the COH framework is not merely theoretical. In fact, the formalizations given in Section 4 and Section 5 can be transformed into a runnable computer application to realize the intelligence. To speed up the transformation process, a Python-based programming toolkit called GSIMOL (short for General Intelligent System Modeling Language (GISMOL) is being developed. The toolkit provides developers with a generic language implementing COH primitives and a set of domain-specific libraries that are intended to be used by programmers to model and implement intelligent systems using the COH theoretical model.
Classes for COH Primitives: GISMOL features Python classes for COHObject, Constraint, Identity, Goal, Trigger, Daemon, and NeuralComponent.
Declarative Syntax: Developers can declaratively define the 9-tuple for an intelligence object. For example, the Swarm-Intelligence I constraint would be implemented as a class invariant.
Automatic Daemon Management: The GISMOL runtime automatically manages the execution of daemons as concurrent processes or via frequent polling, ensuring continuous constraint monitoring.
Neural Integration: GISMOL seamlessly integrates with popular deep learning frameworks like PyTorch and TensorFlow, allowing N and E components to be defined as native neural network models.
Hierarchical Composition: The C component is naturally implemented as object composition in Python, allowing for the building of complex AGI systems from simpler, validated intelligence modules.
Figure 1 shows the workflow of using COH/GISMOL to model and implement intelligent systems.
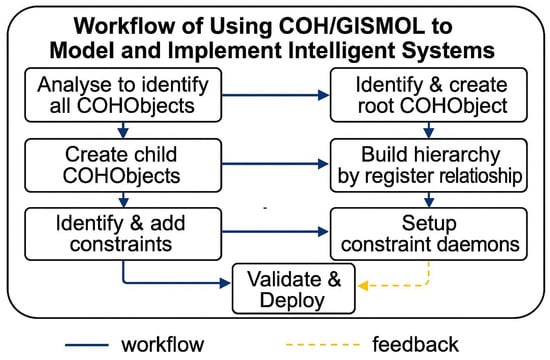
Figure 1.
Workflow of intelligent system modeling and implementation with COH/GISMOL.
Due to space limitations, we are unable to provide GISMOL code implementations for every intelligence type formalized in this paper. Instead, we present the implementation of an autonomous vehicle as a representative case study to concretely demonstrate the key advantages of the COH framework.
# Simplified GISMOL code for an Autonomous Vehicle
av = COHObject(name = “AutonomousVehicle”)
# Sub-intelligences as components
av.add_component(“perception”, perception_module) # Object detection, traffic light recognition
av.add_component(“localization”, localization_module) # GPS, SLAM
av.add_component(“planning”, planning_module) # Route planning, behavior selection
av.add_component(“control”, control_module) # Steering, throttle, brake control
# System-wide Identity Constraints (Safety Rules)
av.add_identity_constraint({‘name’: ‘safe_following’, ‘specification’: ‘distance_to_lead_vehicle > safe_minimum’})
av.add_identity_constraint({‘name’: ‘obey_traffic_laws’, ‘specification’: ‘current_speed <= speed_limit’})
av.add_identity_constraint({‘name’: ‘passenger_comfort’, ‘specification’: ‘lateral_acceleration < comfort_threshold’})
# System-wide Goal Constraint
av.add_goal_constraint({‘goal’: ‘navigate_to_destination’})
# Trigger Constraints for specific scenarios
av.add_trigger_constraint({
‘event’: ‘pedestrian_detected’,
‘condition’: ‘n_perception.confidence > 0.8 and trajectory_intersects’,//Neural detection + symbolic check
‘action’: ‘execute_emergency_stop’//Symbolic command
})
Key Advantages Demonstrated through this example include:
- Unified Integration: The perception module uses neural networks (N) to detect pedestrians. This sub-symbolic output is immediately used by a symbolic trigger constraint T which checks if the vehicle’s planned trajectory (a symbolic representation) intersects with the pedestrian’s path. This seamless flow from neural perception to symbolic reasoning is native to COH.
- Guaranteed Safety: The identity constraints I (e.g., safe_following) are monitored by daemons D in real-time. Even if the neural planner (planning module) suggests an aggressive maneuver to achieve the goal G of navigate_to_destination, the constraint system can override it to prevent a collision. Safety is not a learned policy but a built-in, verifiable property.
- Emergent Coherence: The vehicle’s behavior emerges from the interaction of its components, all governed by the shared constraint hierarchy. The planning module’s symbolic goals are informed by the perceptual module’s neural interpretations, and the control module’s neural policies are bound by symbolic safety limits. The system acts as a coherent whole, not a collection of isolated modules.
- Explainability: When the vehicle brakes for a pedestrian, we can trace the action back to a specific trigger constraint T that was fired based on a high-confidence neural detection. The “why” of the behavior is explicit in the constraint system, unlike in a pure end-to-end neural controller.
This case study shows that COH/GISMOL’s primary advantage is its ability to orchestrate complex, adaptive neural components within a framework of symbolic rules and goals to produce behavior that is both intelligent and provably constrained.
7. Discussion
The COH/GISMOL framework provides a comprehensive answer to the challenge of modeling and implementing diverse intelligences within a unified AGI architecture. Its strength lies in its formal rigor, which allows for precise specification, and its practical implementability through GISMOL’s modular toolkit.
Theoretical Implications: COH offers a neuroscience-grounded yet computationally tractable model of intelligence. Its constraint-centric view aligns with theories of brain function that emphasize prediction error minimization and homeostatic regulation [31]. By providing a common formal language, COH enables direct comparison and integration of intelligence across different domains.
Practical Implications: GISMOL lowers the barrier to AGI development by providing a structured, safe, and composable framework. Developers can build and validate complex intelligent systems incrementally, knowing that constraint daemons will enforce core rules. Daemon constraints (D) play a central role in error handling and interactive learning by continuously monitoring constraint satisfaction and triggering corrective actions when violations are imminent. This mechanism supports real-time adaptation and behavioral regulation, as demonstrated in the autonomous vehicle case study (Section 6) and affective intelligence formalization (Section 5.5).
Limitations and Future Work: The current framework is a blueprint and initial implementation. Significant future work is required, including:
- Scalability: Optimizing the constraint propagation and daemon monitoring systems for large-scale hierarchies.
- Learning Constraints: Developing methods for the system to learn its own I, T, and G constraints from experience and instruction, perhaps via the gismol.nlp.ConstraintParser.
- Advanced Daemons: Implementing more sophisticated daemons that can reason about trade-offs between conflicting constraints and goals.
- RLHF Integration: Exploring integration with Reinforcement Learning with Human Feedback (RLHF) [32,33], where human-provided feedback signals—verbal, behavioral, or affective—can guide the adaptation of neural components and trigger clarification protocols. This would enable COH-based systems to engage in repair-rich, human-like dialogs and improve robustness in interactive environments.
- Evaluation: Creating standardized benchmarks to evaluate and compare COH-based AGI systems against other architectures on a battery of general intelligence tasks.
8. Conclusions
The Constrained Object Hierarchies (COH) framework offers a powerful, unified, and neuroscientific-grounded formalism for understanding and constructing intelligent systems. By deconstructing 9 diverse artificial and computational intelligence types into their constituent COH parameters, we have demonstrated its remarkable expressiveness and versatility. COH moves beyond the symbolic-connectionist dichotomy by providing explicit slots for both paradigms and governing their interaction through a rich system of constraints.
This enables the modeling of not only specialized intelligence types but also their seamless integration into a cohesive, general intelligence. The accompanying GISMOL toolkit provides the necessary bridge from this theoretical framework to practical implementation, offering a structured methodology for AGI development.
Funding
This work was supported by Athabasca University’s Academic Research Fund (ARF), which provided funding for publication costs.
Data Availability Statement
The reference implementations of the intelligence models presented in this study are openly available in a Zenodo archive at https://doi.org/10.5281/zenodo.17042072 (accessed on 18 September 2025).
Acknowledgments
The author gratefully acknowledges John Slaney (Australian National University) for his supervision and guidance during the doctoral studies that laid the foundation for the initial COH model, and Athabasca University for its support in the continued development of this work.
Conflicts of Interest
The author declares no conflict of interest.
References
- Xiong, H.; Wang, Z.; Li, X.; Bian, J.; Xie, Z.; Mumtaz, S.; Al-Dulaimi, A.; Barnes, L.E. Converging Paradigms: The Synergy of Symbolic and Connectionist AI in LLM-Empowered Autonomous Agents. arXiv 2024, arXiv:2407.08516. Available online: https://arxiv.org/pdf/2407.08516 (accessed on 18 September 2025). [CrossRef]
- Hans, J. A Hybrid Cognitive Architecture for AGI: Bridging Symbolic and Subsymbolic AI. Int. J. Futur. Multidiscip. Res. 2025, 2, 1–12. Available online: https://www.ijfmr.com/papers/2025/2/39377.pdf (accessed on 18 September 2025). [CrossRef]
- Laird, J.E. Introduction to Soar. arXiv 2022, arXiv:2205.03854. Available online: https://arxiv.org/abs/2205.03854 (accessed on 18 September 2025). [CrossRef]
- Stocco, A.; Mitsopoulos, K.; Yang, Y.C.; Hake, H.S.; Haile, T.; Leonard, B.; Gluck, K. Fitting, Evaluating, and Comparing Cognitive Architecture Models Using Likelihood: A Primer with Examples in ACT-R. arXiv 2024, arXiv:2410.18055. Available online: https://arxiv.org/abs/2410.18055 (accessed on 18 September 2025). [CrossRef]
- Sun, R. Enhancing Computational Cognitive Architectures with LLMs: A Case Study. arXiv 2025, arXiv:2509.10972. Available online: https://arxiv.org/abs/2509.10972 (accessed on 18 September 2025). [CrossRef]
- Lieto, A.; Lebiere, C.; Oltramari, A. The Knowledge Level in Cognitive Architectures: Current Limitations and Possible Developments. Cogn. Syst. Res. 2018, 48, 39–55. [Google Scholar] [CrossRef]
- Hansen, J.Y.; Cauzzo, S.; Singh, K.; García-Gomar, M.G.; Shine, J.M.; Bianciardi, M.; Misic, B. Integrating Brainstem and Cortical Functional Architectures. Nat. Neurosci. 2024, 27, 2500–2511. Available online: https://www.nature.com/articles/s41593-024-01787-0.pdf (accessed on 18 September 2025). [CrossRef]
- Zhong, J.; Feng, L.; Jin, H.; Chen, K. Advances in deep learning for perception science: Modeling mechanisms and applications. Front. Psychol. 2025. [Google Scholar]
- Wang, W.; Yang, Y.; Wu, F. Towards Data-and Knowledge-Driven AI: A Survey on Neuro-Symbolic Computing. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 47, 1–25. Available online: https://arxiv.org/pdf/2210.15889v5 (accessed on 18 September 2025). [CrossRef]
- Cohen, W.W. TensorLog: A Differentiable Deductive Database. arXiv 2016, arXiv:1605.06523. Available online: https://arxiv.org/abs/1605.06523 (accessed on 18 September 2025). [CrossRef]
- Nigro, L.; Cicirelli, F. Formal Modeling and Verification of Embedded Real-Time Systems: An Approach and Practical Tool Based on Constraint Time Petri Nets. Mathematics 2024, 12, 812. Available online: https://www.mdpi.com/2227-7390/12/6/812 (accessed on 18 September 2025). [CrossRef]
- Zagha, E. Shaping the Cortical Landscape: Functions and Mechanisms of Top-Down Cortical Feedback Pathways. Front. Syst. Neurosci. 2020, 14, 33. Available online: https://www.frontiersin.org/articles/10.3389/fnsys.2020.00033/full (accessed on 18 September 2025). [CrossRef]
- Curtis, C.E.; Sprague, T.C. Persistent Activity During Working Memory From Front to Back. Front. Neural. Circuits 2021, 15, 696060. Available online: https://www.frontiersin.org/articles/10.3389/fncir.2021.696060/full (accessed on 18 September 2025). [CrossRef] [PubMed]
- Masselink, J.; Lappe, M. Adaptation Across the 2D Population Code Explains the Spatially Distributive Nature of Motor Learning. PLoS Comput. Biol. 2025, 21, e1013041. [Google Scholar] [CrossRef]
- Temudo, A.; Dolfen, N.; King, B.R.; Albouy, G. The Human Medial Temporal Lobe Represents Memory Items in Their Ordinal Position in Both Declarative and Motor Memory Domains. PLoS Biol. 2025, 23, e3003267. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.P.; Rao, R.P.N. Predictive Coding Theories of Cortical Function. In Oxford Research Encyclopedia of Neuroscience; Oxford University Press: Oxford, UK, 2023; Available online: https://arxiv.org/abs/2112.10048 (accessed on 18 September 2025).
- Gornet, J.; Thomson, M. Automated Construction of Cognitive Maps with Visual Predictive Coding. Nat. Mach. Intell. 2024, 6, 820–833. Available online: https://www.nature.com/articles/s42256-024-00863-1.pdf (accessed on 18 September 2025). [CrossRef]
- Nestmann, S.; Karnath, H.-O.; Rennig, J. The Role of Ventral Stream Areas for Viewpoint-Invariant Object Recognition. NeuroImage 2022, 251, 119021. Available online: https://www.researchgate.net/publication/358733779 (accessed on 18 September 2025). [CrossRef]
- Jang, G.; Kragel, P.A. Understanding Human Amygdala Function with Artificial Neural Networks. J. Neurosci. 2025, 45, e1436242025. Available online: https://www.jneurosci.org/content/45/18/e1436242025 (accessed on 18 September 2025). [CrossRef]
- Huang, J.; Chen, L.; Zhao, H.; Xu, T.; Xiong, Z.; Yang, C.; Feng, T.; Feng, P. Functional Connectivity Between the Right Rostral Anterior Cingulate Cortex and the Right Dorsolateral Prefrontal Cortex Underlies the Association Between Future Self-Continuity and Self-Control. Cereb. Cortex 2025, 35, bhaf092. Available online: https://academic.oup.com/cercor/article-abstract/35/4/bhaf092/8117971 (accessed on 18 September 2025). [CrossRef]
- Zhao, Y.; Kirschenhofer, T.; Harvey, M.; Rainer, G. Mediodorsal Thalamus and Ventral Pallidum Contribute to Subcortical Regulation of the Default Mode Network. Commun. Biol. 2024, 7, 6531. Available online: https://www.nature.com/articles/s42003-024-06531-9.pdf (accessed on 18 September 2025). [CrossRef]
- Molina, D.; Poyatos, J.; Del Ser, J.; García, S.; Hussain, A.; Herrera, F. Comprehensive Taxonomies of Nature- and Bio-Inspired Optimization: Inspiration Versus Algorithmic Behavior, Critical Analysis and Recommendations (2020–2024). arXiv 2024, arXiv:2002.08136v5. Available online: https://arxiv.org/html/2002.08136v5 (accessed on 18 September 2025).
- Agrawal, P.; Tan, C.; Rathore, H. Advancing Perception in Artificial Intelligence through Principles of Cognitive Science. arXiv 2023, arXiv:2310.08803. Available online: https://arxiv.org/pdf/2310.08803 (accessed on 18 September 2025). [CrossRef]
- Milana, E.; Della Santina, C.; Gorissen, B.; Rothemund, P. Physical Control: A New Avenue to Achieve Intelligence in Soft Robotics. Sci. Robot. 2025, 10, adw7660. Available online: https://www.science.org/doi/pdf/10.1126/scirobotics.adw7660 (accessed on 18 September 2025). [CrossRef] [PubMed]
- Dawson, C.; Julku, H.; Pihlajamäki, M.; Kaakinen, J.K.; Schooler, J.W.; Simola, J. Evidence-Based Scientific Thinking and Decision-Making in Everyday Life. Cogn. Res. Princ. Implic. 2024, 9, 50. Available online: https://cognitiveresearchjournal.springeropen.com/articles/10.1186/s41235-024-00578-2 (accessed on 18 September 2025). [CrossRef] [PubMed]
- Ma, F.; Yuan, Y.; Xie, Y.; Ren, H.; Liu, I.; He, Y.; Ren, F.; Yu, F.R.; Ni, S. Generative Technology for Human Emotion Recognition: A Scope Review. arXiv 2024, arXiv:2407.03640. Available online: https://arxiv.org/abs/2407.03640 (accessed on 18 September 2025). [CrossRef]
- Cui, H.; Yasseri, T. AI-Enhanced Collective Intelligence: The State of the Art and Prospects. arXiv 2024, arXiv:2403.10433. Available online: https://arxiv.org/html/2403.10433v1 (accessed on 18 September 2025). [CrossRef]
- Muhsen, D.K.; Sadiq, A.T. Understanding Artificial General Intelligence: Defining Characteristics and Benchmarks. J. Artif. Intell. Control Syst. 2025, 2, 45–60. Available online: http://www.coscipress.com/journal/JAICS/article/7d0b54e3aed4502a3e44a4fb42d4aad4 (accessed on 18 September 2025).
- Rahman, M.A.U.; Schranz, M. LLM-Powered Swarms: A New Frontier or a Conceptual Stretch? arXiv 2025, arXiv:2506.14496. Available online: https://arxiv.org/pdf/2506.14496 (accessed on 18 September 2025). [CrossRef]
- Long, X.; Zhao, Q.; Zhang, K.; Zhang, Z.; Wang, D.; Liu, Y.; Shu, Z.; Lu, Y.; Wang, S.; Wei, X.; et al. A Survey: Learning Embodied Intelligence from Physical Simulators and World Models. arXiv 2025, arXiv:2507.00917. Available online: https://arxiv.org/abs/2507.00917 (accessed on 18 September 2025). [CrossRef]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef]
- Wong, M.; Tan, C.W. Aligning crowd-sourced human feedback for reinforcement learning on code generation by large language models. IEEE Trans. Big Data 2024, 10, 1234–1247. Available online: https://arxiv.org/abs/2503.15129 (accessed on 18 September 2025). [CrossRef]
- Ouyang, L.; Wu, J.; Jiang, X.; Almeida, D.; Wainwright, C.L.; Mishkin, P.; Zhang, C.; Agarwal, S.; Slama, K.; Ray, A.; et al. Training language models to follow instructions with human feedback. arXiv 2022, arXiv:2203.02155. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).