Teaching Machine Learning to Undergraduate Electrical Engineering Students ^†

Abstract

Proficiency in machine learning (ML) and the associated computational math foundations have become critical skills for engineers. Required areas of proficiency include the ability to use available ML tools and the ability to develop new tools to solve engineering problems. Engineers also need to be proficient in using generative artificial intelligence (AI) tools in a variety of contexts, including as an aid to learning, research, writing, and code generation. Using these tools properly requires a solid understanding of the associated computational math foundation. Without this foundation, engineers will struggle with developing new tools and can easily misuse available ML/AI tools, leading to poorly designed systems that are suboptimal or even harmful to society. Teaching (and learning) these skills can be difficult due to the breadth of skills required. One contribution of this paper is that it approaches teaching this topic within an industrial engineering human factors framework. Another contribution is the detailed case study narrative describing specific pedagogical challenges, including implementation of teaching strategies (successful and unsuccessful), recent observed trends in generative AI, and student perspectives on learning this topic. Although the primary methodology is anecdotal, we also include empirical data in support of anecdotal results.

1. Introduction

With the recent explosive growth of machine learning (ML) tools and ML-based generative artificial intelligence (AI), it is now more important than ever before that engineers are proficient in ML, generative AI, and the associated computational math and data analytics skills. Hai-Dung Do et al. identify AI as a hard skill gap where undergraduate education should be improved to better prepare engineers for Industry 4.0, including the robotics industry [1]. Verma et al. describe the strong growth in ML and AI related positions in conjunction with Industry 4.0 trends, noting the shortage of qualified talent and the need for complementary technical skills, such as data analytics, programming, statistics, and communication [2]. As per Aikins et al., engineers require not only data proficiency, but also the ability to use data to solve real-world problems [3]. More recently, Saroja and Jinwal show that top skills and competencies within India include Python, ML, AI, and data analytics [4], while Alsharif shows a 10-fold increase in Python demand for bachelor’s-level electrical engineering (EE) job skills from 2012 to 2022 [5]. According to Beke, engineering education must cover additional skills, such as communication and the ability to learn continuously to prepare students for Industry 4.0 [6].

These national and global trends are confirmed by our local East Texas A&M University (ETAMU) EE industry advisory board (IAB) and the industry experience of our lead author (G.F.), who observed similar patterns prior to retiring from L3Harris in 2021 as a Senior Fellow. Factors driving this growth include increased ML and generative AI capabilities, greater computational resources, and reduced costs due to open-source platforms such as Python Anaconda, PyTorch, and OpenAI’s ChatGPT [7,8]. Although this paper focuses on electrical engineering, similar trends exist across other engineering disciplines.

Teaching ML and the associated computational math skills to today’s Gen Z students can present challenges for traditional teaching methods, as discussed later in Section 2.3. These challenges are amplified at universities like ETAMU, which serve a large proportion of underrepresented groups in engineering, including underrepresented minority (URM) students, first generation students, and students from low socio-economic status (SES) households [9].

While many studies have discussed teaching Science, Technology, Engineering, and Mathematics (STEM) topics to underrepresented groups [10,11], very little has been published on teaching ML and computational math to underrepresented groups, especially regarding practical implementation of teaching strategies. This gap in literature makes it challenging for educators to implement or replicate specific strategies as discussed later in Section 2. The goal of this paper is to help address this gap in literature by extending and updating earlier work by Fudge [9]. Contributions of this paper include the following:

• Human Factors Pedagogical Framework: The teaching methodology is framed within a human factors perspective, an area of industrial engineering that optimizes human performance in systems [12]. Although human factors can be applied to optimize pedagogy and the associated process for teaching ML and computational math, it is rarely applied in literature.
• Implementation Details: We provide detailed descriptions of both successful and unsuccessful teaching strategies. In addition to previously published strategies [9], we also describe novel strategies, including the resubmit grading policy, oral midterms, specific software requirements, and hands-on visualization activities for understanding the histogram and convolution. Our goal is to provide actionable guidance for other educators.
• Curriculum Integration: This paper shows how key concepts and skills can be taught and reinforced across multiple courses from the first to the final year. We have not seen curriculum integration addressed in the existing ML and computational math education literature.
• Responsible Use of Generative AI: We present strategies to encourage students to properly use generative AI, with attention to issues such as citation, reliability, and tool usage to aid rather than replace engineers in report writing and coding.
• Student Perspective: This paper incorporates student perspectives from student coauthors (W.Z., J.R., and C.B.) representing both Gen Z and Millennial students, who evaluated the assignment and lecture materials for Computing for Electrical Engineers course.

Our methodology is tied directly to our research goals. When this project began in Fall of 2021, our primary research question was as follows: How can pedagogy theory be effectively translated into practice when teaching ML and computational math, especially for students from disadvantaged backgrounds? Thus, our goal was to find effective strategies for teaching complex computational topics previously not covered in our undergraduate curriculum. Accordingly, we developed the following specific research questions for teaching the Computing for Electrical Engineers course:

• RQ1: What ML and computational math skills and concepts do EEs need to learn their sophomore year to be successful in (1) EE internships after their sophomore year and (2) EE positions after graduation?
• RQ2: What are the most effective approaches for teaching these skills and concepts given our demographics? This question is further divided into the following:
  • RQ2a: What are the best general strategies? (I.e., optimal mix of lecture and hands-on activities; methods for working with Gen Z students; grading mechanism; approaches for alleviating stress regarding making errors; etc.)
  • RQ2b: What are the best specific strategies for traditional EE computational methods? (E.g., time/frequency/time-frequency domain analysis, filtering & convolution, Fourier transform, time-frequency spectrogram, sampling, etc.)
  • RQ2c: What are the best specific strategies for teaching recent EE computational methods in ML? (I.e., using ML algorithms properly, recognizing underfit/overfit, visualizing data, etc.)
  • RQ2d: What are the best specific strategies for teaching programming skills for ML and computational math? (I.e., writing reusable, clean well-documented code, and learning new programming languages and development environments.)
  • RQ2e: What strategies are best for teaching engineering report writing skills? (I.e., initially how to structure a report and how to write clearly; more recently, how to cite properly, how to use generative AI appropriately, and how to use report templates.)

RQ1 was initially answered during the Fall 2021 semester by author G.F. based on industry experience, which included leading large multi-disciplinary engineering teams in product development from research through deployment. Since then, the list of required skills and concepts has been revised to incorporate industry trends as reflected by our IAB (see Table 1 in Section 2.2). While the research methodology applies to RQ1, the focus of this paper is on RQ2 since that is where substantial challenges have emerged.

The remainder of this paper is organized as follows: Section 2 provides background information with a literature review to help frame the problem, and to provide context to allow our results to be adapted to fit the needs of faculty at other universities. Section 3 discusses our teaching methodology and the research methodology used to evaluate the teaching methodology. Section 4 focuses on results, including unsuccessful and successful strategies. Section 5 discusses and evaluates the results prior to the conclusions in Section 6.

2. Background and Literature Review

We first discuss and define ML and AI in Section 2.1, followed by a discussion of ML and computational math skills that EEs need in Section 2.2. We then discuss student demographics and Gen Z characteristics in Section 2.3, our EE curriculum in Section 2.4, our human factors framework in Section 2.5, and teaching ML and computational math in Section 2.6.

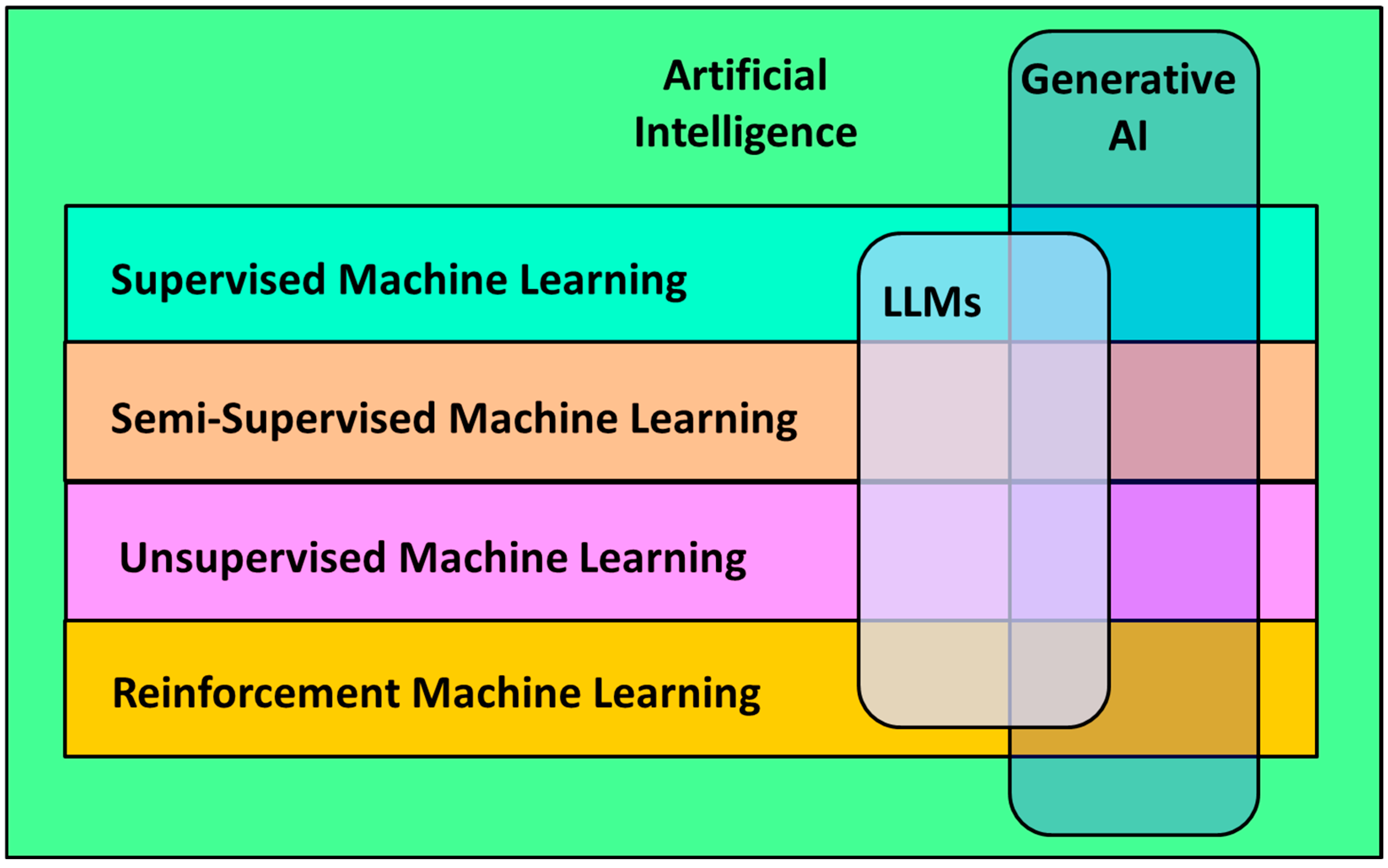
2.1. Machine Learning and AI

Per Raschka et al., the goal of ML is to give “computers the ability to learn from data” to identify and classify patterns, and make useful predictions [7]. Thus, ML relies on automated computational math tools to perform applied statistical analysis. As shown in Figure 1, ML is a subfield of AI that includes (1) supervised learning that uses training labels to learn how to predict on new data without labels, (2) semi-supervised learning that combines labeled and unlabeled data in training, (3) unsupervised learning that identifies patterns in the data, and (4) reinforcement learning that trains via rewards and penalties [7]. Deep learning spans all these areas, and refers to ML architectures such as neural networks that have complex multi-layered models. Although the focus of our undergraduate ML training at ETAMU is on basic supervised and unsupervised learning, the special topics Applied Machine Learning course covers more advanced ML techniques, including deep learning techniques for image classification.

Generative AI is a subfield of AI that uses a variety of ML techniques supplemented by additional AI tools to synthesize (generate) new content based on previously trained content. Generative AI typically relies on large language models (LLMs), especially for generating text, but can use other ML methods as well as non-ML-based AI methods. As Kaswan et al. note, generative AI has broad applications in areas as diverse as chatbots, code creation, language translation, content creation, molecular design, image generation, and generating synthetic data [13]. Author G.F., for example, has used ChatGPT for learning biochemistry, analyzing legacy Python code, writing new MATLAB code, suggesting topics for engineering student projects, and supporting research. According to Bender et al. [14], generative AI exhibits stochastic behavior that tends to reflect the consensus view. This can be useful at times, but it can also cause problems if students are unaware of this tendency.

Another potential problem of generative AI is that it can make major errors, often referred to as “hallucinations” [15]. For example, Munir documents various legal cases involving fictitious citations produced by generative AI tools, leading to disciplinary actions (Munir also provides a detailed explanation as to why LLMs are susceptible to such hallucinations) [16]. Similarly, Jamieson et al. have reported that generative AI regularly produces erroneous Karnaugh maps which lead to faulty digital circuits [17]. Author G.F. has experienced both fake citations and error-prone Karnaugh maps, in addition to other generative AI hallucinations. Students need to keep in mind that AI, while artificial, is not actually intelligent—it can only mimic intelligence.

2.2. Required Skills and Knowledge for Electrical Engineers Working in Machine Learning

One of the challenges of teaching ML is the wide range of skills and areas of conceptual understanding required for effective development and usage of ML tools [9]. Table 1 identifies key ML and computational math skills and concepts for EE students based on standard ML industry references [8], the lead author’s (G.F.) industry experience, and feedback from representatives of the ETAMU EE IAB. While most learning outcomes listed in Table 1 require both conceptual understanding and skills, some are more heavily weighted towards skills (highlighted in light green). The Table 1 arrangement corresponds to how these skills and concepts are covered within the ETAMU EE curriculum lower-level courses (see Table 2 and Figure 2 in Section 2.4).

Table 1. Machine Learning & Computational Math Skills & Concepts for Electrical Engineers.

Skill/Concept	Discussion
Unit conversion skills	Engineering, including ML, often requires unit conversions to support scale changes, plotting, and data visualization. For example, EEs often need to convert from sample rate to frequency.
Estimation skills	Modern computational tools, while sophisticated, can be difficult to use properly, and, even if used properly, will generate erroneous results if the input data is incorrect. Thus, engineers need to be able to estimate to provide a sanity check when using sophisticated computational math tools.
Documentation skills	Based on industry experience, engineers often struggle with developing proper documentation, including reports, code documentation, and proper plot labeling. Proper documentation during development is critical for reproducibility, team collaboration, and transition to production.
Noise, probability, & statistics	ML is essentially applied probability and statistics using automated computational tools. Thus, a solid foundation in probability and statistics is required for ML. Furthermore, given that real-world data is noisy, engineers need to understand how to effectively handle noise in signals and data.
Trigonometry & projections	Both linear and non-linear projections are widely used in ML to reduce the data dimensionality, perform feature extraction, and support visualization. Prior to understanding non-linear projection techniques, engineers must understand linear projections, including trigonometric sine/cosine projections commonly used in engineering, as well as projection via PCA and the DFT as discussed below.
Generative AI skills	Engineers need to know how to properly use generative AI to support coding and documentation, while maintaining critical thinking skills, and while identifying generative AI hallucinations.
Data visualization	Visualization is critical in the data exploration phase of ML, and plays a key role in interpreting and explaining the results and methodology to colleagues, managers, and customers.
ML theory & practice	Engineers need to understand and apply key ML concepts when developing ML code, including supervised vs. unsupervised training, overfit vs. underfit, classification vs. regression vs. clustering, data scrubbing and other preprocessing steps, the curse of dimensionality, performance metrics, and training vs. test.
Software coding skills	Engineers need to be able to develop algorithms to solve problems. Proficiency is needed in both object-oriented and structured coding methods used in languages such as Python and MATLAB. In addition, proficiency in using visual block-diagram tools may be needed since many tools are visual (e.g., Simulink). Engineers also need skills to learn new languages given the variety of ML and computational math platforms. Finally, given typical corporate coding standards, engineers also need to understand software requirements regarding test methodology, style, documentation, naming conventions, etc.
Discrete Fourier Transform (DFT)	The DFT is the standard tool to analyze digitized periodic signals, and is used in ML applications involving periodic signals for feature extraction, dimensionality reduction, and data visualization. The DFT can also be used to implement fast convolution used in ML algorithms such as the convolutional neural network. Understanding the DFT, in turn, requires an understanding of trigonometric projections, Euler’s formula, complex phasors, and inner products.
Convolution & filtering	Convolution is used in a variety of applications, including convolutional neural networks, computing probability distribution functions, and finite impulse response filters. Filtering is used to smooth data and reduce noise (low pass), support edge detection (high pass), and to isolate signals (bandpass/reject).
Matrix math & linear algebra	These skills and concepts are needed to develop algorithms, and to understand and interpret algorithms such as PCA or other dimensionality reduction techniques. Engineers need to understand concepts such as linear independence and matrix rank to properly use tools that solve systems of linear equations.
Sampling theory & practice	ML practitioners need to know when the sampling granularity is sufficient. In addition, an understanding of statistical sampling is critical in ML to avoid biased results caused by poor training data.
Principal Component Analysis (PCA)	PCA is widely used in ML to reduce the data dimensionality prior to training in order to reduce the processing time and, in some cases, to improve the ML classifier performance. PCA is based on eigenvector decomposition of the feature data covariance matrix, followed by replacing the original features with the eigenvectors associated with the largest eigenvalues. Thus, an understanding of eigenvectors and eigenvalues is critical to effective use of PCA in ML.
Optimization theory & practice	ML algorithms rely on optimization for training and hyperparameter optimization. Thus, a basic understanding of optimization theory, and concepts such as step size and learning rate, is required.
Digital logic	Binary number systems, Boolean logic, state machines, and sequential logic flow crop up in numerous areas of ML and computational math, including hypothesis testing and detection, sequential algorithm flow, hidden Markov models, large language models, digital signal processing, etc.
Embedded implementation skills	Due to computational complexity, many ML and computational math algorithms are implemented using graphics processor units (GPUs), field programmable gate arrays (FPGAs), etc., in order to support effective real-world deployment. Engineers with skills in these areas will have more career opportunities.

Table 1. Machine Learning & Computational Math Skills & Concepts for Electrical Engineers.

Skill/Concept	Discussion
Unit conversion skills	Engineering, including ML, often requires unit conversions to support scale changes, plotting, and data visualization. For example, EEs often need to convert from sample rate to frequency.
Estimation skills	Modern computational tools, while sophisticated, can be difficult to use properly, and, even if used properly, will generate erroneous results if the input data is incorrect. Thus, engineers need to be able to estimate to provide a sanity check when using sophisticated computational math tools.
Documentation skills	Based on industry experience, engineers often struggle with developing proper documentation, including reports, code documentation, and proper plot labeling. Proper documentation during development is critical for reproducibility, team collaboration, and transition to production.
Noise, probability, & statistics	ML is essentially applied probability and statistics using automated computational tools. Thus, a solid foundation in probability and statistics is required for ML. Furthermore, given that real-world data is noisy, engineers need to understand how to effectively handle noise in signals and data.
Trigonometry & projections	Both linear and non-linear projections are widely used in ML to reduce the data dimensionality, perform feature extraction, and support visualization. Prior to understanding non-linear projection techniques, engineers must understand linear projections, including trigonometric sine/cosine projections commonly used in engineering, as well as projection via PCA and the DFT as discussed below.
Generative AI skills	Engineers need to know how to properly use generative AI to support coding and documentation, while maintaining critical thinking skills, and while identifying generative AI hallucinations.
Data visualization	Visualization is critical in the data exploration phase of ML, and plays a key role in interpreting and explaining the results and methodology to colleagues, managers, and customers.
ML theory & practice	Engineers need to understand and apply key ML concepts when developing ML code, including supervised vs. unsupervised training, overfit vs. underfit, classification vs. regression vs. clustering, data scrubbing and other preprocessing steps, the curse of dimensionality, performance metrics, and training vs. test.
Software coding skills	Engineers need to be able to develop algorithms to solve problems. Proficiency is needed in both object-oriented and structured coding methods used in languages such as Python and MATLAB. In addition, proficiency in using visual block-diagram tools may be needed since many tools are visual (e.g., Simulink). Engineers also need skills to learn new languages given the variety of ML and computational math platforms. Finally, given typical corporate coding standards, engineers also need to understand software requirements regarding test methodology, style, documentation, naming conventions, etc.
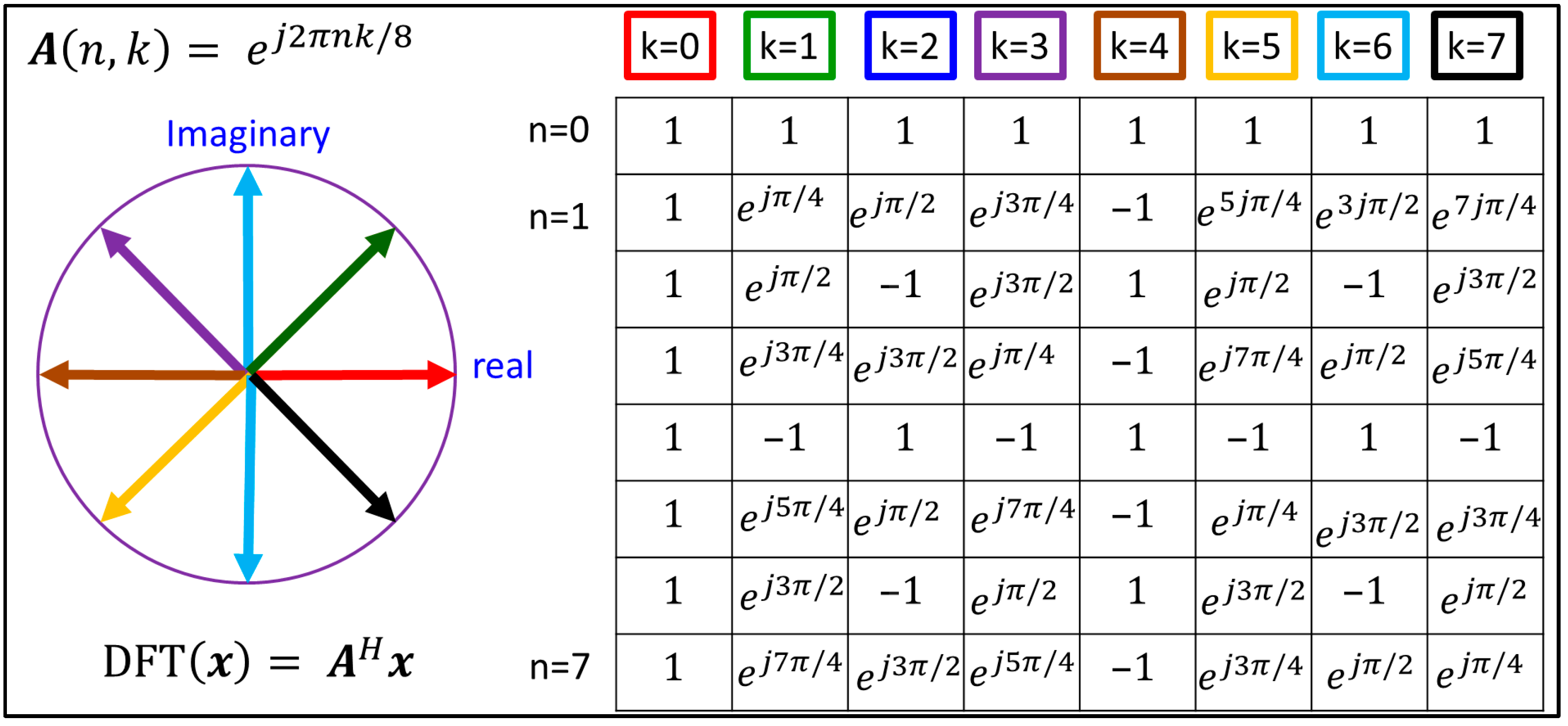
Discrete Fourier Transform (DFT)	The DFT is the standard tool to analyze digitized periodic signals, and is used in ML applications involving periodic signals for feature extraction, dimensionality reduction, and data visualization. The DFT can also be used to implement fast convolution used in ML algorithms such as the convolutional neural network. Understanding the DFT, in turn, requires an understanding of trigonometric projections, Euler’s formula, complex phasors, and inner products.
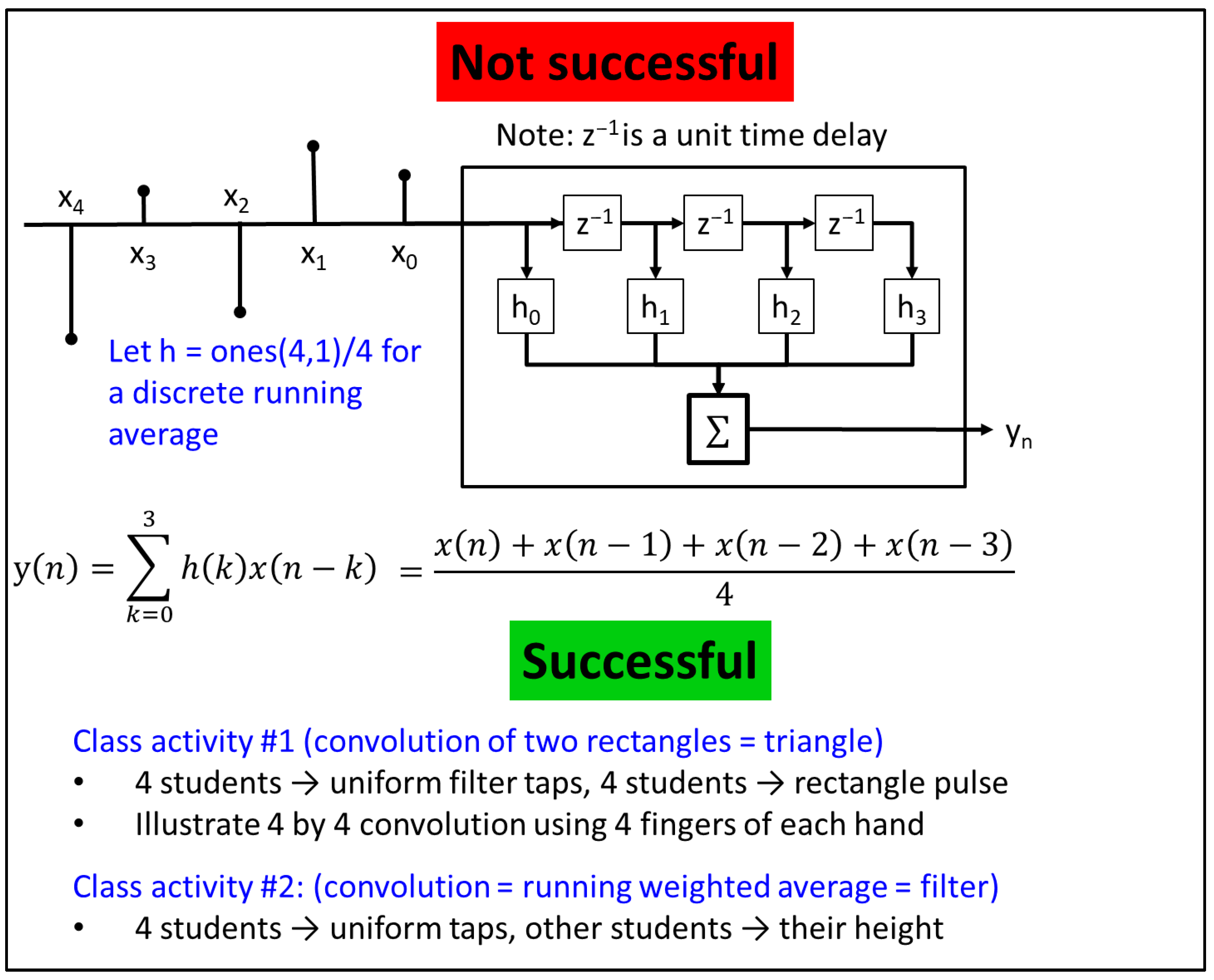
Convolution & filtering	Convolution is used in a variety of applications, including convolutional neural networks, computing probability distribution functions, and finite impulse response filters. Filtering is used to smooth data and reduce noise (low pass), support edge detection (high pass), and to isolate signals (bandpass/reject).
Matrix math & linear algebra	These skills and concepts are needed to develop algorithms, and to understand and interpret algorithms such as PCA or other dimensionality reduction techniques. Engineers need to understand concepts such as linear independence and matrix rank to properly use tools that solve systems of linear equations.
Sampling theory & practice	ML practitioners need to know when the sampling granularity is sufficient. In addition, an understanding of statistical sampling is critical in ML to avoid biased results caused by poor training data.
Principal Component Analysis (PCA)	PCA is widely used in ML to reduce the data dimensionality prior to training in order to reduce the processing time and, in some cases, to improve the ML classifier performance. PCA is based on eigenvector decomposition of the feature data covariance matrix, followed by replacing the original features with the eigenvectors associated with the largest eigenvalues. Thus, an understanding of eigenvectors and eigenvalues is critical to effective use of PCA in ML.
Optimization theory & practice	ML algorithms rely on optimization for training and hyperparameter optimization. Thus, a basic understanding of optimization theory, and concepts such as step size and learning rate, is required.
Digital logic	Binary number systems, Boolean logic, state machines, and sequential logic flow crop up in numerous areas of ML and computational math, including hypothesis testing and detection, sequential algorithm flow, hidden Markov models, large language models, digital signal processing, etc.
Embedded implementation skills	Due to computational complexity, many ML and computational math algorithms are implemented using graphics processor units (GPUs), field programmable gate arrays (FPGAs), etc., in order to support effective real-world deployment. Engineers with skills in these areas will have more career opportunities.

2.3. Student Demographics

Understanding student demographics is essential for adapting teaching strategies. As per [9], our engineering program has a very high percentage of students from underrepresented groups in engineering, including over 50% URMs, many from low SES backgrounds, and many first-generation students. These students can face multiple challenges, including the following:

• Poor academic preparation [18,19]. For example, less than half of our students were proficient in trigonometry prior to starting engineering core courses [9].
• Limited soft skills, along with a fear of engaging with faculty [18,19,20]. Since these same students often need more support, faculty need to be creative when engaging with students and providing support via peers [3,21,22].
• Lack of adequate financial support [20,21]. Many of our students need to work part or full time, and some students even need to support their families, or deal with incarcerated family members [19]. While employment can help develop responsible habits, it also creates problems, including reduced study time, lack of sleep, and coordination challenges on team projects.
• Need to commute [21]. Many of our students commute an hour or more, reducing available study time, and leading to missed classes due to traffic accidents, flat tires, and even closed roads (some students live in rural locations that are inaccessible by road after heavy rains).
• Reduced faculty expectations for URM students [21,23]. Instructors need to set appropriately high expectations.

Another important demographic factor to consider is student age. Most undergraduate students are Generation Z (Gen Z), born from approximately 1997 to 2012 [24]. Gen Z traits include (1) shorter attention spans, (2) a tendency to multitask, (3) a preference for video learning over traditional textbooks, (4) a need for immediate feedback, (5) individualism, (6) proficiency with digital technology, and (7) low information literacy [24,25,26]. Within our engineering program at ETAMU, we also have several older non-traditional students. These students, while facing different challenges than traditional students, are typically more mature and disciplined, and can provide a positive role model for the younger traditional students.

2.4. ETAMU Electrical Engineering Curriculum

The EE program, launched in Fall 2017, continues to evolve through the addition of Circuit Theory II, Computing for Engineers course, and a range of technical electives, including Power Electronics, Electronic Warfare, and Applied Machine Learning. Since the EE section of the Computing for Engineers course is effectively a different course than the legacy Computing for Engineers course (still taught to other engineering majors), we will refer to the EE section by its future Fall 2026 title, Computing for Electrical Engineers. Our most recent curriculum is shown in Table 2.

Table 2. ETAMU Electrical Engineering Curriculum, Fall 2025–Spring 2026.

Year 1		Year 2		Year 3		Year 4
Fall	Spring	Fall	Spring	Fall	Spring	Fall	Spring
Calculus I	Calculus II	Differential Equations	Linear Algebra	Calculus III	Digital Systems & Embedded Controls	Capstone I	Capstone II
Chemistry I	Intro to CS & Programming	Computing for Electrical Engineers **	Circuit Theory I	Circuit Theory II	Continuous Signals & Systems	Electric Machinery	Digital Signal Processing
Intro to Engineering & Technology *	Product Design & Development	Digital Circuits *	Engineering Probability & Statistics **	Electronics I	Electronics II	Technical Electives 1–2	Control Systems
	Physics I	Physics II	Engineering Economic Analysis		Electromagnetics	Technical Elective 3	Technical Electives 4–5 **
Notes regarding EE Technical Electives Technical Elective 1: Antennas Technical Elective 2: Power Electronics Technical Elective 3: Discrete Signals & Systems Technical Electives 4, 5: Electronic Warfare (odd years) or Applied Machine Learning (even years) As an alternative to EE course electives, EE students can take senior level physics electives
* Course discussed in this paper ** Course also includes significant ML content

Table 2. ETAMU Electrical Engineering Curriculum, Fall 2025–Spring 2026.

Year 1		Year 2		Year 3		Year 4
Fall	Spring	Fall	Spring	Fall	Spring	Fall	Spring
Calculus I	Calculus II	Differential Equations	Linear Algebra	Calculus III	Digital Systems & Embedded Controls	Capstone I	Capstone II
Chemistry I	Intro to CS & Programming	Computing for Electrical Engineers **	Circuit Theory I	Circuit Theory II	Continuous Signals & Systems	Electric Machinery	Digital Signal Processing
Intro to Engineering & Technology *	Product Design & Development	Digital Circuits *	Engineering Probability & Statistics **	Electronics I	Electronics II	Technical Electives 1–2	Control Systems
	Physics I	Physics II	Engineering Economic Analysis		Electromagnetics	Technical Elective 3	Technical Electives 4–5 **
Notes regarding EE Technical Electives Technical Elective 1: Antennas Technical Elective 2: Power Electronics Technical Elective 3: Discrete Signals & Systems Technical Electives 4, 5: Electronic Warfare (odd years) or Applied Machine Learning (even years) As an alternative to EE course electives, EE students can take senior level physics electives
* Course discussed in this paper ** Course also includes significant ML content

Although the EE curriculum in Table 2 represents an idealized course flow, many students follow a non-linear path due to inadequate high school preparation, transferring from community colleges, and insufficient financial aid (often coupled with needing to work part time or full time) [9]. Furthermore, even the idealized course flow presents some challenges, such as needing to cover basic linear algebra concepts and matrix math in Computing for Electrical Engineers since it is sequenced prior to Linear Algebra. Similarly, Engineering Probability & Statistics is sequenced after Computing for Electrical Engineers. While the sequencing can make it challenging to teach Computing for Electrical Engineers, the EE students who take this course first understand the application, which helps when they take the more theoretical courses the following semester. One final note is that we do not have any graduate engineering courses or graduate assistants; we have very little research funding, and we focus on teaching undergraduates. Although the core of this paper is centered on Computing for Electrical Engineers, a number of other EE courses have significant computational math content, including foundational courses (blue highlight) and upper-level courses (green highlight).

Figure 2 shows how the concepts and skills in Table 1 are covered by Table 2 lower-level foundational courses. The solid lines indicate primary student learning outcomes, while the dashed lines indicate that the topic is discussed but is not a significant part of the course learning objectives. As can be seen, Computing for Electrical Engineers covers numerous concepts and skills, which is one of the challenges in teaching it.

Figure 2. Mapping of ML and Computational Math Concepts and Skills to Lower-Level Courses.

Figure 2. Mapping of ML and Computational Math Concepts and Skills to Lower-Level Courses.

2.5. Human Factors Framework for Teaching Machine Learning and Computational Math

Human factors (HF) engineering focuses on optimizing human performance within complex systems. When applying to ML and computational math education, HF considers the range of factors impacting instructor and student performance, including demographics, student characteristics, cognitive factors, specific pedagogical techniques (e.g., hands-on and project-based learning), and both instructor and student perspectives. Despite HF’s success in other domains, little work has been done to apply HF to optimize the process of teaching ML and computational math.

Teaching ML and computational math imposes significant cognitive load, especially for students with limited prior exposure. HF principles can provide strategic approaches for addressing these challenges by drawing insights from cognitive psychology, instructional usability, and learner-centered design. Cognitive Load Theory (CLT), a foundational framework in learning and instruction, is based on short-term memory limitations [27]. As per Hollender et al., cognitive load includes (1) intrinsic load based on the inherent complexity of the material, including how many interactive elements a learner must process simultaneously; and (2) extraneous load based on complexity of the learning environment, including poor material presentation [28,29]. When learning ML, the intrinsic load is very high due to its interdependence of multiple computational math domains in conjunction with code writing skills. Since intrinsic load is dependent on the level of expertise of the learner, students with minimal background in computational math and coding often experience elevated cognitive load as they simultaneously manage new conceptual structures and unfamiliar tools [30]. Extraneous load can be minimized through more efficient instructional design, including the use of multimodal delivery, guided manual gestures, and designing interfaces that align with students’ existing mental models and task practices [31,32,33], while taking into account student demographics.

In addition to optimizing cognitive demands, human factors methodology emphasizes learner engagement and empowerment. Learner-centered instruction encourages students to take an active role in constructing knowledge through collaboration and cooperation, rather than just passively listening to the lectures [34]. Active learning, such as in-class coding practice and short team activities, can effectively enhance students’ social and problem-solving skills, as well as their capabilities for self-reliance [34]. Techniques such as role playing, case-based learning, and project-based learning (PBL) can allow students to connect theoretical knowledge with real-world applications and evaluate their own learning performance [34,35,36,37].

These methods are relevant in computational math and ML education, where the abstract nature of the material, steep learning curves, and frequent trial and error during learning can cause cognitive overload and fatigue, leading to excessive failure and high anxiety levels that are detrimental to learning [38]. Although excessive failure can inhibit learning, properly structured failure is important for learning because it triggers neuroplasticity, and supports long-term motivation through neurochemical mechanisms involving dopamine, serotonin, and epinephrine [38]. Furthermore, learning how to deal with uncertainty and failure are critical in real-world engineering. Thus, educators need strategies that lead to productive failure while avoiding excessive anxiety. As a practical application, strategies that encourage students to attempt solutions before receiving instructions have been shown to improve learning outcomes [38]. By integrating CLT, learner-based instruction methods, and neurobiologically informed approaches, it is possible to create high-impact instructional environments that support learners, especially those with minimal prior exposure to technical courses.

2.6. Teaching ML and Computational Math

We will now highlight a few papers that focus on teaching ML and computational math, including benefits and concerns when leveraging generative AI in the educational environment. One method is the “use-modify-create” model, in which students use sample code first and then modify the sample code to solve a closely related problem prior to creating new code to solve a different problem [39,40]. This method is also similar to real-world engineering practice, which mostly involves modifying existing code, rather than starting from scratch.

One of the challenges in learning to develop ML and computational math solutions is poor motivation when students feel overwhelmed by the volume of new skills. Solórzano et al. classified student learning difficulties into three categories, including (1) programming language syntax; (2) programming concepts such as loops, variable assignments, encapsulation, etc.; and (3) strategic knowledge to be able to write code to solve a problem [41]. Solórzano et al. advocate a Virtual Worlds (VWs) environment to maintain motivation while learning programming, however, based on our experience, we are not convinced that learning with VWs readily translates to problem-solving skills in text-based programming languages. However, we agree with Solórzano et al. regarding some of the benefits of the VWs pedagogy, including the constructivist grounding where students learn by doing in a problem-based collaborative environment. The Learning Assistant (LA) approach, in which peers (who have previously taken the course) provide in-class support and after-class tutoring sessions, can also help with motivation [22]. Not only do students appreciate the LA model, but the LA can also help the instructor know what material the students are struggling with the most.

Students also need to understand the ethical considerations when developing ML solutions that are susceptible to bias in the training data, leading to the possibility of harmful effects to individuals or to society in general [42]. A more recent concern in academia is the impact of ChatGPT and similar generative AI. While these tool capabilities can be leveraged to enhance education, there is also the potential of student misuse by not properly citing generative AI support, cheating during exams, or resorting to generative AI instead of working out a solution on their own, which reduces critical thinking skills [15,43]. Given the expectation by our IAB that EEs will know how to use generative AI tools appropriately, we need to teach our students the ethical considerations, strengths, and weaknesses of generative AI, including how to properly test and evaluate generative AI enhanced ML or computational math code.

3. Methods

The methodology is tied directly to the research goals. Therefore, this study involves two interrelated but distinct methodologies linked to RQ2: (1) a teaching methodology grounded in human factors, and (2) a research methodology used to evaluate the teaching methodology.

3.1. Teaching Methodology

The teaching methodology employs industry experience, HF-based instructional design, and pedagogical strategies, such as PBL [37,44,45] and experimentation. The strategies implemented are evaluated and revised using the continuous improvement process shown in Figure 3.

As per Figure 3, the student learning objectives (SLOs) for the new and revised courses that support ML and computational math were initially based on a combination of legacy SLOs and industry experience. As discussed earlier, in the case of Computing for Electrical Engineers, these were based primarily on the industry experience of author G.F.. Once the baseline is established, the SLOs are evaluated every year to ensure alignment with industry using a feedback loop (shown in blue) that includes the EE IAB. The teaching strategies and techniques are also evaluated and revised every year to maximize effectiveness given our student demographics. Finally, the Accreditation Board for Engineering and Technology (ABET) evaluates the overall process at periodic intervals to ensure compliance with accreditation standards. Note that this continuous improvement process can also serve as a framework for educators who want to implement strategies described in this paper (or other research literature). Since the evaluation process is also the basis for the research methodology of this paper, we discuss this topic under research methodology in the next section.

3.2. Research Methodology and Course Effectiveness Assessment

In line with our practice-oriented research goals, this work does not follow a formal experimental design with participants, control groups, or randomized interventions. The research methodology evaluation is based on the same methodology used by the instructor to assess the effectiveness of the teaching strategies and techniques. The assessment tools for Computing for Electrical Engineers include

• Instructor observations

  ⚬

  During in-class hands-on exercises as students work through problems;

  ⚬

  During in-class lectures and office hours as students ask questions.

• Student feedback

  ⚬

  End-of-semester student evaluations;

  ⚬

  Informal student feedback during and after the semester;

  ⚬

  Detailed student analysis by student coauthors.

• Industry feedback
• Assignments

  ⚬

  Homework;

  ⚬

  End-of-semester projects.

• Exams

  ⚬

  Written and oral midterms;

  ⚬

  Written finals.

The instructor observations, student feedback, and industry feedback, while subjective, are useful for evaluating specific teaching strategies and for guiding strategy modifications. Feedback during the semester enables dynamic adaptation, and adjustments to teaching strategies and assignments based on student conceptual understanding and skill development during the semester. Industry feedback validates overall student career readiness, as well as any systemic weaknesses of our program. Interestingly, while the end-of-semester student evaluations for Computing for Electrical Engineers provide useful written feedback (both positive and negative), the numerical evaluations for Computing for Engineers do not correlate positively with student success as measured by empirical methods, and have limited utility.

The detailed student analysis was performed by the three student coauthors (W.Z., J.R., C.B.), who went through the course material and evaluated it based on their own experiences as well as the experiences of their classmates. The evaluation goals included identifying strategies and methods that were effective or ineffective, and recommending approaches to improve the course. One focus for course improvement was the first few weeks based on informal student feedback and instructor observations. Although non-empirical, with three students working independently, the resulting analysis provides valuable insights to supplement the other non-empirical results and to support our empirical results.

The assignments and exams all provide empirical assessment data. However, they have different levels of assessment utility. Since homework can be re-submitted for an improved grade, the homework scores are less useful for empirical analysis, although trend analysis of common errors is useful for instructor evaluation and immediate adjustments. The end-of-semester project scores, while useful, are limited since (1) not all semesters conclude with a final project, (2) the projects are team-based, and (3) the minimum required project scope is modest, with team project difficulty varying significantly. Similarly, the midterm exams (both written and oral) are limited in empirical utility because of their limited scope and lack of consistency from semester to semester.

The written final exam, on the other hand, provides strong empirical assessment evidence since (1) it is comprehensive, and (2) it is similar year-to-year except for difficulty level, which has increased since the course was first taught in 2021. Regarding difficulty level, the quantity of complex problem-solving questions has increased compared to prior years. For example, in the most recent Computing for Electrical Engineers final exam, one of the new questions required students to download a noisy in-phase/quadrature-phase (IQ) dataset with hundreds of pulses varying in signal to noise ratio and pulse width, then write MATLAB code to detect and measure the pulses, and to generate summary statistics of the pulse measurements. With complex problem-solving questions in addition to basic knowledge questions, the final exam also meets the ABET assessment criteria relevant for this course (Student Outcome 1), which requires that students demonstrate “an ability to identify, formulate, and solve complex engineering problems by applying principles of engineering, science, and mathematics” [46]. Since the raw point value assignment methodology has remained consistent for the final exam each year, the final exam scores can be normalized by difficulty level by scaling according to the total raw point value and are thus useful for empirical trend analysis.

In summary, the evaluation methodology combines broad-based anecdotal data with narrowly focused empirical results. Although the anecdotal results are not statistically significant, we present our results within the context of recent research literature to ensure proper grounding. One key advantage of our approach is that it allows us to focus on specific practical lessons learned and strategies that others can adapt for classroom use to aid in teaching these topics. A second advantage is that this approach adapts readily to a continuous approach process; long-term empirical studies with control groups are problematic when the teaching strategies and implementation methods are continually updated. A third advantage is that we are able to include recent observations regarding significant changes over the past year. A final advantage of our methodology is that it considers student perspectives as captured by the three student coauthors based on their learning experience and detailed analysis of course material.

4. Strategies and Results

We now present strategies and results for teaching ML and computational math to our engineering students, starting with general strategies in Section 4.1, followed by strategies for selected courses, including Intro to Engineering & Technology (Section 4.2), Computing for Electrical Engineers (Section 4.3), Engineering Probability and Statistics (Section 4.4), Digital Circuits (Section 4.5), and Applied Machine Learning (Section 4.6).

4.1. General Strategies for Teaching ML and Computational Math

This section describes general strategies based on human factors and the research literature discussed earlier.

Lecture style: Not surprisingly, given Gen Z traits, we have learned that we need to interleave lecture time with hands-on activities during class to avoid student tune-out during lecture-heavy classes.

Digital proficiency: Surprisingly, while most of our students can easily install packages, many of our students lack proficiency in performing low-level tasks, including locating downloaded data, unzipping compressed files, and organizing files on their computer. We have learned to allocate more class time to teach these low-level skills.

Instructor In-Class Problem Solving: Although making mistakes is essential to learning, it also causes stress, which can inhibit learning. We have observed that student fears of making errors in front of their peers can be mitigated by seeing the instructor make occasional errors while working problems from scratch (without notes) in front of the class—if the instructor can make mistakes, then so can the students. Another benefit is that students are more alert as they watch for errors to get extra credit.

Midterm Corrections Exam: In addition to the traditional written midterm exam, we have found that having an additional midterm corrections exam with both written and oral exam components is very effective in helping students master the material so that they do not make the same errors on the final exam (previous strategies, such as reviewing errors during class, providing writing corrections only, assigning homework, and doing quizzes, were not successful). During the oral component, the instructor does not allow notes or, in most cases, even a calculator, which forces students to think through the problem conceptually, and helps develop confidence. Another benefit of the midterm corrections exam is that it reduces the motivation to cheat since once complete, the midterm corrections grade is set to 100% and averaged with the midterm. The primary drawback is the time required for the oral exam component, especially for weaker students.

Assignment Correction Policy: A related strategy that we have found effective is to allow students to correct and resubmit their homework with a resubmit penalty of 10% per resubmission. In addition to observing improved student outcomes, informal student feedback indicates that this policy reduces anxiety and improves student understanding.

Rapid-Fire Verbal Questions: One final general strategy that has proven effective is to call on students by name with rapid-fire questions. Since our class sizes are typically less than 30 students, it is possible to call on most, if not all, students during each class period. Although students report that this is stressful at first, students also acknowledge that the rapid-fire technique helps keep them alert, especially if the rapid-fire name sequence is varied in interesting patterns. This technique also helps students learn their classmates’ names and become comfortable with faculty engagement.

4.2. Intro to Engineering & Technology

This course introduces students to the engineering discipline and provides a solid foundation in fundamental skills needed for later engineering courses, and for success as an engineer. This course uses a combination of traditional homework and project-based assignments to help students learn to apply mathematics to solve engineering problems, acquire team working skills, practice written and verbal communication skills, and develop problem solving and design skills. Specific skills relevant to ML and computational math include (1) unit conversion process, (2) estimation, (3) trigonometry and projections, and (4) report writing, including with the aid of generative AI.

4.2.1. Unit Conversion Process

Although sometimes overlooked in engineering academics, the unit conversion process is a key engineering skill necessary for proper data scaling and visualization, for accurately solving problems, and for peer review by other engineers. Students struggle with this apparently simple concept because it requires multiple sub-skills, including converting a colloquial English problem statement into an algebraic equation with abstract unit variables. Furthermore, this process also teaches students the self-discipline to work carefully and methodically, which is even more critical today given the availability of sophisticated tools that can easily be used incorrectly. An example unit conversion problem with solution is shown below in Figure 4. While this process looks easy, most of our students struggle with unit conversion, and many require one-on-one sessions to master this concept sufficiently to apply it.

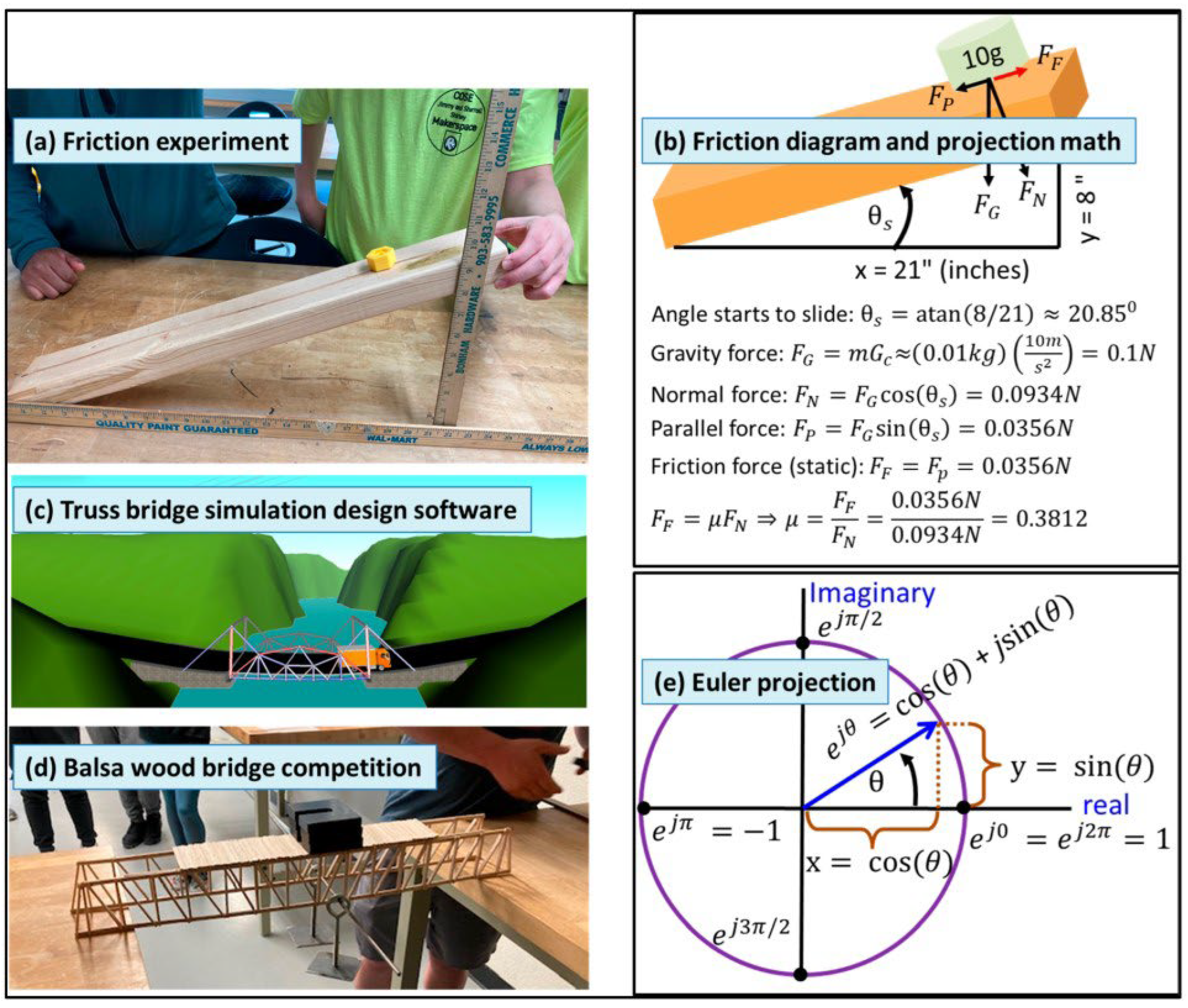
4.2.2. Estimation

Although estimation has always been important as a second check to equations and other analytical solutions, estimation skills are especially important today given how easy it is for engineers to make undetected major errors using powerful computational tools. At the same time, given the Gen Z reliance on tools, most students are reluctant to estimate. Thus, instructors must require students to estimate, starting with their first engineering class, and continuing through graduation. Students also need to see examples to help them understand the need for estimation, such as when a digital entry is off by one decimal place, leading to an order of magnitude error that can easily be caught by comparing with a rough estimate.

An example effective estimation problem is as follows: Estimate the resulting volume of water in liters if the classroom is filled to a depth of a quarter inch of water. This is done as a team exercise, so students can develop teamwork skills. Also, there is a time limit, and students are not given any measurement equipment, forcing students to work together to figure out how to estimate the class dimensions. Afterwards, the instructor compares the average with the median team volume estimates to provide students with sample statistic experience and help them see that the median is robust to outliers. In a different exercise, students estimate the volume of the school pool using only cues from an online image.

4.2.3. Trigonometry and Projections

As discussed in [9], teaching trigonometry via diagrams such as the Euler projection and unit circle diagram shown in panel (e) of Figure 5 was not successful, but starting with the hands-on friction measurement shown in panels (a) and (b) of Figure 5 was successful. In addition, two hands-on bridge design activities help students improve their intuition of force projection. In the first activity, students design truss bridges using freely available bridge simulation software see the Bridge Design Software at https://www.bridgecontest.org/ (accessed 30 June 2025) as shown in panel (c) of Figure 5. With this activity, students quickly learn that triangles are required for stability in truss bridges. The simulation exercise is followed by a balsa wood bridge contest where the students are given a fixed amount of balsa wood to span a gap of two feet with a goal of supporting the maximum weight as shown in panel (d) of Figure 5. Once these activities are complete, students are introduced to Euler’s formula and the corresponding force projection diagram shown in panel (e) of Figure 5. The Euler force projection lesson references the earlier triangle ramp friction experiment of panels (a) and (b) to help students tie theory to real world engineering problems and their experiential learning. This approach has proven successful in teaching force projections. This also helps EE students understand complex rotating phasors and the Fourier Transform when studied in Computing for Electrical Engineers.

As per [9], the hands-on approach improved classroom efficiency, allowing us to add a short unit on probability and statistics covering concepts such as independent and mutually exclusive events via simple coin toss and dice experiments. These concepts are reinforced in a Markov chain example involving tourist island-hopping between three islands Adapted from https://brilliant.org/wiki/markov-chains/ (accessed 30 June 2025). in which students compute the probability of a tourist being on a particular island given their island location earlier in the week.

4.2.4. Reports and Generative AI

Engineering documentation, reports, white papers, professional papers, and peer reviewed papers continue to be important in engineering. Despite advances in generative AI, students still need to know how to write coherent reports because generative AI, while able to improve grammar and spelling, cannot reliability correct incoherent content given the stochastic nature of LLMs.

Our initial (unsuccessful) report strategy focused on a single team-based final project report. The rubric included a significant emphasis on grammar, spelling, and structure. However, this approach did not yield good results because (1) there were no further report exercises for students to incorporate feedback, (2) often, one student wrote the report, and (3) there were no prior shorter reports for students to develop report writing skills.

Our latest successful report strategy requires multiple reports of varying complexity centered around class projects such as the friction and bridge activities shown in Figure 5. Each report uses a template so that students only need to follow the template rather than worry about the report structure (this is closer to industry practice based on the experience of author G.F.). Although collaboration is encouraged, reports are individual, even for team-based projects. Furthermore, the latest grading rubric does not address grammar or spelling unless the overall comprehension is impacted. In addition, students are encouraged to use generative AI to improve their writing with the caveat that they properly cite any generative AI tools. This approach is consistent with inputs from representatives on our EE IAB, who remarked that using generative AI is a common business practice now, and that engineers need to know how to use these tools properly. This approach has led to significantly improved reports that are more readable and which contain more thoughtful analysis of the class activity results. Finally, there is less motivation for students to cheat since (1) no single report constitutes a significant portion of the grade, (2) the focus is on specific class activity results, which makes it difficult for generative AI to write the report, and (3) students are not only allowed, but encouraged, to submit a generative AI enhanced version for an improved grade.

4.3. Computing for Electrical Engineers

As described in [9], we developed a separate EE section of the Computing for Engineers course in the fall of 2021 designed to prepare our students for the local job market, which we refer to here using its future Fall 2026 title, Computing for Electrical Engineers. This section presents an overview of the course in Section 4.3.1, discusses common assignment strategies in Section 4.3.2, describes required coding standards (including the grading rubric) and post-assignment peer-review process in Section 4.3.3, and describes individual assignments and the associated classroom teaching strategies in Section 4.3.4. We also discuss the appropriate use of generative AI in coding in Section 4.3.5, as well as project strategy in Section 4.3.6. We conclude this section with empirical results in Section 4.3.7.

4.3.1. Course Overview

The legacy Computing for Engineers course focused on Excel spreadsheet skills, including pivot tables and regression analysis, along with a very brief introduction to computing using MATLAB and Python. The new Computing for Electrical Engineers course emphasizes (1) computational programming using both structured and objected oriented techniques, (2) matrix math, (3) data visualization, (4) time, frequency, and time-frequency domain analysis, and (5) introductory machine learning.

The course starts with MATLAB, then transitions to Python (supplemented by Jupyter Notebooks) after midterm exams for the unit on machine learning. We selected MATLAB because it is still widely used by EEs, and is both powerful and simple to use. Also, based on our experience, MATLAB is a good language to learn structured programming techniques. We selected Python because it is also widely used in engineering, and because of the wide range of powerful open-source ML and computational math tools available. Furthermore, Python is an excellent language to learn object-oriented programming techniques. Finally, Python, especially when used with the NumPy and Matplotlib Anaconda libraries, has similar syntax as MATLAB, and the Python Spyder integrated development environment (IDE) is similar to the MATLAB IDE. We selected Jupyter Notebooks as a supplement because, based on our observations, they are not useful for teaching software problem-solving skills, but they are a great tool for learning Python syntax and specific Python ML techniques.

As remarked upon in [9], the inaugural course in the Fall 2021 semester lost about two weeks while we paused the course to review basic programming concepts. Another unexpected delay was caused by needing to teach trigonometric projections since the Intro to Engineering & Technology course had not previously been covering this topic, and most students were not proficient in trigonometry. Given these delays, the Fall 2021 semester lacked time to introduce Python, and only had an abbreviated introduction to ML.

The Fall 2022 course was revised to include basic programming skills, and to tie in the trigonometric projections covered in the revised Intro to Engineering & Technology course, leading to a better foundation for using the Fourier Transform as a computational tool, and allowing us to cover more material, including Python ML as originally planned.

However, one problem that we continue to face is that, even with these changes, most students still feel overwhelmed during the first month, leading to high anxiety levels that inhibit learning. In order to improve the course for the upcoming Fall 2025 semester, our three student coauthors (W.Z., J.R., and C.B.) analyzed the Fall 2024 course material as discussed earlier.

4.3.2. Common Assignment Strategies

Computing for Electrical Engineers relies on a set of common homework assignment strategies used throughout the course, including

• PBL: The homework assignments are like mini-projects so that students learn problem-solving skills rather than just syntax. This approach is successful in that once the first Fall 2021 cohort reached their senior year, we began seeing more capstone projects tackle designs with significant ML and computational math components.
• Sequenced learning: The assignments build on each other as the assignments get more sophisticated. Thus, later assignments reinforce concepts from earlier assignments. One problem is that if students fall behind early on, it is difficult to catch up; hence, intervention must be employed early in the semester for students who are struggling. Another problem that we are still working to solve is that the assignment complexity ramps up too quickly over the first month as noted earlier.
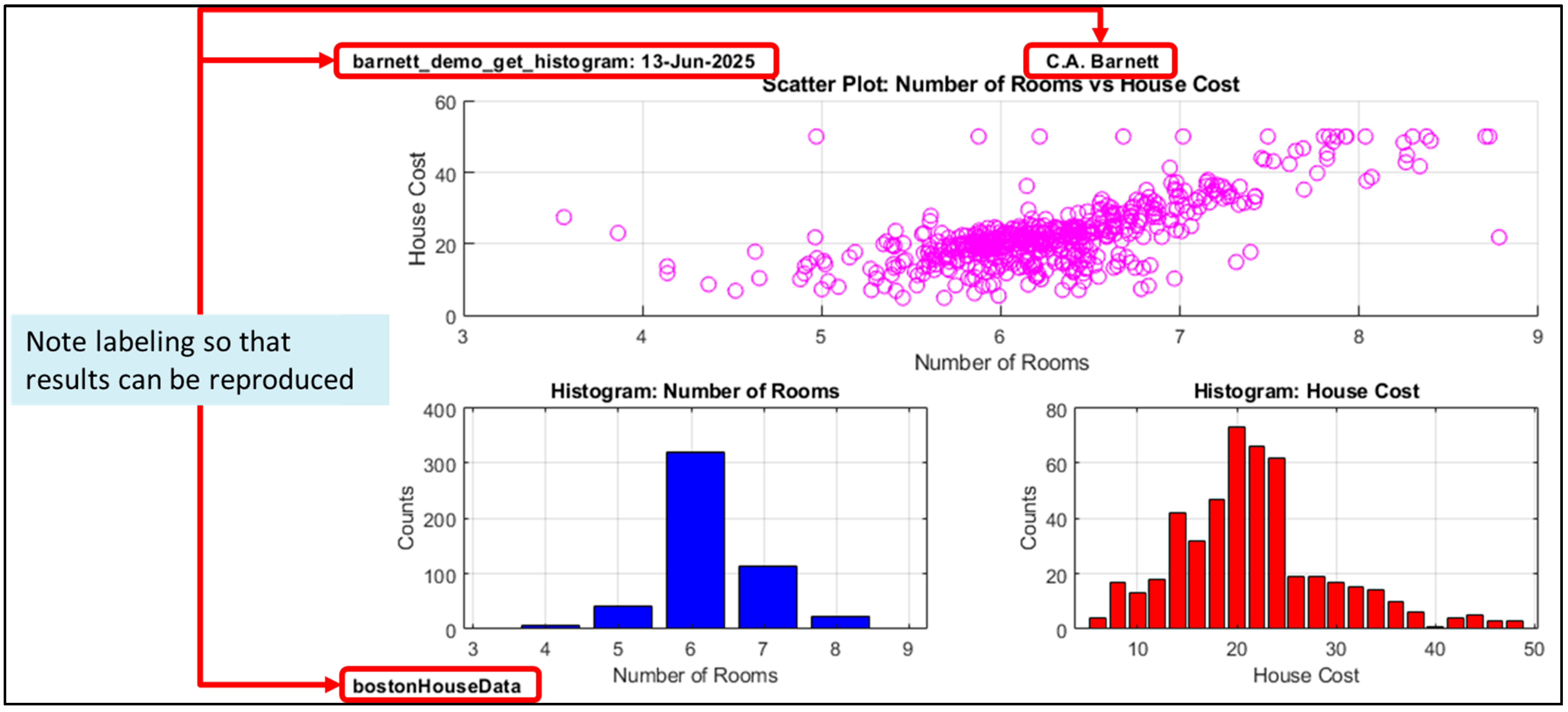
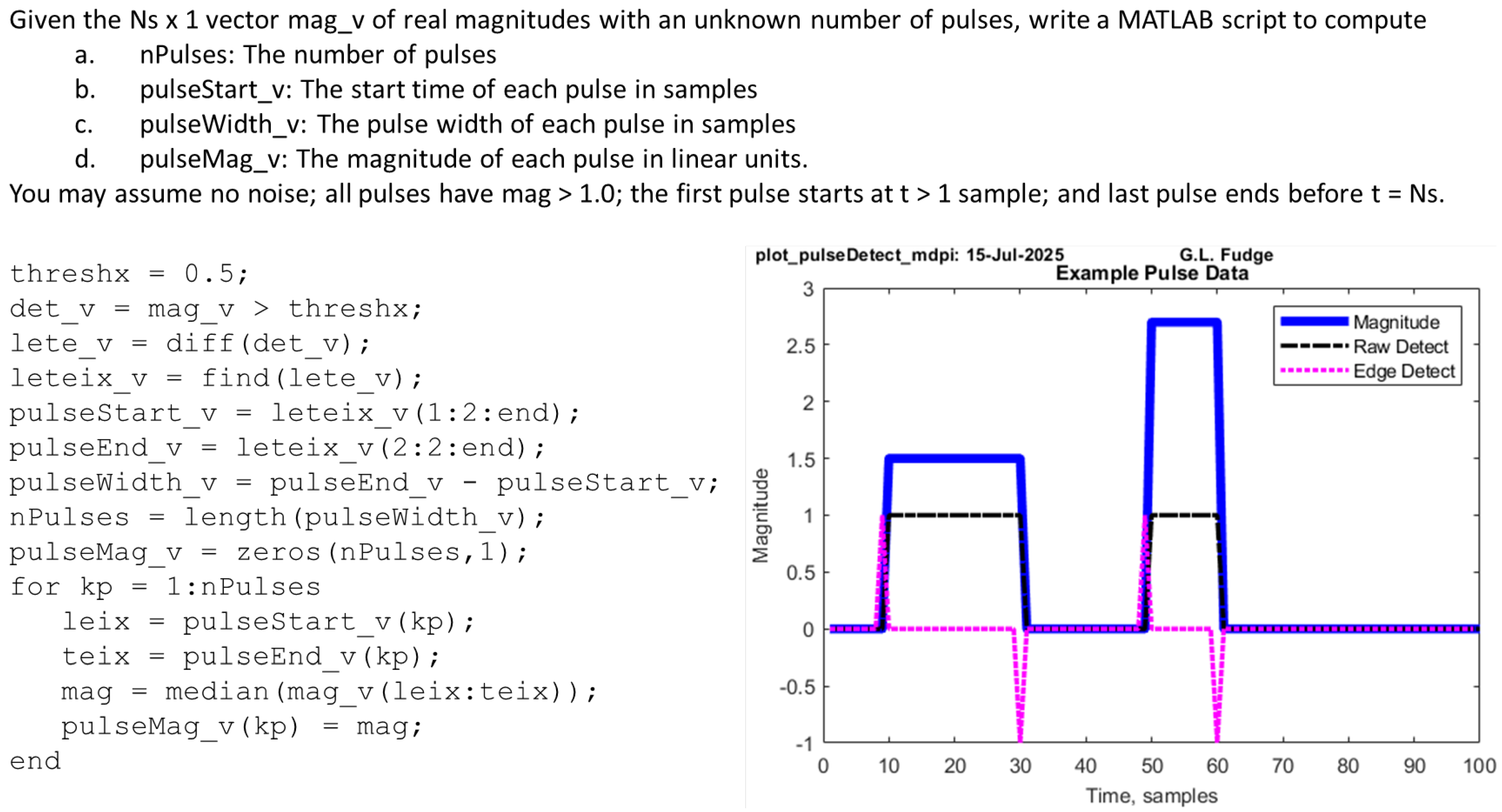
• Data visualization: Each assignment includes visualization plots, which students report is helpful in learning concepts. An example can be seen in Figure 6.
• The “Use-modify-create” plus “save-as” strategy: Students are taught to develop new code by first saving old code that is similar to the new code, then modifying while maintaining the software requirements discussed below. This technique not only helps students, but also improves productivity in industry.
• Peer learning via peer-review, the LA model, and classmate collaboration: The peer pressure involved in submitted code walkthroughs is one of the more effective strategies for motivating students to pay attention to details. Similarly, the LA model has proven effective to provide supplemental tutoring. However, we have observed mixed results with collaboration because some students tend to rely too heavily on their classmates. Thus, while partially successful, the collaboration strategy needs improvement.
• Software requirements and figure labeling: This specific strategy has not been described in the literature previously, so we describe it in more detail below.

Our software requirements approach requires all code submissions to comply with the instructor’s software standards, including (1) code file names, (2) figure numbering method, (3) plot labeling, (4) figure labeling, (5) figure sizing, and (6) internal comments (including the header comments). The first two requirements allow the instructor to run an automated master script that encapsulates and runs each student’s script for all students in the class with non-overlapping figures. The figure labels (see Figure 6) supplement the plot labels (x-axis, y-axis, title) to provide standard information for reproducing and reusing work, and to support rapid grading and classroom discussion during peer review. The common figure sizing simplifies the process of comparing results from different students during peer review, and supports building professional presentations. The internal comments required are similar to industry standards, although less formal and detailed.

We have observed that students struggle with software requirements, so to make it easier for students, we provide generic MATLAB script and function templates, along with compliant examples. Similarly, we provide compliant Python code examples. Students are taught to use the “save-as” method to retain the existing compliant code framework while modifying legacy code or integrating new code.

4.3.3. Grading Rubric

The generic grade rubric applicable to all assignments is discussed and posted so that all students can know what to expect in grading. For example, there is a penalty for each independent code error causing the code to crash (the instructor debugs and corrects each individual error until the code runs or until the penalties reach 50%). Similarly, there is a penalty for each significant template requirement violation. For minor errors, the penalties are smaller, although as the semester progresses, the penalty for minor errors increases to encourage students to maintain code discipline. Although grading the first homework assignment is time consuming, most students quickly learn to follow the coding standards, allowing the instructor’s automated script to run all of the submissions, which greatly accelerates grading. The assignment correction policy discussed earlier provides students with an opportunity to correct their errors and improve their grade.

In addition to providing detailed feedback on each assignment, the instructor runs student submissions for the prior week’s homework and displays the results for class discussion and informal peer review, including identifying individual errors (such as axis labeling, etc.), common errors for the particular assignment, visualization approaches by different students, etc. This is similar to a standard industry peer review, except that the written feedback is from the instructor, although students are expected to provide verbal feedback on submissions during class. Although students find it intimidating at first to have their work displayed and mistakes discussed in class, peer reviews are an important component of engineering in industry, and so it is important that students get familiar with the peer review process. The assignment grading strategies, including informal peer reviews and resubmit policy, have proven effective in developing not only hard skills, but also in developing soft skills such as confidence and maturity in handling errors.

4.3.4. Assignments and Classroom Teaching Strategies

We will now discuss each assignment and associated classroom teaching strategies. Most of the assignments from the Fall 2024 semester are similar to the Fall 2023 assignments discussed in [9], but a few assignments have been revised based on lessons learned. Based on detailed analysis of the course material and recommended changes by our three student authors, we have further revised some of the assignments (especially the earlier assignments) for the Fall 2025 semester. Figure 7 illustrates example homework assignments from the Fall 2024 semester as they would be displayed during peer review. We will now discuss each assignment.

The goal of HW #1 (Noisy Real Sinusoid in panel (a) of Figure 7) is for students to get familiar with the MATLAB IDE, understand scripts and basic plotting methods, be able to simulate real sinusoids with additive white Gaussian noise (AWGN), understand digital frequency, and use running average filters to smooth data. In addition, students must follow the standard software requirements discussed earlier. According to student author analysis, discussing and implementing digital frequency is a good choice for early assignments to familiarize EE students with sinusoids. However, despite simplification from the prior year, after careful analysis of all results, we realized that this assignment still had too many new learning elements, leading to cognitive overload and suboptimal results.

The goal of HW #2 (Inner Product in panel (b) of Figure 7) is for students to learn how to write their own MATLAB functions, and to get familiar with projections via the inner product between vectors. Students develop a demo script to generate and plot two vectors, and a function that returns the inner product of two input vectors. While some students found this assignment easy, others struggled with the concept of encapsulation via functions. The student authors also identified another problem, which was that this week’s lecture covered way too much syntax for students to absorb at one time, and recommended covering only the syntax required during lecture time and providing the extensive syntax lecture notes to the students as reference material only.

The goal of HW #3 (Histogram in panel (c) of Figure 7) is for students to understand data visualization via histograms and scatter plots, to be able to develop the histogram algorithm, and to know how to load data in MATLAB while maintaining compliance with software requirements. Surprisingly, many students struggled with the histogram concept. To address this problem, we designed a classroom activity in which the students physically form the histogram bins. For example, students pick a number from 0.0 to 9.9, then the instructor calls all students with numbers from 0.0 to 1.9 to stand in a line at the front of the class. Then students with numbers from 2.0 to 3.9 form a line next to the first line. We continue this process until we have 5 lines. The students can then visualize the counts for how many students picked numbers in each range. We then discuss how to interpret the x-axis as either bin number (1 through 5 in this case) or as bin center value (1 through 9). This activity successfully helped students understand the histogram based on all feedback mechanisms.

The goal of HW #4 (Low Pass Filter in panel (d) of Figure 7) is for students to understand (1) complex sinusoids by generating a complex rotating phasor; (2) simulation of pulsed signals by multiplying the phasor by a pulse template; (3) signal magnitude of a complex noisy sinusoid; and (4) signal-to-noise ratio (SNR) by calculating SNR = A^2/sigmaX^2 for a complex sinusoid with amplitude A and complex noise standard deviation sigmaX. Students also learn to calculate SNR in dB. During the associated class lecture, we introduce convolution. We originally used a simple discrete time 4-point running average circuit diagram (see the top half of Figure 8) to help illustrate convolution. However, even after walking through this diagram slowly with numerical examples, students were still confused. We then designed a hands-on activity involving student participation. As summarized in the bottom half of Figure 8, four students are selected to represent filter tap multipliers h₀ through h₃, each with a value of 0.25. Another set of four students represent the input data x₀ through x₃, each with a value of 1.0. We then convolve the two rectangles by walking the data students one step at a time through the filter tap students, applying the appropriate multiplication and addition at each time step. The students then verify that the output forms a length six triangle. This exercise is repeated, except that now we have a larger group of data students with values corresponding to their heights to illustrate a simple running average that smooths the height variation. As confirmed by student feedback, instructor observations, and student author analysis, this was a much more successful strategy. We have found that the four-finger convolution example suffices to review convolution since students remember the class activity even after graduation.

The goal of HW #5 (Pulse Detection in panel (e) of Figure 7) is for students to apply earlier lessons by loading a noisy IQ dataset containing simulated pulsed radars and then detecting and measuring the pulses. As can be seen from panel (e) of Figure 7, there are a variety of pulses with varying pulse width, amplitude, and SNR. Students are expected to compute the magnitude, perform low pass filtering to smooth the pulse magnitude, threshold the magnitude, and apply an edge detector in order to find the pulse leading and trailing edges and pulse width. Finally, students estimate the pulse magnitude. This is a very challenging assignment for sophomore level students due to the multiple algorithm steps required. The detected pulses are auto-graded with an instructor script that penalizes student scores for insufficient quantity of detected pulses and for inaccurate measurements of detected pulses. Based on class experience, the instructor needs to go through the algorithm steps carefully, and have students practice writing the code by hand from scratch to be sure they really understand it. Per student author analysis, the running average smoothing demonstration is useful, but one improvement would be to introduce more advanced filter design options available in MATLAB.

The goal of HW #6 (Fourier Transform in panel (f) of Figure 7) is for students to understand how to use and interpret the DFT. One successful strategy to help students understand the power of the DFT is to use the MATLAB sound() command in conjunction with DFT magnitude plots under different digital frequency and noise cases, including negative SNR. Another successful strategy is to relate the DFT magnitude plot to Euler’s formula and to the cosine identity as shown in Figure 9 below. We also illustrate how the Fourier Transform is a projection onto orthogonal frequency axes via the inner product. Finally, we show how the DFT can be computed via matrix-vector multiplication that represents a set of inner products of the desired signal onto a set of discrete rotating phasors as shown in Figure 10 (the phasor diagram is animated so that students can see how the different frequency components rotate at different rates). We have found that all of these strategies, plus review in subsequent courses, are required for our students to understand and properly use the DFT.

The goal of HW #7 (Time Frequency in panel (g) of Figure 7) is for students to understand how to construct a time frequency spectrogram tool using the DFT, then perform time frequency analysis using the spectrogram tool on the same dataset from the HW #5 Pulse Detection assignment. HW #7 builds on earlier assignments, with students comparing visualization in the time domain via simple magnitude smoothing, frequency domain via the DFT magnitude, and time frequency domain via the spectrogram magnitude. Surprisingly, the primary problem that students have on this assignment is with unit conversions to get the time and frequency scales correct. We also have observed that students tend to get careless with the software requirements as the assignments get more challenging. During the homework review, the instructor demonstrates the process of zooming in on the spectrogram, with classroom discussion focusing on comparing individual pulses in the time, frequency, and time frequency domains. In the special topics Electronic Warfare class, students use the spectrogram tool developed in this class to analyze more complex radar signal examples. We have observed that time frequency analysis is also a useful tool to develop student curiosity as they look at spectrograms of different signals.

The goal of HW #8 (Least Squares Regression in panel (h) of Figure 7) is for students to learn ML concepts (regression prediction, overfit, underfit) and more advanced matrix math via least squares polynomial data fit. Students develop their own MATLAB function to compute the linear and quadratic fit coefficients, along with the corresponding root mean square error (RMSE). Students can compare their results with the MATLAB polyfit() and polyval() functions for extra credit. The primary challenge that students have is understanding how to set up the matrix model and the pseudo inverse matrix solution required to generate the least squares polynomial coefficients. Surprisingly, students also struggle with creating test data.

The goal of HW #9 (Python Regression in panel (i) of Figure 7) is to reinforce HW #8 and to introduce students to Python polynomial regression tools within a demo script that meets software requirements. One problem we have observed is that students struggle with understanding Python code, especially the code to support plot labeling.

The goal of HW #10 (Python Classifier in panel (j) of Figure 7) is to introduce students to machine learning classifiers available in Anaconda. As part of the classroom lecture time, the instructor walks students through code modification of a classifier example to change the algorithm and to change the classification data. This method has worked well, although one weakness is that students do not gain experience in developing a classifier from scratch.

Supplemental Assignments. We have found that assigning students to read a short introductory book on ML, such as [47], is a good way to supplement the lecture material for most students. We have also found that YouTube assignments covering MATLAB, Machine Learning, and Linear Algebra are excellent resources for students (see

Table A1. Some Useful Online Resources for ML and Computational Math.

Category (Host)	Site and Discussion
Code (Anaconda)	https://www.anaconda.com/download Includes latest Python, Spyder IDE, NumPy, Matplotlib, Scikit-learn ML algorithms, and many other computational math algorithms in ML, data visualization, statistical analysis, etc.
Code, toy data (Scikit-learn)	https://scikit-learn.org/stable/ Includes many easy-to-use ML algorithms that have common interface methodology, including data visualization, clustering, regression, and classification. Also, various toy datasets for ML beginners.
Data (Kaggle)	https://www.kaggle.com/ Popular site for ML, with a large variety of datasets with descriptions. Also, hosts ML competitions. Account required (free).
Data (UC Irvine)	https://archive.ics.uci.edu/datasets Hundreds of datasets useful for ML. Well organized with suggested types of ML prediction (classification, regression).
Data, code (OpenML)	https://www.openml.org/ Includes a variety of documented datasets. Also can share code and can compare with benchmark information posted by other users.
Book (Raschka)	https://github.com/rasbt/machine-learning-book GitHub site for [7] that includes figures, Jupyter Notebooks associated with the chapters (including Python code examples), and some datasets.
Data, papers (Figshare)	https://figshare.com/browse Contains a large variety of datasets and papers. Can be difficult to navigate to find good data to practice on, but potentially useful for more advanced students.
Video series (Linear Algebra) (3Blue1Brown)	https://www.3blue1brown.com/topics/linear-algebra Intuitive explanations of key concepts in linear algebra with outstanding graphics. Total of 16 videos, most of which are about 10 min long.
Video series (Deep Learning) (3Blue1Brown)	https://www.3blue1brown.com/topics/neural-networks Intuitive explanations of key concepts in deep learning. Total of 7 videos covering neural networks (including gradient descent and backpropagation for training), LLMs, transformers, and attention methods.
Video (Fourier Transform) (3Blue1Brown)	https://www.3blue1brown.com/lessons/fourier-transforms Intuitive explanation of the Fourier Transform with animated graphics that many students and engineers find useful. About 20 min long.
Video (MATLAB) (freeCodeCamp)	https://www.youtube.com/watch?v=7f50sQYjNRA MATLAB Crash Course for Beginners. Useful introduction to basic MATLAB, including the IDE, plots, and equations. About 30 min.
LinkedIn Learning	Machine Learning with Scikit-Learn (43 min) Outstanding introduction to ML, including Jupyter Notebook examples to work through with lecture.
LinkedIn Learning	MATLAB Essential Training (2.5 h) Good introduction to MATLAB that students have found to be very useful.
LinkedIn Learning	Learning FPGA Development (1.15 h) Outstanding introduction to FPGA programming, including Verilog and VHDL.

).

4.3.5. Generative AI in Coding

As discussed earlier, graduating EE students will be expected to be able to use generative AI effectively and appropriately. Based on our experience, generative AI can significantly enhance productivity and is useful for (1) generating tutorial explanations, (2) summarizing the current state of the art, (3) editing reports and other writing to improve readability, (4) literature review (but the citations must be verified), (5) generating class project suggestions, (6) explaining code snippets, (7) generating code snippets and code modules, and (8) generating humorous rhyming verse that can be useful for developing student interest.

However, using generative AI as a tool to improve productivity has some significant drawbacks, including (1) reliability due to the possibility of hallucinations as discussed earlier, (2) potential negative impact on critical thinking skills [15,48], and (3) intellectual property (IP) concerns [13]. Although IP can be a concern within academia, in the context of undergraduate education, the more important issues we face are reliability and impact on critical thinking. Although showing students examples of ChatGPT errors (we have a number of examples) helps students understand the need for verification, we are beginning to see that under the stress of deadlines, students will often skip verification and submit major generative AI errors that should have been caught by inspection of the answer. Starting during the second half of the Spring 2025 semester, we began observing students using generative AI when it would have been simpler (and more reliable) to solve without generative AI.

One strategy we have found effective to ensure students are able to think critically and write code is to have an in-person oral exam in which the students write out algorithm code while explaining via words, diagrams, and plots. Figure 11 shows an example question and expected response code, along with plots showing key intermediate results. A second strategy is to have students develop code during an exam to solve a problem that is beyond the capability of current generative AI (such as the recent final exam that requires students to download a dataset containing hundreds of noisy pulses and then detect and measure the pulses; the dataset is designed to make it difficult for a student to rely on generative AI to answer this question).

4.3.6. Project Strategy

As discussed earlier, in addition to the mini-project homework assignments, in some semesters we concluded with a team project. One problem we observed was that student teams spent too much time deciding how to define their project, including datasets and ML goals. Also, some students will wait until the last minute and put in very little effort, or they will rely on their teammates to do the work. In our experience, the most successful engineering projects in our courses involve competition among small teams of 2–3 students with a well-defined project goal—our students will spend much more time on competition projects than other projects. This is consistent with Herrero-de Lucas et al., who stress that when using PBL, the actual workload for students is less important than the perceived workload [49]. With a lower perceived workload, student engagement, morale, and productivity all increase substantially. Some useful online resources for datasets are listed in Table A1.

4.3.7. Empirical Results

Figure 12 below shows the trend in the final exam scores, which is the key performance assessment (KPA) tool for Computing for Electrical Engineers due to its comprehensive nature and alignment with ABET assessment as discussed earlier. The left plot shows three trends: (1) the non-normalized median scores (blue dashed line with square markers), (2) the test difficulty level (black dashed line with x markers), and (3) the median scores after normalizing by the test difficulty level (magenta line with circle markers). As can be seen, the normalized test scores have shown a consistent upward trend since the course was first rolled out in 2021. At the same time, as indicated by the right plot, the teacher-to-student ratio for this course has declined due to increasing student enrollment and larger class sizes (the ratio includes both the instructor and the peer Learning Assistant). Also, the student demographics have remained nearly constant over this period of time. c in the EE program has been constant at 55% +/− 2 percent over the past few years based on student self-reported data.

4.4. Engineering Probability and Statistics

The Engineering Probability and Statistics course is another foundational course for ML and computational math. However, unlike the Computing for Electrical Engineers course, this course is designed for all engineering majors. Although Engineering Probability and Statistics is taken after the Computing for Electrical Engineers course in the standard sequence, our EE students often take these two courses out of sequence due to a variety of circumstances.

In addition to the material covered in a traditional course, we began revising this course starting in the Spring 2022 semester to include ML towards the end of the semester since ML is a key application area. Except for the project phase, which can include ML or other statistical analysis, the course emphasizes working out problems by hand, or with a calculator rather than using more advanced tools. The motivation behind this strategy is to (a) give the students confidence in applying the principles and in understanding the concepts, and (b) give students a way to verify proper tool usage by comparing the tool solution with a simple hand-worked solution. With tools becoming more complex, and with generative AI able to write code for computational tools, tool usage verification is more important than ever before.

Students are able to understand the importance of verification when this point is emphasized via examples. As a specific example relevant to this course, MATLAB defines its erf() tool as erf(x) = 2/sqrt(pi) * integral from 0 to x of exp(−t^2) dt. At first glance, this looks like the integral of the Standard Normal (Gaussian) probability density function (PDF) and could thus be used directly for Z-score calculations. However, erf(x) is defined for 2-sided integration, and inputs must be scaled by 1/sqrt(2). Thus, erf(1/sqrt(2)) = 0.6827, corresponding to the probability of a Gaussian random variable x falling within one standard deviation of the mean, and erf(2/sqrt(2)) = 0.9545, which corresponds to two standard deviations. Students are expected to know thumb rules for both cases, and are also expected to be able to use these thumb rules to calculate a variety of interval probabilities for non-standardized Gaussian random variables without requiring a calculator. Similarly, in the unit on combinatorics, students are expected to work various combinatorics problems without the use of notes. The strategy of teaching students to solve basic problems by hand without notes (and without calculators for some problems) has proven effective in helping students understand the concepts and in equipping them to use more advanced tools.

During the latter portion of the semester, the emphasis transitions to ML, data visualization, and statistical analysis using Python tools. For example, Figure 13 and Figure 14 below show sample project figures from a two-student team. The dataset analyzed by this team contained various date fruit measurements for seven different types of date fruit (see [50]; the data can also be downloaded from Kaggle.com with a free account https://www.kaggle.com/datasets/muratkokludataset/date-fruit-datasets, accessed 16 July 2025). Figure 13 shows two scatter plots after reducing the feature space from 34 coordinates to 2 coordinates using the nonlinear uniform manifold approximation and projection (UMAP) algorithm. The left plot illustrates UMAP clustering prior to scaling the data by standardization, while the plot shows UMAP clustering after data scaling (these were originally in separate plots; the first author combined the two plots). From these two plots, students can see that (1) as with many ML algorithms, scaling is important in UMAP—without scaling, the features do not cluster as well; and (2) UMAP reveals that while the classes separate reasonably well, there is still some feature overlap with UMAP, and thus achieving 100% classification probability may not be possible.

Figure 14 shows additional visualization and classification results from the second team member. The left panel shows box plots of four features (area, perimeter, solidity, and compactness) for the seven different types of date fruit. The right panel shows classification results using the logistic regression classifier available in Anaconda. The classifier results also illustrate the importance of scaling for logic regression classification (the unscaled training accuracy is T = 0.63 and the verification accuracy is V = 0.60, while the scaled training accuracy is Ts = 0.96 and the verification accuracy is Vs = 0.91).

4.5. Digital Circuits

The Digital Circuits course covers binary numbers, Boolean logic, and simple circuit design to implement Boolean logic. The course is structured as half lecture and half lab, although the instructor can adjust the ratio to optimize outcomes. Key lessons learned from teaching this class include the following: (1) Students need repetition and practice working with binary numbers, including two’s complement and gray codes. (2) Students struggle with Boolean logic and related concepts, such as Karnaugh maps, until they are able to apply these concepts practically by designing and implementing simple circuits. Laboratory exercises using Multisim, followed by the same exercise with a physical breadboard, have proven particularly effective. Another effective strategy is for students to analyze and correct a faulty Karnaugh map produced by generative AI.

4.6. Applied Machine Learning

In the Spring 2024 semester, we introduced Applied Machine Learning as a special topics course since we had a sufficient number of EE students who had taken Computing for Electrical Engineers. The course is structured such that the first half of the course relies on instructor-led lectures with in-class hands-on activities, while most of the second half of the course is based on student team-led seminars. For this portion, each team can select an area of machine learning to explore. They research the topic, then develop a lecture to teach this topic to the rest of the class (including the instructor). The lectures may include hands-on activities, demonstrations, etc.

This was the first time any of our EE courses had been taught with a significant student-led seminar component, but much to the first author’s surprise, this format was extremely successful, with some teams exploring advanced topics not covered in any prior courses. For example, one team developed an image classifier to classify pills (Tylenol, Advil, etc.) in support of a senior capstone project to design and build an automatic pill dispenser (APD). The APD capstone project included a local software interface, pill hoppers, a mechanical device and associated controller to select and dispense the correct pills, and the image classifier to verify that the correct pills were dispensed.

As another example, one of the junior EE students taking Applied Machine Learning advised a senior capstone project on how to implement a convolutional neural network (CNN). This second senior capstone team then developed a time frequency detector and CNN-based modulation classifier for pulsed radar signals that they were able to publish in a peer-reviewed conference in early 2025 [51].

5. Discussion

5.1. Successful Teaching Strategies

Based on feedback from our recent EE graduates, empirical results, and significantly improved undergraduate research capability, our ML and computational math teaching strategies have been successful. To further improve our program, we can consider some clear themes regarding effective teaching strategies.

Project-Based Learning: Consistent with the literature we reviewed, one of the most successful strategies to teach ML and computational math is PBL, including small mini-projects and more substantial projects, and including both team-based and individual projects. Some particular PBL techniques that have proven especially effective include (1) having a mix of team-based and individual projects during the semester; (2) requiring individual reports for most team-based projects; (3) including a competitive component in at least one project; (4) keeping teams small (2 or 3 students) unless the project can be clearly partitioned into enough code development and test segments for all students to participate meaningfully; and (5) having a well-defined project with clear goals.

Experiential Learning: Also consistent with the literature we reviewed, hands-on experiential learning is crucial for our students. For example, teaching projections by starting with Euler’s formula was almost completely ineffective. However, starting with a physical friction on ramp experiment followed by Euler’s formula somewhat later in the semester (after students were comfortable with performing projection calculations for physical situations) was effective.

Avoid Lecture-Heavy Classes: As per the reviewed literature, Gen Z students have limited attention spans when listening to the instructor lecturing. Based on our experience, after 15 to 20 min of lecture, students are ready for a hands-on activity—squeezing in more lecture material is useless if most of the students are zoned out.

Use-Modify-Create: As expected based on the literature, this is an effective strategy for helping students to learn coding skills in ML and computational math, especially in conjunction with the “save-as” method. One potential pitfall of this strategy is that students will sometimes modify code without thinking about what they are doing. Specific techniques to avoid this pitfall include the following: (1) early in the semester, start with a very minimal template, then create a basic demo example that can serve as a template for future examples by having students walk through the code development with the instructor; (2) for some cases, provide an image of the code so that students need to enter the code themselves during class time; and (3) walk through some of the early code examples line-by-line.

Show Students the Code Development Process (Including Making and Correcting Errors): As part of the use-modify-create strategy, instructors need to demonstrate the code development process by developing code examples via this technique while the students observe. Typically, the instructor will make occasional errors. As these occur, the instructor should point them out to the students or challenge the students to find any errors themselves for extra credit. The instructor’s attitude when making errors is critical—in particular, instructors should be able to laugh at their own errors, and should be able to remark to the class that even professors make mistakes (in a humorous tone of voice, especially if the mistake is a simple error). Besides helping students gain familiarity with the coding process, these exercises also help develop an atmosphere in which students can try out new ideas and make mistakes without undue anxiety. As part of this process, instructors need to guide students through the tool development process so that students can gain proficiency in developing their own toolboxes. This not only helps develop student confidence, but also prepares them for industry where they may be required to design new tools or implement tools in an embedded programming environment.

Design Courses to Build on Each Other: We have observed that when courses are specifically designed to build on each other, with the instructor pointing out the cross-course connections, student learning is reinforced, and students appreciate that they cannot just take a course then forget the material. During decades of interviewing candidates in industry, the first author G.F. noted that many candidates, when they did not know how to answer a technical interview question, used the excuse that they had forgotten the material since they had not seen the material in one or two years, with the implicit assumption that they should not be expected to remember material from their coursework (the first author G.F. did not hire any candidates who used this excuse).

Embrace Generative AI: Although fear of generative AI is a common reaction due to the difficulties with detecting cheating, given that industry expects engineers to know how to properly use generative AI, instructors need to embrace generative AI rather than fear it. This means that instructors in courses involving ML and computational math need to personally get familiar with generative AI tools through regular use, reading, and talking to students about generative AI capabilities. Techniques that have proven effective so far in preventing inappropriate use of generative AI include the following: (1) for reports, start out with short reports, use templates, do not overemphasize grammar and spelling, and maximize specific content, such as personal perspective and in-class laboratory results; (2) for code, start out with simple templates that embed software requirements, explain code line-by-line, demonstrate and practice the use-modify-create methodology, show students how to use AI tools to decipher complex code, be sure students understand how to test, verify, and debug code, and include generative AI coding as an in-class exercise and/or as an assignment with a well-defined and limited computational module; and (3) for both code and reports, emphasize the need to cite significant sources, especially generative AI.

Encourage Student Collaboration on Homework: Student collaboration can be an effective learning tool. One problem is students who copy rather than collaborate. A related problem is groupthink, especially if one student dominates the group collaboration while other students merely copy without critically assessing the code or ideas. Techniques for preventing inappropriate use of generative AI are also effective in encouraging proper collaboration. In addition, leaving room for students to pick how their plots look in terms of line style, overlaid or separate plots, etc., can help, especially if a penalty is applied for identical plots from virtually identical code between two or more students. A closely related strategy we have found effective is to hire peer helpers, including Learning Assistants, who have been through the course. Oral and written exams that include coding exercises do not prevent inappropriate collaboration, but they do help identify when a student has been copying without critically thinking about the code.

Allow Code Correction and Resubmission with Modest Penalty: Students uniformly report that the correction and resubmit policy helps them learn better. Also, it allows the instructor to apply heavy penalties for coding errors since the students can correct and resubmit without a major grade penalty. We have not seen this strategy reported in the literature, but it has proven very effective over the past few years.

Peer Reviews: While students typically do not like having their work displayed and discussed in front of the class, we have found that informal peer reviews are an effective strategy, especially if the instructor can help each student see that their classmates are making similar errors. One of the keys to successful peer reviews is to keep the tone light to minimize student anxiety.

Call on Students by Name: Although this may not be possible in larger classrooms, we have found that calling on students by name, especially when doing rapid-fire questions, is effective in engaging students, and also reduces barriers for students to seek faculty support.

Provide Suitable Video & On-Line Resources: As discussed earlier, Gen Z students in particular learn from video, but they need help in finding good sources. Thus, instructors need to provide sample resources and/or guide the search process so that students do not spend too much time searching (as we’ve seen happen). See Table A1 for some useful online resources that we have identified so far.

5.2. Limitations and Future Directions

Although there are advantages to our methodology, there are also some limitations. First, we are not presenting a formal study with screened participants, control groups, or control variables. Aligned with our research goals, the data is anecdotal in nature, and our empirical data reflects the results of multiple teaching strategies rather than individual strategies that can function as control variables. Additionally, the results are based on our students’ demographics and may not be fully generalizable to other institutions or disciplines. Finally, our results are based on a relatively small sample size. For example, the inaugural Computing for Electrical Engineers class consisted of 17 students.

To mitigate the limitations of the assessment methodology, we have (1) provided information on our student demographics, (2) discussed our strategies and results in the context of other empirically based studies, (3) provided specific details on implementation of teaching strategies, and (4) provided a roadmap (Figure 3) that others can adapt for teaching purposes, or for studies with formal assessment methodology.

Although some of our specific strategy implementations are not generalizable to other educational settings (for example, the hands-on convolution exercise is not applicable to language arts), we anticipate that most of the strategies can be applied in other undergraduate engineering settings, and possibly even at the graduate level. Furthermore, some strategies can probably be adapted to non-engineering fields. For example, if the use-modify-create strategy is an effective strategy to help students write better engineering reports, it seems reasonable that this same strategy can be used to support essay writing in the humanities, where such adaptation has not been studied yet.

Moving forward, we plan to expand our approach to Computing for Electrical Engineers in several ways:

• We will replace most of the syntax lecture time with in-class hands-on activities to practice creation of functions, and to practice matrix math computations using both hand calculations and MATLAB. In addition, for the Fall 2025 semester, we will provide a YouTube link to a short lecture introducing MATLAB.
• Students will be taught how to use generative AI effectively so that they can improve their productivity while maintaining critical thinking. We plan to add an exercise in which the student (1) develops their own version of a built-in MATLAB tool, (2) develops a generative AI based version, and (3) compares the three versions (original built-in, hand-coded, generative AI coded). Later in the semester, we will show students how to develop and test more complex code from generative AI (e.g., connected components algorithm). The goal is to get students to emulate the same type of process that engineers have used for decades when using open-source or other externally provided commodity tools, such as the Numerical Recipes series of books that originated in the 1980s [52]. Our contention is that there is no fundamental difference between the appropriate use of generative AI and traditional commodity tools—in either case, the appropriate algorithm module meeting the design requirements must be identified, tested and verified, cited appropriately, and documented (including any IP issues). However, engineers (and instructors of engineers) need to understand key differences between generative AI and traditional commodity tools, including that (1) generative AI solutions are not obtained from a source-controlled tested library and thus require more evaluation and testing to verify; (2) generative AI is not constrained to low-level algorithm modules, but will confidently generate solutions, whether correct or incorrect, to complex problems that normally might require dozens of lower-level major algorithm modules; (3) generative AI does not come with external algorithm documentation; and (4) based on the first author’s personal experience with ChatGPT, generative AI solutions can vary wildly in quality and content, depending on the exact prompt and prompt sequence.
• We plan to modify the team-based project to make it competitive with a common dataset and common goals (visualization, regression, and classification), but with the algorithms and methods open to student decisions. Projects will be evaluated using student peer-review scores in conjunction with a rubric scoring sheet.
• We plan to add a time-frequency exercise in which the students collect and analyze audio data of interest (musical instruments, human speech, birds, etc.). The goal of this exercise is to stimulate curiosity.

Building on the insights discussed above, a future study could employ a longitudinal experimental design with more detailed demographic information and more detailed formal assessment so that specific strategies could be empirically evaluated.

6. Conclusions

We have presented strategies, successful as well as unsuccessful, that we have used in teaching machine learning and computational math to undergraduate electrical engineering students at ETAMU. Some of the strategies are novel and have not been previously published to the best of our knowledge, including the resubmit grading policy for homework assignments and the hands-on student participation activities to help with visualization of the histogram and convolution. Other strategies have been published but adapted for our particular student demographics (most of our engineering students are from underrepresented groups). Also, we have presented strategies in progress to address the proper use of generative AI, including as a coding aid. Details have been included to allow others to adapt these strategies for their institutions.

Common techniques to implement successful strategies include (1) hands-on experiential learning; (2) interleaving lecture material with hands-on activities; (3) implementing strategies to alleviate student stress and to provide an environment where students and instructors can make mistakes; (4) setting high expectations; (5) creating project-based learning and team projects, which are especially important for Gen Z students; and (6) embracing AI instead of ignoring it since it is now being widely adopted by industry.

The primary limitation of our methodology is its anecdotal nature with limited empirical results, including limited sample population from a single university. To help ensure that our results can be generalized and adapted by others, we have provided a significant level of detail, and we have discussed our results in the context of prior published work, including human factors research. To help ensure relevance, three of our authors are students who analyzed the Computing for Electrical Engineers course material, including the associated teaching strategies. We hope that others will find this paper both relevant and useful in teaching machine learning and computational math.