Research on the Application of Federated Learning Based on CG-WGAN in Gout Staging Prediction
Abstract
1. Introduction
- This paper proposes a Conditional Gradient Penalty Wasserstein Generative Adversarial Network (CG-WGAN), which incorporates an optimized gradient penalty mechanism by introducing gout-specific label condition information and feature-aware noise perturbations. This design enables the generation of high-quality medical tabular data and significantly alleviates the issue of category distribution bias caused by non-IID data.
- This paper designs a FedCG-WGAN federated learning framework that avoids the transmission of raw data or model parameters by employing synthetic data sharing instead of traditional parameter aggregation. This approach enables clients to train local personalized prediction models while preserving data privacy and enhancing security.
- Experiments conducted on real-world gout medical records and the MIMIC-III dataset demonstrate that the proposed method improves prediction accuracy by 6.0%, while reducing training time by 32% and communication overhead by 40%, thereby validating its effectiveness and practical applicability.
2. Related Works
2.1. Existing Approaches to Gout Prediction
2.2. Applications of Federated Learning in Healthcare
2.3. Applications of Generative Adversarial Networks in Healthcare
3. Method
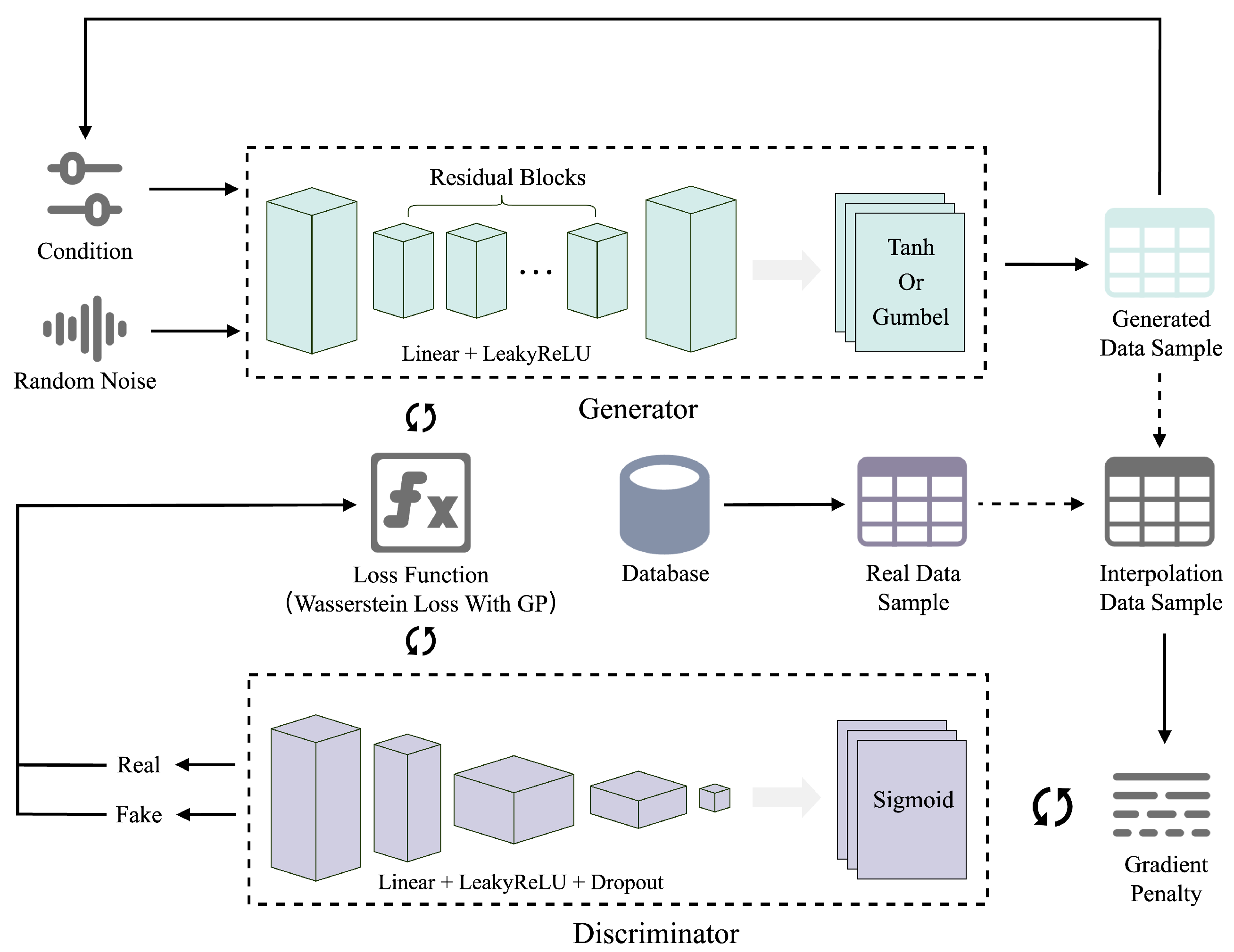
3.1. Improved Generative Adversarial Network CG-WGAN
| Algorithm 1 CG-WGAN training algorithm. |
| Require:
Generator parameters , discriminator parameters , gradient penalty coefficient , number of critic steps Ensure: Updated generator and discriminator
|
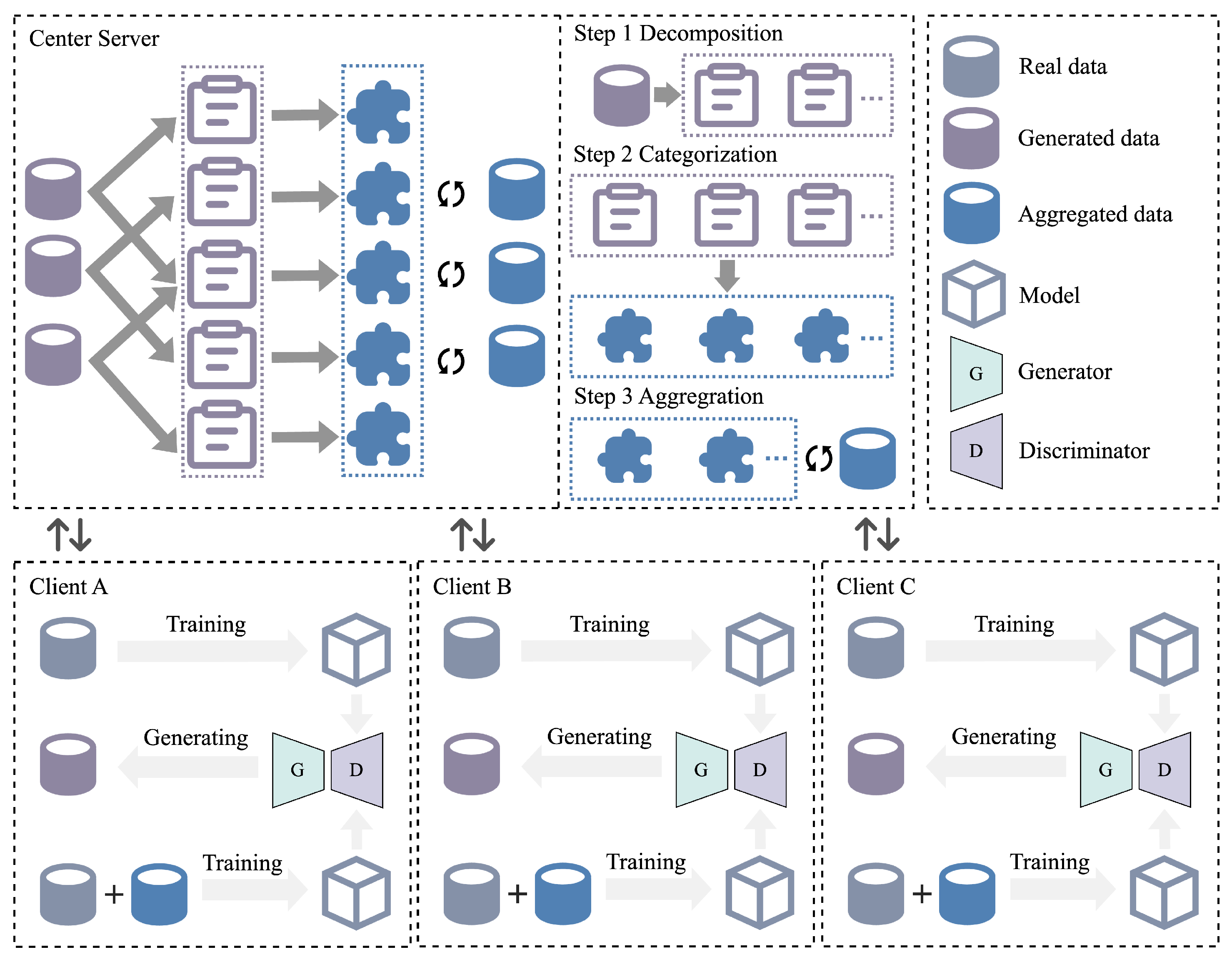
3.2. CG-WGAN-Based Federated Learning Approach
- Local Model Training: Each client k trains a CG-WGAN using its local dataset . The newly generated synthetic samples are defined as in Formula (9). The feature distribution of these samples is evaluated locally. A comprehensive quality score Q is then computed by combining the discriminator confidence score (D-score) and the feature distribution similarity score (F-score). Finally, the synthetic samples, their quality scores, missing labels, and sample counts are uploaded to the central server.where denotes the generator network of the CG-WGAN on client k, is a random noise vector sampled from the noise distribution , and is a conditional label sampled from the local label distribution .
- Verification of Data Quality and Assessment of Data Balance: The central server receives the synthetic data and corresponding quality scores from each client. For the synthetic dataset uploaded by client k, candidate samples satisfying are retained.
- Aggregation and Distribution of Project Data by the Central Server: The server constructs a shared dataset of synthetic cases by aggregating all candidate samples from clients. Based on the missing label categories and the number of missing samples uploaded by each client, the server samples from the shared dataset and distributes the data to each client accordingly. Assuming the missing category for client k is , the server allocates samples from the shared dataset as Formula (10).where denotes the new synthetic dataset received by client k from the server, is the label category of the synthetic sample , and is the number of samples requested by client k for category .
- Client Model Update: After receiving the data distributed by the central server, each client merges the new data with its local dataset to form an updated dataset. This updated dataset is then used to train and update the client’s local model. The loss function is defined as Formula (11).where denotes the loss function minimized with respect to the local model parameters after merging the local and synthetic datasets on client k; ℓ is the cross-entropy loss, and is the local classification model, implemented as XGBoost.
- Model Evolution and Optimization: The above process is repeated multiple times, where each iteration includes retraining the CG-WGAN to generate additional synthetic data and using the updated dataset to train the model. Each client’s model will gradually adapt to the newly generated data and increasingly complex tasks, resulting in a more personalized and accurate model. Algorithm 2 presents the pseudocode of the FedCG-WGAN model.
| Algorithm 2 FedCG-WGAN training algorithm. |
| Require:
Local datasets , communication rounds T, quality threshold Ensure: Personalized models
|
3.3. Convergence Analysis
4. Experiment
4.1. Description of the Dataset
4.2. Pre-Processing of Gout History Data
- Outlier handling: The dataset contained ‘dirty data’, i.e., records with values beyond clinically reasonable ranges (e.g., height = 1888 cm, weight = 300 kg, negative ALT values, or random urine FEUA exceeding 1). Based on clinical guidelines and typical distributions of medical test results, acceptable ranges were defined for each feature, and unreasonable records were removed. A total of 3905 records (approximately 7.1% of the initial dataset) were discarded. The resulting clean dataset was denoted as feature set F1.
- Missing value imputation: The missing rate of each feature in F1 was first calculated. Fifteen features with a missing rate were directly discarded. For the remaining features, different imputation strategies were applied:
- Mean substitution stratified by gender for height and weight.
- Group-wise averages stratified by gender and age for smoking duration.
- Multivariate linear regression using height and weight as predictors for waist and hip circumference.
- Random forest regression for biochemical test items, leveraging feature importance and ensemble predictions.
After imputation, a complete dataset was obtained and denoted as feature set F2. - Feature selection: To improve diagnostic accuracy and ensure privacy, irrelevant or sensitive attributes were removed, including mobile phone numbers, ID numbers, home addresses, and prescription details. This step excluded eight features, resulting in feature set F3.
- Standardization and alignment: To mitigate dataset drift and enhance generalization in the federated setting, F3 underwent standardization and alignment. Continuous features were standardized using Z-scores, categorical features were consistently encoded, and discrepancies in feature naming and units across hospitals were harmonized. This step is essential for alleviating inter-client distribution heterogeneity (non-IID). The final processed dataset was denoted as F4, which was used for all subsequent experiments.
4.3. Experimental Setup
- FedAvg [40] trains models locally on multiple clients and then aggregates the client models by averaging their parameters into a global model.
- FedProx [41] is an improved version of FedAvg that introduces a proximal term to address the issue of non-IID data distribution.
- FedMD [42] utilizes model distillation techniques to integrate knowledge from different clients.
4.4. Experimental Evaluation Indicators
4.4.1. Composite Assessment Method for Data Quality
4.4.2. Quantitative Analysis of Model Performance Improvement
4.4.3. Performance Indicators in Gout Diagnostic Tasks
5. Result and Discussion
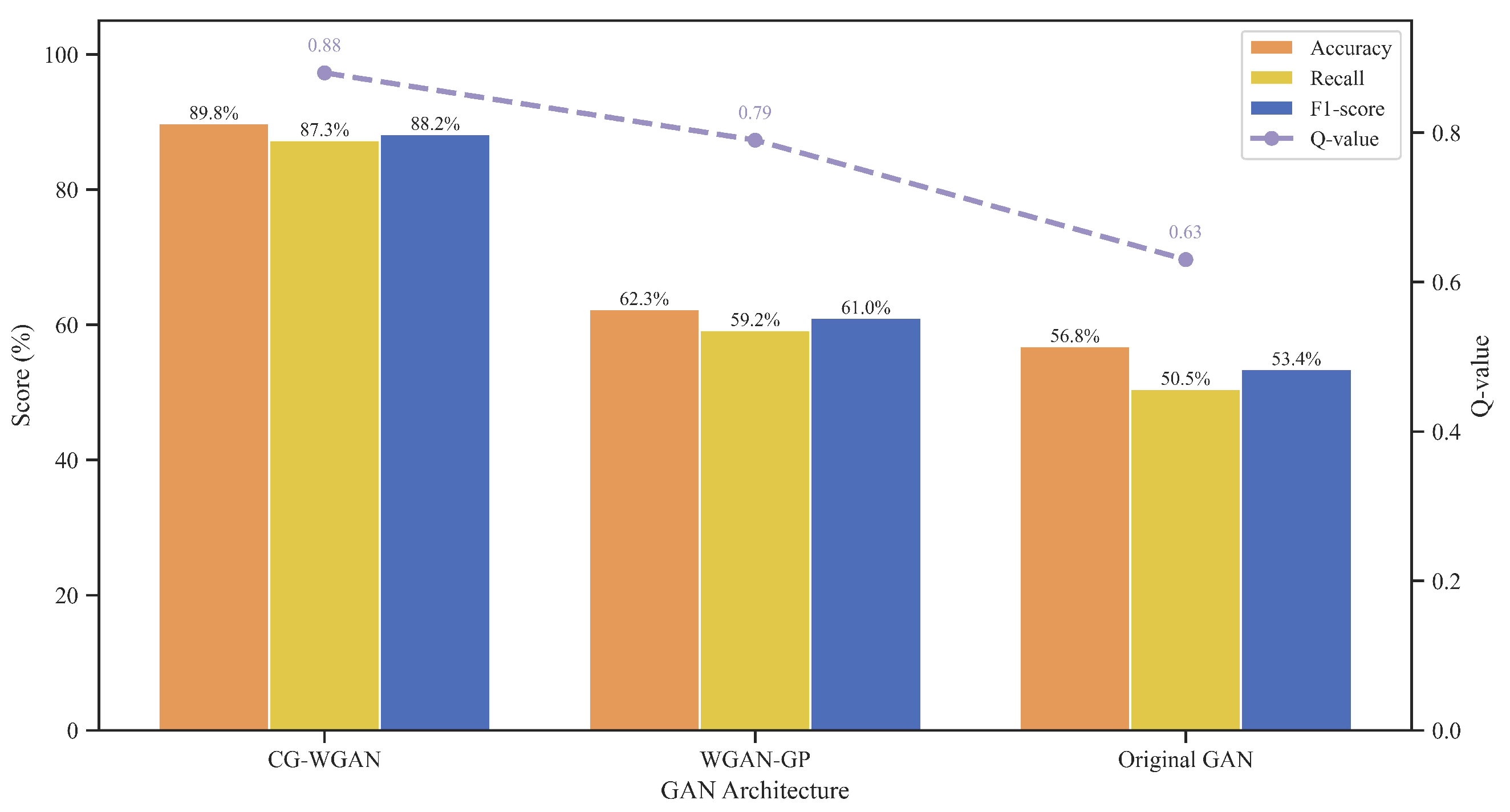
5.1. CG-WGAN Generated Data Quality and Privacy Security Assessment
5.2. Comparison of Model Performance Based on EMRs
5.3. Ablation Experiments and Analysis
5.3.1. Core Component Ablation Experiment
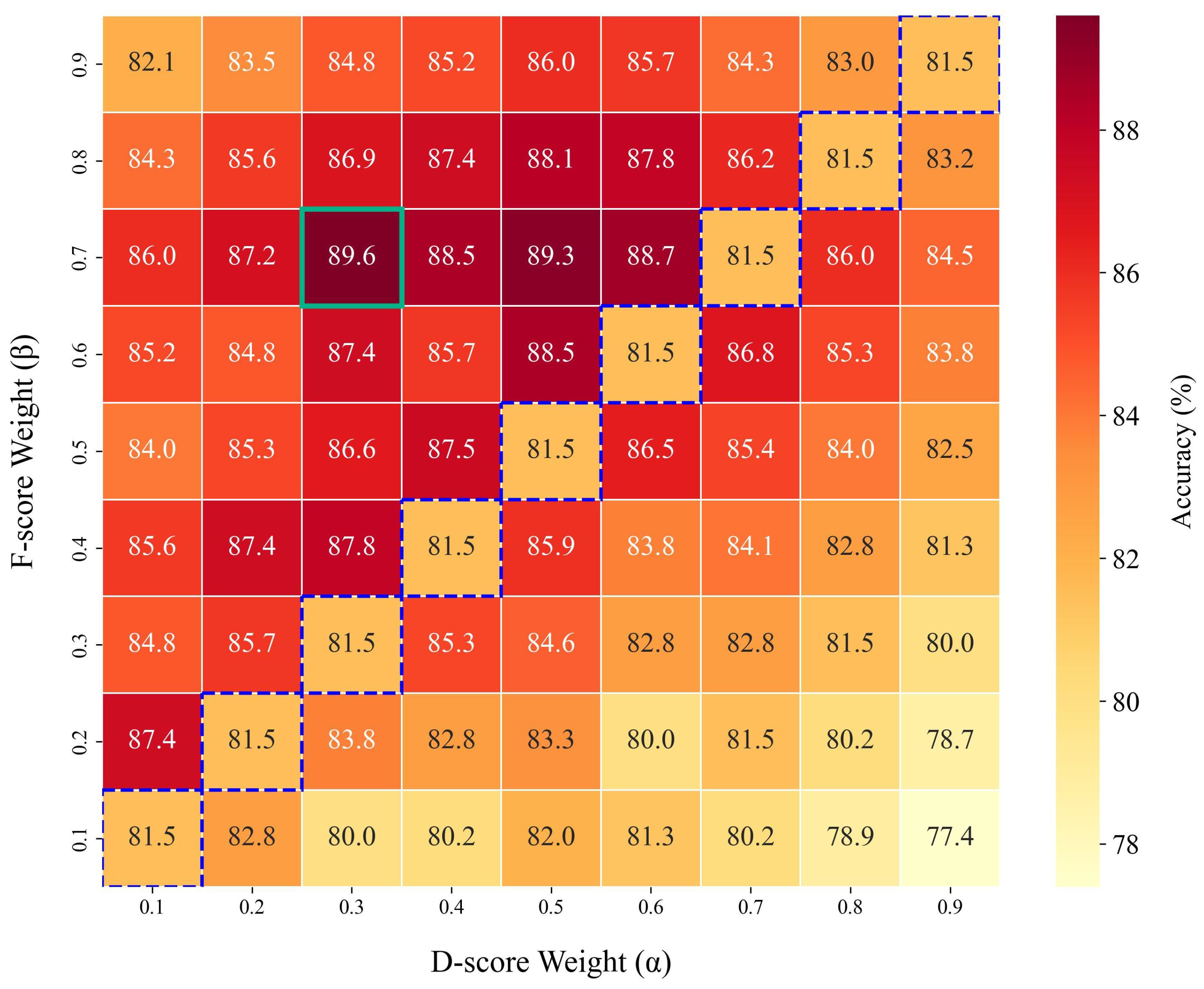
5.3.2. Sensitivity Analysis
5.3.3. Quantitative Analysis of Privacy Risks
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bodakçi, E. How well do we recognise gout disease? Dicle Tıp Derg. 2024, 51, 173–1181. [Google Scholar] [CrossRef]
- Newberry, S.J.; FitzGerald, J.D.; Motala, A.; Booth, M.; Maglione, M.A.; Han, D.; Tariq, A.; O’Hanlon, C.E.; Shanman, R.; Dudley, W.; et al. Diagnosis of gout: A systematic review in support of an American College of Physicians Clinical Practice Guideline. Ann. Intern. Med. 2017, 166, 27–36. [Google Scholar] [CrossRef]
- Brikman, S.; Serfaty, L.; Abuhasira, R.; Schlesinger, N.; Bieber, A.; Rappoport, N. A machine learning-based prediction model for gout in hyperuricemics: A nationwide cohort study. Rheumatology 2024, 63, 2411–2417. [Google Scholar] [CrossRef]
- Zheng, C.; Rashid, N.; Wu, Y.L.; Koblick, R.; Lin, A.T.; Levy, G.D.; Cheetham, T.C. Using natural language processing and machine learning to identify gout flares from electronic clinical notes. Arthritis Care Res. 2014, 66, 1740–1748. [Google Scholar] [CrossRef]
- Tian, P.; Chen, Z.; Yu, W.; Liao, W. Towards asynchronous federated learning based threat detection: A DC-Adam approach. Comput. Secur. 2021, 108, 102344. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, Y.; Wang, D.; Han, Z. FedACS: Federated skewness analytics in heterogeneous decentralized data environments. In Proceedings of the 2021 IEEE/ACM 29th International Symposium on Quality of Service (IWQOS), Tokyo, Japan, 25–28 June 2021; pp. 1–10. [Google Scholar]
- Jeong, E.; Oh, S.; Kim, H.; Park, J.; Bennis, M.; Kim, S.L. Communication-efficient on-device machine learning: Federated distillation and augmentation under non-iid private data. arXiv 2018, arXiv:1811.11479. [Google Scholar]
- Fang, L.; Yin, C.; Zhu, J.; Ge, C.; Tanveer, M.; Jolfaei, A.; Cao, Z. Privacy protection for medical data sharing in smart healthcare. ACM Trans. Multimed. Comput. Commun. Appl. (TOMM) 2020, 16, 1–18. [Google Scholar] [CrossRef]
- Xu, X.; Wu, J.; Yang, M.; Luo, T.; Duan, X.; Li, W.; Wu, Y.; Wu, B. Information leakage by model weights on federated learning. In Proceedings of the 2020 Workshop on Privacy-Preserving Machine Learning in Practice, Virtual, 9 November 2020; pp. 31–36. [Google Scholar]
- El Ouadrhiri, A.; Abdelhadi, A. Differential privacy for deep and federated learning: A survey. IEEE Access 2022, 10, 22359–22380. [Google Scholar] [CrossRef]
- Kanagavelu, R.; Li, Z.; Samsudin, J.; Yang, Y.; Yang, F.; Goh, R.S.M.; Cheah, M.; Wiwatphonthana, P.; Akkarajitsakul, K.; Wang, S. Two-phase multi-party computation enabled privacy-preserving federated learning. In Proceedings of the 2020 20th IEEE/ACM International Symposium on Cluster, Cloud and Internet Computing (CCGRID), Melbourne, VIC, Australia, 11–14 May 2020; pp. 410–419. [Google Scholar]
- Clebak, K.T.; Morrison, A.; Croad, J.R. Gout: Rapid evidence review. Am. Fam. Physician 2020, 102, 533–538. [Google Scholar]
- Han, T.; Chen, W.; Qiu, X.; Wang, W. Epidemiology of gout—Global burden of disease research from 1990 to 2019 and future trend predictions. Ther. Adv. Endocrinol. Metab. 2024, 15, 20420188241227295. [Google Scholar] [CrossRef]
- Lei, T.; Guo, J.; Wang, P.; Zhang, Z.; Niu, S.; Zhang, Q.; Qing, Y. Establishment and validation of predictive model of tophus in gout patients. J. Clin. Med. 2023, 12, 1755. [Google Scholar] [CrossRef] [PubMed]
- Cüre, O.; Bal, F. Application of Machine Learning for Identifying Factors Associated with Renal Function Impairment in Gouty Arthritis Patients. Appl. Sci. 2025, 15, 3236. [Google Scholar] [CrossRef]
- Xiao, L.; Zhao, Y.; Li, Y.; Yan, M.; Liu, Y.; Liu, M.; Ning, C. Developing an interpretable machine learning model for diagnosing gout using clinical and ultrasound features. Eur. J. Radiol. 2025, 184, 111959. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; Chandra, V. Federated learning with non-iid data. arXiv 2018, arXiv:1806.00582. [Google Scholar] [CrossRef]
- Armanious, K.; Jiang, C.; Fischer, M.; Küstner, T.; Hepp, T.; Nikolaou, K.; Gatidis, S.; Yang, B. MedGAN: Medical image translation using GANs. Comput. Med. Imaging Graph. 2020, 79, 101684. [Google Scholar] [CrossRef]
- Fabbri, C. (University of Minnesota, Minneapolis, MN, USA). Conditional Wasserstein Generative Adversarial Networks. Unpublished student paper. 2017. [Google Scholar]
- Aziira, A.; Setiawan, N.; Soesanti, I. Generation of synthetic continuous numerical data using generative adversarial networks. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; Volume 1577, p. 012027. [Google Scholar]
- Chen, D.; Orekondy, T.; Fritz, M. Gs-wgan: A gradient-sanitized approach for learning differentially private generators. Adv. Neural Inf. Process. Syst. 2020, 33, 12673–12684. [Google Scholar]
- Zhao, Z.; Kunar, A.; Birke, R.; Chen, L.Y. Ctab-gan: Effective table data synthesizing. In Proceedings of the Asian Conference on Machine Learning, Bangkok, Thailand, 1–3 December 2021; pp. 97–112. [Google Scholar]
- Xu, L.; Skoularidou, M.; Cuesta-Infante, A.; Veeramachaneni, K. Modeling tabular data using conditional GAN. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates Inc.: Red Hook, NY, USA, 2019. Article No. 659. pp. 1–11. [Google Scholar]
- Engelmann, J.; Lessmann, S. Conditional Wasserstein GAN-based oversampling of tabular data for imbalanced learning. arXiv 2020, arXiv:2008.09202. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Liu, K.; Qiu, G. Lipschitz constrained GANs via boundedness and continuity. Neural Comput. Appl. 2020, 32, 18271–18283. [Google Scholar] [CrossRef]
- Zhou, Z.; Song, Y.; Yu, L.; Wang, H.; Liang, J.; Zhang, W.; Zhang, Z.; Yu, Y. Understanding the effectiveness of lipschitz-continuity in generative adversarial nets. arXiv 2018, arXiv:1807.00751. [Google Scholar] [CrossRef]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved training of wasserstein gans. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Wei, M.; Vogel, C. Generative Adversarial Networks in Federated Learning. In Applications of Artificial Intelligence and Neural Systems to Data Science; Springer: Berlin/Heidelberg, Germany, 2023; pp. 341–350. [Google Scholar]
- Durgadevi, M.; Karthika, S. Generative Adversarial Network (GAN): A general review on different variants of GAN and applications. In Proceedings of the 2021 6th International Conference on Communication and Electronics Systems (ICCES), Coimbatre, India, 8–10 July 2021; pp. 1–8. [Google Scholar]
- Alajaji, S.A.; Khoury, Z.H.; Elgharib, M.; Saeed, M.; Ahmed, A.R.; Khan, M.B.; Tavares, T.; Jessri, M.; Puche, A.C.; Hoorfar, H.; et al. Generative adversarial networks in digital histopathology: Current applications, limitations, ethical considerations, and future directions. Mod. Pathol. 2024, 37, 100369. [Google Scholar] [CrossRef]
- Zheng, M.; Li, T.; Zhu, R.; Tang, Y.; Tang, M.; Lin, L.; Ma, Z. Conditional Wasserstein generative adversarial network-gradient penalty-based approach to alleviating imbalanced data classification. Inf. Sci. 2020, 512, 1009–1023. [Google Scholar] [CrossRef]
- Tan, A.Z.; Yu, H.; Cui, L.; Yang, Q. Towards personalized federated learning. IEEE Trans. Neural Networks Learn. Syst. 2022, 34, 9587–9603. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Sun, G.; Yu, H.; Guizani, M. PerFED-GAN: Personalized federated learning via generative adversarial networks. IEEE Internet Things J. 2022, 10, 3749–3762. [Google Scholar] [CrossRef]
- Ji, X.; Tian, J.; Sun, C.; Zhang, M. PFed-ME: Personalized Federated Learning Based on Model Enhancement. In Proceedings of the International Conference on Intelligent Computing, Tianjin, China, 5–8 August 2024; pp. 263–274. [Google Scholar]
- Johnson, A.E.; Pollard, T.J.; Shen, L.; Lehman, L.w.H.; Feng, M.; Ghassemi, M.; Moody, B.; Szolovits, P.; Anthony Celi, L.; Mark, R.G. MIMIC-III, a freely accessible critical care database. Sci. Data 2016, 3, 160035. [Google Scholar] [CrossRef]
- Özkan, Y.; Demirarslan, M.; Suner, A. Effect of data preprocessing on ensemble learning for classification in disease diagnosis. Commun. Stat.-Simul. Comput. 2024, 53, 1657–1677. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Li, D.; Wang, J. Fedmd: Heterogenous federated learning via model distillation. arXiv 2019, arXiv:1910.03581. [Google Scholar] [CrossRef]




| Gout Staging | Participants | ||
|---|---|---|---|
| Hospital A | Hospital B | Hospital C | |
| Acute arthritis phase | 1008 | 612 | 737 |
| Intermittent phase | 10,009 | 8750 | 9550 |
| Chronic arthritis phase | 8050 | 6110 | 6301 |
| Feature Name | Chi-Square () | ANOVA (F) | Clinical Relevance |
|---|---|---|---|
| Uric acid | 15.2 | 18.6 | Core indicator for staging |
| Systolic BP | 6.8 | 5.4 | Positively correlates with inflammation |
| Joint swelling score | 12.1 | – | Acute-phase specific marker |
| Gender | 1.2 | – | Retained (clinically essential) |
| Model | Local Accuracy | Complete Training Time | Peak Memory Usage |
|---|---|---|---|
| XGBoost | 82.5% | 1250.5 s | 245 MB |
| LightGBM | 81.8% | 1050.2 s | 210 MB |
| CatBoost | 82.1% | 1480.7 s | 290 MB |
| MLP | 78.9% | 1720.3 s | 180 MB |
| Q-Value Threshold | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 |
| RPIR | 1.37 | 1.40 | 1.42 | 1.43 | 1.44 |
| Feature Name | Real Distribution | Synthetic Distribution | Correlation Coefficient |
|---|---|---|---|
| Blood Uric Acid (μmol/L) | 0.96 | ||
| Percentage of Knee Involvement | 68.3% | 66.9% | 0.93 |
| Acute Phase (CRP > 10 mg/L) | 75.1% | 72.3% | 0.94 |
| Incidence of Gouty Stones | 39.8% | 41.6% | 0.91 |
| Percentage of Renal Function Abnormalities | 22.4% | 24.1% | 0.89 |
| Proportion of Combined Hypertension | 43.6% | 41.2% | 0.95 |
| Models Metric | Baseline Methods | Proposed | Improvement | ||||
|---|---|---|---|---|---|---|---|
| FedAvg | FedProx | FedMD | FedCG-WGAN | vs. Best | vs. Avg | ||
| Accuracy | Qingdao Hospitals | 83.2% | 85.1% | 82.5% | 89.6% | ↑4.5% | ↑6.0% |
| MIMIC-III | 78.3% | 80.1% | 77.6% | 85.3% | ↑5.2% | ↑6.7% | |
| Precision | Qingdao Hospitals | 81.6% | 83.5% | 80.8% | 86.3% | ↑2.8% | ↑4.3% |
| MIMIC-III | 76.5% | 78.9% | 75.2% | 87.5% | ↑8.6% | ↑10.3% | |
| Recall | Qingdao Hospitals | 80.9% | 82.7% | 79.4% | 85.5% | ↑2.8% | ↑4.5% |
| MIMIC-III | 75.8% | 77.3% | 74.1% | 83.1% | ↑5.8% | ↑7.3% | |
| F1-score | Qingdao Hospitals | 81.2% | 83.1% | 80.1% | 85.9% | ↑2.8% | ↑4.4% |
| MIMIC-III | 76.1% | 78.1% | 74.7% | 84.2% | ↑6.1% | ↑8.0% | |
| Round Time | Qingdao Hospitals | 142.7 s | 135.4 s | 155.2 s | 97.1 s | ↓38.3 s | ↓47.3 s |
| MIMIC-III | 138.5 s | 130.1 s | 148.7 s | 94.3 s | ↓35.8 s | ↓45.2 s | |
| Comm Cost | Qingdao Hospitals | 12.8 MB | 11.2 MB | 14.6 MB | 7.3 MB | ↓3.9 MB | ↓5.6 MB |
| MIMIC-III | 11.5 MB | 10.3 MB | 13.2 MB | 6.8 MB | ↓3.2 MB | ↓5.1 MB | |
| Accuracy | Recall | F1-Score | Training Stability | |
|---|---|---|---|---|
| 1 | 82.3% | 79.5% | 80.8% | Unstable (mode collapse) |
| 5 | 88.5% | 86.1% | 87.2% | Relatively stable |
| 10 (Default) | 89.8% | 87.3% | 88.2% | Stable |
| 20 | 88.9% | 86.8% | 87.8% | Stable |
| 30 | 87.2% | 84.9% | 86.0% | Stable (slower convergence) |
| Training Data Source | Attack Accuracy | Attack AUC |
|---|---|---|
| Synthetic Data (Q = 0.80) | 51.0% | 0.52 |
| Synthetic Data (Q = 0.85) | 51.2% | 0.53 |
| Synthetic Data (Q = 0.88) | 58.7% | 0.62 |
| Original Data | 68.7% | 0.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhang, K.; Guan, Z.; Ye, Z.; Ma, C.; Huang, H. Research on the Application of Federated Learning Based on CG-WGAN in Gout Staging Prediction. Computers 2025, 14, 455. https://doi.org/10.3390/computers14110455
Wang J, Zhang K, Guan Z, Ye Z, Ma C, Huang H. Research on the Application of Federated Learning Based on CG-WGAN in Gout Staging Prediction. Computers. 2025; 14(11):455. https://doi.org/10.3390/computers14110455
Chicago/Turabian StyleWang, Junbo, Kaiqi Zhang, Zhibo Guan, Zi Ye, Chao Ma, and Hai Huang. 2025. "Research on the Application of Federated Learning Based on CG-WGAN in Gout Staging Prediction" Computers 14, no. 11: 455. https://doi.org/10.3390/computers14110455
APA StyleWang, J., Zhang, K., Guan, Z., Ye, Z., Ma, C., & Huang, H. (2025). Research on the Application of Federated Learning Based on CG-WGAN in Gout Staging Prediction. Computers, 14(11), 455. https://doi.org/10.3390/computers14110455








