Sparse Keyword Data Analysis Using Bayesian Pattern Mining

Abstract

Keyword data analysis aims to extract and interpret meaningful relationships from large collections of text documents. A major challenge in this process arises from the extreme sparsity of document–keyword matrices, where the majority of elements are zeros due to zero inflation. To address this issue, this study proposes a probabilistic framework called Bayesian Pattern Mining (BPM), which integrates Bayesian inference into association rule mining (ARM). The proposed method estimates both the expected values and credible intervals of interestingness measures such as confidence and lift, providing a probabilistic evaluation of keyword associations. Experiments conducted on 9436 quantum computing patent documents, from which 175 representative keywords were extracted, demonstrate that BPM yields more stable and interpretable associations than conventional ARM. By incorporating credible intervals, BPM reduces the risk of biased decisions under sparsity and enhances the reliability of keyword-based technology analysis, offering a rigorous approach for knowledge discovery in zero-inflated text data.

1. Introduction

The exponential growth of digital information has made text data one of the most widely used and important resources in modern data analysis. With the rapid accumulation of documents such as research papers, patents, reports, and online content, extracting useful insights from textual information has become a critical research topic [1,2,3,4,5,6,7]. Among the various approaches to text mining, keyword analysis has played a central role because keywords provide a compact and meaningful representation of document content. By analyzing keywords, researchers can identify emerging themes, discover semantic structures, and capture technological and social trends [1,2,8,9,10,11,12,13,14]. A standard process in keyword analysis begins with constructing a document–keyword matrix, where rows represent documents and columns represent keywords. Each entry in this matrix denotes the frequency with which a keyword occurs in a document. However, in practice, such matrices are characterized by extreme sparsity. That is, extreme sparsity arises because even if a particular keyword appears in only a single document, it is still represented as a separate column in the document–keyword matrix. As a result, that column has a non-zero entry in only one row, while all other rows contain zero, which leads to a highly sparse and zero-inflated structure. This leads to the well-known zero-inflated problem, which has been reported as a major obstacle to the reliable performance of analytical models [3,4,15,16,17,18,19,20,21,22,23]. When sparsity is severe, traditional frequency-based methods may provide unstable or biased results, making it difficult to draw meaningful conclusions.

Over the years, a variety of methods have been proposed to address sparsity in keyword analysis. Classical approaches include weighting schemes such as term frequency–inverse document frequency (TF–IDF) [24,25,26,27], which adjust raw frequencies to better reflect the discriminative power of keywords across documents. More recently, probabilistic models, graph-based approaches, and embedding methods (e.g., Word2Vec, BERT) have been applied to keyword analysis, aiming to capture latent semantic relationships beyond raw co-occurrence counts [3,5,28,29,30,31,32,33,34]. While these methods represent significant progress, they are not free from limitations. Frequency-based and TF–IDF approaches often remain sensitive to sparsity. Graph-based and embedding approaches provide richer representations but may require large corpora, heavy computation, or domain-specific fine-tuning, which can limit their applicability in practice. Moreover, these methods typically rely on point estimates, which may not adequately account for uncertainty in sparse and noisy data. Against this backdrop, Bayesian statistics has recently attracted increasing attention as a powerful tool for handling sparsity and uncertainty in text analysis [16,18,19,20,32]. By incorporating prior information and using posterior distributions, Bayesian methods can provide both point estimates and uncertainty intervals, thereby supporting more robust inference. In particular, Bayesian models have shown promise in zero-inflated count data analysis, such as in biomedical, ecological, and patent domains [16,19,21]. Building on this line of research, Bayesian approaches offer an opportunity to enhance keyword analysis, where sparsity and zero inflation are pervasive. The objective of this study is therefore to develop a robust methodology for sparse keyword data analysis that explicitly addresses the zero-inflated problem. We propose Bayesian Pattern Mining (BPM), which integrates Bayesian inference with association rule mining (ARM). Traditional ARM has been widely used in fields such as market basket analysis and text mining [35,36,37], where it discovers frequent co-occurrence patterns among items or keywords. However, ARM relies only on single-value measures such as support, confidence, and lift, without quantifying the uncertainty of these measures. This limitation becomes critical when analyzing sparse document–keyword matrices, where biased or unstable estimates may lead to incorrect interpretations.

Our proposed BPM framework addresses this challenge by introducing Bayesian inference into pattern mining. Specifically, BPM applies Bayesian priors and likelihoods to association rules, yielding posterior distributions for interestingness measures. From these posterior distributions, BPM derives not only the expected (mean) values but also credible intervals for support, confidence, and lift. This dual estimation enables analysts to make decisions that account for uncertainty, thereby reducing bias and improving robustness in sparse settings. For example, in cases where ARM would produce a misleadingly high confidence due to data sparsity, BPM can reveal wide credible intervals that caution against over-interpretation. Despite the progress achieved by recent text mining methods, there remains a clear research gap between semantic representation and probabilistic uncertainty modeling. Embedding-based and large language model (LLM)-based models (e.g., Word2Vec, BERT, GPT) have advanced the representation of keyword meaning, yet they typically rely on large corpora and deterministic embeddings, without explicitly quantifying the uncertainty caused by data sparsity. Moreover, these approaches seldom address the zero-inflated nature of document–keyword matrix. In contrast, our proposed BPM framework directly incorporates Bayesian inference into rule-based keyword analysis to estimate both the mean and credible intervals of association measures. This enables a rigorous probabilistic treatment of uncertainty, thereby filling a methodological gap in the current literature on sparse text analysis.

The contributions of this paper are fourfold as follows: First, we introduce BPM as a novel approach that combines Bayesian inference with association rule mining to mitigate the zero-inflated sparsity problem in keyword data. Second, we demonstrate how Bayesian credible intervals can enhance the interpretability of association measures, offering a probabilistic framework that extends traditional ARM. Third, using a large-scale dataset of 9436 patent documents in the field of quantum computing, we validate the effectiveness of BPM compared to conventional ARM, showing that BPM provides more stable and reliable keyword associations. Lastly, we illustrate how BPM can support technology forecasting and patent analysis by offering more trustworthy insights into the associative structures among technological keywords. The remainder of this paper is organized as follows. Section 2 reviews the research background, including keyword analysis and association rule mining. Section 3 presents the proposed BPM methodology in detail. Section 4 reports experimental results using the quantum computing patent dataset. Section 5 provides a discussion of theoretical and practical implications, followed by conclusions and future research directions.

2. Research Background

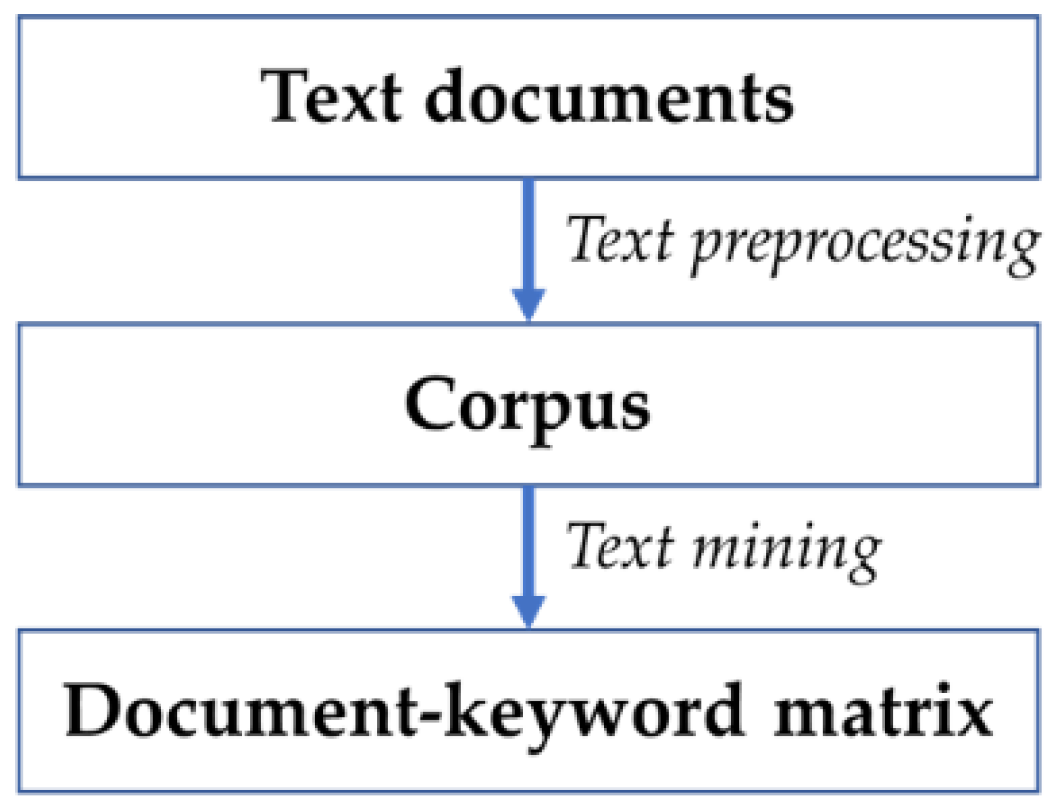
2.1. Keyword Analysis

Keyword analysis is to analyze the document–keyword matrix constructed from the text document data. Figure 1 shows text preprocessing and mining of collected text documents.

We search the text documents related to target issues from diverse resources. By text processing, the collected text documents are changed to a corpus. A corpus is a dataset that has been structured and transformed into a form that can be processed by a computer [24]. Using text mining techniques, we construct the document–keyword matrix from the corpus. Using this matrix, we can perform various keyword analyses. Keyword analysis has been widely used as a fundamental approach in text document studies to capture the social and technological trends of documents. In general, keyword analysis is also to extract the terms that frequently occur in the corpus, followed by quantifying their distribution and statistical significance [24,25,26]. Keywords provide a meaningful representation of document content and build associative structures such as graph or topic models [8]. Most studies have primarily relied on frequency counts to identify keywords occurring in documents. However, keyword analysis methods based on frequency are often limited by the sparsity and skewness of keyword distributions caused by the zero-inflated problem in the document–term matrix [3,20]. To address this problem in the early stages of keyword analysis, Salton and Buckley (1988) introduced weighting schemes such as term frequency–inverse document frequency (TF–IDF) and probabilistic models [25]. So, they enhanced the discriminative power of keywords across documents. Some recent research has used keyword network models based on graph structure, social network analysis, and probabilistic approaches [3,5,28,29,30]. Bayesian keyword analysis has also been actively researched in various fields recently [3,16,30,31]. Jun (2024) proposed a zero-inflated model based on Bayesian statistics to analyze keyword data [3], because Bayesian data analysis provides a way to solve the sparsity problem of zero-overcount data [18,19,32].

Recently, new methods have been actively studied in patent keyword analysis, which extracts and analyzes keywords from patent documents [7,20,31]. These studies have used advanced statistical analysis methods as well as machine learning algorithms for patent keyword analysis. Keyword analysis has been making significant contributions in solving problems in various domains. For example, patent keyword analysis has been used to predict technological trends and understand technological structures within a target domain [33]. In keyword analysis, a fundamental challenge concerns the construction of an appropriate semantic representation of keywords, as traditional frequency-based or co-occurrence methods are often sparse and limited in capturing semantic relations. Recent studies have therefore compared alternative approaches such as co-word networks, word embeddings, and network embeddings, demonstrating that their effectiveness in bibliometric research largely depends on corpus characteristics and analytical objectives [10,34]. There are still many issues to be resolved in the field of keyword analysis, and data sparsity of zero inflation is also a critical issue that needs to be addressed. In our paper, we study an analysis method to solve this problem.

In addition to keyword-based methods, a significant body of research has focused on multiclass text classification and clustering to find latent structures in text corpora. Many of these approaches are grounded in probabilistic modeling, including the use of Dirichlet distributions, multinomial models, and Bayesian inference. For example, Campello et al. (2013) studied density-based clustering and hierarchical density estimation to group documents based on probabilistic similarity measures [38]. Also, Aljalbout et al. (2018) integrated deep learning with clustering to improve representation learning for large-scale corpora [39]. In scientific text analysis, Beltagy et al. (2019) developed pretrained language models such as SciBERT, which showed strong performance not only in classification tasks but also in entity and relation extraction, closely connected to rule mining and keyword association [40]. These previous studies demonstrated that their probabilistic approaches to clustering and classification are powerful tools for text mining, complementing keyword analysis by capturing semantic and structural relationships at multiple levels.

While embedding-based methods such as Word2Vec, BERT, and SciBERT [10,34] provide powerful representations of semantic similarity, they typically assume dense vector spaces and do not directly address the statistical sparsity and uncertainty inherent in document–keyword matrices. LLMs further extend this capability to contextual semantics but are computationally intensive and lack mechanisms to quantify probabilistic confidence in inferred associations. In contrast, BPM focuses on probabilistic rule inference, offering a complementary approach that estimates the reliability of associations rather than semantic proximity.

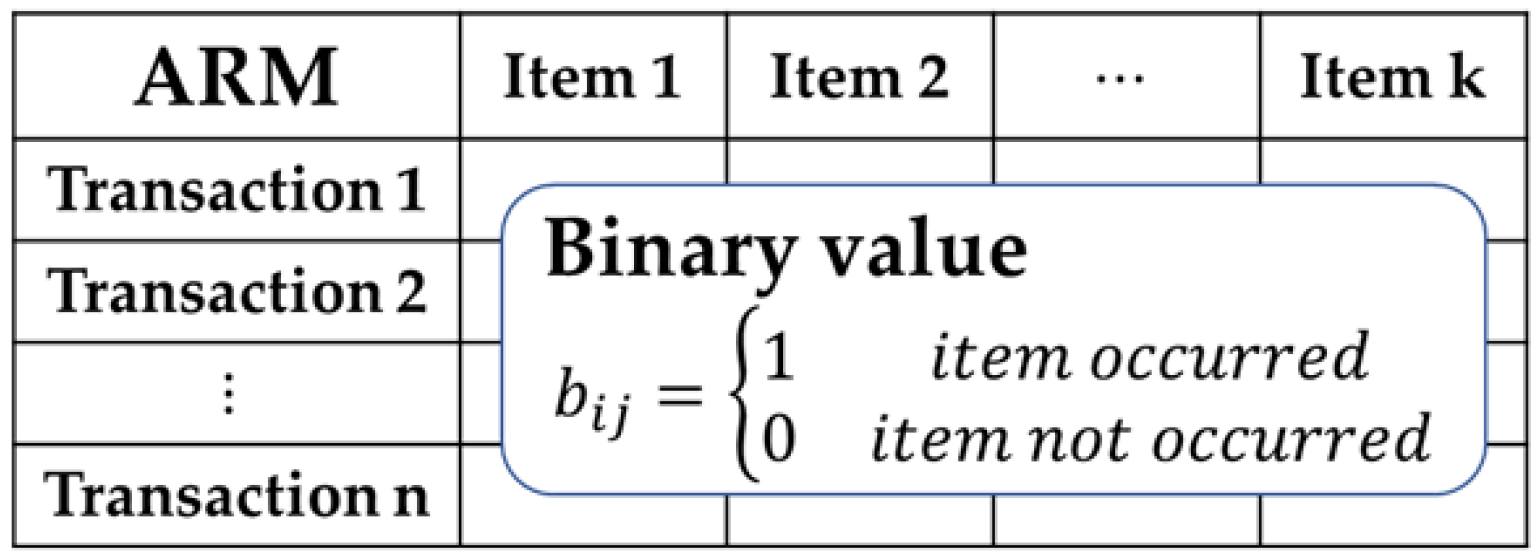
2.2. Association Rule Mining

ARM is a data mining method designed to uncover hidden relationships among items in large datasets [35]. This was introduced as an algorithm for application in market basket analysis. ARM consists of items and transactions. An item is a distinct attribute, object, or keyword that can appear in a dataset. A transaction is a collection of items that occur together in one record, such as a shopping basket or a document. We build a matrix consisting of transactions and items as rows and columns, respectively. Figure 2 shows the transaction–item matrix for ARM.

In Figure 2, each element $b_{ij}$ of this matrix has a binary value of 1 or 0. That is, if the jth item occurs in the ith transaction, $b_{ij}=1$. This matrix is input data for general ARM. To evaluate the performance of rules extracted through ARM, we use three measures: support, confidence, and lift. When an association rule is expressed as $X\to Y$, $X$ is the antecedent item and $Y$ is the consequent item [35,36]. The support of $X\to Y$ is defined as follows [35,36].

$$Support\left(X\to Y\right)=P\left(X\cap Y\right)$$

(1)

In Equation (1), the $Support\left(X\to Y\right)$ is the probability that a transaction contains $X\cap Y$. The confidence of $X\to Y$ is computed by following equation [35,36].

$$Confidence\left(X\to Y\right)={\displaystyle \frac{P\left(X\cap Y\right)}{P\left(X\right)}}$$

(2)

In Equation (2), the $Confidence\left(X\to Y\right)$ is the conditional probability that a transaction having $Y$ given $X$. The remaining measure for evaluating the performance of ARM is lift, which is defined as follows [35,36].

$$Lift\left(X\to Y\right)={\displaystyle \frac{Confidence\left(X\to Y\right)}{P\left(Y\right)}}$$

(3)

The lift value is not a probability in Equation (3). This measure has a value greater than or equal to 0. If the lift value is greater than 1, $X$ and $Y$ are complementary, and if it is less than 1, they are substitutes. Therefore, we find the meaningful rules from given data using support, confidence, and lift measures.

3. Bayesian Pattern Mining for Sparse Keyword Data Analysis

In ARM, three primary measures (support, confidence, and lift) are commonly used to evaluate the strength of associations between items. In this study, these measures are further extended under a Bayesian framework. The term confidence refers to its conventional definition in ARM, representing the conditional probability of observing the consequent given the antecedent. To avoid confusion, the term credible interval is used instead of confidence interval when describing Bayesian posterior intervals. In this paper, we propose a method of Bayesian Pattern Mining, an association rule mining method based on Bayesian inference, to solve the sparsity problem that occurs during keyword data analysis. In general, the keyword data have a zero-inflated problem. That is, since a significant number of elements in the keyword data have zero values, the data sparsity problem occurs due to zero excess. Our proposed method consists of two analysis procedures. The first procedure is to build a document–keyword matrix from the collected text documents to make the data to be used for Bayesian Pattern Mining. The procedure of building document–keyword matrix is shown as follows. Using the result of building document–keyword matrix in Algorithm 1, we perform the BPM to analyze the sparse keyword data as follows.

Algorithm 1 Building Document–Keyword Matrix

Input:     - Document data     - Unique string separator

Output:     - Extracted keywords     - Document–keyword matrix 1. Collecting text data - documents, papers, patents, reports, news articles, legal documents - social media and chat comments, online comments 2. Checking data schema - removing duplicated documents - missing value imputation 3. Normalizing text data - removing spaces, numbers, symbols, etc. - lowercasing, using stopwords by user dictionary 4. Lemmatization and stemming 5. Parsing - corpus, text database 6. Constructing document–keyword matrix - sparse matrix, keyword extraction - each element representing frequency of keywords occurring in each document 7. Changing element value from count to binary - binary document–keyword matrix - using binary matrix for transaction data for association rule mining

The input and output of Algorithm 1 are the collected text documents and document–keyword matrix, respectively. We collect text data from various data sources. The collected data goes through a preprocessing with text mining after data checking such as removing duplicate documents and missing value imputation. Using the data normalizing, lemmatization, stemming, and parsing techniques of text mining, we construct the document–keyword matrix. At this stage, the preprocessing of various text mining such as removing spaces, lowercasing, stemming, and corpus parsing is performed. The rows and columns of the final document–keyword matrix represent documents and keywords, respectively, and each element indicates the frequency of a keyword contained in a document. Typically, the number of keywords is much larger than the number of documents, which causes the document–keyword matrix to become extremely sparse, with most entries equal to zero, thereby giving rise to a zero-inflated problem. In this paper, we study a new method to solve this problem. In Algorithm 1, all non-zero count values in this matrix are changed to one. This binary matrix becomes the transaction data used in the association rule mining.

To solve the sparsity problem of zero inflation that occurs in text data analysis, the method we study in this paper is sparse text data analysis based on Bayesian Pattern Mining (BPM). The BPM, a combination of Bayesian statistics and ARM, is a methodology that infers the uncertainty of association rules probabilistically by reflecting prior knowledge in the model. For example, ARM provides a single value representing the lift measure, but BPM provides not only a single lift value but also a credible interval for the lift, giving you more information to understand and utilize the association rules. This characteristic of BPM enables it to effectively address the sparsity issue inherent in keyword data analysis. Pattern mining is the process of discovering meaningful patterns from data consisting of items and transactions. By applying Bayesian statistics, the significance of patterns is evaluated using posterior distributions derived from the prior distributions and likelihood functions. Algorithm 2 shows the procedure of BPM, from the sparse document–keyword matrix to summary statistics of extracted association rules.

Algorithm 2 Bayesian Pattern Mining

Input:     - sparse document–keyword matrix with binary data

Output:     - means and credible intervals of association rules 1. Constructing 2 × 2 contingency table - X: antecedent item (keyword) - Y: consequent item (keyword) 2. Building posterior distribution - prior: $P~Dirichlet\left({\alpha }_{11},{\alpha }_{10},{\alpha }_{01},{\alpha }_{00}\right)$$, {\alpha }_{ij}>0$ - likelihood: $n|P~Multinomial(N,P)$$, \mathrm{N}=n_{11}+n_{10}+n_{01}+n_{00}$ - posterior: $P|n~Dirichlet({\alpha }_{11}+n_{11},{\alpha }_{10}+n_{10},{\alpha }_{01}+n_{01},{\alpha }_{00}+n_{00})$ 3. Obtaining interesting measures - support: $S\left(X\to Y\right)$ - confidence: $C\left(X\to Y\right)$ - lift: $L\left(X\to Y\right)$ 4. Estimating mean and credible interval - drawing samples from posterior distribution - estimating probability values, expectation, and credible interval

In BPM, each document and keyword in the document–keyword matrix becomes a transaction and item, respectively. In BPM, we use the document–keyword matrix as the transaction–item matrix. The element $f_{ij}$ of this matrix has a value of 0 or 1, as follows.

$$f_{ij}\in \left\{\mathrm{0,1}\right\}, i=1, 2,\dots n, j=1, 2,\dots p$$

(4)

In Equation (4), $n$ and $p$ are the numbers of documents (transactions) and keywords (items), respectively. If the $f_{ij}$ value is 1, it means that the jth keyword is included in the ith document. If the antecedent and consequent of the association rule are represented as X and Y, respectively, the following partition table is created [35,37].

In

Table 1. Contingency table of antecedent and consequent items.

Item	$\mathit{Y}=1$	$\mathit{Y}=0$	Row Sum
$X=1$	$n_{11}$	$n_{10}$	$n_{1·}$
$X=0$	$n_{01}$	$n_{00}$	$n_{0·}$
Column sum	$n_{·1}$	$n_{·0}$	Total sum = N

, each item is a keyword of document–keyword matrix. Also, $n_{ij}$ represents the number of $X=i$ and $Y=j$ ($i,j\in \left\{\mathrm{0,1}\right\}$). Let $p_{ij}$ be the probability of $X=i$ and $Y=j$, $P=\left(p_{11},p_{10},p_{01},p_{00}\right)$ and ${\sum }_{i,j=1}^0{p}_{ij}=1.$ In our BPM, we use the Dirichlet distribution as a prior, $P~Dirichlet\left({\alpha }_{11},{\alpha }_{10},{\alpha }_{01},{\alpha }_{00}\right)$, ${\alpha }_{ij}>0$ in Equation (5).

$$f\left(P\right)={\displaystyle \frac{\mathsf{\Gamma }\left({\alpha }_{11}+{\alpha }_{10}+{\alpha }_{01}+{\alpha }_{00}\right)}{\mathsf{\Gamma }\left({\alpha }_{11}\right)\mathsf{\Gamma }\left({\alpha }_{10}\right)\mathsf{\Gamma }\left({\alpha }_{01}\right)\mathsf{\Gamma }\left({\alpha }_{00}\right)}}{p}_{11}^{{\alpha }_{11}-1}{p}_{10}^{{\alpha }_{10}-1}{p}_{01}^{{\alpha }_{01}-1}{p}_{00}^{{\alpha }_{00}-1}, p_{11},p_{10},p_{01},p_{00}\ge 0$$

(5)

The likelihood function uses a multinomial distribution $n|P~Multinomial(N,P)$, $N=n_{11}+n_{10}+n_{01}+n_{00}$. In this study, we set the Dirichlet prior parameter α = 1 for all elements, corresponding to a uniform noninformative prior. This choice assumes equal prior probability across all possible rule outcomes, reflecting the absence of domain-specific prior knowledge. Such a setting prevents overfitting on rare keyword pairs and provides stable posterior estimates. Alternative α configurations can be employed when prior information about item co-occurrence is available, which will be explored in future work. Using the prior distribution and likelihood function, we derive the posterior distribution as Equation (6).

$$P|n~Dirichlet({\alpha }_{11}+n_{11},{\alpha }_{10}+n_{10},{\alpha }_{01}+n_{01},{\alpha }_{00}+n_{00})$$

(6)

For each interestingness measure (support, confidence, and lift), posterior distributions were estimated using Markov Chain Monte Carlo (MCMC) sampling [41]. The posterior mean represents the expected value under the Bayesian model, while the credible interval corresponds to the 95% highest posterior density (HPD) region, calculated from the 2.5th and 97.5th percentiles of the posterior samples [41]. These credible intervals quantify the uncertainty of each measure and provide a probabilistic interpretation that extends beyond the point estimates obtained from conventional ARM. We derive the interesting measures of association rules from the contingency table and probability distribution as follows.

$$S\left(X\to Y\right)=p_{11}, C\left(X\to Y\right)={\displaystyle \frac{p_{11}}{p_{11}+p_{10}}}, L\left(X\to Y\right)={\displaystyle \frac{p_{11}}{(p_{11}+p_{10})(p_{11}+p_{01})}}$$

(7)

In Equation (7), $S\left(X\to Y\right)$, $C\left(X\to Y\right)$, and $L\left(X\to Y\right)$ are support, confidence, and lift of association rules, respectively. We use samples drawn from the posterior distribution to obtain probability, expectation, and credible interval for each interesting measure. We show how to apply Bayesian inference to association rules with support, confidence, and lift. Lastly, we apply Bayesian inference to association rules, and estimate means and credible intervals of confidence and lift from the association rules in Algorithm 3.

Algorithm 3 Bayesian Inference for Association Rules

Input:     - $\left(n_{11},n_{10},n_{01},n_{00}\right)$ of contingency table     - prior, likelihood (M samples), posterior - threshold $t$ of confidence

Output:     - summary statistics of confidence and lift     - credible intervals of confidence and lift     - probability values of $P(L\left(X\to Y\right)>1)$ and $P(C\left(X\to Y\right)>t)$ 1. Obtaining parameters for posterior distribution - ${\alpha }_{ij}^{*}={\alpha }_{ij}+n_{ij}$ for all elements 2. Drawing M samples from posterior distribution - posterior: $P^{\left(m\right)}~Dirichlet\left({\alpha }_{ij}^{*}\right)$$, {\alpha }_{ij}^{*}>0$ 3. Computing interesting measures per sample - $S\left(X\to Y\right)=p_{11}^{\left(m\right)}$ - $C\left(X\to Y\right)={\displaystyle \frac{p_{11}^{\left(m\right)}}{p_{11}^{\left(m\right)}+p_{10}^{\left(m\right)}}}$ - $L\left(X\to Y\right)={\displaystyle \frac{C\left(X\to Y\right)}{p_{11}^{\left(m\right)}+p_{01}^{\left(m\right)}}}$ 4. Estimating summary statistics - calculating posterior mean and 95% credible intervals - estimating probability values of $P(L\left(X\to Y\right)>1)$$\mathrm{and} P(C\left(X\to Y\right)>t)$

The input of Bayesian inference for association rules are $\left(n_{11},n_{10},n_{01},n_{00}\right)$ of contingency table and M samples drawn from posterior distribution. We determine threshold $t$ of confidence measure in the input. Our output contains the summary statistics of confidence and lift such as mean and credible interval. The output also provides the probability values of $P(L\left(X\to Y\right)>1)$ and $P(C\left(X\to Y\right)>t)$. Step 3 of Algorithm 3 represents how to compute the interesting measures per sample in total M samples. Using the M samples, we estimate the means and 95% credible intervals of confidence and lift. Using the results of Algorithms 1–3, we made a keyword diagram to understand the target domain.

4. Experimental Results

To evaluate the effectiveness of the proposed BPM, we collected patent documents related to quantum computing technology from two major international patent databases: the Korea Intellectual Property Rights Information Service (KIPRIS) and the United States Patent and Trademark Office (USPTO) [42,43]. The collection period spans from March 2015 to March 2025, during which we obtained a total of 9436 patent documents that were either filed or granted in the domain of quantum computing. Before conducting the analysis, we performed several preprocessing steps using text mining techniques. First, duplicate and incomplete documents were removed and missing values were imputed. Next, standard natural language processing procedures were applied, including tokenization, lowercasing, stemming, and lemmatization. Domain-specific stopwords (e.g., general legal terms in patents such as “system,” “method,” or “apparatus”) were also eliminated using a user-defined stopword dictionary. This process resulted in a clean corpus suitable for keyword extraction.

From the processed corpus, we extracted a total of 175 representative keywords. The selection of the 175 representative keywords was based on both frequency and domain relevance. First, only keywords with occurrence frequencies greater than approximately 1000 across the entire corpus were considered. Second, within this subset, we identified those that were relevant to quantum computing by consulting standard references in the field [44,45,46,47,48,49]. In particular, we relied on the introduction sections of these works, which provide an overview of the fundamental concepts and terminology in quantum computing. This ensured that selected keywords not only appeared frequently but also reflected core technical themes, including qubit, entanglement, gate, error correction, algorithms, and simulation. The final set was then categorized into three main technology domains of quantum computing: core, software, and hardware: core technologies (e.g., qubit, entanglement, gate), software and algorithms (e.g., encryption, program, network), and hardware components (e.g., chip, photon, superconduct). Using these keywords, we constructed a document–keyword matrix where rows represent documents and columns represent keywords. An important characteristic of the dataset is its sparsity. Because the number of keywords is much larger than the number of documents, most entries in the document–keyword matrix are zero. Specifically, over 92% of all matrix entries have zero values, indicating the presence of a severe zero-inflated problem. This sparsity highlights the limitations of traditional ARM methods and underscores the necessity of our proposed BPM approach, which incorporates credible intervals to reduce decision bias under zero inflation.

Quantum computing is a computational paradigm based on the principles of quantum mechanics using qubit to achieve speedups beyond classical bit-based computers [44,45,46,47,48,49]. Whereas classical computers represent and process information using bits that take values of either 0 or 1, quantum computers employ qubits that can exist in a superposition of both 0 and 1 simultaneously [46,48]. This enables the solution of certain computational problems with significantly higher efficiency and speed compared to classical computers. So, we analyzed the patents to build technology structure of quantum computing. Figure 3 shows the constructed patent document–keyword matrix.

In Figure 3, the keywords and frequency values of all keywords extracted from patent documents are showed. Since the word endings were removed during the preprocessing of text mining, the keywords shown in Figure 3 represent only the root of each word. For ARM analysis, we converted the count values in this matrix to binary data. That is, all values greater than or equal to 1 were converted to 1. If a specific keyword was included in each patent document, it was represented as 1, otherwise 0. Figure 4 shows resulting binary patent document–keyword matrix.

Among all keywords, we selected the final keywords according to the three technology categories of quantum computing: core, software, and hardware, as shown in

Table 2. Representative keywords related to quantum computing.

Technology Category	Representative Keywords
Core	algorithm, bit, calcul, circuit, comput, entangl, error, gate, Hamiltonian, ion, measur, photon, quantum, qubit, sequenc, signal, simul, state, superconduct, timetrap,
Software	algorithm, authent, circuit, cloud, code, connect, data, electron, encrypt, execut, function, gate, graph, implement, includ, inform, key, logic, model, modul, network, optim, perform, processor, program, random, sampl, secret, secur, simul, structur, technolog,
Hardware	chip, electron, energi, ion, memori, optic, optical, photon, reson, storage, substrat, superconduct, trap

.

According to the keywords, there are also representative keywords that are included in two categories at the same time. For example, the keyword algorithm falls into both the core and software categories. Among them, we selected 25 keywords as follows; atom, bit, calculation, chip, cloud, code, computing, connect, data, electron, encryption, hybrid, inform, logic, memory, network, photon, processor, program, quantum, qubit, random, security, superconduct, and vector. We first show the performance results of ARM in

Table 3. Top 30 rules of ARM by confidence measure.

LHS	RHS	Confidence	Lift	Support
bit	quantum	0.9809	1.0777	0.1271
photon	quantum	0.9806	1.0773	0.0379
chip	quantum	0.9766	1.0730	0.0761
atom	quantum	0.9714	1.0673	0.0255
superconduct	quantum	0.9659	1.0612	0.0669
processor	quantum	0.9596	1.0543	0.0995
qubit	quantum	0.9494	1.0431	0.2134
logic	quantum	0.9493	1.0430	0.0643
program	quantum	0.9489	1.0425	0.0717
hybrid	quantum	0.9424	1.0354	0.0491
computing	quantum	0.9402	1.0329	0.7622
electron	quantum	0.9330	1.0251	0.0792
code	quantum	0.9266	1.0181	0.0583
hybrid	computing	0.9239	1.1396	0.0482
connect	quantum	0.9237	1.0148	0.0870
chip	computing	0.9118	1.1248	0.0710
memory	quantum	0.9000	0.9888	0.0454
inform	quantum	0.8997	0.9885	0.1493
network	quantum	0.8986	0.9872	0.1150
program	computing	0.8949	1.1038	0.0676
calculation	quantum	0.8919	0.9800	0.1603
cloud	computing	0.8857	1.0925	0.0299
vector	quantum	0.8834	0.9706	0.0325
cloud	quantum	0.8762	0.9627	0.0296
atom	computing	0.8735	1.0774	0.0230
superconduct	computing	0.8698	1.0728	0.0602
data	quantum	0.8683	0.9540	0.2066
processor	computing	0.8654	1.0675	0.0897
electron	computing	0.8546	1.0542	0.0725
qubit	computing	0.8535	1.0527	0.1919

.

Table 3 shows the top 30 in descending order of confidence. We made it possible to compare not only the confidence value of each rule, but also the values of lift and support measures. The left-hand side (LHS) and right-hand side (RHS) are the antecedent and consequent items. From the results in Table 3, we see that rules $\left(bit\to quantum\right)$ and $\left(photon\to quantum\right)$ are the largest, followed by $\left(chip\to quantum\right)$ and $\left(atom\to quantum\right)$. For example, the probability of quantum appearing under the condition that the keyword photon appears is 0.9806. This means that knowledge of photons is essential for quantum technology development. Additionally, the lift value of rule $\left(chip\to quantum\right)$ was 1.0773, which was greater than 1. This means that chip and quantum technologies are complementary to each other. We also found that the support value of rule $\left(qubit\to quantum\right)$ is 0.2134, which means that the keywords qubit and quantum appeared together in 21.34% of all patent documents. Next, we show the top 30 ARM rules by lift measure in

Table 4. Top 30 rules of ARM by lift measure.

LHS	RHS	Lift	Confidence	Support
encryption	security	5.9356	0.5567	0.0411
security	encryption	5.9356	0.4382	0.0411
random	encryption	4.9903	0.3684	0.0203
encryption	random	4.9903	0.2747	0.0203
processor	memory	4.9056	0.2474	0.0256
memory	processor	4.9056	0.5085	0.0256
atom	photon	4.3320	0.1673	0.0044
photon	atom	4.3320	0.1139	0.0044
superconduct	chip	4.1792	0.3256	0.0225
chip	superconduct	4.1792	0.2893	0.0225
encryption	cloud	3.6980	0.1250	0.0092
cloud	encryption	3.6980	0.2730	0.0092
random	security	3.6373	0.3411	0.0188
security	random	3.6373	0.2002	0.0188
cloud	random	3.0565	0.1683	0.0057
random	cloud	3.0565	0.1033	0.0057
memory	logic	2.8909	0.1957	0.0099
logic	memory	2.8909	0.1458	0.0099
chip	connect	2.8801	0.2713	0.0211
connect	chip	2.8801	0.2244	0.0211
security	cloud	2.8772	0.0973	0.0091
cloud	security	2.8772	0.2698	0.0091
chip	bit	2.7757	0.3595	0.0280
bit	chip	2.7757	0.2162	0.0280
processor	hybrid	2.6400	0.1377	0.0143
hybrid	processor	2.6400	0.2737	0.0143
superconduct	connect	2.6000	0.2450	0.0170
connect	superconduct	2.6000	0.1800	0.0170
memory	program	2.3940	0.1809	0.0091
program	memory	2.3940	0.1207	0.0091

.

In Table 4, we found that the lift value of ARM rules $\left(encryption\to security\right)$ and $\left(security\to encryption\right)$ are the largest. The lift value is 5.9356. This indicates a very strong interdependence between the two technologies based on keywords encryption and security. This means that as the technology based on encryption is developed, technology based on security is also developed accordingly. The interpretation and use of confidence and support in Table 4 are the same as in Table 3.

As confirmed in Table 3 and Table 4, ARM provides only one value for each of the three measures—confidence, lift, and support. Therefore, we must rely on a single value for decision-making. In analyzing sparse data with zero inflation, the decision process can lead to bias. So, to overcome this problem, we proposed a method of extracting association rules, called BPM.

Table 5. Top 30 rules of BPM by confidence measure.

LHS	RHS	Credible Interval of Confidence Measure			Lift	Support
		Mean	Lower	Upper	Mean	Mean
bit	quantum	0.9804	0.9719	0.9882	1.0773	0.1271
photon	quantum	0.9793	0.9631	0.9910	1.0760	0.0379
chip	quantum	0.9760	0.9636	0.9855	1.0724	0.0761
atom	quantum	0.9696	0.9443	0.9879	1.0654	0.0255
superconduct	quantum	0.9652	0.9496	0.9778	1.0605	0.0669
processor	quantum	0.9590	0.9459	0.9701	1.0538	0.0995
qubit	quantum	0.9493	0.9392	0.9584	1.0430	0.2134
logic	quantum	0.9487	0.9312	0.9647	1.0425	0.0643
program	quantum	0.9480	0.9303	0.9633	1.0417	0.0717
hybrid	quantum	0.9416	0.9192	0.9602	1.0345	0.0491
computing	quantum	0.9401	0.9347	0.9455	1.0330	0.7622
electron	quantum	0.9327	0.9159	0.9492	1.0250	0.0792
code	quantum	0.9261	0.9053	0.9443	1.0175	0.0583
hybrid	computing	0.9231	0.8977	0.9454	1.1388	0.0482
connect	quantum	0.9230	0.9047	0.9399	1.0142	0.0870
chip	computing	0.9117	0.8904	0.9312	1.1246	0.0710
inform	quantum	0.8993	0.8836	0.9137	0.9883	0.1493
memory	quantum	0.8992	0.8710	0.9243	0.9879	0.0454
network	quantum	0.8983	0.8814	0.9152	0.9870	0.1150
program	computing	0.8947	0.8716	0.9155	1.1036	0.0676
calculation	quantum	0.8917	0.8764	0.9065	0.9799	0.1603
cloud	computing	0.8839	0.8466	0.9171	1.0903	0.0299
vector	quantum	0.8825	0.8450	0.9145	0.9696	0.0325
cloud	quantum	0.8745	0.8362	0.9075	0.9608	0.0296
atom	computing	0.8721	0.8282	0.9104	1.0757	0.0230
superconduct	computing	0.8693	0.8413	0.8944	1.0721	0.0602
data	quantum	0.8680	0.8540	0.8819	0.9539	0.2066
processor	computing	0.8652	0.8416	0.8863	1.0674	0.0897
electron	computing	0.8538	0.8282	0.8780	1.0531	0.0725
qubit	computing	0.8532	0.8373	0.8679	1.0526	0.1919

shows the top 30 association rules of BPM by confidence measure.

In Table 5, the confidence measure provides three values such as mean, lower, and upper. The mean of confidence in Table 5 is the same concept as the confidence of ARM in Table 3. The BPM enables us to make unbiased decisions about association rules because it provides credible intervals for confidence that ARM does not. In this paper, we obtained a 95% credible interval. We also illustrate the top 30 rules of BPM by lift measure in

Table 6. Top 30 rules of BPM by lift measure.

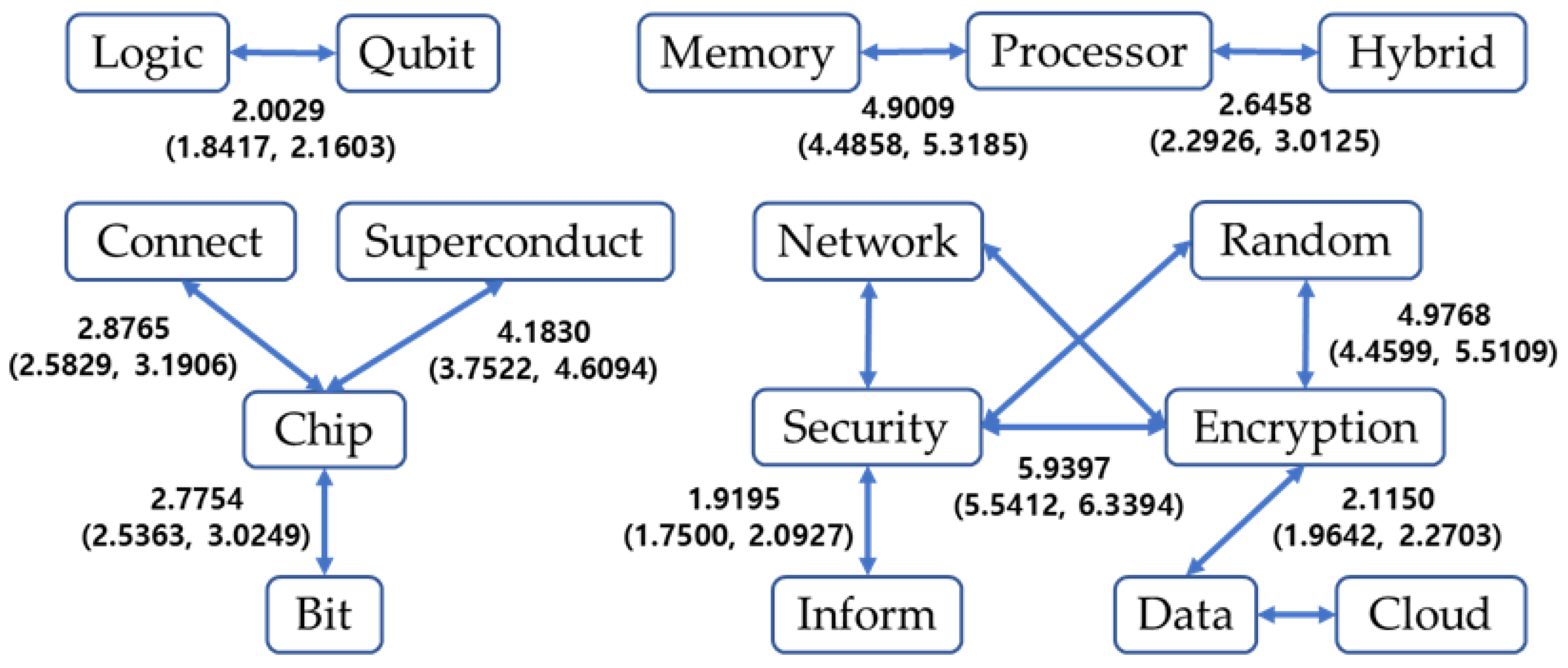
LHS	RHS	Credible Interval of Lift Measure			Confidence	Support
		Mean	Lower	Upper	Mean	Mean
security	encryption	5.9397	5.5412	6.3394	0.4380	0.0411
encryption	security	5.9312	5.5399	6.3563	0.5568	0.0411
encryption	random	4.9807	4.4713	5.5169	0.2744	0.0203
random	encryption	4.9768	4.4599	5.5109	0.3680	0.0203
processor	memory	4.9091	4.4942	5.3458	0.2478	0.0256
memory	processor	4.9009	4.4858	5.3185	0.5086	0.0256
chip	superconduct	4.1867	3.7600	4.6149	0.2902	0.0225
superconduct	chip	4.1830	3.7522	4.6094	0.3263	0.0225
security	random	3.6474	3.2506	4.0597	0.2012	0.0188
random	security	3.6309	3.2322	4.0481	0.3406	0.0188
connect	chip	2.8765	2.5829	3.1906	0.2244	0.0211
chip	connect	2.8743	2.5706	3.2114	0.2708	0.0211
bit	chip	2.7764	2.5242	3.0326	0.2164	0.0280
chip	bit	2.7754	2.5363	3.0249	0.3598	0.0280
processor	hybrid	2.6458	2.2926	3.0125	0.1382	0.0143
hybrid	processor	2.6424	2.2901	2.9987	0.2741	0.0143
superconduct	connect	2.6076	2.3019	2.9425	0.2460	0.0170
connect	superconduct	2.6054	2.2929	2.9412	0.1806	0.0170
data	cloud	2.3239	2.0822	2.5532	0.0788	0.0187
cloud	data	2.3211	2.0941	2.5495	0.5520	0.0187
network	security	2.2942	2.0781	2.5122	0.2154	0.0275
security	network	2.2903	2.0867	2.5047	0.2930	0.0275
encryption	data	2.1150	1.9642	2.2703	0.5033	0.0371
data	encryption	2.1129	1.9585	2.2696	0.1561	0.0371
logic	qubit	2.0029	1.8417	2.1603	0.4504	0.0305
qubit	logic	2.0005	1.8366	2.1706	0.1357	0.0305
security	inform	1.9195	1.7500	2.0927	0.3184	0.0298
inform	security	1.9175	1.7436	2.0918	0.1800	0.0298
encryption	network	1.9101	1.6762	2.1574	0.2445	0.0180
network	encryption	1.9085	1.6822	2.1442	0.1412	0.0180

.

Similar to the results of confidence in Table 5, Table 6 presents the mean of the lift measure and the lower and upper limits of the 95% credible interval. We found that the lift values for rules, $\left(encryption\to security\right)$ and $\left(security\to encryption\right)$ were identical, with a mean of 5.9397. This result was similar to that in Table 4. In addition, Table 6 provided the lower and upper values of the credible interval, 5.5412 and 6.3394, as well as the mean lift. In other words, the keywords encryption and security have a highly complementary relationship, with lift values ranging from a minimum of 5.5412 to a maximum of 6.3394 at the 95% confidence level, thereby enabling efficient decision-making. Using the results in Table 5, we constructed the keyword diagram shown in Figure 5.

From the results of Figure 5, we verified that all keywords influence the keywords quantum and computing. Also, keyword computing affects keyword quantum. All arrows have a mean and credible interval of the confidence measure. For example, the confidence value of association rule $\left(computing\to quantum\right)$ is 0.9401, and its credible interval is the bounds between 0.9347 and 0.9455. Next, we show another keyword diagram by lift measure in Figure 6.

From the results in Figure 6, we can see that there are four keyword components for quantum computing. The smallest component is the rule consisting of two keywords (logic and qubit), with a lift value of 2.0029, and the lower and upper bounds of the credible interval from 1.8417 to 2.1603, respectively. In this paper, we used the R data language and its packages to perform our experiments [50,51].

5. Discussion and Implications

5.1. Theoretical Implications

The experimental results of this study provide several important insights into both the theoretical development of text mining methodologies and their practical applications in real-world contexts. In this section, we discuss the implications of our proposed BPM method, highlighting how it differs from existing approaches and how it contributes to the field of keyword data analysis. This study makes a methodological contribution by extending the classical framework of ARM with Bayesian inference. While ARM has been widely used to extract frequent co-occurrence patterns in document–keyword matrices [35,36,37], it is limited in that it provides only single-value measures of support, confidence, and lift. Such point estimates are particularly vulnerable to bias and instability in sparse and zero-inflated datasets, where the majority of matrix entries are zero [3,20]. By contrast, BPM introduces a probabilistic framework in which these measures are derived from posterior distributions, enabling the estimation of both mean values and credible intervals. This extension allows analysts to incorporate uncertainty directly into decision-making, thus reducing the likelihood of biased interpretations. To our knowledge, this is one of the first attempts to explicitly integrate Bayesian credible intervals into rule-based keyword analysis. In this respect, BPM not only strengthens the theoretical underpinnings of association rule mining but also bridges the gap between statistical zero-inflated modeling [16,18,21] and text mining approaches.

5.2. Practical Implications

From a practical standpoint, BPM provides an effective tool for analyzing sparse keyword datasets across a variety of application domains. In our case study of 9436 quantum computing patent documents collected from KIPRIS and USPTO, BPM revealed reliable associations among 175 extracted keywords. These results can inform technology forecasting, competitive intelligence, and strategic planning by identifying stable relationships among emerging technologies. Unlike embedding-based models (e.g., Word2Vec, BERT) that require large-scale corpora and heavy computation [10,34], BPM can be applied effectively in situations where datasets are small, domain-specific, or highly sparse. Moreover, BPM does not require training large neural architectures, which makes it more accessible to practitioners in fields such as intellectual property management, R&D strategy, and policymaking. By providing credible intervals for association measures, BPM also enhances interpretability, allowing decision-makers to gauge the robustness of results before acting on them.

5.3. Differentiation from Existing Work

This research also differs from existing studies in important ways. Traditional frequency-based methods such as TF–IDF [25,27] or co-word analysis capture keyword salience but do not quantify the uncertainty associated with sparsity. Recent advances using semantic embeddings or LLMs [10,34] provide richer representations of meaning but often fail to address the structural sparsity of document–keyword matrices. Furthermore, prior zero-inflated modeling research has been primarily applied to regression analysis or biomedical count data [16,18,21], rather than to association rules in text mining. By directly embedding Bayesian inference into ARM, our BPM approach introduces a unique mechanism for mitigating decision bias under sparsity. This methodological innovation positions BPM as a complementary tool that can coexist with semantic and embedding-based methods. In future work, BPM could be integrated with semantic embeddings to leverage both probabilistic inference and semantic representation, thereby enhancing the reliability and applicability of keyword-based text mining across diverse domains.

In this study, we focused primarily on single-word keywords in constructing the document–keyword matrix. The motivation for this choice is that our goal is not to perform topic modeling or semantic phrase extraction, but to evaluate associative relationships between items (keywords) using confidence and lift measures. Nevertheless, the proposed BPM framework is not restricted to single terms. Since n-grams such as bigrams and trigrams (e.g., quantum computing, quantum entanglement, quantum cryptography) can also be represented as items in the transaction–item matrix, our method can be extended to incorporate them. Future research will consider this extension to enhance the discriminatory power of the analysis.

Although the extracted rules were ranked quantitatively according to confidence and lift measures (Table 5 and Table 6), this study did not incorporate external expert validation or semantic comparison for evaluating the relevance of the extracted rules. The purpose of our work was to introduce a probabilistic framework that quantifies uncertainty in rule strength through Bayesian credible intervals, providing an internal measure of reliability rather than an external relevance assessment. Nevertheless, integrating expert judgment or external validation, for example, comparing rule patterns with domain knowledge or large language model outputs, represents an important direction for future research. This combination of statistical and semantic validation could further enhance the interpretability and applicability of BPM.

6. Conclusions

In this paper, we proposed BPM as a novel approach for analyzing sparse and zero-inflated keyword data. Unlike traditional ARM, which provides only point estimates of support, confidence, and lift, BPM incorporates Bayesian inference to estimate both the mean values and credible intervals of these measures. This dual estimation enables more robust and unbiased decision-making in the presence of sparsity, which is a critical limitation of conventional keyword analysis methods. To verify the effectiveness of our approach, we applied BPM to a dataset of 9436 patent documents related to quantum computing collected from KIPRIS and USPTO over a ten-year period (2015–2025). From these documents, 175 representative keywords were extracted after preprocessing, and a highly sparse document–keyword matrix was constructed. Our experimental results showed that BPM can provide interpretable and stable associations between keywords, with credible intervals that reduce the risk of biased interpretation under zero-inflated conditions.

This study contributes to the literature in three ways: (i) it introduces a Bayesian extension of ARM that addresses the zero-inflated sparsity problem in keyword data, (ii) it demonstrates the empirical utility of BPM through a large-scale patent analysis in the field of quantum computing, and (iii) it highlights the theoretical and practical implications of incorporating uncertainty into rule-based keyword analysis. Nevertheless, some limitations remain.

Furthermore, we acknowledge that the empirical validation used ARM as the only baseline, since BPM was developed as a direct Bayesian extension of ARM. However, to strengthen future evaluation, BPM will be compared with embedding-based and LLM-based approaches that provide semantic representations of keyword relationships. Combining semantic embedding with Bayesian inference may enable a more comprehensive framework that captures both semantic proximity and probabilistic uncertainty, thereby enhancing interpretability and predictive capability.

This study focused on improving ARM and therefore used ARM as the primary baseline. While comparisons with state-of-the-art semantic or embedding-based approaches such as TF–IDF, word embeddings, or LLMs were not conducted, future work will explore integrating BPM with such methods to combine probabilistic inference and semantic representation. We also plan to extend BPM to other domains, including social media and biomedical text, to further demonstrate its versatility.

In conclusion, BPM provides a probabilistic framework that enhances the interpretability and reliability of keyword data analysis. By explicitly addressing sparsity and zero-inflated problems, our approach lays a foundation for future studies that seek to combine Bayesian inference with modern text mining techniques to achieve more comprehensive and trustworthy insights.