1. Introduction
Many prior studies in volumetric dataset analysis and rendering have focused on performance-related issues, especially computation time and analysis/rendering quality (e.g., [
1]). Particular items that have been considered in such studies have included factors such as data staging, rendering construction strategies, salient feature detection, highlighting, etc. (e.g., [
2,
3,
4,
5]). The work here considers a type of performance issue that has received somewhat less consideration—the energy consumption for computing certain volume features (i.e., descriptors) that have been used in the analyses and renderings of scientific datasets. The descriptors here have particularly been used in the direct volume rendering (DVR) mode of scientific visualisation, especially in ray-cast DVR. The work here goes beyond simply measuring energy consumption; however, the investigations of several strategies for reducing energy consumption for descriptor computation are also reported.
As such, this work can lead to three larger benefits. First, it can aid in finding the environmental impacts of the analysis and rendering of scientific datasets. Second, it can aid in making key pieces of scientific dataset analysis and rendering processes more energy efficient, potentially improving battery life for battery-powered computers performing such tasks. Third, it can aid analysis and rendering to have less demand on the power grid (and, thus, possibly help in lowering greenhouse gas emissions in regions where power generation produces them).
Two descriptors are considered in this paper: gradients and curvatures. These two descriptors are fundamental for a number of volume analysis and rendering approaches, such as in DVR. In particular, in DVR gradients and curvatures are used in determining shadings (e.g., [
6]). One example of such use is DVR that employs opacity-based composition processes utilizing gradient- and/or curvature-based transfer functions coupled with Phong or Phong-like illumination schemes to produce end renderings. Curvature-based descriptors have also been used in point cloud-based studies, for example, in computational fluid simulations [
7]—as well as in range image applications (e.g., [
8]).
There are a number of gradient and curvature computation methods that have been reported in the literature. Some details of such methods are described later, in
Section 2 of this paper. Beyond DVR, there are volume data analysis applications reported for isosurfacing, registration (e.g., [
9]), etc., and classic speed and accuracy studies have been carried out in such domains (with the importance of accuracy receiving increased recent attention, as in [
10]). However, focus here is on them as components that commonly enable DVR end renderings.
This paper is an extended version of work previously presented in a conference paper [
11]. The extensions include many new, additional experimental results, including experiments using 67% more datasets than the prior work as well as new imagery, with these expressed in approximately twice the number of tables.
The remainder of this work is organised as follows. In
Section 2, the background for the direct volume rendering’s employment of the descriptors of interest here, gradients and curvature, is described. Some background about the research community’s prior interests in CPU energy consumption, including some discussion of mechanisms for measuring such consumption, is also discussed there. In
Section 3, approaches for potentially reducing gradient and curvature descriptor computation energy use that were considered for this effort are described.
Section 4 provides details of both the experimental setup employed for this effort and the experiments conducted to comparatively analyse energy usage. The paper concludes in
Section 5.
2. Background
Ray-cast direct volume rendering is one popular way to visualise volumetric data, often in conjunction with gradient-based shading. A number of gradient-based shading ray-cast schemes exist. Some such schemes compute gradients during ray marching while others march over pre-computed gradients to provide suitable rendering rates [
12]. Curvature-based transfer functions are also a popular approach for adding shape-based cues to DVRs [
13]. The use of curvature for shape cues requires the determination of curvature values at each location within the volume, and, as in the case of gradients, these curvatures could be either pre-computed or computed during marching. Consequently, consideration of the energy footprint associated with direct volume rendering requires not just determination of the energy usage during a given renderer’s marching or compositing steps but also consideration of the energy usage of any base descriptor computations (even if not all descriptor computation is performed in real time during marching).
In this study, we focus on gradient and curvature descriptors typically associated with ray-cast direct volume rendering. Specifically, we focus on the energy usage of (1) the commonly used central differencing (and associated higher-order methods) for gradient estimation and (2) two common methods for determining curvature values that have previously been used in conjunction with curvature-based transfer functions for DVR [
13,
14]. This section first briefly describes related studies on energy usage. It then provides background details on the specific gradient estimation and curvature determination methods considered in our studies (reported later).
2.1. CPU Energy-Usage Measurement and Prior Studies Thereof
Recently, Jay et al. [
15] reported that approximately 6% of world power use can be ascribed to digital activity. Their report also noted that this percentage is growing. While the Jay et al. report has likely increased the focus on the energy usage of computing, even prior to their report many works introduced schemes to measure and/or reduce energy usage (often with a focus on CPU energy usage). However, the energy usage of specific software components is typically unexplored and thus unknown [
16], with a few exceptions. One exception is the use of complexity plot visualisations to consider the energy cost of matrix multiplication [
17]. However, to our knowledge no prior works have specifically studied the energy usage associated with the computation of the descriptors used by classic volume dataset visualisation (in particular, gradient estimation and surface curvature determination). Some methods for computing gradients and curvatures have been studied on the bases of their
accuracy and/or run
time (e.g., gradients were considered in [
18]). Unfortunately, such studies provide very limited insight into the energy usage associated with such computation, because prior studies of energy usage have found that energy usage is not always correlated with execution time [
17,
19].
In recent years, the measurement of CPU energy usage has been simplified by the fact that some modern processors (including Sandy Bridge and later Intel CPUs) provide a means to internally measure energy usage. Intel provides this functionality via the Running Average Power Limit (RAPL) circuitry [
20]. The RAPL circuitry estimates the CPU’s energy usage via a model that incorporates hardware counters, leakage, and temperature. The studies of energy usage, presented later in this work, consider the energy usage of a RAPL-capable processor (in conjunction with the Performance API (PAPI) software [
21] (version 6.0.0), which supports RAPL measurements).
Some prior works were able to measure energy usage on Intel processors, even prior to the inclusion of RAPL. For example, Seng et al. [
22] placed 5w resistors inline with the Vcc trace to the processor core and used this setup to measure code energy use on a Pentium 4 CPU. They observed that, with regards to C++ code, some code exhibits energy efficiency improvements when compiler-based loop unrolling is used. However, they also observed that this energy saving does not apply to all C++ code. Later, other work found that using very large loop unrolling factors (>1024) on x86-64 processors may substantially increase energy consumption [
23].
Some prior works have also considered energy usage on non-Intel processors. For example, Vasilakis [
24] has studied instruction level energy usage on ARM Cortex-A7 and Cortex-A15 CPUs. To measure processor energy usage, those studies polled a set of current sensing chips present on the development board used. The studies found that, on such CPUs, identical instructions use less energy when an L1 cache hit occurs compared to when an L1 cache miss occurs. Additionally, they found that, compared to integer instructions, floating point instructions typically use more energy on such CPUs, with division instructions exhibiting especially high energy usage. Further, the studies found that the presence of data dependencies between instructions may result in significantly higher energy usage (compared to otherwise identical instructions without such dependencies).
Some prior works have studied the relative energy efficiencies of different programming languages. One such work is that of Pereira et al. [
25], which reported that C/C++ code tends to be more energy efficient than other languages. (That finding motivated the use of C/C++ for the work here.)
A tabular summary of some of the related, prior work that studied energy-efficient computation is shown in
Table 1. Foci have ranged from the system and high-level language programming to individual machine instructions.
In our own studies concerning the energy efficiency of C/C++ code (which also motivates the work here), we have found that the energy efficiency of such code can sometimes be increased via the use of compiler directives to inline, frequently called functions. We also found that the compiler general optimisation level (e.g., -O1, -O2, or -O3) and arithmetic optimisation settings (e.g., gcc’s -ffast-math option) can also, for some code, influence energy consumption (e.g., some code we examined in preliminary studies exhibited its lowest energy use when compiled with the -O2 or -O3 optimisation levels, combined with -ffast-math).
2.2. Methods for Gradient Estimation
The studies here consider four methods for gradient estimation within volumetric data. One method that is considered is the classic central differencing gradient estimator. For a point
within a volume,
V, where
denotes the value at coordinate location
within the volume, it is computed in one direction within a volume according to
The other directional gradients are computed analogously. In this paper, this gradient computation method is denoted as central.
Another method that is considered estimates the gradient using the differences between adjacent voxels, computed in one direction at
according to
The other directional gradients are computed analogously. In this paper, this gradient computation method is denoted as inter.
Also considered are two variations using third-order polynomials (one centred on either side of the voxel). The first variant is computed is one direction at
according to
The second variant is computed in the same direction and location according to
The other directional gradients are computed analogously. In this paper, the first variant is denoted as 3order_a and the second as 3order_b.
Finally, a method that uses fourth-order polynomials is considered. It computes the gradient in one direction at
according to
The other directional gradients are computed analogously. In this paper, this gradient computation method is denoted as 4order.
2.3. Methods for Surface Curvature Determination
The studies here consider two methods for determining surface curvature in volumetric data. Both of these methods determine curvature using a two-step process. In the first step, all necessary derivatives (i.e., first, second, and mixed partial derivatives) are estimated at each point within the volume. In the second step, these estimated derivatives are used, in conjunction with a standard surface curvature formulation (i.e., the one presented in [
13]), to compute the two principal component curvature values at each point within the volume.
The two methods considered differ in how they estimate the derivatives.
OP, which is the first method, determines surface curvature using derivatives estimated via convolutions with kernels sampled from specially constructed orthogonal polynomials [
14]. This
OP has one parameter: the kernel size,
N. In general, smaller
N values allow for better localisation, while larger kernels are more robust to noise. In our studies here, we follow the guidance of a prior report’s findings that suggest a value of
suitably balances these factors [
14].
TE, which is the second method, determines surface curvature using derivatives estimated via convolutions with kernels constructed from the Taylor expansion [
13]. This method has two parameters: the continuity and accuracy properties of the kernels. In our studies here, we, as with the
OP method, follow a prior report’s recommendations on parameter value selection and use kernels with
continuity and fourth-order accuracy [
14].
3. Energy Optimisation Approaches
Our energy optimisation approaches are described in this section. We were inspired to take these approaches by observations made in prior works (i.e., those described in
Section 2.1). Our approaches attempt to reduce energy usage via a variety of strategies, including loop unrolling, mathematics optimisations, general compiler settings, data organisation strategies, etc. First, we describe such strategies for gradient estimation. Then, we describe the strategies applied to determining surface curvature in volumetric data.
3.1. Energy-Saving Approaches for Gradient Estimation
For gradient estimation, one focus was on loop overhead reduction because gradient estimation is a loop-driven process that passes over the volumetric dataset elements. Reduction of loop overhead could limit (1) the exercise of loop prediction logic and (2) certain other loop-carried operations, in turn lowering energy consumption, which may underlie prior findings that loop unrolling sometimes yields energy savings. Another focus was arithmetic computation optimisation, since the higher-order polynomial-based gradients involve somewhat intensive floating-point computations in each step of the process. To realise these foci, we devised three potentially energy-saving strategies for gradient estimation.
The first strategy, which focuses on loop overhead, is to unroll the loops that perform the passes over the volume for each gradient estimator. Here, such unrolling was performed via gcc/g++’s -funroll-all-loops option. We denote this strategy as Unroll.
The second strategy explores reducing some floating-point computation overhead. It involves avoiding checks for certain floating point computation conditions. It was performed here via the -ffast-math compiler option. We denote this strategy as Fast.
The third strategy, which focuses to some extent on both loop and computation overhead, involves using a higher level of compiler optimisation (
-O3) compared to a baseline implementation (e.g.,
-O2). This level of optimisation includes two features in particular that may benefit the descriptor computations: it attempts to reuse some computations, especially memory loads and stores between loop iterations, and it attempts to find and eliminate arithmetic subexpressions [
33]. (Another motivation: some prior work has found this level of compiler optimisation tends to reduce energy usage.) We denote this strategy as
O3.
3.2. Energy-Saving Approaches for Curvature Determination
For curvature determination in volumetric data, we devised six approaches to potentially save energy. They are described here.
Three of the strategies are the strategies also used for gradient estimation. These are the
Unroll,
Fast, and
O3 strategies described in
Section 3.1.
Our fourth strategy aims to organise and stage memory accesses in an efficient manner. It was motivated based on prior findings that an increased L1 cache hit rate may result in energy savings [
24]. Both the
OP and
TE methods utilise convolution to estimate derivatives. Due to the multidimensionality of volumetric data, convolution, which requires accessing neighbouring data points in every axial direction in order to perform the necessary multiplications/additions, often results in an inefficient use of memory as non-contiguous regions of memory are traversed. The strategy works to increase memory efficiency during convolution by carefully computing and storing intermediate convolution terms across the volume, which later allows avoiding large and/or unpredictable strides that may result in a less efficient use of memory. We denote this strategy as
Bespoke.
Specifically, the Bespoke strategy works as follows. First, as a pre-processing step, a list of the unique values in the convolution kernels for the respective curvature method is computed (e.g., for the TE method, a list of all the unique values present in the first and second derivative continuous, fourth-order accurate convolution kernels is manually constructed). We use k to denote this list of unique values in the kernels (of which there are such values, denoted as through ). Next, during run time, variants of the original input volume (denoted as v) are produced, with each of these variants representing the multiplication of each value in v by one of the values in k (requiring extra memory, where is the number of values contained in v) (i.e., one variant volume consists of the original volume with each of its entries scaled by ; another one consists of entries scaling by , etc.). These multiplications proceed sequentially in memory in order to help ensure cache efficiency. Once the scaled volumes are produced, the convolution is completed via summing the relevant entries of these variant volumes.
Our fifth strategy seeks to reduce data dependencies. It is motivated by prior findings that data dependencies within code often result in increased energy usage [
24]. (Moreover, our own studies have found that the increase in energy usage is especially notable when such code contains few additional instructions to be executed between the dependent ones.) To increase the number of instructions available to be executed between dependent instructions, we developed a software pipelined version of the code that computes the final curvature values from the estimated derivatives. We denote this strategy as
Pipeline.
Our sixth strategy seeks to increase data locality by blocking. Increased locality of reference is known to improve cache efficiency, leading to improved computation speed, which motivated us to determine if such increased locality could also reduce energy consumption. It uses a blocked approach to traverse the volume while producing final results. We denote this strategy as Blocking. (Our experiments, presented later, tried various block sizes from up to . To save space, Blocking in conjunction with a specific blocksize, n, will be denoted as Blockingn.)
4. Experimental Setup and Results
In this section, we report on the energy usage of gradient and curvature descriptor computation for a baseline realisation on x86, which is probably the most common CPU environment for most desktop scientific computation. We focus on CPU-based computation here as that is one of the oft-used modes for computing descriptors for the DVRs of sensed volume data (such as CT or MR scans of industrial or patient subjects). We also report experiments that evaluate the energy-saving strategies that were attempted. Lastly, analyses of accuracy and memory effects are presented.
First, we detail the testing setup. Experiments were performed on a computer equipped with an Intel Core i5-8279U processor and 16 GB of RAM (as that matched the one used in some prior energy-usage reports). The operating system used was a minimal install of Ubuntu Server 22.04.1 AMD64. The CPU governor mode was set to “performance” (using the cpufreq-set utility). All experimental code was written in C/C++. Double precision floats were used in all curvature and gradient computations. The code was compiled with gcc/g++ 11.3.0. PAPI was used to measure energy usage (via RAPL). All experiments were run as the root user (to allow access to the energy measurement hardware) on a single core.
We believe that, while the experiments here were performed on the Intel Core i5-8279U CPU, many of the findings are likely applicable to all similar Intel processors.
4.1. Test Conditions and Energy Measurement
To evaluate the energy usage (and savings, if any) associated with each of the approaches, we ran, on several volume datasets, each of the gradient estimation and curvature determination methods using different combinations of the strategies previously described. In total, 8 variants of each gradient estimation method were tested (including a Baseline variant compiled with -O2 and using no other energy optimisation strategies) and 70 variants of each curvature determination method were tested (including a Baseline variant compiled with -O2 and using no other energy optimisation approaches). Relative energy use versus the baselines were then found.
To measure energy, PAPI was used to determine total energy usage (in Joules), , of the RAPL PP0 plus the RAPL DRAM domains during just the curvature determination/gradient estimation steps (i.e., excluding I/O associated with loading the data or writing the results). The RAPL PP0 domain represents the power usage of all the processor cores and excluding the DRAM or GPU. The RAPL DRAM domain represents the power usage of the DRAM. This measurement of PP0 + DRAM thus represents the sum of the CPU and DRAM power usage of each method (n.b., we chose to include the DRAM domain because some of the energy-saving strategies, such as Bespoke, utilise more memory compared to the baseline, and the inclusion of the DRAM domain ensures that the extra memory usage associated with this is accounted for).
To ensure consistent results, each variant was run five times and the trimmed means of the PP0 and DRAM domains were computed, with those two values then summed to give the final energy-usage measurement.
4.2. The Datasets and Visualisation
Our experiments consider three types of volumetric data: Marschner-Lobb (
ML),
Foot, and
Genus3. These datasets were used in prior curvature and gradient studies (e.g., [
14,
18]). ML and Genus3 are synthetic data, while Foot is sensed. Foot is size
. Genus3 is size
. Three different-size ML datasets are considered: ML128 (
), ML256 (
), and ML512 (
). All volumes were stored as double precision floating point data. ML256 was considered with and without Gaussian noise (
). This noise-added version is denoted as ML256n.
A slice image of Foot is shown in
Figure 1a and a DVR using a curvature-based transfer function is shown in
Figure 1b;
Figure 1b demonstrates one visualisation usage involving the descriptors considered here.
4.3. Gradient Estimation
Table 2 and
Table 3 show gradient energy-usage results on
Foot and
Genus3, respectively.
Table 4,
Table 5 and
Table 6 show gradient energy-usage results on
ML128,
ML256, and
ML512, respectively (n.b.,
Table 4,
Table 5 and
Table 6 all represent additional experimentation over our prior work). The first rows in each table present energy-usage outcomes for the baseline computations while other rows show energy-usage change (as a percentage of Baseline) from the use of one of the strategies or combinations of strategies.
Bold values show the variant with the lowest energy usage. Cell colouring on a red–green scale indicates the degree of improvement.
With the Baseline variant, inter exhibits the lowest energy usage for all analysed datasets. On average, central uses approximately 1.1 times more energy than inter, 3order_a uses approximately 1.26 times more energy than inter, 3order_b uses approximately 1.29 times more energy than inter, and 4order uses approximately 1.54 times more energy than inter.
Here, all of the lowest energy-usage variants make use of the Unroll strategy. The lowest energy variants often make use of multiple strategies (e.g., O3 and Unroll). Alone, Fast typically had a negligible effect.
For all of the gradient methods, the combination of the Fast and Unroll strategies typically exhibits the lowest (or among the lowest) energy usage. Thus, it appears the Fast and Unroll strategies in combination may be a suitable choice for practitioners aiming to reduce energy consumption associated with common gradient estimation strategies.
4.4. Curvature Determination Results
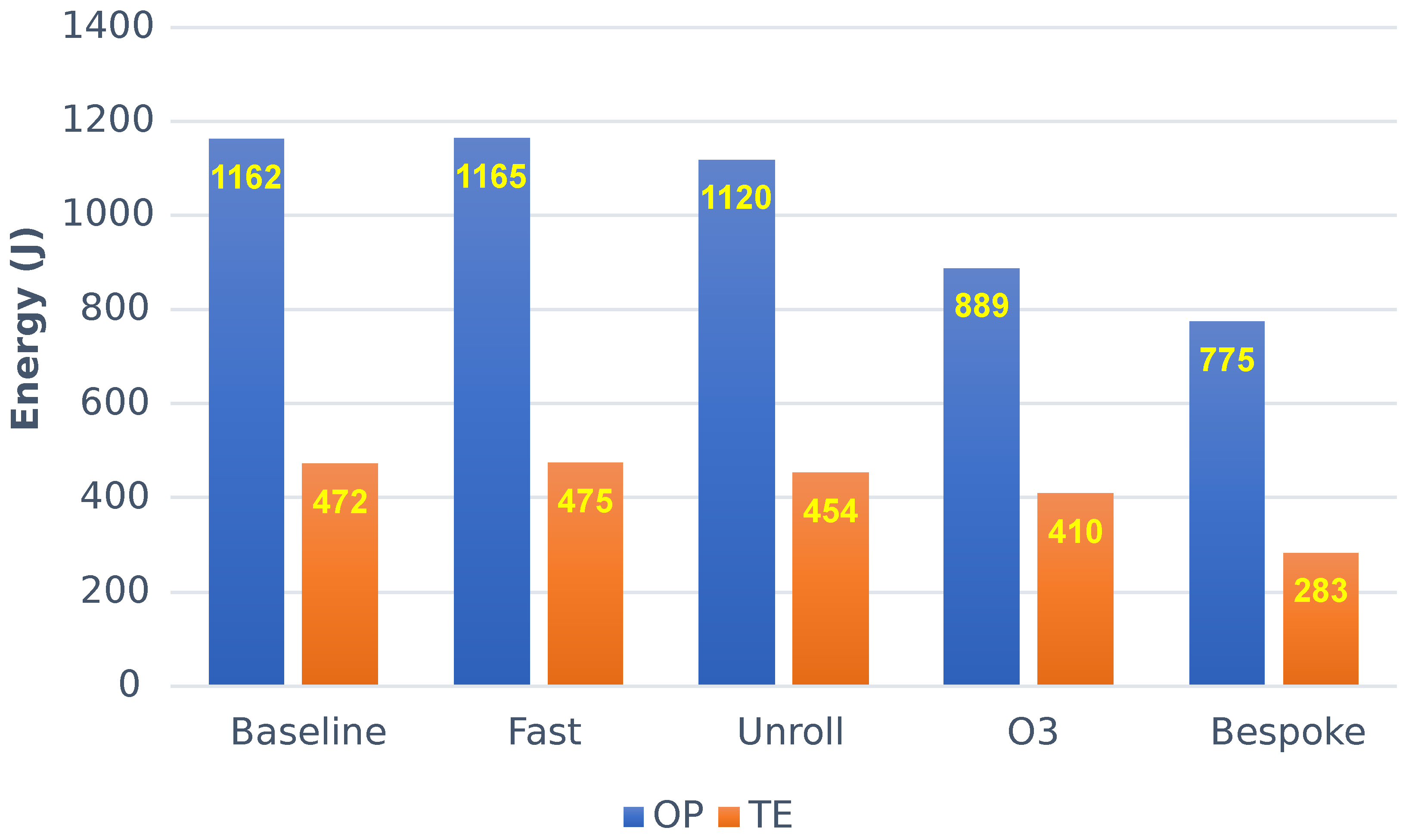
Table 7 shows a selection of curvature determination energy-usage results on the
ML512 dataset for isolated approaches vs. the baseline. Its first row presents the energy-usage outcomes for the baseline computations for the curvature methods. The table again uses the energy differences and colour coding used earlier. These isolated approach results are visualised in
Figure 2. The energy usage (in J) of each isolated approach is shown, overlaid on each bar in the figure.
Table 8 and
Table 9 show energy-usage results for other combinations of approaches (n.b.,
Table 7,
Table 8 and
Table 9 and
Figure 2 all represent additional experimentation over our prior work). Since the
Bespoke approach is the best approach in isolation, the remainder of the reported results will analyse
Bespoke in conjunction with the other approaches. (We actually tested other combinations as well, but we do not report them here, as they are inferior to the combinations including
Bespoke.)
Table 8 shows a selection of such energy results on the ML512 dataset for blocking-based approaches in conjunction with the single best isolated approach,
Bespoke.
Table 9 shows a variety of other combinations of approaches. The best results were the combinations
Bespoke,
O3,
Unroll,
Fast in the case of
OP and
Bespoke,
O3,
Fast in the case of
TE. These same variants also exhibited the lowest energy usage on the
volumes (not shown here).
It is not always the case that the most energy-efficient realisation is the fastest realisation. For the
TE results in
Table 7,
Table 8 and
Table 9, for example, the least energy-consuming combination is
Bespoke, O3, Fast. However, the fastest execution was achieved by the combination of
Bespoke, O3, Unroll, Fast.
Table 10 shows a selection of execution times on the
ML256 dataset.
ML256n (not shown here) exhibits nearly identical execution times.
Table 11 shows a selection of energy-usage results on the
Genus3 dataset. Here, the best combination of approaches is
Bespoke, O3, Fast for
TE and
Bespoke, Blocking32, O3, Unroll, Fast for
OP.
For all datasets, the use of the
Bespoke strategy alone produces large energy savings. Using the
O3 strategy alone also produces notable energy savings. Combining
Bespoke with
O3 typically results in further energy savings, although sometimes only if also combined with at least one other strategy. For example, the combination of one or, especially, both with
Fast typically results in additional energy savings.
Unroll in isolation offers a modest improvement, but it was less effective in combination with other strategies. The
Bespoke strategy commonly uses a little more energy in its memory-related processing but substantially less energy for other parts of processing, according to reports gathered from RAPL.
Table 12 shows selected energy uses (broken out by PP0 and DRAM) on the
ML256 dataset. These results reveal that the
Bespoke strategy very effectively trades off higher memory usage for overall power reduction. For example, in the case of
Bespoke, O3 for
OP on the
ML256 dataset, 2.42 J more DRAM energy is used, but an energy saving of 42.92 J is achieved in PP0 (compared to
O3 alone).
Use of Blocking and Pipeline often did not produce substantial energy savings. Changes in block size had little impact in the performance of the Blocking approach.
4.5. Accuracy Considerations
For some codes, the use of certain instruction optimisation settings, in particular mathematics-based optimisation settings, can affect the accuracy of results. To test if our strategies incurred such effects, we compared the outputs of the different methods on the ML256 dataset. In summary, our finding is that the optimisations used in our strategies appear to not meaningfully degrade accuracy for gradients or curvatures, as discussed next.
For the gradient determination on the ML256 dataset, for all but one of the gradient methods the most energy-efficient realisation had no difference in gradient values versus the baseline realisation. For the one that did differ, the difference was approximately .
For OP-based curvature determination on the ML256 dataset, the most energy-efficient realisation had a maximal difference in curvature values of versus the baseline realisation. (That is, no single curvature value from energy-optimal OP differed by more than from the corresponding value in the baseline result.) For TE’s curvatures for ML256, the most energy-efficient realisation’s values never had a difference (versus the baseline) of more than .
Based on these results on the ML256 dataset, we expect similar results in the general case; the use of the energy optimisation approaches here can enable achievement of more power-optimal volume data analysis and visualisation apparently without a meaningful impact on accuracy.
4.6. Analyses
The Bespoke strategy produced, relative to the other strategies, the most significant energy savings. To determine some of the underlying causes of this occurrence, we explored aspects of its behaviour via Intel’s VTune tool. The report and analysis using VTune here is based on a run of the OP curvature determination on the ML256 dataset.
In particular, we found that the Bespoke strategy was able to utilise the memory access capability of the system more effectively. On this CPU, the maximum memory bandwidth is 20 GB/s. OP using Bespoke and O3 together utilised a maximal bandwidth of 14 GB/s, whereas OP using O3 alone utilised a maximal bandwidth of just 6.7 GB/s. Additionally, for these scenarios the average bandwidths utilised, respectively, were 7.96 GB/s and 1.69 GB/s.
Additionally, OP using Bespoke and O3 together incurred approximately a factor-of-four improvement in the number of loads and stores incurred by OP using O3 alone. Specifically, OP using Bespoke and O3 incurred loads and stores. OP with O3 incurred loads and stores.
Thus, the Bespoke strategy has a major benefit of effectively organising and staging the data to allow much more optimal use of the memory channel, decreasing both time and energy consumption.
5. Conclusions and Future Work
This study has considered the energy usage for computing two descriptors, gradients and curvatures, that have been widely utilised in volume data analysis and rendering (e.g., in DVR). Several approaches for potentially reducing energy usage in those computations were also described and explored. Some approaches, including the Bespoke approach, which aims to decrease energy usage by organising memory accesses associated with convolution in a cache-efficient manner, along with the Pipeline and Blocking approaches, are applicable only to the curvature determination process. Of these, the Bespoke approach was among the most successful and was employed by all of the most energy-efficient curvature determination variants. The O3, Unroll, and Fast approaches are applicable to both curvature determination and gradient estimation. Of these, the O3 and Fast approaches were among the most successful when applied to curvature determination, with all of the most energy-efficient curvature determination variants employing both O3 and Fast. In the case of gradient estimation, the Fast and Unroll strategies in combination may be a suitable general purpose choice.
In gradient descriptor computation, an approximately 20% energy saving was achieved by the approaches investigated here. In curvature descriptor computation, approximately a factor-of-two energy saving was achieved by the approaches. Given that the work was carried out in C/C++, already an energy-efficient environment [
25], these results are especially significant. In summary, the findings here could be employed in the form of energy-efficient routines called by volume analysis or rendering tasks, providing widespread general benefit.
As the current work has focused on computation on CPUs, one unexplored area that could be considered in future work is the energy consumption of gradient and curvature descriptor computation on GPUs. For example, computation on Nvidia GPUs is one suitable focus, as recent work has reported [
15] that the NVidia Management Library (NVML) API allows quite accurate power consumption determination (i.e., within 5% of actual usage), at least on Fermi-class and newer GPUs (n.b., power consumption determination using the built-in power sensor on earlier Nvidia GPUs, such as Tesla-class GPUs, may be less accurate, according to a report by Burtscher et al. [
34]).