Abstract
This paper introduces a novel approach to the creation and application of confusion matrices for error pattern discovery in spellchecking for the Croatian language. The experimental dataset has been derived from a corpus of mistyped words and user corrections collected since 2008 using the Croatian spellchecker available at ispravi.me. The important role of confusion matrices in enhancing the precision of spellcheckers, particularly within the diverse linguistic context of the Croatian language, is investigated. Common causes of spelling errors, emphasizing the challenges posed by diacritic usage, have been identified and analyzed. This research contributes to the advancement of spellchecking technologies and provides a more comprehensive understanding of linguistic details, particularly in languages with diacritic-rich orthographies, like Croatian. The presented user-data-driven approach demonstrates the potential for custom spellchecking solutions, especially considering the ever-changing dynamics of language use in digital communication.
1. Introduction
Throughout written history, spelling errors have been influenced by various factors. Back in the time when people used to handwrite on paper, mistyping was result of their poor familiarity with spelling rules and orthography standards or a sign of some medical symptoms like dysgraphia. With the widespread acceptance of printing presses and typewriters, much later computers with their keyboards as standard input devices, and nowadays smartphones with virtual keyboards, a whole new set of problems opened up related to the fact that people are not perfect and simply make mistakes while using a device. In the short history of spellchecking from the late 1950s to 2020, Mitton [1] described the development of spellcheckers from dictionary lookup, affix stripping, correction, confusion sets, and edit distance to the use of gigantic databases. A comprehensive survey by Hladek et al. [2] summarizes the theoretical framework and provides an overview of the approaches developed from 1991 to 2019 related to the field of automatic spelling error detection, followed by spelling error correction.
Apart from mistyping, a common cause of spelling errors is poor knowledge of spelling rules, which applies to speakers of almost all languages. However, some languages use letters with diacritical marks (also called “diacritics”) or accents that are written by users as simpler variants that are easily accessible on the virtual keyboard on the screen or do not require multiple keystrokes.
Within natural language processing, the use of confusion matrices in spellchecking plays an important role in identifying and correcting misspelled words, improving the accuracy of language processing. Confusion matrices are particularly valuable tools in the context of spellchecking, as they provide a systematic way to analyze the performance of spellchecking algorithms by identifying the frequency of correct and incorrect correction candidates. In the field of natural language processing, confusion matrices are generally used for the descriptive statistical analysis and the visualization of words, phonemes, or tokens, but they can also be used as a starting point for exploratory analysis. In this regard, each row and each column represent a language token corpus, thereby identifying the frequency of their mutual occurrence.
The paper discusses the creation and possible application of a confusion matrix for the Croatian language derived from a dataset of mistyped words and their corrections provided by users while using the Croatian spellchecker available at https://ispravi.me/ (accessed on 31 December 2023) since 2003. The important role of confusion matrices in improving the precision of spellchecker tools, especially in the diverse linguistic context of the Croatian language, is investigated. Common causes of spelling errors are identified and analyzed, highlighting the challenges posed by the use of diacritics. The aim of the paper is to contribute to the further development of spellchecking technologies and enable a more comprehensive understanding of linguistic details, especially in languages with diacritical orthography such as Croatian.
The remainder of this paper is organized as follows: Section 2 provides insight into related research in the field of spellchecking, with particular emphasis on the use of confusion matrices, as well as on spellchecking in the Croatian language. Section 3 describes in more detail the spellchecking service that provided the data for the research and describes the language and the types of errors that users make. Section 4 describes the process of matrix creation, and Section 5 discusses each of the created matrices and highlights the implications of the obtained data. Section 6 concludes the paper and provides further insight into future work that can be based on this user data-driven confusion matrix.
2. Related Work
This section provides an exploration of the significance of confusion matrices in spellchecking, examines language technologies within the Slavic language family, and sheds light onto the language technologies and tools for the Croatian language.
2.1. Confusion Matrix
The confusion matrix is a crucial tool in natural language processing, particularly in spellchecking, as it helps in identifying and correcting misspelled words. In general, a confusion matrix lists the number of times one thing was confused with another [3]. The study of confusion matrices has been widely explored in the field of computer science, linguistics, natural language processing (NLP), and speech recognition.
In the context of NLP, Almutir and Nadeem [4] use confusion matrices to evaluate the performance of named-entity recognition systems by analyzing the discrepancies between predicted and actual entity labels. Pienaar and Snyman use them for the identification of eleven official South African languages [5]. Abandah et al. [6] use confusion matrix to correct spelling mistakes in Arabic with insufficient datasets to train the correction models.
In one study [7], the authors present a new approach to Chinese spellchecking (CSC) that prioritizes contextual similarity over traditional character similarity. The authors challenge the conventional methods of CSC; they introduce a curriculum learning framework to train models in a human-like, progressive manner that is adaptable for different CSC models. They conducted extensive experiments on the SIGHAN datasets and demonstrated superior performance over previous state-of-the-art methods, proving that focusing on contextual information significantly improves the accuracy and efficiency of spellchecking in Chinese. This research not only advances CSC but also points to a broader shift towards contextual understanding in natural language processing. In [8], the authors introduce the “Fintech Key-Phrase” dataset, a significant contribution to natural language processing in the Chinese financial high-technology sector. This dataset, comprising over 12,000 human-annotated key phrases from Chinese management discussions and analyses, addresses the lack of data resources in this domain. Key features include domain-specific content, high-quality annotations, and comprehensive evaluations, including consistency and quality assessments. The utility of the dataset is demonstrated through its integration with advanced information retrieval systems and ChatGPT for text augmentation, showing notable improvements in key-phrase extraction accuracy and coverage. Furthermore, in [9], the author compares the grammatical and semantic properties of effective constructions in English and Uzbek. The study investigates resultative structures in English, such as participles and complex objects, and compares them to similar linguistic constructs in Uzbek, with a particular emphasis on complex participles and specific suffixes that indicate resultative meanings. The study explores the differences and similarities in how these two languages use lexical, grammatical, and semantic elements to convey actions and outcomes, revealing the nuanced interaction of language units in expressing resultative meanings.
In the domain of speech recognition, Phatak et al. [10] employ confusion matrices to assess the accuracy of speech recognition systems and to identify patterns of misrecognition, aiding in the refinement of acoustic and language models. Xu et al. [11] discuss the generation of phonetic confusion matrices to enhance speech recognition performance, demonstrating the wide applicability of confusion matrices in language-related tasks.
Confusion matrices are integral to spellchecking systems, enabling the analysis of spelling correction accuracy and the identification of common spelling errors. Kernighan et al. [12] use confusion matrices to propose and sort a list of candidate corrections for misspelled words in one of the early spellcheckers named “correct,” which is based on the idea of a noisy channel. They are also given considerable mention in Appendix B, of an online version of a textbook on speech and language processing by Jurafski and Martin [3].
2.2. Slavic Languages
The causes of spelling errors for the English language have been studied extensively [2]. Factors such as language interference, lack of awareness of spelling rules, and even the dissimilarity between writing systems of different languages have been highlighted as a significant cause of spelling errors. Furthermore, the use of digital tools, such as spelling software, has been explored in addressing spelling errors [13,14]. However, Slavic languages, particularly Croatian, have not been studied to such an extent [15].
The history of spellchecking in Slavic languages is deeply intertwined with the linguistic diversity and unique characteristics of these languages. The Slavic languages, traditionally divided into three distinct branches—West Slavic, South Slavic, and East Slavic [16]—have evolved over centuries, each with its own orthographic and phonetic peculiarities. The study by Golubovic and Gooskens [17] provides valuable insights into the linguistic distinctions within the Slavic language family.
The development of language technologies for Slavic languages has been a subject of interest, as highlighted by the work of Nouza et al. [18], which addresses the challenges posed by Slavic languages in automatic speech recognition (ASR) systems. The unique orthographic and morphosyntactic features of pre-modern Slavic varieties have also been the focus of research, as demonstrated by the work of Pedrazzini and Eckhoff [19], who developed a scalable Early Slavic dependency parser trained on modern language data to resemble the orthography and morphosyntax of pre-modern varieties. The linguistic diversity and historical evolution of Slavic languages have also been studied in the context of language contact and borrowing, as evidenced by the research of Adamou et al. [20], which explores borrowing and contact intensity in Slavic minority languages.
Substantial research related to n-gram systems and spellchecking has been conducted on language technologies for individual languages. For the Polish language, n-gram models were presented by Banasiak et al. [21] and Ziółko et al. [22]. Rozovskaya developed a minimally supervised model for spelling correction and evaluated its performance on datasets annotated for spelling errors in Russian [23]. Sorokin presented an algorithm for the automatic correction of spelling errors at the sentence level for Russian [24]; Richter et al. presented a statistical text corrector tool, Korektor [25], for the Czech language; and Ramasamy et al. presented its improvements [26]. Hladek et al. [27] described a method to automatically propose and choose a spelling correction in Slovak. However, some of the problems are common to the whole language group.
The restoration of diacritic characters in Slavic languages is a significant area of research, aiming to accurately reconstruct the original orthographic forms of words. This process is particularly crucial in languages with diacritics, such as Czech, Croatian, and Polish. The restoration of diacritics involves the identification and insertion of diacritic marks to ensure the correct pronunciation and semantic interpretation of words. Research in this area encompasses various techniques, including character-based machine learning models [28]. Náplava et al. [29] propose a new architecture for diacritics restoration based on contextualized embeddings, particularly BERT, and evaluate it using 12 languages with diacritics, including Croatian. The restoration of diacritics is essential for accurate language processing and understanding in Slavic languages, and ongoing research continues to advance the development of effective diacritic restoration methods.
The research in this area has contributed to a deeper understanding of the orthographic, phonetic, and morphosyntactic features of Slavic languages, paving the way for the development of language technologies tailored to the specific needs of these languages.
2.3. Croatian Language
The Croatian language, belonging to the South Slavic branch, has a distinct orthographic system, which has influenced the development of spellchecking tools.
An innovative approach to large-scale n-gram system creation applied to the Croatian language is presented in [30]. This study highlights the efforts to develop language technologies specific to Croatian. Additionally, Šoić and Vuković [31] utilize a Croatian language network for building a solution capable of generating spoken notifications in Croatian, demonstrating the practical applications of language technologies in the Croatian context. Šantić et al. [32] describe a system for automatic diacritic restoration in Croatian texts, which combines dictionary lookup and statistical language modeling, achieving high levels of accuracy.
The advantages of online spellchecking specifically in the Croatian context, emphasizing the relevance and impact of spellchecking tools for the Croatian language, are described in [33]. This highlights the growing significance of spellchecking technologies in addressing linguistic challenges unique to Croatian.
The history of spellchecking in the Croatian language reflects concerted efforts to develop language technologies tailored to the unique linguistic characteristics of Croatian. The research in this area has contributed to the advancement of spellchecking tools and language technologies specific to Croatian, addressing the linguistic, sociocultural, and technological aspects of spellchecking in the Croatian language.
3. The Croatian Language and Common Spelling Errors
Croatia is home to the population of 4 million and is situated in Southeast Europe, on the east coast of the Adriatic Sea up to the Pannonian basin. The official language is Croatian, which belongs to the group of Slavic languages and is spoken by approximately 8 million people. It is used by Croats in Croatia and in Bosnia and Herzegovina (one of three official languages), and also in neighboring countries (in some of them as a recognized minority language). It is based on the Latin writing system, and its orthography is mostly phonetical.
Figure 1 shows a Croatian QWERTZ keyboard layout. The alphabet consists of 30 letters, 5 of them vowels. It is characterized by the usage of five letters with diacritics:

Figure 1.
Standard Croatian keyboard layout [34].
- “č”, pronounced like “ch” in the English word “checker”;
- “ć”, pronounced like “tj” in the Dutch word “Aantjes”;
- “đ”, pronounced like “Gi” in the Italian word “Giulia”;
- “š”, pronounced like “sh” in the English word “shop”;
- “ž”, pronounce like “J” in the Portuguese word “Joaquim”.
Three digraphs are treated as individual letters:
- “dž”, pronounced like “j” in the English word “job”;
- “nj”, pronounced like “ñ” in the Spanish word “señora”;
- “lj”, pronounced like “ll” in the Spanish word “Castilla”.
The sound system uses two diphthongs—short and long “ě”, which are written down as “je” and “ije”. Foreign names borrow their original orthography, effectively extending the number of letters used in writing. Names from non-Latin scripts are transliterated according to Croatian rules, but in practice, often English transliteration is used. Abbreviations are written in capital letters.
The five letters with diacritics and two diphthongs are a great source of confusion for a large part of population. The three basic groups of spelling mistakes are:
- Orthography- or grammar-related errors;
- The substitution of diacritics with non-diacritics;
- Random mistyping.
3.1. Orthography- and Grammar-Related Errors
Croatian is a highly inflected language: verbs conjugate for gender, number, and tense; pronouns, nouns, adjectives, and certain numerals decline in seven cases. Nouns come in masculine, feminine, and neutral genders, and the grammatical gender of a noun affects the morphology of the surrounding adjectives, pronouns, and verbs. The abundance of orthography rules in Croatian can contribute to frequent misspellings, even among proficient speakers.
The process of orthography standardization lasted for many years, and the final orthography standard is available from the Institute for Croatian Language and Linguistics [35], but several other orthography handbooks are still in use. Orthography-related misspellings can be divided into several common types, described in the following subsections.
3.1.1. Diphthongs
In standard Croatian, the common Slavic vowel “ě” (/ie/) is reproduced as a diphthong, which is written either as “ije” or “je”, but the proper variant depends on the word:
- Long /ie/—as in “tijesto” [dough] or “vijest” [news];
- Short /ie/—as in “mjesto” [place] or “vjera” [faith].
Usually, writing one instead of the other results in an easily identifiable non-word spelling error, but sometimes, adding or removing the “i” can be ambiguous. One of the notorious errors is substituting “slijedeći” for “sljedeći”—the former is used in the phrase “slijedeći zeca, završio sam u šumi” [by following the rabbit, I ended up in the forest], and the other can be used in the phrase “sljedeći dan” [next day] or “sljedeći put” [next time]. Similar examples are “svijetleći” [while one was lighting] and “svjetleći” [the one which emits light] or “zahtjeva” [genitive of the plural of noun request] and “zahtijeva” [verb (s/he) requests] [13].
3.1.2. Diacritic Letters
Another type of common orthography error is confusing diacritic letters:
- “č” for “ć”, e.g., “mač” [sward] becomes “mać”, “ručak” [lunch] becomes “rućak”, “četvrtak” [Thursday] becomes “ćetvrtak”;
- “ć” for “č”, e.g., “ćup” [cup] becomes “čup”, “maćeha” [stepmother] becomes “mačeha”.
As in the previous case, substitution usually leads to a non-word error, but sometimes, amusing real-word errors occur: “spavačica” [sleeping woman] vs. “spavaćica” [sleeping dress], “kuče” [small dog] vs. “kuće” [houses], “vraćati” [to return] vs. “vračati” [to cast a spell]. All those words are valid words with common usage, and detecting them as errors presents a contextual challenge.
3.1.3. Preposition “s/sa”
The third common error involves the preposition “s” or “sa” [with]. “Sa” as a preposition is used when the following word starts with “s”, “z”, “š”, “ž”, “ks”, or “ps”; in all other cases, “s” is grammatically correct. Substituting one for the other is common, but the error is trivial to detect and correct.
3.1.4. Negation of Verbs
Another common error is writing negations of verbs. They are typically formed by placing the particle “ne” [not] before the verb (e.g., “ne znam” [I do not know], “ne mogu” [I cannot]), with exceptions “neću” [I will not], “nemoj” [do not], “nemam” [I do not have], and “nedostajati” [to miss]. A common error is omitting the space after the particle “ne”, where instead of two words, one error word is formed (e.g., “neznam”, “nemogu”, etc.).
3.1.5. Future Tense
In Croatian, the future tense is formed by using the future tense of the auxiliary verb “biti” [to be], which may be “će/ćeš/ćemo/ćete” [will], depending on the personal pronouns used. The structure is similar to the English future tense, where “will” is combined with the infinitive form of the verb (e.g., “ja ću pisati” [I will write]). If the personal pronoun is omitted, the proper form of future tense inverts the position of the verb and the auxiliary verb “ću/ćeš/ćemo/ćete” (e.g., “pisat ću”). However, many people mistakenly write the main verb in the infinitive form, with the letter “i” at the end (e.g., “pisati ću”).
3.1.6. Assimilation of Consonants
The assimilation of consonants is a phonological phenomenon that occurs when adjacent consonants influence each other in terms of their pronunciation:
- Assimilation by voicing, where the voicing quality of one consonant is influenced by the voicing of a neighboring consonant that immediately follows it (e.g., “vrabac” and “vrapca” [sparrow in nominative and genitive forms], “težak” and “teška” [heavy (male and female)], “svat” and “svadba” [wedding guest and wedding]);
- Assimilation by place of articulation, which involves the modification of a consonant’s place of articulation to match that of a nearby consonant (e.g., “list” and “lišće” [leaf, singular vs. plural], “grozd” and “grožđe” [grape, singular vs. plural]).
These assimilatory processes contribute to the overall fluidity and ease of pronunciation in connected speech, making language production more efficient and natural. However, the assimilation of consonants can also lead to spelling errors with users not familiar with orthography rules (e.g., writing “vrabca” instead of “vrapca”).
3.2. Swapping Letters with Diacritical Marks
The second group of spelling errors stems from the fact that letters with diacritics traditionally were often substituted with their simpler variants without diacritics, especially back in the old days when keyboards and character sets did not provide support for them (e.g., ASCII character set). That substitution is still present in instant messaging and on smartphone chat apps: people write “macka” instead of “mačka” [cat], “cvjetic” instead of “cvjetić” [small flower], “skola” instead of “škola” [school], “zena” instead of “žena” [woman]. The letter “đ” is sometimes written as “d”, but may also be written as “dj”, although “dj” is also a legitimate digraph in Croatian—“đubre” [trash] can often be written as “dubre” or “djubre”, but the word “djevojka” [girl] is a correct word that starts with “dj” and cannot be substituted with “đevojka” because that is not a valid Croatian word (but is a valid Montenegrin word).
Furthermore, words with any of the letters “c”, “č”, or “ć” in the same position are regular words (e.g., “placa”—genitive of colloquial for market; “plača”—genitive for the noun cry; “plaća”—salary or [s/he] pays).
In most cases, using letters without diacritics is a deliberate choice the user makes to speed up typing and by itself it does not constitute a true spelling error. Words written that way are understandable from the surrounding context, even if writing in such a way introduces real-word “errors”, like when “što” [what] becomes “sto” [a hundred], “žemlja” [sort of bun] becomes “zemlja” [ground] and so on. Surely, converting words back to diacritics is a big challenge, which requires contextual spellchecking and an n-gram language model. For this task, the employed word databases enable the creation of confusion sets, since the number of such words is not too high (Table 1).

Table 1.
The list of letters in the Croatian language that can be substituted with one another and cause a real-word error, with letter pairs, the number of words from the presented database that have these letters at the same position, and examples of such words.
3.3. Mistypings
Mistypings in writing can happen for a variety of causes, most of which are triggered by a combination of factors that affect the accuracy of keyboard input. Simple human error is one common cause, in which fingers inadvertently press the wrong keys owing to misplacement or a brief break in concentration. Fatigue and distractions can also lead to typos because fatigued or distracted typists are more likely to make mistakes.
In fast-paced typing conditions, the layout of the keyboard and the proximity of certain keys may result in inadvertent keystrokes. Furthermore, unfamiliarity with a specific keyboard layout, whether QWERTY, QWERTZ, AZERTY, or others, can add to typos, especially when users transfer between devices or regional settings. Mistypings in writing can also be caused by hearing impairment, particularly when individuals rely on auditory guidance for typing accuracy. Furthermore, individuals with hearing impairments must rely on autocorrect and spellcheck technologies to assure the accuracy of their written communication. While autocorrect and predictive text algorithms are useful, they might cause errors if they misread the intended words.
Those mistypings result either in a non-word error, which is easy to find and correct, or in a real-word error, which requires more sophisticated solutions based on understanding of the word’s context.
3.4. Words from Foreign Languages and Slang
A significant share of users of the ispravi.me spellchecking service comes from Bosnia and Herzegovina, Serbia, and Montenegro, with their text written in Serbian. However, certain nuances arise from the linguistic similarities and distinctions between the Croatian and Serbian languages. Although these South Slavic languages have a shared linguistic ancestry, they have diverged over time, resulting in differences in vocabulary, spelling, and grammatical subtleties. Croatian spellcheckers may not reliably identify Serbian-specific vocabulary, phrases, or grammatical patterns, which could result in incorrect evaluations or omissions while reviewing for errors.
Such problems arise in diphthong use—the short and long /ie/ are in Croatian written as “je” and “ije”, while in the Serbian language, both are written as “e” (e.g., in Croatian we write “rijeka” [river], “mlijeko” [milk], “pjevati” [to sing]; in Serbian, those words become “reka”, “mleko” and “pevati”. In most cases, the usage of a Serbian word will be marked as a spelling error, but sometimes, it may cause a real-word error (e.g., Croatian: “ljeti” [during the summer], Serbian: “leti”—in Croatian it means [he/she/it flies]).
The modern Croatian language has also experienced the increasing influence of English words on various domains, particularly in the realms of technology, business, and popular culture. As Croatia is connected globally and engages in international exchanges, English terms often find their way into everyday conversations and written texts. This infusion of English vocabulary poses a challenge for spellchecking in Croatian texts and extends possible spelling errors.
3.5. Ispravi.me—Croatian Online Spellchecker
Almost thirty years ago, in March 1994, the spellchecker for the Croatian language was introduced as an online email service, starting from a small corpus of 100,000 words derived from a Croatian–English dictionary and a corpus of words in English borrowed from the Unix spelling program. In 2003, email service was transferred to the World Wide Web, and the usage of the service has grown ever since. During the email phase, the service only listed suspicious words, without offering corrections. The suggested corrections were added as the service migrated to the web. Each time users chose the proper correction candidate, the pair “error word → correct word” was logged on the server. That gave us a huge dataset, published in [36].
The architecture of the Croatian Academic Spelling Checker (Croatian: “Hrvatski akademski spelling checker”, abbreviated as “Hascheck” and pronounced as “Hašek”, as it was known for more than 20 years) is extensively described in [37].
Briefly, as the text arrives for analysis, the Extractor block extracts valid tokens and removes them from further processing. Non-recognized tokens are then passed to the Classifier, which forwards them to the Guesser and the Corrector, which consult the Dictionary and suggest corrections in the final report sent to the user. Learning is performed offline and is supervised by an administrator. Learning is based on the data collected during usage (statistics, logs, input text, and reports). As the result of the learning process, the dictionary is updated under human supervision, thus improving the spellchecker’s functionality.
Spellchecking is not based on a static corpus; it is based on live traffic, created by real people of all sorts of professions—journalists, scientists, translators, writers, lawyers—but also by regular people who just use it to spellcheck their personal correspondence. Unlike static newspaper or book corpus, ispravi.me’s growing crowdsourced database includes modern words, slang, abbreviations, named entities, etc.
The dictionary is organized in three word-list files: word types, name types, and English types. The initial word type file was derived back in the 1970s from the English–Croatian Lexicographic Corpus (ECLC), which produced 100,000 words that may occur written in small letters only, with an initial capital letter at the start of a sentence, or in capital letters only. In 30 years, the word type file grew to 1,108,164 tokens as of December 2023.
The left-hand side of the ECLC was used to produce 70,528 different English word types. The reasoning for the inclusion of English words is this: as the modern lingua franca, English, often comes mixed with Croatian words. Words that are shared between languages were removed from the English types on file. It is the only dictionary file that has not changed at all since it was created.
The name type file contains all the case-sensitive elements of writing: proper and other names, abbreviations, and acronyms, as well as names with the unusual use of small and capital letters, like LaTeX. It also contains words from foreign languages that appear in Croatian writing in their original orthography. The file started empty, but over the course of learning, it increased to 1,088,606 name types as of December 2023.
The service is available online at https://ispravi.me/ (accessed on 31 December 2023) [correct.me], and as of December 2023, according to the collected server statistics and Google Analytics data, it serves almost 12,000 user sessions per day. From 2003 until December 2023, Hascheck processed almost 62 million texts which form a corpus of 15.8 gigatokens (Gtokens). The service registered usage by almost 2 million IP addresses.
The ispravi.me server keeps track of spelling errors that were found in received texts and suggestions sent to the user, text statistics (number of different classes of errors, number of words and characters in incoming texts), and valid words selected by users from the list of suggested words. Incoming texts are subjected to n-gram analysis, which over the years has resulted in an n-gram system for Croatian language [38]. After n-gram processing, incoming texts are removed from the server for reasons of maintaining user privacy.
In [36] the authors presented an extensive dataset containing a total of 33,382,330 entries of the form “error word → correct word” collected between December 2008 and March 2023 compiled from the contributions of nearly 900,000 users of ispravi.me, the most popular Croatian online spellchecking service. In this huge dataset, the authors identified 5,584,226 unique “error word → correct word” pairs. In total, 5,296,266 unique words were misspelled, which the authors corrected to a total of 1,530,329 words. The authors use this dataset as a foundation for the creation of a letter-level confusion matrix for the Croatian language. Every record of the dataset includes the record date, the ID of the request, the error word, the correct word chosen by user, and the Damerau–Levenshtein edit distance. A sample of the dataset is given in Table 2.

Table 2.
A sample of the dataset of misspelled words and their corrections.
4. Confusion Matrix
A vital tool in natural language processing, especially for spellchecking, is the confusion matrix, which aids in locating and correcting misspelled words by providing probabilities that one word will be transformed into another.
In order to measure how close the error word is to the correct word (edit distance), the Damerau–Levenshtein metric is used to identify the minimum number of insertions, deletions, substitutions, or transpositions of a single character needed to transform the error word into a correct one [39]. If the correct word can be generated using only one transformation, the edit distance between the error word and the correct word is 1. If two basic transformations are required, then the edit distance is 2, and this pattern continues accordingly.
The confusion matrices will provide counts, relative frequencies, or probabilities indicating that a given spelling mistake happened at a given location in the word. For example, a substitution matrix for Croatian will be a square matrix of 30 × 30 letters, which represents the number of times one letter was incorrectly used instead of another. A transposition matrix will tell us how many times two letters were erroneously swapped.
The relative frequencies of inserting or deleting a specific letter can depend on either the preceding or the following character. Both approaches are utilized and will be detailed in the subsequent section. In order to calculate the relative frequency for each edit, a confusion matrix is required that records the counts of these errors.
4.1. Creation of Confusion Matrices
To create the confusion matrices, a subset of the ispravi.me dataset for the period 2008–2016 was used, which contained a total of 1,011,307 unique pairs of “error word → correct word”. Those pairs appeared 3,489,162 times in the texts users corrected through the ispravi.me web service interface.
During the process of matrix creation, the letters from the Croatian alphabet were converted to lowercase. The letters “dž”, “lj”, and “nj” were omitted from the analysis because they are digraphs and always written as two letters (even though the UTF-8 character set supports them as one letter, that option is seldom used). Restricting the matrix to the Croatian alphabet, the English letters “q”, “w”, “x”, and “y”, which are not part of the Croatian alphabet, were omitted, even though they appear in English words and in the named entities database.
After excluding words containing letters that do not belong to Croatian alphabet, the entries in the form “error word → correct word” where the Damerau–Levenshtein edit distance (the selected measure of choice) between the error and correct word was equal to 1 were extracted. That left a corpus of 824,959 unique pairs that contained 3,009,996 transformations that were subsequently further analyzed.
4.2. Types of Matrices
The task that followed was to parse the errors and create the matrices. Iterating over the list of all pairs with edit distance 1, it was determined which of the four types of edits—insertions, deletions, substitution, or transpositions—occurred using the following Algorithm 1:
| Algorithm 1: Determining the type of an edit for a given pair of [error, correct] | |
| 1: | for each pair [error, correct] do |
| 2: | if DL_edit_distance(error, correct) = 1 then |
| 3: | if length (error) > length (correct) then |
| 4: | return {insertion} |
| 5: | elseif length(error) < length(correct) then |
| 6: | return {deletion} |
| 7: | elseif diff (error, correct) = 1 then |
| 8: | return {substitution} |
| 9: | else |
| 10: | return {transposition} |
| 11: | end if |
| 12: | end if |
| 13: | end for |
Table 3 summarizes the types of identified transformations. Among all errors, substitution dominates: if sorted by descending frequency, in the first 10 errors, 6 are the result of substitution, 3 of insertion, and 1 of deletion.

Table 3.
Number and share of detected Damerau–Levenshtein edit distance 1 transformations.
4.3. Conditioning Insertion and Deletion on Both the Previous and Following Letters
Although similar to research results from four confusion matrices (e.g., [12]), one for each transformation type, due to the nature of the most common errors in Croatian, two subvariants of both deletions and insertions (conditioning on the previous and the following letter) were used. More precisely, a total six confusion matrices were created:
- insertionCondOnFollowing—letter Y inserted in front of letter X (X → YX);
- insertionCondOnPrevious—Y inserted after X (X → XY);
- deletionCondOnFollowing—Y deleted in front of X (YX → X);
- deletionCondOnPrevious—Y deleted after X (XY → X);
- Substitution—Y substituted for X (X → Y);
- Transposition—switching adjacent X and Y (XY → YX).
The reason for the choice of six matrices is explained in Section 3: common errors are inserting “i” before “j”, deleting “i” before “j”, and inserting or deleting “a” after “s”. So, conditioning on both the previous and following character in insertions and deletions is appropriate:
- insertionCondOnFollowing is convenient when it is necessary to track where “i” was mistyped before “j”; otherwise, those errors would be spread to all the cases where “i” was added after any other letter in the insertionCondOnPrevious;
- insertionCondOnPrevious is convenient to track errors where “sa” was wrongly used instead of “s” [with]; otherwise, the insertions of “a” before space characters in insertionCondOnFollowing must be tracked;
- deletionCondOnFollowing is convenient to track where “i” was mistakenly deleted before “j”; otherwise, those errors would be spread to all the cases where “i” was deleted after any other letter in deletionCondOnPrevious;
- deletionCondOnPrevious is convenient to track errors where “sa” should be a proper preposition instead of “s”, as one would need to track “a” missing before the space, which would include cases where “na” [on] was misspelled as “n”, “za” [for] as “z”, “da” [yes] as “d, “ja” [I] as “j”, etc. in deletionCondOnFollowing.
Table 4 gives clear insight into the most common orthography-related mistakes explained earlier in the paper: writing “je” instead of “ije”, converting diacritics, and the wrong usage of “s” and “sa” prepositions. The ten most common errors account for 48.92% of all errors in the presented dataset.

Table 4.
Ten most common transformations in the studied dataset.
4.4. Space and Word Boundaries
Apart from the 30 letters of Croatian alphabet, the insertion and deletion matrices contain one more column and two more rows. The space character is present in both a row and a column (represented as “˽”), since the dataset contained a number of spelling errors containing two-word expressions:
- “sa tobom” → “s tobom” [with you]—“a” deleted in front of a space;
- “bi smo” → “bismo” [(we) would]—space inserted after “i” or before “s”;
- “neznam” → “ne znam” [I do not know]—space deleted after “e” or before “z”;
- “oprostiti ću” → “oprostit ću” [I will forgive you]—“i” inserted before space”, etc.
A space in the error word is the result of the ispravi.me spellchecker targeting the exact type of the common error. Had the spellchecking been restricted to just one word, it would not be possible to find this mistake. Explanations for both errors are given in Section 3.1.
The word boundary (represented as “@”, as in [12], meaning the beginning or the end of a word) is in the last row because the character can be inserted or deleted at the beginning or the end of the word:
- Insertion: “adodati” or “dodatia” → “dodati” [to add];
- Deletion: “apsodija” or “rapsodij” → “rapsodija” [rhapsody];
- The option existed to remove those two characters to maintain matrices at 30 × 30 letters, but this could lead to inconsistencies since the total count of errors would not be the same when conditioned on the previous or the following letter.
4.5. Content of the Confusion Matrices
Using a subset of data from the authors’ extensive dataset [36], three matrices for each type of error with the following values were created:
- Number of times the error occurred;
- Relative frequencies of an error on a given letter;
- Relative frequencies of an error with respect to the whole analyzed subset.
The data from all three matrices are already available online as a result of the authors’ previous study [40]. In each of the published matrices, by selecting the value in the row/column intersection, examples from the dataset for each type of error may be provided.
Regarding the terms used in the paper for the description of frequencies, it is important to emphasize that the term relative frequency was used instead of probability. Also, for obtained values in confusion matrices, the term relative frequencies was used instead of probabilities. These two concepts are related, but they have some subtle differences. Both represent measures used to describe the likelihood of events; however, the relative frequency is based on observed data from observations, while probability is a theoretical measurement of the likelihood of an event occurring. Since the presented research is based on observed data, the correct term, relative frequency, was used instead of probability.
5. Discussion
In the following section, numerical tables with a heatmap-like visualization of a confusion matrix for each type of edit are presented. In all six confusion matrices shown below, the rows represent the letter X, the columns represent the letter Y, and the number at the intersection represents the relative frequencies (RFs) of errorXY and is displayed as −log10(RF(errorXY)) for the given type of spelling error, rounded to two decimal places. The logarithmic scale is used in this paper due to the limited space, since the original values that are available online [40] contain too many decimal places to be presented.
A log scale with heatmap-like visualization offers a good insight into our conclusions about error patterns in the Croatian language. However, when using the matrix, we strongly recommend using the data availabe online, as relative frequency values are significantly more precise than the log-scale values presented in this paper.
The matrices should be read as follows. For example, in the insertionCondOnPrevious, at the intersection of row “j” and column “i” is number 0.65, which means that the relative frequency of “i” being mistakenly added after “j” is 10−0.65, which amounts to 0.22387. In [40], available online, the value at that intersection is presented more precisely as 0.225095 or 22.5095%.
The lower the value in the matrix, the greater the relative frequency of this error. In each table, the values are colored to visualize the most frequent errors: the color of each cell can gradually change from green (high cell values—low relative frequency) to red (low cell values—high relative frequency).
Rows and columns for digraphs “dž”, “lj”, and “nj” are omitted from all matrices. Space and word boundary are omitted from the substitution and transposition matrices since they have no significant associated counts.
5.1. “insertionCondOnFollowing” Matrix
Table 5 presents the relative frequencies of errors where X was mistyped as YX (X → YX). The two most frequent errors, accounting for almost a half of all insertion errors, are:

Table 5.
“insertionCondOnFollowing”—relative frequencies of errors with edit distance 1 where letter Y was mistyped before X, i.e., X was mistyped as YX (X → YX).
- Wrong usage of the preposition “s/sa”—recorded as “a” added before space, as explained in Section 3.1.3.—representing 24.25% of all insertion errors (in the matrix, it is represented as the value 0.62 at the intersection of row “˽” and column “a”. As suggested, we refer the reader to our online data, and at that intersection is the value 0.242453, which is the relative frequency of that type of error (−log10 0.24243 is 0.615372437, rounded to 0.62 in this table). Examples of such mistakes are also available in [40] by clicking on the cell value. Some of the notable examples include (“sa tim” instead of “s tim” [with that], or “sa drugim” instead of “s drugim” [with another].
- Inserting “i” in front of “j”, as explained in 3.1.1., with over 100,000 occurrences of that type (22.51% of all insertion errors), the most common being writing “riješenje” instead of “rješenje” [solution] (intersection of row “j” and column “i”).
5.2. “insertionCondOnPrevious” Matrix
Table 6 presents the relative frequencies of errors where X was mistyped as XY (X → XY). Here, the error of writing “sa” instead of “s” is the most frequent, accounting for almost a quarter of all insertion errors. The only error that exceeds the 5% share is adding “i” after “v”, which is due to the “ije/je” subcase (e.g., “uvijet” instead of “uvjet” [condition], “savijet” instead of “savjet” [advice]). Other notable mentions include adding “i” after “r”, “l”, “t”, “m”, “c”, “p”, and “d” (intersection of column “i” and rows “r”, “l”, “t”, “m”, “c”, “p”, and “d”. This illustrates why conditioning on the previous character makes more sense for that type of error.

Table 6.
“insertionCondOnPrevious”—relative frequencies of errors where X was mistyped as XY (X → XY).
It is worth considering the differences in treating insertion errors when X and Y are the same letter (duplication), e.g., writing “zebbra” instead of “zebra”. When the correct and wrong words are matched, the first occurrence of a duplicate letter is considered correct (X); the second is considered an error (Y). So, in the insertionCondOnFollowing matrix, the second letter is considered the wrong letter inserted before the next character; therefore, the main diagonal of Table 4 is empty.
In the insertionCondOnPrevious matrix, the duplicate letter inserted after the correct one produces X → XX, so the main diagonal has values. The dataset shows that the most duplicated letter is “i”, with word “niije” written instead of “nije” [not] most often.
5.3. “deletionCondOnFollowing” Matrix
Table 7 presents the relative frequencies of errors where YX was mistyped as X (YX → X). The error of deleting an “i” in front of “je” is the most frequent of this type of error (intersection of row “j” and column “i”). The most common errors of this type are writing “uvjek” instead of “uvijek” [always] and “promjeniti” instead of “promijeniti” [to change].

Table 7.
“deletionCondOnFollowing”—relative frequencies of errors where YX was mistyped as X (YX → X).
As expected, the deletion matrix conditioned on the removal of letter Y in front of letter X reveals the common error of the wrong usage of “ije” and “je”, where “i” was removed from the proper form. This error accounts for 23.73% of all spelling errors in the dataset.
This matrix also shows cases where “j” was removed in before “e”, which happens mostly when texts in Serbian come for processing and use words that in Croatian contain “je” but in Serbian are written without “j” (e.g., “ponedjeljak” [Monday] is written as “ponedeljak”, “gdje” [where] as “gde”, or “čovjek” [human] as “čovek”). Since this error falls under an edit distance of 1, corrections to proper Croatian forms are offered. This particular error accounts for 4.57% of all errors.
Another error that is visible in this matrix (3.9% of all errors) is removal of the letter “i” in front of a space, which often happens when the infinitive of the verb is used in its shortened form—e.g., “ponoviti UZV” [to repeat the ultrasound] is spelled as “ponovit UZV”.
5.4. “deletionCondOnPrevious” Matrix
Table 8 shows the relative frequencies of errors where XY was erroneously written as X (XY → X). It is not that obvious to find the winner here, but upon closer examination, it is noticeable that the letter “i” (represented by column “i”) deleted after “d”, “r”, “v”, “l”, or “m” (represented in their rows) has greater frequency, which is actually a consequence of removing “i” before “j”, where letters “d”, “r”, “v”, “l”, or “m” should stand before “i”. To illustrate this, “primjetiti” should be “primijetiti” [to notice], “poslje” should be “poslije” [after], and “djete” should be “dijete” [child]. This clearly illustrates the need for the deletionCondOnFollowing matrix, where all these examples would fall under one mistake, deleting “i” before “j”.

Table 8.
“deletionCondOnPrevious”—relative frequencies of errors where XY was mistyped as X (XY → X).
The observations about the main diagonal in the insertion matrices are valid here as well. Even though two duplicate consecutive letters are not characteristic for Croatian, certain compound words feature them—e.g., “preddiplomski” [undergraduate], “najjači” [the strongest] or “samoobrana” [self-defense]. The main diagonal of the deletionCondOnFollowing matrix is empty because when the letter is erroneously missing (e.g., “samobrana”), the second letter “o” is considered missing and is accounted for in the intersection of row “b” and column “o”. In deletionCondOnPrevious, it is counted in the intersection of row “o” and column “o”, as it is treated as “o” missing after “o”. However, this kind of error is negligible across the whole dataset because words with duplicate characters are far less frequent than others.
5.5. “Substitution” Matrix
Table 9 gives insight into the relative frequencies of errors where X was mistyped as Y (X → Y).

Table 9.
“Substitution”—relative frequencies of errors where X was mistyped as Y (X → Y).
Here, writing “č” instead of “ć” is the most common error—it happens in 16% of all substitutions (row “ć”, column “č”), with most notable examples being “mogučnost” instead of “mogućnost” [possibility] and “čemo” instead of “ćemo” [we will]. However, writing “ć” instead of “č” happens half as often (row “č”, column “ć”), e.g., “naćin” instead of “način” [way, method] and “inaće” instead of “inače” [otherwise]. Also, this matrix shows that often both “ć” and “č” are substituted with “c”, “đ” with “d” (but less often, as “đ” is not a frequent character”), “š” is substituted with “s”, and “ž” with “z”. Substituting “đ” with “dj” produces an error of Damerau–Levenshtein distance 2 (one substitution and one insertion) and is not accounted for in this research. Substituting “dž” with “dz” is also common (even though “dž” is even less frequent than “đ”) but is accounted for in the substitution of “ž” with “z” already because the data was analyzed at character level. Another spelling error that can be observed from the data is related to assimilation of consonants. The substitution of “t” with letter “d” (ranked 11th, with a relative frequency of 0.010049) in examples such as “predpostavljam” (proper form: “pretpostavljam” [I assume]) or “predhodno” (proper form: “prethodno” [previous]) is a consequence of users’ unawareness of the assimilation rule, where “d” in front of “p” should become “t”. Other errors are also observable but are not prominent (e.g., “pretstavlja” instead of the proper “predstavlja” [presents], “sretstva” instead of the proper “sredstva” [means, resources], “substanca” instead of the proper “supstanca” [substance], “drugčije” instead of the proper “drukčije” [differently], etc.).
5.6. “Transposition” Matrix
Table 10 shows the relative frequencies of errors where adjacent letters XY were misspelled as YX (XY → YX).

Table 10.
“Transposition”—relative frequencies of errors where XY was mistyped as Y (XY → YX).
Unlike in other presented confusion matrices, in this case, the deviations from random typos were not observed. Even though some errors dominate, compared to other types of errors, they show a more uniform distribution where even proximity of keys on the keyboard does not contribute much to the error.
It seems that the letter “a” is transposed more frequently, either with a group of letters that are usually typed with the right hand or adjacent letters typed with the left hand. For example, “pozdarv” is often written instead of “pozdrav” [greeting] (row “r”, column “a”) and “stavri” instead of “stvari” [things] (row “v”, column “a”).
This may lead to the conclusion that different speeds at which the left and right hands work can have a notable impact on the correct spelling of the written text. In cases where there is a significant imbalance in typing speed between the two hands or even between two fingers of one hand, errors can occur because one hand or finger is faster than the other. This discrepancy can lead to typos, misspellings, or even omitted letters, as the faster hand may accidentally skip characters or anticipate the next ones before they have been typed correctly.
Disparity in typing speed becomes even more noticeable when typing fast and can potentially compromise the overall accuracy of the written content. This emphasizes the importance of refining typing skills and maintaining a harmonious balance between the left and right hands to improve typing and spelling and, subsequently, produce error-free text.
5.7. Implementation of Confusion Matrices in Spellchecking
As a proof of concept, we used our matrices in the process of sorting correction candidate words in a list of possible corrections offered to the user. After selecting all the possible correction candidates with edit distance 1, we sorted the correction candidates based on the product of the relative frequency of the correction candidate word from our unigram corpus and the relative frequency of a given type of error that could convert the correct word to the wrong word. For example, given the error word “prjetili”, the only two correction candidates are “prijetili” [threatened], and “pretili” [obese]:
- The relative frequency of the word “prijetili” in our corpus is 2.4966 × 10−6. In order to mistype “prijetili” as “prjetili”, a deletion of character “i” in front of “j” is required, and according to Table 7, deletionCondOnFollowing at [40] (row “j”, column “i”), the relative frequency of such an event is 0.237323. The product of those two values is 5.925 × 10−7.
- The relative frequency of the word “pretili” is 6.85977 × 10−7. For mistyping “pretili” to “prjetili”, we need to find the relative frequency of “j” inserted before “e” in Table 5 insertionCondOnFollowing—it is 0.007118. The product of the two values is 4.88278 × 10−9.
Therefore, the word “prijetili” is offered as the first choice. However, the sentence, “Naši susjedi su prjetili.” could be either “Naši susjedi su prijetili.” [Our neighbors threatened.] or “Naši susjedi su pretili.” [Our neighbors are obese.], which clearly shows the need to take into account the context. Although initial results of the implementation of our matrices show promising results, this research is still ongoing.
5.8. Log Charts
When spelling errors occur, users are more likely to label them as typos than to admit their poor knowledge of the orthography (i.e., spelling) rules. The difference is clear: if someone writes “adn” or “teh” instead of “and” or “the”, it is a typo. However, if a person writes “than” instead of “then” or “wellcome” instead of “welcome” it may be assumed it is not a typo but a sign of unfamiliarity with orthography rules.
It is possible to use the data from the presented matrices to visualize the relative frequencies of the errors on a logarithmic scale and try to determine which of the explanations for the error is more likely: is it a typo, is it a lack of proficiency in orthography, or are users simply saving time by replacing a letter with a simpler variation that requires fewer keystrokes?
The relative frequencies of spelling errors from the confusion matrices are shown graphically in Figure 2a–f according to the principle of rank-size distribution in decreasing order of size. The rank of each error type is shown on the x-axis, and the corresponding relative frequency is shown on the y-axis. Due to the large range of magnitudes, the values on both axes are on a logarithmic scale in order to make their dependence visible.
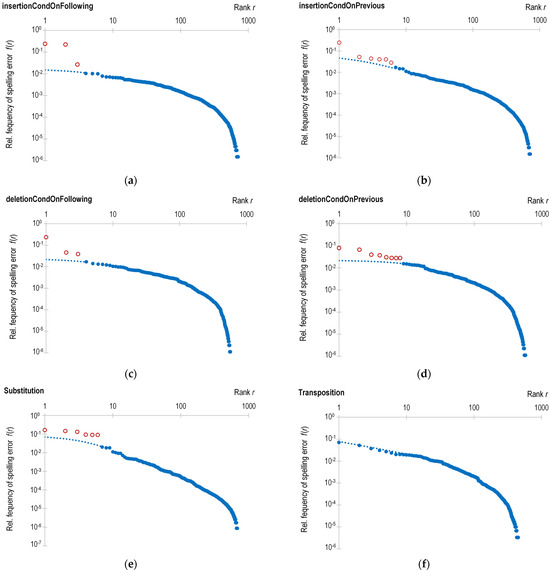
Figure 2.
Log–log plot of relative frequencies of spelling errors for the (a) insertion of letter Y conditioned on the previous character, (b) insertion of letter Y conditioned on the following character, (c) deletion of letter Y conditioned on the previous character, (d) deletion of letter Y conditioned on the following character, (e) substitution where X was mistyped, and (f) transposition where adjacent letters XY were mistyped as YX. The red dots represent deviations from the rank-size distribution expected trend (indicated by the blue dashed curve).
This way of visualizing data corresponds to the Zipf–Mandelbrot distribution [41], an empirical law that is often used for describing linguistic phenomena, e.g., in a certain language, the frequency of each word is inversely proportional to its rank in the frequency distribution.
As can be seen from Figure 2a–e, the points corresponding to the higher ranks are distributed as if forming a smooth and regular curve, while for lower ranks, the values of the points may deviate significantly upwards from the supposed curve. However, in the case of a transposition spelling error, as shown in Figure 2f, points of a lower rank do not have a specified observed deviation. This fact confirms that transposition errors are random in nature.
In all other cases, there are individual errors that deviate significantly from randomness and are marked by red dots in Figure 2a–e. Such an approach could be used to identify spelling error outliers, i.e., extremely frequent errors, as explained in the discussion section. In future related research, modeling of the curve will be performed, so the level of deviation from the curve will enable an objective quantitative judgment of what is a spelling error and what is due to ignorance.
6. Conclusions
Spellcheckers are indispensable tools in the current digital age, both for everyday writing and for professional communication. They can quickly identify and correct spelling errors, improving the readability and quality of texts, especially for non-native speakers. These tools are more than just error correctors. They also help users to improve their language skills. In the professional field, e.g., for academic papers or legal documents, the accuracy of spellchecking is essential.
Our research, based on an experimental dataset derived from a long-term collection of mistyped words and user corrections, presents a novel approach to leveraging confusion matrices for spellchecking error pattern discovery and the improvement of spellchecker precision in the Croatian language. Our findings contribute to the advancement of Croatian spellchecking technologies, particularly in providing a more accurate offering of correction candidates. Our work offers a deeper understanding of linguistic specifics, particularly in underresourced languages with rich orthographies like Croatian.
The study has uncovered subtle statistical properties of spelling errors in the Croatian language, emphasizing the development of spellcheckers and the crucial role of confusion matrices in refining suggested corrections. The user-generated data from the Croatian spellchecker ispravi.me has been examined to provide insights into common spelling errors which may be used for the creation of confusion matrices based on the linguistic details of the Croatian language.
The research conducted shows the importance of using user data to improve the accuracy of spellchecking algorithms. By examining the frequency and patterns of corrections, matrices were created that not only statistically evaluate the performance of current spellcheckers but also provide a basis for future improvements to these important digital tools on the web and mobile devices. The implications of the data obtained go beyond spellcheckers and provide a deeper understanding of the linguistic challenges posed by the use of diacritics and the accessibility of virtual keyboards.
Concerning future development, the user-driven confusion matrices presented in this paper pave the way for further advances in the field of spellchecking, especially in languages with unique orthographic features. The context-dependent nature of the presented approach opens new possibilities for more accurate and linguistically informed correction suggestions, thus contributing to the ongoing evolution of language processing tools.
Finally, it is important to emphasize the dynamic nature of language use and the need for adaptive technologies. Future research efforts could use the findings reported in this study to improve spellcheckers, investigating additional aspects of language data in order to improve the overall user experience in different linguistic contexts. Such a user-centric approach extends the scope of spellchecking and also emphasizes the importance of incorporating user data to customized language processing tools for achieving better performance and user satisfaction.
Author Contributions
Conceptualization, G.G. and M.H.; methodology, G.G. and M.S.; software, G.G. and M.S.; validation, M.M. and M.S.; formal analysis, M.M.; investigation, M.S. and G.G.; resources, G.G.; data curation, G.G. and M.M.; writing—original draft preparation, G.G.; writing—review and editing, M.S., M.H. and M.M.; visualization, M.S.; supervision, G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The dataset is described in [32]. The results obtained on a subset of the dataset which are presented in this paper are available in detail at https://ispravi.me/confusion (accessed on 31 December 2023).
Acknowledgments
We express our heartfelt gratitude to Šandor Dembitz, whose visionary leadership has been instrumental in advancing language technologies and spellchecking for the Croatian language. His outstanding contribution reflects not only a brilliant mind but also a commitment to innovation. We appreciate Dembitz’s dedication to the development of the spellchecking service, which has significantly enhanced the language landscape for Croatian.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mitton, R. Fifty Years of Spellchecking. Writ. Syst. Res. 2010, 2, 1–7. [Google Scholar] [CrossRef]
- Hládek, D.; Staš, J.; Pleva, M. Survey of Automatic Spelling Correction. Electronics 2020, 9, 1670. [Google Scholar] [CrossRef]
- Jurafsky, D.; Martin, J.H. Speech and Language Processing: An Introduction to Natural Language Processing, Computational Linguistics, and Speech Recognition, 1st ed.; Prentice Hall PTR: Hoboken, NJ, USA, 2000. [Google Scholar]
- Almutiri, T.; Nadeem, F. Markov Models Applications in Natural Language Processing: A Survey. Int. J. Inf. Technol. Comput. Sci. 2022, 14, 1–16. [Google Scholar] [CrossRef]
- Pienaar, W.; Snyman, D.P. Spelling Checker-Based Language Identification for the Eleven Official South African Languages. In Proceedings of the Twenty-First Annual Symposium of the Pattern Recognition Association of South Africa, Stellenbosch, South Africa, 22–23 November 2010. [Google Scholar]
- Abandah, G.; Suyyagh, A.; Khedher, M.Z. Correcting Arabic Soft Spelling Mistakes Using BiLSTM-Based Machine Learning. Int. J. Adv. Comput. Sci. Appl. 2022, 13, 815–829. [Google Scholar] [CrossRef]
- Zhang, D.; Li, Y.; Zhou, Q.; Ma, S.; Li, Y.; Cao, Y.; Zheng, H.-T. Contextual Similarity Is More Valuable Than Character Similarity: An Empirical Study for Chinese Spell Checking. In Proceedings of the ICASSP 2023—IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Jin, W.; Zhao, B.; Zhang, Y.; Sun, G.; Yu, H. Fintech Key-Phrase: A New Chinese Financial High-Tech Dataset Accelerating Expression-Level Information Retrieval. ACM Trans. Asian Low-Resour. Lang. Inf. Process. 2023, 22, 1–37. [Google Scholar] [CrossRef]
- Davlatova, M. Semantic Properties of Effective Constructions in English and Uzbek Languages. E3S Web Conf. 2023, 420, 10027. [Google Scholar] [CrossRef]
- Phatak, S.A.; Lovitt, A.; Allen, J.B. Consonant Confusions in White Noise. J. Acoust. Soc. Am. 2008, 124, 1220–1233. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Wang, Y.; Metze, F. EM-Based Phoneme Confusion Matrix Generation for Low-Resource Spoken Term Detection. In Proceedings of the 2014 IEEE Spoken Language Technology Workshop (SLT), South Lake Tahoe, NV, USA, 7–10 December 2014; pp. 424–429. [Google Scholar]
- Kernighan, M.D.; Church, K.W.; Gale, W.A. A Spelling Correction Program Based on a Noisy Channel Model. In Proceedings of the COLING 1990 Volume 2: Papers Presented to the 13th International Conference on Computational Linguistics, Helsinki, Finland, 20–25 August 1990. [Google Scholar]
- Cekaite, A. Collaborative Corrections with Spelling Control: Digital Resources and Peer Assistance. Int. J. Comput. Support. Collab. Learn. 2009, 4, 319–341. [Google Scholar] [CrossRef]
- Mossige, M.; Arendal, E.; Kongskov, L.; Svendsen, H.B. How Do Technologies Meet the Needs of the Writer with Dyslexia? An Examination of Functions Scaffolding the Transcription and Proofreading in Text Production Aimed towards Researchers and Practitioners in Education. Dyslexia 2023, 29, 408–425. [Google Scholar] [CrossRef] [PubMed]
- META-NET White Paper Series Key Results and Cross-Language Comparison. Available online: http://www.meta-net.eu/whitepapers/overview (accessed on 12 April 2023).
- Sussex, R.; Cubberley, P. The Slavic Languages; Cambridge University Press: Cambridge, UK, 2006; ISBN 9780521223157. [Google Scholar]
- Golubović, J.; Gooskens, C. Mutual Intelligibility between West and South Slavic Languages. Russ. Linguist. 2015, 39, 351–373. [Google Scholar] [CrossRef]
- Nouza, J.; Safarik, R.; Cerva, P. ASR for South Slavic Languages Developed in Almost Automated Way. In Proceedings of the Interspeech 2016, ISCA, San Francisco, CA, USA, 8–12 September 2016; pp. 3868–3872. [Google Scholar]
- Pedrazzini, N.; Eckhoff, H.M. OldSlavNet: A Scalable Early Slavic Dependency Parser Trained on Modern Language Data. Softw. Impacts 2021, 8, 100063. [Google Scholar] [CrossRef]
- Adamou, E.; Breu, W.; Scholze, L.; Shen, R.X. Borrowing and Contact Intensity: A Corpus-Driven Approach from Four Slavic Minority Languages. J. Lang. Contact 2016, 9, 513–542. [Google Scholar] [CrossRef]
- Banasiak, D.; Mierzwa, J.; Sterna, A. Extended N-Gram Model for Analysis of Polish Texts. In Man-Machine Interactions 5; Springer: Berlin/Heidelberg, Germany, 2018; pp. 355–364. [Google Scholar]
- Ziolko, B.; Skurzok, D.; Michalska, M. Polish N-Grams and Their Correction Process. In Proceedings of the 2010 4th International Conference on Multimedia and Ubiquitous Engineering, IEEE, Cebu, Philippines, 11–13 August 2010; pp. 1–5. [Google Scholar]
- Rozovskaya, A. Spelling Correction for Russian: A Comparative Study of Datasets and Methods. In Proceedings of the International Conference on Recent Advances in Natural Language Processing (RANLP 2021), Varna, Bulgaria, 6–8 September 2021; Mitkov, R., Angelova, G., Eds.; INCOMA Ltd.: Moscow, Russia, 2021; pp. 1206–1216. [Google Scholar]
- Sorokin, A. Spelling Correction for Morphologically Rich Language: A Case Study of Russian. In Proceedings of the 6th Workshop on Balto-Slavic Natural Language Processing, Association for Computational Linguistics, Stroudsburg, PA, USA, 4 April 2017; pp. 45–53. [Google Scholar]
- Richter, M.; Stranak, P.; Rosen, A. Korektor—A System for Contextual Spell-Checking and Diacritics Completion. In Proceedings of the COLING 2012: Posters, Mumbai, India, 8–15 December 2012; Kay, M., Boitet, C., Eds.; The COLING 2012 Organizing Committee: Mumbai, India; pp. 1019–1028. [Google Scholar]
- Ramasamy, L.; Rosen, A.; Stranák, P. Improvements to Korektor: A Case Study with Native and Non-Native Czech. In Proceedings of the ITAT 2015: Information Technologies—Applications and Theory, Slovensky Raj, Slovakia, 17–21 September 2015. [Google Scholar]
- Hladek, D.; Stas, J.; Juhar, J. Unsupervised Spelling Correction for Slovak. Adv. Electr. Electron. Eng. 2013, 11, 2013. [Google Scholar] [CrossRef]
- Stankevičius, L.; Lukoševičius, M.; Kapočiūtė-Dzikienė, J.; Briedienė, M.; Krilavičius, T. Correcting Diacritics and Typos with a ByT5 Transformer Model. Appl. Sci. 2022, 12, 2636. [Google Scholar] [CrossRef]
- Náplava, J.; Straka, M.; Straková, J. Diacritics Restoration Using BERT with Analysis on Czech Language. Prague Bull. Math. Linguist. 2021, 116, 27–42. [Google Scholar] [CrossRef]
- Dembitz, Š.; Gledec, G.; Sokele, M. An Economic Approach to Big Data in a Minority Language. Procedia Comput. Sci. 2014, 35, 427–436. [Google Scholar] [CrossRef]
- Šoić, R.; Vuković, M. N-Gram Based Croatian Language Network: Application in a Smart Environment. J. Commun. Softw. Syst. 2022, 18, 63–71. [Google Scholar] [CrossRef]
- Šantić, N.; Šnajder, J.; Dalbelo Bašić, B. Automatic Diacritics Restoration in Croatian Texts. In Proceedings of the 2nd International Conference The Future of Information Sciences (INFuture 2009), Zagreb, Croatia, 4–6 November 2009; pp. 309–318. [Google Scholar]
- Dembitz, Š.; Gledec, G.; Randić, M. Spellchecker. In Wiley Encyclopedia of Computer Science and Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Wikimedia Commons contributors Croatian Keyboard Layout 2010. Available online: https://commons.wikimedia.org/wiki/File:Croatian_keyboard_layout.jpg (accessed on 31 December 2003).
- Institute for Croatian Language and Linguistics Hrvatski Pravopis (Croatian Ortography). Available online: http://pravopis.hr/ (accessed on 31 December 2023).
- Gledec, G.; Horvat, M.; Mikuc, M.; Blašković, B. A Comprehensive Dataset of Spelling Errors and Users’ Corrections in Croatian Language. Data 2023, 8, 89. [Google Scholar] [CrossRef]
- Dembitz, Š.; Gledec, G.; Blašković, B. Architecture of Hascheck—An Intelligent Spellchecker for Croatian Language; LNAI; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6277, ISBN 3642153895. [Google Scholar]
- Gledec, G.; Šoić, R.; Dembitz, Š. Dynamic N-Gram System Based on an Online Croatian Spellchecking Service. IEEE Access 2019, 7, 149988–149995. [Google Scholar] [CrossRef]
- Damerau, F.J. A Technique for Computer Detection and Correction of Spelling Errors. Commun. ACM 1964, 7, 171–176. [Google Scholar] [CrossRef]
- Srdić, I.; Gledec, G. Confusion Matrices for Croatian Language. Available online: https://ispravi.me/confusion/ (accessed on 31 December 2023). (In Croatian).
- Mandelbrot, B. An Informational Theory of the Statistical Structure of Language. In Communication Theory; Academic Press: Princeton, NJ, USA, 1953; pp. 486–502. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).