Least Squares Minimum Class Variance Support Vector Machines
Abstract
1. Introduction
2. Literature Review on SVMs
2.1. Support Vector Machines (SVMs)
2.2. Least Squares Support Vector Machines (LSSVMs)
2.3. Minimum Class Variances Support Vector Machines (MCVSVMs)
3. New Method: LS-MCVSVM
4. Addressing Singularity Using Principal Projections
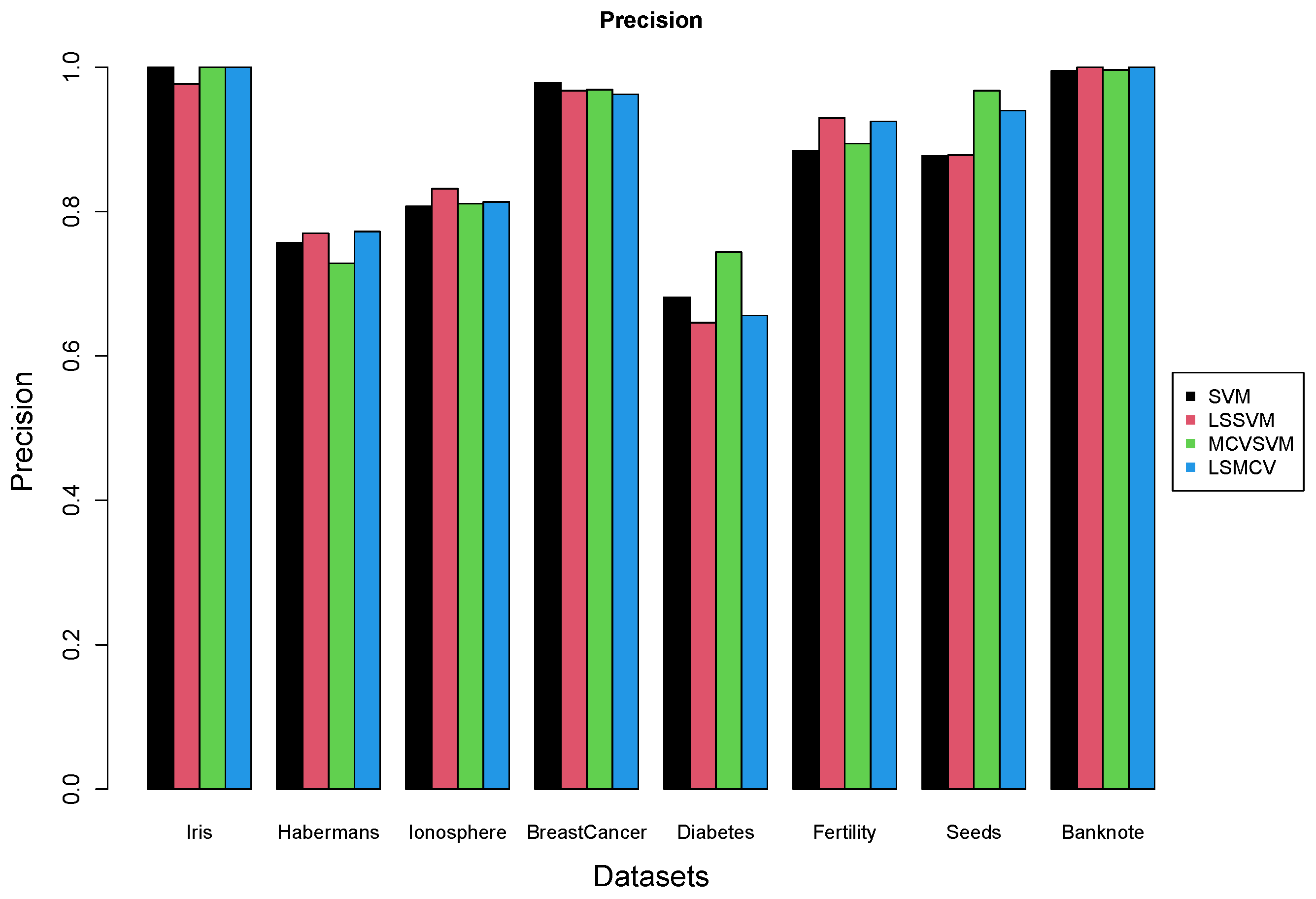
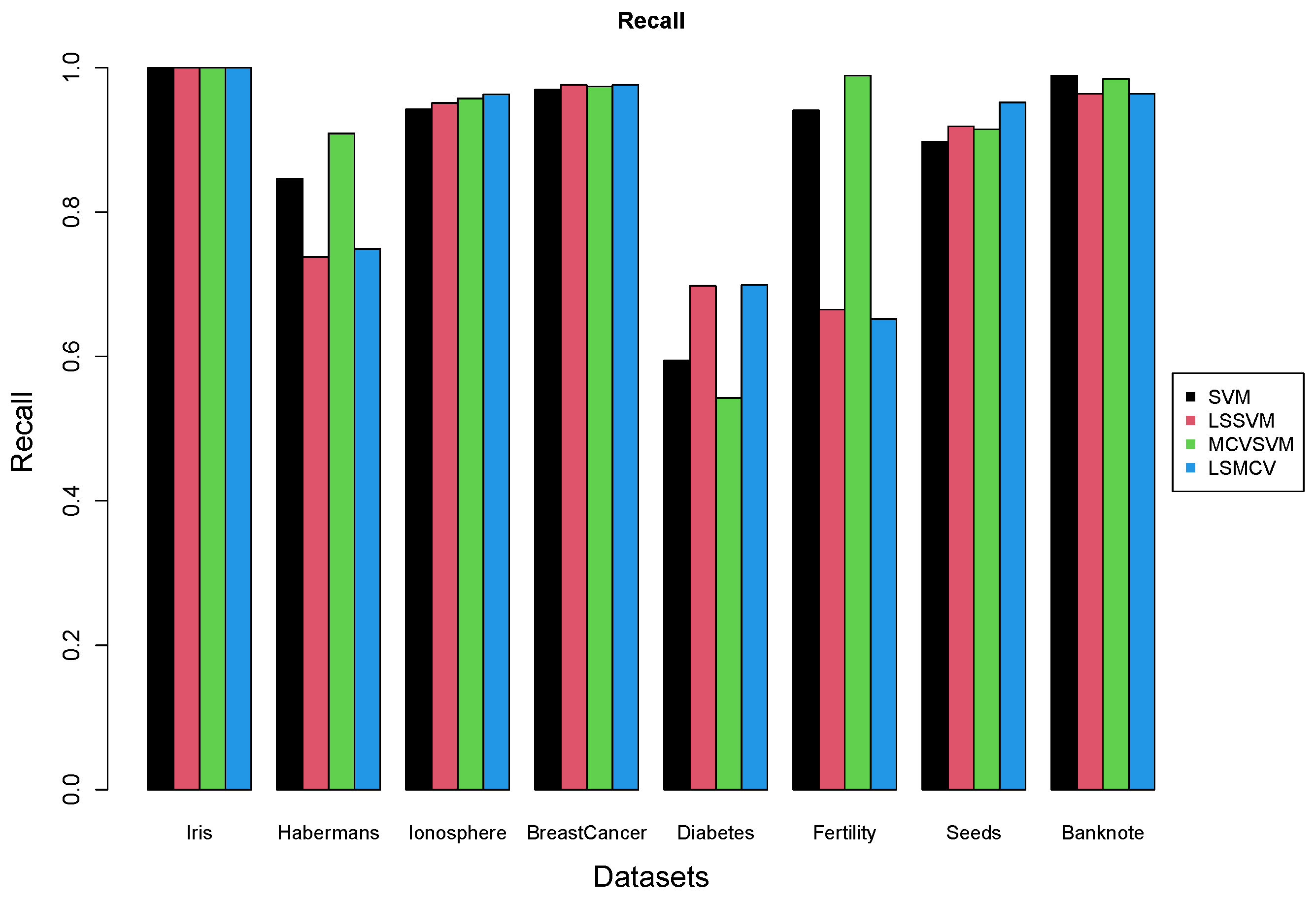
5. Real Data Experiments
6. Conclusions
Other Approaches and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Liu, W.; Ci, L.; Liu, L. A New Method of Fuzzy Support Vector Machine Algorithm for Intrusion Detection. Appl. Sci. 2020, 10, 1065. [Google Scholar] [CrossRef]
- Razaque, A.; Mohamed, B.H.F.; Muder, A.; Munif, A.; Bandar, A. Improved Support Vector Machine Enabled Radial Basis Function and Linear Variants for Remote Sensing Image Classification. Sensors 2021, 21, 4431. [Google Scholar] [CrossRef] [PubMed]
- Panup, W.; Wachirapong, R.; Rabian, W. A Novel Twin Support Vector Machine with Generalized Pinball Loss Function for Pattern Classification. Symmetry 2022, 14, 289. [Google Scholar] [CrossRef]
- Han, K.-X.; Chien, W.; Chiu, C.-C.; Cheng, Y.-T. Application of Support Vector Machine (SVM) in the Sentiment Analysis of Twitter DataSet. Appl. Sci. 2020, 10, 1125. [Google Scholar] [CrossRef]
- Sheykhmousa, M.; Mahdianpari, M.; Ghanbari, H.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support Vector Machine Versus Random Forest for Remote Sensing Image Classification: A Meta-Analysis and Systematic Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6308–6325. [Google Scholar] [CrossRef]
- Ehsan, H.; Lahmer, T.; Kumari, V.; Jadhav, K. Application of Support Vector Machine Modeling for the Rapid Seismic Hazard Safety Evaluation of Existing Buildings. Energies 2020, 13, 3340. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Zafeiriou, S.; Tefas, A.; Pitas, I. Minimum Class Variance Support Vector Machines. IEEE Trans. Image Process. 2006, 16, 2551–2564. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.A. The Use of Multiple Measurements in Taxonomic Problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Fisher, R.A. Iris. UCI Machine Learning Repository. 1988. Available online: https://archive.ics.uci.edu/dataset/53/iris (accessed on 23 January 2024). [CrossRef]
- Haberman, S. Haberman’s Survival. UCI Machine Learning Repository. 1999. Available online: https://archive.ics.uci.edu/dataset/43/haberman+s+survival (accessed on 23 January 2024). [CrossRef]
- Sigillito, V.; Wing, S.; Hutton, L.; Baker, K. Ionosphere. UCI Machine Learning Repository. 1989. Available online: https://archive.ics.uci.edu/dataset/52/ionosphere (accessed on 23 January 2024). [CrossRef]
- Wolberg, W. Breast Cancer Wisconsin (Original). UCI Machine Learning Repository. 1992. Available online: https://archive.ics.uci.edu/dataset/15/breast+cancer+wisconsin+original (accessed on 23 January 2024). [CrossRef]
- Kahn, M. Diabetes. UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/dataset/34/diabetes (accessed on 23 January 2024). [CrossRef]
- Gil, D.; Girela, J. Fertility. UCI Machine Learning Repository. 2013. Available online: https://archive.ics.uci.edu/dataset/244/fertility (accessed on 23 January 2024). [CrossRef]
- Charytanowicz, M.; Niewczas, J.; Kulczycki, P.; Kowalski, P.; Lukasik, S. Seeds. UCI Machine Learning Repository. 2012. Available online: https://archive.ics.uci.edu/dataset/236/seeds (accessed on 23 January 2024). [CrossRef]
- Lohweg, V. Banknote Authentication. UCI Machine Learning Repository. 2013. Available online: https://archive.ics.uci.edu/dataset/267/banknote+authentication (accessed on 23 January 2024). [CrossRef]
- Panayides, M.; Artemiou, A. LSMCV-SVM Comparisons with Other SVMs. Zenodo. 2024. Available online: https://zenodo.org/records/10476188 (accessed on 23 January 2024). [CrossRef]
- Veropoulos, K.; Campbell, C.; Cristianini, N. Controlling the sensitivity of support vector vector machines. In Proceedings of the Sixteenth International Joint Conference on Artificial Intelligence (IJCAI ’99), Workshop ML3, Stockholm, Sweden, 31 July–6 August 1999; pp. 55–60. [Google Scholar]
- Artemiou, A.; Shu, M. A cost based reweighed scheme of Principal Support Vector Machine. Top. Nonparamet. Stat. Springer Proc. Math. Stat. 2014, 74, 1–22. [Google Scholar]
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- Artemiou, A.; Dong, Y.; Shin, S.J. Real-time sufficient dimension reduction through principal least squares support vector machines. Pattern Recognit. 2021, 112, 107768. [Google Scholar] [CrossRef]
- Jang, H.J.; Shin, S.J.; Artemiou, A. Principal weighted least square support vector machine: An online dimension-reduction tool for binary classification. Comput. Stat. Data Anal. 2023, 187, 107818. [Google Scholar] [CrossRef]
- Li, B.; Artemiou, A.; Li, L. Principal Support Vector Machines for linear and nonlinear sufficient dimension reduction. Ann. Stat. 2011, 39, 3182–3210. [Google Scholar] [CrossRef]
- Wang, X.-M.; Wang, S.-T. Least-Square-based Minimum Class Variance Support Vector Machines. Jisuanji Gongcheng Comput. Eng. 2010, 36, 12. [Google Scholar]

| Dataset | Observations | Features | Source, Citation |
|---|---|---|---|
| Iris | 150 | 4 | /53/iris, [11] |
| Haberman’s | 306 | 3 | /43/haberman+s+survival, [12] |
| Ionosphere | 351 | 34 | /52/ionosphere, [13] |
| Breast Cancer | 699 | 9 | /15/breast+cancer+wisconsin+original, [14] |
| Diabetes | ≈253,000 | 21 | /891/cdc+diabetes+health+indicators, [15] |
| Fertility | 100 | 10 | /244/fertility, [16] |
| Seeds | 210 | 7 | /dataset/236/seeds, [17] |
| Banknote | 1372 | 5 | /267/banknote+authentication, [18] |
| Algorithm | SVM | LS SVM | MCV SVM | LSMCV SVM | |
|---|---|---|---|---|---|
| Datasets | |||||
| Iris | 0 (0) | 0 (0) | 0 (0) | 0 (0) | |
| Haberman’s | 0.27 (0.002) | 0.25 (0.002) | 0.27 (0.002) | 0.25 (0.002) | |
| Ionosphere | 0.14 (0.002) | 0.14 (0.002) | 0.14 (0.002) | 0.14 (0.002) | |
| Breast Cancer | 0.04 (0.000) | 0.04 (0.000) | 0.04 (0.000) | 0.04 (0.000) | |
| Diabetes | 0.24 (0.001) | 0.23 (0.001) | 0.24 (0.001) | 0.23 (0.001) | |
| Fertility | 0.17 (0.010) | 0.12 (0.005) | 0.17 (0.009) | 0.12 (0.005) | |
| Seeds | 0.07 (0.001) | 0.06 (0.001) | 0.04 (0.001) | 0.03 (0.001) | |
| Banknote | 0.01 (0.000) | 0.03 (0.000) | 0.01 (0.000) | 0.03 (0.000) | |
| Algorithm | SVM | LS SVM | MCV SVM | LSMCV | |
|---|---|---|---|---|---|
| Datasets | |||||
| Iris | 0.229 | 0.00931 | 0.205 | 0.0207 | |
| Haberman’s | 0.953 | 0.0305 | 0.783 | 0.0334 | |
| Ionosphere | 1.29 | 0.0593 | 1.12 | 0.0784 | |
| Breast Cancer | 8.79 | 0.241 | 6.34 | 0.217 | |
| Diabetes | 10.4 | 0.342 | 8.003 | 0.307 | |
| Fertility | 0.139 | 0.00786 | 0.125 | 0.016 | |
| Seeds | 0.441 | 0.0164 | 0.372 | 0.0224 | |
| Banknote | 59.3 | 1.67 | 49.1 | 1.42 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panayides, M.; Artemiou, A. Least Squares Minimum Class Variance Support Vector Machines. Computers 2024, 13, 34. https://doi.org/10.3390/computers13020034
Panayides M, Artemiou A. Least Squares Minimum Class Variance Support Vector Machines. Computers. 2024; 13(2):34. https://doi.org/10.3390/computers13020034
Chicago/Turabian StylePanayides, Michalis, and Andreas Artemiou. 2024. "Least Squares Minimum Class Variance Support Vector Machines" Computers 13, no. 2: 34. https://doi.org/10.3390/computers13020034
APA StylePanayides, M., & Artemiou, A. (2024). Least Squares Minimum Class Variance Support Vector Machines. Computers, 13(2), 34. https://doi.org/10.3390/computers13020034









