Multispectral Image Generation from RGB Based on WSL Color Representation: Wavelength, Saturation, and Lightness
Abstract
1. Introduction
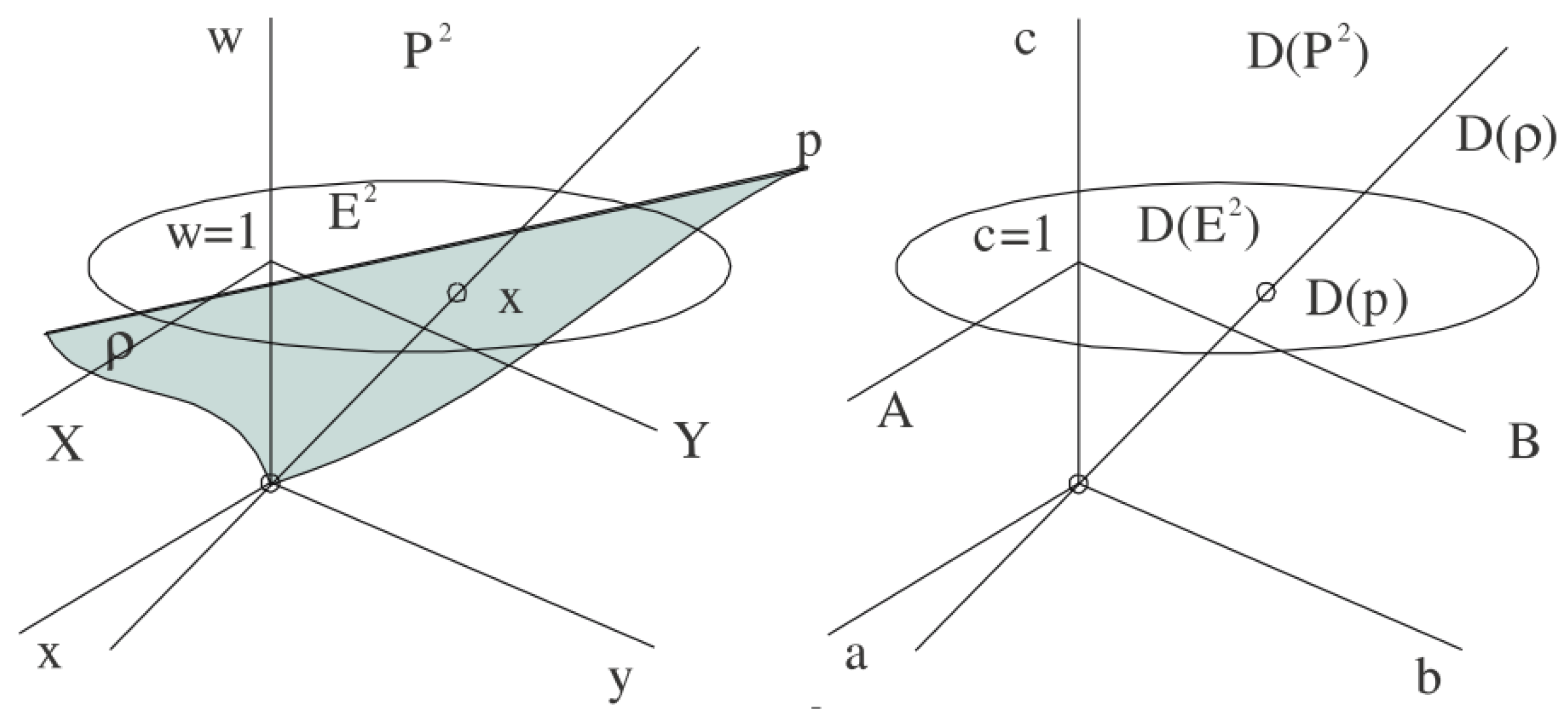
2. Projective Space and Duality
Principle of Duality
3. Color and Color Representation
3.1. RGB Color System
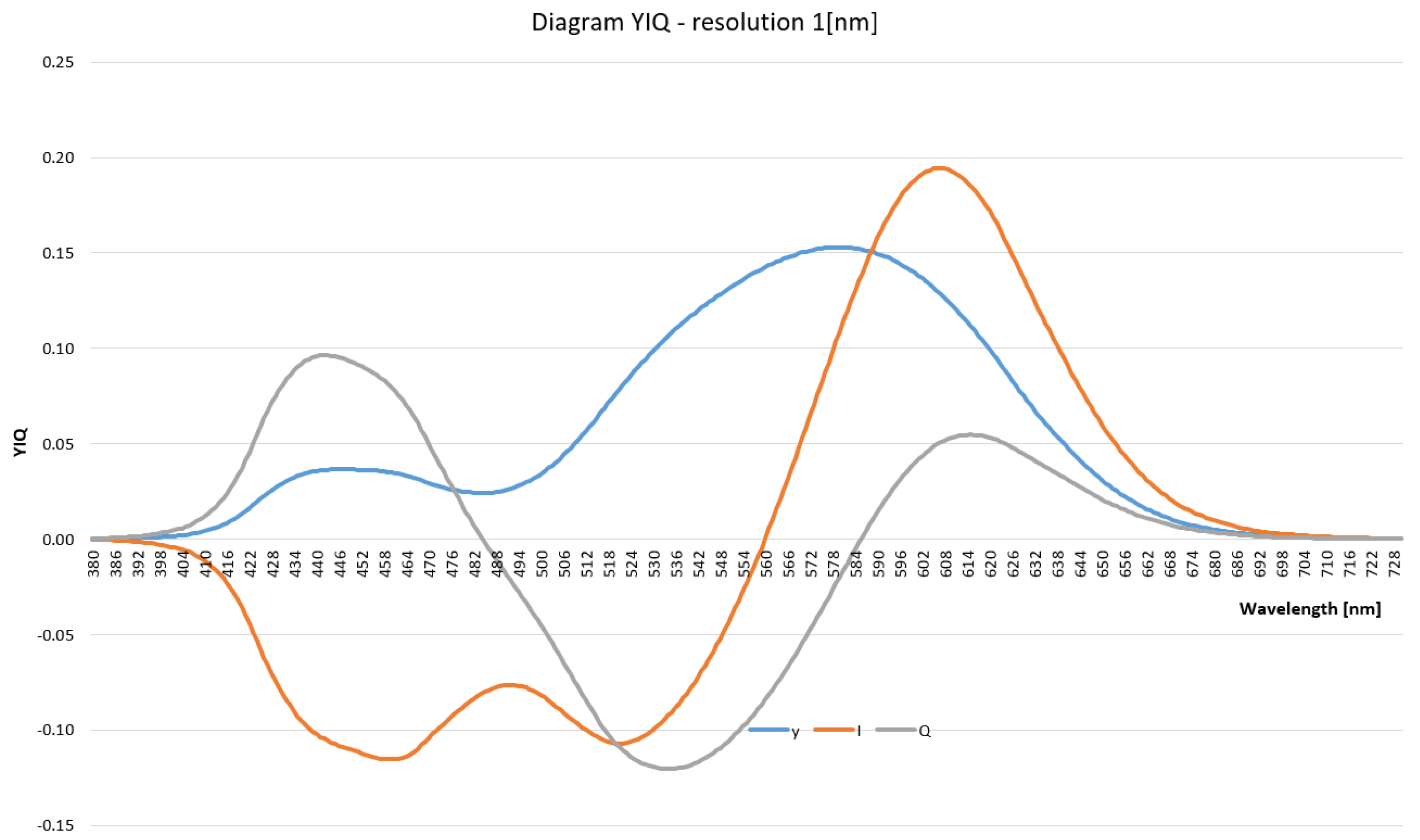
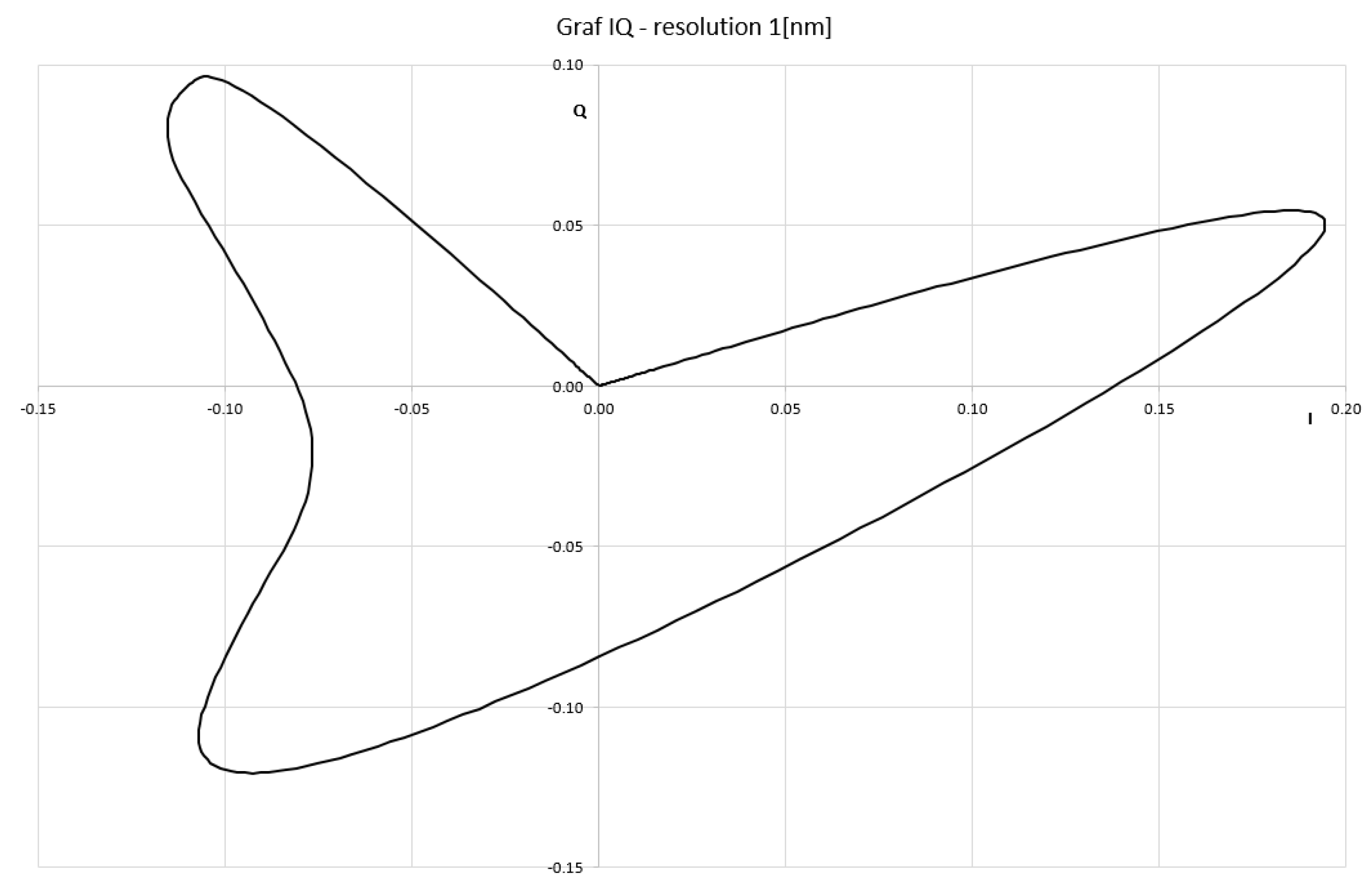
3.2. YIQ Color System
3.3. HSI Color System
- Saturation (S), represents a distance of a color c from a diagonal of the RGB cube;
- Intensity (I) or lightness (L);
- Hue (H), represents human color sense. The hue is represented as an angle, i.e., , where , , represents red (R), green (G), blue (B) colors in RGB.
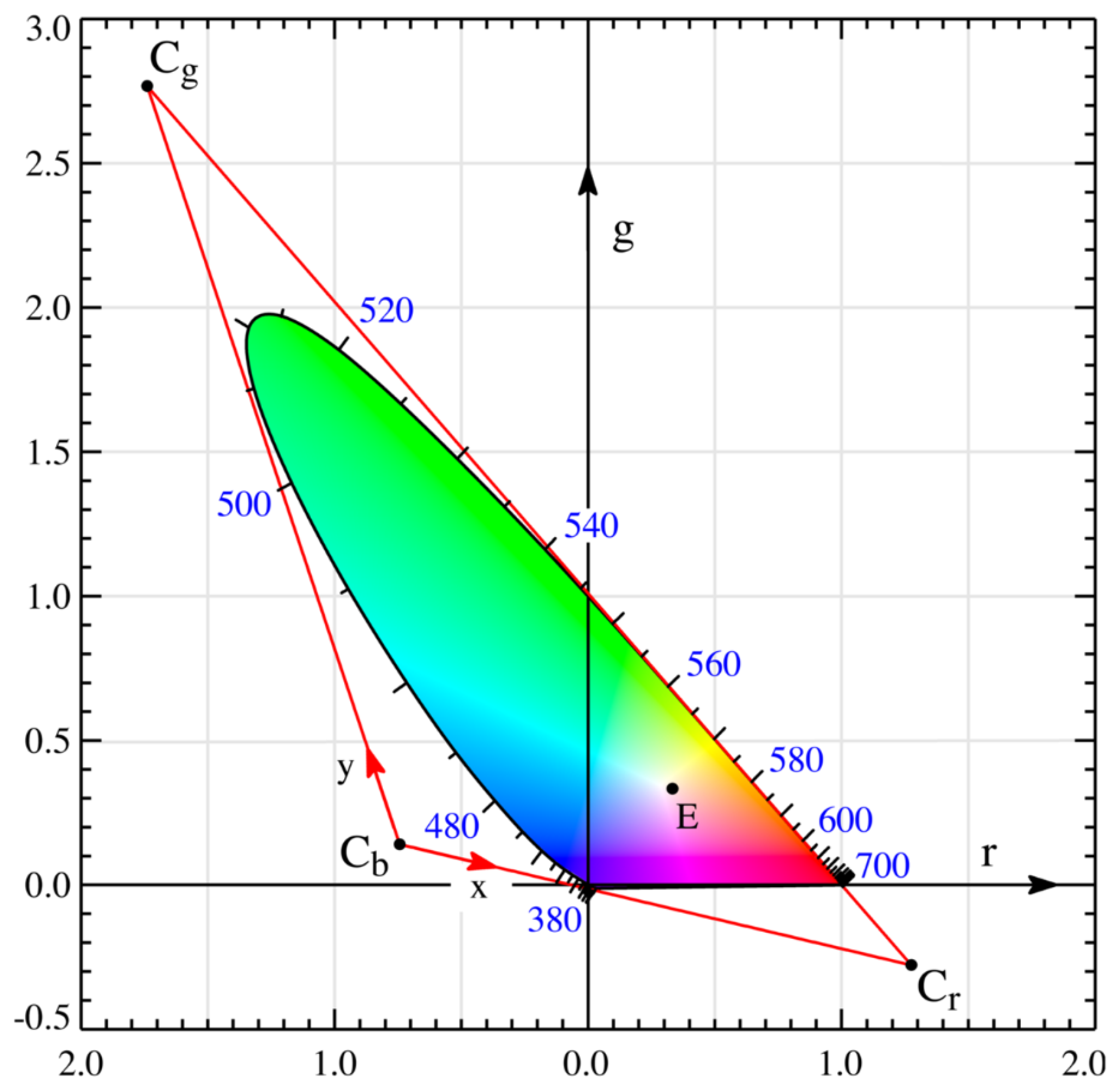
3.4. CIE-xy Color System
4. Wavelength Computation from RGB
- Recompute the RGB values for the spectral curve using a resampling factor ;
- Compute the rainbow curve samples with 100% color saturation;
- Uniformly resample the rainbow curve with a fine resolution using the scaling factor to obtain RGB values for each point;
- Obtain relevant wavelengths on and ;
- Project the rainbow curve points to (for the sector) and (for the sector) lines to find the relevant points on the x-axis and y-axis, respectively;
- Interpolate the wavelengths corresponding to these relevant points from the resampled RGB values obtained in step 1.
- Compute the relevant position of the point D using the projection on either or , depending on whether C is in the or sector;
- Use the r or g value of the point D as an index to the table with the interpolated wavelengths, applying the scaling factor and the offset k as follows:
- Compute the relevant position of the point D using the projection on either or , depending on whether C is in the or sector.
- saturation within the RGB cube, i.e., 100% means that the color of a pixel is on the face of the RGB cube;
- saturation within the natural variety of colors, i.e., covering also colors outside of the RGB cube.
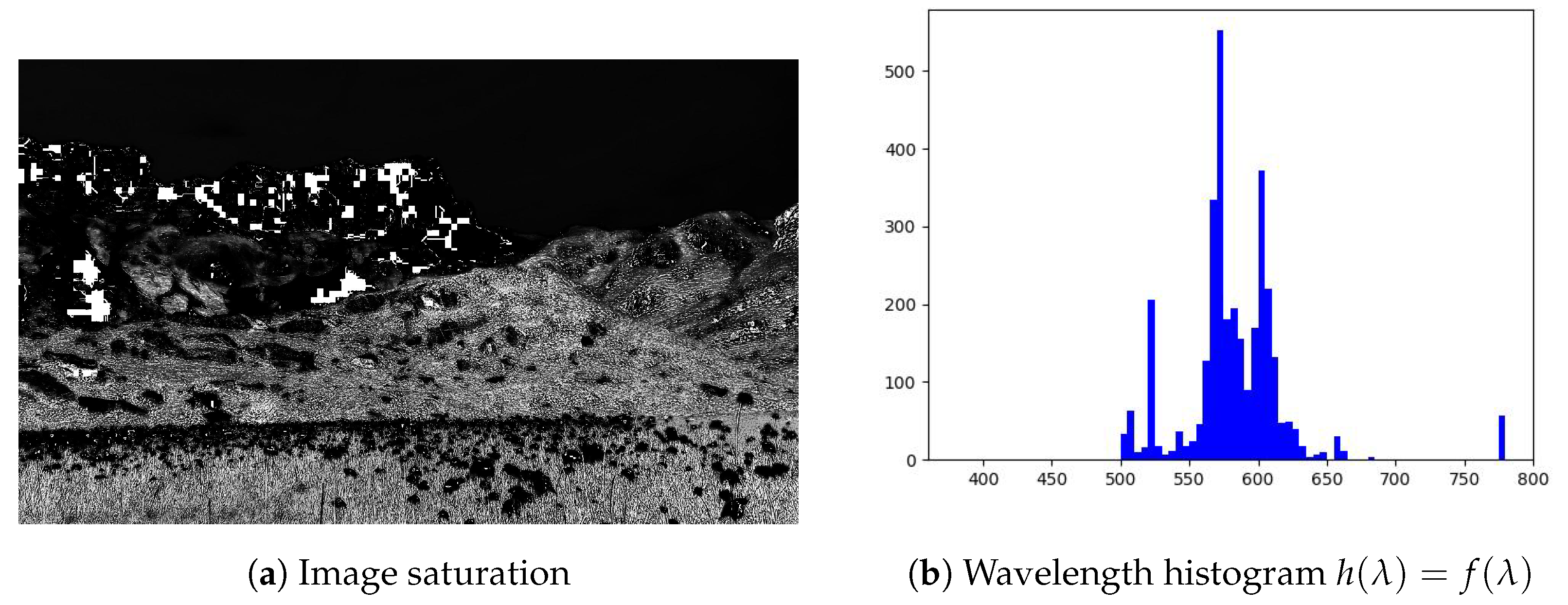
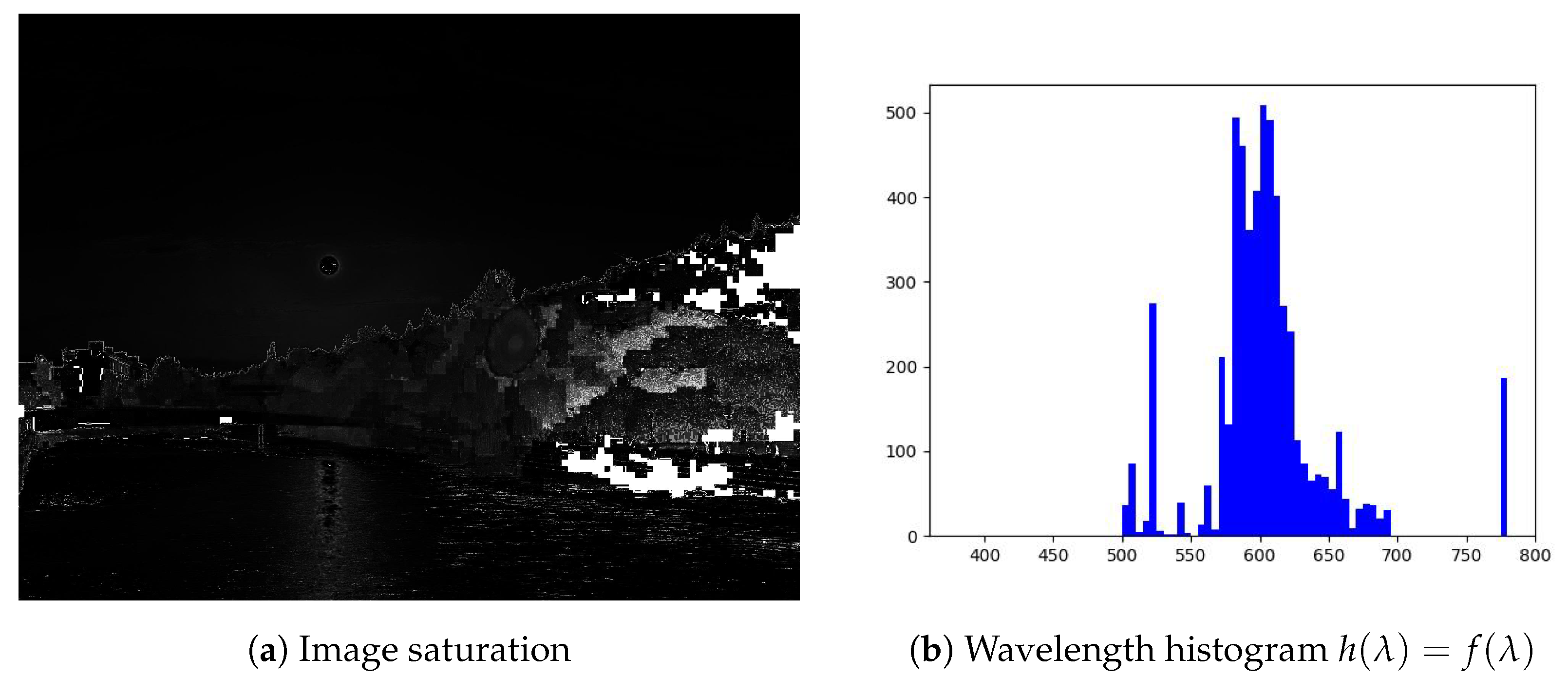
5. Experimental Results
6. Conclusions
- Look-up table generation: The use of a precomputed look-up table for wavelength conversion allows for fast and efficient processing of RGB images. Once the table is generated, it can be used for all images without the need for repeated calculations.
- Simple run-time: The actual wavelength extraction using the look-up table involves simple linear interpolation, which is computationally efficient and convenient for processing large images.
- Wide range of applications: The method opens up various applications in image processing, computer vision, and astro-image processing. Using wavelength information instead of traditional gray-scale or RGB values can provide valuable insights and may lead to novel image analysis techniques.
- Potential for future exploration: The potential use of the XYZ color system, which eliminates negative values, can be an interesting direction for future research and development. Exploring other color spaces and their implications on image processing and analysis could yield valuable results.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. RGB Trichromatic Coefficients
| r | g | b | r | g | b | ||
|---|---|---|---|---|---|---|---|
| 380 | 0.00003 | −0.00001 | 0.00117 | 580 | 0.24526 | 0.13610 | −0.00108 |
| 385 | 0.00005 | −0.00002 | 0.00189 | 585 | 0.27989 | 0.11686 | −0.00093 |
| 390 | 0.00010 | −0.00004 | 0.00359 | 590 | 0.30928 | 0.09754 | −0.00079 |
| 395 | 0.00017 | −0.00007 | 0.00647 | 595 | 0.33184 | 0.07909 | −0.00063 |
| 400 | 0.00030 | −0.00014 | 0.01214 | 600 | 0.34429 | 0.06246 | −0.00049 |
| 405 | 0.00047 | −0.00022 | 0.01969 | 605 | 0.34756 | 0.04776 | −0.00038 |
| 410 | 0.00084 | −0.00014 | 0.03707 | 610 | 0.33971 | 0.03557 | −0.00030 |
| 415 | 0.00139 | −0.00070 | 0.06637 | 615 | 0.32265 | 0.02583 | −0.00022 |
| 420 | 0.00211 | −0.00110 | 0.11541 | 620 | 0.29708 | 0.01828 | −0.00015 |
| 425 | 0.00266 | −0.00143 | 0.18575 | 625 | 0.26348 | 0.01253 | −0.00011 |
| 430 | 0.00218 | −0.00119 | 0.24769 | 630 | 0.22677 | 0.00833 | −0.00008 |
| 435 | 0.00036 | −0.00021 | 0.29012 | 635 | 0.19233 | 0.00537 | −0.00005 |
| 440 | −0.00261 | 0.00149 | 0.31228 | 640 | 0.15968 | 0.00334 | −0.00003 |
| 445 | −0.00673 | 0.00379 | 0.31860 | 645 | 0.12905 | 0.00199 | −0.00002 |
| 450 | −0.01213 | 0.00678 | 0.31670 | 650 | 0.10167 | 0.00116 | −0.00001 |
| 455 | −0.01874 | 0.01046 | 0.31166 | 655 | 0.07857 | 0.00066 | −0.00001 |
| 460 | −0.02608 | 0.01485 | 0.29821 | 660 | 0.05932 | 0.00037 | 0.00000 |
| 465 | −0.03324 | 0.01977 | 0.27295 | 665 | 0.04366 | 0.00021 | 0.00000 |
| 470 | −0.03933 | 0.02538 | 0.22991 | 670 | 0.03149 | 0.00011 | 0.00000 |
| 475 | −0.04471 | 0.03183 | 0.18592 | 675 | 0.02294 | 0.00006 | 0.00000 |
| 480 | −0.04939 | 0.03914 | 0.14494 | 680 | 0.01687 | 0.00003 | 0.00000 |
| 485 | −0.05364 | 0.04713 | 0.10968 | 685 | 0.01187 | 0.00001 | 0.00000 |
| 490 | −0.05814 | 0.05689 | 0.08257 | 690 | 0.00819 | 0.00000 | 0.00000 |
| 495 | −0.06414 | 0.06948 | 0.06246 | 695 | 0.00572 | 0.00000 | 0.00000 |
| 500 | −0.07173 | 0.08536 | 0.04776 | 700 | 0.00410 | 0.00000 | 0.00000 |
| 505 | −0.08120 | 0.10593 | 0.03688 | 705 | 0.00291 | 0.00000 | 0.00000 |
| 510 | −0.08901 | 0.12860 | 0.02698 | 710 | 0.00210 | 0.00000 | 0.00000 |
| 515 | −0.09356 | 0.15262 | 0.01842 | 715 | 0.00148 | 0.00000 | 0.00000 |
| 520 | −0.09264 | 0.17468 | 0.01221 | 720 | 0.00105 | 0.00000 | 0.00000 |
| 525 | −0.08473 | 0.19113 | 0.00830 | 725 | 0.00074 | 0.00000 | 0.00000 |
| 530 | −0.07101 | 0.20317 | 0.00549 | 730 | 0.00052 | 0.00000 | 0.00000 |
| 535 | −0.05316 | 0.21083 | 0.00320 | 735 | 0.00036 | 0.00000 | 0.00000 |
| 540 | −0.03152 | 0.21466 | 0.00146 | 740 | 0.00025 | 0.00000 | 0.00000 |
| 545 | −0.00613 | 0.21487 | 0.00023 | 745 | 0.00017 | 0.00000 | 0.00000 |
| 550 | 0.02279 | 0.21178 | −0.00058 | 750 | 0.00012 | 0.00000 | 0.00000 |
| 555 | 0.05514 | 0.20588 | −0.00105 | 755 | 0.00008 | 0.00000 | 0.00000 |
| 560 | 0.09060 | 0.19702 | −0.00130 | 760 | 0.00006 | 0.00000 | 0.00000 |
| 565 | 0.12840 | 0.18522 | −0.00138 | 765 | 0.00004 | 0.00000 | 0.00000 |
| 570 | 0.16768 | 0.17087 | −0.00135 | 770 | 0.00003 | 0.00000 | 0.00000 |
| 575 | 0.20715 | 0.15429 | −0.00123 | 775 | 0.00001 | 0.00000 | 0.00000 |
| 580 | 0.24526 | 0.13610 | −0.00108 | 780 | 0.00000 | 0.00000 | 0.00000 |
References
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Faugeras, O.; Luong, Q.T.; Papadopoulou, T. The Geometry of Multiple Images: The Laws That Govern The Formation of Images of a Scene and Some of Their Applications; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Starck, J.L.; Murtagh, F.; Bijaoui, A. Image Processing and Data Analysis: The Multiscale Approach; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Szeliski, R. Computer Vision: Algorithms and Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Burger, W.; Burge, M.J. Digital Image Processing: An Algorithmic Introduction Using Java, 2nd ed.; Springer Publishing Company: New York, NY, USA, 2016. [Google Scholar]
- Wang, M.; Lai, C.H. A Concise Introduction to Image Processing Using C++, 1st ed.; Chapman & Hall/CRC: London, UK, 2008. [Google Scholar]
- Nassau, K. (Ed.) Color for Science, Art and Technology, 1st ed.; North Holland: Amsterdam, The Netherlands, 1998; p. 490. [Google Scholar]
- Hall, R. Illumination and Color in Computer Generated Imagery; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Jackson, R.; MacDonald, L.; Freeman, K. Computer Generated Color: A Practical Guide to Presentation and Display; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1994. [Google Scholar]
- Stone, M. Field Guide to Digital Color; A. K. Peters, Ltd.: Natick, MA, USA, 2002. [Google Scholar]
- Giorgianni, E.J.; Madden, T.E. Digital Color Management: Encoding Solutions; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1998. [Google Scholar]
- Hoffmann, M. Digital signal processing mathematics. CAS—CERN Accel. Sch. Course Digit. Signal Process. 2008. [Google Scholar]
- Hrdina, J.; Vašík, P.; Matoušek, R.; Návrat, A. Geometric algebras for uniform colour spaces. Math. Methods Appl. Sci. 2018, 41, 4117–4130. [Google Scholar] [CrossRef]
- Ohta, N.; Robertson, A.R. Colorimetry: Fundamentals and Applications; Wiley: Hoboken, NJ, USA, 2006; pp. 1–334. [Google Scholar] [CrossRef]
- Hornak, P. Svetelna Technika (Lighting Technology); Alfa: Bratislava, Slovakia, 1989; p. 247. [Google Scholar]
- Skala, V. Length, Area and Volume Computation in Homogeneous coordinates. Int. J. Image Graph. 2006, 6, 625–639. [Google Scholar] [CrossRef]
- Keller, P.A. Electronic Display Measurement: Concepts, Techniques, and Instrumentation; John Wiley&Sons: London, UK, 1997; p. 325. [Google Scholar]
- Zhou, W.; Zhang, X.; Wang, H.; Gao, S.; Lou, X. Raw Bayer Pattern Image Synthesis for Computer Vision-oriented Image Signal Processing Pipeline Design. arXiv 2021, arXiv:2110.12823. Available online: https://arxiv.org/pdf/2110.12823.pdf (accessed on 12 September 2023).
- Park, J.; Chong, J. Pattern Transformation Method for Digital Camera with Bayer-Like White-RGB Color Filter Array. IEICE Trans. Inf. Syst. 2015, E98.D, 2021–2025. [Google Scholar] [CrossRef]
- Poomrittigul, S.; Ogawa, M.; Iwahashi, M.; Kiya, H. Reversible color transform for Bayer color filter array images. APSIPA Trans. Signal Inf. Process. 2013, 2, e5. [Google Scholar] [CrossRef]
- Mohammed, S.K.; Rahman, K.M.M.; Wahid, K.A. Lossless Compression in Bayer Color Filter Array for Capsule Endoscopy. IEEE Access 2017, 5, 13823–13834. [Google Scholar] [CrossRef]
- Li, D.; Wang, M.; Jiang, J. China’s high-resolution optical remote sensing satellites and their mapping applications. Geo-Spat. Inf. Sci. 2021, 24, 85–94. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, X.; Wang, S.; Zhang, L. Advances in spaceborne hyperspectral remote sensing in China. Geo-Spat. Inf. Sci. 2021, 24, 95–120. [Google Scholar] [CrossRef]
- Zhao, B.; Gao, L.; Liao, W.; Zhang, B. A new kernel method for hyperspectral image feature extraction. Geo-Spat. Inf. Sci. 2017, 20, 309–318. [Google Scholar] [CrossRef]
- Roy, P. Spectral reflectance characteristics of vegetation and their use in estimating productive potential. Proc. Plant Sci. 1989, 99, 59–81. [Google Scholar] [CrossRef]
- Gates, D.M.; Keegan, H.J.; Schleter, J.C.; Weidner, V.R. Spectral properties of plants. Appl. Opt. 1965, 4, 11–20. [Google Scholar] [CrossRef]
- Ouzounis, T.; Rosenqvist, E.; Ottosen, C.O. Spectral Effects of Artificial Light on Plant Physiology and Secondary Metabolism: A Review. HortSci. Horts 2015, 50, 1128–1135. [Google Scholar] [CrossRef]
- Carranza-García, M.; Galán-Sales, F.J.; Luna-Romera, J.M.; Riquelme, J.C. Object detection using depth completion and camera-LiDAR fusion for autonomous driving. Integr. Comput. Aided Eng. 2022, 29, 241–258. [Google Scholar] [CrossRef]
- Chakraborty, D.; Singh, S.; Dutta, D. Segmentation and classification of high spatial resolution images based on Hölder exponents and variance. Geo-Spat. Inf. Sci. 2017, 20, 39–45. [Google Scholar] [CrossRef][Green Version]
- Verma, G.; Kumar, M. Under-water image enhancement algorithms: A review. In Proceedings of the AIP Conference Proceedings, Mathura, India, 24–26 December 2023; Volume 2721, p. 040031. [Google Scholar] [CrossRef]
- Vince, J. Geometric Algebra: An Algebraic System for Computer Games and Animation, 1st ed.; Springer Publishing Company: New York, NY, USA, 2009. [Google Scholar]
- Skala, V. Intersection Computation in Projective Space using Homogeneous Coordinates. Int. J. Image Graph. 2008, 8, 615–628. [Google Scholar] [CrossRef]
- Lengyel, E. Mathematics for 3D Game Programming and Computer Graphics, 3rd ed.; Course Technology Press: Boston, MA, USA, 2011. [Google Scholar]
- Skala, V.; Karim, S.; Kadir, E. Scientific Computing and Computer Graphics with GPU: Application of Projective Geometry and Principle of Duality. Int. J. Math. Comput. Sci. 2020, 15, 769–777. [Google Scholar]
- Johnson, M. Proof by Duality: Or the Discovery of “New” Theorems. Math. Today 1996, 138–153. [Google Scholar]
- Skala, V.; Kuchař, M. The hash function and the principle of duality. In Proceedings of the Computer Graphics International Conference, CGI, Hong Kong, China, 6 July 2001; pp. 167–174. [Google Scholar]
- Arokiasamy, A. Homogeneous coordinates and the principle of duality in two dimensional clipping. Comput. Graph. 1989, 13, 99–100. [Google Scholar] [CrossRef]
- Skala, V. Duality, barycentric coordinates and intersection computation in projective space with GPU support. WSEAS Trans. Math. 2010, 9, 407–416. [Google Scholar]
- Skala, V. Projective geometry, duality and Plücker coordinates for geometric computations with determinants on GPUs. In Proceedings of the International Conference of Numerical Analysis and Applied Mathematics (ICNAAM 2016), Rhodes, Greece, 19–25 September 2017; Volume 1863. [Google Scholar] [CrossRef]
- Skala, V. Geometric Transformations and Duality for Virtual Reality and Haptic Systems. Commun. Comput. Inf. Sci. 2014, 434 Pt I, 642–647. [Google Scholar] [CrossRef]
- Skala, V. Duality and intersection computation in projective space with GPU support. In Proceedings of the International Conference on Applied Mathematics, Simulation, Modelling, Corfu Island, Greece, 22–25 July 2010; pp. 66–71. [Google Scholar]
- Skala, V. Geometry, duality and robust computation in engineering. WSEAS Trans. Comput. 2012, 11, 275–293. [Google Scholar]
- Zapletal, J.; Vaněček, P.; Skala, V. RBF-based image restoration utilising auxiliary points. In Proceedings of the Computer Graphics International Conference, CGI, Victoria, BC, Canada, 26–29 May 2009; pp. 39–43. [Google Scholar] [CrossRef]
- Uhlir, K.; Skala, V. Radial basis function use for the Restoration of damaged images. In Computer Vision and Graphics (ICCVG 2004), Computational Imaging and Vision; Springer: Dordrecht, The Netherlands, 2006; Volume 32, pp. 839–844. [Google Scholar] [CrossRef]
- Hassan, M.F.; Adam, T.; Rajagopal, H.; Paramesran, R. A hue preserving uniform illumination image enhancement via triangle similarity criterion in HSI color space. Vis. Comput. 2022. [Google Scholar] [CrossRef]
- Plataniotis, K.N.; Venetsanopoulos, A.N. Color Image Processing and Applications; Springer: Berlin, Germany, 2010; p. 355. [Google Scholar] [CrossRef]
- Ma, S.; Ma, H.; Xu, Y.; Li, S.; Lv, C.; Zhu, M. A low-light sensor image enhancement algorithm based on HSI color model. Sensors 2018, 18, 3583. [Google Scholar] [CrossRef]
- Skala, V.; Bellot, T.C.L.; Berault, X. Wavelength Computation from RGB. Lect. Notes Comput. Sci. 2023, 13957 LNCS, 423–430. [Google Scholar] [CrossRef]
- Skala, V. Barycentric coordinates computation in homogeneous coordinates. Comput. Graph. 2008, 32, 120–127. [Google Scholar] [CrossRef]
- Skala, V. A Brief Survey of Clipping and Intersection Algorithms with a List of References. Informatica 2023, 34, 169–198. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skala, V. Multispectral Image Generation from RGB Based on WSL Color Representation: Wavelength, Saturation, and Lightness. Computers 2023, 12, 182. https://doi.org/10.3390/computers12090182
Skala V. Multispectral Image Generation from RGB Based on WSL Color Representation: Wavelength, Saturation, and Lightness. Computers. 2023; 12(9):182. https://doi.org/10.3390/computers12090182
Chicago/Turabian StyleSkala, Vaclav. 2023. "Multispectral Image Generation from RGB Based on WSL Color Representation: Wavelength, Saturation, and Lightness" Computers 12, no. 9: 182. https://doi.org/10.3390/computers12090182
APA StyleSkala, V. (2023). Multispectral Image Generation from RGB Based on WSL Color Representation: Wavelength, Saturation, and Lightness. Computers, 12(9), 182. https://doi.org/10.3390/computers12090182






