Comparison between an RSSI- and an MCPD-Based BLE Indoor Localization System ^†

Abstract

IPS is a crucial technology that enables medical staff and hospital management to accurately locate and track persons or assets inside medical buildings. Among other technologies, readily available BLE can be exploited to achieve an energy-efficient and low-cost solution. This work presents the design, implementation and comparison of a RSSI-based and a MCPD-based indoor localization system. The implementation is based on a lightweight wkNN algorithm that processes RSSI and MCPD distance data from connection-less BLE Beacons. The designed hardware and firmware are implemented around the state-of-the-art SoC for BLE, the nRF5340 from Nordic Semiconductor. Experimental evaluation with real-time data processing has been evaluated and presented in a 7.3 m × 8.9 m room with furniture and six beacon nodes. The experimental results on randomly chosen validation points within the room show an average error of only 0.50 m for the MCPD approach, whereas the RSSI approach achieved an error of 1.39 m.

1. Introduction

The complexity of medical buildings, such as hospitals, clinics and nursing facilities, is increasing every day due to the increasing number of patients/hosts [1]. Moreover, the complexity increases due to new equipment and technologies offered to the staff, ranging from medical equipment to electronic medical data storage. In recent years, we have been assisting with the introduction of information technology location-aware devices and systems for healthcare environments that are exploiting different IoT technologies [1,2]. The main goal of those emerging IPS is enabling medical staff and hospital management to accurately locate and track assets or even persons inside the medical buildings [1]. Among other scenarios where IPS can be exploited, promising hospital scenarios could become a reality for IPS in the near future: finding equipment and other medical devices inside a hospital or a building is often a complicated and time-consuming task. In large hospitals, time is crucial, and having a fast and reliable way to identify the location of equipment could save lives [3]. Moreover, the vision is to have a next-generation nurse smart-calling system that is able to locate the nearest nurse in the medical building. This can make medical work more efficient [4], e.g., to locate and track medical equipment, which simultaneously helps identify paths of infection [5]. In further steps, the IPS can lead to more freedom for patients and can help medical staff to track patients inside the hospital or in large indoor areas. This could especially be helpful when patients with a critical disease, such as dementia, get lost in the medical building. These are only a few examples of how an IPS can improve the internal functionalities inside a hospital.

Advances in electronics, computer sciences, miniaturization and wireless communication enable energy-efficient communication among battery-operated smart devices inside the IoT paradigm [6,7]. The presence of a smart device allowing the discovery, communication and data analysis is the key enabling factor for the real development and deployment of IoT applications such as IPS [1]. Wireless communication technologies enable IPS with a precision down to a few centimeters [8]. The development of a functional localization system accurate to one meter could be applied to many application scenarios, especially within the medical section. In addition to the highest possible precision, this should also be cost-effective and as easy to set up as possible—which guarantees a large application area. GPS is a well-known and established technology to precisely identify a location—however, it is well-known that it cannot be used indoors [9,10]. Different systems and technologies have been investigated and proposed in the recent literature, and a few of them are available on the market to address the need for indoor localization, including systems that use cameras or other combinations of sensors [11]. However, emerging research is investigating new ways of using wireless communication to enable accurate indoor localization [9,12].

The most promising wireless technologies for meter-precision indoor localization are WLAN [13], UWB [14,15], RFID [16], BLE [17] and LoRa [18], including combinations with GPS [19]. Many researchers have been investigating the possibility of using WLAN for the fact that it is pervasive in all buildings and it has a long-range—however, the high energy consumption for a battery-powered system and the not excellent accuracy in the detection are the main weaknesses. Due to the ultra-wideband and the nature of the technology [14], the solutions based on UWB allow very high accuracy of less than 30 cm in a radius of tenths of meters—however, current UWB modules still have a too high power consumption, around 55 mW [15], which reduces its use in a real-application scenario where the IoT device needs to last months with a coin battery. RFID allows the achievement of very low-energy consumption as many tags can even work without any supply. Moreover, the passive tags achieve the most accurate cm accuracy [20]. But the operative range is restricted to the small range of less than 2 m [21], while the active tags for extending the ranges are affected by larger energy consumption and bigger antennas. Long-Range sub-giga wireless communication such as LoRa [22] have been investigated to provide localization information. However, the range achieved is in the order of several hundred meters, which makes them not suitable for high-precision indoor localization. Some researchers combined LoRa with GPS to achieve below-meter accuracy with real-time kinematics, however, this solution works only outdoors [19]. BLE 5.x offers an optimal trade-off of accuracy, range, energy consumption and availability in all modern phones that have been exploited by many recent works, including the novel features of estimation of the AoA enabled from the 5.2 version of BLE [23], which also allows for ranging applications [24]. Figure 1 gives an overview of the most exploited wireless technologies for indoor localization with some key parameters such as range, accuracy and energy efficiency when supplied by batteries.

Although technology is advancing wireless communications, indoor localization systems are still prone to errors—attenuated by software algorithms. Many previous works focusing on the use of CNN have been proposed as a competitive solution, especially for WLAN [25] and BLE [26]. CNN are improving the precision performance on the one hand, and on the other hand, CNN models are designed to be executed on a CPU or GPU, requiring data to be transmitted from the mobile sensor node to an external computer engine through wired or wireless communication. Recently, a new generation of mobile smart IoT is attracting academic and industrial researchers, using MCU, which are supposed to bring computing capabilities toward the “edge” to perform real-time computation [27,28]. Edge computing offers the following advantages:

• lower energy consumption for the data transmission between IoT devices and remote processing;
• longer battery lifetime;
• significantly shorter latency compared to remote computation;
• user comfort;
• security and privacy improvements, as the data are processed locally [27].

This paper focuses on the design and implementation of a low-cost and battery-operated hardware and software system for an indoor localization system. In particular, the system is based on BLE 5.2 using the low-power general-purpose multi-protocol SoC nRF5340 from Nordic Semiconductor. Our study presents an evaluation and comparison of two localization technologies based on BLE: MCPD and RSSI. While RSSI has been analyzed in depth in previous research, MCPD is relatively new, and little research exists on it. Notably, to the best of our knowledge, this is the first comparison of the two methods under BLE. By comparing the performance of the wkNN algorithm using MCPD and RSSI methods, our research contributes to the existing literature on IPS. The implementation of the wkNN algorithm, together with MCPD and RSSI, is described, in detail, in this paper. We hereby present the following contributions:

• On the software side, the paper compares the performance of wkNN for the two different ranging methods based on BLE: One being based on MCPD, the other on RSSI.
• The design of the anchors and the mobile nodes are presented and evaluated with experimental results showing an overall accuracy of the implemented algorithm below 1 m using MCPD and below 2 m using RSSI on average for a 7.3 m × 8.9 m room.

2. Background on BLE-Based Localization

Ranging-based localization of a moving target, in general, requires the availability of multiple fixed anchors [29], which can be arranged in two ways: In the first variant, a mobile device receives packets from the fixed anchors and records the distance. The other method would be to have multiple fixed receivers and a mobile device as a transmitter of the packets. Figure 2 illustrates the two options where the white pentagon in the middle identifies the mobile tag. The four circles in the corners are the BLE anchors that are fixed.

The former configuration achieves a higher energy efficiency of the mobile device, as it can wake up autonomously and decide when to receive messages and must not be connected to the anchors. In addition, all calculations can be carried out on the receiver—thus, the beacon themselves do not need to communicate with each other.

Therefore, the approach with the sending anchors is used in this work.

2.1. Ranging Technologies

The distance itself can be obtained in different ways. The classical way of ranging between two BLE devices is by using the RSSI [30]. With the addition of Direction Finding to BLE, novel devices have the capability of incoming phase measurements using IQ sampling and can exploit this also for ranging.

2.1.1. RSSI-Based Ranging

All BLE devices are capable of measuring the power of an incoming signal, called RSSI. To enable RSSI-based ranging, the decrease in signal strength has to be clarified with the increase in distance in a medium such as air. A well-known mathematical model is the logarithmic distance loss model [31]. In this model, the decrease in signal strength is assumed to be logarithmic decreasing with the increasing distance [32]. Equation (1) illustrates the model used for the RSSI value to approximate the distance.

$$\mathit{RSSI}\left(d\right)=\mathit{RSSI}\left(d_0\right)-10n·{log}_{10}\left(\frac{d}{d_0}\right)$$

(1)

where d is the estimated distance, $d_0$ describes a self-defined reference distance, $\mathit{RSSI}\left(\right)$ is the function that assigns the expected signal strength to each distance and n is the path loss parameter given by the properties of the environment.

Figure 3 shows the decay evaluated by Equation (1) based on approximations performed in a room with the received RSSI values of the nRF5340 for both beacon and receiver and a transmission power of 0 dBm.

However, although the theoretical concept describes a strong relationship between distance and path loss, RSSI-based localization is not considered robust [33]. The reasons for this include inaccurate measurement of the incoming signal strength, different antenna gains depending on the antenna rotation and, in particular, dependence on the transport medium and the environment. In particular, obstructed line of sight and reflections from objects generate strong deviations in the received signal strength.

2.1.2. MCPD-Based Ranging

The BLE 5.2 amendment adds functionality for direction finding using BLE. Measuring the IQ components of the incoming signal, devices having multiple antennas can detect the direction of an incoming signal ($\theta$) using the formula in Equation (2),

$$\theta =arccos\left(\frac{\Delta \varphi ·\lambda }{2\pi ·l}\right)$$

(2)

where l is the distance between the two antennas, $\lambda$ is the wavelength of the signal and $\Delta \varphi$ is the measured phase difference of the incoming signal at the different antennas.

Although not explicitly stated in the definition of BLE direction finding, the distance between two devices can also be determined by this IQ data. Two signals of different frequencies traveling through space will experience a different IQ component. The measured phase $\varphi$ can be formulated using Equation (3) [34],

$$\varphi =4\pi ·\frac{d·f}{c}$$

(3)

where d is the distance between the devices, f is the propagation frequency and c is the propagation speed. As this function is surjective but not injective, we have an ambiguity when trying to find the distance for a measured phase shift $\varphi$. Using MCPD, this ambiguity can be eliminated. The initiator of the measurement transmits a signal with a frequency $f_1$. The reflector retransmits the signal (after a fixed amount of time, which correlates with a fixed phase shifts $\Phi$) back to the initiator on the same frequency—where the initiator measures the obtained phase shift ${\varphi }_1$.

$${\varphi }_1=4\pi ·\frac{d·f_1}{c}+\Phi$$

(4)

The procedure is then repeated on a second frequency $f_2$, and the initiator obtains the phase shift ${\varphi }_2$.

$${\varphi }_2=4\pi ·\frac{d·f_2}{c}+\Phi$$

(5)

Using this information, the initiator can then, using invertable Equation (6), calculate the distance between the devices.

$$d=\frac{c}{4\pi }\frac{{\varphi }_2-{\varphi }_1}{f_2-f_1}$$

(6)

In practical applications, this procedure is repeated using multiple different frequencies and solved using least squares to minimize errors introduced during the measurement. This technology has been analyzed in a controlled environment by Zand et al. [24] and then evaluated in a multipath-rich environment by Lu et al. [35] using a DA14695 SoC of Renesas (back then Dialog Semiconductors). The experiment was carried out in an empty experimental building with four anchors in a 6 m × 6 m square arrangement, fixed 160 cm above ground. The tag was fixed in the center 50 cm above ground. The achieved accuracy lies within 25 cm in the x-direction and 10 cm in the y-direction.

The implementation in our work is based on the Nordic Distance Toolbox and their implementation of MCPD using the IFFT.

2.2. Localization Algorithms

The most used setting for localization applications with multiple anchors is trilateration [36], which is also used by GPS.

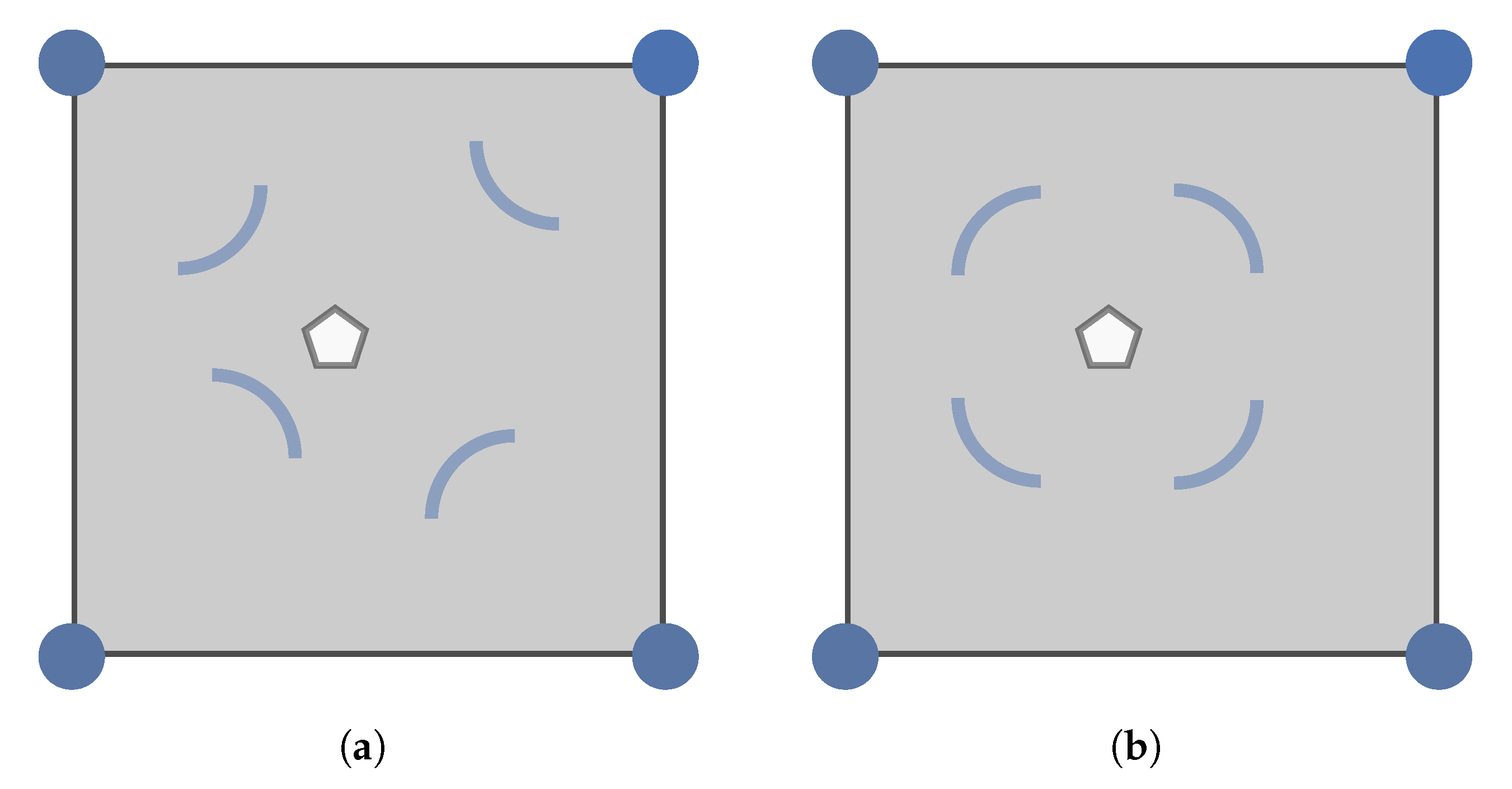
2.2.1. Trilateration

Trilateration [37] is a method where the distance between the target/beacon ($d_i$) and at least three known reference positions (${\left[x_i,y_i,z_i\right]}^{\top }$) are used, to calculate the position of the target (in 3D space). The equations for trilateration are shown in Equation (7) and lead to the target position when solved for the unknown coordinate ${\left[x,y,z\right]}^{\top }$.

$$d_i=\sqrt{{(x-x_i)}^2+{(y-y_i)}^2+{(z-z_i)}^2}$$

(7)

As the exact distance $d_i$ is usually not known (noise, measurement uncertainty, …), additional reference points should be added to the linear system of equations. As the system gets overdetermined, regression methods, such as Gauss’s least squares [38], have to be used to find the most probable position.

Although more references improve the performance of trilateration, it still relies on good, qualitative measurements of the distances. As this is, especially with RSSI, not necessarily given, the performance of trilateration is known to be poor [39]. In order to improve localization accuracy, wkNN has been used in this paper.

2.2.2. Weighted k-Nearest Neighbors Indoor Localization Algorithm

The wkNN algorithm is one of the most widely used algorithms to improve the performance of indoor localization based on RSSI [40]. Moreover, the algorithm can be implemented directly on the MCU, as it does only require memory to store the training data (one value per trainings position and anchor) and little computational resources. This algorithm belongs to the category of supervised learning and requires that the position of the beacons and the positions of the training points are known. Section 3.2 explains the experimental setup used to acquire the data set. Through a previous training (fingerprint), the RSSI and MCPD values from each beacon (vector with six values) at each position are determined. Due to the nature of wkNN, only positions within the trained positions can be estimated.

wkNN [41] is a complement to kNN. In the first step, as shown in Algorithm 1, the distance between the measurement m and all training measurements $t\left[·\right]$ is calculated using a choosable norm. The term “distance” is here used as $d\left[i\right]={∥m-t\left[i\right]∥}_n$, where $t\left[i\right]$ is the training data of training i and ${∥·∥}_n$ is the euclidian (${∥·∥}_2$) or Chebyshev (${∥·∥}_{\infty }$) norm.

Then k smallest distances are taken to form a weighted arithmetic mean of the k closest training positions $p\left[i\right]$ by using the reciprocal of the estimated distance $d\left[i\right]$ to the receiver. The result then corresponds to the estimated position $p_{\mathit{est}}$. The weighting assigns a very high value to the training position with a difference close to zero, while the others split the remainder, promoting convergence to the nearest positions. It is important to note that only positions within the area spanned by the training positions can be correctly detected.

Algorithm 1 wkNN-based localization.

function wkNN($S,m,k$)             ▹S: list of training positions i       $d\leftarrow$[]                                       ▹m: measurement vector       for $i\in S$do                             ▹k: # closest neighbors to select            $d\left[i\right]\leftarrow {∥m\left[i\right]-t\left[i\right]∥}_n$)       end for       $d\leftarrow$SortAscending(d)       $K\leftarrow$GetKClosestNeighbors(d,k)       $w\leftarrow$[]       for $i\in K$ do            $w\left[i\right]\leftarrow \frac{1}{d\left[i\right]}$       end for       $p_{\mathit{est}}\leftarrow \frac{1}{{\sum }_{i}w\left[i\right]}·\left({\displaystyle \sum _i}\left(w\left[i\right]·p\left[i\right]\right)\right)$ end function

3. Materials and Methods

3.1. System Architecture

This paper presents both the beacons and the receiver that were developed based on the BLE 5.3 SoC nRF5340 from Nordic Semiconductor. This was the most advanced BLE chip including BLE Direction Finding at the beginning of the design, as it had the lowest power consumption among all available chips both for the radio interface as well as in terms of computational efficiency. This SoC contains a dual-core ARM Cortex-M33 microcontroller for the user firmware.

Beacon and Receiver Nodes

Figure 4 shows the prototype and block diagram of the node developed and implemented in this work. The node is designed to operate from a 3.7 V LiPo battery, which is used to power the nRF5340 (u-blox Nora B106 module with a ProAnt PCB antenna) using a 1.8 V buck converter, represented by the MCU block in Figure 4b. The node is designed for low power consumption and a small footprint (see Figure 4a). To provide an extended battery lifetime, the nodes are equipped with a can be charged using USB-C.

The average power consumption of the node is around 0.185 mW when advertising/measuring every 100 ms for RSSI and 1.850 mW for MCPD. When increasing the measurement interval for MCPD to 1.5 s (see Section 4.5, possible due to the low variance), the power consumption can be reduced to 0.122 mW, resulting in a runtime of 92 days for RSSI and 139 days for MCPD on the 110 mAh LiPo battery.

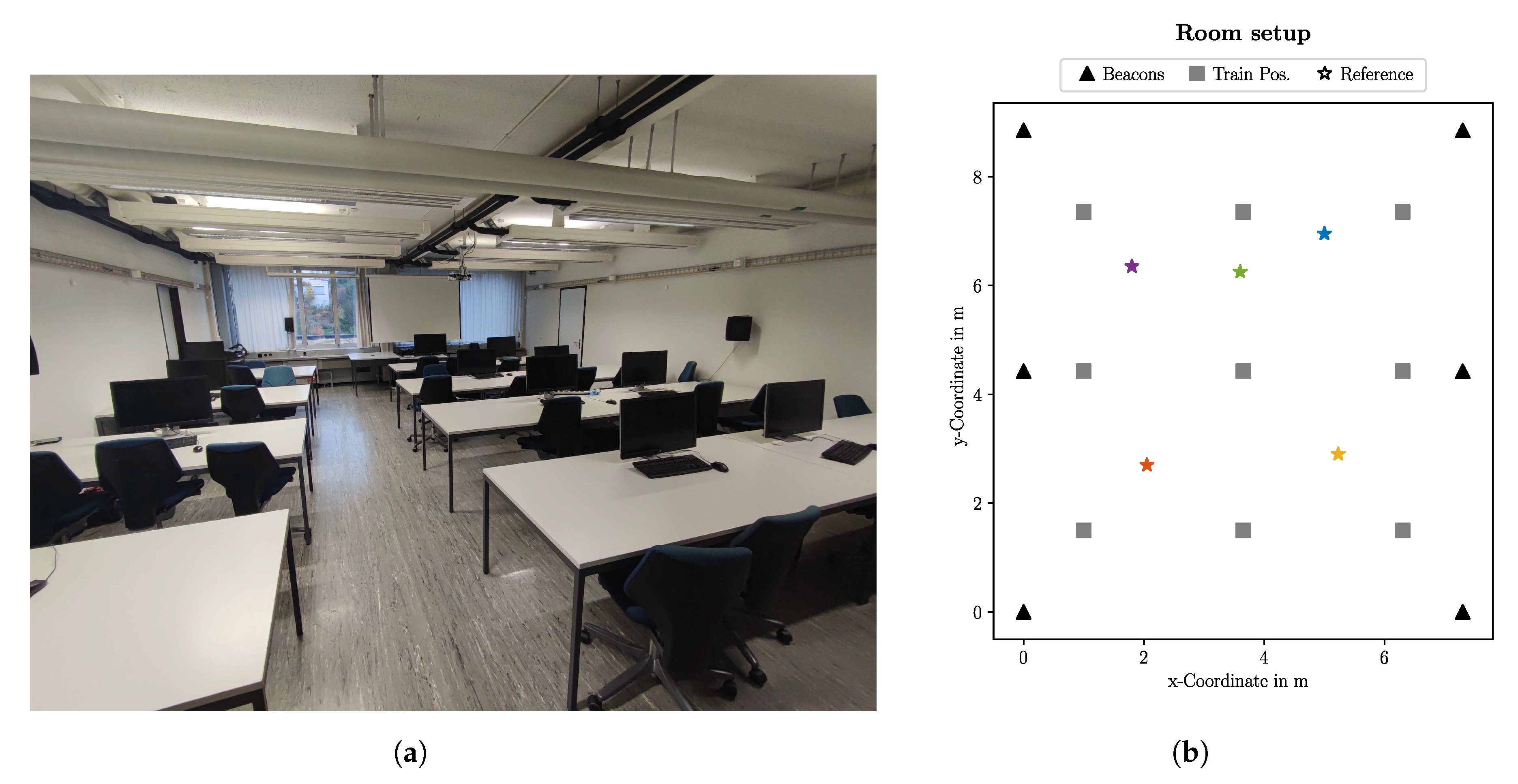
3.2. Experimental Setup

To evaluate the designed prototypes and algorithm, six beacons were distributed equally in the room, as shown in Figure 5. The beacons were placed at a height of 1.8 m above floor level at the edges and side walls of the room. The height was chosen so that the signal is blocked as little as possible, as there are usually no or only a few objects at this height. Figure 5a shows the classroom used for the experimental evaluation with an area of 7.3 × 8.9 m. Additionally, Figure 5b shows the nine training positions and the five validation positions. The edge beacons were mounted on a 45° angle towards the room (see Figure 6a). During the measurements, the receiver node was statically placed on a table, pointing with the antenna always in the same direction (see Figure 6b). Obstacles in the room were the chairs, desks and monitors, which were around 1 m high, as shown in Figure 5a.

It is important to note that the implemented algorithm is evaluated as a regression problem and not as a classification problem of the nine known positions. This is performed to obtain a more realistic and useful system that can be used in an IPS for medical applications. To obtain a proper validation of the algorithm, the validation positions are chosen randomly and different from the training positions.

4. Results

The wkNN algorithm in Algorithm 1 was implemented using both the euclidian (2-norm) and Chebyshev (∞-norm) norms and with $k\in \{3,5\}$. The raw measurement results of the two ranging technologies were then used as an input in the different wkNN configurations.

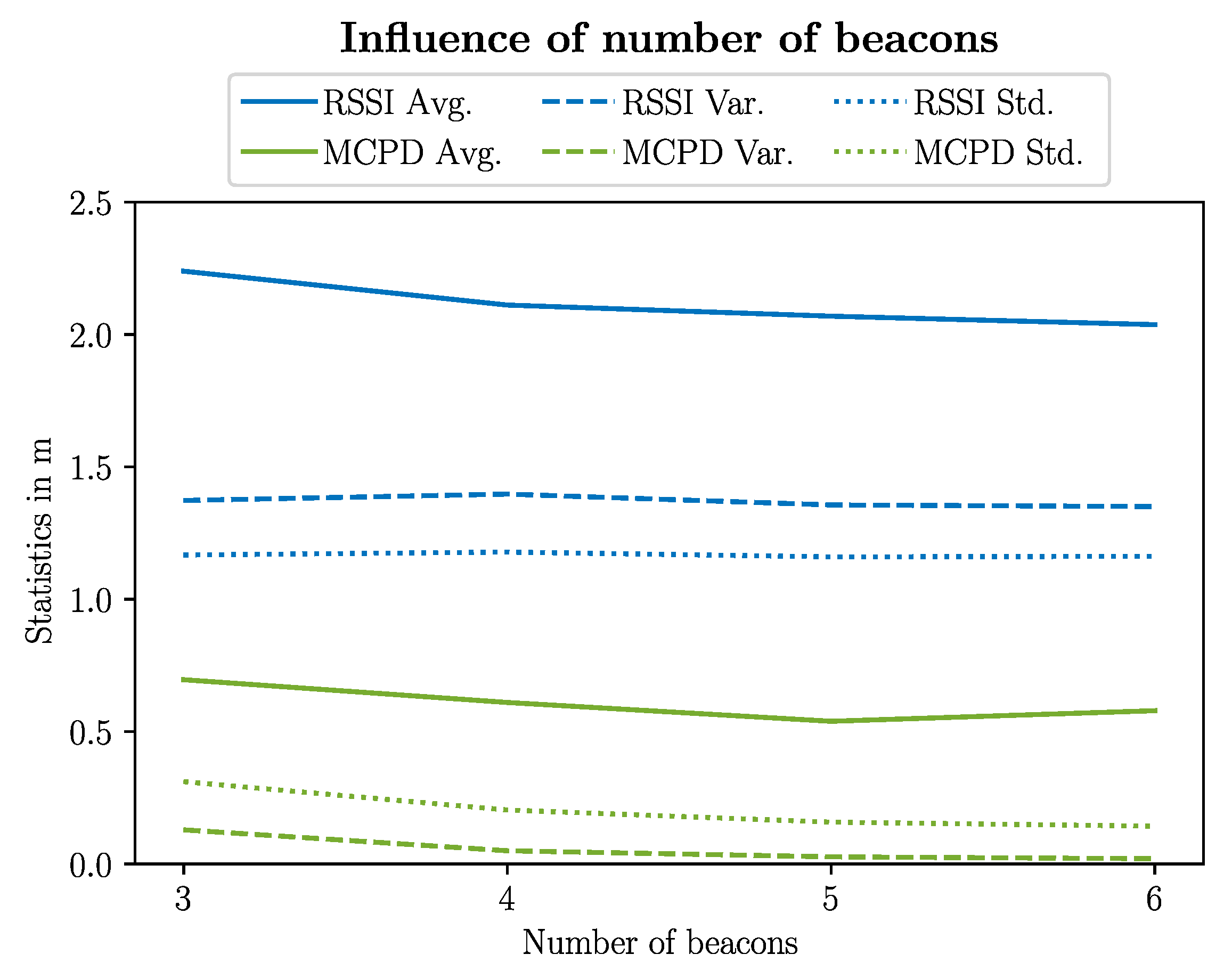
4.1. Influence of the Number of Beacons for the Localization Accuracy

Since the number of beacons in the room is relatively high, which is unlikely in a realistic scenario, the algorithm was evaluated for all possibilities of “6 choose x”, with $x\in \{3,4,5,6\}$. Thus, the performance of all combinations of the available beacons could be analyzed. For the following evaluations, an estimation is performed for every single measurement we took (no a priori averaging of the raw data).

To keep the overview, only the euclidian norm for $k=3$ is considered in this part. The results with $k=3$ were always better than with $k=5$, and the euclidian norm was always better than the Chebyshev norm for RSSI, and for MCPD never more than 20 cm worse.

Table 1. Analysis of the data for the selected amount of badges in the room and for both methods RSSI and MCPD, using $k=3$ and the euclidian norm.

	Number of Beacons
Avg. Statistics	3		4		5		6
	RSSI	MCPD	RSSI	MCPD	RSSI	MCPD	RSSI	MCPD
Avg.	2.239 m	0.696 m	2.111 m	0.610 m	2.069 m	0.539 m	2.037 m	0.579 m
Var.	1.373 m	0.129 m	1.397 m	0.050 m	1.356 m	0.027 m	1.350 m	0.020 m
Std.	1.167 m	0.311 m	1.178 m	0.204 m	1.160 m	0.158 m	1.162 m	0.143 m
Min.	0.048 m	0.067 m	0.048 m	0.145 m	0.095 m	0.115 m	0.245 m	0.245 m
Max.	5.379 m	2.702 m	5.111 m	1.441 m	5.027 m	0.879 m	4.990 m	0.786 m

shows the influence of the number of beacons on the accuracy. For each category, the average results over all combinations using x beacons are shown.

When it comes to the number of beacons; a higher number of beacons generally corresponds to an improvement in accuracy, as can be seen in Figure 7; only with a change from five to six beacons did the performance of MCPD slightly degrade. On average, the accuracy is improved by 3.08% for RSSI and 6.075% for MCPD when adding one more beacon to the room. Notably, precision is also improved by similar percentage points for all nodes, as both the variance and the standard deviation also decreases when more beacons are added.

The selection of the subset of beacons can have a significant influence on the accuracy. As can be seen in Figure 8, depending on which three beacons of the six are used for the calculation of wkNN, the outcome has a large variation. For example, the best selection of three beacons for RSSI achieved a 32.6% improved result when compared to the worst selection of three beacons. For MCPD, the effect was even higher, where the deviation was 52.9%.

4.2. Results When First Averaging 15 Measurements before Estimation, Using 6 Beacons

For further analysis, the case with six beacons is considered, as all available data are taken into account, and measurement inaccuracies can be better filtered out.

Table 2. Average error of the different wkNN configurations and ranging technologies when averaging 15 measurements.

Method	$\mathit{k}=3$		$\mathit{k}=5$
	2-Norm	∞-Norm	2-Norm	∞-Norm
RSSI	1.369 m	1.410 m	1.766 m	1.999 m
MCPD	0.577 m	0.501 m	0.753 m	0.788 m

shows the estimation error on the validation positions when first averaging all measurements (15 per position) before performing the estimation using all six beacons.

The configurations of the wkNN algorithm leading to the best results for both the RSSI-based and the MCPD-based approach are looked at in more detail in the following.

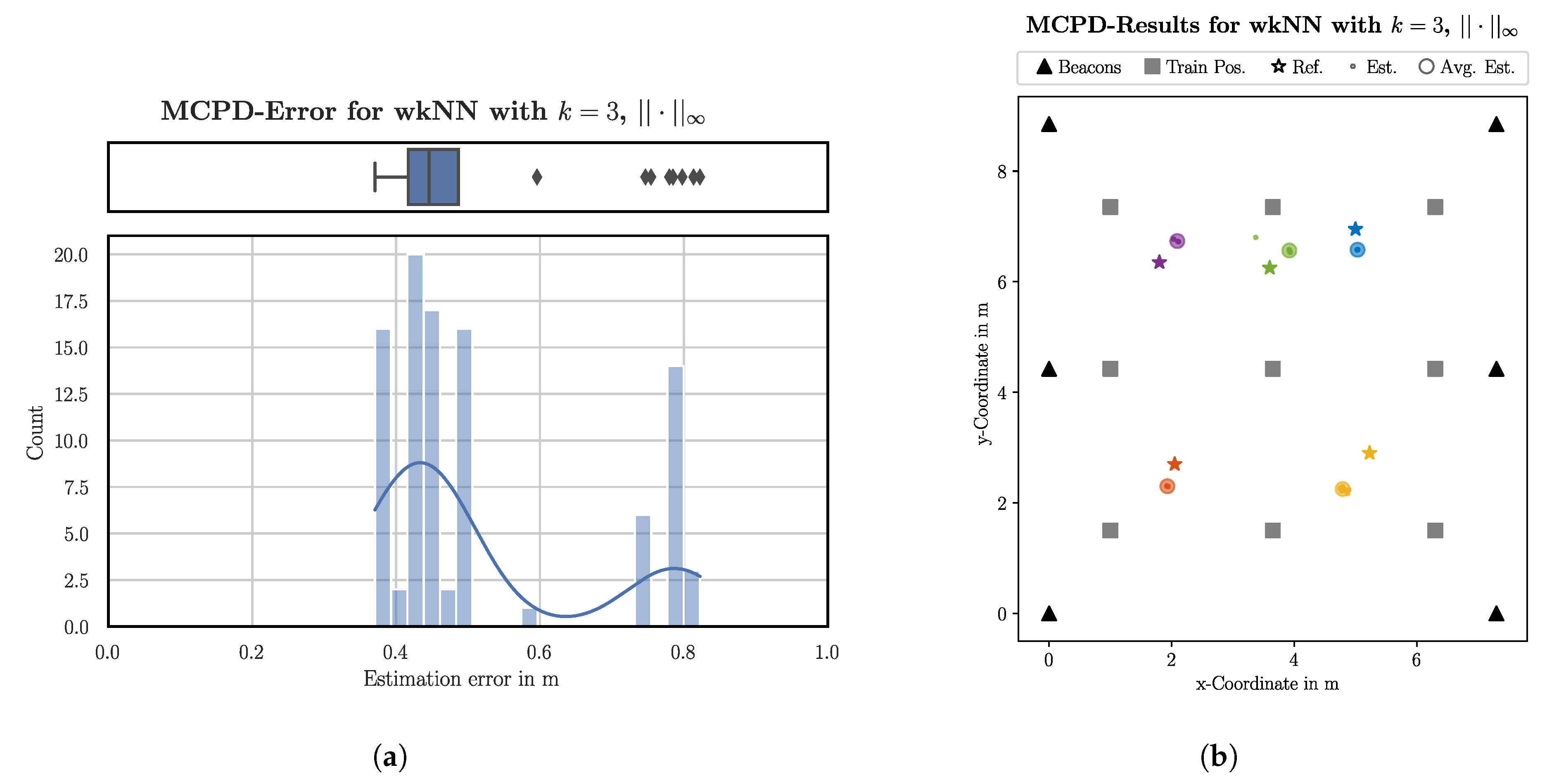
4.3. Results for MCPD Using $k=3$ and the Chebyshev Norm

Applying wkNN to every single measurement of MCPD leads to an average error of 0.52 m with a variance of 0.02 m and a standard deviation of 0.16 m. The best measurement showed an error of 0.35 m, whereas the worst had an error of 0.79 m. Figure 9 shows the histogram and boxplot of all the individual measurements, and on the right side, a map containing the estimations of all individual measurements as well as the estimation result when averaging all measurements (before estimation).

4.4. Results for RSSI Using $k=3$ and the Euclidian Norm

The average error when estimating the position using a single RSSI measurement is 2.04 m. The variance of 1.35 m and the standard deviation of 1.16 m already indicate the difficulty when performing wkNN estimations using RSSI. The maximal error was 4.99 m, and the minimal estimation error was 0.35 m. Figure 10 shows the larger variation of the RSSI estimate when compared to the MCPD estimate, considering a single RSSI measurement.

4.5. Discussion

For both ranging technologies, $k=3$ leads to an improvement of between 23.4% and 36.4% over $k=5$. The chosen norm has a much smaller influence and depending on the used ranging technology, the result changes: For RSSI-based measurements, the euclidian norm performs 2.9% better than the Chebyshev norm, whereas, for the MCPD-based measurement, the Chebyshev norm performs better by 13.2%. Considering only the best configuration of wkNN for both ranging technologies, the MCPD approach leads to a 63.4% decreased average estimation error than RSSI when first averaging the measurements before performing the estimation and by 74.9% when not averaging the measurements.

Due to the small variance of only 0.02 m in the MCPD estimation with individual measurements, the averaging of the measurement before estimation decreases the average error of MCPD by only 3.6%. This is insofar noticeable, as power consumption can be drastically decreased since single measurements are already reliable enough to perform an accurate estimation. On the other hand, RSSI suffers from huge variance in the measurements and estimation (1.35 m). Averaging 15 measurements to perform the estimation can decrease the error by 32.9%, with the trade-off of a slower estimation or higher power consumption. Comparing this to the original paper [17], it seems slightly worse. This can be explained by

• In the original paper, the validation is performed at the same position as the training; the estimation error there can, therefore, be attributed to the variance of the RSSI measurement and not the performance of the algorithm (and linearity between the position) itself.
• Here only 15 measurements have been used to perform the estimation, whereas, in the original paper, 1000 measurements were used.
• A different node design, with a different SoC and antenna design, has been used.

Taking this aspect into account and assuming an estimation interval of 1.5 s (i.e., 1 sample of MCPD for 15 samples of RSSI, collected every 100 ms), the current consumption of MCPD can be reduced to $\approx 33.3$ $\mathsf{\mu }$A by still having a 62.0% improved estimation accuracy over RSSI.

5. Conclusions

This paper presents and compares the design and implementation of an indoor localization hardware-software system that enables localization and tracking in medical applications based on RSSI and MCPD measurements. The used algorithm is the lightweight wkNN that can run on an ARM Cortex-M33 microcontroller. Experimental results in a 7.3 × 8.9 m room have shown the superiority in the accuracy of the MCPD method over the RSSI method. Even with an amount of only three beacons, an accuracy below 1 m can be achieved, which can be improved when adding more beacons. In particular, due to the small variance in the measurements with MCPD, an accuracy of 0.52 m, on average, can be achieved with a single measurement and 6 beacons, while with RSSI, despite the averaging of 15 measurements, a significantly higher average deviation of 1.39 m is achieved. The average current consumption of the beacons is around 50 $\mathsf{\mu }$A at 3.7 V, resulting in a long lifetime of at least three months when powered by a small LiPo battery of 110 mAh. The advantages of the novel MCPD-based ranging is the more and more upcoming availability of BLE Direction Finding, leading to energy-efficient, low-cost and more accurate localization systems than the previously RSSI-based ones.