Abstract
Technology-based in-home reading and spelling programs have the potential to compensate for the lack of sufficient instructions provided at schools. However, the recent COVID-19 pandemic showed the immaturity of the existing remote teaching solutions. Consequently, many students did not receive the necessary instructions. This paper presents a model for developing intelligent reading and spelling programs. The proposed approach is based on an optimization model that includes artificial neural networks and linear regression to maximize the educational value of the pedagogical content. This model is personalized, tailored to the learning ability level of each user. Regression models were developed for estimating the lexical difficulty in the literacy tasks of auditory and visual lexical decision, word naming, and spelling. For building these regression models, 55 variables were extracted from French lexical databases that were used with the data from lexical mega-studies. Forward stepwise analysis was conducted to identify the top 10 most important variables for each lexical task. The results showed that the accuracy of the models (based on root mean square error) reached 88.13% for auditory lexical decision, 89.79% for visual lexical decision, 80.53% for spelling, and 83.86% for word naming. The analysis of the results showed that word frequency was a key predictor for all the tasks. For spelling, the number of irregular phoneme-graphemes was an important predictor. The auditory word recognition depended heavily on the number of phonemes and homophones, while visual word recognition depended on the number of homographs and syllables. Finally, the word length and the consistency of initial grapheme-phonemes were important for predicting the word-naming reaction times.
1. Introduction
Lockdowns during the COVID-19 pandemic have highlighted an urgent need for high-quality technology-based in-home educational programs. However, even before the pandemic, there was always a need for such programs due to the important number of students with severe reading and spelling difficulties. For example, In 2010, a large-scale study evaluated the reading skills of around 800,000 young French adults (age 17 or older) in terms of reading automaticity, vocabulary knowledge, and comprehension [1]. The results showed that 20.4% were not effective readers. Among them, 5.7% had very weak reading skills, and 5.1% had severe reading difficulties. The alarming statistics obtained from such studies encouraged many researchers to search for more effective instructional approaches. Ubiquitous technologies, such as computers, tablets, and smartphones, have great potential for home-based reading approaches. They offer many advantages, such as unlimited access to instructional material, the possibility of personalization, and relieving the burden on the teachers.
It is highly recommended for reading and writing instructions to be systematic [2,3]. However, this is a difficult task for teachers who have limited time and linguistic knowledge. New technologies have the potential to offer systematic instructional approaches. In the scientific literature, there are various technology-based approaches for reading and spelling instructions (e.g., [4,5,6,7,8]). However, these programs are often evaluated as black boxes, and their content management systems are either rudimentary [9,10], or not explicit, as highlighted by a recent review [11]. These problems motivated the research community to develop systematic models from basic levels. In this context, this paper aims at addressing this problem by proposing an intelligent model for in-home reading and spelling instructions dedicated to children of elementary and pre-elementary grades. Due to its flexibility, this intelligent model can be used in a wide variety of reading and spelling tasks. This approach is made of a model for presenting optimal instructional content and regression models based on artificial neural networks and linear regressions. The objective of the optimization model is to maximize the educational value of each training session. This model is constrained by the ability level of each user. The meta-heuristic method of genetic algorithm (GA) is used to solve the optimization problem.
However, to be efficient, the optimization model requires accurate parameters. Lexical difficulty is one of the most important parameters, it depends on many lexical and sub-lexical variables. Unraveling the weight of each variable and the intertwined relationships between them is a complex problem. In addition, lexical difficulty highly depends on the nature of the task. For example, a word may be easy to read but difficult to write. For solving this complex problem, four lexical skills that cover most of the reading and spelling tasks were identified. They are auditory and visual word recognition (represented by auditory and visual lexical decision tasks), word decoding (represented by word naming) and spelling. The data of French lexical mega-studies were used with the data of 55 French lexical and sub-lexical variables (extracted from Lexique 3.83 [12,13], and Lexique Infra [14]) to build the lexical difficulty models. For auditory and visual lexical decisions, the MEGALEX [15] database was used. For the spelling task, the database published in the EOLE book [16] was used and the Chronolex database [17] was used for the word naming task.
Combining lexical and sub-lexical databases with the databases of the mega-studies created a database that included 25,776 words for the visual lexical decision. However, the auditory lexical decision had 15,842 words, the spelling task had 11,373 words, and the word-naming task had 1481 words. Since the number of lexical and sub-lexical variables was high (55 variables), forward stepwise analysis was used to identify the key variables for the linear regression and the artificial neural network models. For each model, the top 10 variables were identified. Then, the linear regression and the ANN models were built using these ten variables. The accuracy of the models was evaluated using 10-fold cross validation method.
The objective of this study is to contribute to the fields of educational technology and applied linguistics by proposing and evaluating an intelligent model for technology-based reading and spelling programs. An optimization model solved by the meta-heuristic approach of genetic algorithm is proposed to provide optimal instructional content for the learners with considering specific difficulty levels. For accurately parametrizing this optimization model, four predictive models of lexical difficulty are designed based on artificial neural networks (ANN) and linear regression. In order to identify the most important set of variables in each lexical difficulty model, a forward stepwise analysis is carried out. For each of the predictive models, the top 10 variables are identified through the forward stepwise analysis. The results showed that the neural network models performed marginally better than the linear regression models in terms of the accuracy of auditory word recognition, visual word recognition, spelling, and word-naming tasks.
The main contribution of this research in the domains of educational technology and applied linguistics are as follows:
- -
- An intelligent model that can be adopted for various technology-based reading and spelling tasks is proposed and evaluated.
- -
- The model adapts to the ability level of the learner and presents educational content that is neither too difficult, nor too easy. Hence, it complies with learning theories, such as the flow theory [18,19].
- -
- The model takes into accounts the length of the instructional sessions. Therefore, the instructor can remotely choose the minimum and the maximum length of the instructional session.
- -
- The model adapts the presented content based on the previous session of the learner.
- -
- The number of irregular phoneme-grapheme associations, word frequency, and minimum phoneme–grapheme associations are important for predicting the success of spelling.
- -
- The number of phonemes, homophones, and word frequency are important for the auditory lexical decision task.
- -
- The word frequency, number of homographs and syllables are the most important variables for the visual lexical decision task.
- -
- The number of letters, word frequency, and initial grapheme–phoneme consistency are important for the word naming of monosyllabic, monomorphemic words.
The obtained results are beneficial for people with reading difficulties, particularly in the conditions of the lack of sufficient instructions in schools. The provision of the training tool presented in this paper could improve the acquisition of reading skills by learners and represent important added value for society by opening opportunities for education to people. The workflow of the conducted research is presented in the diagram of Figure 1.
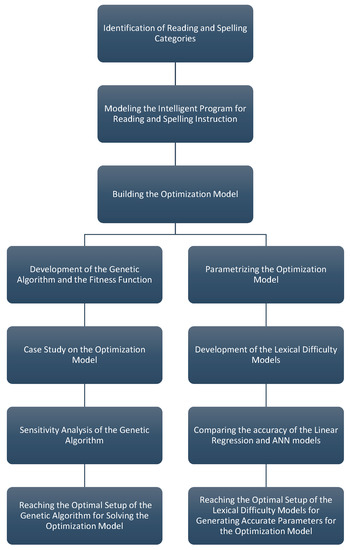
Figure 1.
The workflow of the conducted research.
The proposed approach is described in Section 2. The data collection and the experimentation procedures are presented in Section 3. Section 4 provides a detailed analysis of the results obtained from the proposed models. Section 5 presents the discussion of the results and the limitations of this study. Finally, the conclusion and the research perspectives are presented in Section 6.
2. Proposed Approach: Intelligent Reading and Spelling Instruction
It is highly recommended for the reading and writing tasks to be systematic [2,3]. Additionally, technology-based programs have the potential to offer systematic instruction. However, the main challenge of technology-based in-home reading and spelling programs is the personalization of the instructional content for each individual and providing the optimal content for each training session. This paper presents a generalizable intelligent model that could be applied to various instructional tasks.
Early reading and spelling programs in elementary and pre-elementary grades consist mainly of the six categories: the phonological awareness, phonics, spelling, vocabulary, comprehension, and fluency. The contents of most of the tasks in these early literacy categories are either sub-lexical units, words, word lists, sentences, or full texts. In order to be systematic in organizing the instructional contents, two parameters are essential: the difficulty level and the educational value of each content material. An optimal instructional session should offer the content that maximizes the educational value with a limited difficulty level so that it does not surpass the ability level of the learner. This is an optimization problem to be solved before each instructional session.
The educational value of a content material can be marked by frequency values. If the content is made of single words, learning the highly frequent words brings more educational value to the learner. However, estimating the word difficulty level is a more complex process. Calculating lexical difficulty depends on many lexical and sub-lexical variables. In addition, the lexical difficulty depends highly on the task. In this article, the lexical and sub-lexical databases were used with the data obtained from lexical mega-studies. These databases were used to estimate the lexical difficulty for four main lexical skills (visual and auditory word recognition, word decoding and spelling). The methods of linear regression and artificial neural networks were used for modeling the lexical difficulties.
The architecture of the intelligent model for reading and spelling instruction is illustrated in Figure 2. A detailed description of each module of this system is presented in the following sections.
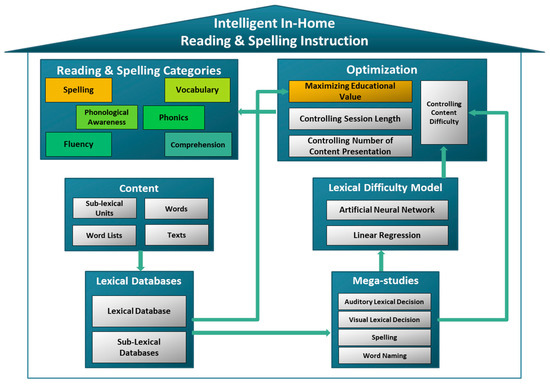
Figure 2.
The system architecture of the intelligent reading and spelling instruction.
2.1. Reading and Spelling Categories
The National Reading Panel has suggested that phonological awareness, phonics, vocabulary, comprehension, and fluency programs are essential for a balanced reading instruction [20]. Subsequently, it was shown that progress in reading does not guarantee progress in spelling. Hence, spelling should be addressed separately [21].
Phonological awareness is defined as “the understanding of different ways that oral language can be divided into smaller components and manipulated” [22]. It includes abilities, such as isolating, adding, deleting, and substituting the smaller units of the language, e.g., syllable and phoneme [11]. Phonological awareness could be instructed at an early age before the introduction of the written language. On the other hand, phonics focuses on teaching how to decode the orthography. It refers to “various approaches designed to teach children about the orthographic code of the language and the relationships of spelling patterns to sound patterns” [23].
Vocabulary is “the knowledge of meanings of words” [24]. The vocabulary instruction can be indirect, such as encouraging students to engage in reading activities, or it can be direct by teaching new words individually. Comprehension is the goal of reading, it is defined as “the construction of meaning of a written or spoken communication through a reciprocal, holistic interchange of ideas between the interpreter and the message in a particular communicative context” [25]. Strategies, such as summarizing, self-questioning, and paraphrasing, are used to enhance the comprehension of the reader [26]. Fluency is the highest level in reading. It “combines accuracy, automaticity, and oral reading prosody. When taken together, they facilitate the reader’s construction of meaning” [27]. Practices such as repeated reading and increasing independent and recreational reading are often used to increase fluency [20]. Finally, for the instruction of spelling, the common interventions are based on phonics, graphotactics, spelling rules, and morphological instructions [28].
Instructional content of the aforementioned literacy categories is mainly in the form of words, word lists, sentences, or full texts. In cases of phonological awareness and phonics, the content is often in the form of sub-lexical units. However, even in these cases, it is preferred to teach the sub-lexical units in the context of real words. Therefore, the instructional content of most of the reading and spelling tasks can be organized by individual words. The words used in the instructional content can contain the sub-lexical units that represent the target of phonological awareness and phonics. They can also be the building blocks of the texts used in vocabulary, spelling, comprehension, and fluency instructions.
2.2. Optimization
According to the Lev Vygotsky’s zone of proximal development, most of the development happens when the instructional content is slightly more difficult than what the user is actually capable of doing on his/her own [29]. The flow theory proposed by Mihaly Csikszentmihalyi confirms that the peak of motivation is reached when there is a balance between the task’s difficulty and the individual’s abilities [18]. When the material is too difficult, the user will get frustrated or anxious, and if the learning material is too easy, the user feels bored. Therefore, the learning program should provide the content with maximum educational value while remaining close to the user’s ability level. These intelligent characteristics are essential for any in-home interventional programs. Traditionally, it is the role of the instructor to choose the appropriate content. However, for the in-home approach, the intelligent component of the literacy program must play the role of the instructor.
Maximizing the educational value of a training session while keeping the session’s difficulty level within the learner’s abilities is an optimization problem. Modeling and solving this optimization problem require deep linguistic knowledge and high computation power, which cannot be provided by teachers. Modeling and solving this optimization problem are the main objectives of this research.
The knapsack model is an optimization method used in previous research in education [30]. The characteristics of this model allow modeling reading and spelling tasks. In the knapsack problem, for the given items, each with their associated weights and values, a set of items that produce the highest total value, without surpassing the weight limit, should be selected. In the case of this study, the items are the single words, the weights are the difficulty level of words (lexical difficulty), and since learning more frequent words is more valuable for the learner, the value parameter of each word is represented by its lexical frequency.
The total value of the selected items is maximized by the objective function of this optimization model. Therefore, an item with a high value has a greater probability to be selected. Three constraints were considered for this optimization model:
- -
- The constraint on the maximum difficulty: ensures that the selected items for the training session remain within the defined weight limit (difficulty level). It includes an upper weight (UW) for the upper limit of the content’s difficulty to avoid frustration and a lower weight (LW) for the lower limit of the content’s easiness to avoid boringness
- -
- The constraint on the session length: defines the maximum number of selected items within a defined boundaries. The upper number (UN) and the lower number (LN) are the maximum and the minimum number of items that could be selected (for a training session), respectively.
- -
- The constraint limiting the number of presentations (P): defines the maximum number of times that a content material can be presented to the user. This constraint ensures that a word will not be displayed to the learner more than a fixed number of times.
The proposed optimization model is presented below:
The objective function maximizes the value of each training session formulated as the following:
where is the value of the item (learning content), and is one if the item is selected, and zero if the item is not selected.
Subject to the following constraints:
The constraint on the difficulty level of each training session:
where is the weight (difficulty) of the item, LW is the minimum allowed weight, and the UW is the maximum allowed weight.
The constraint on the number of items in each training session:
where LN is the lower limit on the number of selected item, and the UN is the lower limit on the number of selected items.
The constraint on the number of presentations for each reading material:
where is the number of times a learning item is presented to the learner. P is the upper limit on the number of presentations for each item.
Where:
Table 1 presents the variables and parameters of the optimization model. is the variable and are the parameters of the model.

Table 1.
The notation for the variable and parameters of the optimization model.
2.3. Genetic Algorithm
The proposed optimization model is a NP-complete problem. Therefore, when the size of the problem is big, there is no known method to quickly find the best solution. The meta-heuristic method of genetic algorithm (GA) is effective in approximating computationally complex models. Hence, it was adopted to solve this problem.
The first step of implementing the genetic algorithm was to define the nature of the genes. In this context, the genes were binary values where each gene represented a single instructional material. This can be a single word, word list, question, sentence, or text. If the gene is equal to zero, this means that the material is not selected but if the gene is equal to one, this means that the material is selected. The second step was to define the chromosome. In this context, the chromosome is an array of binary values (genes). The size of the chromosome is identical to the size of the content. The third step was the random creation of chromosomes for the first population. At the beginning of this step, the chromosomes with all-zero genes are created. Then, for each chromosome, a number of genes (equal to the length of the session) are selected randomly and set to one.
In the fourth step, a piecewise function was developed as the fitness function to evaluate the feasibility and suitability of each solution for this optimization problem. This function divided the solutions into the categories of strictly infeasible, mildly infeasible, feasible but not suitable, and feasible and suitable.
The first category of strictly infeasible happened when the selected items had a total weight more than the maximum allowed weight. For this category, the big-M (penalty) method was used by assigning a big negative number to the fitness function and reducing the total weight. Therefore, when two infeasible solutions were compared, the solution having the lower total weight had a better fitness value. Using this method converged the solutions towards feasible areas.
The second category of mildly infeasible referred to the solutions that satisfies the weight constraint but violated the constraint of the session length. For this category, a small-M (penalty) was used and multiplied by the degree of the deviation from the allowed session length. Using this method converged the session lengths towards the allowed boundaries.
For the third category of feasible but not suitable, the value of the fitness function remained negative but closer to zero than the big-M or small-M values. This third state occurred when the main constraints on total weight and session length were respected but violating the constraint on the number of presentations. In this situation, the value of the fitness function was set to the extent of the deviation from the constraint. Therefore, in the case of having two similar solutions where the constraint on the number of presentations is violated, the solution having less deviation was regarded as a fitter solution. This converged the solutions towards the feasible areas.
For the fourth category of feasible and suitable, the fitness function was always positive. It was equal to the total value of the selected reading materials.
The following piecewise function used for computing the fitness (F) of the solutions is presented below and its parameters are presented in Table 2:

Table 2.
The parameters of the fitness function.
2.4. Lexical Difficulty Model
The optimization model proposed in this paper could lead to accurate solutions if its parameters are set accurately. Lexical difficulty level represents the weight parameter of the model. However, estimating lexical difficulty is complex as tens of lexical and sub-lexical variables affect lexical difficulty. The order of their importance is not fully known and the relationships between the variables are complex.
Previous studies have shown that particularly for beginners in reading, word length is a better predictor of lexical difficulty [31,32]. In addition, the effect of word length is more important for less skilled readers and people with reading disorders such as dyslexia or pure alexia [33]. Word-length can be presented by the number of letters, graphemes, phonemes, syllables, or morphemes. Another important variable is lexical frequency. Its effect on word naming and lexical decision times has been shown [34,35]. Another key variable affecting lexical difficulty is the orthographic consistency. It includes grapheme to phoneme (GP) mapping consistency (feed-forward consistency) and phoneme to grapheme (PG) mapping consistency (feedback consistency). It was shown that both of these variables have effects on word recognition [36]. In addition, the number of consonant clusters, the number of neighbors (words that differ only in one letter or one phoneme), and the number of homophones can affect lexical difficulty [37,38,39,40], respectively.
Lexical difficulty depends on the task. For example, in a reading task, the word may be considered easy, but it may prove difficult in writing. This is particularly the case for French language, which has an asymmetric orthography, meaning that writing is often more challenging than reading [41]. Moreover, one word may be difficult for a particular age but easy for another age. These layers of complexity create a challenge in the accurate estimation of lexical difficulty. To solve this problem, regression models based on linear regression and artificial neural networks were used in this research to estimate lexical difficulty in French language. Four lexical skills of visual and auditory word recognition, word decoding, and spelling were studied and modelled using linear regression and artificial neural networks.
Linear regression requires a relatively a small amount of data, it is computationally fast, easy to understand and interpret. However, it is not accurate in handling non-linearity, which represents its main drawback. Since most of real-life cases include non-linearity, linear regression fails to capture their underlying relationships. On the other hand, artificial neural networks have the capacity of modeling most complex problems. They can handle both linearity and non-linearity. Depending on the number of hidden layers and the number of neurons in each layer, it can provide significant computational power. However, it requires considerably more input-output data to reach acceptable accuracy than linear regression models. In addition, the understanding and interpretation of artificial networks model is much more difficult. Furthermore, its training time can be significantly longer than linear regression. Since linear regression and artificial neural networks allow different possibilities, both models were used in this study for the creation of lexical difficulty models. The comparison of their accuracy could provide guidance for using the most appropriate model. These models and the evaluation of their accuracies are presented in Section 4.
The data needed for building lexical difficulty models fit within two categories. The first category is the outcome data of behavioral mega-studies that tested the lexical tasks for thousands of words with human subjects. The second category is the lexical and sub-lexical databases that contain tens of quantified characteristics for each word.
3. Methodology and Data Collection
This section presents the data collection procedure, the methods used for the implementation of the approach, and the data analysis.
3.1. French Lexical Mega-Studies
For building the lexical difficulty models, French lexical mega-studies were used to collect the data for auditory and visual lexical decision, word naming, and spelling. These databases are the result of behavioral mega-studies in which the lexical tasks of numerous words were tested with many human subjects. In word naming, the subjects were requested to read a word aloud, the time taken for reading was recorded. In auditory lexical decision, the pronunciation of a word is played. The subjects had to decide whether it is a real word or a pseudoword, the reaction time to provide the answer was recorded. In the visual lexical decision task, a written word is presented. The subjects were requested to indicate whether the word is a real word or a pseudoword, and the reaction time was recorded. In the spelling task, a word is pronounced, then the subjects were requested to write its spelling for which the errors and the correct answers were recorded.
For the spelling task, the database published in the EOLE book [16] was used. This database contains the results of spelling task for around 12,000 words tested with many students in over 2000 classrooms in France. In this work, Béatrice and Philipe Pothier collected the average spelling success-rate of students for all the words across the five grades of the primary school in France. For the auditory and visual lexical decision tasks, MEGALEX database [15] was selected. It includes the decision times and accuracies of 28,466 words for visual lexical decision and 17,876 words for auditory lexical decision. For the word-naming task, Chronolex database [17] was selected, including 1482 monosyllabic and monomorphemic words.
3.2. French Lexical and Sub-Lexical Variables
In this study, the French language was used for creating lexical difficulty models. The Lexique 3 database [12,13] was used for the general lexical variables and the Lexique-Infra [14] was used for sub-lexical variables. Both databases contain the data of approximately 140,000 French words. These two databases were combined with selecting only quantified variables. The result led to 55 lexical and sub-lexical variables for which the list is presented in Table 3. All the quantified data were normalized to a value ranging from 0 to 1. The frequency of words was calculated by averaging the frequency values in books and films available in the Lexique 3 database. Since these average frequencies were dispersed, the standard frequency index (SFI) formula was used to homogenize them before the normalization process. The formula below was adopted from the Manulex database [42], originally proposed by John B. Carroll [43]. SFI is the standard frequency index, and c is the word count.

Table 3.
The lexical and sub-lexical variables.
The lexical and sub-lexical database that contains 55 variables was combined with the databases of the four lexical tasks. The overlapping data generated four databases with 11,373 words for the spelling task, 25,776 words for the visual lexical decision, 15,842 words for the auditory lexical decision, and 1481 words for the word-naming task. Furthermore, the output data was the success rates for the spelling task and the reaction times for word-naming database. The output data for the lexical decision tasks were both the reaction times and error rates. However, the latter was not included in building the regression models. This decision was made because the subjects involved in these tasks were adults form whom the number of errors for most of the words was significantly low. Hence, the reaction time was considered as a more pertinent indicator of word recognition difficulty. In addition, for the lexical decision tasks, the standardized reaction times were used instead of the raw reaction times. Finally, all these data were normalized to values ranging from 0 to 1.
3.3. Forward Stepwise Method
The forward stepwise method was used to identify the top 10 lexical and sub-lexical variables for building each lexical difficulty model. If none of the variables were dropped for building the lexical difficulty model, the model could become unnecessarily complex. Some of the independent variables did not significantly affect the dependent variable. In addition, despite the significant effect of some variables, they have strong collinearity with other variables.
To overcome these problems, the forward stepwise analysis was used for the identification of the most important variables for each lexical difficulty model. The initiation of the forward stepwise method was carried out with a model without any variable (called NULL model). Subsequently, the variable having the most predictive value was selected and added to the model. In the following step, the new model was tested with all the other variables, and again the variable that added the most predictive value was kept in the model. This process can be ended when the change in the predictive value becomes not significant. The process of forward stepwise analysis was performed for both linear regression and artificial neural network. For the forward stepwise linear regression, the selection criterion was the probability of F (p-value). For the forward stepwise artificial neural network, the selection criterion was the mean absolute error () computed by the following the formula:
where: is the real value, is the predicted value, and N is the number of data points.
For evaluating the accuracy of the models, a second error rate was used together with the MAE to obtain a more complete understanding of the accuracy of the model. This error rate is the root mean square error () computed by the following equation:
where is the real value and is the predicted value. N is the total number of data points.
Extensive training time was provided to allow the model selecting the variables accurately. In artificial neural network technical terms, each time the model is trained with the whole dataset, an Epoch is completed. In this study, the ANN models had 1000 epochs for recording their highest accuracy. In each step, all the models were compared to select the model having the better accuracy. Long training time was allowed because, with each step, the differences between the variables were narrowed and the selection of better variable required high precision. For the identification of the top 10 variables among 55 lexical variables, the forward stepwise method required training 505 models for each lexical task. Building 505 models with 1000 training epochs and shuffling all the training sets for each epoch required extensive computation time.
3.4. Computation of the Accuracy of Lexical Difficulty Models
For the evaluation of the final accuracy of the lexical difficulty models, 10-fold cross-validation method was used. The dataset was divided into 10 equal-sized (randomly selected) subsets. Then, one subset (test set) was kept for the validation of the model and the remaining nine folds were used for training the model. When the training of the model was completed, the test set was used to evaluate its accuracy and the accuracy metrics of RMSE and MAE were recorded. Then, another subset was used as a new test set and the model was trained with the remaining subsets. This process was repeated ten times and the average RMSE and MAE were calculated. This cross-validation process was followed for both linear regression and artificial neural network models.
4. Results
This section presents the performance evaluation of the optimization model and the sensitivity analysis of the genetic algorithm. Then, the linear regression and ANN forward stepwise analyses are presented for auditory and visual lexical decision, word naming, and spelling.
4.1. Case Study on the Optimization Model
As a case study, a database of 315 Dolch sight words [44] was prepared. The weight parameters representing difficulty levels were distinguished by the word length. The frequency levels of words were used as the value parameter of the optimization model. For the Genetic Algorithm, an Adam chromosome was constructed with 315 binary genes, with each gene representing one word. For each generation, the population size is equal to 50. Further, 25% of the new generation were selected as the fittest solutions of the past generation, which were passed directly to the new generation (elite selection) and 75% were created through crossover. There was a 20% chance of mutation among this 75%.
To create new offspring, a uniform crossover with a mixed probability of 0.5 was used. A partial shuffle mutation with the probability rate of 20% was used. The iteration number (generation number) was chosen as the termination method of the algorithm. However, it was also possible to terminate the algorithm based on time. A time-based termination strategy guaranteed that the algorithm took the same time to initiate across all the devices. However, for slower devices, the solution could be less optimal. On the other hand, the iteration-based termination offered the same level of performance by the algorithm.
The algorithm was set to terminate after the 100th generation. It returned the fittest chromosome, which was converted to words. This problem was solved using a laptop (MSI Stealth Pro) with a processor of Intel Core i7 2.80 GHz, 16 GB RAM, 8 GB GeForce GTX 1070 graphics card. It took, on average, 1070 milliseconds to finish the algorithm. However, for AWS cloud computing service with 3 GB of RAM, it took on average 168 milliseconds, which was more than six times faster. It is important to note that although 1 s is acceptable for the user, the local PC that tested the algorithm had relatively powerful specifications. When the algorithm is performed on mobile devices or any device with low computation power, cloud computing provides a faster and more accurate solution.
4.2. Sensitivity Analysis of the Genetic Algorithm
The analysis of the efficiency of the structural choices in the genetic algorithm was carried out. Series of tests were performed in the cloud-computing version of the optimization model. The first analysis investigated the performance of the GA for different numbers of generations concerning the objective function (total value) and the computation time (milliseconds). For each iteration, the algorithm was performed ten times for which the averages of total value and computation times were recorded. Figure 3 depicts the obtained results, showing the linear relationship between time and the number of generations. However, the optimal value reached an asymptote.
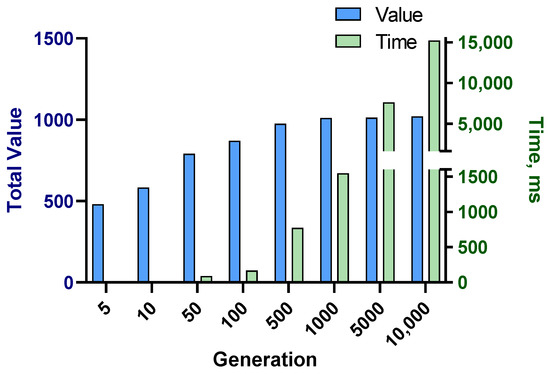
Figure 3.
The average performance of the model for different generation numbers of the GA.
Figure 4 illustrates the analysis of the size of the population and its effect on the execution time and the obtained optimal value. The model was executed 20 times for each population size, for which the averages of the total value and the computation time were recorded. The analysis revealed the linear relationship between the population size and the computation time, but the total value reached an asymptote. The important question was to determine the most effective population size for a fixed computation time. Hence, the GA’s termination was set to 200 milliseconds, the algorithm was executed 20 times for each population size, and the averages of total value and computation time were recorded (Figure 5). The results showed that the population sizes of 100 and 150 were the most efficient. However, when the population size increased further, the total value decreased.
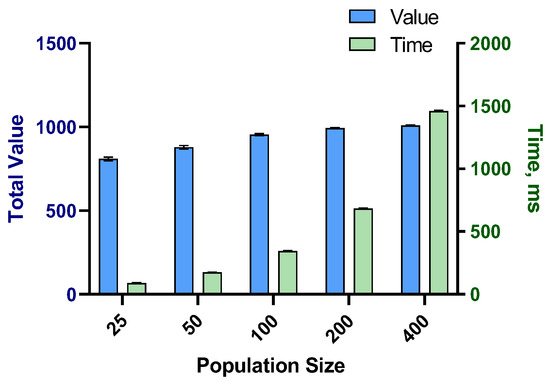
Figure 4.
The average performance of the model for different population sizes of the GA.
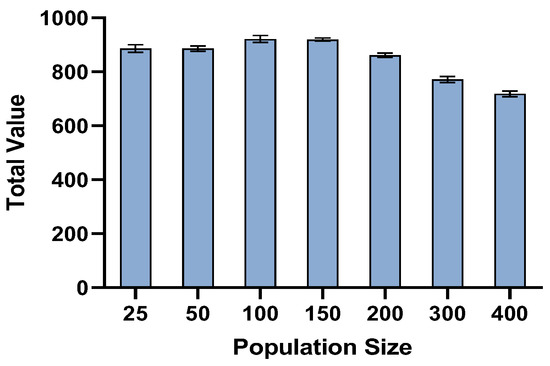
Figure 5.
Average total value for different population sizes for a fixed computation time (200 ms).
Another analysis was carried out on the performance of the model with four crossover functions. In uniform crossover (with the mixed probability of 0.5), each gene of the offspring was taken from one parent based on a 50–50 percent chance. Therefore, each parent’s contribution to the offspring was around 50%. in one-point crossover, one point in both parents was selected randomly, and all the genes beyond that point were swapped between the two parents to produce the two offspring. In two-point crossover, two points were selected in parent chromosomes, and the genes between these two points were swapped between the two parents. In the three-parent crossover, the genes of two of the parent chromosomes were compared. When the two parents had the same gene, this common gene was transferred to the offspring. However, if the genes were different, the gene from the third parent was chosen for the offspring. The algorithm with each crossover was performed ten times for which the average time and value were calculated. The results are presented in Figure 6. This shows the advantage of uniform crossover compared to two-point, one-point, and three-parent crossovers. Despite the longer time required to perform uniform crossover, the increase in performance was considerable.
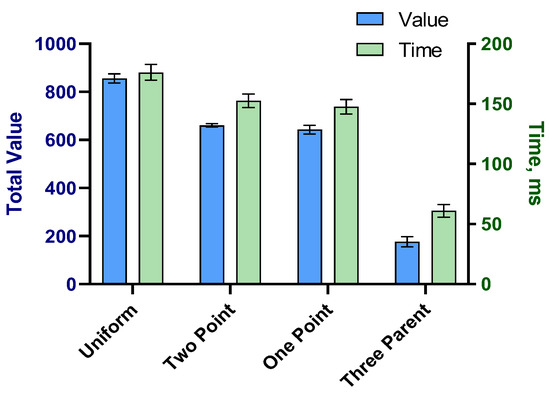
Figure 6.
Comparison of four crossover functions.
The same analysis was performed for the mutation types. Five mutation functions were studied by executing the model 30 times for each mutation type with recording the averages of time and value. In partial shuffle mutation, two points were randomly chosen and the sequence between these two points was shuffled. In displacement mutation, one part of the chromosome (a sequence of genes) was chosen randomly, and then, this part was removed and placed at a random position in the chromosome. In insertion mutation, a single gene was randomly selected and removed from the chromosome, then placed in another random position. In reverse sequence mutation, a random part of the chromosome was chosen (a sequence of genes), and their sequence was reversed. Finally, in the twors mutation, two randomly chosen genes swapped positions. The results of the tests on mutation functions are presented in Figure 7. The results were close, but the performance of partial shuffle mutation was slightly better than other functions in terms of the total value. Additionally, the computation times were close, with a minimum of 159 milliseconds and a maximum of 164 milliseconds.
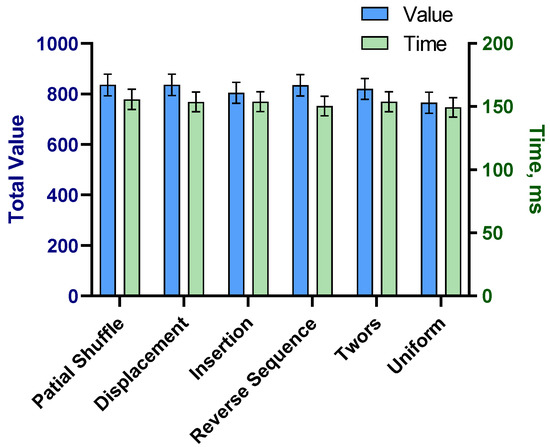
Figure 7.
Comparison of five mutation functions.
Another parameter related to mutation was the mutation probability. In order to find the optimal mutation probability, eight probabilities were tested. The algorithm was executed 30 times for each probability and the average total values and computation times were calculated. The results presented in Figure 8 shows that 20% and 25% mutation rates produced higher total value. However, the 20% percent mutation rate was slightly faster.
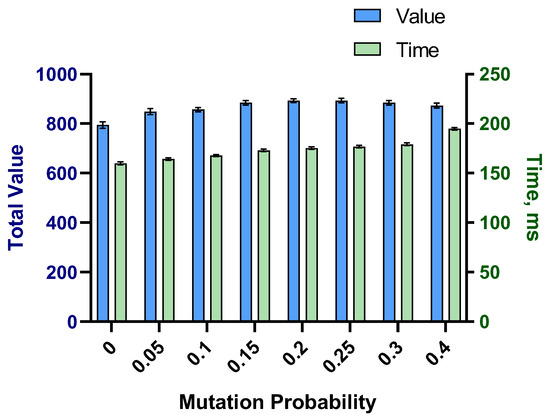
Figure 8.
Comparison of the model performance for different mutation probabilities.
The selection methods of chromosomes for passing to the next generation was studied by comparing four selection methods. The first method was Elite selection in which the fittest chromosomes were selected for passing to the next generation. Roulette wheel is a fitness-proportionate selection method in which the probability of selection for each chromosome is based on its fitness. Therefore, the fitter individuals have a higher probability of being selected. Stochastic universal sampling is also a fitness-proportionate selection method which ensured that this proportionality is kept in the selection because this is not guaranteed by the classic roulette wheel selection. In tournament selection, several competitions are held with a number of chromosomes and the winning chromosomes are selected as the fittest chromosomes. The key element in tournament selection is the size of the competitions. If the size is small, weak chromosomes have more chance to be selected. However, if the size of competitions is big, weaker chromosomes have less chance to be selected.
Each selection type was tested by executing the algorithm 30 times to obtain the average performance. The results presented in Figure 9 shows that the elite selection method resulted in higher total values and a faster computation time.
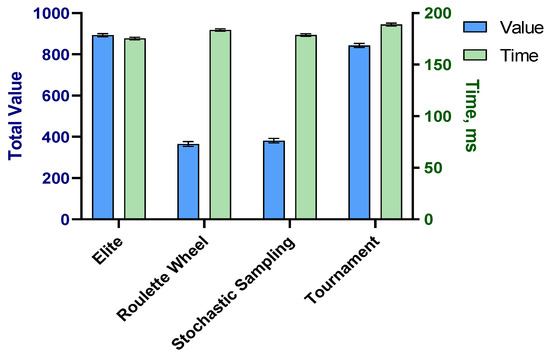
Figure 9.
Comparison of four selection functions.
4.3. Regression Models for Auditory Word Recognition
This section presents the forward stepwise analysis of the auditory lexical decision using linear regression and artificial neural networks. The accuracy of the two models was compared with the mean absolute error (MAE) and the root mean squared error (RMSE). Table 4 shows that the number of phonemes in the word was the most important variable for predicting the auditory lexical decision’s reaction time. The frequency, number of homophones, number of syllables, and is-lemma (is the word a lemma) were the next important variables. The two forward stepwise models resulted in eight similar variables and two different variables.

Table 4.
Forward stepwise analysis of the auditory lexical decision task.
Figure 10 illustrates the progress of the forward stepwise analysis on the measure of root mean square error (RMSE). The diagram shows that as the steps progressed, the difference between the two models became bigger and the ANN produced the lower error rate. Nevertheless, the difference between the two approaches remained marginal.
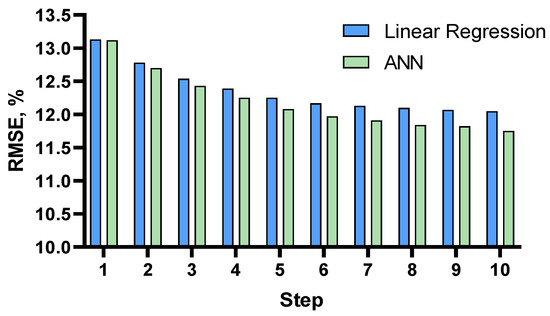
Figure 10.
The RMSE percentage of the forward stepwise analysis of the auditory lexical decision task.
The linear regression and ANN models with the selected 10 variables were constructed and trained. The analysis of their accuracies using the 10-fold cross-validation method led to the following results:
The average error rates of the linear regression model:
- -
- RMSELR = 12.05% (SD = 0.22)
- -
- MAELR = 9.60% (SD = 0.16)
The average error rates of the ANN model (with two hidden layers of 20 neurons):
- -
- RMSEANN = 11.87% (SD = 0.12)
- -
- MAEANN = 9.42% (SD = 0.17).
The difference between the average error rates of the two models:
- -
- RMSEDIFF = 0.18%
- -
- MAEDIFF = 0.18%
The similarity of the linear regression and ANN performance reveals that either the task had low non-linearity or the data size was not sufficient for detecting any complex relationship. The models were also constructed and trained with all the 55 lexical variables, and the analysis of their accuracies using the 10-fold cross-validation led to the following results:
The average error rates of the linear regression:
- -
- MAELR-All = 9.49 (SD = 0.17)
- -
- RMSELR-All = 11.92 (SD = 0.17)
The average error rates of the ANN model (with two hidden layers of 20 neurons):
- -
- MAEANN-All = 9.25 (SD = 0.14)
- -
- RMSEANN-All = 11.67 (SD = 0.14)
The results of the analysis are illustrated in Figure 11.
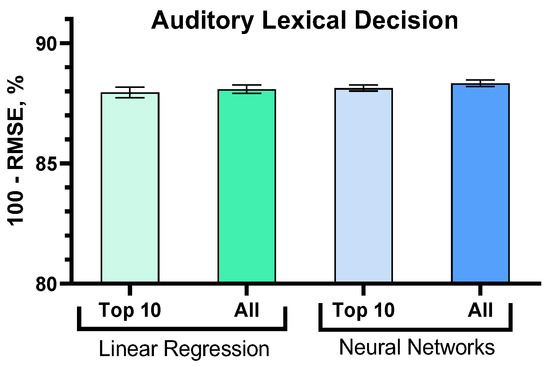
Figure 11.
Comparison of the accuracy of the linear regression and ANN models.
4.4. Regression Models for Visual Word Recognition
Table 5 presents the forward stepwise analysis results on visual lexical decision using linear regression and ANN. The word frequency was the most important variable in predicting the reaction time of the visual lexical decision task. The two forward stepwise models resulted in five similar variables and five different variables. The five similar variables were the frequency, number of homographs, number of syllables, phonological unicity point, and number of morphemes.

Table 5.
Forward stepwise analysis of the visual lexical decision task.
Figure 12 illustrates the progress of the forward stepwise analysis on the measure of RMSE. Similar to the auditory lexical decision, the diagram shows that as the steps progressed, the difference between the two models became bigger and the ANN produced the lower error rate compared to linear regression. However, the difference between the two models remained marginal.
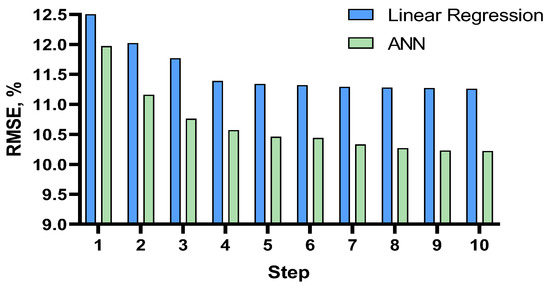
Figure 12.
The RMSE percentage of the forward stepwise analysis of the visual lexical decision task.
The linear regression and ANN models with the selected 10 variables were constructed and trained. The analysis of their accuracies using the 10-fold cross-validation method led to the following results:
The average error rates of the linear regression model:
- -
- RMSELR = 11.26% (SD = 0.22)
- -
- MAELR = 8.87% (SD = 0.17)
The average error rates of the ANN model (with two hidden layers of 20 neurons):
- -
- RMSEANN = 10.21% (SD = 0.16)
- -
- MAEANN = 7.92% (SD = 0.14)
The difference between the average error rates of the two models:
- -
- RMSEDIFF = 1.05%
- -
- MAEDIFF = 0.95%.
The models were also trained with all the 55 lexical variables and the analysis of their accuracies using the 10-fold cross-validation method led to the following results:
The average error rates of the linear regression model:
- -
- MAELR-All = 8.87 (SD = 0.18)
- -
- RMSELR-All = 11.15 (SD = 0.24)
The average error rates of the ANN model:
- -
- MAEANN-All = 7.82 (SD = 0.16)
- -
- RMSEANN-All = 10.04 (SD = 0.17)
The results of the analysis are illustrated in Figure 13.
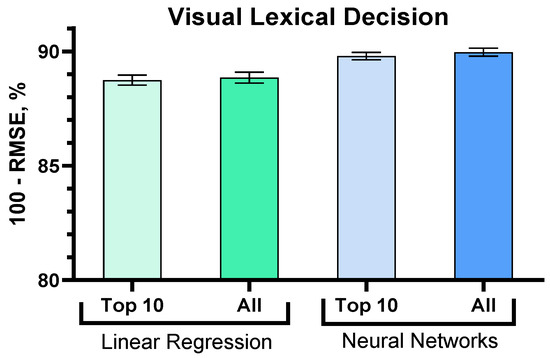
Figure 13.
Comparison of the accuracy of the linear regression and the ANN models.
4.5. Regression Models for Word Spelling
The stepwise analysis of spelling task using linear regression and the ANN was carried out (Table 6). It should be noted that in the EOLE database [16] each word has five spelling success rates that represent the five primary school grades. Therefore, the number of the dataset was 56,865. The grade variable was included in the models by default. The two forward stepwise models (linear regression and ANN) resulted in six similar variables and four different variables. The six similar variables were the number of phoneme-grapheme irregularity, frequency, minimum consistency of phoneme–grapheme associations, consistency of the last phoneme-grapheme association, number of grapheme-phoneme irregularities, and the average frequency of phonological syllables.

Table 6.
The results of the forward stepwise analysis of the spelling task.
Figure 14 illustrates the progress of the forward stepwise analysis on the measure of RMSE. Similar to the two other tasks, the diagram shows that as the steps progressed, the difference between the two models increased and ANN produced a lower error rate. The difference between these models remained marginal but it is more sizable when compared to the two lexical decision tasks.
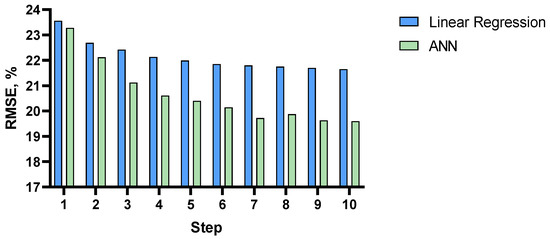
Figure 14.
Root Mean Square Error for the forward stepwise analysis of the visual lexical decision task.
The linear regression and ANN models with the selected 10 variables were constructed and trained. The analysis of their accuracies using the 10-fold cross-validation method led to the following results:
The average error rates of the linear regression model:
- -
- RMSELR = 21.65% (SD = 0.13)
- -
- MAELR = 17.50% (SD = 0.12)
The average error rates of the ANN model (with two hidden layers of 20 neurons):
- -
- RMSEANN = 19.47% (SD = 0.27)
- -
- MAEANN = 15.17% (SD = 0.25)
The difference between the average error rates of the two models:
- -
- RMSEDIFF = 2.18%
- -
- MAEDIFF = 2.33%.
The models were also trained with all the 55 lexical variables and the analysis of their accuracies using the 10-fold cross-validation method led to the following results:
The average error rates of the linear regression model:
- -
- MAELR-All = 17 (SD = 0.1)
- -
- RMSELR-All = 21.15 (SD = 0.11)
The average error rates of the ANN model:
- -
- MAEANN-All = 13.26 (SD = 0.14)
- -
- RMSEANN-All = 16.96 (SD = 0.19)
The results of the analysis are illustrated in Figure 15.
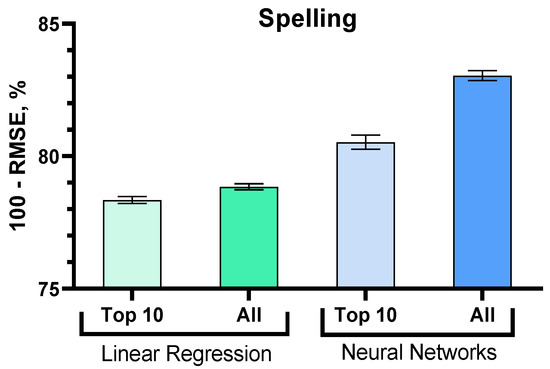
Figure 15.
Comparison of the accuracy of the linear regression and ANN models.
The EOLE database [16] has the advantage of being tested with children of the five primary grades in France. Each word in the database included the average spelling success-rate for each of the five grades. The result of the forward stepwise analysis for each grade is presented in Table 7. These results showed that the number of phoneme–grapheme irregularities (countregTo_PG) was the most important variable for all five grades. The next important variable was word frequency. However, word frequency was less important in the first grade, but it became more important considering the standardized coefficients in the grade-by-grade analysis. On the other hand, it was noticed that voisorth variable representing the number of orthographic neighbors, was initially important but this decreased with each grade. The minimum consistency of phoneme-grapheme associations was a stable variable across the five grades. However, the importance of the average trigram frequency in the word (TrigrFreqTo) increased by each grade. Lastly, final phoneme–grapheme consistency was a stable predictor of spelling success in the French language but its importance marginally decreased by each grade.

Table 7.
Grade-based forward stepwise linear regression for the spelling task.
4.6. Regression Model for Word-Naming
For the word-naming task, only 1481 words were available in the database. Hence, the ANN model could not produce accurate results. For this reason, only forward stepwise linear regression was carried out for which the results are presented in Table 8. The most important variable was the number of letters. The consistency of the initial grapheme–phoneme association was the next important variable. The third variable was the frequency. The three next variables were related to the initial grapheme-phoneme and phoneme-grapheme associations. It should be noted that this task was performed with only monosyllabic, monomorphemic words for which the results may not be generalizable to all words. The results from the 10-fold cross validation produced the average error rates of 16.14% for RMSE (SD = 1.07) and 13.02% MAE (SD = 0.78). Furthermore, the 10-fold cross-validation of the linear regression, including all the 55 lexical variables, yielded the root mean square error (RMSE) = 16.09% (SD = 0.94) and the mean absolute error (MAE) = 12.83% (SD = 0.81).

Table 8.
Forward stepwise analysis of the word-naming task.
5. Discussion
The results of this study showed that the word frequency remained among the most influential variables in predicting the outcome of lexical tasks. This is in line with the results of other studies [45,46]. However, the results also showed that the prediction of lexical difficulty depended on the type of the task and each task was affected by a different set of lexical and sub-lexical variables. The spelling task depended heavily on phoneme-grapheme irregularity and consistency variables. The number of irregular phoneme-grapheme associations and the minimum consistency value of phoneme–grapheme associations in the word are the most important variables in the prediction of spelling. In addition, the final phoneme-grapheme consistency value played a more prominent role than the initial and middle grapheme-phoneme associations. This may be due to the specific characteristic of the French language that has highly inconsistent final phoneme–grapheme associations.
The reaction times from the auditory lexical decision relied heavily on the number of phonemes which is a measure of the word length. This was caused by the nature of the task, as explained by the authors of the MEGALEX database [15]. The users could respond as soon as the sound of the word started playing. Since users often waited until the end of the word’s pronunciation, the words with more phonemes caused longer reaction time. Apart from the word length effect, the number of homophones is an important variable in predicting auditory lexical decision. Homophones are words that have the same pronunciations but different meanings. In an auditory lexical decision task, a high number of homophones reduced the reaction time in recognizing that the word is not a pseudoword. The auditory lexical decision is a good representative of auditory word recognition. However, deciding whether the word is real or pseudoword is not the ultimate level of word recognition. Contrary to the results, high homophones, in theory, should slow down the user in the extraction of the meaning. The same applies to the number of homographs and visual lexical decision. Homographs are words with the same spelling but with different meanings. The results of this study showed that a higher number of homographs facilitates the visual lexical decision. However, this may be the opposite in normal reading in which a high number of homographs may induce confusion and slow down the reader.
Apart from frequency and number of homographs, the phonological unicity point (puphon) is another variable with an important facilitatory effect on the visual lexical decision. This variable calculates the number of phonemes required (since the beginning of its pronunciation) for its recognition as a unique word. It was not expected for this variable to appear among the most important variables for predicting visual lexical decision. After examining the manual of the Lexique 3 database [13,47], it was noticed that the phonological and orthographic unicity points were only generated for lemmas (canonical form of a word). The words that were not lemma had zero for their unicity points. This means that the puphon and puorth variables at times conveyed the unicity points, but they also conveyed whether the word was a lemma or not. This additional information could explain this effect. However, the orthographic unicity point also conveyed the information about lemmas but the results showed its limited importance. For further interpretation of these results, the Lexique 3 database was investigated, and it was revealed that the orthographic unicity point contained almost double zeros (90879) compared to the zero values in the variable representing the phonological unicity point (48784). This additional information contained in the puphon variable made it a more important variable for the analysis.
The key variables for the for estimating the reaction time of the word-naming task are: the letter number, word frequency, initial grapheme-phoneme, and phoneme-grapheme consistency and the number of homographs. The Chronolex database [17] only contained monosyllabic and monomorphemic words. For future studies, it is necessary to investigate whether the initial grapheme–phoneme association consistencies keep their importance in naming multisyllabic words. The importance of the number of letters in the word-naming task could be due to the extra time required to finish articulating longer words.
The Lexique-Infra database [14] used as the source of sub-lexical variables is a comprehensive database containing around 140,000 words. However, more variables could be included to increase the accuracy of the lexical difficulty models. Particularly, as the minimum consistency variables were important in predicting spelling success, minimum grapheme–phoneme frequency variables should have been useful for predicting the spelling task. A grapheme-phoneme relationship may be completely consistent but very rare. In this case, minimum frequency variables convey more important information than the consistency variables. The number of graphemes is another missing variable. Current results showed that the number of syllables is an important variable representing the word-length for the lexical decision tasks, while the number of letters is more important for the spelling and word-naming task. However, this result was obtained without considering the number of graphemes.
The linear regression and ANN models had approximately similar accuracy, but ANN models marginally outperformed linear regression models. However, the results of these models showed that the advantage of ANN was dependent on the size of the training set. Figure 16 shows the accuracy difference between ANN and linear regression models in terms of the training size. The relationship shows that more datasets are necessary to obtain better performance of the ANN models.
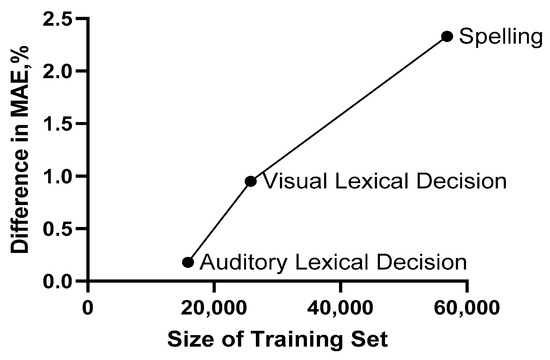
Figure 16.
The relationship between the size of the training sets and the extra accuracy produced by the ANN model compared to linear regression models.
After estimating the word difficulties, the next big challenge is to estimate the user’s ability level. The spelling difficulty model in this study was grade-based. Therefore, the difficulty of the session could be set by the grade level of the learner, but the process is less accurate for other tasks. One solution is to use a coefficient for each grade and allow greater difficulty for higher grades. It should be noted that the difference between the grades becomes smaller as they progress. The data of the spelling task showed this fading difference. The average spelling success rate of the first graders was 17.87%, while the second graders were 13.68% higher than the first graders. The differences between the following grades were 13.21%, 10.28%, and 8.56%. However, the generalization of this trend to other reading tasks requires further investigations.
The intelligent model reported in this study brings a new contribution to the development of instructional programs. Moreover, there is no similar approaches reported in the previous research for the technology-based reading instruction. Hence, the evaluation of this model in comparison with similar models was not possible.
6. Conclusions and Research Perspectives
This paper presents a model for intelligent technology-based reading and spelling tasks. An optimization model is proposed to provide optimal instructional content for the learners with considering specific difficulty levels of the contents. The meta-heuristic approach of genetic algorithm was developed to solve the optimization problem, and the most optimal setup for the genetic algorithm was analyzed. To obtain accurate solutions, the parameters of the optimization model should be set with precision. Notably, the difficulty level of the instructional materials should be accurately estimated. In this paper, the lexical difficulty models of four lexical tasks were developed based on linear regression and artificial neural networks. The databases from lexical mega-studies were combined with lexical and sub-lexical databases. This resulted in 55 lexical and sub-lexical variables and 15,842 words for auditory word recognition, 25,776 words for visual word recognition, 1481 words for word naming, and 11,373 words for spelling task.
For building lexical difficulty models, each task was analyzed with 55 lexical and sub-lexical variables. In order to identify the most important set of variables, the forward stepwise analysis was carried out for both the artificial neural networks and linear regressions. The top 10 variables for each of the lexical tasks were identified when comparing the accuracies of the models. The neural network models performed marginally better than the linear regression models. The auditory word recognition task reached 88.13% accuracy calculated by the 10-fold cross validation based on the root mean square error (RMSE). The accuracy was 89.79% for visual word recognition, 80.53% for spelling task, and 83.86% for word-naming task.
The spelling models showed that variables, such as the number of irregular phoneme–grapheme associations, word frequency, and minimum phoneme–grapheme associations, are important in predicting spelling success. The auditory lexical decision task depended highly on the number of phonemes, homophones, and word frequency. For the visual lexical decision task, word frequency, number of homographs, and syllables are among the most important variables. Finally, for the word naming of monosyllabic, monomorphemic words, the number of letters, word frequency, and initial grapheme–phoneme consistency are important variables.
The research presented in this paper presents a contribution to the development of intelligent technology-based reading and spelling instruction. However, in order to differentiate the types of learning, such as skill and knowledge acquisition, the reported optimization model needs more elaboration to include additional instructional constraints. Additional lexical and sub-lexical variables could be also included in the creation of lexical difficulty models. Finally, the lexical difficulty models could be used as a stepping-stone for the creation of sentence difficulty models.
Author Contributions
Conceptualization, H.J. and S.G.; Methodology, H.J. and S.G.; Validation, H.J.; Formal analysis, H.J., S.G. and I.A.S.; investigation, H.J. and S.G.; resources, H.J.; data curation, H.J.; writing—original draft preparation, H.J.; writing—review and editing, S.G.; visualization, S.G. and I.A.S.; supervision, S.G.; project administration, H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- De La Haye, F.; Gombert, J.-E.; Rivière, J.-P.; Rocher, T. Les éValuations en Lecture Dans Le Cadre de la Journée Défense ET Citoyenneté: Année 2010; Ministère de L’Education Nationale, de la Jeunesse ET de la Vie Associative: Paris, France, 2011; pp. 12–13.
- Ehri, L.C.; Nunes, S.R.; Stahl, S.A.; Willows, D.M. Systematic phonics instruction helps students learn to read: Evidence from the National Reading Panel’s meta-analysis. Rev. Educ. Res. 2001, 71, 393–447. [Google Scholar] [CrossRef]
- Graham, S.; Harris, K.R. Strategy instruction and the teaching of writing. Handb. Writ. Res. 2006, 5, 187–207. [Google Scholar]
- Lyytinen, H. Helping Dyslexic Children with GraphoGame Digital Game-Based Training Tool (An Interview). Psychol. Sci. Educ. 2018, 23, 84–86. [Google Scholar] [CrossRef]
- Abrami, P.C.; Lysenko, L.; Borokhovski, E. The effects of ABRACADABRA on reading outcomes: An updated meta-analysis and landscape review of applied field research. J. Comput. Assist. Learn 2020, 36, 260–279. [Google Scholar] [CrossRef]
- Görgen, R.; Huemer, S.; Schulte-Körne, G.; Moll, K. Evaluation of a digital game-based reading training for German children with reading disorder. Comput. Educ. 2020, 150, 103834. [Google Scholar] [CrossRef]
- Steenbeek-Planting, E.G.; Boot, M.; de Boer, J.C.; Van de Ven, M.; Swart, N.M.; van der Hout, D. Evidence-based psycholinguistic principles to remediate reading problems applied in the playful app Letterprins: A perspective of quality of healthcare on learning to read. In Games for Health; Springer: Berlin/Heidelberg, Germany, 2013; pp. 281–291. [Google Scholar]
- Klatte, M.; Bergström, K.; Steinbrink, C.; Konerding, M.; Lachmann, T. Effects of the Computer-Based Training Program Lautarium on Phonological Awareness and Reading and Spelling Abilities in German Second-Graders. In Reading and Dyslexia; Literacy Studies; Lachmann, T., Weis, T., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 16, pp. 323–339. ISBN 978-3-319-90804-5. [Google Scholar]
- Steenbeek-Planting, E.G.; van Bon, W.H.J.; Schreuder, R. Improving word reading speed: Individual differences interact with a training focus on successes or failures. Read. Writ. 2012, 25, 2061–2089. [Google Scholar] [CrossRef]
- Steenbeek-Planting, E.G.; van Bon, W.H.J.; Schreuder, R. Improving the reading of bisyllabic words that involve context-sensitive spelling rules: Focus on successes or on failures? Read. Writ. 2013, 26, 1437–1458. [Google Scholar] [CrossRef]
- Jamshidifarsani, H.; Garbaya, S.; Lim, T.; Blazevic, P.; Ritchie, J.M. Technology-based reading intervention programs for elementary grades: An analytical review. Comput. Educ. 2019, 128, 427–451. [Google Scholar] [CrossRef]
- New, B.; Pallier, C.; Ferrand, L.; Matos, R. Une base de données lexicales du français contemporain sur internet: LEXIQUETM//A lexical database for contemporary french: LEXIQUETM. L’année Psychol. 2001, 101, 447–462. [Google Scholar] [CrossRef]
- New, B. Lexique 3: Une nouvelle base de données lexicales. In Proceedings of the Actes de la Conférence Traitement Automatique des Langues Naturelles (TALN 2006), Leuven, Belgique, 10–13 April 2006. [Google Scholar]
- Gimenes, M.; Perret, C.; New, B. Lexique-Infra: Grapheme-phoneme, phoneme-grapheme regularity, consistency, and other sublexical statistics for 137,717 polysyllabic French words. Behav. Res. 2020, 52, 2480–2488. [Google Scholar] [CrossRef]
- Ferrand, L.; Méot, A.; Spinelli, E.; New, B.; Pallier, C.; Bonin, P.; Dufau, S.; Mathôt, S.; Grainger, J. MEGALEX: A megastudy of visual and auditory word recognition. Behav. Res. 2018, 50, 1285–1307. [Google Scholar] [CrossRef]
- Pothier, B.; Pothier, P. Echelle D’acquisition en Orthographe Lexicale: Pour L’école Élémentaire: Du CP au CM2; Retz: Paris, France, 2004. [Google Scholar]
- Ferrand, L.; Brysbaert, M.; Keuleers, E.; New, B.; Bonin, P.; Méot, A.; Augustinova, M.; Pallier, C. Comparing word processing times in naming, lexical decision, and progressive demasking: Evidence from Chronolex. Front. Psychol. 2011, 2, 306. [Google Scholar] [CrossRef]
- Csikszentmihalyi, M. Finding Flow: The Psychology of Engagement with Everyday Life; Basic Books: New York, NY, USA, 1997. [Google Scholar]
- Csikszentmihalyi, M.; Abuhamdeh, S.; Nakamura, J. Flow. In Flow and the Foundations of Positive Psychology; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar] [CrossRef]
- National Reading Panel (US); National Institute of Child Health and Human Development (US). Report of the National Reading Panel: Teaching Children to Read: An Evidence-Based Assessment of the Scientific Research Literature on Reading and Its Implications for Reading Instruction: Reports of the Subgroups; National Institute of Child Health and Human Development, National Institutes of Health: North Bethesda, MD, USA, 2000.
- Mehta, P.D.; Foorman, B.R.; Branum-Martin, L.; Taylor, W.P. Literacy as a Unidimensional Multilevel Construct: Validation, Sources of Influence, and Implications in a Longitudinal Study in Grades 1 to 4. Sci. Stud. Read. 2005, 9, 85–116. [Google Scholar] [CrossRef]
- Chard, D.J.; Dickson, S.V. Phonological Awareness: Instructional and Assessment Guidelines. Interv. Sch. Clin. 1999, 34, 261–270. [Google Scholar] [CrossRef]
- Stahl, S.A. Saying the “p” word: Nine guidelines for exemplary phonics instruction. Read. Teach. 1992, 45, 618–625. [Google Scholar] [CrossRef]
- Hiebert, E.H.; Kamil, M.L. Teaching and Learning Vocabulary: Bringing Research to Practice; Routledge: New York, NY, USA, 2005. [Google Scholar]
- Harris, T.L.; Hodges, R.E. The Literacy Dictionary: The Vocabulary of Reading and Writing; ERIC: Washington, DC, USA, 1995. [Google Scholar]
- Ponce, H.R.; López, M.J.; Mayer, R.E. Instructional effectiveness of a computer-supported program for teaching reading comprehension strategies. Comput. Educ. 2012, 59, 1170–1183. [Google Scholar] [CrossRef]
- Kuhn, M.R.; Schwanenflugel, P.J.; Meisinger, E.B. Aligning Theory and Assessment of Reading Fluency: Automaticity, Prosody, and Definitions of Fluency. Read. Res. Q. 2010, 45, 230–251. [Google Scholar] [CrossRef]
- Galuschka, K.; Görgen, R.; Kalmar, J.; Haberstroh, S.; Schmalz, X.; Schulte-Körne, G. Effectiveness of spelling interventions for learners with dyslexia: A meta-analysis and systematic review. Educ. Psychol. 2020, 55, 1–20. [Google Scholar] [CrossRef]
- Shabani, K.; Khatib, M.; Ebadi, S. Vygotsky’s Zone of Proximal Development: Instructional Implications and Teachers’ Professional Development. Engl. Lang. Teach. 2010, 3, 237–248. [Google Scholar] [CrossRef]
- Zandi Atashbar, N.; Rahimi, F. Optimization of Educational Systems Using Knapsack Problem. Int. J. Mach. Learn. Comput. 2012, 2, 552. [Google Scholar] [CrossRef]
- Zoccolotti, P.; De Luca, M.; Di Pace, E.; Gasperini, F.; Judica, A.; Spinelli, D. Word length effect in early reading and in developmental dyslexia. Brain Lang. 2005, 93, 369–373. [Google Scholar] [CrossRef] [PubMed]
- Joseph, H.S.S.L.; Liversedge, S.P.; Blythe, H.I.; White, S.J.; Rayner, K. Word length and landing position effects during reading in children and adults. Vis. Res. 2009, 49, 2078–2086. [Google Scholar] [CrossRef] [PubMed]
- Barton, J.J.S.; Hanif, H.M.; Eklinder Björnström, L.; Hills, C. The word-length effect in reading: A review. Cogn. Neuropsychol. 2014, 31, 378–412. [Google Scholar] [CrossRef]
- Balota, D.A.; Cortese, M.J.; Sergent-Marshall, S.D.; Spieler, D.H.; Yap, M.J. Visual word recognition of single-syllable words. J. Exp. Psychol. Gen. 2004, 133, 283. [Google Scholar] [CrossRef] [PubMed]
- Yap, M.J.; Balota, D.A. Visual word recognition of multisyllabic words. J. Mem. Lang. 2009, 60, 502–529. [Google Scholar] [CrossRef]
- Lacruz, I.; Folk, J.R. Feedforward and Feedback Consistency Effects for High- and Low-Frequency Words in Lexical Decision and Naming. Q. J. Exp. Psychol. Sect. A 2004, 57, 1261–1284. [Google Scholar] [CrossRef]
- Wijayathilake, M.A.D.K.; Parrila, R. Predictors of word reading skills in good and struggling readers in Sinhala. Writ. Syst. Res. 2014, 6, 120–131. [Google Scholar] [CrossRef]
- Pollatsek, A.; Perea, M.; Binder, K.S. The effects of “neighborhood size” in reading and lexical decision. J. Exp. Psychol. Hum. Percept. Perform. 1999, 25, 1142–1158. [Google Scholar] [CrossRef] [PubMed]
- Mulatti, C.; Reynolds, M.G.; Besner, D. Neighborhood effects in reading aloud: New findings and new challenges for computational models. J. Exp. Psychol. Hum. Percept. Perform. 2006, 32, 799–810. [Google Scholar] [CrossRef]
- Ferrand, L.; Grainger, J. Homophone interference effects in visual word recognition. Q. J. Exp. Psychol. Sect. A 2003, 56, 403–419. [Google Scholar] [CrossRef]
- Ecalle, J.; Magnan, A. L’apprentissage de la Lecture et Ses Difficultés, 2nd ed.; Dunod: Ile-de-France, France, 2015. [Google Scholar]
- Lété, B.; Sprenger-Charolles, L.; Colé, P. MANULEX: A grade-level lexical database from French elementary school readers. Behav. Res. Methods Instrum. Comput. 2004, 36, 156–166. [Google Scholar] [CrossRef] [PubMed]
- Carroll, J.B. An alternative to Juilland’s usage coefficient for lexical frequencies, and a proposal for a standard frequency index (SFI). Comput. Stud. Humanit. Verbal Behav. 1970, 3, 61–65. [Google Scholar]
- Dolch, E.W. A Basic Sight Vocabulary. Elem. Sch. J. 1936, 36, 456–460. [Google Scholar] [CrossRef]
- Vlasov, M.S.; Odonchimeg, T.; Sainbaiar, V.; Gromoglasova, T.I. Word Frequency Effect in Lexical Decision Task: Evidence from Mongolian. Humanit. Soc. Sci. 2019, 12, 1954–1964. [Google Scholar] [CrossRef]
- Brysbaert, M.; Mandera, P.; Keuleers, E. The Word Frequency Effect in Word Processing: An Updated Review. Curr. Dir. Psychol. Sci. 2018, 27, 45–50. [Google Scholar] [CrossRef]
- New, B.; Pallier, C.; Ferrand, L. Manuel de Lexique 3. Behav. Res. Methods Instrum. Comput. 2005, 36, 516–524. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).