Meshfree Interpolation of Multidimensional Time-Varying Scattered Data

Abstract

Interpolating and approximating scattered scalar and vector data is fundamental in resolving numerous engineering challenges. These methodologies predominantly rely on establishing a triangulated structure within the data domain, typically constrained to the dimensions of 2D or 3D. Subsequently, an interpolation or approximation technique is employed to yield a smooth and coherent outcome. This contribution introduces a meshless methodology founded upon radial basis functions (RBFs). This approach exhibits a nearly dimensionless character, facilitating the interpolation of data evolving over time. Specifically, it enables the interpolation of dispersed spatio-temporally varying data, allowing for interpolation within the space-time domain devoid of the conventional “time-frames”. Meshless methodologies tailored for scattered spatio-temporal data hold applicability across a spectrum of domains, encompassing the interpolation, approximation, and assessment of data originating from various sources, such as buoys, sensor networks, tsunami monitoring instruments, chemical and radiation detectors, vessel and submarine detection systems, weather forecasting models, as well as the compression and visualization of 3D vector fields, among others.

1. Introduction

Data interpolation and approximation represent recurrent tasks spanning numerous domains. Typically, interpolation is employed for datasets denoted as $h_i=f\left({\mathbf{x}}_{\mathbf{i}}\right)$ where $h_i$ corresponds to a value at position ${\mathbf{x}}_{\mathbf{i}}\in \mathrm{\Omega }$. The data domain is represented by $\mathrm{\Omega }$ within the Euclidean space $E^d$, usually with dimensions $d=2$ or $d=3$. Notably, the tessellation of the data domain does not invariably hinge upon the Delaunay triangulation (DT).

The values $h_i$ may manifest as scalars or vectors, exemplified by parameters such as wind velocity $(v_x,v_y,v_z)$. In spatio-temporal data instances, an implicit expectation emerges wherein a fixed and known correspondence between points yields spatio-temporal meshes featuring unchanging point connectivity across temporal frames $t_i$ and $t_{i+1},$ if domain tessellation is adopted. It warrants mention that in scenarios where the spatial domain $\mathrm{\Omega }\in E^3$, the spatio-temporal context requires tessellation within $E^4$.

A customary technique for tessellation resides in the Delaunay triangulation (DT) [1]. Nevertheless, it is imperative to acknowledge that its computational complexity increases as $O\left(N^{\lceil d/2+1\rceil }\right)$, resulting in $O\left(N^2\right)$ for $d=2$ and $O\left(N^3\right)$ for $d=3$ or $d=4$ [1]. Furthermore, the dimensionality of the data introduces a significant increase in computational demands, engendering numerical robustness concerns.

In addition to computational intricacies, ensuring the requisite smoothness of the final interpolation of $h_i$ values presents a formidable challenge when triangular or tetrahedral meshes are utilized for data domain representation. This methodology holds relevance in spatio-temporal scenarios where data are “framed” for a designated “time-slice” $t_i$ with fixed, known point connectivity.

However, many problems here require interpolating scattered spatio-temporal data in a “non-framed” manner. Examples encompass sensor networks, buoyant devices outfitted with sensors at sea, and situations where data sources operate sporadically, such as tsunami detection and the identification of ships and submarines. Such sensors experience transient connectivity, yielding energy conservation benefits while posing challenges in their detection.

2. Spatio-Temporal Data Classification

Interpolation and approximation are usually made for the “ordered” data domains, e.g., rectangular, triangular, and tetrahedral meshes. In CAD systems, the parametric space is used for interpolation, e.g., for parametric curves and surfaces. The data domain can be classified as follows:

• ordered:

  –

  structured:

  *

  regular, e.g., a rectangular mesh where all elements have the same size, triangular meshes with a constant vertex valency.

  *

  irregular, e.g., a rectangular mesh, but elements have different-sized triangular meshes with non-constant vertex valencies.

  –

  unstructured, e.g., general triangular or tetrahedral meshes.

• unordered:

  –

  clustered—points form clusters in the data domain.

  –

  scattered—points are generally scattered across the domain.

The domain data can also be classified as static or dynamic in space and time; see

Table 1. The classification of spatio-temporal datasets.

		Temporal Property
		Static	Dynamic
Spatial Property	Static	$h=f\left(\mathbf{x}\right)$	$h=f(\mathbf{x},t)$
	Dynamic	$h=f\left(\mathbf{x}\right(t\left)\right)$	$h=f\left(\mathbf{x}\right(t),t)$

. It can be seen that the case $h=f\left(\mathbf{x}\right(t),t)$ represents interpolation of a scalar value h on the d-dimensional domain of $\mathbf{x}\left(t\right)\in \mathrm{\Omega }\left(t\right)$, where the position $\mathbf{x}\left(t\right)$ is changing within time t. It should be noted that the $\mathrm{\Omega }\left(t\right)$ is not generally constant in time.

Now, the case of the scattered spatio-temporal domain is dynamic in both, i.e., $h\left(t\right)=f\left(\mathbf{x}\right(t),t)$ can be classified further as follows:

• framed in time—points lie on a hyperplane $\rho \in E^d$ for the given time slice $t_i$.
• framed in space—all points for the given slice in the given $E^d$ space are given (limited to the $(x,t)$ case, i.e., $x\in R^1$).
• unframed in space and time—just an unordered “heap of points” scattered in space-time.

Also, the points in the $\mathrm{\Omega }$ domain might be with known mutual point correspondences, i.e., a geometrical trajectory of a point can be reconstructed, e.g., using the sensor’s ID, or without any similar information, i.e., the sensor’s ID is not available. A typical example can be free-floating buoys (not attached), e.g., measuring value radiations that transmit information only if the measured values are outside the expected interval.

The following describes a general approach to scattered spatio-temporal data interpolation using radial basis functions (RBFs).

3. Radial Basis Functions

Several radial basis functions (RBFs) have been introduced by various authors [2,3,4]. The RBF interpolation is based on a solution of a linear system of equations $\mathbf{Ax}=\mathbf{b}$ and consists of two major steps:

• The weight $\mathbf{\lambda }$ computation, Equations (1) and (2); this will be explained later.
• Interpolated function $h\left(\mathbf{x}\right)$ computation for the value $\mathbf{x}$, Equation (1).

The RBFs can be categorized into two major groups:

• “Global” RBFs: These RBFs have a global impact and include functions like the following:

  –

  Polyharmonic spline (PHS):

  $\phi \left(r\right)=r^{2k-1},k=1,2,\dots$    $\phi \left(r\right)=r^{k}lnr,k=1,2,\dots$

  –

  Thin-plate spline (TPS): $\phi \left(r\right)=r^{2k}lnr,k=1,2,\dots$

  In the actual implementation, $\phi \left(r\right)=r^{2}ln{r}^2$ is used as $r^{2}lnr=\frac{1}{2}{r}^{2}ln{r}^2$.

  –

  Gaussian: $\phi \left(r\right)=e^{-\alpha r^2}$.

  –

  Multiquadric: $\phi \left(r\right)=\sqrt{1+\alpha r^2}$.

  –

  Inverse quadratic: $\phi \left(r\right)=\frac{1}{1+\alpha r^2}$.

  –

  Inverse multiquadratic: $\phi \left(r\right)=\frac{1}{\sqrt{1+\alpha r^2}}$.

  In these functions, $\alpha >0$ is a shape parameter, and $r\in (0,\infty )$. The global RBFs lead to dense (full) matrix $\mathbf{A}$, in some cases ill-conditioned.
• “Local” RBFs (Compactly Supported RBFs or CS-RBFs): These RBFs have non-zero positive values only on the interval $(0,1)$, see Figure 1a. Some examples of these functions are listed in

  Table 2. Wendland’s Compactly Supported RBF (CS-RBF) ${(·)}_{+}$ indicates that the value of the expression is zero for $r\ge 1$.

  ID	RBF	Function	ID	RBF	Function
  1	${\phi }_{1,0}$	${(1-r)}_{+}$	2	${\phi }_{1,1}$	${(1-r)}_{+}^3(3r+1)$
  3	${\phi }_{1,2}$	${(1-r)}_{+}^5(8r^2+5r+1)$	4	${\phi }_{3,0}$	${(1-r)}_{+}^2$
  5	${\phi }_{3,1}$	${(1-r)}_{+}^4(4r+1)$	6	${\phi }_{3,2}$	${(1-r)}_{+}^6(35r^2+18r+3)$
  7	${\phi }_{3,3}$	${(1-r)}_{+}^8(32r^3+25r^2+8r+3)$	8	${\phi }_{5,0}$	${(1-r)}_{+}^3$
  9	${\phi }_{5,1}$	${(1-r)}_{+}^3(5r+1)$	10	${\phi }_{5,2}$	${(1-r)}_{+}^7(16r^2+7r+1)$

  . CS-RBFs usually lead to a sparse matrix $\mathbf{A}$ and depend on the shape parameter $\alpha$. Additional CS-RBFs, such as the “bump CS-RBF” based on Gaussian, have also been proposed.

There are two steps in the RBF interpolation:

• The “global” functions lead to full RBF matrices, usually ill-conditioned [2]. Also, for large data processing, the size of matrix $\mathbf{A}$ is very high and the block matrix approach has to be taken [5]; in the St.Helen case, over $6.7\times$ 10${}^6$ points were processed and it led to a ${10}^6\times {10}^6$ matrix.
  Some RBFs depend on a “proper” selection of the shape parameter $\alpha$ and are very sensitive, especially if the polynomial $P_k\left(\mathbf{x}\right)$ is used [6].
• The “local” functions lead to sparse RBF matrices if the shape parameter $\alpha$ is chosen appropriately. If the RBF matrix is positive definite, iterative methods can be used. It usually leads to a faster solution. Also, space partitioning can be used to obtain a faster solution of the RBF weights $\mathbf{\lambda }$ followed by an interpolation between neighbor cells in actual value computation. The whole domain $\mathrm{\Omega }$ is split into cells $\omega$ and weights $\mathbf{\lambda }$ are computed for each cell $\omega$ together with some points from the neighbor cells; see Figure 1b. The final interpolated value is determined by a linear interpolation covering the neighbor cells [7].

It should be noted that the radial basis functions have the shape parameter $\alpha$, which influences the precision of the final interpolation and the choice of the value might be critical [8,9,10].

4. RBF Interpolation

The radial basis function (RBF) interpolation is based on the mutual distances between points within the data domain $\mathrm{\Omega }$ [2,11,12,13,14,15,16,17,18,19]. RBFs find widespread use in various applications, including those discussed [10,20,21,22].

RBF interpolation takes the following form:

$$h\left(\mathbf{x}\right)=\sum _{j=1}^N{\lambda }_j\phi (\parallel \mathbf{x}-{\mathbf{x}}_j\parallel )=\sum _{j=1}^N{\lambda }_j\phi \left(r_j\right)$$

(1)

where $r_j$ represents the distance from point $\mathbf{x}$ to point ${\mathbf{x}}_j$, ${\lambda }_j$ represents weight, and $\phi (·)$ is the RBF kernel function used.

Since the parameter r in the function $\phi \left(r\right)$ is a distance between two points in a d-dimensional space, the interpolation is inseparable by dimension. The RBF $\phi \left(r\right)$ will be given later. For each point ${\mathbf{x}}_i$, the interpolating function must take on the value $h_i$. This leads to a system of linear equations:

$$h_i=h\left({\mathbf{x}}_i\right)=\sum _{j=1}^N{\lambda }_j\phi (\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel )=\sum _{j=1}^N{\lambda }_j\phi \left(r_{ij}\right),i=1,\dots ,N$$

(2)

where ${\lambda }_j$ represents unknown weights for each radial basis function, N is the number of given points, and $\phi \left(r\right)$ is the radial basis function itself. Then Equation (2) can be written in matrix form as:

$$\mathbf{A}\mathbf{\lambda }=\mathbf{h}$$

(3)

or using ${\phi }_{ij}=\phi \left(r_{ij}\right)=\phi (\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel )$ as:

$$\left[\begin{array}{ccccc}{\phi }_{11}& \cdots & {\phi }_{1j}& \cdots & {\phi }_{1N}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\phi }_{i1}& \cdots & {\phi }_{ij}& \cdots & {\phi }_{iN}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\phi }_{N1}& \cdots & {\phi }_{Nj}& \cdots & {\phi }_{NN}\end{array}\right]\left[\begin{array}{c}{\lambda }_1\\ ⋮\\ {\lambda }_i\\ ⋮\\ {\lambda }_N\end{array}\right]=\left[\begin{array}{c}{h}_1\\ ⋮\\ h_i\\ ⋮\\ h_N\end{array}\right]$$

(4)

The interpolated value $h\left(\mathbf{x}\right)$ at point $\mathbf{x}$ is computed using Equation (1).

Additional orthogonal functions can be added to ensure positive definiteness of the system [2,6,23,24]. However, it might lead to the ill-conditionality of the linear system of equations in some cases [24]. In the case of an additional polynomial $P_k\left({\mathbf{x}}_i\right)$ of degree k, we have

$$h\left({\mathbf{x}}_i\right)=\sum _{j=1}^N{\lambda }_j\phi (\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel )+P_k\left({\mathbf{x}}_i\right),i=1,\dots ,N$$

(5)

It is worth noting that the matrix size is nearly independent of the dimension and has a size of approximately $(N\times N)$, which is advantageous for solving large systems of linear equations [5]. For example, in the case of a bilinear polynomial $P_1(x,y)$:

$$P_1(x,y)=a_0+a_{1}x+a_{2}y+a_{3}xy$$

(6)

Additional orthogonal conditions, in the case of the polynomial $P_1(x,y)$ in Equation (6), are to be applied:

$$\sum _{j=1}^N{\lambda }_j=0,\sum _{j=1}^N{\lambda }_j{x}_j=0,\sum _{j=1}^N{\lambda }_j{y}_j=0,\sum _{j=1}^N{\lambda }_j{x}_j{y}_j=0$$

(7)

The conditions in Equation (7) lead to a compact formulation of RBF interpolation:

$$\left[\begin{array}{cc}\mathbf{A}& \mathbf{P}\\ {\mathbf{P}}^{\mathbf{T}}& \mathbf{0}\end{array}\right]\left[\begin{array}{c}\mathbf{\lambda }\\ \mathbf{a}\end{array}\right]=\left[\begin{array}{c}\mathbf{h}\\ \mathbf{0}\end{array}\right]$$

(8)

In Equation (8), the matrix $\mathbf{P}$ represents the polynomial, $\mathbf{\lambda }$ is the vector of the RBF weights, the vector $\mathbf{a}$ contains the resulting polynomial coefficients, and $\mathbf{h}$ represents the given values at the given points ${\mathbf{x}}_i\in \mathrm{\Omega }$. The matrix ${\mathbf{P}}^{\mathbf{T}}$ represents the additional orthogonal conditions as defined in Equation (7).

However, when using the polynomial $P_k\left(\mathbf{x}\right)$:

• RBF interpolation is not invariant to rotation and translation except when $P_0\left(\mathbf{x}\right)=a_0$ is used, i.e., contains only a scalar value.
• Interpolation, represented by $\mathbf{\lambda }$ and $\mathbf{a}$, depends on the physical units used for the vector $\mathbf{x}$.
• The polynomial used might be counter-productive in cases with a large range of domain data [6,24].

RBF interpolation results in a linear system of equations $\mathbf{Ax}=\mathbf{b}$. It is a significant advantage of the RBF methods, as sophisticated numerical methods have been developed.

4.1. Distance

The RBF methods are based on distances. The distance between points ${\mathbf{x}}_i$ and ${\mathbf{x}}_j$, denoted as $r_{ij}=\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel$, is defined as follows:

• For spatial data (time-independent), the Euclidean norm ${\parallel ·\parallel }_2$ is typically used:

  $$r_{ij}=\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel =\sqrt{\sum _{k=1}^d{({}^k{x}_i-{}^k{x}_j)}^2}=\sqrt{{({\mathbf{x}}_i-{\mathbf{x}}_j)}^T({\mathbf{x}}_i-{\mathbf{x}}_j)}$$

  (9)

  where ${}^k{x}_i$ represents the $k^{th}$ element of the vector ${\mathbf{x}}_i$.
  It should be noted that the norm ${\parallel ·\parallel }_1$ is also used, e.g., in fuzzy systems.
• For spatio-temporal data (time-varying), the distance is calculated as

  $$r_{ij}=\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel =\sqrt{\sum _{k=1}^d{({}^k{x}_i-{}^k{x}_j)}^2+{\beta }^2{(t_i-t_j)}^2}$$

  (10)

  where ${}^k{x}_i$ again represents the $k^{th}$ element of the vector ${\mathbf{x}}_i$. The coefficient $\beta$ has physical units of $[m/s]$ and reflects the speed of the physical phenomena, such as the speed of sound in water or the speed of light, etc.
  Unfortunately, $\beta =1$ is usually taken in many applications regardless of physical reasoning and possible influence on the final interpolated values.
• Another approach is to use the radial basis function $\phi \left(r\right)$ with a multiplicative exponential time term:

  $$\varphi \left(r\right(t),t)=\phi \left(r\right)e^{-k_{1}t}\mathrm{or}\varphi \left(r\right(t),t)=\phi \left(r\right)e^{-(k_1{t}^2+k_{2}t+k_3)}$$

  (11)

  where $k_1$, $k_2$, and $k_3$ are constants, as discussed in Ku [25].
  Such an approach is usually taken in solutions of partial differential equations (PDEs).
  If the points $\mathbf{x}$ are not static, i.e., $\mathbf{x}=\mathbf{x}\left(t\right)$, then the mutual distances of points are not constant and they are time-dependent, i.e., $r_{ij}=r_{ij}\left(t\right)$.
  The radial basis functions mentioned above are used for interpolation, approximation, and solving ordinary differential equations (ODEs) and partial differential equations (PDEs), among other applications.

In the case of RBF approximation with a polynomial, a direct application of the Least Square Error methods (LSE) leads to incorrect results.

4.2. Normalized RBF

Normalized RBF (N-RBF) is a modification of the standard RBF used in RBF neural network-related applications [26]. It is given in the following form:

$$h\left(\mathbf{x}\right)=\frac{{\sum }_{j=1}^N{\lambda }_j\phi \parallel \mathbf{x}-{\mathbf{x}}_j\parallel )}{{\sum }_{j=1}^N\phi \parallel \mathbf{x}-{\mathbf{x}}_j\parallel }=\frac{{\sum }_{j=1}^N{\lambda }_j\phi \left(r_j\right)}{{\sum }_{j=1}^N\phi \left(r_j\right)}$$

(12)

where $r_j$ is the distance from point $\mathbf{x}$ to point ${\mathbf{x}}_j$.

It can be seen that denominator values in Equation (12) can be zero, or close to zero, i.e., ${\sum }_{j=1}^N\phi \parallel \mathbf{x}-{\mathbf{x}}_j\parallel \to 0$ for some values $\mathbf{x}$, which would lead to instability as $h\left(\mathbf{x}\right)\to \infty$. However, the N-RBFs are used in the RBF neural network applications [26] as the projective linearity is kept.

4.3. Squared Normalized RBF

Some RBFs $\phi \left(r\right)$ used for interpolation and approximation are not strictly positive, such as $r^{2}ln\left(r\right)$ (Thin-Plate Spline—TPS), which is negative on the interval $(0,1)$. In such cases, the Euclidean norm should be used for more robust computation. It should be noted that $r^{2}log\left(r\right)=\frac{1}{2}{r}^{2}log\left(r^2\right)$ is to be used as no $\sqrt{r^2}$ computation is needed; only the values of the weights ${\lambda }_j$ are doubled. Also, there is a direct connection between the matrix conditionality and numerical robustness [27].

The Squared Normalized RBF (SN-RBF) is defined as follows:

$$h\left(\mathbf{x}\right)=\frac{{\sum }_{j=1}^N{\lambda }_j\phi (\parallel \mathbf{x}-{\mathbf{x}}_j\parallel )}{\sqrt{{\sum }_{j=1}^N{\phi }^2(\parallel \mathbf{x}-{\mathbf{x}}_j\parallel )}}=\frac{{\sum }_{j=1}^N{\lambda }_j\phi \left(r_j\right)}{\sqrt{{\sum }_{j=1}^N{\phi }^2\left(r_j\right)}}$$

(13)

where $r_j=\parallel \mathbf{x}-{\mathbf{x}}_j\parallel$ is the distance from point $\mathbf{x}$ to point ${\mathbf{x}}_j$.

This is essentially the Euclidean normalization of each row of the matrix $\mathbf{A}$ in Equation (4), which leads to slightly better numerical conditionality of the linear system of equations.

In the case of interpolation, Equation (13) must be valid for all given points ${\mathbf{x}}_i\in \mathrm{\Omega }$:

$$h\left({\mathbf{x}}_i\right)=\frac{{\sum }_{j=1}^N{\lambda }_j\phi (\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel )}{\sqrt{{\sum }_{j=1}^N{\phi }^2(\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel )}}=\frac{{\sum }_{j=1}^N{\lambda }_j\phi \left(r_{ij}\right)}{\sqrt{{\sum }_{j=1}^N{\phi }^2\left(r_{ij}\right)}},i=1,\dots ,N$$

(14)

It leads to:

$$\sum _{j=1}^N{\lambda }_j\phi (\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel )=h\left({\mathbf{x}}_i\right)\sqrt{\sum _{j=1}^N{\phi }^2(\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel )},i=1,\dots ,N$$

(15)

In the case of interpolation with an added polynomial $P_k\left(\mathbf{x}\right)$ of degree k, Equation (14) becomes:

$$h\left(\mathbf{x}\right)=\frac{{\sum }_{j=1}^N{\lambda }_j\phi (\parallel \mathbf{x}-{\mathbf{x}}_j\parallel )}{\sqrt{{\sum }_{j=1}^N{\phi }^2(\parallel \mathbf{x}-{\mathbf{x}}_j\parallel )}}+P_k\left(\mathbf{x}\right)$$

(16)

The additional orthogonal conditions are to be added, as discussed in Equation (7). The polynomial $P_k\left(\mathbf{x}\right)$ improves the conditionality of the RBF matrix and provides a rough approximation of the given data. However, it might be counter-productive in some cases.

The SN-RBF in Equation (16) can be rewritten as:

$$h\left({\mathbf{x}}_i\right)=\frac{{\sum }_{j=1}^N{\lambda }_j\phi (\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel )}{\sqrt{{\sum }_{j=1}^N{\phi }^2(\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel )}}+P_k\left({\mathbf{x}}_i\right)=\frac{{\sum }_{j=1}^N{\lambda }_j\phi \left(r_{ij}\right)}{\sqrt{{\sum }_{j=1}^N{\phi }^2\left(r_{ij}\right)}}+P_k\left({\mathbf{x}}_i\right),i=1,\dots ,N$$

(17)

where $r_{ij}=\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel$.

It is important to note that this approach replaces $O\left(N^2\right)$ division operations with $O\left(N\right)$ multiplications. The given values $h\left({\mathbf{x}}_i\right)$ are just multiplied by the values $\sqrt{{\sum }_{j=1}^N{\phi }^2\left(r_{ij}\right)}$. This also enhances the robustness of computation, especially for large values of N.

Equation (17) can be modified similarly to Equation (15) to:

$$\sum _{j=1}^N{\lambda }_j\phi \left(r_{ij}\right)+P_k\left({\mathbf{x}}_i\right)\sqrt{\sum _{j=1}^N{\phi }^2\left(r_{ij}\right)}=h\left({\mathbf{x}}_i\right)\sqrt{\sum _{j=1}^N{\phi }^2\left(r_{ij}\right)},i=1,\dots ,N$$

(18)

As $\sqrt{{\sum }_{j=1}^N{\phi }^2\left(r_{ij}\right)}$ is a constant for the $i^{th}$ row ($i=1,\dots ,N$), Equation (18) can be simplified:

$$\sum _{j=1}^N{\lambda }_j\phi \left(r_{ij}\right)+q_i{P}_k\left({\mathbf{x}}_i\right)=q_{i}h\left({\mathbf{x}}_i\right),i=1,\dots ,N$$

(19)

where $q_i=\sqrt{{\sum }_{j=1}^N{\phi }^2\left(r_{ij}\right)}$.

Then the system of linear equations for the SN-RBF interpolation has the following form:

$$\left[\begin{array}{ccccccc}{\phi }_{11}& \dots & {\phi }_{1N}& q_1& q_1{x}_1& q_1{y}_1& q_1{x}_1{y}_1\\ ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& ⋮\\ {\phi }_{N1}& \dots & {\phi }_{NN}& q_N& q_N{x}_N& q_N{y}_N& q_N{x}_n{y}_N\\ 1& 1& 1& 0& 0& 0& 0\\ x_1& \dots & x_N& 0& 0& 0& 0\\ y_1& \dots & y_N& 0& 0& 0& 0\\ x_1{y}_1& \dots & x_N{y}_N& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}{\lambda }_1\\ ⋮\\ {\lambda }_N\\ a_0\\ a_1\\ a_2\\ a_3\end{array}\right]=\left[\begin{array}{c}{q}_1{h}_1\\ ⋮\\ q_N{h}_N\\ 0\\ 0\\ 0\\ 0\end{array}\right]$$

(20)

which can be expressed more compactly as

$$\left[\begin{array}{cc}\mathbf{A}& \mathbf{QP}\\ {\mathbf{P}}^{\mathbf{T}}& \mathbf{0}\end{array}\right]\left[\begin{array}{c}\mathbf{\lambda }\\ \mathbf{a}\end{array}\right]=\left[\begin{array}{c}\mathbf{Q}\mathbf{h}\\ \mathbf{0}\end{array}\right]$$

(21)

where $\mathbf{Q}=diag[q_1,\dots ,q_N]$ is a diagonal matrix and $q_i>0$, $i=1,\dots ,N$ in the case of SN-RBFs. However, in the approximation case, i.e., the matrix $\mathbf{A}$ is $(N\times M),N>M$, the polynomial part has to be handled differently, and the Least Square Method (LSE) cannot be used directly [28].

4.4. RBF Approximation

Approximation using RBF with a polynomial leads to Equation (22), which is formally similar to Equation (8). However, the RBF matrix is $N\times M$, where $N>M$.

$$\left[\begin{array}{cc}\mathbf{A}& \mathbf{P}\\ {\mathbf{P}}^{\mathbf{T}}& \mathbf{0}\end{array}\right]\left[\begin{array}{c}\mathbf{\lambda }\\ \mathbf{a}\end{array}\right]=\left[\begin{array}{c}\mathbf{h}\\ \mathbf{0}\end{array}\right]$$

(22)

If the Least Square Method were to be used directly, it would lead to a matrix:

$$\left[\begin{array}{cc}{\mathbf{A}}^T\mathbf{A}+{\mathbf{P}}^T\mathbf{P}& {\mathbf{A}}^T\mathbf{P}\\ {\mathbf{P}}^T\mathbf{A}& {\mathbf{P}}^T\mathbf{P}\end{array}\right]$$

(23)

where values without physical units ${\mathbf{A}}^T\mathbf{A}$ would be summed with ${\mathbf{P}}^T\mathbf{P}$ values having physical units (m${}^2$). This means that it is an incorrect solution.

The correct solution can be obtained using Lagrange multipliers and an error r minimization:

$$\mathbf{A}\mathbf{\lambda }+\mathbf{P}\mathbf{a}=\mathbf{h},r=\parallel \mathbf{A}\mathbf{\lambda }+\mathbf{P}\mathbf{a}-\mathbf{h}\parallel$$

(24)

Using the conditions for a minimum of r:

$$\frac{\partial r^2}{\partial \mathbf{\lambda }}={\mathbf{A}}^T\mathbf{A}\mathbf{\lambda }+{\mathbf{A}}^T\mathbf{P}\mathbf{a}-{\mathbf{A}}^T\mathbf{h}=\mathbf{0},\frac{\partial r^2}{\partial \mathbf{a}}={\mathbf{P}}^T\mathbf{A}\mathbf{\lambda }+{\mathbf{P}}^T\mathbf{P}\mathbf{a}-{\mathbf{P}}^T\mathbf{h}=\mathbf{0}$$

(25)

It leads to the correct solution of RBF approximation:

$$\left[\begin{array}{cc}{\mathbf{A}}^T\mathbf{A}& {\mathbf{A}}^T\mathbf{P}\\ {\mathbf{P}}^T\mathbf{A}& {\mathbf{P}}^T\mathbf{P}\end{array}\right]\left[\begin{array}{c}\mathbf{\lambda }\\ \mathbf{a}\end{array}\right]=\left[\begin{array}{c}{\mathbf{A}}^T\mathbf{h}\\ {\mathbf{P}}^T\mathbf{h}\end{array}\right]$$

(26)

However, this leads to numerical problems due to an ill-conditioned RBF matrix [24,29].

5. RBF Interpolation Example

For the demonstration of RBF spatio-temporal scattered data interpolation properties, we use rainfall data from Peninsular Malaysia in 2007, sourced from the Malaysian Meteorology Department [30]. These data are static from a spatial perspective but dynamic in the temporal dimension.

5.1. Algorithm Based on Triangulation and Timmer Patches

One approach to interpolate these data is to tessellate the domain, see Figure 2, subdivide the mesh, and smooth it. Ali [30] employed Delaunay triangulation based on 25 major meteorological station positions and used cubic Timmer triangular patches for the triangular surface representation and interpolation. Algorithm 1 outlines Ali’s approach and is used to generate the final triangular surface also using triangular mesh subdivision with the Timmer patches.

Algorithm 1 Ali’s Scattered Data Interpolation Algorithm

1: Input: Data points 2: Triangulate the domain using Delaunay triangulation. 3: Specify derivatives at data points using [31], then assign Timmer coordinates values for each triangular patch. 4: Generate triangular patches of the surfaces using cubic Timmer triangular patches. 5: Output: Surface reconstruction.

It is important to note that additional operations are required to obtain a smooth surface over the triangular mesh generated by Ali’s algorithm, or other interpolation techniques on tessellated data can be used [32].

Figure 2. The tessellation of Peninsular Malaysia; data taken from [33].

Figure 2. The tessellation of Peninsular Malaysia; data taken from [33].

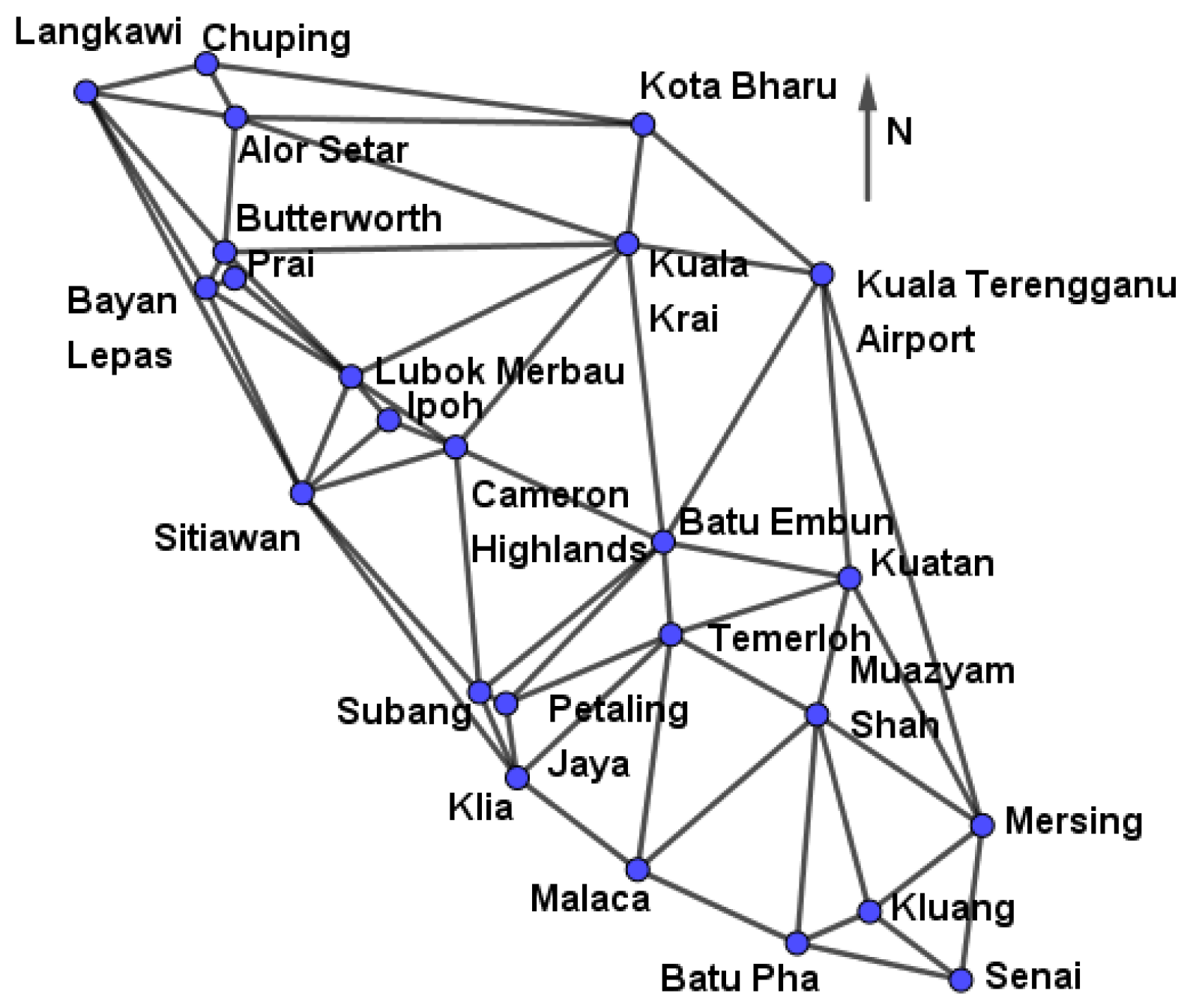
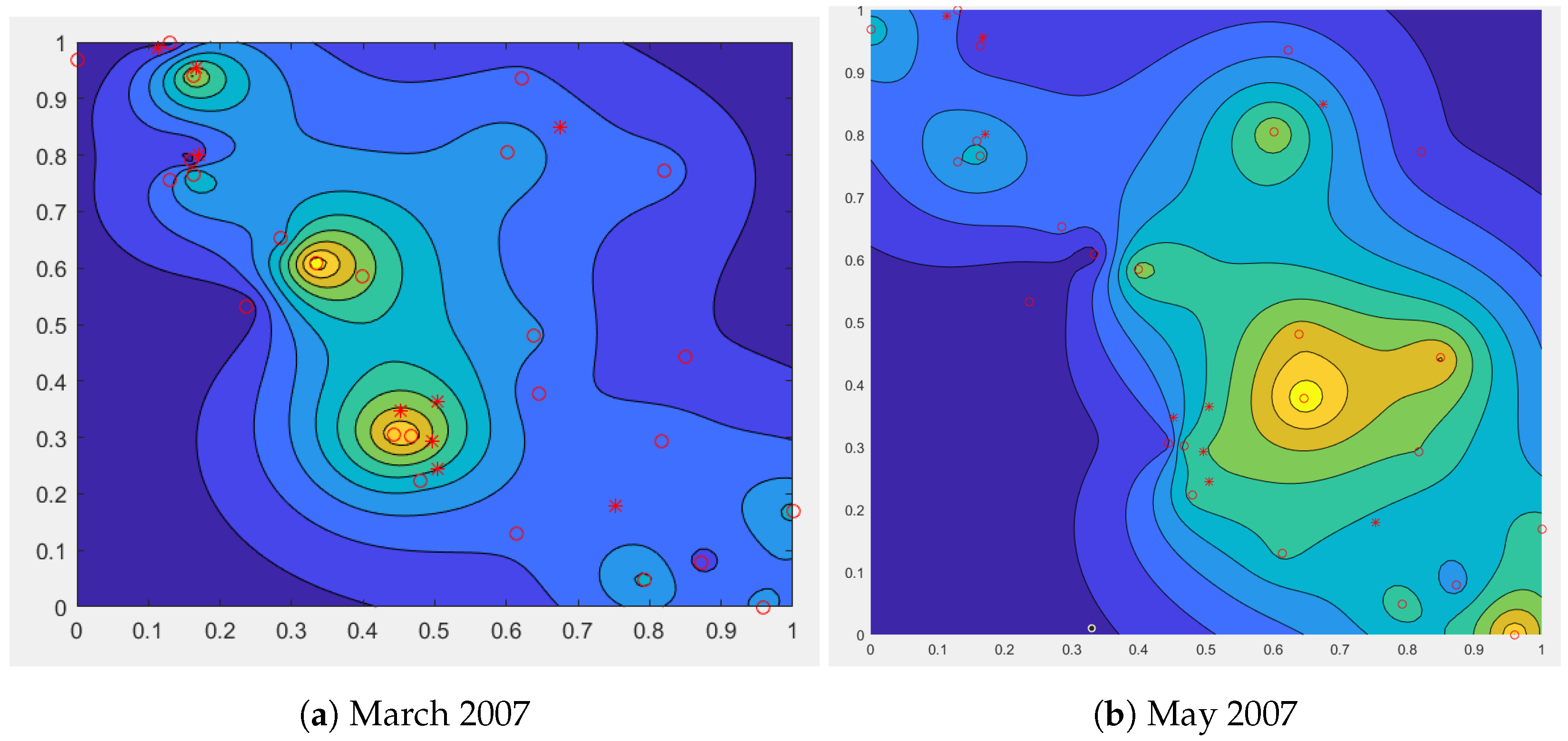
In the following section, we present a solution based on RBF interpolation.

5.2. RBF Interpolation

The RBF approach leads to a smooth surface automatically. However, interpolation on borders might not be reliable. Examples of the data SN-RBF interpolation are presented in figures in Figure 3. The SN-RBF with the Gauss function and bilinear polynomial was used; parameters $\alpha =0.255$ and $\beta =1$ in Equation (10).

The 3D views of the rainfall interpolated data are presented in Figure 4 and Figure 5. It should be noted that the $\alpha$ shape parameter has to be set reasonably. Note, that there are several suboptimal shape parameters [8,9,34].

5.3. Experimental Comparison

In RBF interpolation and approximation evaluation, standard testing functions are usually used and errors are evaluated.

The testing functions have been normalized to the data domain $[0,1]\times [0,1]$ and their values to $[0,1]$ for easier mutual comparison. It should be noted that:

• use of “global” functions leads to full RBF matrices, which are usually ill-conditioned;
• “local” functions are sensitive to the shape parameter $\alpha$ choice; in the following tests, $\alpha =1$ was taken;
• additional polynomial use leads to loss of invariance and to additional problems in large spans of data [24].

In the experiments conducted, the following items have been evaluated:

• RBF matrix conditionality:

  $$\kappa \left(\mathbf{A}\right)=\frac{|{\lambda }_{max}\left(\mathbf{A}\right)|}{|{\lambda }_{min}\left(\mathbf{A}\right)|}$$

  where $\lambda$ are eigenvalues of the matrix $\mathbf{A}$.
  Note that the angular conditionality might be used for large matrices $\mathbf{A}$.
• Root Mean Square Error (RMSE):

  $$RMSE=\sqrt{\sum _{i=1}^n\frac{{(x_i-h\left(x_i\right))}^2}{n}}$$
• Coefficient $R^2$:

  $$R^2=1-\frac{{\sum }_{i=1}^n{(x_i-h\left(x_i\right))}^2}{{\sum }_{i=1}^n{(x_i-\overline{x})}^2},$$
• Maximum error $e_{max}$:

  $$e_{max}=\underset{i}{max}\left(\right|x_i-h\left(x_i\right)\left|\right)$$

The following testing functions were used:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill F_1(x,y)=0.75e^{-\left(\frac{{(9x-2)}^2+{(9y-2)}^2}{4}\right)}+0.75e^{-(\frac{{(9x+1)}^2}{49}+\frac{9y+1}{10})}\\ \hfill +0.5e^{-\left(\frac{{(9x-7)}^2+{(9y-3)}^2}{4}\right)}-0.2e^{-({(9x-4)}^2+{(9y-7)}^2)}\\ \hfill F_2(x,y)=\frac{1}{9}(tanh(9y-9x)+1)\\ \hfill F_3(x,y)=\frac{1}{6}\frac{1.25+cos\left(4.5y\right)}{1+{(3x-1)}^2}\\ \hfill F_4(x,y)=\frac{1}{3}{e}^{-\frac{81}{16}{(x-0.5)}^2+{(y-0.5)}^2}\\ \hfill F_5(x,y)=\frac{1}{3}{e}^{-\frac{81}{4}{(x-0.5)}^2+{(y-0.5)}^2}\\ \hfill F_6(x,y)=\frac{1}{9}\sqrt{64-81({(x-0.5)}^2+{(y-0.5)}^2)}-0.5\end{array}\end{array}$$

(27)

Experimental results are presented in

Table 3. The experimental results: RBF interpolation with 121 points generated; F—testing function.

F	RBF	Norm.	Degree	Conditionality	RMSE	${\mathbf{R}}^2$	${\mathbf{e}}_{\mathbf{max}}$
1	${(1-r)}_{+}^7(16r^2+7r+1)$	no	-	$3.73\times {10}^{04}$	0.002	1.000	0.011
2	${(1-r)}_{+}^6(35r^2+18r+3)$	no	-	$9.76\times {10}^{04}$	0.004	1.000	0.016
3	$\frac{1}{\alpha +r^2}$	no	-	$2.10\times {10}^{16}$	0.000	1.000	0.001
4	$\frac{1}{\alpha +r^2}$	no	-	$2.10\times {10}^{16}$	0.000	1.000	0.000
5	$\frac{1}{\alpha +r^2}$	no	-	$2.10\times {10}^{16}$	0.000	1.000	0.001
6	$\frac{1}{\alpha +r^2}$	no	-	$2.10\times {10}^{16}$	0.000	1.000	0.000
1	${(1-r)}_{+}^7(16r^2+7r+1)$	yes	-	$3.88\times {10}^{04}$	0.001	1.000	0.011
2	${(1-r)}_{+}^7(16r^2+7r+1)$	yes	-	$3.88\times {10}^{04}$	0.004	1.000	0.018
3	${(1-r)}_{+}^7(16r^2+7r+1)$	yes	-	$3.88\times {10}^{04}$	0.000	1.000	0.001
4	$\frac{1}{\alpha +r^2}$	yes	-	$2.30\times {10}^{16}$	0.000	1.000	0.000
5	$\frac{1}{\alpha +r^2}$	yes	-	$2.30\times {10}^{16}$	0.000	1.000	0.001
6	$\frac{1}{\alpha +r^2}$	yes	-	$2.30\times {10}^{16}$	0.000	1.000	0.000
1	${(1-r)}_{+}^7(16r^2+7r+1)$	no	0	$4.42\times {10}^{04}$	0.001	1.000	0.011
2	${(1-r)}_{+}^7(16r^2+7r+1)$	no	0	$4.42\times {10}^{04}$	0.004	1.000	0.015
3	$\frac{1}{\alpha +r^2}$	no	0	$2.12\times {10}^{16}$	0.000	1.000	0.001
4	$\frac{1}{\alpha +r^2}$	no	0	$2.12\times {10}^{16}$	0.000	1.000	0.000
5	$\frac{1}{\alpha +r^2}$	no	0	$2.12\times {10}^{16}$	0.000	1.000	0.001
6	$\frac{1}{\alpha +r^2}$	no	0	$2.12\times {10}^{16}$	0.000	1.000	0.000
1	${(1-r)}_{+}^7(16r^2+7r+1)$	no	1	$4.71\times {10}^{04}$	0.001	1.000	0.011
2	${(1-r)}_{+}^7(16r^2+7r+1)$	no	1	$4.71\times {10}^{04}$	0.004	1.000	0.015
3	$\frac{1}{\alpha +r^2}$	no	1	$2.13\times {10}^{16}$	0.000	1.000	0.001
4	$\frac{1}{\alpha +r^2}$	no	1	$2.13\times {10}^{16}$	0.000	1.000	0.000
5	$\frac{1}{\alpha +r^2}$	no	1	$2.13\times {10}^{16}$	0.000	1.000	0.001
6	$\frac{1}{\alpha +r^2}$	no	1	$2.13\times {10}^{16}$	0.000	1.000	0.000
1	${(1-r)}_{+}^7(16r^2+7r+1)$	no	2	$4.89\times {10}^{04}$	0.001	1.000	0.011
2	${(1-r)}_{+}^7(16r^2+7r+1)$	no	2	$4.89\times {10}^{04}$	0.004	1.000	0.015
3	$\frac{1}{\alpha +r^2}$	no	2	$2.08\times {10}^{16}$	0.000	1.000	0.001
4	$\frac{1}{\alpha +r^2}$	no	2	$2.08\times {10}^{16}$	0.000	1.000	0.000
5	$\frac{1}{\alpha +r^2}$	no	2	$2.08\times {10}^{16}$	0.000	1.000	0.001
6	$\frac{1}{\alpha +r^2}$	no	2	$2.08\times {10}^{16}$	0.000	1.000	0.000

for the interpolation case with the uniform sampling and in

Table 4. Experimental results: RBF approximation with 121 points generated; F—testing function.

F	RBF	Norm.	Degree	Conditionality	RMSE	${\mathbf{R}}^2$	${\mathbf{e}}_{\mathbf{max}}$
1	${(1-r)}_{+}^3(3r+1)$	no	-	$2.02\times {10}^{03}$	0.013	0.997	0.060
1	${(1-r)}_{+}^7(16r^2+7r+1)$	no	-	$4.80\times {10}^{02}$	0.015	0.996	0.058
2	$\frac{1}{\alpha +r^2}$	no	-	$3.23\times {10}^{07}$	0.029	0.996	0.063
3	$\frac{1}{\alpha +r^2}$	no	-	$3.23\times {10}^{07}$	0.004	1.000	0.014
4	$\sqrt{\alpha +r^2}$	no	-	$2.78\times {10}^{09}$	0.001	1.000	0.003
5	${(1-r)}_{+}^3(3r+1)$	no	-	$2.02\times {10}^{03}$	0.020	0.996	0.053
6	$r^{2}log\left(r\right)$	no	-	$5.78\times {10}^{02}$	0.000	1.000	0.001
1	${(1-r)}_{+}^7(16r^2+7r+1)$	yes	-	$4.68\times {10}^{02}$	0.012	0.998	0.059
1	${(1-r)}_{+}^8(32r^2+25r^2+8r+3)$	yes	-	$1.44\times {10}^{02}$	0.018	0.994	0.058
2	$\frac{1}{\alpha +r^2}$	yes	-	$3.17\times {10}^{07}$	0.030	0.995	0.064
2	${(1-r)}_{+}^7(16r^2+7r+1)$	yes	-	$4.68\times {10}^{02}$	0.029	0.996	0.067
3	${(1-r)}_{+}^7(16r^2+7r+1)$	yes	-	$4.68\times {10}^{02}$	0.004	1.000	0.014
4	$\frac{1}{\alpha +r^2}$	yes	-	$3.17\times {10}^{07}$	0.001	1.000	0.004
5	${(1-r)}_{+}^7(16r^2+7r+1)$	yes	-	$4.68\times {10}^{02}$	0.020	0.996	0.044
6	$e^{-\alpha r^2}$	yes	-	$5.79\times {10}^{12}$	0.001	1.000	0.002
1	${(1-r)}_{+}^7(16r^2+7r+1)$	no	0	$4.34\times {10}^{05}$	0.010	0.998	0.057
1	${(1-r)}_{+}^8(32r^2+25r^2+8r+3)$	no	0	$3.70\times {10}^{04}$	0.017	0.995	0.054
2	${(1-r)}_{+}^6(35r^2+18r+3)$	no	0	$1.56\times {10}^{06}$	0.028	0.996	0.063
3	${(1-r)}_{+}^5(8r^2+5r+1)$	no	0	$2.01\times {10}^{07}$	0.003	1.000	0.010
4	$\frac{1}{\alpha +r^2}$	no	0	$1.11\times {10}^{15}$	0.002	1.000	0.004
5	${(1-r)}_{+}^3(3r+1)$	no	0	$5.15\times {10}^{06}$	0.019	0.996	0.055
5	${(1-r)}_{+}^6(35r^2+18r+3)$	no	0	$1.56\times {10}^{06}$	0.020	0.996	0.054
6	$r^{2}log\left(r\right)$	no	0	$1.04\times {10}^{06}$	0.000	1.000	0.001
1	${(1-r)}_{+}^7(16r^2+7r+1)$	no	1	$5.45\times {10}^{05}$	0.008	0.999	0.052
1	${(1-r)}_{+}^8(32r^2+25r^2+8r+3)$	no	1	$4.43\times {10}^{04}$	0.016	0.995	0.049
2	${(1-r)}_{+}^6(35r^2+18r+3)$	no	1	$1.61\times {10}^{06}$	0.028	0.996	0.062
3	${(1-r)}_{+}^5(8r^2+5r+1)$	no	1	$2.34\times {10}^{07}$	0.003	1.000	0.010
4	$\sqrt{\alpha +r^2}$	no	1	$1.28\times {10}^{18}$	0.002	1.000	0.003
5	${(1-r)}_{+}^3(3r+1)$	no	1	$5.70\times {10}^{06}$	0.019	0.996	0.055
5	${(1-r)}_{+}^6(35r^2+18r+3)$	no	1	$1.61\times {10}^{06}$	0.020	0.996	0.054
6	$r^{2}log\left(r\right)$	no	1	$1.64\times {10}^{06}$	0.000	1.000	0.001
1	${(1-r)}_{+}^7(16r^2+7r+1)$	no	2	$4.19\times {10}^{06}$	0.008	0.999	0.052
1	${(1-r)}_{+}^8(32r^2+25r^2+8r+3)$	no	2	$4.09\times {10}^{05}$	0.016	0.995	0.048
2	${(1-r)}_{+}^6(35r^2+18r+3)$	no	2	$3.64\times {10}^{07}$	0.028	0.996	0.062
3	$\frac{1}{\alpha +r^2}$	no	2	$1.76\times {10}^{15}$	0.003	1.000	0.008
4	$\frac{1}{\sqrt{\alpha +r^2}}$	no	2	$6.11\times {10}^{16}$	0.001	1.000	0.002
5	${(1-r)}_{+}^5(8r^2+5r+1)$	no	2	$2.72\times {10}^{07}$	0.010	0.999	0.023
6	$\frac{1}{\alpha +r^2}$	no	2	$1.76\times {10}^{15}$	0.000	1.000	0.000

for the approximation case; points of importance were detected [5]. Figure 6, Figure 7, Figure 8 and Figure 9 present typical results of the RBF interpolation. It can be seen that the error is high at the border, which is a typical behavior of RBF interpolation.

6. Discussion

The RBF interpolation methods presented above are intended for spatio-temporal scattered data interpolation, generally in d-dimensional space. The main advantages are:

• the final interpolation is inherently smooth;
• if CS-RBFs are used, the RBF matrix is sparse;
• computational complexity is nearly independent of dimensionality and mainly depends on the number of data points;
• an explicit formal analytical formula for the final interpolation is obtained in the form $\mathbf{Ax}=\mathbf{b}$ (a solution is equivalent to the outer product (extended cross product) application [10]);
• if the RBF $\phi \left(r\right)$ is positive definite, iterative methods can be employed for solving linear systems of equations;
• the SN-RBF enhances numerical stability by effectively normalizing each row of the RBF matrix;
• solving linear systems of equations $\mathbf{Ax}=\mathbf{b}$ is equivalent to the outer product (extended cross-product) use; standard symbolic operations can be applied for further processing without the need for numerical evaluation;
• block matrix decomposition may be utilized for large datasets, resulting in faster computation [5,7].

However, the selection of the shape parameter $\alpha$ seems to be critical, and optimal choice is still an open question [8,9,10]. Additionally, RBFs find applications in solving partial differential equations (PDEs) and surface reconstruction of acquired data [21,22,35,36,37,38,39].

7. Conclusions

This contribution introduces a new form of normalized radial basis function (RBF) called Squared Normalized RBF (SN-RBF) for spatio-temporal data with normalization of RBF matrix rows. The main potential use is expected in sensor networks, where sensors may not have fixed positions, and data are not synchronized in time, i.e., in time slots. The proposed SN-RBF formulation not only provides better RBF matrix conditionality but also enhances the suitability of RBF interpolation for various applications. (Related papers are available at http://afrodita.zcu.cz/~skala/Publication-RBF.htm (accessed on 10 November 2023)).

The presented SN-RBF interpolation method is particularly advantageous for scattered spatio-temporal interpolation scenarios. For instance, it can be applied to cases where sensors transmit data only when physical phenomena reach values outside the expected range or when sensors change their positions, such as surveillance sensors in marine environments.

Future research will focus on analyzing the sensitivity of the shape parameter $\alpha$, evaluating the applicability of the thin-plate spline (TPS) function ($r^{2}lnr$) for large datasets, assessing the conditionality of resulting RBF matrices, and developing visualization methods for spatio-temporal data in 2D+T and 3D+T, which cannot be visualized effectively using traditional methods like contour plots or 3D projections.