Application of Feature Selection Approaches for Prioritizing and Evaluating the Potential Factors for Safety Management in Transportation Systems
Abstract
:1. Introduction
2. Methodology
2.1. Artificial Neural Networks (ANNs)
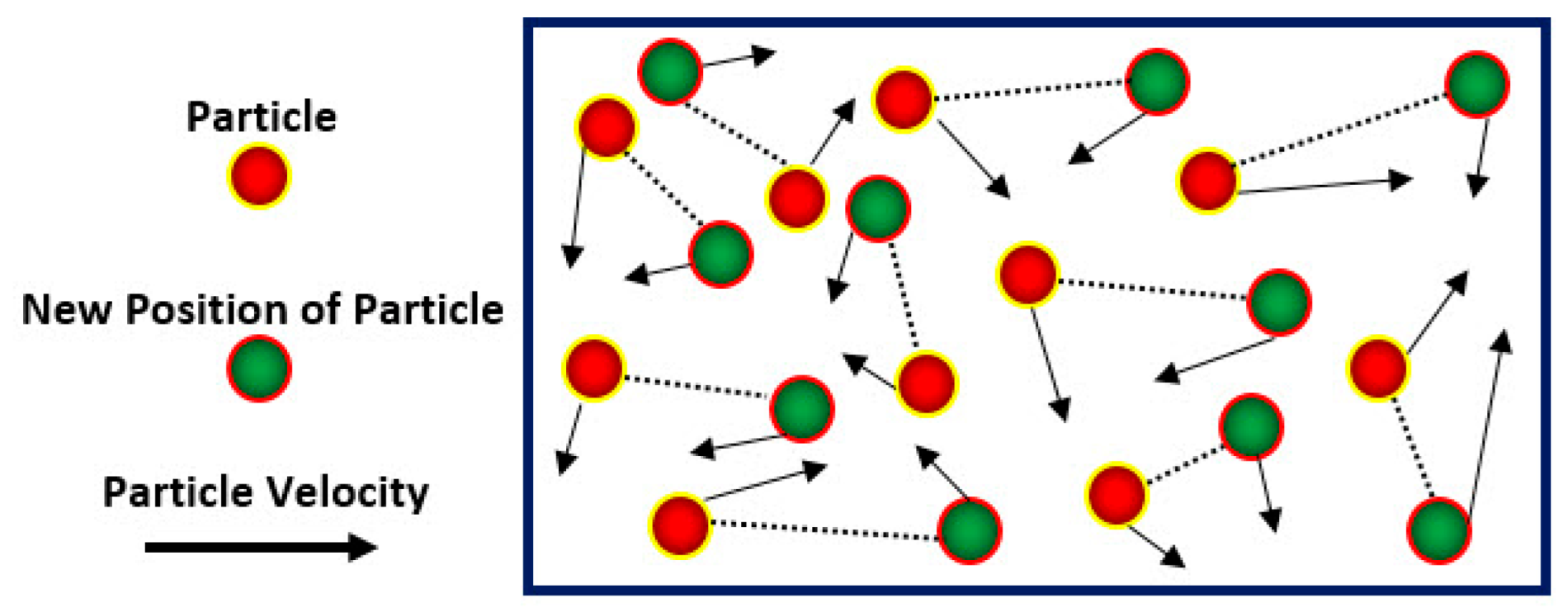
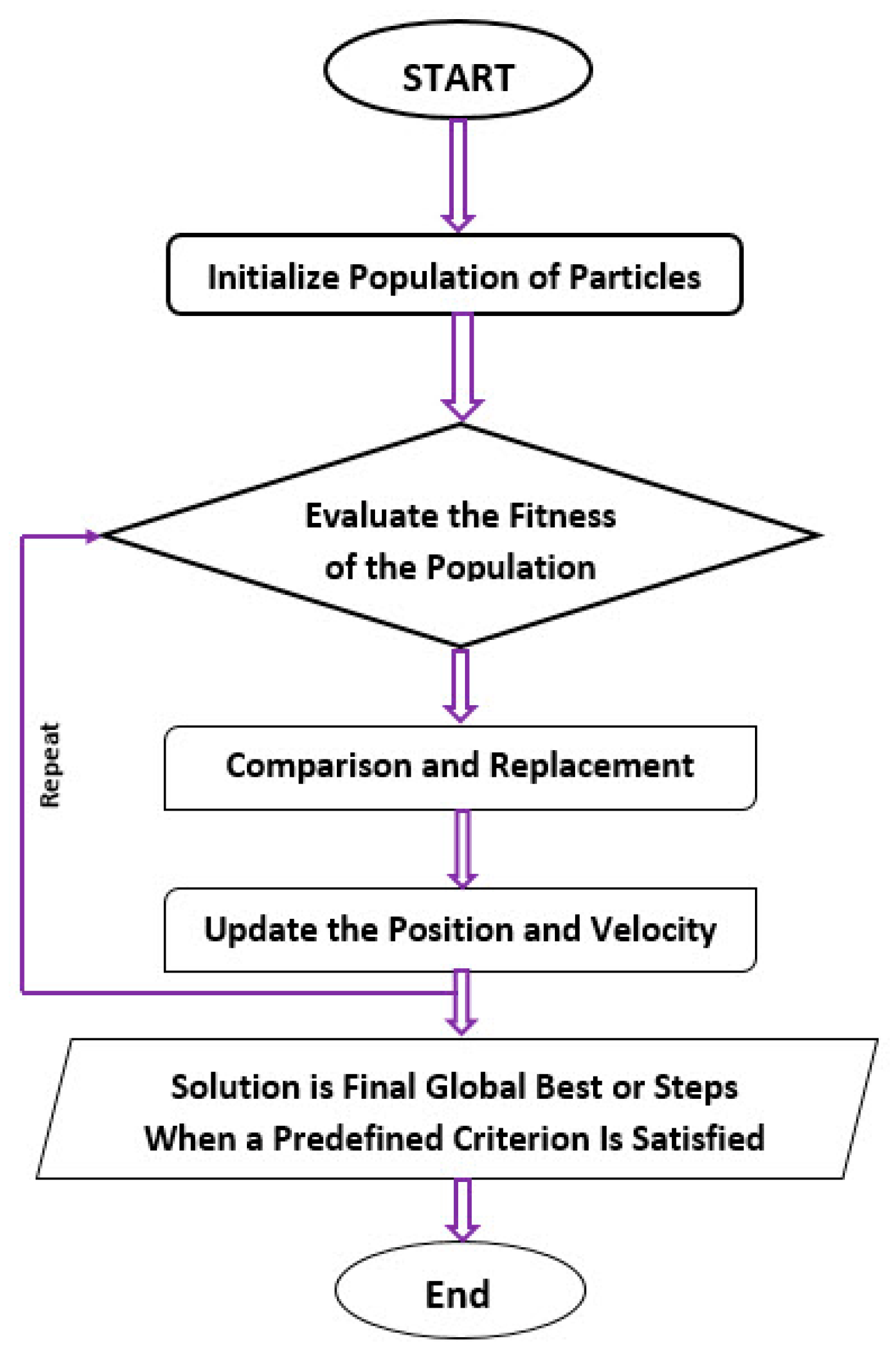
2.2. Particle Swarm Optimization (PSO)
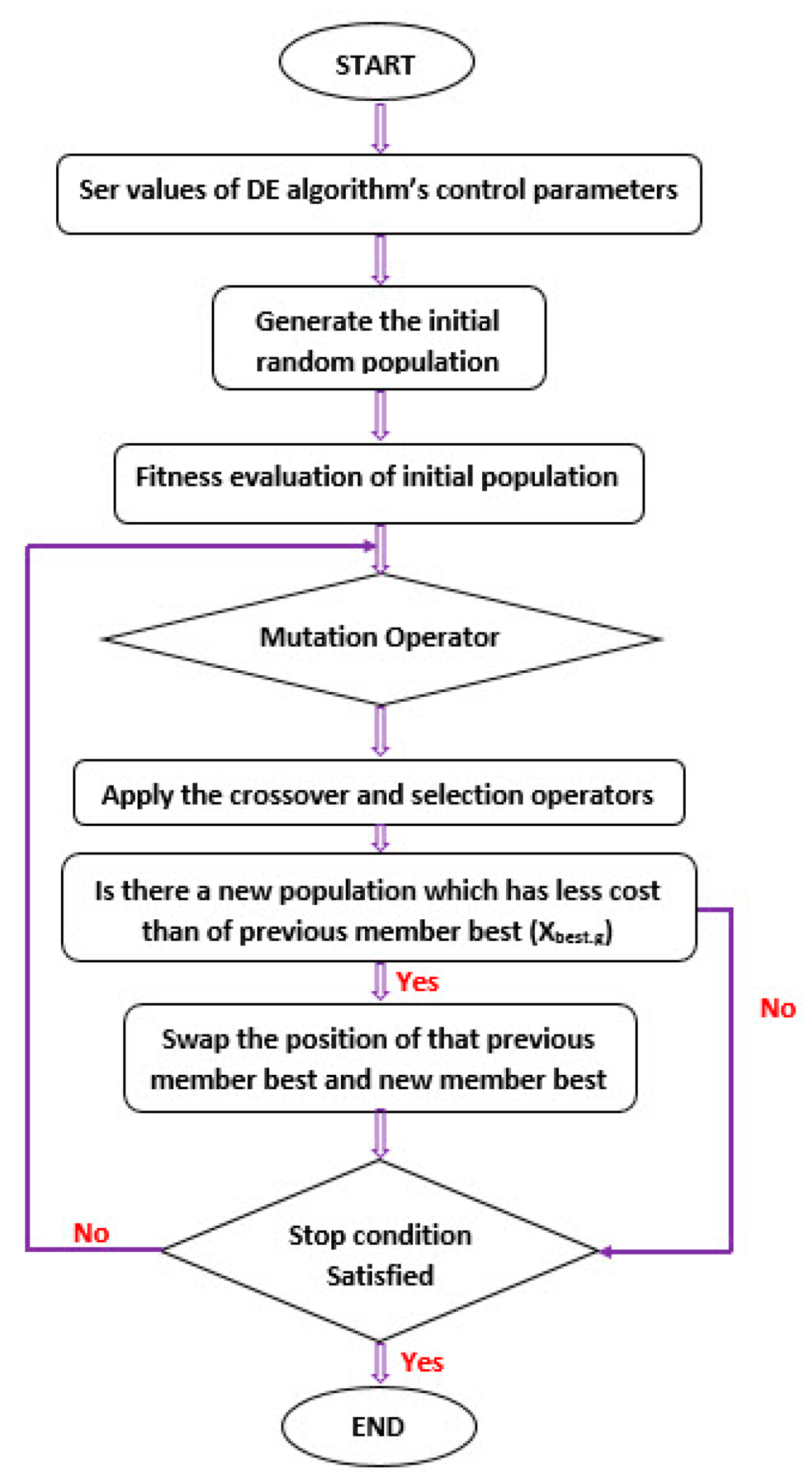
2.3. Differential Evolution (DE)
2.4. Data Description
3. Results and Discussion
3.1. Modelling by ANN-PSO
3.2. Modeling by ANN-DE
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdelwahab, H.T.; Abdel-Aty, M.A. Development of artificial neural network models to predict driver injury severity in traffic accidents at signalized intersections. Transp. Res. Rec. 2001, 1746, 6–13. [Google Scholar] [CrossRef]
- Abdelwahab, H.T.; Abdel-Aty, M.A. Artificial neural networks and logit models for traffic safety analysis of toll plazas. Transp. Res. Rec. 2002, 1784, 115–125. [Google Scholar] [CrossRef]
- Sayed, T.; Brown, G.; Navin, F. Simulation of traffic conflicts at unsignalized intersections with TSC-Sim. Accid. Anal. Prev. 1994, 26, 593–607. [Google Scholar] [CrossRef]
- Abduljabbar, R.; Dia, H.; Liyanage, S.; Bagloee, S.A. Applications of artificial intelligence in transport: An overview. Sustainability 2019, 11, 189. [Google Scholar] [CrossRef]
- Imprialou, M.; Quddus, M. Crash data quality for road safety research: Current state and future directions. Accid. Anal. Prev. 2019, 130, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Mussone, L.; Bassani, M.; Masci, P. Analysis of factors affecting the severity of crashes in urban road intersections. Accid. Anal. Prev. 2017, 103, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Sayed, T.; Mannering, F. Modeling traffic conflicts for use in road safety analysis: A review of analytic methods and future directions. Anal. Meth. Accid. Res. 2021, 29, 100142. [Google Scholar] [CrossRef]
- Yang, D.; Xie, K.; Ozbay, K.; Yang, H. Fusing crash data and surrogate safety measures for safety assessment: Development of a structural equation model with conditional autoregressive spatial effect and random parameters. Accid. Anal. Prev. 2021, 152, 105971. [Google Scholar] [CrossRef]
- Lord, D.; Mannering, F. The statistical analysis of crash-frequency data: A review and assessment of methodological alternatives. Transp. Res. Part A Policy Pract. 2010, 44, 291–305. [Google Scholar] [CrossRef]
- Schlögl, M.; Stütz, R. Methodological considerations with data uncertainty in road safety analysis. Accid. Anal. Prev. 2019, 130, 136–150. [Google Scholar] [CrossRef]
- Zheng, L.; Sayed, T. Application of Extreme Value Theory for Before-After Road Safety Analysis. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 1001–1010. [Google Scholar] [CrossRef]
- Abdel-Aty, M.A.; Radwan, A. Modeling traffic accident occurrence and involvement. Accid. Anal. Prev. 2000, 32, 633–642. [Google Scholar] [CrossRef]
- Huang, H.; Abdel-Aty, M. Multilevel data and Bayesian analysis in traffic safety. Accid. Anal. Prev. 2010, 42, 1556–1565. [Google Scholar] [CrossRef] [PubMed]
- Chong, M.M.; Abraham, A.; Paprzycki, M. Traffic accident analysis using decision trees and neural networks. arXiv 2004, arXiv:cs/0405050. [Google Scholar]
- Darcin, A.; Bulent, A. A neural network (NN) model to predict intersection crashes based upon driver, vehicle and roadway surface characteristics. J. Sci. Res. Essays 2010, 5, 2832–2836. [Google Scholar]
- Astarita, V.; Giofré, V.P.; Guido, G.; Vitale, A. Investigating road safety issues through a microsimulation model. Procedia-Soc. Behav. Sci. 2011, 20, 226–235. [Google Scholar] [CrossRef]
- Guido, G.; Astarita, V.; Giofré, V.P.; Vitale, A. Safety performance measures: A comparison between microsimulation and observational data. Procedia-Soc. Behav. Sci. 2011, 20, 217–225. [Google Scholar] [CrossRef]
- Moghaddam, F.R.; Afandizadeh, S.; Ziyadi, M. Prediction of accident severity using artificial neural networks. Int. J. Civ. Eng. 2011, 9, 41–48. [Google Scholar]
- Young, W.; Sobhani, A.; Lenné, M.G.; Sarvi, M. Simulation of safety: A review of the state of the art in road safety simulation modelling. Accid. Anal. Prev. 2014, 66, 89–103. [Google Scholar] [CrossRef]
- Gallelli, V.; Guido, G.; Vitale, A.; Vaiana, R. Effects of calibration process on the simulation of rear-end conflicts at roundabouts. J. Traffic Transp. Eng. 2019, 6, 175–184. [Google Scholar] [CrossRef]
- Shankar, V.; Mannering, F.; Barfield, W. Statistical analysis of accident severity on rural freeways. Accid. Anal. Prev. 1996, 28, 391–401. [Google Scholar] [CrossRef]
- Astarita, V.; Festa, D.C.; Giofré, V.P.; Guido, G. Surrogate Safety Measures from Traffic Simulation Models a Comparison of different Models for Intersection Safety Evaluation. Transp. Res. Procedia 2019, 37, 219–226. [Google Scholar] [CrossRef]
- Karimi, A.; Bassani, M.; Boroujerdian, A.M.; Catani, L. Investigation into passing behavior at passing zones to validate and extend the use of driving simulators in two-lane roads safety analysis. Accid. Anal. Prev. 2020, 139, 105487. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.; Huang, H.; Pei, X.; Wong, S.C. Modeling nonlinear relationship between crash frequency by severity and contributing factors by neural networks. Anal. Meth. Accid. Res. 2016, 10, 12–25. [Google Scholar] [CrossRef]
- Halim, Z.; Kalsoom, R.; Bashir, S.; Abbas, G. Artificial intelligence techniques for driving safety and vehicle crash prediction. Artif. Intell. Rev. 2016, 46, 351–387. [Google Scholar] [CrossRef]
- Ait-Mlouk, A.; Gharnati, F.; Agouti, T. An improved approach for association rule mining using a multi-criteria decision support system: A case study in road safety. Eur. Transp. Res. Rev. 2017, 9, 1–13. [Google Scholar] [CrossRef]
- Fernandes, B.; Vicente, H.; Ribeiro, J.; Analide, C.; Neves, J. Evolutionary Computation on Road Safety. In Proceedings of the International Conference on Hybrid Artificial Intelligence Systems, Oviedo, Spain, 20–22 June 2018; Springer: Cham, Switzerland, 2018; pp. 647–657. [Google Scholar]
- Xu, Y.; Ye, Z.; Wang, Y.; Wang, C.; Sun, C. Evaluating the influence of road lighting on traffic safety at accesses using an artificial neural network. Traffic Inj. Prev. 2018, 19, 601–606. [Google Scholar] [CrossRef]
- Silva, P.B.; Andrade, M.; Ferreira, S. Machine learning applied to road safety modeling: A systematic literature review. J. Transp. Eng. 2020, 7, 775–790. [Google Scholar] [CrossRef]
- Boukerche, A.; Tao, Y.; Sun, P. Artificial intelligence-based vehicular traffic flow prediction methods for supporting intelligent transportation systems. Comput. Netw. 2020, 182, 107484. [Google Scholar] [CrossRef]
- Afework, A.; Sipos, T. Modelling of accidents for four lane non-urban highways using artificial neural networks technique. In Proceedings of the 2020 IEEE 14th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 21–23 May 2020; pp. 47–52. [Google Scholar]
- Guido, G.; Haghshenas, S.S.; Haghshenas, S.S.; Vitale, A.; Astarita, V.; Haghshenas, A.S. Feasibility of stochastic models for evaluation of potential factors for safety: A case study in Southern Italy. Sustainability 2020, 12, 7541. [Google Scholar] [CrossRef]
- Guido, G.; Haghshenas, S.S.; Haghshenas, S.S.; Vitale, A.; Gallelli, V.; Astarita, V. Development of a binary classification model to assess safety in transportation systems using GMDH-type neural network algorithm. Sustainability 2020, 12, 6735. [Google Scholar] [CrossRef]
- Tonni, S.I.; Aka, T.A.; Antik, M.M.; Taher, K.A.; Mahmud, M.; Kaiser, M.S. Artificial intelligence based driver vigilance system for accident prevention. In Proceedings of the 2021 International Conference on Information and Communication Technology for Sustainable Development (ICICT4SD), Dhaka, Bangladesh, 27–28 February 2021; pp. 412–416. [Google Scholar]
- Ministero delle Infrastrutture e dei Trasporti. Studio di Valutazione dei Costi Sociali dell’incidentalità Stradale; Direzione Generale per la Sicurezza Stradale: Rome, Italy, 2012.
- Wang, K.; Shirani-Bidabadi, N.; Shaon, M.R.R.; Zhao, S.; Jackson, E. Correlated mixed logit modeling with heterogeneity in means for crash severity and surrogate measure with temporal instability. Accid. Anal. Prev. 2021, 160, 106332. [Google Scholar] [CrossRef]
- Ghasedi, M.; Sarfjoo, M.; Bargegol, I. Prediction and analysis of the severity and number of suburban accidents using logit model, factor analysis and machine learning: A case study in a developing country. SN Appl. Sci. 2021, 3, 1–16. [Google Scholar] [CrossRef]
- Yan, X.; He, J.; Zhang, C.; Liu, Z.; Qiao, B.; Zhang, H. Single-vehicle crash severity outcome prediction and determinant extraction using tree-based and other non-parametric models. Accid. Anal. Prev. 2021, 153, 106034. [Google Scholar] [CrossRef] [PubMed]
- Haghshenas, S.S.; Haghshenas, S.S.; Geem, Z.W.; Kim, T.H.; Mikaeil, R.; Pugliese, L.; Troncone, A. Application of harmony search algorithm to slope stability analysis. Land 2021, 10, 1250. [Google Scholar] [CrossRef]
- Guido, G.; Haghshenas, S.S.; Vitale, A.; Astarita, V. Challenges and Opportunities of Using Data Fusion Methods for Travel Time Estimation. In Proceedings of the 2022 8th International Conference on Control, Decision and Information Technologies (CoDIT), Istanbul, Turkey, 17–20 May 2022; Volume 1, pp. 587–592. [Google Scholar]
- Guido, G.; Haghshenas, S.S.; Haghshenas, S.S.; Vitale, A.; Gallelli, V.; Astarita, V. Prioritizing the Potential Smartification Measures by Using an Integrated Decision Support System with Sustainable Development Goals (a Case Study in Southern Italy). Safety 2022, 8, 35. [Google Scholar] [CrossRef]
- Guido, G.; Shaffiee Haghshenas, S.; Shaffiee Haghshenas, S.; Vitale, A.; Astarita, V.; Park, Y.; Geem, Z.W. Evaluation of Contributing Factors Affecting Number of Vehicles Involved in Crashes Using Machine Learning Techniques in Rural Roads of Cosenza, Italy. Safety 2022, 8, 28. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Shaffiee Haghshenas, S.; Jalali, S.M.E.; Zare, S.; Mikaeil, R. Developing the Rule of Thumb for Evaluating Penetration Rate of TBM, Using Binary Classification. Geotech. Geol. Eng. 2022, 40, 4685–4703. [Google Scholar] [CrossRef]
- Amiri, A.M.; Sadri, A.; Nadimi, N.; Shams, M. A comparison between artificial neural network and hybrid intelligent genetic algorithm in predicting the severity of fixed object crashes among elderly drivers. Accid. Anal. Prev. 2020, 138, 105468. [Google Scholar] [CrossRef]
- Qian, Y.; Zhang, X.; Fei, G.; Sun, Q.; Li, X.; Stallones, L.; Xiang, H. Forecasting deaths of road traffic injuries in China using an artificial neural network. Traffic Inj. Prev. 2020, 21, 407–412. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Behnood, A.; Arashpour, M. Predicting the compressive strength of normal and High-Performance Concretes using ANN and ANFIS hybridized with Grey Wolf Optimizer. Constr. Build. Mater. 2020, 232, 117266. [Google Scholar] [CrossRef]
- Naderpour, H.; Rafiean, A.H.; Fakharian, P. Compressive strength prediction of environmentally friendly concrete using artificial neural networks. J. Build. Eng. 2018, 16, 213–219. [Google Scholar] [CrossRef]
- Naderpour, H.; Fakharian, P. Predicting the torsional strength of reinforced concrete beams strengthened with FRP sheets in terms of artificial neural networks. J. Struct. Constr. Eng. 2018, 5, 20–35. [Google Scholar]
- Mikaeil, R.; Shaffiee Haghshenas, S.; Ozcelik, Y.; Shaffiee Haghshenas, S. Development of intelligent systems to predict diamond wire saw performance. J. Soft Comput. Civ. Eng. 2017, 1, 52–69. [Google Scholar]
- Eidgahee, D.R.; Jahangir, H.; Solatifar, N.; Fakharian, P.; Rezaeemanesh, M. Data-driven estimation models of asphalt mixtures dynamic modulus using ANN, GP and combinatorial GMDH approaches. Neural Comput. Appl. 2022, 1–26. [Google Scholar] [CrossRef]
- Se, C.; Champahom, T.; Jomnonkwao, S.; Ratanavaraha, V. Motorcyclist injury severity analysis: A comparison of Artificial Neural Networks and random parameter model with heterogeneity in means and variances. Int. J. Inj. Contr. Saf. Promot. 2022, 1–16. [Google Scholar] [CrossRef]
- Ali, G.A.; Tayfour, A. Characteristics and prediction of traffic accident casualties in Sudan using statistical modeling and artificial neural networks. Int. J. Transp. Sci. Technol. 2012, 1, 305–317. [Google Scholar] [CrossRef]
- Sanayei, R.; Vafaeinejad, A.; Karami, J.; Zanjirabad, H.A. A model development on GIS-driven data to predict temporal daily collision through integrating Discrete Wavelet Transform (DWT) and Artificial Neural Network (ANN) algorithms; case study: Tehran-Qazvin freeway. Geocarto Int. 2021, 1–17. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Yoon, T. Road surface conditions forecasting in rainy weather using artificial neural networks. Saf. Sci. 2021, 140, 105302. [Google Scholar] [CrossRef]
- Huang, J.; Koopialipoor, M.; Armaghani, D.J. A combination of fuzzy Delphi method and hybrid ANN-based systems to forecast ground vibration resulting from blasting. Sci. Rep. 2020, 10, 19397. [Google Scholar] [CrossRef]
- Mikaeil, R.; Haghshenas, S.S.; Sedaghati, Z. Geotechnical risk evaluation of tunneling projects using optimization techniques (case study: The second part of Emamzade Hashem tunnel). Nat. Hazards 2019, 97, 1099–1113. [Google Scholar] [CrossRef]
- Abbasi, E.; Hadji Hosseinlou, M. The Importance of Exercise and General Mental Health on Prediction of Property-Damage-Only Accidents among Taxi Drivers in Tehran: A Study Using ANFIS-PSO and Regression Models. J. Adv. Transp. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Noori, A.M.; Mikaeil, R.; Mokhtarian, M.; Haghshenas, S.S.; Foroughi, M. Feasibility of intelligent models for prediction of utilization factor of TBM. Geotech. Geol. Eng. 2020, 38, 3125–3143. [Google Scholar] [CrossRef]
- Amiri, A.M.; Nadimi, N.; Yousefian, A. Comparing the efficiency of different computation intelligence techniques in predicting accident frequency. IATSS Res. 2020, 44, 285–292. [Google Scholar] [CrossRef]
- Shaffiee Haghshenas, S.; Pirouz, B.; Shaffiee Haghshenas, S.; Pirouz, B.; Piro, P.; Na, K.S.; Geem, Z.W. Prioritizing and analyzing the role of climate and urban parameters in the confirmed cases of COVID-19 based on artificial intelligence applications. Int. J. Environ. Res. Public Health 2020, 17, 3730. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-international conference on neural networks, Perth, WA, Australia, 27 November 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Xu, X.; Zeng, Z.; Wang, Y.; Ash, J. Crash Density and Severity Prediction Using Recurrent Neural Networks Combined with Particle Swarm Optimization. In Proceedings of the International Conference on Management Science and Engineering Management, Ontario, ON, Canada, 5–8 August 2019; Springer: Cham, Switzerland, 2019; pp. 566–580. [Google Scholar]
- Armaghani, D.J.; Koopialipoor, M.; Marto, A.; Yagiz, S. Application of several optimization techniques for estimating TBM advance rate in granitic rocks. J. Rock Mech. Geotech. Eng. 2019, 11, 779–789. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Minimizing the real functions of the ICEC’96 contest by differential evolution. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 842–844. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Pan, X.; Zhou, W.; Lu, Y.; Sun, N. Prediction of network traffic of smart cities based on DE-BP neural network. IEEE Access 2019, 7, 55807–55816. [Google Scholar] [CrossRef]
- Dormishi, A.; Ataei, M.; Mikaeil, R.; Khalokakaei, R.; Haghshenas, S.S. Evaluation of gang saws’ performance in the carbonate rock cutting process using feasibility of intelligent approaches. Eng. Sci. Technol. Int. J. 2019, 22, 990–1000. [Google Scholar] [CrossRef]
- Aryafar, A.; Mikaeil, R.; Haghshenas, S.S.; Haghshenas, S.S. Application of metaheuristic algorithms to optimal clustering of sawing machine vibration. Measurement 2018, 124, 20–31. [Google Scholar] [CrossRef]
- World Health Organization. Global Status Report on Road Safety; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Elvik, R. A comprehensive and unified framework for analysing the effects on injuries of measures influencing speed. Accid. Anal. Prev. 2019, 125, 63–69. [Google Scholar] [CrossRef]
- Eboli, L.; Guido, G.; Mazzulla, G.; Pungillo, G. Experimental relationships between operating speeds of successive road design elements in two-lane rural highways. Transport 2017, 32, 2138–2145. [Google Scholar] [CrossRef]
- Camacho-Torregrosa, F.J.; Pérez-Zuriaga, A.M.; Campoy-Ungría, J.M.; García-García, A. New geometric design consistency model based on operating speed profiles for road safety evaluation. Accid. Anal. Prev. 2013, 61, 33–42. [Google Scholar] [CrossRef]






| Data Field Type | Variable | Code/Unit | Description | Percentage of Total Crashes |
|---|---|---|---|---|
| Traffic flow characteristics | AADT (veh/day) | 1 | <5000 | 6.9 |
| 2 | 5000–9999 | 4.7 | ||
| 3 | 10,000–14,999 | 54.8 | ||
| 4 | >14,999 | 33.6 | ||
| Avg Speed (km/h) | Not coded | Min. 28 | 100 | |
| Max. 122 | ||||
| Avg. 85.29 | ||||
| Speed Limit (km/h) | 1 | 50 | 26.3 | |
| 2 | 70 | 31.2 | ||
| 3 | 90 | 17.6 | ||
| 4 | 110 | 0.8 | ||
| 5 | 130 | 24.1 | ||
| Environment characteristics | Light Conditions | 0 | Daylight | 66.8 |
| 1 | Nighttime | 33.2 | ||
| Day of the Week | 0 | Weekend or Holiday | 30 | |
| 1 | Weekday | 70 | ||
| Location environment | Road classification | 1 | Highway | 37.5 |
| 2 | Other | 62.5 | ||
| Accident characteristic | Number of Vehicles | 1 | 1 | 31.6 |
| 2 | 2 | 52 | ||
| 3 | 3 or more | 16.4 | ||
| Accident Type | 1 | Collision with vehicle | 68.6 | |
| 2 | Collision with pedestrian | 3 | ||
| 3 | Collision with obstacle | 7.2 | ||
| 4 | Other | 21.3 |
| Control Parameters | Values for the Best Developed Model of Urban Area | Values for the Best Developed Model of Rural Area |
|---|---|---|
| Number of hidden layers | 5 | 5 |
| Swarm size | 15 | 20 |
| Individual learning factor (C1) | 1.49 | 1.49 |
| Social learning factor (C2) | 1.49 | 1.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guido, G.; Shaffiee Haghshenas, S.; Shaffiee Haghshenas, S.; Vitale, A.; Astarita, V. Application of Feature Selection Approaches for Prioritizing and Evaluating the Potential Factors for Safety Management in Transportation Systems. Computers 2022, 11, 145. https://doi.org/10.3390/computers11100145
Guido G, Shaffiee Haghshenas S, Shaffiee Haghshenas S, Vitale A, Astarita V. Application of Feature Selection Approaches for Prioritizing and Evaluating the Potential Factors for Safety Management in Transportation Systems. Computers. 2022; 11(10):145. https://doi.org/10.3390/computers11100145
Chicago/Turabian StyleGuido, Giuseppe, Sami Shaffiee Haghshenas, Sina Shaffiee Haghshenas, Alessandro Vitale, and Vittorio Astarita. 2022. "Application of Feature Selection Approaches for Prioritizing and Evaluating the Potential Factors for Safety Management in Transportation Systems" Computers 11, no. 10: 145. https://doi.org/10.3390/computers11100145
APA StyleGuido, G., Shaffiee Haghshenas, S., Shaffiee Haghshenas, S., Vitale, A., & Astarita, V. (2022). Application of Feature Selection Approaches for Prioritizing and Evaluating the Potential Factors for Safety Management in Transportation Systems. Computers, 11(10), 145. https://doi.org/10.3390/computers11100145











