More Plausible Models of Body Ownership Could Benefit Virtual Reality Applications †
Abstract
:1. Introduction
2. Theory
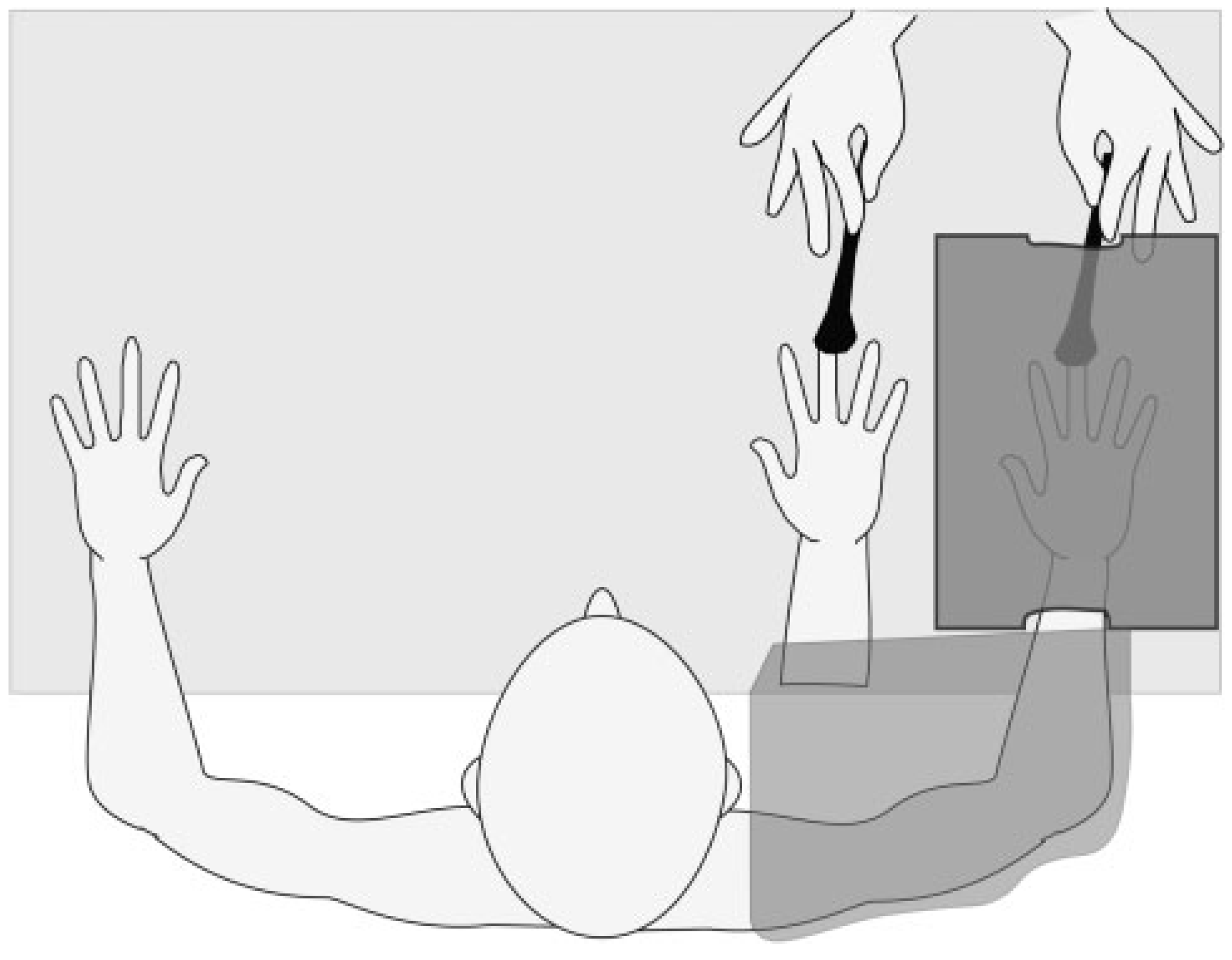
2.1. The Rubber Hand Illusion
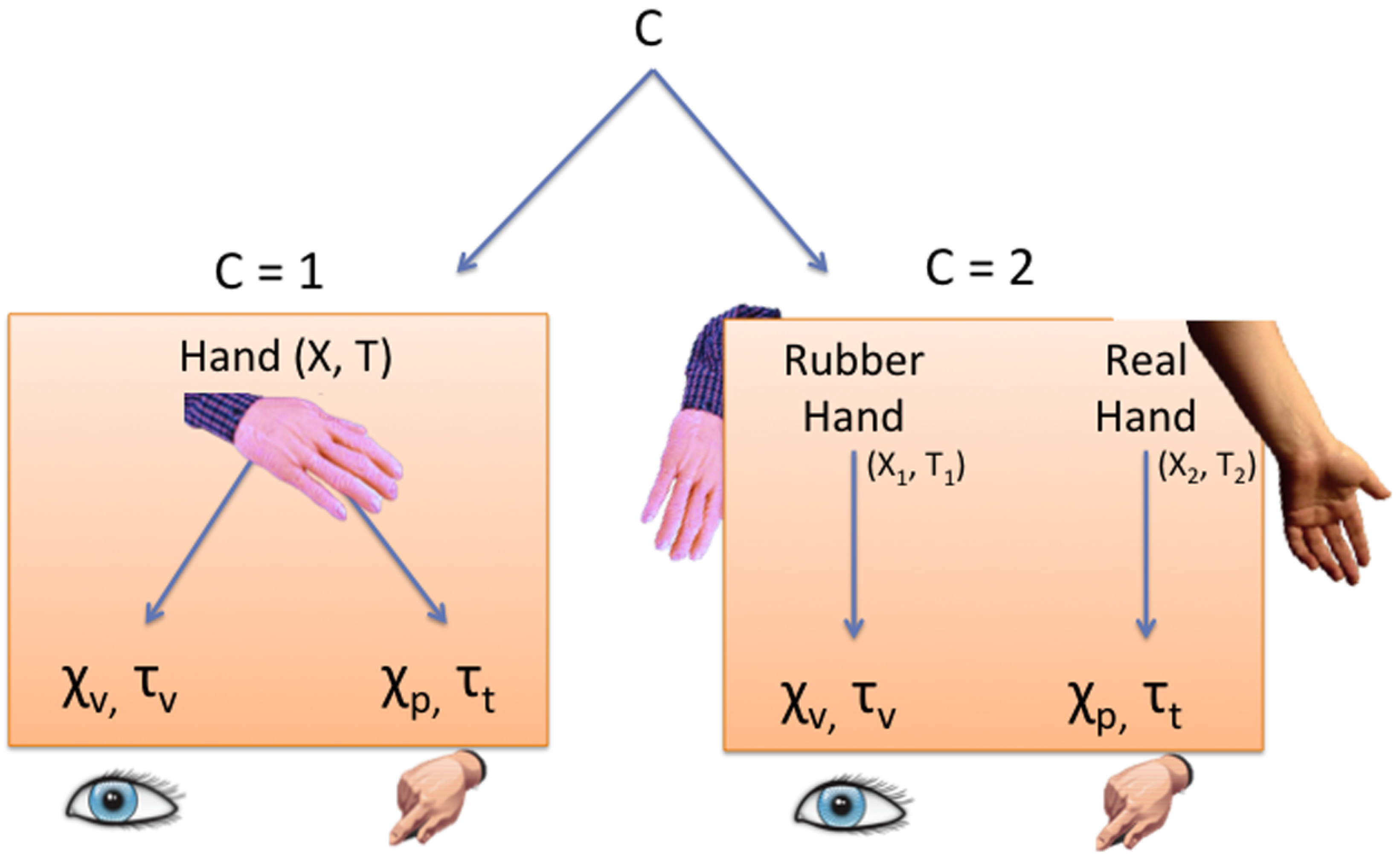
2.2. The BCIBO Model
2.3. Related Works
2.4. Specification of the BCIBO Model
2.5. Critique of the Model
3. Results
3.1. Change in the Sensory Priors
3.2. Truncated Model
3.2.1. Truncation Bounds
Proprioceptive Input
Spatial Visual Input
Temporal Input
- and
- .
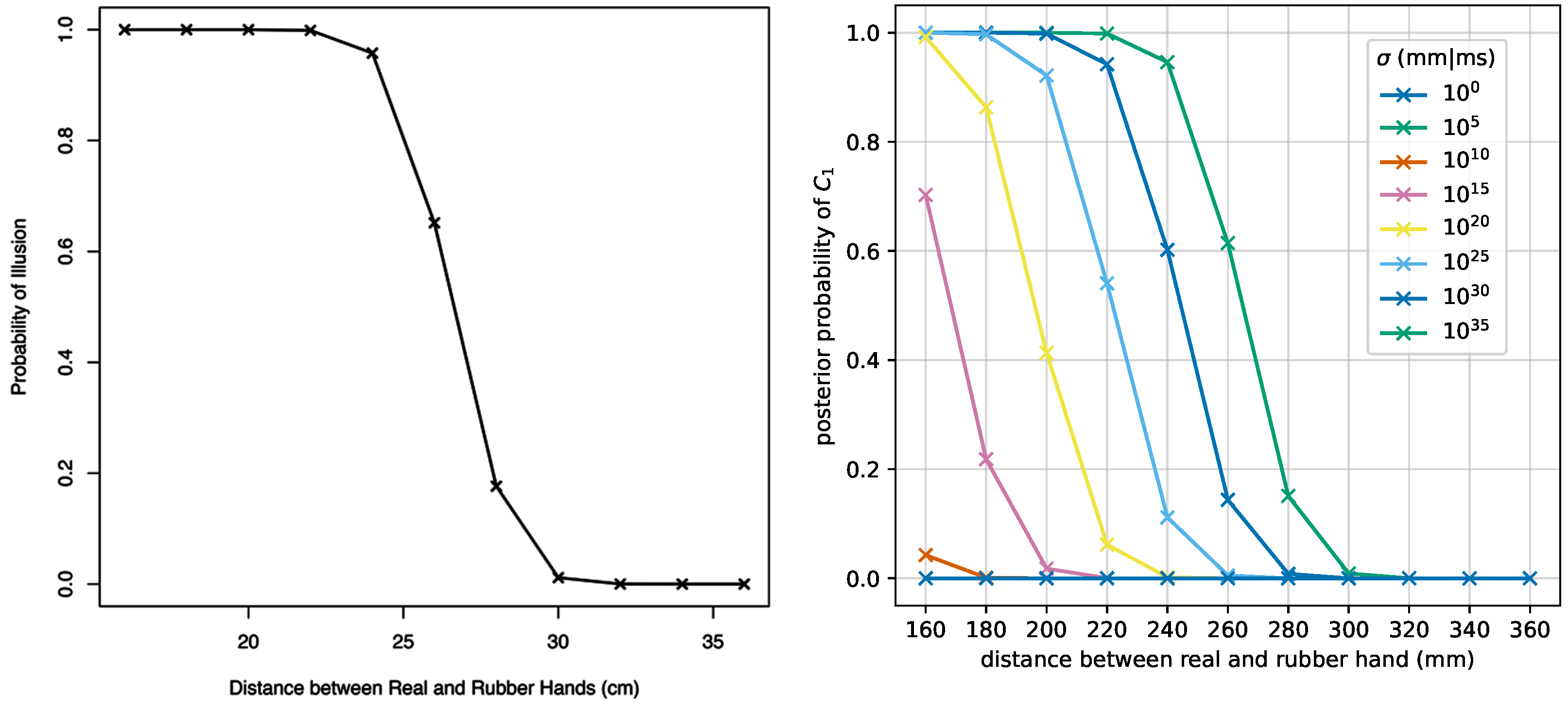
3.2.2. Simulation Run
3.3. Change in the Model Prior
4. Discussion
4.1. Limitations and Future Work
4.2. Applications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BCIBO | Bayesian Causal Inference of Body Ownership |
| BOI | body ownership illusion |
| EEG | electroencephalography |
| GUI | graphical user interface |
| HMD | head-mounted display |
| MDPI | Multidisciplinary Digital Publishing Institute |
| RHI | rubber hand illusion |
| SEM | standard error of the mean |
| VR | virtual reality |
| common cause model | |
| separate causes model | |
| X | inferred position of the rubber/real hand |
| T | inferred time point of the brush stroke |
| spatial visual input | |
| (spatial) proprioceptive input | |
| temporal visual input | |
| (temporal) tactile input |
Appendix A. Model Specifications
Appendix A.1. Original Model
Appendix A.2. Truncated Model
Appendix A.3. Changes in the Model Prior
References
- Samad, M.; Chung, A.J.; Shams, L. Perception of Body Ownership Is Driven by Bayesian Sensory Inference. PLoS ONE 2015, 10, e0117178. [Google Scholar] [CrossRef] [PubMed]
- Schubert, M.; Endres, D. The Bayesian Causal Inference of Body Ownership Model: Use in VR and Plausible Parameter Choices. In Proceedings of the 2021 IEEE Conference on Virtual Reality and 3D User Interfaces Abstracts and Workshops (VRW), Lisbon, Portugal, 27 March–1 April 2021; pp. 67–70. [Google Scholar] [CrossRef]
- Botvinick, M.; Cohen, J. Rubber Hands ‘Feel’ Touch That Eyes See. Nature 1998, 391, 756. [Google Scholar] [CrossRef] [PubMed]
- Neustadter, E.S.; Fineberg, S.K.; Leavitt, J.; Carr, M.M.; Corlett, P.R. Induced Illusory Body Ownership in Borderline Personality Disorder. Neurosci. Conscious. 2019, 5, niz017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsakiris, M. The Sense of Body Ownership. In The Oxford Handbook of the Self; Oxford University Press: Oxford, UK, 2011; pp. 180–203. [Google Scholar]
- Lewis, E.; Lloyd, D.M. Embodied Experience: A First-Person Investigation of the Rubber Hand Illusion. Phenomenol. Cogn. Sci. 2010, 9, 317–339. [Google Scholar] [CrossRef]
- Körding, K.P.; Beierholm, U.; Ma, W.J.; Quartz, S.; Tenenbaum, J.B.; Shams, L. Causal Inference in Multisensory Perception. PLoS ONE 2007, 2, e943. [Google Scholar] [CrossRef] [Green Version]
- Hohwy, J. The Predictive Mind, 1st ed.; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Magnotti, J.F.; Ma, W.J.; Beauchamp, M.S. Causal Inference of Asynchronous Audiovisual Speech. Front. Psychol. 2013, 4, 798. [Google Scholar] [CrossRef] [Green Version]
- Geisler, W.S.; Kersten, D. Illusions, Perception and Bayes. Nat. Neurosci. 2002, 5, 508–510. [Google Scholar] [CrossRef]
- Riemer, M.; Bublatzky, F.; Trojan, J.; Alpers, G.W. Defensive Activation during the Rubber Hand Illusion: Ownership versus Proprioceptive Drift. Biol. Psychol. 2015, 109, 86–92. [Google Scholar] [CrossRef]
- Makin, T.R.; Holmes, N.P.; Ehrsson, H.H. On the Other Hand: Dummy Hands and Peripersonal Space. Behav. Brain Res. 2008, 191, 1–10. [Google Scholar] [CrossRef]
- Armel, K.C.; Ramachandran, V.S. Projecting Sensations to External Objects: Evidence from Skin Conductance Response. Proc. R. Soc. Biol. Sci. 2003, 270, 1499–1506. [Google Scholar] [CrossRef] [Green Version]
- Reader, A.T.; Trifonova, V.S.; Ehrsson, H.H. The Rubber Hand Illusion Does Not Influence Basic Movement. 2021. Available online: https://doi.org/10.31219/osf.io/6dyzq (accessed on 12 August 2021). [CrossRef]
- Schürmann, T.; Vogt, J.; Christ, O.; Beckerle, P. The Bayesian Causal Inference Model Benefits from an Informed Prior to Predict Proprioceptive Drift in the Rubber Foot Illusion. Cogn. Process. 2019, 20, 447–457. [Google Scholar] [CrossRef]
- Chancel, M.; Ehrsson, H.H.; Ma, W.J. Uncertainty-Based Inference of a Common Cause for Body Ownership. 2021. Available online: https://doi.org/10.31219/osf.io/yh2z7 (accessed on 12 August 2021). [CrossRef]
- Crea, S.; D’Alonzo, M.; Vitiello, N.; Cipriani, C. The Rubber Foot Illusion. J. Neuroeng. Rehabil. 2015, 12, 77. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Flögel, M.; Kalveram, K.T.; Christ, O.; Vogt, J. Application of the Rubber Hand Illusion Paradigm: Comparison between Upper and Lower Limbs. Psychol. Res. 2015, 80, 298–306. [Google Scholar] [CrossRef] [PubMed]
- Christ, O.; Elger, A.; Schneider, K.; Rapp, A.; Beckerle, P. Identification of Haptic Paths with Different Resolution and Their Effect on Body Scheme Illusion in Lower Limbs. Tech. Assist. Rehabil. 2013, 1–4. Available online: https://www.ige.tu-berlin.de/fileadmin/fg176/IGE_Printreihe/TAR_2013/paper/Session-10-Event-1-Christ.pdf (accessed on 12 August 2021).
- Jones, S.A.H.; Cressman, E.K.; Henriques, D.Y.P. Proprioceptive Localization of the Left and Right Hands. Exp. Brain Res. 2010, 204, 373–383. [Google Scholar] [CrossRef] [PubMed]
- van Beers, R.J.; Sittig, A.C.; Denier van der Gon, J.J. The Precision of Proprioceptive Position Sense. Exp. Brain Res. 1998, 122, 367–377. [Google Scholar] [CrossRef]
- Hirsh, I.J.; Sherrick, C.E., Jr. Perceived Order in Different Sense Modalities. J. Exp. Psychol. 1961, 62, 423–432. [Google Scholar] [CrossRef] [PubMed]
- Riemer, M.; Trojan, J.; Beauchamp, M.; Fuchs, X. The Rubber Hand Universe: On the Impact of Methodological Differences in the Rubber Hand Illusion. Neurosci. Biobehav. Rev. 2019, 104, 268–280. [Google Scholar] [CrossRef]
- Bars, I.; Terning, J.; Nekoogar, F. Extra Dimensions in Space and Time; Multiversal Journeys; Springer: New York, NY, USA, 2010. [Google Scholar]
- Jones, M.; Love, B.C. Bayesian Fundamentalism or Enlightenment? On the Explanatory Status and Theoretical Contributions of Bayesian Models of Cognition. Behav. Brain Sci. 2011, 34, 169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bowers, J.S.; Davis, C.J. Bayesian Just-so Stories in Psychology and Neuroscience. Psychol. Bull. 2012, 138, 389–414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, D.M. Spatial Limits on Referred Touch to an Alien Limb May Reflect Boundaries of Visuo-Tactile Peripersonal Space Surrounding the Hand. Brain Cogn. 2007, 64, 104–109. [Google Scholar] [CrossRef]
- Kilteni, K.; Normand, J.M.; Sanchez-Vives, M.V.; Slater, M. Extending Body Space in Immersive Virtual Reality: A Very Long Arm Illusion. PLoS ONE 2012, 7, e40867. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miller, M.R.; Crapo, R.; Hankinson, J.; Brusasco, V.; Burgos, F.; Casaburi, R.; Coates, A.; Enright, P.; van der Grinten, C.P.M.; Gustafsson, P.; et al. General Considerations for Lung Function Testing. Eur. Respir. J. 2005, 26, 153–161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reeves, S.L.; Varakamin, C.; Henry, C.J. The Relationship between Arm-Span Measurement and Height with Special Reference to Gender and Ethnicity. Eur. J. Clin. Nutr. 1996, 50, 398–400. [Google Scholar] [PubMed]
- Federal Statistical Office of Germany. Körpermaße nach Altersgruppen und Geschlecht-Statistisches Bundesamt. Available online: https://web.archive.org/web/20210514201250/https://www.destatis.de/DE/Themen/Gesellschaft-Umwelt/Gesundheit/Gesundheitszustand-Relevantes-Verhalten/Tabellen/liste-koerpermasse.html (accessed on 12 August 2021).
- Kammers, M.P.M.; de Vignemont, F.; Verhagen, L.; Dijkerman, H.C. The Rubber Hand Illusion in Action. Neuropsychologia 2009, 47, 204–211. [Google Scholar] [CrossRef]
- Durgin, F.H.; Evans, L.; Dunphy, N.; Klostermann, S.; Simmons, K. Rubber Hands Feel the Touch of Light. Psychol. Sci. 2007, 18, 152–157. [Google Scholar] [CrossRef] [Green Version]
- Abdulkarim, Z.; Hayatou, Z.; Ehrsson, H.H. Sustained Rubber Hand Illusion after the End of Visuotactile Stimulation with a Similar Time Course for the Reduction of Subjective Ownership and Proprioceptive Drift. 2021. Available online: https://doi.org/10.31234/osf.io/wt82m (accessed on 12 August 2021). [CrossRef]
- Litwin, P. Extending Bayesian Models of the Rubber Hand Illusion. Multisens. Res. 2020, 33, 127–160. [Google Scholar] [CrossRef] [PubMed]
- Motyka, P.; Litwin, P. Proprioceptive Precision and Degree of Visuo-Proprioceptive Discrepancy Do Not Influence the Strength of the Rubber Hand Illusion. Perception 2019, 48, 882–891. [Google Scholar] [CrossRef] [PubMed]
- Kalckert, A.; Ehrsson, H.H. Moving a Rubber Hand That Feels Like Your Own: A Dissociation of Ownership and Agency. Front. Hum. Neurosci. 2012, 6, 40. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goh, G.S.; Lohre, R.; Parvizi, J.; Goel, D.P. Virtual and Augmented Reality for Surgical Training and Simulation in Knee Arthroplasty. Arch. Orthop. Trauma Surg. 2021. [Google Scholar] [CrossRef]
- Bailenson, J.N.; Yee, N.; Blascovich, J.; Beall, A.C.; Lundblad, N.; Jin, M. The Use of Immersive Virtual Reality in the Learning Sciences: Digital Transformations of Teachers, Students, and Social Context. J. Learn. Sci. 2008, 17, 102–141. [Google Scholar] [CrossRef] [Green Version]
- Kokkinara, E.; Slater, M. Measuring the Effects through Time of the Influence of Visuomotor and Visuotactile Synchronous Stimulation on a Virtual Body Ownership Illusion. Perception 2014, 43, 43–58. [Google Scholar] [CrossRef] [Green Version]
- Kilteni, K.; Groten, R.; Slater, M. The Sense of Embodiment in Virtual Reality. Presence Teleoper. Virtual Environ. 2012, 21, 373–387. [Google Scholar] [CrossRef] [Green Version]
- Matamala-Gomez, M.; Maselli, A.; Malighetti, C.; Realdon, O.; Mantovani, F.; Riva, G. Virtual Body Ownership Illusions for Mental Health: A Narrative Review. J. Clin. Med. 2021, 10, 139. [Google Scholar] [CrossRef]
- Keizer, A.; van Elburg, A.; Helms, R.; Dijkerman, H.C. A Virtual Reality Full Body Illusion Improves Body Image Disturbance in Anorexia Nervosa. PLoS ONE 2016, 11, e0163921. [Google Scholar] [CrossRef] [PubMed]
- Pichiorri, F.; Morone, G.; Petti, M.; Toppi, J.; Pisotta, I.; Molinari, M.; Paolucci, S.; Inghilleri, M.; Astolfi, L.; Cincotti, F.; et al. Brain–Computer Interface Boosts Motor Imagery Practice during Stroke Recovery. Ann. Neurol. 2015, 77, 851–865. [Google Scholar] [CrossRef]
- Braun, N.; Debener, S.; Spychala, N.; Bongartz, E.; Sörös, P.; Müller, H.H.O.; Philipsen, A. The Senses of Agency and Ownership: A Review. Front. Psychol. 2018, 9, 535. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freina, L.; Ott, M. A Literature Review on Immersive Virtual Reality in Education: State of the Art and Perspectives. In The International Scientific Conference eLearning and Software for Education; Carol I National Defence University Publishing House: Bucharest, Romania, 2015; Volume 11, pp. 133–141. [Google Scholar]
- Tang, Y.M.; Ng, G.W.Y.; Chia, N.H.; So, E.H.K.; Wu, C.H.; Ip, W.H. Application of Virtual Reality (VR) Technology for Medical Practitioners in Type and Screen (T&S) Training. J. Comput. Assist. Learn. 2021, 37, 359–369. [Google Scholar] [CrossRef]
- Skarbez, R.; Brooks, F.P., Jr.; Whitton, M.C. A Survey of Presence and Related Concepts. ACM Comput. Surv. 2017, 50, 96:1–96:39. [Google Scholar] [CrossRef]
- Slater, M.; Sanchez-Vives, M.V. Enhancing Our Lives with Immersive Virtual Reality. Front. Robot. AI 2016, 3, 74. [Google Scholar] [CrossRef] [Green Version]
- Müns, A.; Meixensberger, J.; Lindner, D. Evaluation of a Novel Phantom-Based Neurosurgical Training System. Surg. Neurol. Int. 2014, 5, 173. [Google Scholar] [CrossRef] [PubMed]
- Horvitz, E.; Breese, J.; Heckerman, D.; Hovel, D.; Rommelse, K. The Lumière Project: Bayesian User Modeling for Inferring the Goals and Needs of Software Users. In Proceedings of the Fourteenth Conference on Uncertainty in Artificial Intelligence, UAI’98, Madison, Wisconsin, 24–26 July 1998; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1998; pp. 256–265. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schubert, M.; Endres, D. More Plausible Models of Body Ownership Could Benefit Virtual Reality Applications. Computers 2021, 10, 108. https://doi.org/10.3390/computers10090108
Schubert M, Endres D. More Plausible Models of Body Ownership Could Benefit Virtual Reality Applications. Computers. 2021; 10(9):108. https://doi.org/10.3390/computers10090108
Chicago/Turabian StyleSchubert, Moritz, and Dominik Endres. 2021. "More Plausible Models of Body Ownership Could Benefit Virtual Reality Applications" Computers 10, no. 9: 108. https://doi.org/10.3390/computers10090108
APA StyleSchubert, M., & Endres, D. (2021). More Plausible Models of Body Ownership Could Benefit Virtual Reality Applications. Computers, 10(9), 108. https://doi.org/10.3390/computers10090108






