Approximated Mixed-Integer Convex Model for Phase Balancing in Three-Phase Electric Networks

Abstract

With this study, we address the optimal phase balancing problem in three-phase networks with asymmetric loads in reference to a mixed-integer quadratic convex (MIQC) model. The objective function considers the minimization of the sum of the square currents through the distribution lines multiplied by the average resistance value of the line. As constraints are considered for the active and reactive power redistribution in all the nodes considering a $3\times 3$ binary decision variable having six possible combinations, the branch and nodal current relations are related to an extended upper-triangular matrix. The solution offered by the proposed MIQC model is evaluated using the triangular-based three-phase power flow method in order to determine the final steady state of the network with respect to the number of power loss upon the application of the phase balancing approach. The numerical results in three radial test feeders composed of 8, 15, and 25 nodes demonstrated the effectiveness of the proposed MIQC model as compared to metaheuristic optimizers such as the genetic algorithm, black hole optimizer, sine–cosine algorithm, and vortex search algorithm. All simulations were carried out in MATLAB 2020a using the CVX tool and the Gurobi solver.

1. Introduction

Three-phase electric networks are the most common topology at medium- and low-voltage distribution levels to supply electricity to residential, industrial, and commercial users in urban and rural areas [1,2]. Owing to the asymmetry of the impedances and the power consumptions, which can have single-, two-, and three-phase connections, the number of energy losses occurring in these networks is considerably higher than it would have been in a perfect symmetric case [3]. To reduce the number of power losses in such asymmetric grids, there exists a number of methodologies such as the ones based on the installation of shunt devices (disperse generators, capacitors, static distribution compensators, etc.), reconfiguration of the feeder, and phase balancing, among others. The first two approaches require higher levels of investment relating to acquisition, installation, and maintenance of electrical components, as these methodologies entail the introduction of new devices to the grid; however, the phase balancing approach requires no such high investments, as this methodology only requires working groups to be sent to reconfigure the load points based on the phase balancing optimal plan, which means that there is no need for new devices to be included [4].

In the existing literature, several different approaches have been proposed for solving the phase balancing problem. Most of them are based on master–slave optimization strategies using metaheuristics and three-phase power flow methods. Some of the most recurrent optimization approaches are the Chu and Beasley genetic algorithms (CBGA) [3,5,6], particle swarm optimization [7], vortex search algorithm (VSA) [8], simulated annealing [9], black hole optimizer (BHO) [3], differential evolution algorithm [10], and sine–cosine algorithm (SCA) [11]. A characteristic of these methodologies is that the master stage is entrusted with the responsibility of determining the connection of the loads in all the nodes using an integer codification, which is then transferred to the slave stage where the asymmetric power flow problem is evaluated to determine the number of power losses, which would guide the exploration through the solution space. Even if the master–slave optimization methodologies are simple to implement, they do not guarantee the global optimum finding, as they use random search criteria that require statistical studies to verify their efficiency level.

In this study, we propose a simplified version of the mixed-integer quadratic model recently introduced in [1] to solve the problem of optimal phase balancing by neglecting the effect of voltage drops in the distribution lines. The main advantage of our proposed mixed-integer quadratic convex (MIQC) model is that this model guarantees a global optimal solution with the use of branch and bound with interior point methods available in optimization packages such as CVX in MATLAB with the Gurobi solver. In addition, in order to validate the feasibility and optimality of the solution, a triangular-based three-phase power flow method has been implemented to determine the initial and final power losses in the network. The numerical results of the present study demonstrate the effectiveness and robustness of the proposed MIQC model as compared to metaheuristic optimizers such as the genetic algorithms, SCA, BHO, and VSA in three individual radial test feeders composed of 8, 15, and 25 nodes.

The remainder of this paper is organized as follows. In Section 2, we present the proposed MIQC model to demonstrate the phase balancing problem in three-phase asymmetric networks; in Section 3, we present the solution methodology for the phase balancing problem, which evaluates the solution offered by the MIQC model in the triangular-based power flow method for asymmetric networks so as to determine the level of power loss reduction after implementing the phase balancing plan. In Section 4, we present the main characteristics of the test feeders employed in the numerical validations, which are composed of 8, 15, and 25 nodes that are operated at medium-voltage levels with radial structures. In Section 5, we present the computational implementations and shows the results of comparisons of the model with metaheuristics. Finally, in Section 6, we present the study’s concluding remarks and also highlights a few possible future developments.

2. Proposed Mixed-Integer Approximation

The optimal phase balancing problem in three-phase unbalanced distribution networks is a classical and widely studied optimization problem in electrical distribution systems [5]. The complete optimization model of the grid involves a general mixed-integer nonlinear programming (MINLP) model due to (i) the presence of binary variables associated with the load connection in the model that can be modeled with a binary matrix with $3\times 3$ dimensions [1] and (ii) the intrinsic nonlinearity of the power balance constraints in their three-phase form, i.e., the products among voltages and trigonometric functions [12,13]. However, to address the problem of phase balancing in three-phase unbalanced networks, here, we propose a simplified mixed-integer convex model that would allow for the redistribution of all the loads by considering the ideal voltages for all the buses of the network as well as Kirchhoff’s first law in all the nodes of the network. Note that the simplicity of our model lies in the elimination of the right-hand-side part of the power balance equations which contains trigonometric functions that relate the voltage magnitudes and angles through the nodal admittance matrix by assuming that all the voltages are exactly $1.00$ pu with their respective phase angles. Moreover, note that these assumptions make it possible for the exact MINLP model to transform into an approximated mixed-integer convex approach. The proposed optimization model is described in the following section.

2.1. Objective Function Formulation

The objective function of the proposed approximated MIQC model for load redistribution in three-phase networks is the minimization of the square components of the current (real and imaginary parts) at each three-phase line. This objective function is formulated in Equation (1) as follows:

$$\begin{array}{c}\hfill minz=\sum _{l\in \mathcal{L}}\sum _{f\in \mathcal{F}}{R}_l^{\mathrm{ave}}\left({\left(J_{lf}^r\right)}^2+{\left(J_{lf}^i\right)}^2\right),\end{array}$$

(1)

Here, z represents the objective function value, and $J_{lk}^r$ and $J_{lk}^i$ are the real and imaginary parts of the current through line l in phase f, respectively. $R_l^{\mathrm{ave}}$ is a parameter that calculates the average resistance value of the three-phase line. Note that $\mathcal{L}$ is the set containing all the lines of the network, and $\mathcal{F}$ is the set that consists of all the phases of the network.

2.2. Set of Constraints

The set of constraints associated with the load redistribution in all the nodes of the networks takes the active and reactive power connections at each node into account, as well as the calculation of the ideal net injected current in nodes and current flows in lines. The complete set of constraints is presented as follows:

$$\begin{array}{c}\hfill P_{kf}^d=\sum _{g\in \mathcal{F}}{x}_{kfg}{P}_{kg}^d,\left\{\forall k\in \mathcal{N},\forall f\in \mathcal{F}\right\}\end{array}$$

(2)

$$\begin{array}{c}\hfill Q_{kf}^d=\sum _{g\in \mathcal{F}}{x}_{kfg}{Q}_{kg}^d,\left\{\forall k\in \mathcal{N},\forall f\in \mathcal{F}\right\}\end{array}$$

(3)

$$\begin{array}{c}\hfill I_{kf}^r=\frac{P_{kf}^d}{V_{kf}},\left\{\forall k\in \mathcal{N},\forall f\in \mathcal{F}\right\}\end{array}$$

(4)

$$\begin{array}{c}\hfill I_{kf}^i=\frac{Q_{kf}^d}{V_{kf}},\left\{\forall k\in \mathcal{N},\forall f\in \mathcal{F}\right\}\end{array}$$

(5)

$$\begin{array}{c}\hfill J_{lf}^r=\sum _{k\in \mathcal{N}}\sum _{g\in f}{T}_{lfkg}{I}_{kf}^r,\left\{\forall l\in \mathcal{L},\forall f\in \mathcal{F}\right\}\end{array}$$

(6)

$$\begin{array}{c}\hfill J_{lf}^i=\sum _{k\in \mathcal{N}}\sum _{g\in f}{T}_{lfkg}{I}_{kf}^i,\left\{\forall l\in \mathcal{L},\forall f\in \mathcal{F}\right\}\end{array}$$

(7)

Here, $P_{kf}^d$ and $Q_{kf}^d$ are the final active and reactive power consumptions at node k in the phase f; $P_{kg}^d$, and $Q_{kg}^d$ are the initial active and reactive power demands at node k in the phase g; $x_{kfg}$ is a binary variable (binary $3\times 3$ matrix) that determines whether the demand connected at node k in the phase g is transferred to the phase f; $I_{kf}^r$ and $I_{kf}^i$ are the real and imaginary components of the current demanded at node k in the phase f, respectively; $V_{kf}$ is the ideal voltage magnitude at node k in the phase f, and $T_{lfkg}$ is the matrix that allows for the calculation of the branch currents once the demanded currents of the nodes are defined. Note that $\mathcal{F}$ and $\mathcal{N}$ are the sets that contain all the phases and nodes of the network, respectively.

2.3. Model Characteristics

The optimization model defined from (1) to (7) has the following characteristics:

• It is an optimization model with a set of linear integer constraints and a quadratic objective function that produces a mixed-integer quadratic programming model that can be solved completely with the combination of the branch and bound method and linear interior point methods [14].
• The objective function corresponds to a sensibility function that guides the exploration through the solution space; in other words, it is a performance indicator. However, to determine the real number of power losses, the evaluation of a three-phase power flow method is required [8].
• Equations (4) and (5) do not consider the effect of the voltage angle in the calculation of the real and imaginary parts of the currents, since the magnitude of the currents in all the branches (see Equations (6) and (7)) used in the objective function remains unaltered independent of the angle assigned to the voltages.
• The inputs of the optimization model corresponds to the average resistance value $\left(R_l^{\mathrm{ave}}\right)$ per distribution line, the initial active and reactive power demands in all the nodes and phases $\left(P_{kg}^d\right)$ and $\left(Q_{kg}^d\right)$, respectively, and the triangular-based matrix to calculate branch currents from the the nodal ones, i.e., $T_{lfkg}$. In addition, the main outputs of the optimization model are the objective function value and the final load redistribution at each node, which is provided by the final value of the variable $x_{kfg}$.

It is worth mentioning that the proposed mixed-integer quadratic convex model was based on the convex formulation that was recently proposed in [11], which neglected the effect of the currents through the lines and the objective function associated with the total load consumption at the terminals of the substation, while our proposal includes a sensitive index in the objective function related to the minimization of the power losses under ideal voltage conditions considering the branch current calculations.

3. Optimization Methodology

The solution of the MIQC model defined from (1) to (7) is addressed by the combination of the branch and bound method with an interior point method available in the convex optimization package CVX in the MATLAB programming environment using an MIQC tool [1]. However, as previously mentioned, the solution of the MIQC proposed model does not generate the real value of the power losses of the network; the proposed optimization model approximates the grid variables associated with the voltage profiles. Therefore, it is necessary to evaluate the final load configurations provided in the variables $P_{kf}^d$ and $Q_{kf}^d$. This evaluation was conducted using a three-phase power flow approach, which is briefly presented in the following section.

3.1. Three-Phase Power Flow Method

The solution of the three-phase power flow problem in three-phase networks is an important task in the static analysis of electrical networks. The power flow problem is, in general, a complex numerical problem as it is composed of a set of nonlinear nonconvex equations that include products among voltage variables. In the literature on three-phase networks, several numerical methods have been reported, including the Newton–Raphson method [15], sweep backward/forward method [16], graph-based methods [17], and the triangular-based power flow method [6]. Here, we have adopted the use of the triangular-based method to solve the power flow problem in three-phase networks.

The general recursive formula for the triangular-based power flow method for three-phase networks having loads with $Y$—connections and those that are solidly grounded is presented in Equation (8).

$$\begin{array}{c}\hfill {\mathbb{V}}_{3\phi }^{t+1}={\mathbf{1}}_{3\phi }{V}_{13\phi }-{\mathbf{T}}_{3\phi }^T{\mathbf{Z}}_{3\phi }{\mathbf{T}}_{3\phi }{\mathbf{diag}}^{-1}\left({\mathbb{V}}_{3\phi }^{t,🟉}\right){\mathbb{S}}_{3\phi }^{🟉}.\end{array}$$

(8)

Here, ${\mathbb{V}}_{3\phi }\in {\mathcal{C}}^{3(n-1)\times 1}$ is a vector of the three-phase voltage in all the demand nodes; $V_{13\phi }\in {\mathcal{C}}^{3\times 1}$ is the three-phase voltage at terminals of the substation; ${\mathbf{T}}_{3\phi }\in {\mathcal{R}}^{3b\times 3(n-1)}$ is the upper-triangular matrix that relates nodal currents with branch currents, ${\mathbf{1}}_{3\phi }\in {\mathcal{R}}^{3(n-1)\times 3}$ is a rectangular matrix filled by $3\times 3$ identity matrices, ${\mathbf{Z}}_{3\phi }\in {\mathcal{R}}^{3b\times 3b}$ is the primitive three-phase impedance matrix that contains the information pertaining to all the branches of the network, and ${\mathbb{S}}_{3\phi }\in {\mathcal{C}}^{3(n-1)\times 1}$ is the vector that contains all the complex demands of the network. Note that n and b represent the number of nodes and branches of the network, respectively, and $z^{🟉}$ corresponds to the conjugate operator of the complex variable z. In addition, t represents an iterative counter.

The convergence of the recursive Formula (8) can be ensured by applying the Banach fixed-point theorem, as recently demonstrated by the authors of [6]. In addition, this convergence is achieved when $max\left\{\left|\left|{\mathbb{V}}_{3\phi }^{t+1}\right|-\left|{\mathbb{V}}_{3\phi }^t\right|\right|\right\}\le \epsilon$, where $\epsilon$ is the maximum tolerance error that is typically assigned as $1\times {10}^{-10}$.

3.2. General Solution Methodology

The optimization methodology for solving the problem of phase balancing in three-phase networks using the proposed MIQC model in conjunction with the triangular-based power flow formulation defined by the recursive Formula (8) is summarized in Algorithm 1.

Algorithm 1: Approximate solution of the phase balancing problem by combining the MIQC model with the triangular-based power flow method

Data: Define the test feeder under study 1 Calculate the three-phase power flow matrices; 2 Calculate the initial solution of the three-phase power flow problem using Equation (8); 3 Report the initial grid power losses; 4 Construct the MIQC model (1)–(7); 5 Solve the MIQC model using a mixed-integer quadratic programming tool; 6 Evaluate the solution of the MIQC model in the power flow Formula (8);       Result: Report the final grid power losses

4. Test Feeders

To validate the proposed methodology in order to solve the problem of phase balancing in three-phase asymmetric networks, we employed three test feeders composed of 8, 15, and 25 nodes. All of these test feeders correspond to radial distribution networks operated at medium-voltage levels.

4.1. 8-Bus Test Feeder

The 8-bus system is a radial distribution network operated at the substation bus with a nominal line-to-line voltage of $11$ kV. The electrical configuration of the test feeder is depicted in Figure 1. In this system, phase a absorbs 1005 kW and 485 kvar, phase b absorbs 785 kW and 381 kvar, and phase c absorbs 1696 kW and 821 kvar. The initial state of this system with respect to power losses was 13.9925 kW.

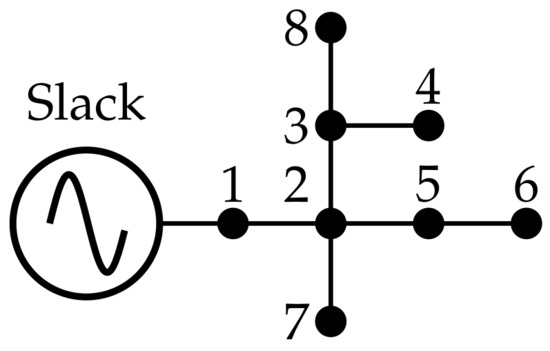
Figure 1. Connection among the nodes in the 8-bus test feeder.

The information regarding impedances and loads for this test system are presented in Table 1 and Table 2, respectively.

Table 1. Demand information and distribution line parameters of the 8-bus test system (all powers in kW and kvar).

Line	Node i	Node j	Cond.	Length (mi)	${\mathit{P}}_{\mathit{ja}}$	${\mathit{Q}}_{\mathit{ja}}$	${\mathit{P}}_{\mathit{jb}}$	${\mathit{Q}}_{\mathit{jb}}$	${\mathit{P}}_{\mathit{jc}}$	${\mathit{Q}}_{\mathit{jc}}$
1	1	2	1	1	519	250	259	126	515	250
2	2	3	2	1	0	0	259	126	486	235
3	2	5	3	1	0	0	0	0	226	109
4	2	7	3	1	486	235	0	0	0	0
5	3	4	4	1	0	0	0	0	324	157
6	3	8	5	1	0	0	267	129	0	0
7	5	6	6	1	0	0	0	0	145	70

Table 2. Impedance information for the type of conductors in the 8-node test system.

Conductor		Impedance Matrix ($\mathbf{\Omega }/$mi)
	$0.093654+j0.0402930$	$0.031218+j0.0134310$	$0.031218+j0.0134310$
1	$0.031218+j0.0134310$	$0.093654+j0.0402930$	$0.031218+j0.0134310$
	$0.031218+j0.0134310$	$0.031218+j0.0134310$	$0.093654+j0.0402930$
	$0.156090+j0.0671550$	$0.052030+j0.0223850$	$0.052030+j0.0223850$
2	$0.052030+j0.0223850$	$0.156090+j0.0671550$	$0.052030+j0.0223850$
	$0.052030+j0.0223850$	$0.052030+J0.0223850$	$0.156090+j0.0671550$
	$0.046827+j0.0201465$	$0.015609+j0.0067155$	$0.015609+j0.0067155$
3	$0.015609+j0.0067155$	$0.046827+j0.0201465$	$0.015609+j0.0067155$
	$0.015609+j0.0067155$	$0.015609+j0.0067155$	$0.046827+j0.0201465$
	$0.031218+j0.0134310$	$0.010406+j0.0044770$	$0.010406+j0.0044770$
4	$0.010406+j0.0044770$	$0.031218+j0.0134310$	$0.010406+j0.0044770$
	$0.010406+j0.0044770$	$0.010406+j0.0044770$	$0.031218+j0.0134310$
	$0.062436+j0.0268620$	$0.020812+j0.0089540$	$0.020812+j0.0089540$
5	$0.020812+j0.0089540$	$0.062436+j0.0268620$	$0.020812+J0.0089540$
	$0.020812+j0.0089540$	$0.020812+j0.0089540$	$0.062436+j0.0268620$
	$0.078045+j0.0335775$	$0.026015+j0.0111925$	$0.026015+j0.0111925$
6	$0.026015+j0.0111925$	$0.078045+j0.0335775$	$0.026015+j0.0111925$
	$0.026015+j0.0111925$	$0.026015+j0.0111925$	$0.078045+j0.0335775$

4.2. 15-Bus System

The 15-bus system is a three-phase asymmetric distribution network built with 15 nodes and 14 lines. The line-to-line voltage in the terminals of the substation (i.e., node 1) is 13.2 kV. A schematic single-line diagram of this test feeder is displayed in Figure 2.

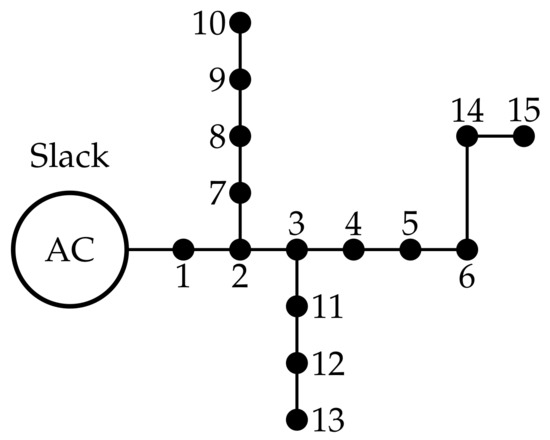
Figure 2. Single-line diagram of the 15-bus system.

The total active and reactive power consumptions in this system are 9605 kW and 5226 kvar for phase a, 6480 kW and 4940 kvar for phase b, and 11977 kW and 8778 kvar for phase c, respectively. Note that, with this load distribution, the total power loss of this system is 134.2472 kW. The parametric information of this test feeder is reported in Table 3. It is worth mentioning that the information of the impedance matrices for this system is the same used in the 8-bus test feeder [18].

Table 3. Demand information for the 15-bus test feeder (all power values are in kW and kvar).

Line	Node i	Node j	Cond.	Length (ft)	${\mathit{P}}_{\mathit{ja}}$	${\mathit{Q}}_{\mathit{ja}}$	${\mathit{P}}_{\mathit{jb}}$	${\mathit{Q}}_{\mathit{jb}}$	${\mathit{P}}_{\mathit{jc}}$	${\mathit{Q}}_{\mathit{jc}}$
1	1	2	1	603	0	0	725	300	1100	600
2	2	3	2	776	480	220	720	600	1040	558
3	3	4	3	825	2250	1610	0	0	0	0
4	4	5	3	1182	700	225	0	0	996	765
5	5	6	4	350	0	0	820	700	1220	1050
6	2	7	5	691	2500	1200	0	0	0	0
7	7	8	6	539	0	0	960	540	0	0
8	8	9	6	225	0	0	0	0	2035	1104
9	9	10	6	1050	1519	1250	1259	1200	0	0
10	3	11	3	837	0	0	259	126	1486	1235
11	11	12	4	414	0	0	0	0	1924	1857
12	12	13	5	925	1670	486	0	0	726	509
13	6	14	4	386	0	0	850	752	1450	1100
14	14	15	2	401	486	235	887	722	0	0

4.3. 25-Bus System

The 25-bus system is a radial distribution network operated at substation terminals with a line-to-line voltage of 4.16 kV. The electrical configuration of the test feeder is depicted in Figure 3. In this system, phase a absorbs 946 kW and 648 kvar, phase b absorbs 573.6 kW and 430.6 kVAr, and phase c absorbs 771.8 kW and 554 kvar. With these power load consumptions, the total power loss in this test feeder is 75.4207 kW.

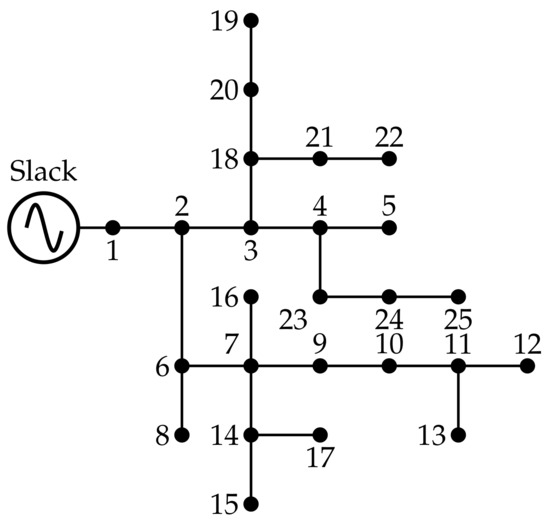
Figure 3. Single-line diagram of the 25-bus system.

The electrical information of the constant power consumptions and distribution line impedances for this test system are presented in Table 4 and Table 5, respectively. This parametric information was taken from [6].

Table 4. Loads and lines parameters of the 25-bus test system (all powers are in kW and kvar).

Line	Node i	Node j	Cond.	Length (ft)	${\mathit{P}}_{\mathit{ja}}$	${\mathit{Q}}_{\mathit{ja}}$	${\mathit{P}}_{\mathit{jb}}$	${\mathit{Q}}_{\mathit{jb}}$	${\mathit{P}}_{\mathit{jc}}$	${\mathit{Q}}_{\mathit{jc}}$
1	1	2	1	1000	0	0	0	0	0	0
2	2	3	1	500	36	21.6	28.8	19.2	42	26.4
3	2	6	2	500	43.2	28.8	33.6	24	30	30
4	3	4	1	500	57.6	43.2	4.8	3.4	48	30
5	3	18	2	500	57.6	43.2	38.4	28.8	48	36
6	4	5	2	500	43.2	28.8	28.8	19.2	36	24
7	4	23	2	400	8.6	64.8	4.8	3.8	60	42
8	6	7	2	500	0	0	0	0	0	0
9	6	8	2	1000	43.2	28.8	28.8	19.2	3.6	2.4
10	7	9	2	500	72	50.4	38.4	28.8	48	30
11	7	14	2	500	57.6	36	38.4	28.8	60	42
12	7	16	2	500	57.6	4.3	3.8	28.8	48	36
13	9	10	2	500	36	21.6	28.8	19.2	32	26.4
14	10	11	2	300	50.4	31.7	24	14.4	36	24
15	11	12	3	200	57.6	36	48	33.6	48	36
16	11	13	3	200	64.8	21.6	33.6	21.1	36	24
17	14	15	2	300	7.2	4.3	4.8	2.9	6	3.6
18	14	17	3	300	57.6	43.2	33.6	24	54	38.4
19	18	20	2	500	50.4	36	38.4	28.8	54	38.4
20	18	21	3	400	5.8	4.3	3.4	2.4	5.4	3.8
21	20	19	3	400	8.6	6.5	4.8	3.4	6	4.8
22	21	22	3	400	72	50.4	57.6	43.2	60	48
23	23	24	2	400	50.4	36	43.2	30.7	4.8	3.6
24	24	25	3	400	8.6	6.5	4.8	2.9	6	4.2

Table 5. Impedance matrix for the type of conductors in the 25-bus test system.

Conductor		Impedance Matrix ($\mathbf{\Omega }/$mi)
	$0.3686+j0.6852$	$0.0169+j0.1515$	$0.0155+j0.1098$
1	$0.0169+j0.1515$	$0.3757+j0.6715$	$0.0188+j0.2072$
	$0.0155+j0.1098$	$0.0188+j0.2072$	$0.3723+j0.6782$
	$0.9775+j0.8717$	$0.0167+j0.1697$	$0.0152+j0.1264$
2	$0.0167+j0.1697$	$0.9844+j0.8654$	$0.0186+j0.2275$
	$0.0152+j0.1264$	$0.0186+j0.2275$	$0.9810+j0.8648$
	$1.9280+j1.4194$	$0.0161+j0.1183$	$0.0161+j0.1183$
3	$0.0161+j0.1183$	$1.9308+j1.4215$	$0.0161+j0.1183$
	$0.0161+j0.1183$	$0.0161+j0.1183$	$1.9337+j1.4236$

5. Computational Validations

The computational validations of the proposed optimization methodology were carried out in the MATLAB programming environment using the CVX optimization package with the Gurobi solver on a personal computer AMD Ryzen 7 3700U, 2.3 GHz, 16 GB RAM with 64-bit Windows 10 Home Single Language. To compare the numerical results of the proposed MIQC model with combinatorial optimization methods, we implemented different optimization techniques based on metaheuristics such as the CBGA [5], BHO [6], SCA [6], VSA [8], and the improved version of the CBGA recently presented in [6]. Note that all of the metaheuristic optimizers were set with a population size of 10 individuals and 1000 iterations.

5.1. 8-Bus Systems

Table 6 presents numerical values for the solution of the phase balancing problem in the 8-bus system applying the proposed MIQC formulation with the triangular-based power flow method, as well as the findings from comparing it with metaheuristic approaches.

Table 6. Numerical results for the 8-bus system.

Method	Power Losses (kW)	Reduction (%)
Benchmark case	13.9925	—
Classical CBGA	10.5869	24.34
BHO	10.5869	24.34
SCA	10.5869	24.34
VSA	10.5869	24.34
Improved CBGA	10.5869	24.34
MIQC	10.5869	24.34

The numerical results of the 8-bus system presented in Table 6 show that (i) the proposed MIQC model and all the comparative methods reach the same optimal solution, which corresponds to a reduction of $3.4056$ kW, i.e., 24.34%; and (ii) the value of $10.5969$ kW corresponds to the global optimum of the solution of the phase balancing problem in the 8-bus system. This was confirmed after evaluating the solution space using an exhaustive search in DigSILENT. It is important to mention that the dimension of the solution space in the 8-bus system is defined as $6^{n-1,}$ i.e., $6^7$ = 279,936.

Note that the key advantage of the proposed MIQC model is that the solution obtained is the same each time it runs, which ensures the global optimum value for the mathematical model (1) to (8), whereas all of the metaheuristic techniques present oscillations and require multiple evaluations so as to study their efficiency using statistical indices [19].

5.2. 15-Bus Systems

The solutions of the phase balancing problem for the 15-bus system with the MIQC model and metaheuristic optimizers are presented in Table 7.

Table 7. Numerical results for the 15-bus system.

Method	Power Losses (kW)	Reduction (%)
Benchmark case	134.2472	—
Classical CBGA	109.2236	18.64
BHO	110.0025	18.06
SCA	109.3973	18.51
VSA	109.3217	18.57
Improved CBGA	109.1980	18.66
MIQC	109.2539	18.62

From the solutions in Table 7, the following observations can be made: (i) The proposed MIQC model allows for a reduction in the number of power losses by approximately $18.62\%$, i.e., 24.9933 kW with respect to the benchmark case. In addition, this corresponds to the third better solution for the 15-bus system, only suppurated by the classical and improved Chu and Beasley genetic algorithms. (ii) The worst method for the 15-bus system is the BHO method with a final reported power loss of $110.0025$ kW, which corresponds to the 18.06% reduction of the benchmark case. (iii) All of the optimization methods reported in Table 7 allow for a reduction in power losses higher than 18%. The best result obtained with the improved CBGA was 18.66%, which is only 0.04% better than the proposed MIQC model.

5.3. 25-Bus System

The solutions of the phase balancing problem in the 25-bus system with the proposed MIQC model as well as the comparative metaheuristic methods are presented in Table 8.

Table 8. Numerical results for the 25-bus system.

Method	Power Losses (kW)	Reduction (%)
Benchmark case	75.4207	—
Classical CBGA	72.2919	4.15
BHO	72.3735	4.04
SCA	72.3047	4.13
VSA	72.2888	4.15
Improved CBGA	72.3142	4.12
MIQC	72.2816	4.16

The numerical results in Table 8 show that (i) the best solution is obtained by the proposed MIQC model with a $4.16\%$ reduction, i.e., 3.1391 kW; (ii) the second-best solution is reached using the VSA method with an objective function of 72.2888 kW, i.e., $4.15\%$; and (iii) all the comparative methods, as well as the proposed MIQC model, allow for decreasing the number of power losses higher than 4.00%, with the worst approach being the BHO, which results in a reduction of only $4.04\%$.

It is important to mention that the proposed MIQC model offers the best solution for the 25-bus system that has a solution space with dimensions of $6^{24}$, i.e., more than $4.70\times {10}^{18}$ possible solutions. This confirms the efficiency of the proposed model in solving the phase balancing problem, as it produces results similar to those of the classical metaheuristic methods, which has a major advantage of not requiring statistical evaluations as the solution of the convex model is always the same (global optimization properties of the mixed-integer convex models).

5.4. Statistical Analysis

To demonstrate that the proposed MIQC model is effective in solving the phase-swapping problem in three-phase asymmetric networks, here, we present the statistical analysis of each of the comparative metaheuristic optimization methods in the 25-bus test feeder. For each one of the metaheuristic approaches, 10 individuals in the populations are assigned, along with the use of 1000 iterations and 100 consecutive repetitions. In Table 9, we present the behavior of each one of the comparative approaches regarding the maximum, minimum, mean, and standard deviation of each one of the combinatorial approaches as well as the behavior of the proposed MIQC model.

Table 9. Statistical behavior of the comparative methodologies in the 25-bus system.

Method	Minimum (kW)	Maximum (kW)	Mean (kW)	Std. Deviation (kW)
Classical CBGA	72.2919	72.3316	72.3164	0.0147
BHO	72.3735	72.4718	72.4177	0.0276
SCA	72.3047	72.3415	72.3262	0.0131
VSA	72.2888	72.3520	72.3228	0.0165
Improved CBGA	72.3142	72.3849	72.3290	0.0206
MIQC	72.2816	72.2816	72.2816	1.0256 $\times {10}^{-16}$

Numerical results in Table 9 show that:

✓

All of the metaheuristic optimizers have mean values for power losses higher than $72.3100$ kW, which are at least $0.0284$ kW higher than the best optimal solution reached by the proposed MIQC model. This value implies that among all the simulation cases, the proposed approach improves the average solution of the metaheuristics by about $0.03\%$. Even if this improvement in the final number of power losses is small when the metaheuristic and the proposed model are compared, this implies that with only one evaluation, the convex reformulation offers better numerical performance, while the combinatorial methods require multiple simulations to find a good solution, with the main problem being that each evaluation may find different local optimal solutions.

✓

The standard deviation indicates that all the solutions provided by the proposed MIQC model are the same, i.e., this methodology, due to the convexity of each node in the branch and bound method, allows the finding of the global optimum of the problem, which is noninsurable with the metaheuristic optimizers owing to the random processes used to explore and exploit the solution space. Note that the standard deviation of the MIQC model is a billion times smaller than all of the metaheuristics, which confirms that the convex reformulation is 100% effective, while the effectiveness of metaheuristic methods ranges between $10\%$ and $30\%$. However, one of the main problems with metaheuristics is that a high dependence on the programmer can affect the final results since the selection of the parameters is key for their implementation [20].

Regarding processing time, it is important to mention that all the optimization methods, i.e., the metaheuristics and the proposed MIQC model, take less than 150 s, which is considered small for solving a complex optimization problem, as in the case of the phase-swapping problem that has a billion different possible combinations for solving the problem. This confirms the effectiveness of the proposed approach in providing practical solutions for the three-phase asymmetric electrical networks.

6. Conclusions and Future Works

An approximated MIQC model combined with the triangular-based power flow method for asymmetric distribution networks was proposed in this study in order to solve the optimal phase balancing problem in medium-voltage distribution grids. The numerical results for three test feeders composed of 8, 15, and 25 nodes demonstrate that the proposed MIQC model reaches the optimal solution in the 8- and 25-bus systems with reductions in the power losses of $24.34\%$ and $4.16\%$, respectively, relative to the benchmark cases. In the case of the 15-bus system, the solution reported by the proposed MIQC model is only supported by the Chu and Beasley genetic approaches (CBGA). However, the difference among these methodologies was found to be only $0.04\%$, which demonstrates that the proposed optimization methodology adequately solves the phase balancing problem with the main advantage that it does not require statistical evaluations owing to the properties of the convex optimization; this is not the case for the metaheuristic optimization methods, as was demonstrated in the 25-bus system where the standard deviation for the MIQC model was a billion times smaller than the metaheuristic methods.

Note that the main advantage of the proposed MIQC model is that it is independent of the solution space size, which is measured as $6^{n-1}$. The solution is consistent and allows for important reductions with regard to power losses without considering the effect of the power balance equations in the approximated model. However, the evaluation of its results in the triangular-based power flow method ensures that the solution is feasible and also has better numerical performance than metaheuristic methods such as BHO, SCA, and VSA.

Owing to the contributions of this study, in the future, it will be possible to (i) obtain a convex approximation of the power balance equations using conic programming in order to obtain a general mixed-integer conic model to solve the phase balancing problem exactly and (ii) use the proposed MIQC model to solve the phase balancing problem in three-phase networks, including renewable energy resources and battery energy storage systems, from the point of view of economic dispatch operations.