Robust Permutation Test of Intraclass Correlation Coefficient for Assessing Agreement
Simple Summary
Abstract
1. Introduction
2. Intraclass Correlation Coefficient and Measurement of Agreement
3. Permutation Test of Intraclass Correlation Coefficient of Agreement with Two Raters
- For n pairs of i.i.d. observations , , …, , estimate the ICC(2,1) as .
- Estimate the approximated variance by
- Calculate the studentized statistic .
- Randomly shuffle for B times. For each permutation, calculate the permuted studentized statistic , .
- Calculate the p-value by
- Reject if .
4. Simulations
- Multivariate normal (MVN) with mean zero and identity covariance.
- Exponential given as where , , and u are uniformly distributed on the two-dimensional unit circle.
- Circular given as the uniform distribution on a two-dimensional unit circle.
- where and , where W and Z are i.i.d. random variables.
- Multivariate t-distribution (MVT) with 5 degrees of freedom.
- Mixture of two bivariate normal distributions. Given as where , , . We use a range of values: 0.1, 0.3, 0.6 and 0.9 to simulate different degrees of dependency between X and Y (MVNX_1, MVNX_3, MVNX_6, MVNX_9).
- Absolute normal distribution (ABNORM). , where Z follows standard normal distribution and X follows a folded standard normal distribution, thus Y has a non-constant variance.
- Binomial normal distribution (BINORM). , where , , and Y is defined to follow a normal distribution with mean 0 and a standard deviation dependent on .
- Squared normal distribution (SQNORM). , and Y is a quadratic function of X and a standard normal error.
- Uniform distribution (UNIF). and , where W and Z are independent variables following . This represents a scenario of dependency due to contrained support
5. Real World Examples
5.1. Inter-Rater Agreement in CT Radiomics
5.2. Inter-Rater Reliability for iTUG Test
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Approximation of ICC(2,1) to Pearson Correlation for Two Raters
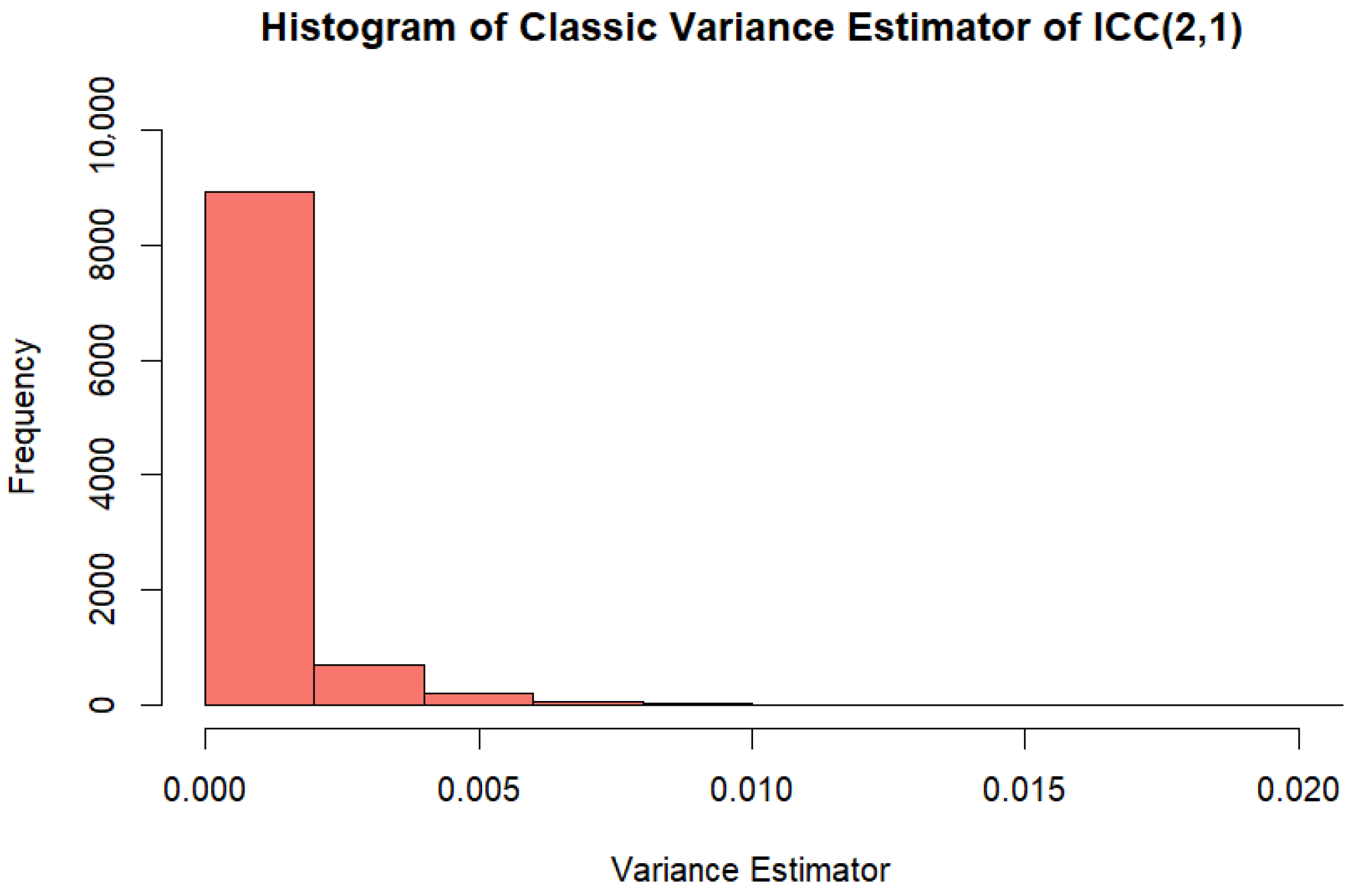
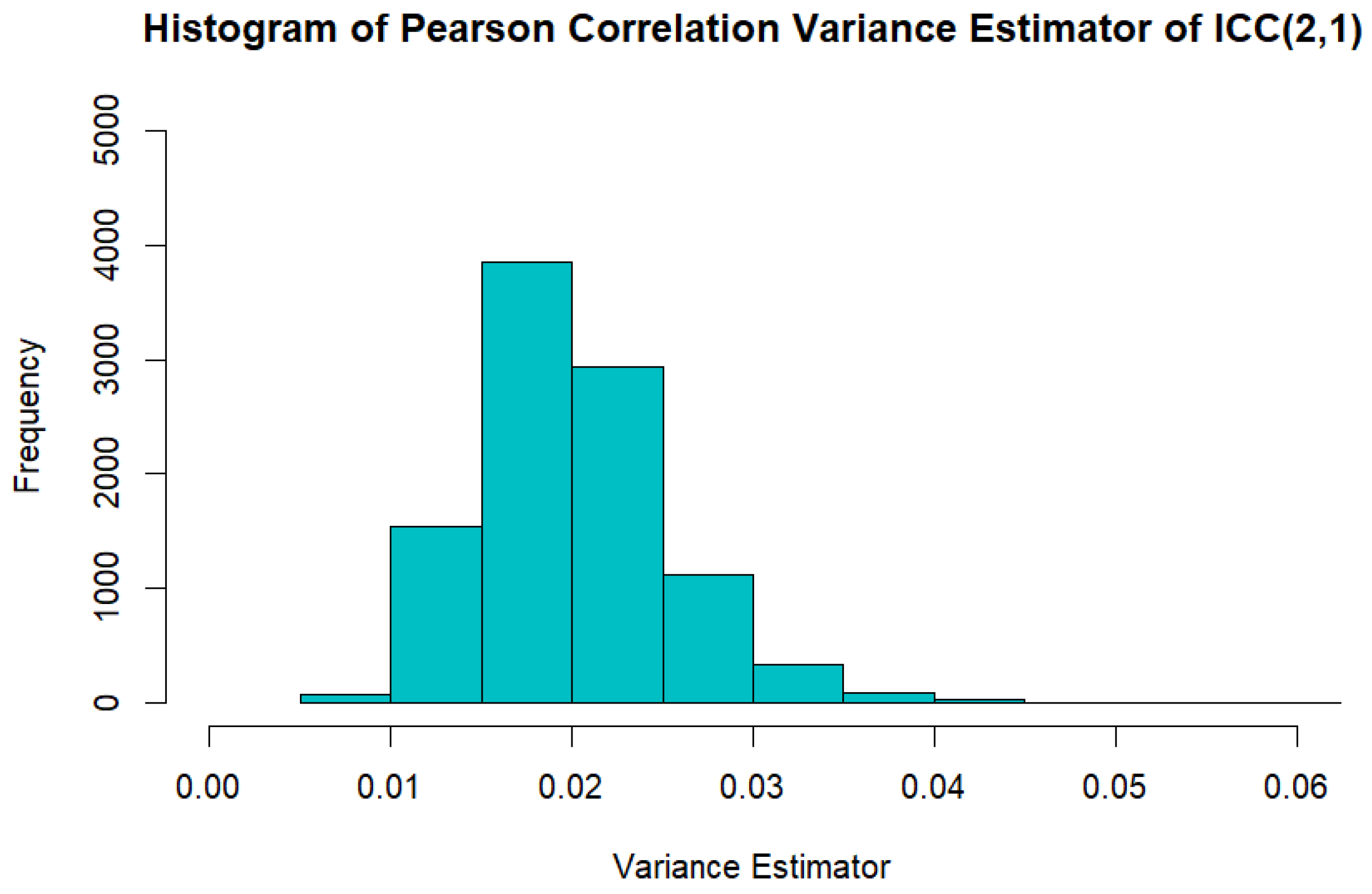
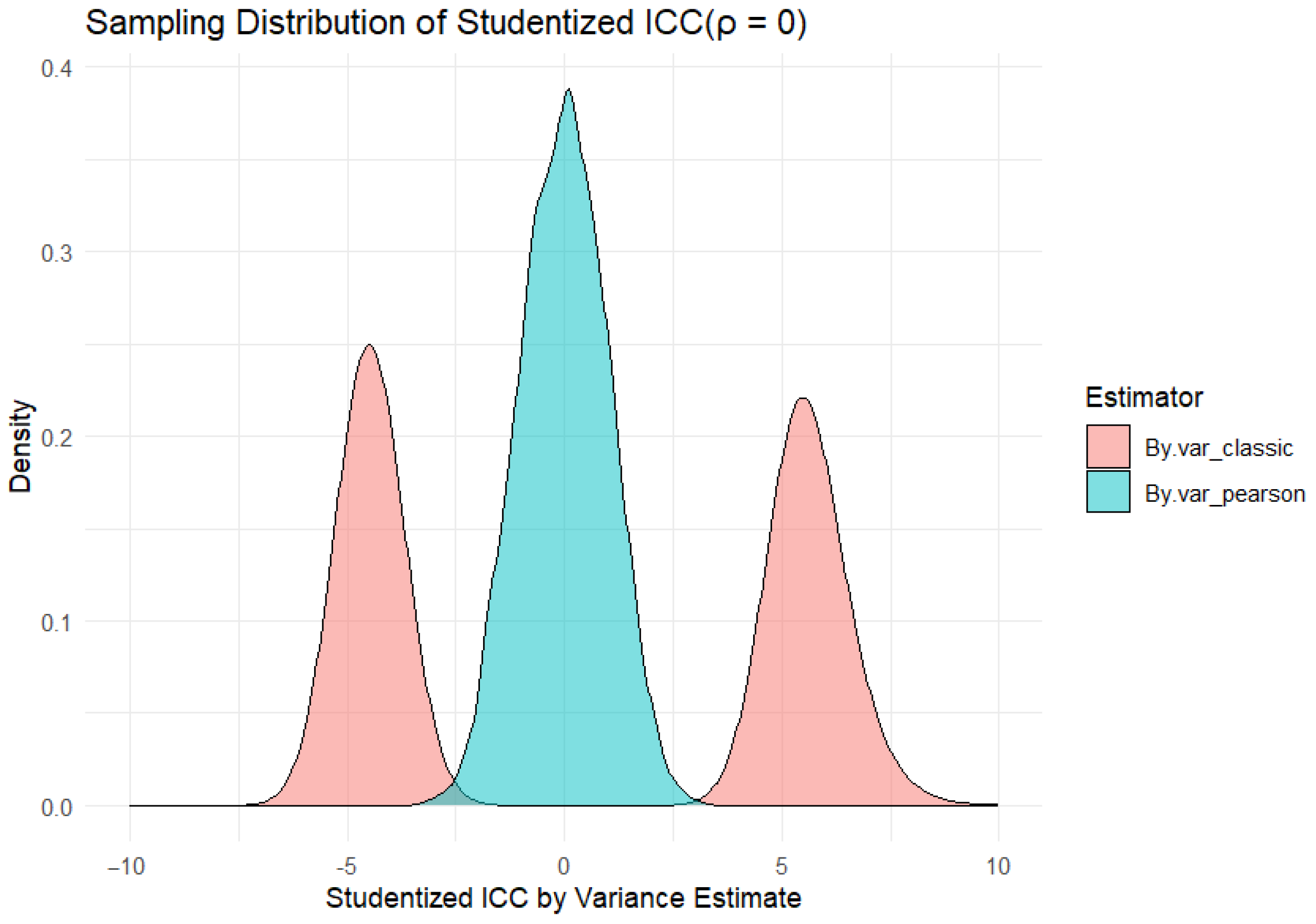
Appendix B. Comparison of Large Sample Variance Estimator and Variance Estimator Based on Pearson Correlation When
References
- Bartko, J.J. The intraclass correlation coefficient as a measure of reliability. Psychol. Rep. 1966, 19, 3–11. [Google Scholar] [CrossRef] [PubMed]
- Bartko, J.J. On various intraclass correlation reliability coefficients. Psychol. Bull. 1976, 83, 762. [Google Scholar] [CrossRef]
- Lahey, M.A.; Downey, R.G.; Saal, F.E. Intraclass correlations: There’s more there than meets the eye. Psychol. Bull. 1983, 93, 586. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D. A note on the use of the intraclass correlation coefficient in the evaluation of agreement between two methods of measurement. Comput. Biol. Med. 1990, 20, 337–340. [Google Scholar] [CrossRef]
- Leyland, A.H.; Groenewegen, P.P. Intraclass correlation coefficient (ICC). In Encyclopedia of Quality of Life and Well-Being Research; Springer International Publishing: Cham, Switzerlands, 2024; pp. 3643–3644. [Google Scholar][Green Version]
- de Raadt, A.; Warrens, M.J.; Bosker, R.J.; Kiers, H.A. A comparison of reliability coefficients for ordinal rating scales. J. Classif. 2021, 38, 519–543. [Google Scholar] [CrossRef]
- Wu, S.; Crespi, C.M.; Wong, W.K. Comparison of methods for estimating the intraclass correlation coefficient for binary responses in cancer prevention cluster randomized trials. Contemp. Clin. Trials 2012, 33, 869–880. [Google Scholar] [CrossRef] [PubMed]
- Xue, C.; Yuan, J.; Lo, G.G.; Chang, A.T.; Poon, D.M.; Wong, O.L.; Zhou, Y.; Chu, W.C. Radiomics feature reliability assessed by intraclass correlation coefficient: A systematic review. Quant. Imaging Med. Surg. 2021, 11, 4431. [Google Scholar] [CrossRef]
- Hade, E.M.; Murray, D.M.; Pennell, M.L.; Rhoda, D.; Paskett, E.D.; Champion, V.L.; Crabtree, B.F.; Dietrich, A.; Dignan, M.B.; Farmer, M.; et al. Intraclass correlation estimates for cancer screening outcomes: Estimates and applications in the design of group-randomized cancer screening studies. J. Natl. Cancer Inst. Monogr. 2010, 2010, 97–103. [Google Scholar] [CrossRef] [PubMed]
- Dinkel, J.; Khalilzadeh, O.; Hintze, C.; Fabel, M.; Puderbach, M.; Eichinger, M.; Schlemmer, H.P.; Thorn, M.; Heussel, C.P.; Thomas, M.; et al. Inter-observer reproducibility of semi-automatic tumor diameter measurement and volumetric analysis in patients with lung cancer. Lung Cancer 2013, 82, 76–82. [Google Scholar] [CrossRef]
- Pleil, J.D.; Wallace, M.A.G.; Stiegel, M.A.; Funk, W.E. Human biomarker interpretation: The importance of intra-class correlation coefficients (ICC) and their calculations based on mixed models, ANOVA, and variance estimates. J. Toxicol. Environ. Health Part B 2018, 21, 161–180. [Google Scholar] [CrossRef]
- Lin, L.I.-K. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef] [PubMed]
- DiCiccio, C.J.; Romano, J.P. Robust permutation tests for correlation and regression coefficients. J. Am. Stat. Assoc. 2017, 519, 1211–1220. [Google Scholar] [CrossRef]
- Hutson, A.D.; Yu, H. A robust permutation test for the concordance correlation coefficient. Pharm. Stat. 2021, 20, 696–709. [Google Scholar] [CrossRef]
- Hutson, A.D.; Yu, H. Exact inference around ordinal measures of association is often not exact. Comput. Methods Programs Biomed. 2023, 240, 107725. [Google Scholar] [CrossRef]
- Yu, H.; Hutson, A.D. Inferential procedures based on the weighted Pearson correlation coefficient test statistic. J. Appl. Stat. 2024, 51, 481–496. [Google Scholar] [CrossRef]
- Bourredjem, A.; Cardot, H.; Devilliers, H. Asymptotic Confidence Interval, Sample Size Formulas and Comparison Test for the Agreement Intra-Class Correlation Coefficient in Inter-Rater Reliability Studies. Stat. Med. 2024, 43, 5060–5076. [Google Scholar] [CrossRef] [PubMed]
- Tian, L.; Cappelleri, J.C. A new approach for interval estimation and hypothesis testing of a certain intraclass correlation coefficient: The generalized variable method. Stat. Med. 2004, 23, 2125–2135. [Google Scholar] [CrossRef]
- McGraw, K.O.; Wong, S.P. Forming inferences about some intraclass correlation coefficients. Psychol. Methods 1996, 1, 30. [Google Scholar] [CrossRef]
- Shrout, P.E.; Fleiss, J.L. Intraclass correlations: Uses in assessing rater reliability. Psychol. Bull. 1979, 86, 420. [Google Scholar] [CrossRef]
- Liljequist, D.; Elfving, B.; Skavberg Roaldsen, K. Intraclass correlation—A discussion and demonstration of basic features. PLoS ONE 2019, 14, e0219854. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Hutson, A.D. A robust Spearman correlation coefficient permutation test. Commun. Stat.-Theory Methods 2024, 53, 2141–2153. [Google Scholar] [CrossRef] [PubMed]
- Bier, G.; Bier, S.; Bongers, M.N.; Othman, A.; Ernemann, U.; Hempel, J.-M. Value of computed tomography texture analysis for prediction of perioperative complications during laparoscopic partial nephrectomy in patients with renal cell carcinoma. PLoS ONE 2018, 13, e0195270. [Google Scholar] [CrossRef] [PubMed]
- van Lummel, R.C.; Walgaard, S.; Hobert, M.A.; Maetzler, W.; van Dieën, J.H.; Galindo-Garre, F.; Terwee, C.B. Intra-Rater, Inter-Rater and Test-Retest Reliability of an Instrumented Timed Up and Go (iTUG) Test in Patients with Parkinson’s Disease. PLoS ONE 2016, 11, e0151881. [Google Scholar] [CrossRef] [PubMed]
| Distribution | n | F-Test | Fisher’s Z Test | Permute | Stu Permute |
|---|---|---|---|---|---|
| MVN | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 | |||||
| Exp | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 | |||||
| Circular | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 | |||||
| t4.1 | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 | |||||
| MVT | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 | |||||
| MVNX_1 | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 | |||||
| MVNX_3 | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 | |||||
| MVNX_6 | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 | |||||
| MVNX_9 | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 | |||||
| MVN4_5 | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 | |||||
| SQNORM | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 | |||||
| ABSNORM | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 | |||||
| BINORM | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 | |||||
| UNIF | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| 200 |
| N | F Test | Fisher’s Z Test | Permute | Stu Permute | |
|---|---|---|---|---|---|
| 0.2 | 10 | 0.131 | 0.103 | 0.127 | 0.121 |
| 25 | 0.268 | 0.237 | 0.257 | 0.250 | |
| 50 | 0.375 | 0.399 | 0.373 | 0.360 | |
| 100 | 0.651 | 0.636 | 0.655 | 0.637 | |
| 200 | 0.884 | 0.880 | 0.883 | 0.877 | |
| 0.4 | 10 | 0.342 | 0.271 | 0.327 | 0.256 |
| 25 | 0.654 | 0.643 | 0.651 | 0.601 | |
| 50 | 0.915 | 0.894 | 0.911 | 0.897 | |
| 100 | 0.993 | 0.994 | 0.994 | 0.991 | |
| 200 | >0.999 | >0.999 | >0.999 | >0.999 | |
| 0.6 | 10 | 0.655 | 0.561 | 0.626 | 0.454 |
| 25 | 0.953 | 0.959 | 0.946 | 0.922 | |
| 50 | 0.997 | 0.999 | 0.999 | 0.997 | |
| 100 | >0.999 | >0.999 | >0.999 | >0.999 | |
| 200 | >0.999 | >0.999 | >0.999 | >0.999 |
| Variable | F Test | Fish’s Z Test | Permute | Stu Permute |
|---|---|---|---|---|
| Tumor volume | <0.001 | <0.001 | <0.001 | 0.012 |
| Tumor longaxis | <0.001 | <0.001 | <0.001 | <0.001 |
| Tumor shortaxis | <0.001 | <0.001 | <0.001 | <0.001 |
| Tumor attenuation | <0.001 | <0.001 | <0.001 | <0.001 |
| Tumor attenuation SD | <0.001 | <0.001 | <0.001 | <0.001 |
| Tumor skewness | <0.001 | <0.001 | <0.001 | <0.001 |
| Tumor kurtosis | <0.001 | <0.001 | <0.001 | <0.001 |
| Tumor entropy | <0.001 | <0.001 | <0.001 | <0.001 |
| Tumor uniformity | <0.001 | <0.001 | <0.001 | 0.004 |
| Tumor MPP | <0.001 | <0.001 | <0.001 | <0.001 |
| Tumor UPP | 0.175 | 0.175 | 0.070 | 0.024 |
| Kidney attenuation | <0.001 | <0.001 | <0.001 | <0.001 |
| Kidney attenuation SD | <0.001 | <0.001 | <0.001 | <0.001 |
| Kidney skewness | 0.036 | 0.037 | 0.046 | 0.066 |
| Kidney kurtosis | 0.365 | 0.364 | 0.316 | 0.350 |
| Kidney entropy | 0.458 | 0.458 | 0.252 | <0.001 |
| Kidney uniformity | 0.309 | 0.313 | 0.048 | 0.006 |
| Kidney MPP | <0.001 | <0.001 | <0.001 | <0.001 |
| Kidney UPP | 0.061 | 0.064 | 0.042 | <0.001 |
| Day | Durations | F Test | Fisher’s Z Test | Permute | Stu Permute |
|---|---|---|---|---|---|
| 1 | iTUG | 0.156 | 0.160 | 0.080 | 0.002 |
| TUG | <0.001 | <0.001 | <0.001 | <0.001 | |
| SitSt | 0.002 | 0.004 | 0.004 | 0.002 | |
| SitSt Flex | <0.001 | <0.001 | <0.001 | 0.034 | |
| SitSt Ext | 0.038 | 0.045 | 0.026 | 0.096 | |
| StSit | <0.001 | <0.001 | <0.001 | 0.002 | |
| StSit Flex | <0.001 | <0.001 | <0.001 | 0.002 | |
| StSit Ext | <0.001 | <0.001 | <0.001 | 0.002 | |
| 2 | iTUG | <0.001 | <0.001 | <0.001 | <0.001 |
| TUG | <0.001 | <0.001 | <0.001 | <0.001 | |
| SitSt | 0.004 | 0.003 | 0.004 | 0.056 | |
| SitSt Flex | 0.284 | 0.289 | 0.252 | 0.228 | |
| SitSt Ext | 0.001 | 0.001 | 0.004 | 0.096 | |
| StSit | <0.001 | <0.001 | <0.001 | <0.001 | |
| StSit Flex | <0.001 | <0.001 | <0.001 | <0.001 | |
| StSit Ext | <0.001 | <0.001 | <0.001 | 0.008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, M.; Hutson, A.D.; Yu, H. Robust Permutation Test of Intraclass Correlation Coefficient for Assessing Agreement. Cancers 2025, 17, 2713. https://doi.org/10.3390/cancers17162713
Fang M, Hutson AD, Yu H. Robust Permutation Test of Intraclass Correlation Coefficient for Assessing Agreement. Cancers. 2025; 17(16):2713. https://doi.org/10.3390/cancers17162713
Chicago/Turabian StyleFang, Mengyu, Alan David Hutson, and Han Yu. 2025. "Robust Permutation Test of Intraclass Correlation Coefficient for Assessing Agreement" Cancers 17, no. 16: 2713. https://doi.org/10.3390/cancers17162713
APA StyleFang, M., Hutson, A. D., & Yu, H. (2025). Robust Permutation Test of Intraclass Correlation Coefficient for Assessing Agreement. Cancers, 17(16), 2713. https://doi.org/10.3390/cancers17162713







