Label Distribution Learning for Automatic Cancer Grading of Histopathological Images of Prostate Cancer
Abstract
:Simple Summary
Abstract
1. Introduction
| Authors | Origin of Dataset or Dataset Name | Size of Dataset | Diagnostic Performance of Systems | Comment |
|---|---|---|---|---|
| Nagpal et al. [22] |
|
|
|
|
| Arvaniti et al. [27] |
|
|
|
|
| Lucas et al. [20] |
|
|
|
|
| Bulten et al. [19] |
|
|
|
|
| Egevad et al. [18] |
|
|
|
|
| Kwak et al. [16] | National Institutes of Health. |
|
|
|
| Singhal et al. [15] |
|
|
|
|
2. Materials and Methods
2.1. Dataset
2.2. Baseline Convolutional Neural Network
2.3. Proposed CNN with LDL
2.4. Implementation Details
2.5. Evaluation of CNNs
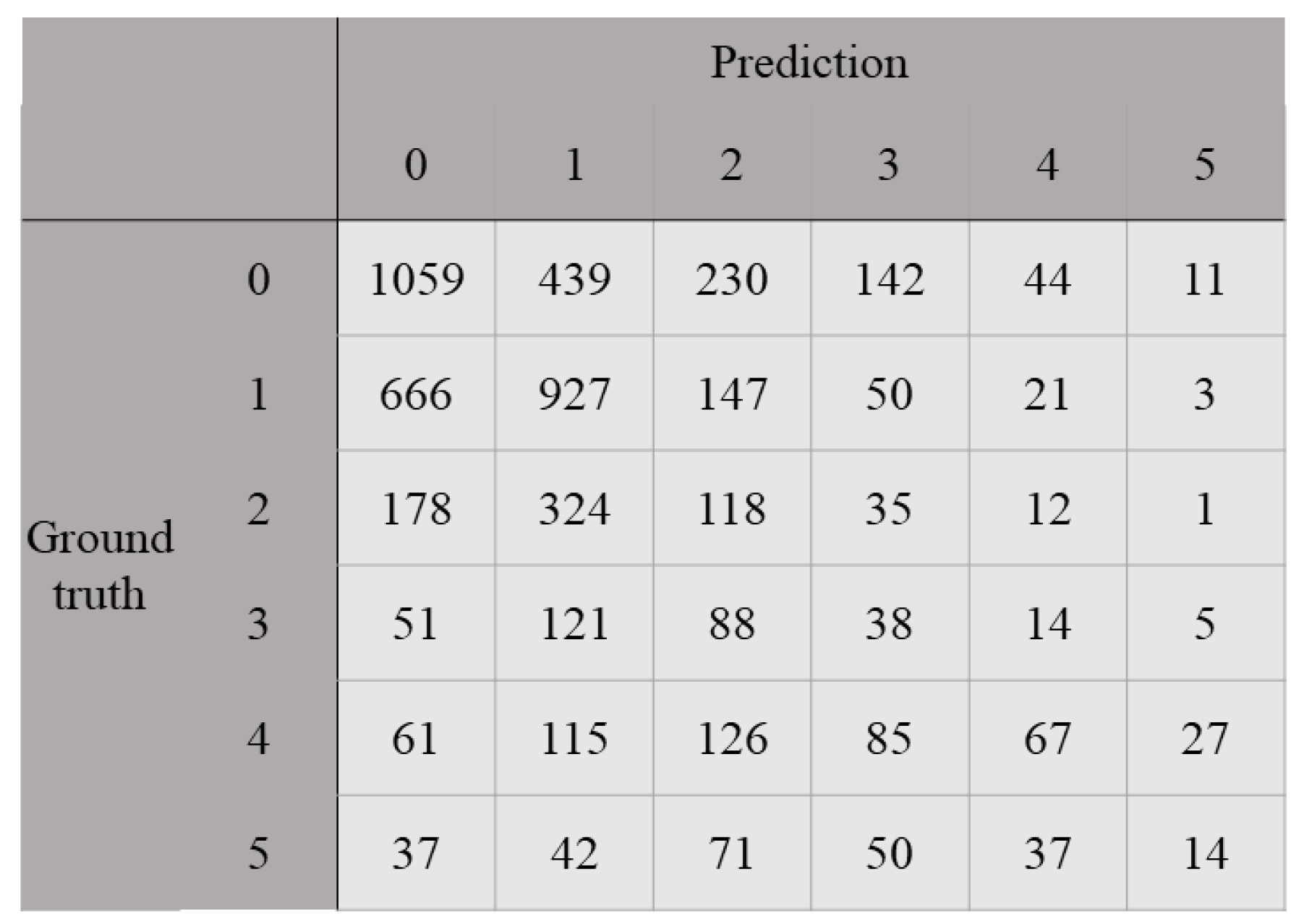
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Siegel, R.L.; Miller, K.D.; Fuchs, H.E.; Jemal, A. Cancer statistics, 2022. CA Cancer J. Clin. 2022, 72, 7–33. [Google Scholar] [CrossRef] [PubMed]
- Gleason, D.F. Histologic grading of prostate cancer: A perspective. Hum. Pathol. 1992, 23, 273–279. [Google Scholar] [CrossRef] [PubMed]
- Epstein, J.I.; Egevad, L.; Amin, M.B.; Delahunt, B.; Srigley, J.R.; Humphrey, P.A. The 2014 international society of urological pathology (ISUP) consensus conference on gleason grading of prostatic carcinoma definition of grading patterns and proposal for a new grading system. Am. J. Surg. Pathol. 2016, 40, 244–252. [Google Scholar] [CrossRef]
- Ozkan, T.A.; Eruyar, A.T.; Cebeci, O.O.; Memik, O.; Ozcan, L.; Kuskonmaz, I. Interobserver variability in Gleason histological grading of prostate cancer. Scand. J. Urol. 2016, 50, 420–424. [Google Scholar] [CrossRef]
- Allsbrook, W.C.; Mangold, K.A.; Johnson, M.H.; Lane, R.B.; Lane, C.G.; Epstein, J.I. Interobserver reproducibility of Gleason grading of prostatic carcinoma: General pathologist. Hum. Pathol. 2001, 32, 81–88. [Google Scholar] [CrossRef]
- Di Loreto, C.; Fitzpatrick, B.; Underhill, S.; Kim, D.H.; Dytch, H.E.; Galera-Davidson, H.; Bibbo, M. Correlation Between Visual Clues, Objective Architectural Features, and Interobserver Agreement in Prostate Cancer. Am. J. Clin. Pathol. 1991, 96, 70–75. [Google Scholar] [CrossRef]
- Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional neural networks: An overview and application in radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [CrossRef]
- Moribata, Y.; Kurata, Y.; Nishio, M.; Kido, A.; Otani, S.; Himoto, Y.; Nishio, N.; Furuta, A.; Onishi, H.; Masui, K.; et al. Automatic segmentation of bladder cancer on MRI using a convolutional neural network and reproducibility of radiomics features: A two-center study. Sci. Rep. 2023, 13, 628. [Google Scholar] [CrossRef]
- Noguchi, S.; Nishio, M.; Sakamoto, R.; Yakami, M.; Fujimoto, K.; Emoto, Y.; Kubo, T.; Iizuka, Y.; Nakagomi, K.; Miyasa, K.; et al. Deep learning-based algorithm improved radiologists’ performance in bone metastases detection on CT. Eur. Radiol. 2022, 32, 7976–7987. [Google Scholar] [CrossRef]
- Matsuo, H.; Nishio, M.; Kanda, T.; Kojita, Y.; Kono, A.K.; Hori, M.; Teshima, M.; Otsuki, N.; Nibu, K.-i; Murakami, T. Diagnostic accuracy of deep-learning with anomaly detection for a small amount of imbalanced data: Discriminating malignant parotid tumors in MRI. Sci. Rep. 2020, 10, 19388. [Google Scholar] [CrossRef]
- Steiner, D.F.; Macdonald, R.; Liu, Y.; Truszkowski, P.; Hipp, J.D.; Gammage, C.; Thng, F.; Peng, L.; Stumpe, M.C. Impact of Deep Learning Assistance on the Histopathologic Review of Lymph Nodes for Metastatic Breast Cancer. Am. J. Surg. Pathol. 2018, 42, 1636–1646. [Google Scholar] [CrossRef] [PubMed]
- Woerl, A.C.; Eckstein, M.; Geiger, J.; Wagner, D.C.; Daher, T.; Stenzel, P.; Fernandez, A.; Hartmann, A.; Wand, M.; Roth, W.; et al. Deep Learning Predicts Molecular Subtype of Muscle-invasive Bladder Cancer from Conventional Histopathological Slides. Eur. Urol. 2020, 78, 256–264. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.W.; Tafe, L.J.; Linnik, Y.A.; Vaickus, L.J.; Tomita, N.; Hassanpour, S. Pathologist-level classification of histologic patterns on resected lung adenocarcinoma slides with deep neural networks. Sci. Rep. 2019, 9, 3358. [Google Scholar] [CrossRef]
- Bulten, W.; Kartasalo, K.; Chen, P.H.C.; Ström, P.; Pinckaers, H.; Nagpal, K.; Cai, Y.; Steiner, D.F.; van Boven, H.; Vink, R.; et al. Artificial intelligence for diagnosis and Gleason grading of prostate cancer: The PANDA challenge. Nat. Med. 2022, 28, 154–163. [Google Scholar] [CrossRef]
- Singhal, N.; Soni, S.; Bonthu, S.; Chattopadhyay, N.; Samanta, P.; Joshi, U.; Jojera, A.; Chharchhodawala, T.; Agarwal, A.; Desai, M.; et al. A deep learning system for prostate cancer diagnosis and grading in whole slide images of core needle biopsies. Sci. Rep. 2022, 12, 3383. [Google Scholar] [CrossRef]
- Kwak, J.T.; Hewitt, S.M. Nuclear Architecture Analysis of Prostate Cancer via Convolutional Neural Networks. IEEE Access 2017, 5, 18526–18533. [Google Scholar] [CrossRef]
- Ren, J.; Sadimin, E.; Foran, D.J.; Qi, X. Computer aided analysis of prostate histopathology images to support a refined Gleason grading system. In Proceedings of the Medical Imaging 2017, Image Processing, SPIE, Orlando, FL, USA, 24 February 2017; p. 101331V. [Google Scholar] [CrossRef]
- Egevad, L.; Swanberg, D.; Delahunt, B.; Ström, P.; Kartasalo, K.; Olsson, H.; Berney, D.M.; Bostwick, D.G.; Evans, A.J.; Humphrey, P.A.; et al. Identification of areas of grading difficulties in prostate cancer and comparison with artificial intelligence assisted grading. Virchows Arch. 2020, 477, 777–786. [Google Scholar] [CrossRef]
- Bulten, W.; Pinckaers, H.; van Boven, H.; Vink, R.; de Bel, T.; van Ginneken, B.; van der Laak, J.; Hulsbergen-van de Kaa, C.; Litjens, G. Automated deep-learning system for Gleason grading of prostate cancer using biopsies: A diagnostic study. Lancet Oncol. 2020, 21, 233–241. [Google Scholar] [CrossRef]
- Lucas, M.; Jansen, I.; Savci-Heijink, C.D.; Meijer, S.L.; de Boer, O.J.; van Leeuwen, T.G.; de Bruin, D.M.; Marquering, H.A. Deep learning for automatic Gleason pattern classification for grade group determination of prostate biopsies. Virchows Arch. 2019, 475, 77–83. [Google Scholar] [CrossRef]
- Jiménez del Toro, O.; Atzori, M.; Otálora, S.; Andersson, M.; Eurén, K.; Hedlund, M.; Rönnquist, P.; Müller, H. Convolutional neural networks for an automatic classification of prostate tissue slides with high-grade Gleason score. In Proceedings of the Medical Imaging 2017, Digital Pathology, SPIE, Orlando, FL, USA, 1 March 2017; p. 101400O. [Google Scholar] [CrossRef]
- Nagpal, K.; Foote, D.; Liu, Y.; Chen, P.H.C.; Wulczyn, E.; Tan, F.; Olson, N.; Smith, J.L.; Mohtashamian, A.; Wren, J.H.; et al. Development and validation of a deep learning algorithm for improving Gleason scoring of prostate cancer. NPJ Digit. Med. 2019, 2, 48. [Google Scholar] [CrossRef]
- Linkon, A.H.M.; Labib, M.M.; Hasan, T.; Hossain, M.; Jannat, M.E. Deep Learning in Prostate Cancer Diagnosis and Gleason Grading in Histopathology Images: An Extensive Study. Informatics in Medicine Unlocked; Elsevier: Amsterdam, The Netherlands, 2021; p. 100582. [Google Scholar] [CrossRef]
- Geng, X.; Yin, C.; Zhou, Z.H. Facial age estimation by learning from label distributions. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2401–2412. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; He, B.; Ou, Y.; Li, B.; Wang, K. Topic-based label distribution learning to exploit label ambiguity for scene classification. Neural Comput. Appl. 2021, 33, 16181–16196. [Google Scholar] [CrossRef]
- Wu, X.; Wen, N.; Liang, J.; Lai, Y.K.; She, D.; Cheng, M.M.; Yang, J. Joint acne image grading and counting via label distribution learning. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October 2019–2 November 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; pp. 10641–10650. [Google Scholar] [CrossRef]
- Arvaniti, E.; Fricker, K.S.; Moret, M.; Rupp, N.; Hermanns, T.; Fankhauser, C.; Wey, N.; Wild, P.J.; Rüschoff, J.H.; Claassen, M. Automated Gleason grading of prostate cancer tissue microarrays via deep learning. Sci. Rep. 2018, 8, 12054. [Google Scholar] [CrossRef] [PubMed]
- Bulten, W.; Litjens, G.; Pinckaers, H.; Ström, P.; Eklund, M.; Kartasalo, K.; Demkin, M.; Dane, S. The PANDA challenge: Prostate cANcer graDe Assessment using the Gleason grading system. In Proceedings of the 23rd International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 2020), Lima, Peru, 19 March 2020. [Google Scholar] [CrossRef]
- Prostate cANcer graDe Assessment (PANDA) Challenge | Kaggle. Available online: https://www.kaggle.com/c/prostate-cancer-grade-assessment (accessed on 6 January 2023).
- GitHub—Kentaroy47/Kaggle-PANDA-1st-Place-Solution: 1st Place Solution for the Kaggle PANDA Challenge. Available online: https://github.com/kentaroy47/Kaggle-PANDA-1st-place-solution (accessed on 6 January 2023).
- RistKaggleWorkshop_20200924_PANDA_1st—Google Slide. Available online: https://docs.google.com/presentation/d/1Ies4vnyVtW5U3XNDr_fom43ZJDIodu1SV6DSK8di6fs/edit#slide=id.p (accessed on 6 January 2023).
- Tan, M.; Le, Q.V. EfficientNet: Rethinking model scaling for convolutional neural networks. In Proceedings of the 36th International Conference of Machine Learning PMLR 2019, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 10691–10700. [Google Scholar]
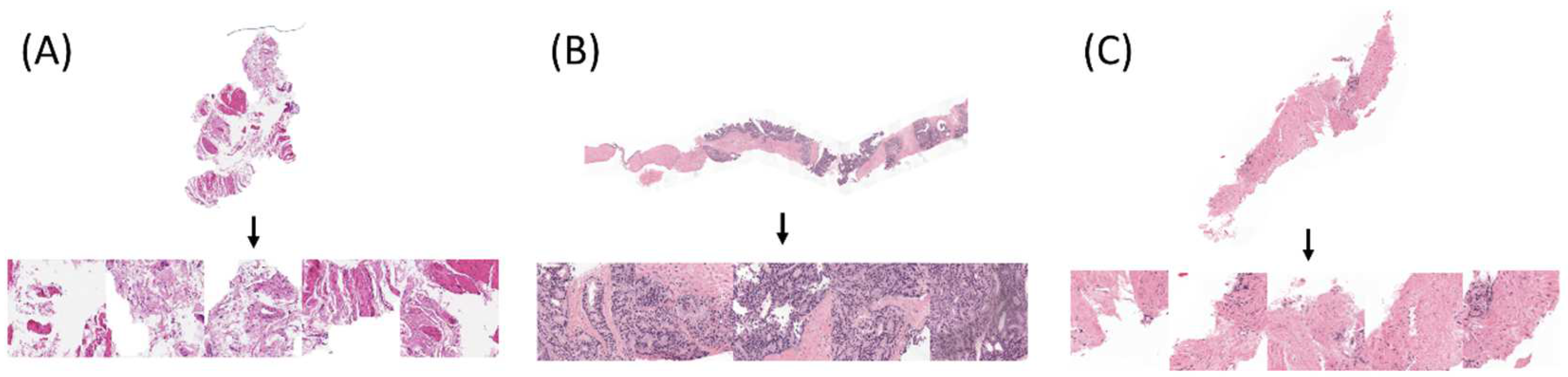
| KERRYPNX | Radboud University Medical Center | Karolinska Institute |
|---|---|---|
| Number of WSIs | N = 5160 | N = 5456 |
| Frequency of ISUP scores | ISUP score 0, N = 967 | ISUP score 0, N = 1925 |
| ISUP score 1, N = 852 | ISUP score 1, N = 1814 | |
| ISUP score 2, N = 675 | ISUP score 2, N = 668 | |
| ISUP score 3, N = 925 | ISUP score 3, N = 317 | |
| ISUP score 4, N = 768 | ISUP score 4, N = 481 | |
| ISUP score 5, N = 973 | ISUP score 5, N = 251 | |
| Annotators | trained students | a single experienced pathologist |
| Usage in this study | development set (training/validation sets) | unseen test set |
| CNN | Cross-Validated QWK | Cross-Validated Accuracy |
|---|---|---|
| Baseline CNN | 0.820 | 0.545 |
| Proposed CNN of EfficientNet B0 with LDL | 0.817 | 0.646 |
| Proposed CNN of EfficientNet B1 with LDL | 0.836 | 0.663 |
| Proposed CNN of EfficientNet B2 with LDL | 0.840 | 0.667 |
| Proposed CNN of EfficientNet B3 with LDL | 0.850 | 0.680 |
| Proposed CNN of EfficientNet B4 with LDL | 0.840 | 0.663 |
| Proposed CNN of EfficientNet B5 with LDL | 0.832 | 0.654 |
| CNN | Cross-Validated QWK | Cross-Validated Accuracy |
|---|---|---|
| Proposed CNN with LDL (D = 18) | 0.850 | 0.680 |
| Proposed CNN with LDL (D = 12) | 0.842 | 0.609 |
| Proposed CNN with LDL (D = 30) | 0.835 | 0.683 |
| Proposed CNN with LDL (D = 60) | 0.839 | 0.700 |
| CNN | QWK | Accuracy |
|---|---|---|
| Baseline CNN | 0.240 | 0.247 |
| Proposed CNN of EfficientNet B3 with LDL (D = 18) | 0.301 | 0.249 |
| Proposed CNN of EfficientNet B3 with LDL (D = 60) | 0.364 | 0.407 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nishio, M.; Matsuo, H.; Kurata, Y.; Sugiyama, O.; Fujimoto, K. Label Distribution Learning for Automatic Cancer Grading of Histopathological Images of Prostate Cancer. Cancers 2023, 15, 1535. https://doi.org/10.3390/cancers15051535
Nishio M, Matsuo H, Kurata Y, Sugiyama O, Fujimoto K. Label Distribution Learning for Automatic Cancer Grading of Histopathological Images of Prostate Cancer. Cancers. 2023; 15(5):1535. https://doi.org/10.3390/cancers15051535
Chicago/Turabian StyleNishio, Mizuho, Hidetoshi Matsuo, Yasuhisa Kurata, Osamu Sugiyama, and Koji Fujimoto. 2023. "Label Distribution Learning for Automatic Cancer Grading of Histopathological Images of Prostate Cancer" Cancers 15, no. 5: 1535. https://doi.org/10.3390/cancers15051535
APA StyleNishio, M., Matsuo, H., Kurata, Y., Sugiyama, O., & Fujimoto, K. (2023). Label Distribution Learning for Automatic Cancer Grading of Histopathological Images of Prostate Cancer. Cancers, 15(5), 1535. https://doi.org/10.3390/cancers15051535







