Early Evolution in Cancer: A Mathematical Support for Pathological and Genomic Evidence in Clear Cell Renal Cell Carcinoma
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
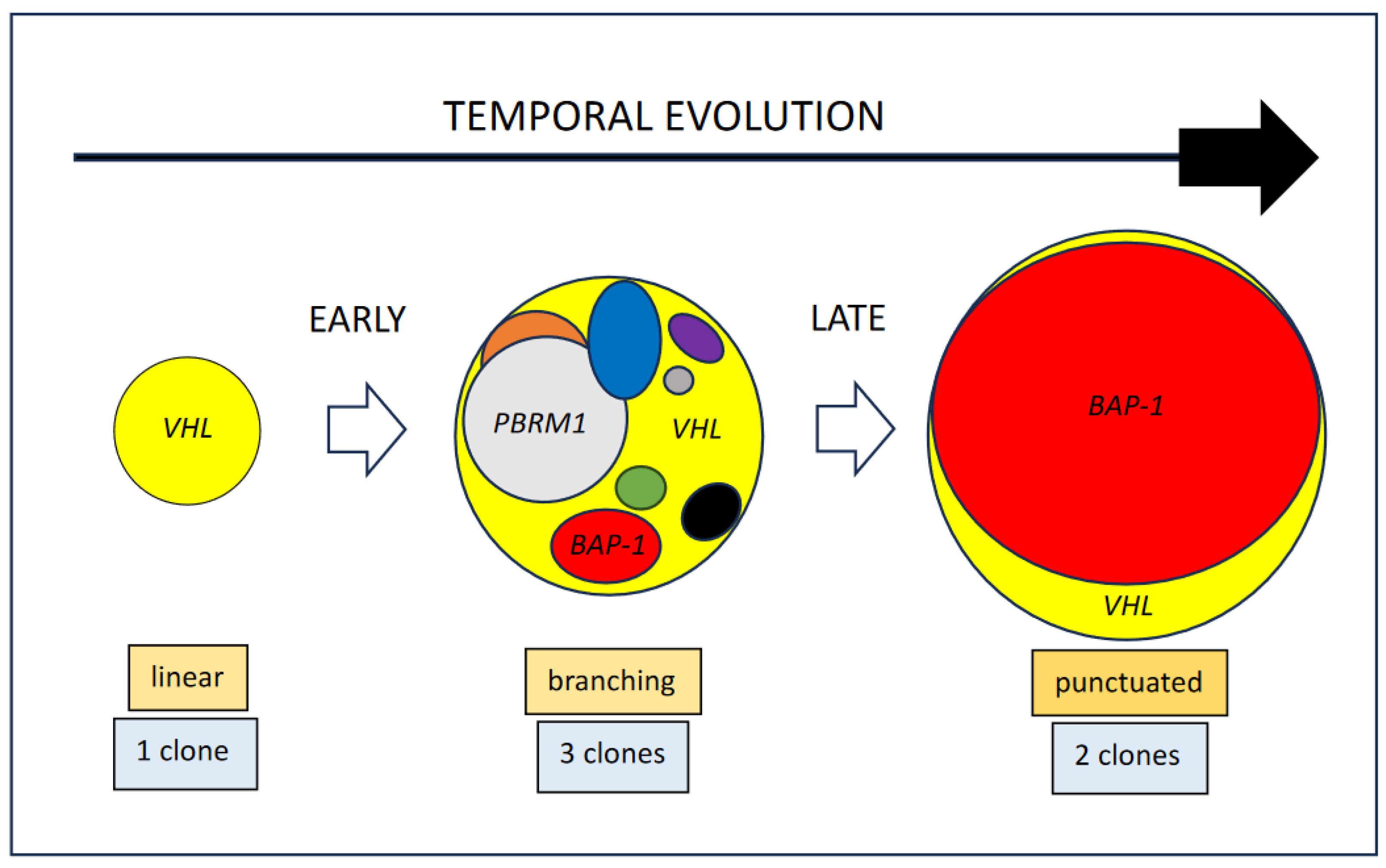
2.1. Clinical Context
2.2. The Hawk-Dove Game
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
(0,1) if zA < xA < zA +1/n
(((n − 1)v/c − n + nxA)/(nxA − 1),1) if xA > zA + 1/n,
(v/2)(1 − v/c) + (v/2c)((v(n − 1) + cn(1 − xA))/(n − 1)) if zA ≤ xA ≤ zA + 1/n
References
- Siegel, R.L.; Miller, K.D.; Wagle, N.S.; Jemal, A. Cancer statistics, 2023. CA Cancer J. Clin. 2023, 73, 17–48. [Google Scholar] [CrossRef] [PubMed]
- Trpkov, K.; Hes, O.; Williamson, S.R.; Adeniran, A.J.; Agaimy, A.; Alaghehbandan, R.; Amin, M.B.; Argani, P.; Chen, Y.B.; Cheng, L.; et al. New developments in existing WHO entities and evolving molecular concepts: The Genitourinary Pathology Society (GUPS) update on renal neoplasia. Mod. Pathol. 2021, 34, 1392–1424. [Google Scholar] [CrossRef] [PubMed]
- Turajlic, S.; Swanton, C.; Boshoff, C. Kidney cancer: The next decade. J. Exp. Med. 2018, 215, 2477–2479. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, B.A.; Oli, M.W.; Oli, M.K. Eco-oncology: Applying ecological principles to understand and manage cancer. Ecol. Evol. 2020, 10, 8538–8553. [Google Scholar] [CrossRef] [PubMed]
- Axelrod, R.; Pienta, K.J. Cancer as a social dysfunction. Why cancer research needs new thinking. Mol. Cancer Res. 2018, 16, 1346–1347. [Google Scholar] [CrossRef] [PubMed]
- Davis, A.; Gao, R.; Navin, N. Tumor evolution: Linear, branching, neutral, or punctuated? Biochim. Biophys. Acta Rev. Cancer 2017, 1867, 151–161. [Google Scholar] [CrossRef] [PubMed]
- Turajlic, S.; Xu, H.; Litchfield, K.; Rowan, A.; Horswell, S.; Chambers, T.; O’Brien, T.; Lopez, J.I.; Watkins, T.B.K.; Nicol, D.; et al. Deterministic evolutionary trajectories influence primary tumor growth: TRACERx Renal. Cell 2018, 173, 595–610. [Google Scholar] [CrossRef] [PubMed]
- Archetti, M.; Pienta, K.J. Cooperation among cancer cells: Applying game theory to cancer. Nat. Rev. Cancer 2019, 19, 110–117. [Google Scholar] [CrossRef]
- Laruelle, A.; Rocha, A.; Manini, C.; López, J.I.; Inarra, E. Effects of heterogeneity on cancer: A game theory perspective. Bull. Math. Biol. 2023, 85, 72. [Google Scholar] [CrossRef]
- Manini, C.; Laruelle, A.; Rocha, A.; López, J.I. Convergent insights into intratumor heterogeneity. Trends Cancer 2023. [Google Scholar] [CrossRef]
- Mitchell, T.J.; Turajlic, S.; Rowan, A.; Nicol, D.; Farmery, J.H.R.; O’Brien, T.; Martincorena, I.; Tarpey, P.; Angelopoulos, N.; Yates, L.R.; et al. Timing the landmark events in the evolution of clear cell renal cell cancer: TRACERx Renal. Cell 2018, 173, 611–623. [Google Scholar] [CrossRef] [PubMed]
- Bailey, C.; Black, J.R.M.; Reading, J.L.; Litchfield, K.; Turajlic, S.; McGranahan, N.; Jamal-Hanjani, M.; Swanton, C. Tracking cancer evolution through the disease course. Cancer Discov. 2021, 11, 916–932. [Google Scholar] [CrossRef]
- Maynard-Smith, J.; Price, G.R. The logic of animal conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Maruyama, T.; Fujita, Y. Cell competition in mammals. Novel homeostatic machinery for embryonic development and cancer prevention. Curr. Opin. Cell Biol. 2017, 48, 106–112. [Google Scholar] [CrossRef] [PubMed]
- Inarra, E.; Laruelle, A. Artificial distinction and real discrimination. J. Theor. Biol. 2012, 305, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Fu, X.; Lopez, J.I.; Rowan, A.; Au, L.; Fendler, A.; Hazell, S.; Xu, H.; Horswell, S.; Shepherd, S.T.C.; et al. Selection of metastasis competent subclones in the tumour interior. Nat. Ecol. Evol. 2021, 5, 1033–1045. [Google Scholar] [CrossRef]
- Manini, C.; López-Fernández, E.; Lawrie, C.H.; Laruelle, A.; Angulo, J.C.; López, J.I. Clear cell renal cell carcinomas with aggressive behavior display low intratumor heterogeneity at the histological level. Curr. Urol. Rep. 2022, 23, 93–97. [Google Scholar] [CrossRef]
- Kim, K.; Zhou, Q.; Christie, A.; Stevens, C.; Ma, Y.; Onabolu, O.; Chintalapati, S.; Mckenzie, T.; Tcheuyap, V.T.; Woolford, L.; et al. Determinants of renal cell carcinoma invasion and metastatic competence. Nat. Commun. 2021, 12, 5760. [Google Scholar] [CrossRef]
- West, J.; Adler, F.; Gallaher, J.; Strobl, M.; Brady-Nicholls, R.; Brown, J.; Roberson-Tessi, M.; Kim, E.; Noble, R.; Viossat, Y.; et al. A survey of open questions in adaptive therapy. Bridging mathematics and clinical translation. eLife 2023, 12, e84263. [Google Scholar] [CrossRef]
- Goyette, M.A.; Lipsyc-Sharf, M.; Polyak, K. Clinical and translational relevance of intratumor heterogeneity. Trends Cancer 2023, 9, 726. [Google Scholar] [CrossRef]
- Zhang, L.L.; Kan, M.; Zhang, M.M.; Yu, S.S.; Xie, H.J.; Gu, Z.H.; Wang, H.N.; Zhao, S.X.; Zhou, G.B.; Song, H.D.; et al. Multiregion sequencing reveals the intratumor heterogeneity of driver mutations in TP53-driven non-small cell lung cancer. Int. J. Cancer 2017, 140, 103–108. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Yu, T.; Zhao, X.; Gao, X.; Zhao, Y.; Liu, G. Intratumor heterogeneity: A new perspective on colorectal cancer research. Cancer Med. 2020, 9, 7637–7645. [Google Scholar] [CrossRef] [PubMed]
- Guo, M.; Peng, Y.; Gao, A.; Du, C.; Herman, J.G. Epigenetic heterogeneity in cancer. Biomark. Res. 2019, 7, 23. [Google Scholar] [CrossRef] [PubMed]
- Kikutake, C.; Yoshihara, M.; Sato, T.; Saito, D.; Suyama, M. Pan-cancer analysis of intratumor heterogeneity associated with patient prognosis using multidimensional measures. Oncotarget 2018, 9, 37689–37699. [Google Scholar] [CrossRef]
- Dong, L.Q.; Shi, Y.; Ma, L.J.; Yang, L.X.; Wang, X.Y.; Zhang, S.; Wang, Z.C.; Duan, M.; Zhang, Z.; Liu, L.Z.; et al. Spatial and temporal clonal evolution of intrahepatic cholangiocarcinoma. J. Hepatol. 2018, 69, 89–98. [Google Scholar] [CrossRef]
- Swanton, C. Intratumor heterogeneity: Evolution through space and time. Cancer Res. 2012, 72, 4875–4882. [Google Scholar] [CrossRef]
- Morris, L.G.; Riaz, N.; Desrichard, A.; Şenbabaoğlu, Y.; Hakimi, A.A.; Makarov, V.; Reis-Filho, J.S.; Chan, T.A. Pan-cancer analysis of intratumor heterogeneity as a prognostic determinant of survival. Oncotarget 2016, 7, 10051–10063. [Google Scholar] [CrossRef]
| Hawk | Dove | |
|---|---|---|
| Hawk | (v − c)/2 | v |
| Dove | 0 | v/2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laruelle, A.; Manini, C.; López, J.I.; Rocha, A. Early Evolution in Cancer: A Mathematical Support for Pathological and Genomic Evidence in Clear Cell Renal Cell Carcinoma. Cancers 2023, 15, 5897. https://doi.org/10.3390/cancers15245897
Laruelle A, Manini C, López JI, Rocha A. Early Evolution in Cancer: A Mathematical Support for Pathological and Genomic Evidence in Clear Cell Renal Cell Carcinoma. Cancers. 2023; 15(24):5897. https://doi.org/10.3390/cancers15245897
Chicago/Turabian StyleLaruelle, Annick, Claudia Manini, José I. López, and André Rocha. 2023. "Early Evolution in Cancer: A Mathematical Support for Pathological and Genomic Evidence in Clear Cell Renal Cell Carcinoma" Cancers 15, no. 24: 5897. https://doi.org/10.3390/cancers15245897
APA StyleLaruelle, A., Manini, C., López, J. I., & Rocha, A. (2023). Early Evolution in Cancer: A Mathematical Support for Pathological and Genomic Evidence in Clear Cell Renal Cell Carcinoma. Cancers, 15(24), 5897. https://doi.org/10.3390/cancers15245897








