Algorithm-Based Risk Identification in Patients with Breast Cancer-Related Lymphedema: A Cross-Sectional Study
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Alternative Clustering into Two BCRL Risk Groups
3. Results
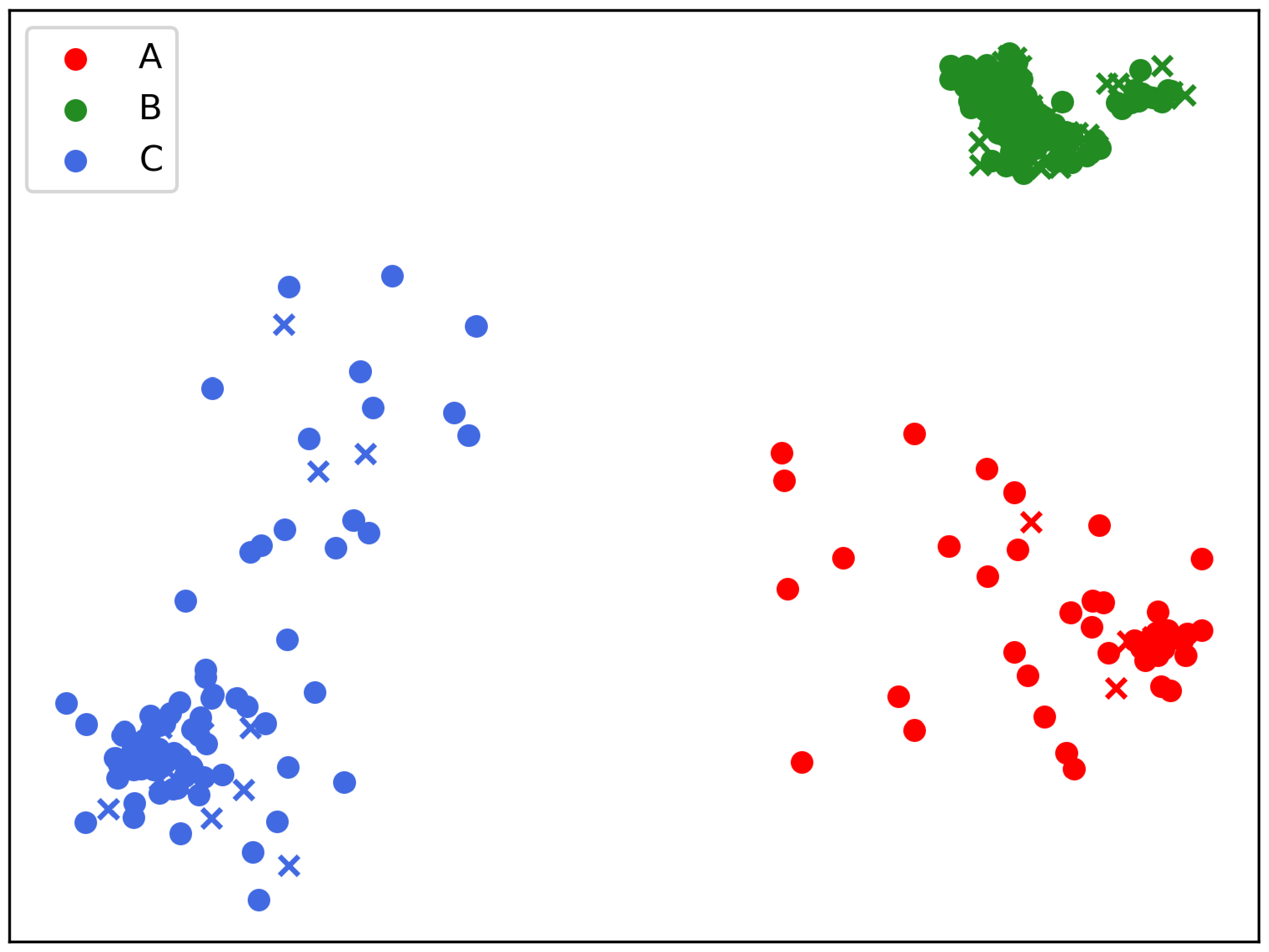
3.1. Statistics on Three Clusters (A, B, C)
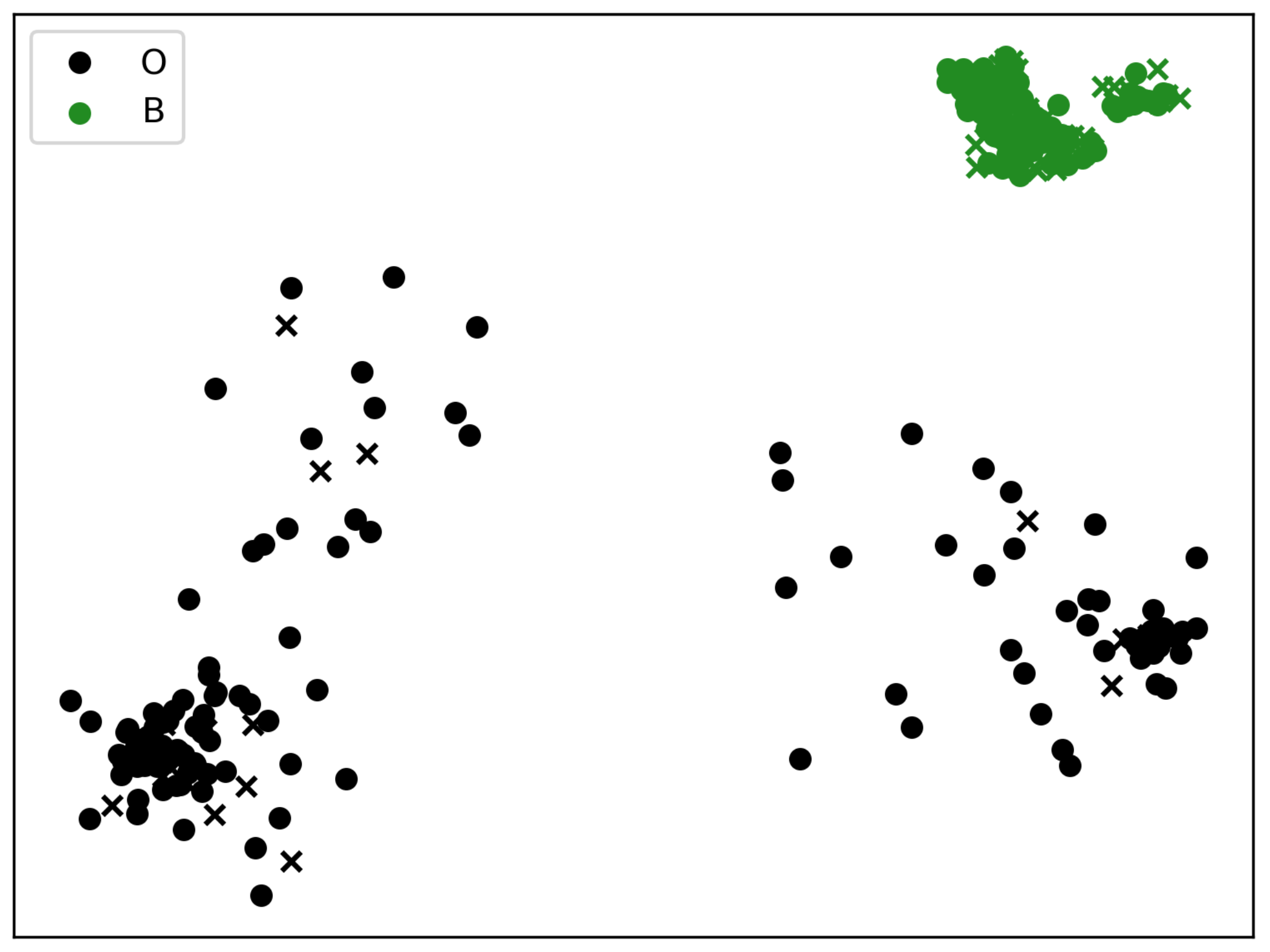
3.2. Statistics on Two Clusters (B vs. “Others”)
3.2.1. Ordinal and Categorical Variables Analysis
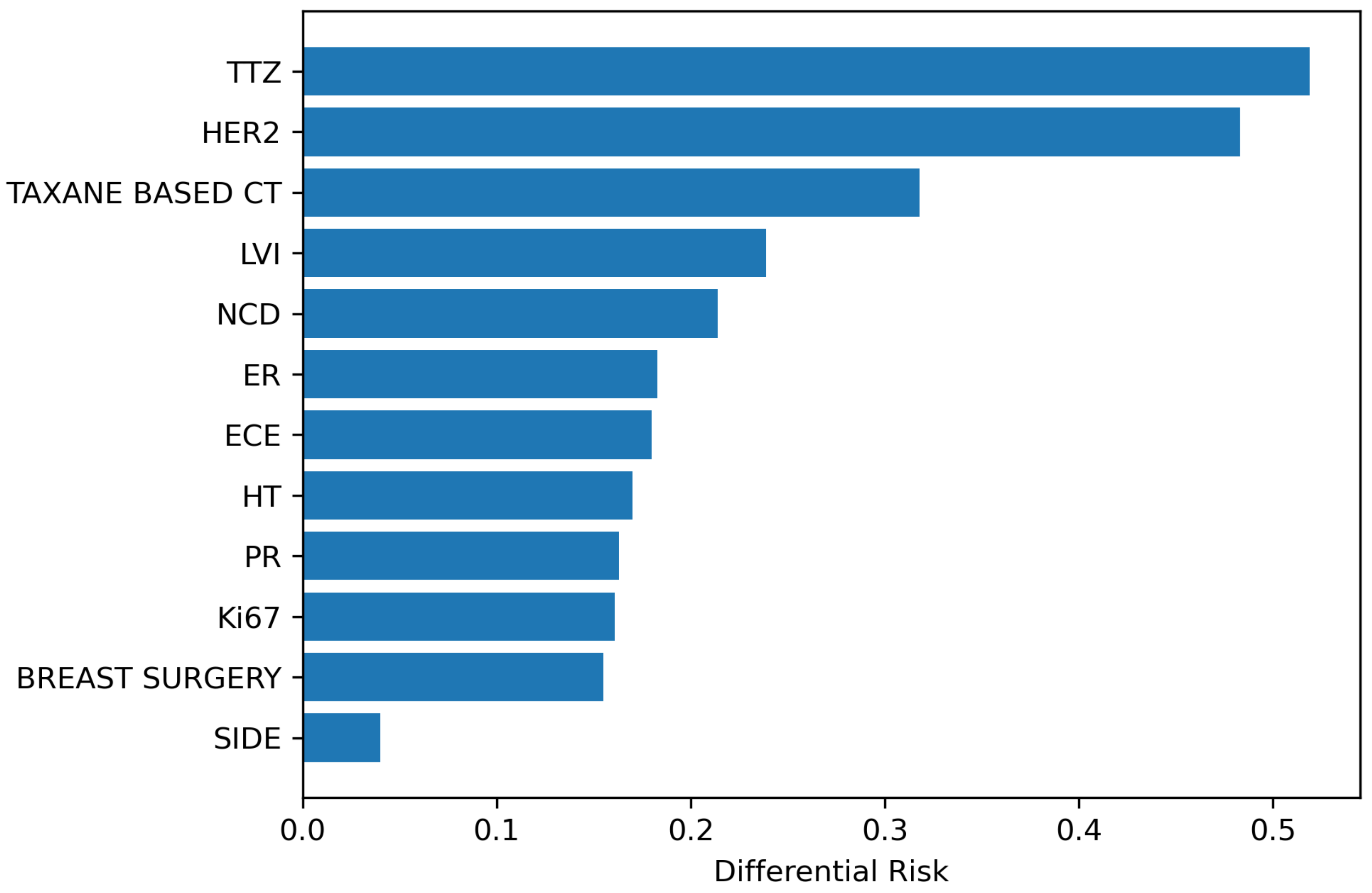
3.2.2. Binary Variables Analysis
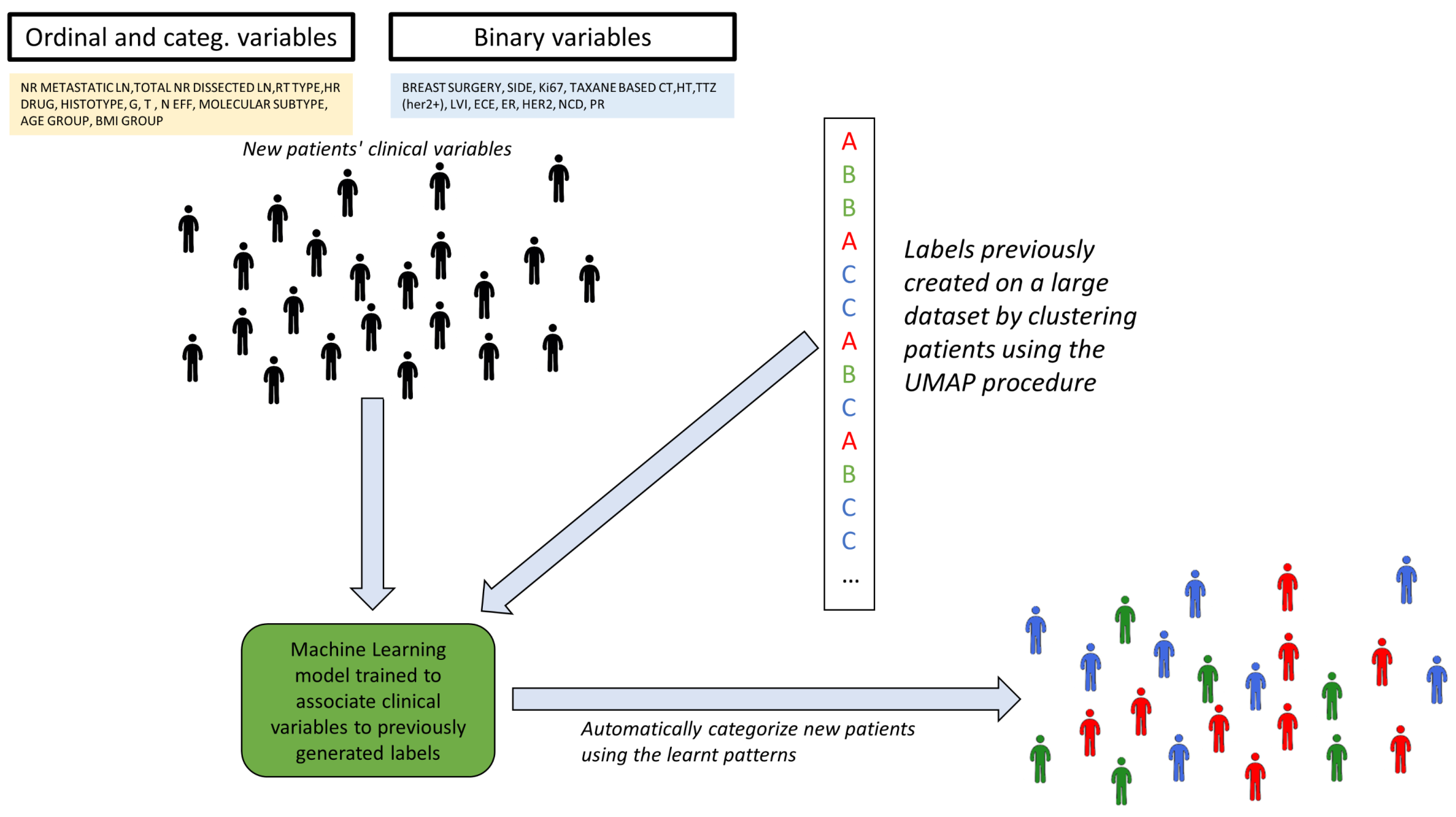
3.3. Demonstration of Automatic Patient Categorization
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABC | Adaptive Gradient Classifier |
| BA | Balanced Accuracy |
| BC | Breast Cancer |
| BCRL | Breast cancer-related lymphedema |
| CV | Cross-Validation |
| ET | Randomized decision trees |
| GMM | Gaussian mixture model |
| HR-QoL | Health-Related Quality of Life |
| LDA | Linear Discriminant Analysis |
| LR | Logistic Regression |
| MLD | Manual lymphatic drainage |
| RF | Random Forest |
| RR | Relative Risk |
| SD | Standard Deviation |
| UMAP | Uniform Manifold Approximation and Projection |
Appendix A. Characteristics of the Clinical Variables
| Variable | Mean | Median | SD | SE | Levels | Range |
|---|---|---|---|---|---|---|
| NR METASTATIC LN | 5.2959 | 2.0 | 7.2157 | 0.4208 | 33 | [0, 37] |
| TOTAL NR DISSECTED LN | 24.9626 | 24.0 | 8.6692 | 0.5056 | 42 | [2, 58] |
| RT TYPE | 1.1565 | 1.0 | 0.9997 | 0.0583 | 4 | [0, 3] |
| HR DRUG | 4.0442 | 5.0 | 2.1197 | 0.1236 | 6 | [0, 6] |
| HISTOTYPE | 1.4082 | 1.0 | 1.2652 | 0.0738 | 8 | [1, 9] |
| G | 2.3673 | 2.0 | 0.591 | 0.0345 | 3 | [1, 3] |
| T | 1.6803 | 1.0 | 0.8703 | 0.0508 | 4 | [1, 4] |
| N | 1.6054 | 1.0 | 0.8015 | 0.0467 | 3 | [1, 3] |
| MOLECULAR SUBTYPE | 1.8844 | 1.0 | 1.2143 | 0.0708 | 5 | [1, 5] |
| AGE 1 | 59.823 | 61.0 | 12.879 | 0.7511 | 56 | [26, 88] |
| BMI | 26.926 | 26.03 | 5.8085 | 0.3388 | 264 | [14.4, 57.2] |
| BREAST SURGERY | 1.4048 | 1.0 | 0.4917 | 0.0287 | 2 | [0, 1] |
| SIDE | 1.4728 | 1.0 | 0.5001 | 0.0292 | 2 | [1, 2] |
| Ki67 | 1.4184 | 1.0 | 0.4941 | 0.0288 | 2 | [1, 2] |
| TAXANE BASED CT | 0.5136 | 1.0 | 0.5007 | 0.0292 | 2 | [0, 1] |
| HT | 0.8537 | 1.0 | 0.354 | 0.0206 | 2 | [0, 1] |
| TTZ | 0.0918 | 0.0 | 0.2893 | 0.0169 | 2 | [0, 1] |
| LVI | 0.3571 | 0.0 | 0.48 | 0.028 | 2 | [0, 1] |
| ECE | 0.619 | 1.0 | 0.4864 | 0.0284 | 2 | [0, 1] |
| ER | 0.8741 | 1.0 | 0.3322 | 0.0194 | 2 | [0, 1] |
| HER2 | 0.1088 | 0.0 | 0.312 | 0.0182 | 2 | [0, 1] |
| NCD | 0.6565 | 1.0 | 0.4757 | 0.0277 | 2 | [0, 1] |
| PR | 0.7925 | 1.0 | 0.4062 | 0.0237 | 2 | [0, 1] |
Appendix B. Binary Variables Cross-Tables
| BREAST SURGERY | BCRL (Unaffected) | BCRL (Affected) |
|---|---|---|
| 1 | 128 | 47 |
| 2 | 96 | 23 |
| SIDE | BCRL (Unaffected) | BCRL (Affected) |
|---|---|---|
| 1 | 109 | 46 |
| 2 | 115 | 24 |
| TAXANE BASED CT | BCRL (Unaffected) | BCRL (Affected) |
|---|---|---|
| 0 | 121 | 22 |
| 1 | 103 | 48 |
| HT | BCRL (Unaffected) | BCRL (Affected) |
|---|---|---|
| 0 | 29 | 14 |
| 1 | 195 | 56 |
| LVI | BCRL (Unaffected) | BCRL (Affected) |
|---|---|---|
| 0 | 153 | 36 |
| 1 | 71 | 34 |
| ECE | BCRL (Unaffected) | BCRL (Affected) |
|---|---|---|
| 0 | 84 | 28 |
| 1 | 140 | 42 |
| ER | BCRL (Unaffected) | BCRL (Affected) |
|---|---|---|
| 0 | 26 | 11 |
| 1 | 198 | 59 |
| HER2 | BCRL (Unaffected) | BCRL (Affected) |
|---|---|---|
| 0 | 206 | 56 |
| 1 | 18 | 14 |
| NCD | BCRL (Unaffected) | BCRL (Affected) |
|---|---|---|
| 0 | 75 | 26 |
| 1 | 149 | 44 |
| PR | BCRL (Unaffected) | BCRL (Affected) |
|---|---|---|
| 0 | 40 | 21 |
| 1 | 184 | 49 |
| TTZ | BCRL (Unaffected) | BCRL (Affected) |
|---|---|---|
| 0 | 211 | 56 |
| 1 | 13 | 14 |
| Ki67 | BCRL (Unaffected) | BCRL (Affected) |
|---|---|---|
| 1 | 137 | 34 |
| 2 | 87 | 36 |
Appendix C. Additional Tables for the Three Clusters Categorization
| Cluster A | Cluster C | Cluster B | |
|---|---|---|---|
| BCRL |
Appendix D. Additional Tables for the Two Clusters Categorization
| Variable | Cluster | Test Type | p |
|---|---|---|---|
| SIDE | B | test | 0.0022 |
| TTZ | B | test | 0.0279 |
| LVI | B | test | 0.0628 |
| HER2 | B | test | 0.0636 |
Appendix E. Future Developments
References
- Nardin, S.; Mora, E.; Varughese, F.M.; D’Avanzo, F.; Vachanaram, A.R.; Rossi, V.; Saggia, C.; Rubinelli, S.; Gennari, A. Breast cancer survivorship, quality of life, and late toxicities. Front. Oncol. 2020, 10, 864. [Google Scholar] [CrossRef] [PubMed]
- D’egidio, V.; Sestili, C.; Mancino, M.; Sciarra, I.; Cocchiara, R.; Backhaus, I.; Mannocci, A.; De Luca, A.; Frusone, F.; Monti, M.; et al. Counseling interventions delivered in women with breast cancer to improve health-related quality of life: A systematic review. Qual. Life Res. 2017, 26, 2573–2592. [Google Scholar] [CrossRef] [PubMed]
- de Sire, A.; Losco, L.; Cisari, C.; Gennari, A.; Boldorini, R.; Fusco, N.; Cigna, E.; Invernizzi, M. Axillary web syndrome in women after breast cancer surgery referred to an Oncological Rehabilitation Unit: Which are the main risk factors? A retrospective case-control study. Eur. Rev. Med. Pharmacol. Sci. 2020, 24, 8028–8035. [Google Scholar] [PubMed]
- Lippi, L.; de Sire, A.; Losco, L.; Mezian, K.; Folli, A.; Ivanova, M.; Zattoni, L.; Moalli, S.; Ammendolia, A.; Alfano, C.; et al. Axillary Web Syndrome in Breast Cancer Women: What Is the Optimal Rehabilitation Strategy after Surgery? A Systematic Review. J. Clin. Med. 2022, 11, 3839. [Google Scholar] [CrossRef] [PubMed]
- Park, S.B.; Tamburin, S.; Schenone, A.; Kleckner, I.R.; Velasco, R.; Alberti, P.; Kanzawa-Lee, G.; Lustberg, M.; Dorsey, S.G.; Mantovani, E.; et al. Optimal outcome measures for assessing exercise and rehabilitation approaches in chemotherapy-induced peripheral-neurotoxicity: Systematic review and consensus expert opinion. Expert Rev. Neurother. 2022, 22, 65–76. [Google Scholar] [CrossRef] [PubMed]
- Lippi, L.; de Sire, A.; Folli, A.; Maconi, A.; Polverelli, M.; Vecchio, C.; Fusco, N.; Invernizzi, M. Effects of ultrasound-guided injection combined with a targeted therapeutic exercise in breast cancer women with subacromial pain syndrome: A randomized clinical study. J. Pers. Med. 2022, 12, 1833. [Google Scholar] [CrossRef]
- de Sire, A.; Losco, L.; Lippi, L.; Spadoni, D.; Kaciulyte, J.; Sert, G.; Ciamarra, P.; Marcasciano, M.; Cuomo, R.; Bolletta, A.; et al. Surgical treatment and rehabilitation strategies for upper and lower extremity lymphedema: A comprehensive review. Medicina 2022, 58, 954. [Google Scholar] [CrossRef]
- de Sire, A.; Invernizzi, M.; Lippi, L.; Cisari, C.; Özçakar, L.; Franchignoni, F. Blurred lines between axillary web syndrome and Mondor’s disease after breast cancer surgery: A case report. Ann. Phys. Rehabil. Med. 2020, 63, 365–367. [Google Scholar] [CrossRef]
- Yang, S.; Chu, S.; Gao, Y.; Ai, Q.; Liu, Y.; Li, X.; Chen, N. A narrative review of cancer-related fatigue (CRF) and its possible pathogenesis. Cells 2019, 8, 738. [Google Scholar] [CrossRef]
- Invernizzi, M.; Corti, C.; Lopez, G.; Michelotti, A.; Despini, L.; Gambini, D.; Lorenzini, D.; Guerini-Rocco, E.; Maggi, S.; Noale, M.; et al. Lymphovascular invasion and extranodal tumour extension are risk indicators of breast cancer related lymphoedema: An observational retrospective study with long-term follow-up. BMC Cancer 2018, 18, 935. [Google Scholar] [CrossRef]
- Hill, W.F.; Deban, M.; Platt, A.; Rojas-Garcia, P.; Jost, E.; Temple-Oberle, C. Immediate Lymphatic Reconstruction during Axillary Node Dissection for Breast Cancer: A Systematic Review and Meta-analysis. Plast. Reconstr. Surg. Glob. Open 2022, 10, e4291. [Google Scholar] [CrossRef]
- Asdourian, M.S.; Skolny, M.N.; Brunelle, C.; Seward, C.E.; Salama, L.; Taghian, A.G. Precautions for breast cancer-related lymphoedema: Risk from air travel, ipsilateral arm blood pressure measurements, skin puncture, extreme temperatures, and cellulitis. Lancet Oncol. 2016, 17, e392–e405. [Google Scholar] [CrossRef]
- Shaitelman, S.F.; Chiang, Y.J.; Griffin, K.D.; DeSnyder, S.M.; Smith, B.D.; Schaverien, M.V.; Woodward, W.A.; Cormier, J.N. Radiation therapy targets and the risk of breast cancer-related lymphedema: A systematic review and network meta-analysis. Breast Cancer Res. Treat. 2017, 162, 201–215. [Google Scholar] [CrossRef]
- Vicini, F.; Shah, C.; Arthur, D. The Increasing Role of Lymphedema Screening, Diagnosis and Management as Part of Evidence-Based Guidelines for Breast Cancer Care. Breast J. 2016, 3, 358–359. [Google Scholar] [CrossRef]
- Sayegh, H.E.; Asdourian, M.S.; Swaroop, M.N.; Brunelle, C.L.; Skolny, M.N.; Salama, L.; Taghian, A.G. Diagnostic methods, risk factors, prevention, and management of breast cancer-related lymphedema: Past, present, and future directions. Curr. Breast Cancer Rep. 2017, 9, 111–121. [Google Scholar] [CrossRef]
- Erickson, V.S.; Pearson, M.L.; Ganz, P.A.; Adams, J.; Kahn, K.L. Arm edema in breast cancer patients. J. Natl. Cancer Inst. 2001, 93, 96–111. [Google Scholar] [CrossRef]
- Ahmed, H.S. Biochemical Changes Related with Temporomandibular Joint Disorders and Inflammatory Arthritis. Biomed. Pharmacol. J. 2017, 10, 2085–2090. [Google Scholar] [CrossRef]
- Slaghmuylder, Y.; Pype, P.; Van Hecke, A.; Lauwerier, E. Development of an intervention aimed at the prevention and treatment of chronic pain in breast cancer survivors: An intervention mapping approach. Pat. Edu. Couns. 2022, 108, 107618. [Google Scholar] [CrossRef]
- International Society of Lymphology. The diagnosis and treatment of peripheral lymphedema: 2013 Consensus Document of the International Society of Lymphology. Lymphology 2013, 46, 1–11. [Google Scholar]
- Executive Committee. The diagnosis and treatment of peripheral lymphedema: 2016 consensus document of the International Society of Lymphology. Lymphology 2016, 49, 170–184. [Google Scholar]
- Witte, M.; Bernas, M. Evolution of the 2020 international society of lymphology consensus document parallels advances in lymphology: An historical perspective. Lymphology 2020, 53, 1–2. [Google Scholar] [PubMed]
- O’Donnell, T.F., Jr.; Allison, G.M.; Iafrati, M.D. A systematic review of guidelines for lymphedema and the need for contemporary intersocietal guidelines for the management of lymphedema. J. Vasc. Surg. Venous Lymphat. Disord. 2020, 8, 676–684. [Google Scholar] [CrossRef] [PubMed]
- Runowicz, C.D.; Leach, C.R.; Henry, N.L.; Henry, K.S.; Mackey, H.T.; Cowens-Alvarado, R.L.; Cannady, R.S.; Pratt-Chapman, M.L.; Edge, S.B.; Jacobs, L.A.; et al. American cancer society/American society of clinical oncology breast cancer survivorship care guideline. CA Cancer J. Clin. 2016, 66, 43–73. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, F.; Costa, A.; Senkus, E.; Aapro, M.; André, F.; Barrios, C.; Bergh, J.; Bhattacharyya, G.; Biganzoli, L.; Cardoso, M.; et al. 3rd ESO–ESMO international consensus guidelines for advanced breast cancer (ABC 3). Breast 2017, 31, 244–259. [Google Scholar] [CrossRef] [PubMed]
- Invernizzi, M.; Kim, J.; Fusco, N. Quality of life in breast cancer patients and survivors. Front. Oncol. 2020, 10, 620574. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Yang, Y.; Zhang, X.; Li, W.; Li, H.; Mu, D. Manual lymphatic drainage for breast cancer-related lymphedema: A systematic review and meta-analysis of randomized controlled trials. Clin. Breast Cancer 2022, 22, e664–e673. [Google Scholar] [CrossRef]
- Hayes, S.C.; Singh, B.; Reul-Hirche, H.; Bloomquist, K.; Johansson, K.; Jönsson, C.; Plinsinga, M.L. The Effect of Exercise for the Prevention and Treatment of Cancer-related Lymphedema: A Systematic Review with Meta-analysis. Med. Sci. Sport. Exerc. 2022, 54, 1389–1399. [Google Scholar] [CrossRef]
- Ferrillo, M.; Migliario, M.; Marotta, N.; Lippi, L.; Antonelli, A.; Calafiore, D.; Ammendolia, V.; Fortunato, L.; Renò, F.; Giudice, A.; et al. Oral health in breast cancer women with vitamin D deficiency: A machine learning study. J. Clin. Med. 2022, 11, 4662. [Google Scholar] [CrossRef]
- Fu, M.R.; Wang, Y.; Li, C.; Qiu, Z.; Axelrod, D.; Guth, A.A.; Scagliola, J.; Conley, Y.; Aouizerat, B.E.; Qiu, J.M.; et al. Machine learning for detection of lymphedema among breast cancer survivors. Mhealth 2018, 4, 17. [Google Scholar] [CrossRef]
- Wei, X.; Lu, Q.; Jin, S.; Li, F.; Zhao, Q.; Cui, Y.; Jin, S.; Cao, Y.; Fu, M.R. Developing and validating a prediction model for lymphedema detection in breast cancer survivors. Eur. J. Oncol. Nurs. 2021, 54, 102023. [Google Scholar] [CrossRef]
- Gianfrancesco, M.A.; Tamang, S.; Yazdany, J.; Schmajuk, G. Potential biases in machine learning algorithms using electronic health record data. JAMA Intern. Med. 2018, 178, 1544–1547. [Google Scholar] [CrossRef]
- Moreau, J.T.; Baillet, S.; Dudley, R.W. Biased intelligence: On the subjectivity of digital objectivity. BMJ Health Care Inform. 2020, 27, e100146. [Google Scholar] [CrossRef]
- Gillespie, T.C.; Sayegh, H.E.; Brunelle, C.L.; Daniell, K.M.; Taghian, A.G. Breast cancer-related lymphedema: Risk factors, precautionary measures, and treatments. Gland. Surg. 2018, 7, 379. [Google Scholar] [CrossRef]
- Sarker, I.H. Deep learning: A comprehensive overview on techniques, taxonomy, applications and research directions. SN Comput. Sci. 2021, 2, 420. [Google Scholar] [CrossRef]
- Palla, K.; Knowles, D.A.; Ghahramani, Z. Relational learning and network modelling using infinite latent attribute models. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 37, 462–474. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Diaz-Papkovich, A.; Anderson-Trocmé, L.; Gravel, S. A review of UMAP in population genetics. J. Hum. Genet. 2021, 66, 85–91. [Google Scholar] [CrossRef]
- Dorrity, M.W.; Saunders, L.M.; Queitsch, C.; Fields, S.; Trapnell, C. Dimensionality reduction by UMAP to visualize physical and genetic interactions. Nat. Commun. 2020, 11, 1537. [Google Scholar] [CrossRef]
- Hozumi, Y.; Wang, R.; Yin, C.; Wei, G.W. UMAP-assisted K-means clustering of large-scale SARS-CoV-2 mutation datasets. Comput. Biol. Med. 2021, 131, 104264. [Google Scholar] [CrossRef]
- Allaoui, M.; Kherfi, M.L.; Cheriet, A. Considerably improving clustering algorithms using UMAP dimensionality reduction technique: A comparative study. In Proceedings of the International Conference on Image and Signal Processing, Marrakech, Morocco, 4–6 June 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 317–325. [Google Scholar]
- Nascimben, M.; Rimondini, L.; Corà, D.; Venturin, M. Polygenic risk modeling of tumor stage and survival in bladder cancer. BioData Min. 2022, 15, 23. [Google Scholar] [CrossRef]
- Reynolds, D.A. Gaussian mixture models. Encyclopedia of biometrics 2009, 741, 659–663. [Google Scholar]
- DiSipio, T.; Rye, S.; Newman, B.; Hayes, S. Incidence of unilateral arm lymphoedema after breast cancer: A systematic review and meta-analysis. Lancet Oncol. 2013, 14, 500–515. [Google Scholar] [CrossRef] [PubMed]
- Press, S.J.; Wilson, S. Choosing between logistic regression and discriminant analysis. J. Am. Stat. Assoc. 1978, 73, 699–705. [Google Scholar] [CrossRef]
- Piramuthu, S. Input data for decision trees. Expert Syst. Appl. 2008, 34, 1220–1226. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Askari, A.; d’Aspremont, A.; El Ghaoui, L. Naive feature selection: Sparsity in naive bayes. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Online, 26–28 August 2020; pp. 1813–1822. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Grollemund, V.; Chat, G.L.; Secchi-Buhour, M.S.; Delbot, F.; Pradat-Peyre, J.F.; Bede, P.; Pradat, P.F. Development and validation of a 1-year survival prognosis estimation model for Amyotrophic Lateral Sclerosis using manifold learning algorithm UMAP. Sci. Rep. 2020, 10, 13378. [Google Scholar] [CrossRef]
- Invernizzi, M.; Michelotti, A.; Noale, M.; Lopez, G.; Runza, L.; Giroda, M.; Despini, L.; Blundo, C.; Maggi, S.; Gambini, D.; et al. Breast cancer systemic treatments and upper limb lymphedema: A risk-assessment platform encompassing tumor-specific pathological features reveals the potential role of trastuzumab. J. Clin. Med. 2019, 8, 138. [Google Scholar] [CrossRef]
- Soran, A.; D’Angelo, G.; Begovic, M.; Ardic, F.; Harlak, A.; Samuel Wieand, H.; Vogel, V.G.; Johnson, R.R. Breast cancer-related lymphedema–what are the significant predictors and how they affect the severity of lymphedema? Breast J. 2006, 12, 536–543. [Google Scholar] [CrossRef]
- Jammallo, L.S.; Miller, C.L.; Singer, M.; Horick, N.K.; Skolny, M.N.; Specht, M.C.; O’Toole, J.; Taghian, A.G. Impact of body mass index and weight fluctuation on lymphedema risk in patients treated for breast cancer. Breast Cancer Res. Treat. 2013, 142, 59–67. [Google Scholar] [CrossRef]
- Helyer, L.K.; Varnic, M.; Le, L.W.; Leong, W.; McCready, D. Obesity is a risk factor for developing postoperative lymphedema in breast cancer patients. Breast J. 2010, 16, 48–54. [Google Scholar] [CrossRef]
- Morfoisse, F.; Tatin, F.; Chaput, B.; Therville, N.; Vaysse, C.; Métivier, R.; Malloizel-Delaunay, J.; Pujol, F.; Godet, A.C.; De Toni, F.; et al. Lymphatic vasculature requires estrogen receptor-α signaling to protect from lymphedema. Arterioscler. Thromb. Vasc. Biol. 2018, 38, 1346–1357. [Google Scholar] [CrossRef]
- De Vrieze, T.; Gebruers, N.; Nevelsteen, I.; Tjalma, W.A.; Thomis, S.; De Groef, A.; Dams, L.; Van der Gucht, E.; Devoogdt, N. Physical activity level and age contribute to functioning problems in patients with breast cancer-related lymphedema: A multicentre cross-sectional study. Support. Care Cancer 2020, 28, 5717–5731. [Google Scholar] [CrossRef]
- Park, J.E.; Jang, H.J.; Seo, K.S. Quality of life, upper extremity function and the effect of lymphedema treatment in breast cancer related lymphedema patients. Ann. Rehabil. Med. 2012, 36, 240–247. [Google Scholar] [CrossRef]
- Tsauo, J.Y.; Hung, H.C.; Tsai, H.J.; Huang, C.S. Can ICF model for patients with breast-cancer-related lymphedema predict quality of life? Support. Care Cancer 2011, 19, 599–604. [Google Scholar] [CrossRef]
- Saleh, H.A.; Rageh, T.M.; Alhassanin, S.A.; Megahed, M.A. Upper limb lymphedema related to breast cancer therapy: Incidence, risk factors, diagnostic techniques, risk reduction and optimal management. Int. Surg. J. 2018, 5, 3633–3639. [Google Scholar] [CrossRef]
- Pinto, M.; Gimigliano, F.; Tatangelo, F.; Megna, M.; Izzo, F.; Gimigliano, R.; Iolascon, G. Upper limb function and quality of life in breast cancer related lymphedema: A cross-sectional study. Eur. J. Phys. Rehabil. Med. 2013, 49, 665–673. [Google Scholar]
- Pereira, A.C.P.R.; Koifman, R.J.; Bergmann, A. Incidence and risk factors of lymphedema after breast cancer treatment: 10 years of follow-up. Breast 2017, 36, 67–73. [Google Scholar] [CrossRef]
- Ahmed, R.L.; Schmitz, K.H.; Prizment, A.E.; Folsom, A.R. Risk factors for lymphedema in breast cancer survivors, the Iowa Women’s Health Study. Breast Cancer Res. Treat. 2011, 130, 981–991. [Google Scholar] [CrossRef]
- Hayes, S.; Sipio, T.D.; Rye, S.; López, J.A.; Saunders, C.; Pyke, C.; Bashford, J.; Battistutta, D.; Newman, B. Prevalence and prognostic significance of secondary lymphedema following breast cancer. Lymphat. Res. Biol. 2011, 9, 135–141. [Google Scholar] [CrossRef]
- Invernizzi, M.; Runza, L.; de Sire, A.; Lippi, L.; Blundo, C.; Gambini, D.; Boldorini, R.; Ferrero, S.; Fusco, N. Integrating augmented reality tools in breast cancer related lymphedema prognostication and diagnosis. JoVE J. Vis. Exp. 2020, 156, e60093. [Google Scholar] [CrossRef] [PubMed]
- Alfano, C.M.; Zucker, D.S.; Pergolotti, M.; Ness, K.K.; Jones, L.W.; Price, N.D.; Schmitz, K.H.; Ligibel, J.A. A precision medicine approach to improve cancer rehabilitation’s impact and integration with cancer care and optimize patient wellness. Curr. Phys. Med. Rehabil. Rep. 2017, 5, 64–73. [Google Scholar] [CrossRef]
- Korpan, M.I.; Crevenna, R.; Fialka-Moser, V. Lymphedema: A therapeutic approach in the treatment and rehabilitation of cancer patients. Am. J. Phys. Med. Rehabil. 2011, 90, S69–S75. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, D.V.; Pereira, E.M.; Cardoso, J.S. Machine learning interpretability: A survey on methods and metrics. Electronics 2019, 8, 832. [Google Scholar] [CrossRef]
- Kocak, Z.; Overgaard, J. Risk factors of arm lymphedema in breast cancer patients. Acta Oncol. 2000, 39, 389–392. [Google Scholar]
- McLaughlin, S.A.; Brunelle, C.L.; Taghian, A. Breast Cancer-Related Lymphedema: Risk Factors, Screening, Management, and the Impact of Locoregional Treatment. J. Clin. Oncol. Off. J. Am. Soc. Clin. Oncol. 2020, 38, 2341–2350. [Google Scholar] [CrossRef]
- Ugur, S.; Arıcı, C.; Yaprak, M.; Mescı, A.; Arıcı, G.A.; Dolay, K.; Ozmen, V. Risk factors of breast cancer-related lymphedema. Lymphat. Res. Biol. 2013, 11, 72–75. [Google Scholar] [CrossRef]
- Warren, L.E.; Miller, C.L.; Horick, N.; Skolny, M.N.; Jammallo, L.S.; Sadek, B.T.; Shenouda, M.N.; O’Toole, J.A.; MacDonald, S.M.; Specht, M.C.; et al. The impact of radiation therapy on the risk of lymphedema after treatment for breast cancer: A prospective cohort study. Int. J. Radiat. Oncol. Biol. Phys. 2014, 88, 565–571. [Google Scholar] [CrossRef]
- Kwan, M.L.; Darbinian, J.; Schmitz, K.H.; Citron, R.; Partee, P.; Kutner, S.E.; Kushi, L.H. Risk factors for lymphedema in a prospective breast cancer survivorship study: The Pathways Study. Arch. Surg. 2010, 145, 1055–1063. [Google Scholar] [CrossRef]


| Variable | Type | Description |
|---|---|---|
| NR METASTATIC LN | Ord. | Number of metastatic lymph nodes |
| TOTAL NR DISSECTED LN | Ord. | Number of dissected lymph nodes |
| RT TYPE | Cat. | Types of radiation therapy (breast, supraclavicular fossa, chest wall) |
| HR DRUG | Cat. | Type of estrogen therapy before breast cancer |
| HISTOTYPE | Cat. | Characterization of lymph node histology |
| G | Ord. | Breast cancer grading |
| T | Ord. | TNM staging system: size or direct extent of the primary tumor |
| N | Ord. | TNM staging system: degree of spread to regional lymph nodes |
| MOLECULAR SUBTYPE | Cat. | Luminal A, Luminal B, ERBB2/HER2-amplified or Triple-negative |
| AGE | Cont. | Age of the patient at diagnosis |
| BMI | Cont. | Body Index Mass |
| BREAST SURGERY | Bin. | Type of breast surgery (quadrantectomy, mastectomy) |
| SIDE | Bin. | Side of breast cancer |
| Ki67 | Bin. | Ki67 expression (low or high ) |
| TAXANE BASED CT | Bin. | Underwent the Taxane-based Chemotherapy |
| HT | Bin. | Hormone therapy |
| TTZ | Bin. | Trastuzumab therapy |
| LVI | Bin. | Presence of Lymphovascular invasion |
| ECE | Bin. | Presence of Extracapsular Extension |
| ER | Bin. | Estrogen receptors |
| HER2 | Bin. | Human Epidermal Growth Factor Receptor 2 |
| NCD | Bin. | Presence of comorbidities |
| PR | Bin. | Progesterone receptor |
| Variable | Num of Neighbors | Learning Rate | Minimal Distance | Spread | Metric |
|---|---|---|---|---|---|
| Ordinal | 44 | 0.0005 | 0.2 | 1.5 | Canberra |
| Binary | 38 | 0.5 | 0.99 | 3 | Correlation |
| Patients | Percentages % | |||||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | Margin | A | B | C | Margin | |
| Absence of BCRL | 41 | 106 | 77 | 224 | 13.94 | 36.05 | 26.19 | 76.19 |
| Presence of BCRL | 4 | 50 | 16 | 70 | 1.36 | 17.0 | 5.44 | 23.80 |
| Margin Total | 45 | 156 | 93 | 294 | 15.3 | 53.0 | 31.63 | 100 |
| Cluster A | Cluster C | Cluster B | Margin Total | |
|---|---|---|---|---|
| Presence of BCRL | 4 | 16 | 50 | 70 |
| Absence of BCRL | 41 | 77 | 106 | 224 |
| Margin Total | 45 | 93 | 156 | 294 |
| Patients | Percentages % | |||||
|---|---|---|---|---|---|---|
| O | B | Margin | O | B | Margin | |
| Absence of BCRL | 118 | 106 | 224 | 40.13 | 36.05 | 76.19 |
| Presence of BCRL | 20 | 50 | 70 | 6.8 | 17.0 | 23.80 |
| Margin Total | 138 | 156 | 294 | 46.93 | 53.06 | 100 |
| Cluster A | Cluster C | Cluster B | |
|---|---|---|---|
| Joint Probability of BCRL among all patients | |||
| Conditional Probability that a patient has BCRL | |||
| given the patient belongs to cluster A, B, or C | |||
| Conditional Probability that a patient suffering | |||
| BCRL belongs to cluster A, B, or C |
| Variable | Clusters B vs. O | Clusters B vs. O |
|---|---|---|
| Patients without BCRL | Patients with BCRL | |
| NR METASTATIC LN | *** | *** |
| TOTAL NR DISSECTED LN | - | - |
| G | *** | ** |
| T | * | - |
| N | *** | * |
| AGE GROUP | *** | *** |
| BMI GROUP | - | * |
| Presence of BCRL | Absence of BCRL | |||
|---|---|---|---|---|
| Variable | Cluster O | Cluster B | Cluster O | Cluster B |
| RT TYPE | 1 | 1 | 1 | 1 |
| HR DRUG | 6 | 0 | 6 | 0 |
| HISTOTYPE | 1 | 1 | 1 | 1 |
| MOLECULAR SUBTYPE | 1 | 1 | 1 | 1 |
| Variable | Cluster B Risk | Cluster O Risk | Absolute Risk Diff. |
|---|---|---|---|
| BREAST SURGERY | 0.257 | 0.102 | 0.155 |
| SIDE | 0.192 | 0.152 | 0.040 |
| Ki67 | 0.337 | 0.176 | 0.161 |
| TAXANE BASED CT | 0.318 | 0 | 0.318 |
| HT | 0.316 | 0.146 | 0.17 |
| TTZ | 0.519 | 0 | 0.519 |
| LVI | 0.406 | 0.167 | 0.239 |
| ECE | 0.303 | 0.123 | 0.18 |
| ER | 0.328 | 0.145 | 0.183 |
| HER2 | 0.483 | 0 | 0.483 |
| NCD | 0.354 | 0.14 | 0.214 |
| PR | 0.301 | 0.138 | 0.163 |
| Two Clusters (B, O) | Three Clusters (A, B, C) | |||
|---|---|---|---|---|
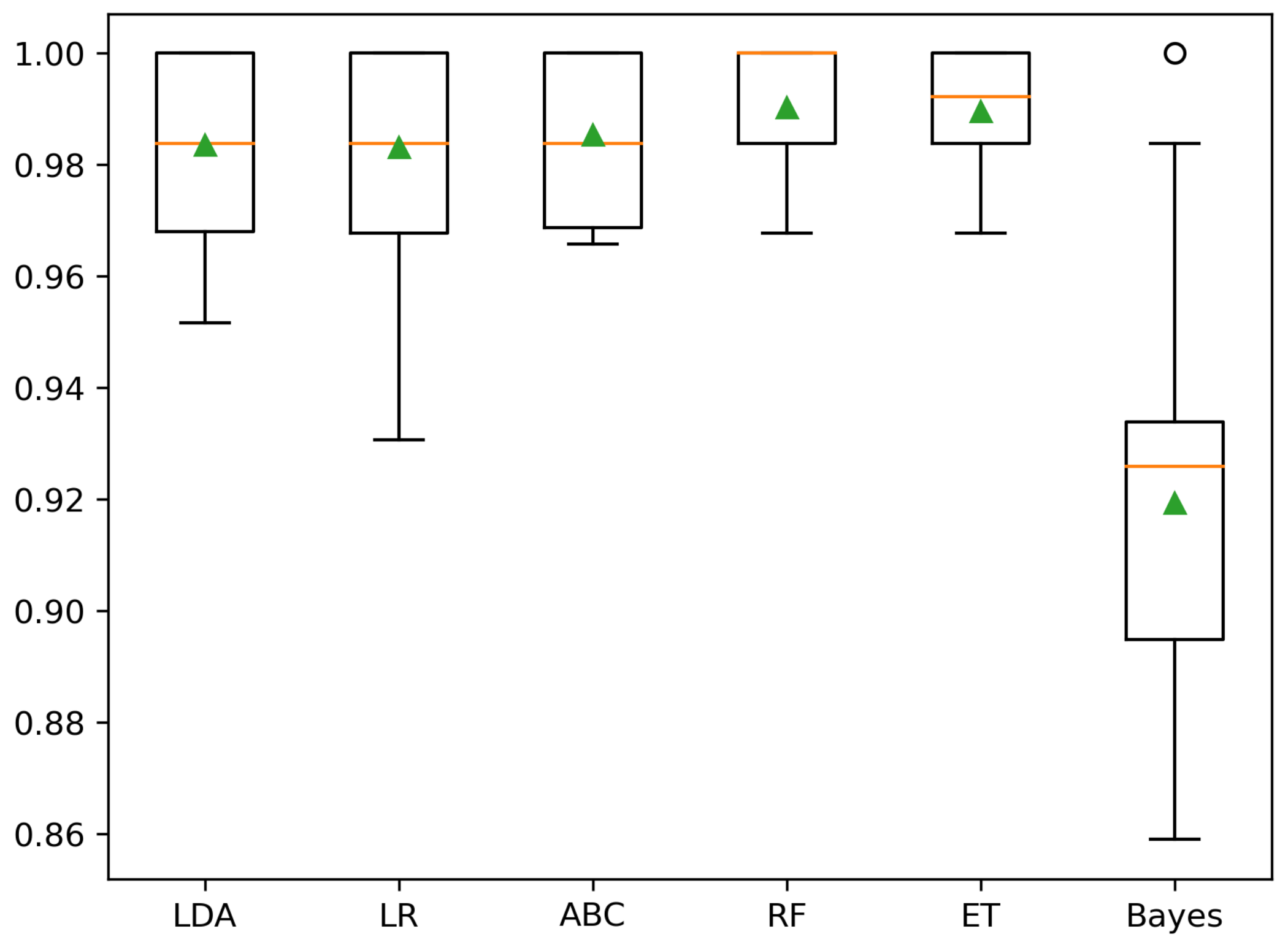
| Classifier | Mean BA (%) | SD BA (%) | Mean BA (%) | SD BA (%) |
| Dummy | 51.3 | 32.5 | ||
| LDA | 98.4 | 95.7 | ||
| LR | 98.3 | 98.0 | ||
| ABC | 98.5 | 96.6 | ||
| RF | 99.0 | 99.4 | ||
| ET | 99.0 | 98.1 | ||
| Bayes | 91.9 | 86.1 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nascimben, M.; Lippi, L.; de Sire, A.; Invernizzi, M.; Rimondini, L. Algorithm-Based Risk Identification in Patients with Breast Cancer-Related Lymphedema: A Cross-Sectional Study. Cancers 2023, 15, 336. https://doi.org/10.3390/cancers15020336
Nascimben M, Lippi L, de Sire A, Invernizzi M, Rimondini L. Algorithm-Based Risk Identification in Patients with Breast Cancer-Related Lymphedema: A Cross-Sectional Study. Cancers. 2023; 15(2):336. https://doi.org/10.3390/cancers15020336
Chicago/Turabian StyleNascimben, Mauro, Lorenzo Lippi, Alessandro de Sire, Marco Invernizzi, and Lia Rimondini. 2023. "Algorithm-Based Risk Identification in Patients with Breast Cancer-Related Lymphedema: A Cross-Sectional Study" Cancers 15, no. 2: 336. https://doi.org/10.3390/cancers15020336
APA StyleNascimben, M., Lippi, L., de Sire, A., Invernizzi, M., & Rimondini, L. (2023). Algorithm-Based Risk Identification in Patients with Breast Cancer-Related Lymphedema: A Cross-Sectional Study. Cancers, 15(2), 336. https://doi.org/10.3390/cancers15020336










