Comparative Analysis of Three Predictive Models of Performance Indicators with Results-Based Management: Cancer Data Statistics in a National Institute of Health
Abstract
Simple Summary
Abstract
1. Introduction
1.1. Results-Based Management to Address the Problem of Improving Public Health Services
1.2. Performance Indicators and Predictive Models for Measuring Healthcare Results with RBM
1.2.1. Predictive Models for Measuring Healthcare Results
1.2.2. ARIMA Model
1.2.3. Exponential Smoothing (ES) Model
- Exponential models are surprisingly accurate.
- Formulating an exponential model is relatively easy.
- The user understands how the model works.
- Very few calculations are required to use the model.
- Computer storage requirements are low due to the limited use of historical data.
- Accuracy tests related to model performance are easy to calculate.
1.2.4. Linear Regression Model (LR)
1.3. Other Management Models for Measuring Healthcare Performance
Other Models with Statistical Methods to Measure Healthcare Results
1.4. Problem Statement
2. Materials and Methods
2.1. Design
2.2. Procedure for Measuring the Performance of Each Model
2.3. Predictive Statistical Methods Used to Measure Performance Results
2.3.1. Linear Regression
2.3.2. ARIMA
2.3.3. Stationary
2.3.4. Differencing
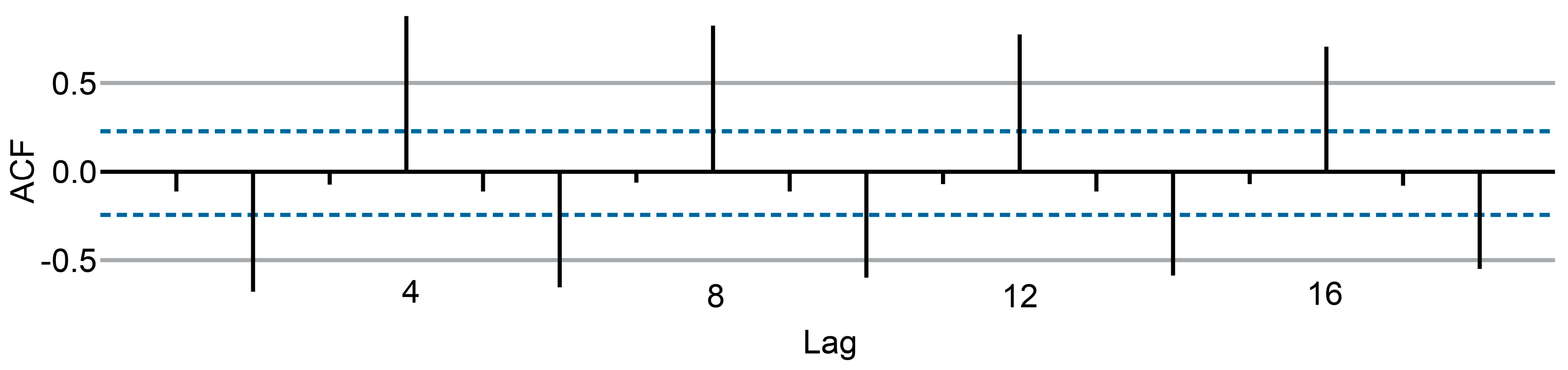
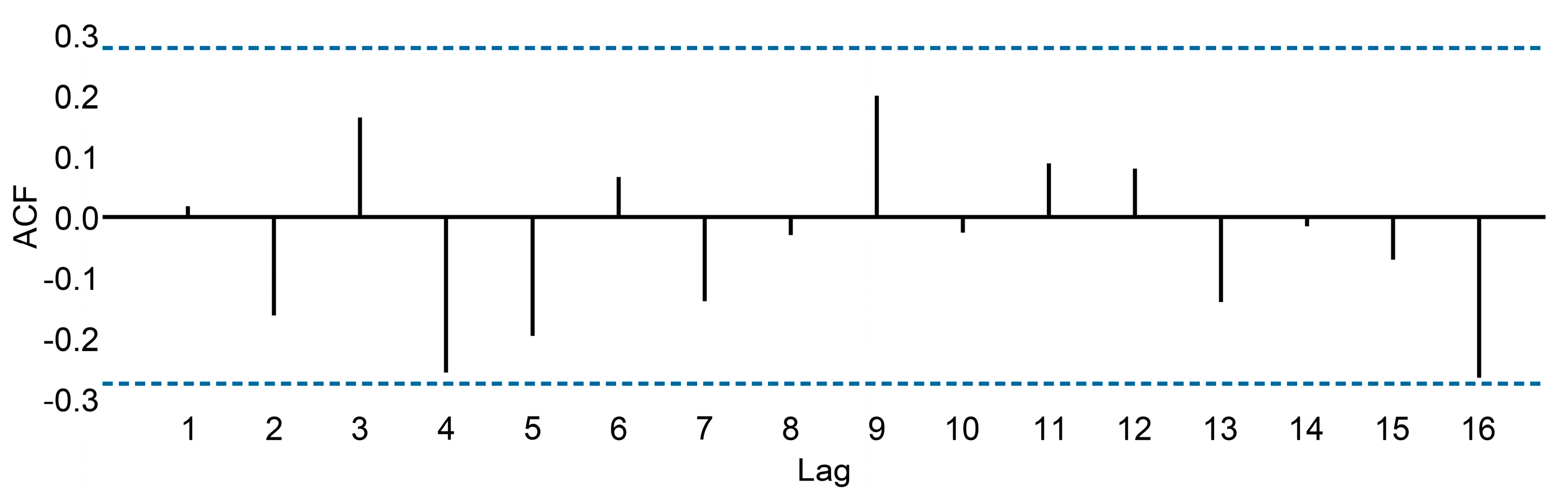
2.3.5. Autocorrelation
- r4 is higher than the values for the other lags. This is due to the seasonal pattern in the data: the peaks tend to be four quarters apart, and the troughs tend to be two quarters apart.
- r2 is more negative than the values for the other lags because troughs tend to be two quarters behind peaks.
- The dashed blue lines indicate whether the correlations are significantly different from zero.
2.3.6. White Noise
2.3.7. Autoregressive AR(p)
2.3.8. Moving Average component MA(q)
2.3.9. Exponential Smoothing
2.4. Ethical Considerations
2.5. Statistical Analysis
3. Results
3.1. Cancer Data Statistics
3.2. The Best Predictive Model That Fit the Data with the Lowest Error
3.3. Predictive Model Results
3.3.1. ARIMA
3.3.2. Linear Regression
3.3.3. Exponential Smoothing (Table 2)
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Serra, A.; Figueroa, V.; Saz, Á. Modelo Abierto de Gestión Para Resultados en el Sector Público, Banco Interamericano de Desarrollo (BID); Centro Latinoamericano de Administración para el Desarrollo: Washington, DC, USA, 2007. [Google Scholar]
- Kravariti, F.; Tasoulis, K.; Scullion, H.; Khaled, M. Talent management and performance in the public sector: The role of organisational and line managerial support for development. Int. J. Hum. Resour. Manag. 2023, 34, 1782–1807. [Google Scholar] [CrossRef]
- Dwivedi, Y.K.; Hughes, D.L.; Coombs, C.; Constantiou, I.; Duan, Y.; Edwards, J.S.; Gupta, B.; Lal, B.; Misra, S.; Prashant, P.; et al. Impact of COVID-19 pandemic on information management research and practice: Transforming education, work and life. Int. J. Inf. Manag. 2020, 55, 102211. [Google Scholar] [CrossRef]
- Star, S.; Russ-Eft, D.; Braverman, M.T.; Levine, R. Performance Measurement and Performance Indicators: A Literature Review and a Proposed Model for Practical Adoption. Hum. Resour. Dev. Rev. 2016, 15, 151–181. [Google Scholar] [CrossRef]
- Zurynski, Y.; Herkes-Deane, J.; Holt, J.; McPherson, E.; Lamprell, G.; Dammery, G.; Meulenbroeks, I.; Halim, N.; Braithwaite, J. How can the healthcare system deliver sustainable performance? A scoping review. BMJ Open 2022, 24, 12. [Google Scholar] [CrossRef]
- Diario Oficial de la Federación. Ley de Presupuesto y Responsabilidad Hacendaria; Última Reforma Publicada DOF: Mexico City, Mexico, 2006. [Google Scholar]
- Burlea-Schiopoiu, A.; Ferhati, K. The managerial implications of the key performance indicators in healthcare sector: A cluster analysis. Healthcare 2020, 9, 19. [Google Scholar] [CrossRef]
- Khalifa, M.; Khalid, P. Developing strategic health care key performance indicators: A case study on a tertiary care hospital. Procedia Comput. Sci. 2015, 63, 459–466. [Google Scholar] [CrossRef]
- Oncioiu, I.; Kandzija, V.; Petrescu, A.; Panagoreţ, I.; Petrescu, M. Managing and measuring performance in organizational development. Econ. Res.-Ekon. Istraživanja 2022, 35, 915–928. [Google Scholar] [CrossRef]
- Vázquez, M.-L.; Vargas, I.; Unger, J.-P.; De Paepe, P.; Mogollón-Pérez, A.S.; Samico, I.; Albuquerque, P.; Eguiguren, P.; Cisneros, A.I.; Rovere, M.; et al. Evaluating the effectiveness of care integration strategies in different healthcare systems in Latin America: The EQUITY-LA II quasi-experimental study protocol. BMJ Open 2015, 7, 37. [Google Scholar] [CrossRef]
- Duarte, D.; Walshaw, C.; Ramesh, N. A comparison of time-series predictions for healthcare emergency department indicators and the impact of COVID-19. Appl. Sci. 2021, 11, 3561. [Google Scholar] [CrossRef]
- Rubio, L.; Gutiérrez-Rodríguez, A.J.; Forero, M.G. EBITDA index prediction using exponential smoothing and ARIMA model. Mathematics 2021, 9, 2538. [Google Scholar] [CrossRef]
- Schaffer, A.; Dobbins, T.; Pearson, S. Interrupted time series analysis using autoregressive integrated moving average (ARIMA) models: A guide for evaluating large-scale health interventions. BMC Med. Res. Methodol. 2021, 21, 58. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Heng, B.H.; Seow, Y.T.; Seow, E. Forecasting daily attendances at an emergency department to aid resource planning. BMC Emerg. Med. 2009, 9, 1. [Google Scholar] [CrossRef] [PubMed]
- Afilal, M.; Yalaoui, F.; Dugardin, F.; Amodeo, L.; Laplanche, D.; Blua, P. Forecasting the emergency department patients flow. J. Med. Syst. 2016, 40, 175. [Google Scholar] [CrossRef] [PubMed]
- Milner, P.C. Ten-year follow-up of ARIMA forecasts of attendances at accident and emergency departments in the trent region. Stat. Med. 1997, 16, 2117–2125. [Google Scholar] [CrossRef]
- De Livera, A.; Hyndman, R.; Snyder, R. Forecasting Time Series with Complex Seasonal Patterns Using Exponential Smoothing. J. Am. Stat. Assoc. 2011, 106, 1513–1527. [Google Scholar] [CrossRef]
- Williams, B.M.; Durvasula, P.K.; Brown, D.E. Urban freeway traffic flow prediction: Application of seasonal autoregressive integrated moving average and exponential smoothing models. Transp. Res. Rec. 1998, 1644, 132–141. [Google Scholar] [CrossRef]
- Kotillova, A.; Koprinska, I. Statistical and Machine Learning Methods for Electricity Demand Prediction in Neural Information Processing; Springer: Berlin/Heidelberg, Germany, 2012; pp. 535–542. ISBN 978-3-642-34480-0. [Google Scholar]
- Köppelová, J.; Jindrová, A. Application of exponential smoothing models and arima models in time series analysis from telco area. Agris On-Line Pap. Econ. Inform. 2019, 11, 73–84. [Google Scholar] [CrossRef][Green Version]
- Palacios-Cruz, L.; Pérez, M.; Rivas-Ruiz, R.; Talavera, J.O. Investigación clínica XVIII. Del juicio clínico al modelo de regresión lineal. Rev. Méd. Inst. Mex. Seguro Soc. 2013, 51, 656–661. [Google Scholar]
- Turner, S.; Karahalios, A.; Forbes, A.; Taljaard, M.; Grimshaw, J.; McKenzie, J. Comparison of six statistical methods for interrupted time series studies: Empirical evaluation of 190 published series. BMC Med. Res. Methodol 2021, 21, 134. [Google Scholar] [CrossRef]
- Tsitsiashvili, G.; Losev, A. Safety Margin Prediction Algorithms Based on Linear Regression Analysis Estimates. Mathematics 2022, 10, 2008. [Google Scholar] [CrossRef]
- Halunga, A.G.; Orme, C.D.; Yamagata, T. A heteroskedasticity robust Breusch–Pagan test for Contemporaneous correlation in dynamic panel data models. J. Econom. 2017, 198, 209–230. [Google Scholar] [CrossRef]
- Jayakumar, D.; Sulthan, A. Exact distribution of Cook’s distance and identification of influential observations, Hacettepe. J. Math. Stat. 2015, 44, 165–178. [Google Scholar] [CrossRef]
- Johnstone, I.M.; Velleman, P.F. The resistant line and related regression methods. J. Am. Stat. Assoc. 1985, 80, 1041–1054. [Google Scholar] [CrossRef]
- Donald, R.M. Interactive Data Analysis: A Practical Primer; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Velleman, P.; Hoaglin, D. Applications, Basics, and Computing of Exploratory Data Analysis; Duxbury Press: Belmont, CA, USA, 1981. [Google Scholar]
- Zakowska, I.; Godycki-Cwirko, M. Data envelopment analysis applications in primary health care: A systematic review. Fam. Pract. 2020, 37, 147–153. [Google Scholar] [CrossRef] [PubMed]
- Aeenparast, A.; Farzadi, F.; Maftoon, F.; Zandian, H.; Yazdeli, M. Quality of hospital bed performance studies based on pabon lasso model. Int. J. Hosp. Res. 2015, 4, 143–148. [Google Scholar]
- Schmidt, K.; Aumann, I.; Hollander, I.; Damm, K.; von der Schulenburg, J.M. Applying the analytic hierarchy process in healthcare research: A systematic literature review and evaluation of reporting. BMC Med. Inform. Decis. Mak. 2015, 15, 112. [Google Scholar] [CrossRef]
- Betto, F.; Sardi, A.; Garengo, P.; Sorano, E. The evolution of balanced scorecard in healthcare: A systematic review of its design, implementation, use, and review. Int. J. Environ. Res. Public Health 2022, 19, 10291. [Google Scholar] [CrossRef]
- Mahapatra, P.; Berman, P. Using hospital activity indicators to evaluate performance in Andhra Pradesh, India. Int. J. Health Plann. Manag. 1994, 9, 199–211. [Google Scholar] [CrossRef]
- Kiadaliri, A.A.; Jafari, M.; Gerdtham, U.G. Frontier-based techniques in measuring hospital efficiency in Iran: A systematic review and meta-regression analysis. BMC Health Serv. Res. 2013, 13, 312. [Google Scholar] [CrossRef]
- Pecchia, L.; Martin, J.L.; Ragozzino, A.; Vanzanella, C.; Scognamiglio, A.; Mirarchi, L.; Morgan, S.P. User needs elicitation via analytic hierarchy process (AHP). A case study on a computed tomography (CT) scanner. BMC Med. Inform. Decis. Mak. 2013, 13, 2. [Google Scholar] [CrossRef]
- Dolan, J.G.; Boohaker, E.; Allison, J.; Imperiale, T.F. Patients’ preferences and priorities regarding colorectal cancer screening. Med. Decis. Making 2013, 33, 59–70. [Google Scholar] [CrossRef] [PubMed]
- Mühlbacher, A.C.; Kaczynski, A. Der analytic hierarchy process (AHP): Eine methode zur entscheidungsunterstützung im gesundheitswesen. Pharm. Econ. Ger. Res. Artic. 2013, 11, 119–132. [Google Scholar] [CrossRef]
- Pierce, E. A balanced scorecard for maximizing data performance. Front. Big Data 2022, 5, 821103. [Google Scholar] [CrossRef]
- Hegazy, M.; Hegazy, K.; Eldeeb, M. The balanced scorecard: Measures that drive performance evaluation in auditing firms. J. Account. Audit. Financ. 2022, 37, 902–927. [Google Scholar] [CrossRef]
- Waluyo, M.; Huda, S.; Soetjipto, N.; Sumiati; Handoyo. Analysis of balance scorecards model performance and perspective strategy synergized by SEM. MATEC Web Conf. 2016, 58, 02003. [Google Scholar] [CrossRef]
- Byrne, B.M. Structural Equation Modeling With LISREL, PRELIS, and SIMPLIS: Basic Concepts, Applications, and Programming; Psychology Press: New York, NY, USA, 1998. [Google Scholar]
- McGlinn, K.; Yuce, B.; Wicaksono, H.; Howell, S.; Rezgui, Y. Usability evaluation of a web-based tool for supporting holistic building energy management. Autom. Constr. 2017, 84, 154–165. [Google Scholar] [CrossRef]
- Lavy, S.; Garcia, J.; Dixit, M. Establishment of KPIs for facility performance measurement: Review of literature. Facilities 2010, 28, 440–464. [Google Scholar] [CrossRef]
- Shohet, I.M.; Lavy, S. Facility maintenance and management: A health care case study. Int. J. Strateg. Prop. Manag. 2017, 21, 170–182. [Google Scholar] [CrossRef]
- World Health Organization; Regional Office for Europe; European Observatory on Health Systems and Policies; Rechel, B.; Stephen, W.; Nigel, E.; Barrie, D.; Martin, M.; Pieter, D.; Jonathan, E.; et al. Investing in Hospitals of the Future. World Health Organization, Regional Office for Europe. Available online: https://apps.who.int/iris/handle/10665/326414 (accessed on 22 March 2023).
- Gawin, B.; Marcinkowski, B. Business intelligence in facility management: Determinants and benchmarking scenarios for improving energy efficiency. Inf. Syst. Manag. 2017, 34, 347–358. [Google Scholar] [CrossRef]
- Diong, B.; Zheng, J.; Ginn, M. Establishing the foundation for energy management on university campuses via data analytics. In Conference Proceedings—IEEE SOUTHEASTCON; Institute of Electrical and Electronics Engineers Inc.: Fort Lauderdale, FL, USA, 2015; pp. 9–12. [Google Scholar]
- Demirdöğen, G.; Işık, Z.; Arayici, Y. Determination of business intelligence and analytics-based healthcare facility management key performance indicators. Appl. Sci. 2022, 12, 651. [Google Scholar] [CrossRef]
- Ahmed, V.; Aziz, Z.; Tezel, A.; Riaz, Z. Challenges and drivers for data mining in the AEC sector. Eng. Constr. Archit. Manag. 2018, 25, 1436–1453. [Google Scholar] [CrossRef]
- Fan, C.; Xiao, F.; Li, Z.; Wang, J. Unsupervised data analytics in mining big building operational data for energy efficiency enhancement: A review. Energy Build. 2018, 159, 296–308. [Google Scholar] [CrossRef]
- Ioannidis, D.; Tropios, P.; Krinidis, S.; Stavropoulos, G.; Tzovaras, D.; Likothanasis, S. Occupancy driven building performance assessment. J. Innov. Digit. Ecosyst. 2016, 3, 57–69. [Google Scholar] [CrossRef]
- Yafooz, W.M.S.; Bakar, Z.B.A.; Fahad, S.K.A.; Mithun, A.M. Business intelligence through big data analytics, data mining and machine learning. In Data Management, Analytics and Innovation; Sharma, N., Chakrabarti, A., Balas, V.E., Eds.; Springer: Singapore, 2020; pp. 217–230. [Google Scholar]
- Ghandour, Z.; Siciliani, L.; Straume, O.R. Investment and quality competition in healthcare markets. J. Health Econ. 2022, 82, 102588. [Google Scholar] [CrossRef]
- Yu Andieva, E.; Ivanov, R.N. Constructing the measuring system in industry 4.0 concept. J. Phys. Conf. Ser. 2019, 1260, 032002. [Google Scholar] [CrossRef]
- Méndez Prado, S.M.; Zambrano Franco, M.J.; Zambrano Zapata, S.G.; Chiluiza García, K.M.; Everaert, P.; Valcke, M. A Systematic Review of Financial Literacy Research in Latin America and The Caribbean. Sustainability 2022, 14, 3814. [Google Scholar] [CrossRef]
- Saturno-Hernández, P.J.; Martínez-Nicolás, I.; Poblano-Verástegui, O.; Vértiz-Ramírez, J.J.; Suárez-Ortiz, E.C.; Magaña-Izquierdo, M.; Kawa-Karasik, S. Implementation of quality of care indicators for third-level public hospitals in Mexico. Salud Publica Mex. 2017, 59, 227–235. [Google Scholar] [CrossRef] [PubMed]
- Kirschke, S.; Avellán, T.; Benavides, L.; Caucci, S.; Hahn, A.; Müller; Rubio, C. Results-based management of wicked problems? Indicators and comparative evidence from Latin America. Environ. Policy Gov. 2023, 33, 3–16. [Google Scholar] [CrossRef]
- Chen, S.; Wang, X.; Zhao, J.; Zhang, Y.; Kan, X. Application of the ARIMA model in forecasting the incidence of tuberculosis in anhui during COVID-19 pandemic from 2021 to 2022. Infect. Drug Resist. 2022, 15, 3503–3512. [Google Scholar] [CrossRef]
- Luo, L.; Luo, L.; Zhang, X.; He, X. Hospital daily outpatient visits forecasting using a combinatorial model based on ARIMA and SES models. BMC Health Serv. Res. 2017, 17, 469. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; University of Michigan, Holden-Day: Ann Arbor, MI, USA, 1976. [Google Scholar]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: The forecast package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Diario Oficial de la Federación. Ley Federal de Transparencia y Acceso a la Información Pública Gubernamental; Última Reforma Publicada: Mexico City, Mexico, 2006. [Google Scholar]

| Year | Cause of Death | Cause of Morbidity | Cause of Hospital Outpatient |
|---|---|---|---|
| 2016 3798 patients | Tumors and neoplasm (2)/33.7%/64 patients | Acute Lymphoblastic Leukemia (1)/13.5%/1024 patients Malignant Tumor (3)/2.3%/176 patients | Tumors and neoplasm (1)/33.4%/2534 patients |
| 2017 3768 patients | Tumors and neoplasm (1)/42.7%/73 patients | Acute Lymphoblastic Leukemia (1)/13%/1006 patients Malignant Tumor (2)/2.9%/108 patients | Tumors and neoplasm (1)/33.3%/2581 patients |
| 2018 4130 patients | Tumors and neoplasm (2)/24.3%/43 patients | Acute Lymphoblastic Leukemia (1)/13.3%/1060 patients Malignant Tumor (2)/3.2%/399 patients | Tumors and neoplasm (1)/34%/2628 patients |
| 2019 3591 patients | Tumors and neoplasm (1)/35%/62 patients | Acute Lymphoblastic Leukemia (1)/11.2%/915 patients Malignant Tumor (2)/2.8%/273 patients | Tumors and neoplasm (1)/32.1%/2341 patients |
| 2021 2386 patients | Tumors and neoplasm (1)/34.2%/51 patients | Acute Lymphoblastic Leukemia (1)/12.5%/670 patients Malignant Tumor (2)/1.3%/68 patients | Tumors and neoplasm (1)/29.7%/1597 patients |
| Position among the main causes appear in parenthesis/Percentage from total/Number of patients | |||
| Performance Indicator’s Name | Predictive Model | MAE | Deviation Standard | p Value |
|---|---|---|---|---|
| Bed occupancy rate | ARIMA(2,0,1) | 2.3117 | 2.2368 | 0.017 * |
| LR | 2.2453 | 1.5129 | 0.003 | |
| ES | 2.5845 | 1.8873 | NA | |
| Hospital admissions through emergency department | ARIMA(3,2,1) noconstant | 0.1292 | 0.0789 | 0.252 * |
| LR | 1.1620 | 1.5129 | 0.000 | |
| ES | 1.1325 | 1.3363 | NA | |
| Bed turnover rate | ARIMA(1,0,1) noconstant | 0.5129 | 0.6295 | 0.028 * |
| LR | 0.3320 | 0.2181 | 0.004 | |
| ES | 0.3841 | 0.2655 | NA | |
| Bed rotation index | ARIMA(1,0,1) noconstant | 0.7388 | 1.6067 | 0.180 * |
| LR | 0.3012 | 0.1925 | 0.000 | |
| ES | 0.3447 | 0.2225 | NA | |
| Percentage of emergency Admissions | ARIMA(1,0,1) noconstant | 2.2322 | 3.3174 | 0.025 * |
| LR | 1.3884 | 1.5952 | 0.025 | |
| ES | 1.4450 | 1.5600 | NA | |
| Major surgery index | ARIMA(1,0,1) noconstant | 2.4514 | 1.8210 | −2.756 * |
| LR | 1.8183 | 1.5148 | 0.001 | |
| ES | 1.8642 | 1.8720 | NA | |
| Mortality rate | ARIMA(1,0,0) noconstant | 5.5113 | 6.5088 | 0.805 * |
| LR | 3.0747 | 2.2742 | 0.688 | |
| ES | 3.1302 | 2.2275 | NA | |
| Percentage of scheduled consults granted | ARIMA(1,0,0) noconstant | 0.9754 | 2.0528 | 0.135 * |
| LR | 0.3594 | 0.2322 | 0.151 | |
| ES | 0.3887 | 0.2552 | NA | |
| First time consults index | ARIMA(3,0,1) noconstant | 2.4413 | 5.3074 | −1.589 * |
| LR | 1.5087 | 1.2620 | 0.483 | |
| ES | 1.5472 | 1.1538 | NA | |
| Proportion of subsequent consultants with relation to the first time | ARIMA(4,0,1) | 1.5178 | 1.3511 | −2.865 * |
| LR | 1.3400 | 1.3552 | 0.000 | |
| ES | 1.7370 | 1.6261 | NA |
| Criteria ARIMA Used | Value/Type | p Value | |
|---|---|---|---|
| Bed occupancy rate | dfuller CV z(t) 95% = −3.6 | −3.5740 | 0.0321 |
| dfuller best difference | 0 | ||
| dfuller value, trend, constant (a,b,c) | 0.1621 (b) | 0.263 (b) | |
| ARIMA(2,0,1)/IC 95% (ar,ma) | Ma | 0.017 | |
| Hospital admissions through emergency department | dfuller CV z(t) 95% = −3.6 | −5.6590 | 0.0001 |
| dfuller best difference | 2 | ||
| dfuller value, trend, constant (a,b,c) | 0.7877 (c) | 0.375 (c) | |
| ARIMA(1,2,3)/IC 95% | Ma | 0.002 | |
| Bed turnover rate | dfuller CV z(t) 95% = −3.6 | −4.1860 | 0.0047 |
| dfuller best difference | 0 | ||
| dfuller value, trend, constant (a,b,c) | −0.0350 (b) | 0.125 (b) | |
| ARIMA(1,0,1) noconstant/IC 95% (ar,ma) | Ma | 0.028 | |
| Beds rotation index | dfuller CV z(t) 95% = −3.6 | −4.5910 | 0.0011 |
| dfuller best difference | 0 | ||
| dfuller value, trend, constant (a,b,c) * | 0.0239 | 0.180 (b) | |
| ARIMA(1,0,1) noconstant/IC 95% (ar,ma) | Ma | 0.000 | |
| Percentage of emergency admissions | dfuller CV z(t) 95% = −3.6 | −5.4260 | 0.000 |
| dfuller best difference | 2 | ||
| dfuller value, trend, constant (a,b,c) * | 0.1703 | 0.197 (b) | |
| ARIMA(4,2,0) noconstant/IC 95% (ar,i) | Ar | 0.042 (L2) | |
| Major surgery index | dfuller CV z(t) 95% = −3.6 | −4.0760 | 0.0068 |
| dfuller best difference | 1 | ||
| dfuller value, trend, constant (a,b,c) * | −0.0103 | 0.942 (b) | |
| ARIMA(1,1,1) noconstant/IC 95% | Ar | 0.973 | |
| Mortality rate | dfuller CV z(t) 95% = −3.6 | −4.8190 | 0.0004 |
| dfuller best difference | 0 | ||
| dfuller value, trend, constant (a,b,c) * | 0.0405 | 0.805 (b) | |
| ARIMA(1,0,0) noconstant/IC 95% (ar) | Ar | 0.000 | |
| Percentage of scheduled appointments granted | dfuller CV z(t) 95% = −3.6 | −3.9990 | 0.0088 |
| dfuller best difference | 0 | ||
| dfuller value, trend, constant (a,b,c)* | 0.0405 | 0.135 (b) | |
| ARIMA(1,0,0) noconstant/IC 95% (ar) | Ar | 0.000 | |
| First time consults index | dfuller CV z(t) 95% = −3.6 | −3.8820 | 0.0088 |
| dfuller best difference | 1 | ||
| dfuller value, trend, constant (a,b,c) * | 1.1924 | 0.242 (c) | |
| ARIMA(2,1,1) noconstant/IC 95% | Ar | 0.752 (L1) | |
| Proportion of subsequent consults with relation to the first time | dfuller CV z(t) 95% = −3.6 | −3.6460 | 0.0262 |
| dfuller best difference | 1 | ||
| dfuller value, trend, constant (a,b,c) * | −0.1540 | 0.902 (c) | |
| ARIMA(2,1,1) noconstant/IC 95% | Ar | 0.646 (L1) |
| Performance Indicator | Shapiro Wilk p-Value (1) | Cook’s Distance (2) | Breusch Pagan p-Value (3) |
|---|---|---|---|
| Bed occupancy rate | 0.027 | 0 > 1 | 0.3976 |
| Hospital admissions through emergency department | 0.000 | 2 > 1 | 0.0001 |
| Bed turnover rate | 0.085 | 0 > 1 | 0.4146 |
| Bed rotation index | 0.409 | 0 > 1 | 0.5580 |
| Percentage of emergency admissions | 0.000 | 1 > 1 | 0.0000 |
| Major surgery index | 0.568 | 0 > 1 | 0.6507 |
| Mortality rate | 0.263 | 1 > 1 | 0.4861 |
| Percentage of scheduled consults granted | 0.999 | 0 > 1 | 0.7536 |
| First time consults index | 0.209 | 0 > 1 | 0.3049 |
| Proportion of subsequent consultant with relation to the first time | 0.899 | 1 > 1 | 0.5265 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Salazar, J.; Toledano-Toledano, F. Comparative Analysis of Three Predictive Models of Performance Indicators with Results-Based Management: Cancer Data Statistics in a National Institute of Health. Cancers 2023, 15, 4649. https://doi.org/10.3390/cancers15184649
Martínez-Salazar J, Toledano-Toledano F. Comparative Analysis of Three Predictive Models of Performance Indicators with Results-Based Management: Cancer Data Statistics in a National Institute of Health. Cancers. 2023; 15(18):4649. https://doi.org/10.3390/cancers15184649
Chicago/Turabian StyleMartínez-Salazar, Joel, and Filiberto Toledano-Toledano. 2023. "Comparative Analysis of Three Predictive Models of Performance Indicators with Results-Based Management: Cancer Data Statistics in a National Institute of Health" Cancers 15, no. 18: 4649. https://doi.org/10.3390/cancers15184649
APA StyleMartínez-Salazar, J., & Toledano-Toledano, F. (2023). Comparative Analysis of Three Predictive Models of Performance Indicators with Results-Based Management: Cancer Data Statistics in a National Institute of Health. Cancers, 15(18), 4649. https://doi.org/10.3390/cancers15184649





