Quantifying the Growth of Glioblastoma Tumors Using Multimodal MRI Brain Images
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Information
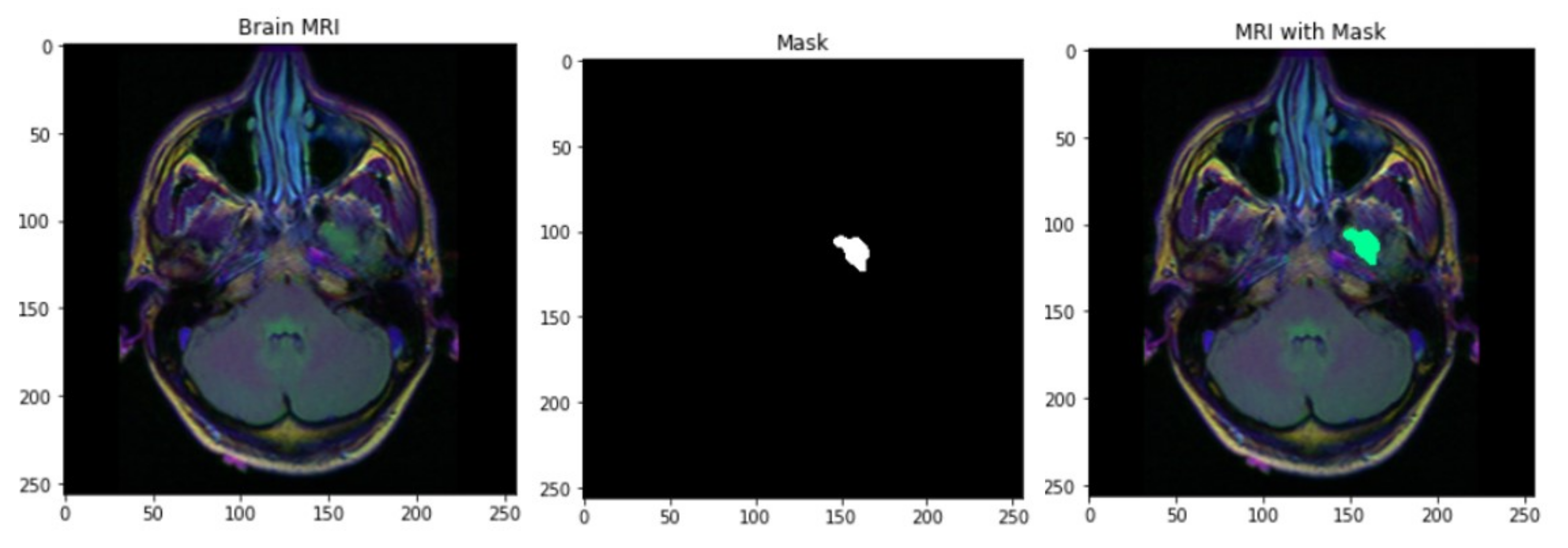
2.2. Preprocessing and Image Segmentation
2.3. Quantification of the Tumor Growth Prediction
2.4. Bayesian Regression of the Eventual Volume for Other Radiomic Features
2.5. Handling the Heterogeneity among Oncogenes
3. Results
3.1. Simulation Study
3.2. Real Data Analysis: Canonical Measurement Metrics
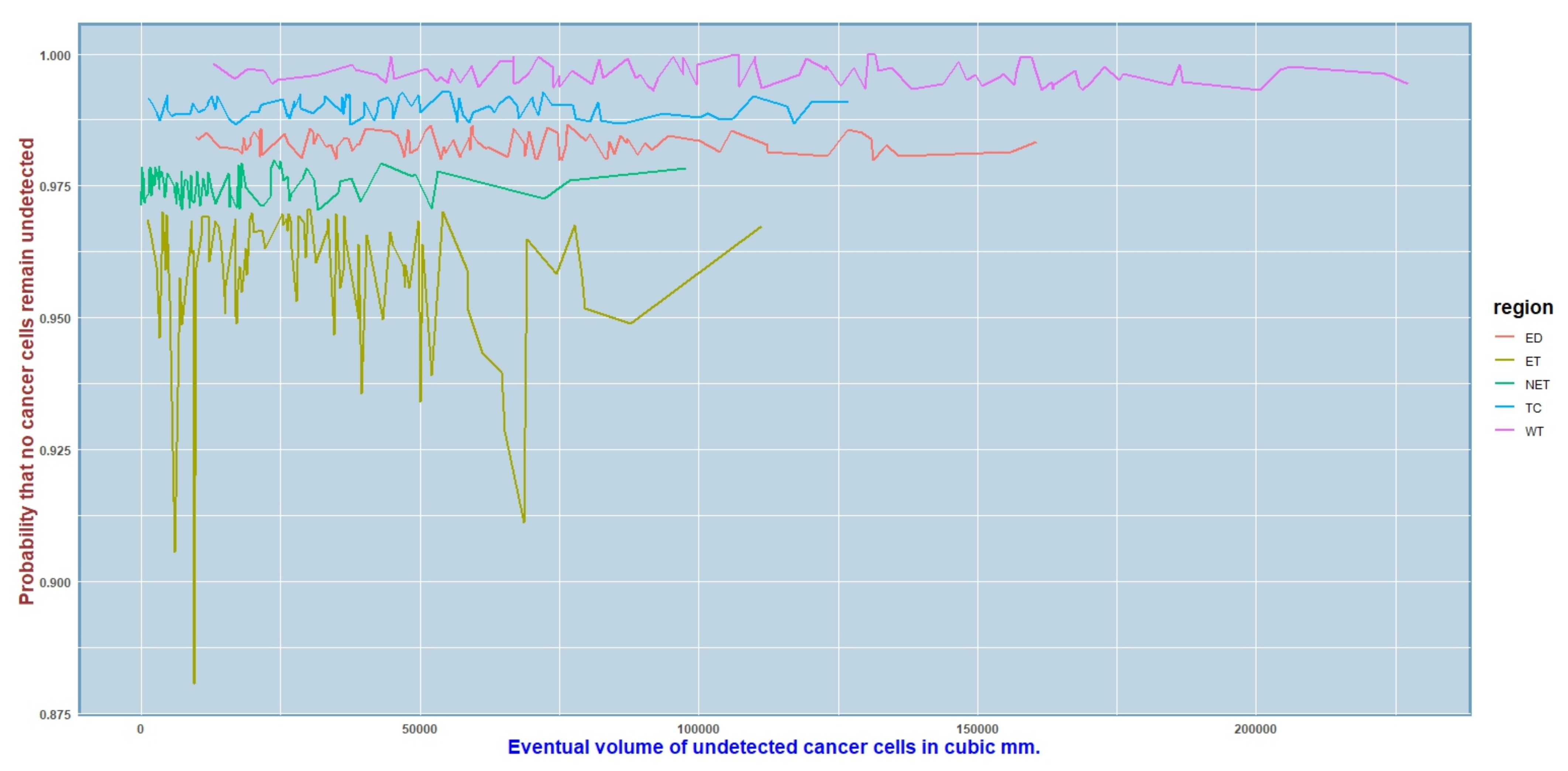
3.3. Real Data Analysis: Prediction of the Eventual Volume of GBM
3.4. Real Data Analysis: Outcome of the Bayesian Regression Model
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GBM | Glioblastoma Multiforme |
| ROIs | Regions of Interest |
| ET | GD-Enhancing Tumor |
| TC | Tumor core |
| WT | Whole Tumor |
| ED | Edema |
| NET | Non-Enhancing Tumor |
Appendix A. Background behind Deriving the Model
Appendix B. The Probability Model
Appendix C. Finding the Likelihood Function
Appendix D. Choice of Prior and Posterior
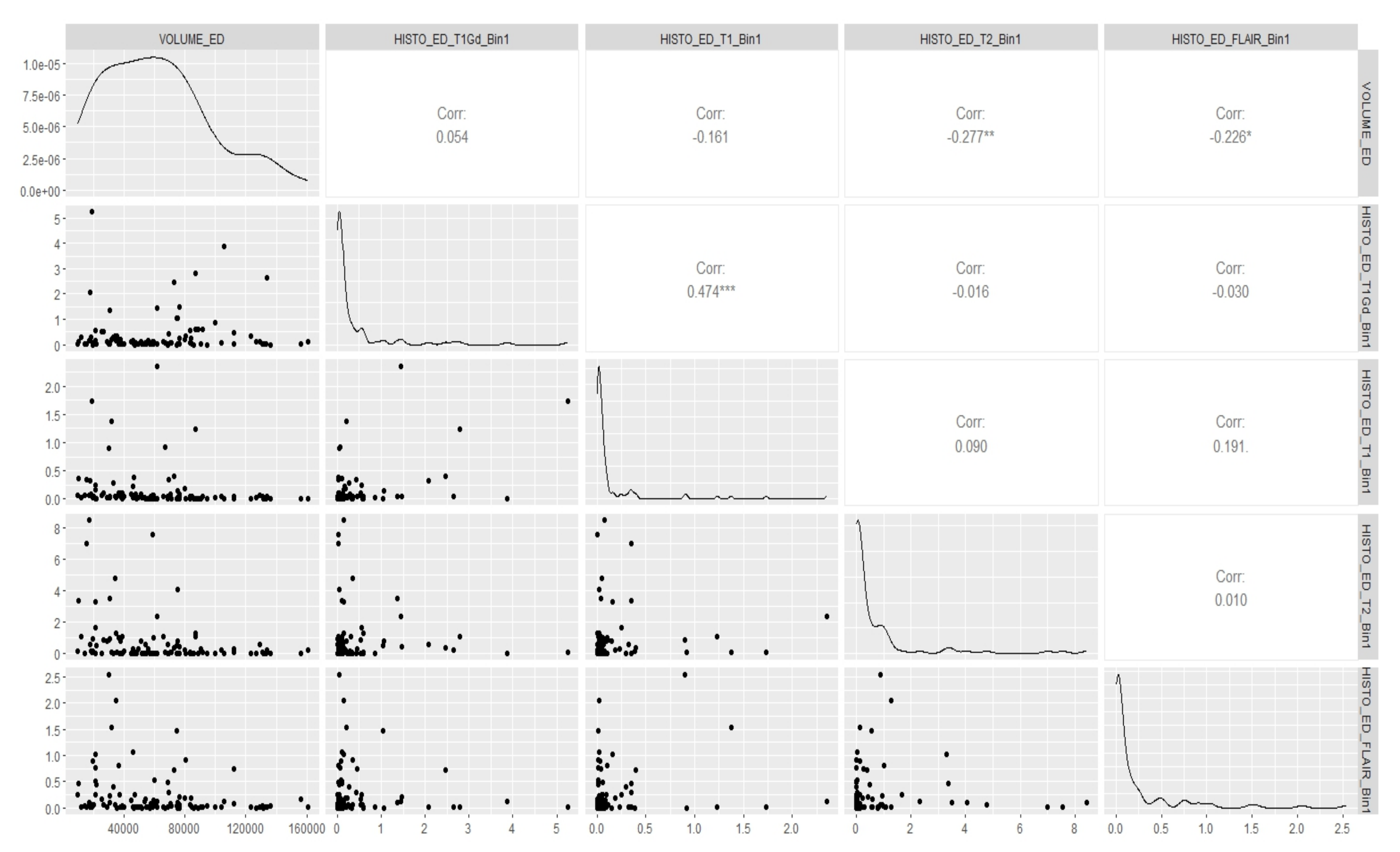
Appendix E. Canonical Measurement Metrics—Correlation Plots
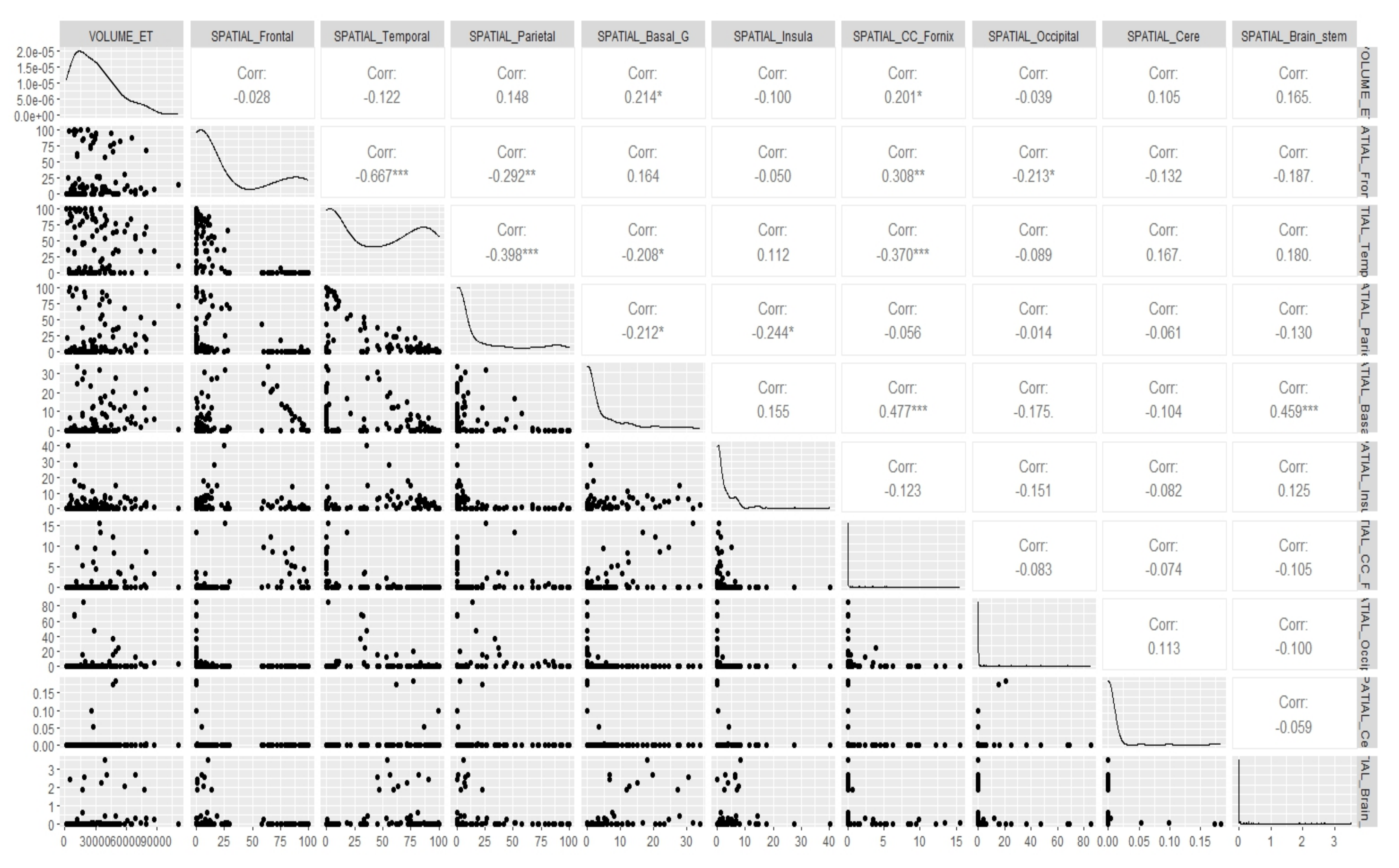

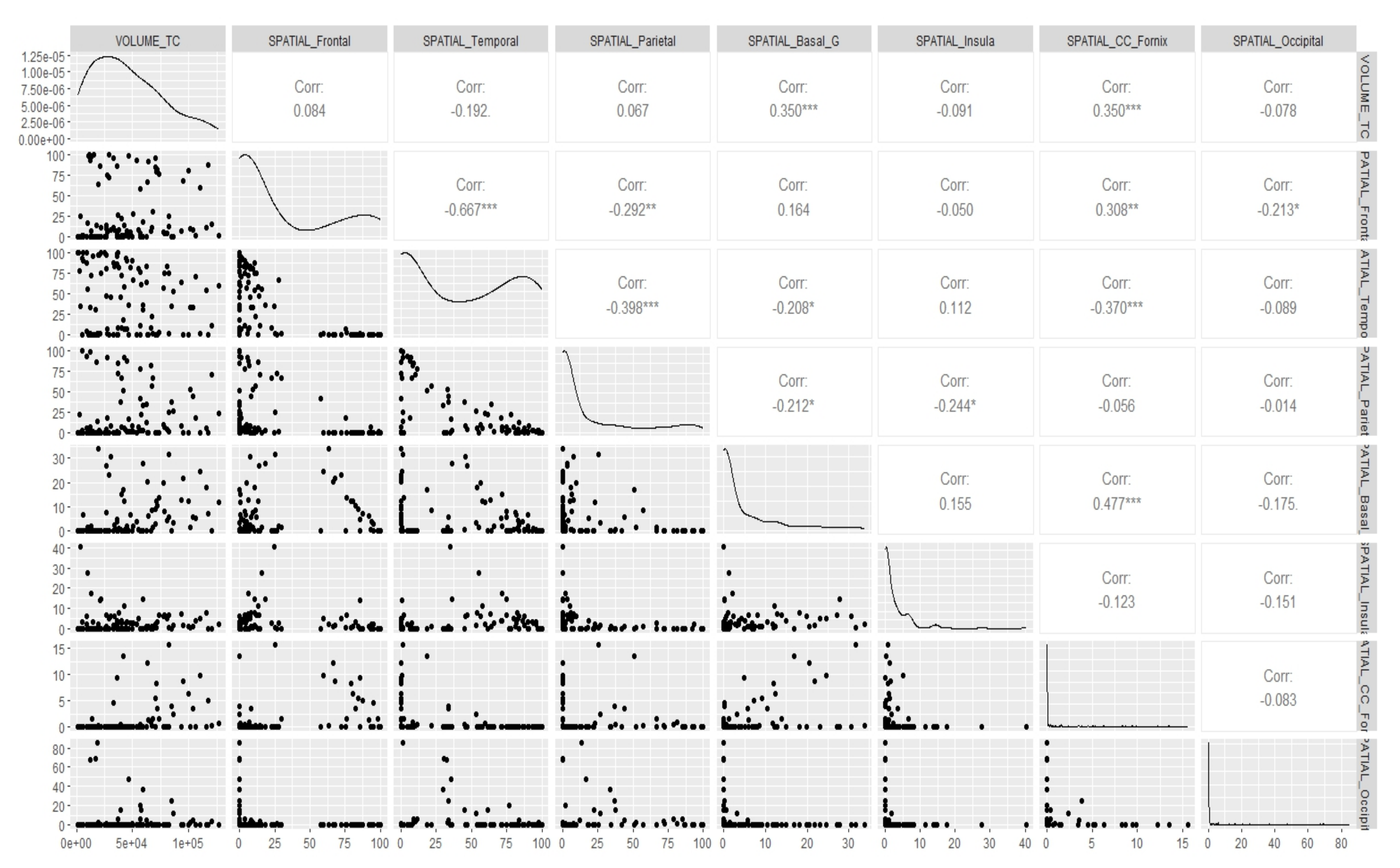
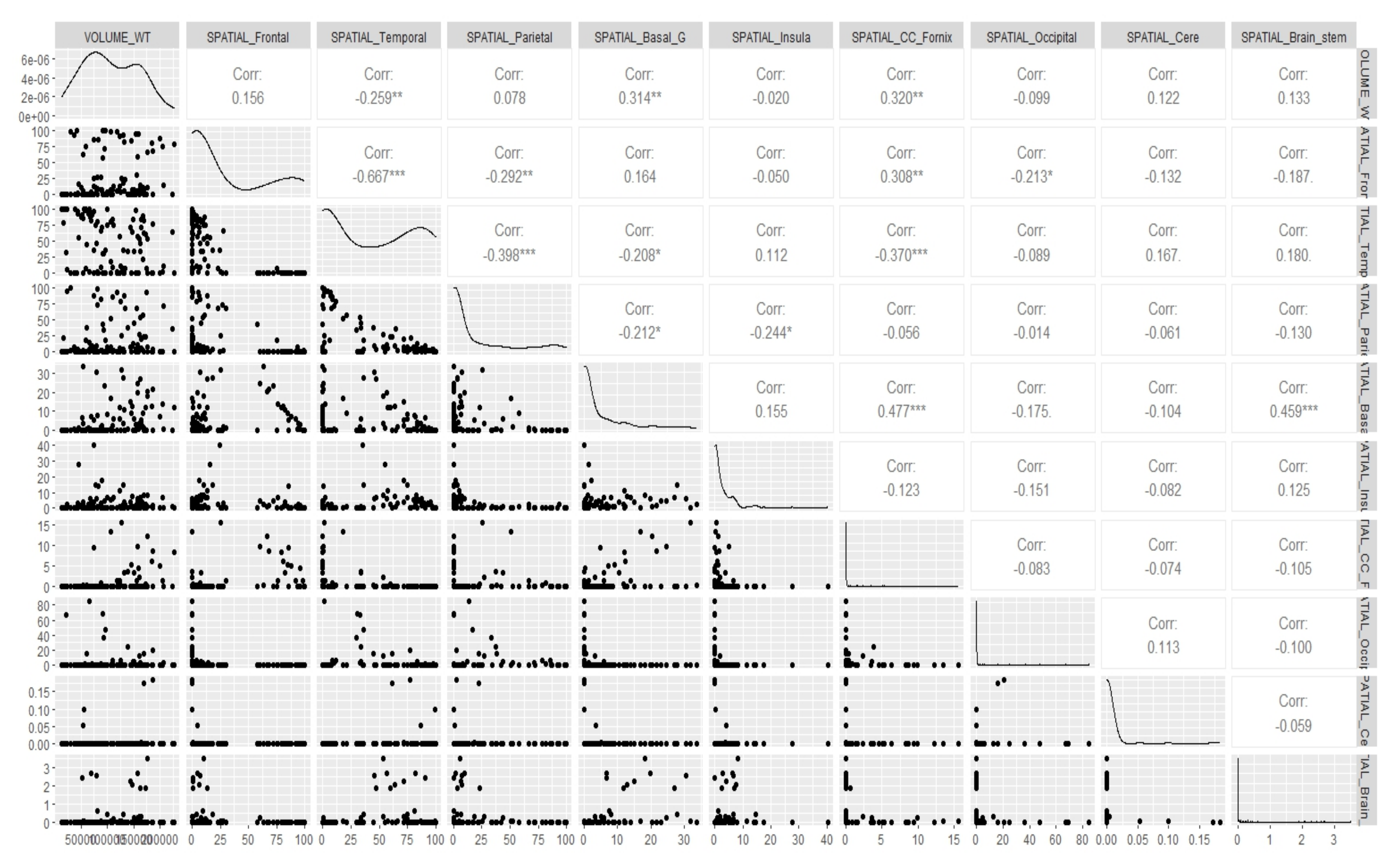

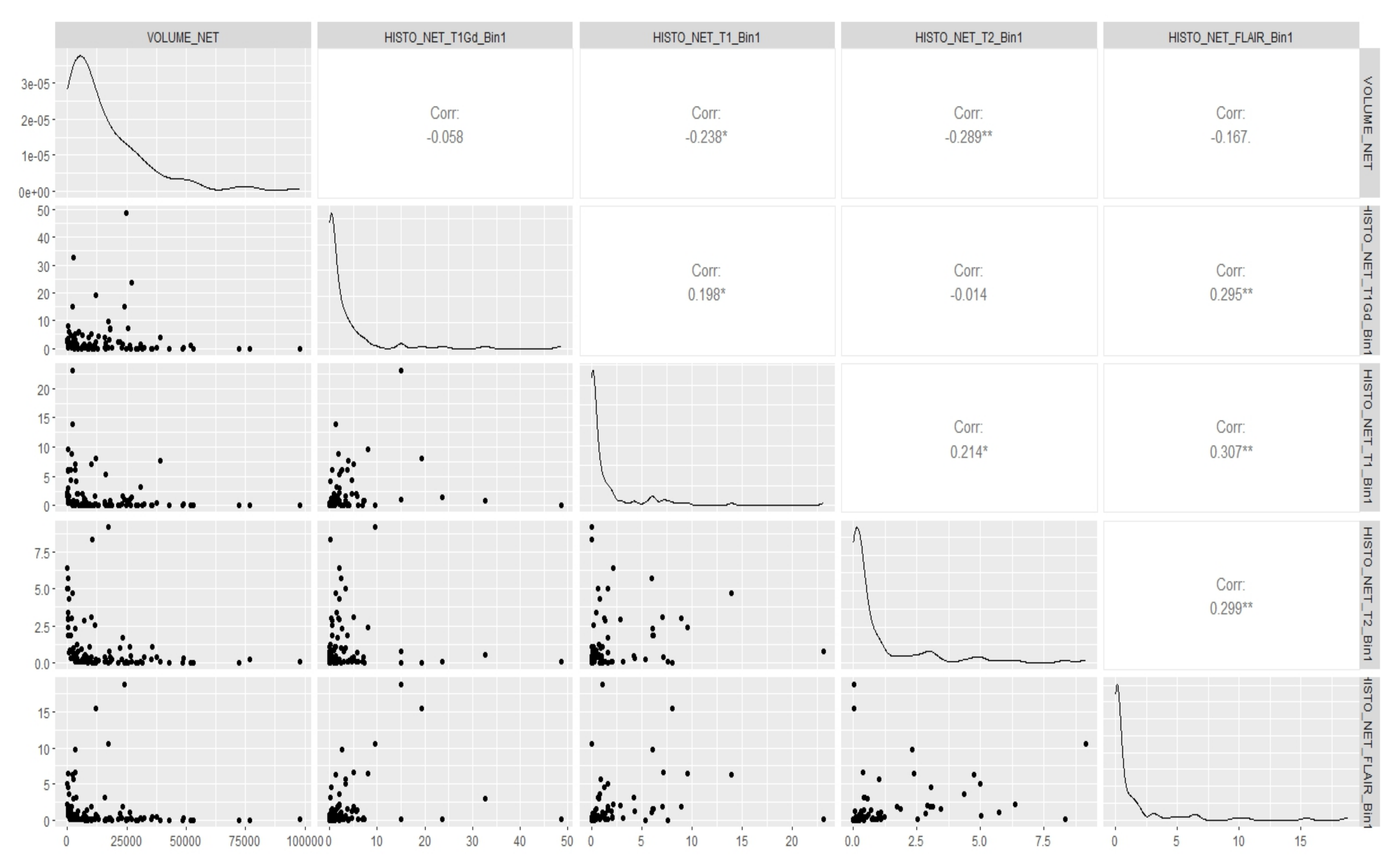
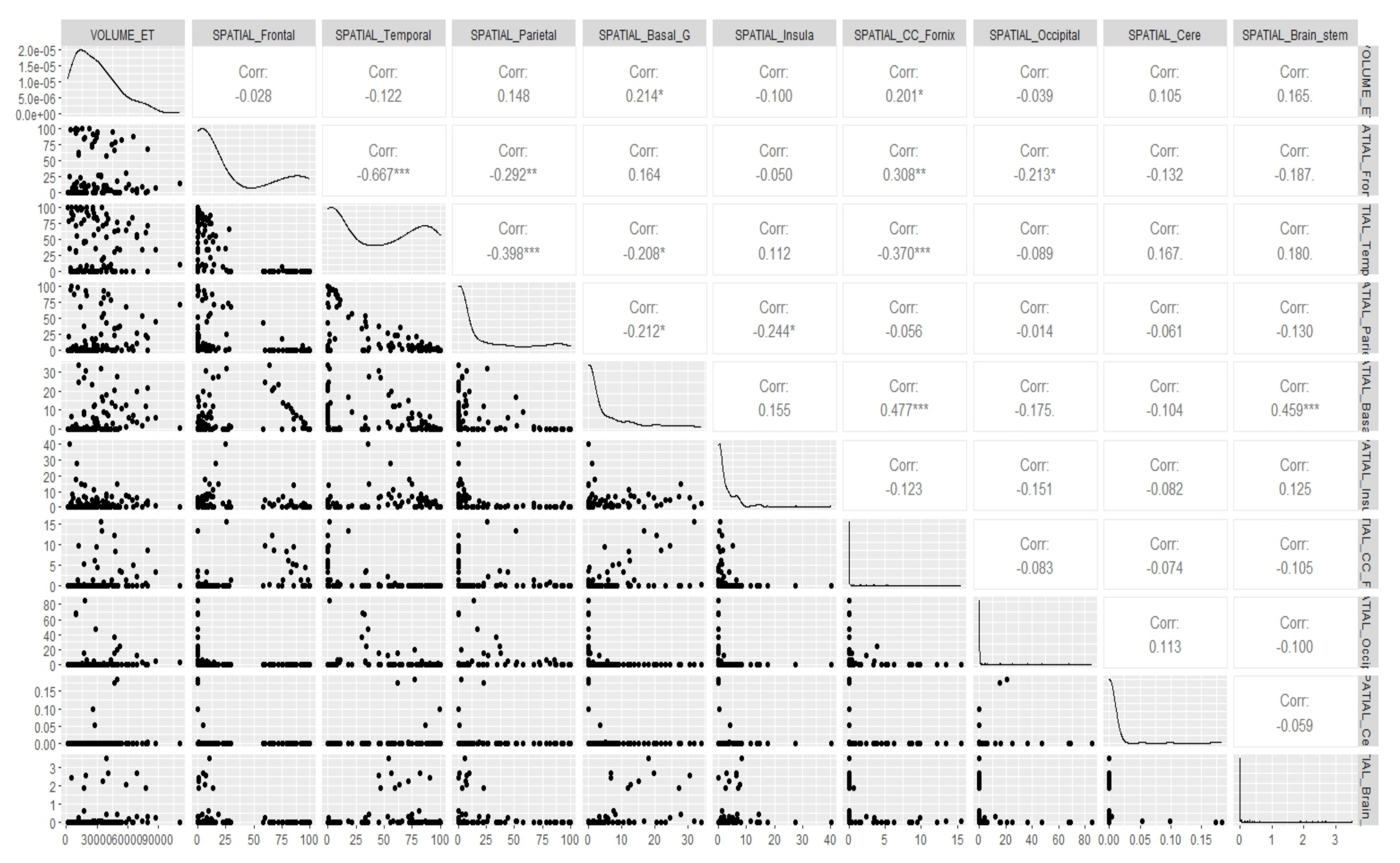

References
- Marini, B.L.; Benitez, L.L.; Zureick, A.H.; Salloum, R.; Gauthier, A.C.; Brown, J.; Wu, Y.M.; Robinson, D.R.; Kumar, C.; Lonigro, R.; et al. Blood-brain barrier–adapted precision medicine therapy for pediatric brain tumors. Transl. Res. 2017, 188, 27.e1–27.e14. [Google Scholar] [CrossRef] [PubMed]
- Stallard, S.; Savelieff, M.G.; Wierzbicki, K.; Mullan, B.; Miklja, Z.; Bruzek, A.; Garcia, T.; Siada, R.; Anderson, B.; Singer, B.H.; et al. CSF H3F3A K27M circulating tumor DNA copy number quantifies tumor growth and in vitro treatment response. Acta Neuropathol. Commun. 2018, 6, 80. [Google Scholar] [CrossRef] [PubMed]
- Vermeulen, P.; Gasparini, G.; Fox, S.; Toi, M.; Martin, L.; McCulloch, P.; Pezzella, F.; Viale, G.; Weidner, N.; Harris, A.; et al. Quantification of angiogenesis in solid human tumours: An international consensus on the methodology and criteria of evaluation. Eur. J. Cancer 1996, 32, 2474–2484. [Google Scholar] [CrossRef] [PubMed]
- Vermeulen, P.; Gasparini, G.; Fox, S.; Colpaert, C.; Marson, L.; Gion, M.; Beliën, J.; De Waal, R.; Van Marck, E.; Magnani, E.; et al. Second international consensus on the methodology and criteria of evaluation of angiogenesis quantification in solid human tumours. Eur. J. Cancer 2002, 38, 1564–1579. [Google Scholar] [CrossRef] [PubMed]
- Linzey, J.R.; Marini, B.L.; Pasternak, A.; Smith, C.; Miklja, Z.; Zhao, L.; Kumar-Sinha, C.; Paul, A.; Harris, N.; Robertson, P.L.; et al. Development of the CNS TAP tool for the selection of precision medicine therapies in neuro-oncology. J. Neuro-Oncol. 2018, 137, 155–169. [Google Scholar] [CrossRef] [PubMed]
- Hieber, S.E.; Bikis, C.; Khimchenko, A.; Schweighauser, G.; Hench, J.; Chicherova, N.; Schulz, G.; Müller, B. Tomographic brain imaging with nucleolar detail and automatic cell counting. Sci. Rep. 2016, 6, 32156. [Google Scholar] [CrossRef]
- Heuvelmans, M.A.; Vliegenthart, R.; de Koning, H.J.; Groen, H.J.; van Putten, M.J.; Yousaf-Khan, U.; Weenink, C.; Nackaerts, K.; de Jong, P.A.; Oudkerk, M. Quantification of growth patterns of screen-detected lung cancers: The NELSON study. Lung Cancer 2017, 108, 48–54. [Google Scholar] [CrossRef]
- Kipps, C.; Hodges, J.; Fryer, T.; Nestor, P. Combined magnetic resonance imaging and positron emission tomography brain imaging in behavioural variant frontotemporal degeneration: Refining the clinical phenotype. Brain 2009, 132, 2566–2578. [Google Scholar] [CrossRef]
- Studholme, C.; Hill, D.L.; Hawkes, D.J. Automated three-dimensional registration of magnetic resonance and positron emission tomography brain images by multiresolution optimization of voxel similarity measures. Med. Phys. 1997, 24, 25–35. [Google Scholar] [CrossRef]
- Chaddad, A.; Kucharczyk, M.J.; Daniel, P.; Sabri, S.; Jean-Claude, B.J.; Niazi, T.; Abdulkarim, B. Radiomics in glioblastoma: Current status and challenges facing clinical implementation. Front. Oncol. 2019, 9, 374. [Google Scholar] [CrossRef]
- Chen, J.; Han, P.; Dahiya, S. Glioblastoma: Changing concepts in the WHO CNS5 classification. Indian J. Pathol. Microbiol. 2022, 65, 24. [Google Scholar]
- Ohgaki, H.; Kleihues, P. Epidemiology and etiology of gliomas. Acta Neuropathol. 2005, 109, 93–108. [Google Scholar] [CrossRef] [PubMed]
- Appin, C.L.; Brat, D.J. Biomarker-driven diagnosis of diffuse gliomas. Mol. Asp. Med. 2015, 45, 87–96. [Google Scholar] [CrossRef] [PubMed]
- Kabat, G.C.; Etgen, A.M.; Rohan, T.E. Do Steroid Hormones Play a Role in the Etiology of Glioma? Steroid Hormones and Glioma. Cancer Epidemiol. Biomarkers Prev. 2010, 19, 2421–2427. [Google Scholar] [CrossRef]
- Wang, J.; Yao, L.; Zhao, S.; Zhang, X.; Yin, J.; Zhang, Y.; Chen, X.; Gao, M.; Ling, E.A.; Hao, A.; et al. Granulocyte-colony stimulating factor promotes proliferation, migration and invasion in glioma cells. Cancer Biol. Ther. 2012, 13, 389–400. [Google Scholar] [CrossRef]
- Dolacek, T.; Propp, J.; Stroup, N. CBTRUS statistical report: Primary brain and central nervous system tumors diagnosed in the United States in 2006–2010. Neuro-Oncology 2012, 14, v1-49. [Google Scholar] [CrossRef]
- Yuan, J.X.; Bafakih, F.F.; Mandell, J.W.; Horton, B.J.; Munson, J.M. Quantitative analysis of the cellular microenvironment of glioblastoma to develop predictive statistical models of overall survival. J. Neuropathol. Exp. Neurol. 2016, 75, 1110–1123. [Google Scholar] [CrossRef]
- Urbańska, K.; Sokołowska, J.; Szmidt, M.; Sysa, P. Glioblastoma multiforme—An overview. Contemp. Oncol. Onkol. 2014, 18, 307–312. [Google Scholar]
- Karcher, S.; Steiner, H.H.; Ahmadi, R.; Zoubaa, S.; Vasvari, G.; Bauer, H.; Unterberg, A.; Herold-Mende, C. Different angiogenic phenotypes in primary and secondary glioblastomas. Int. J. Cancer 2006, 118, 2182–2189. [Google Scholar] [CrossRef]
- Rockne, R.; Rockhill, J.; Mrugala, M.; Spence, A.; Kalet, I.; Hendrickson, K.; Lai, A.; Cloughesy, T.; Alvord, E.; Swanson, K. Predicting the efficacy of radiotherapy in individual glioblastoma patients in vivo: A mathematical modeling approach. Phys. Med. Biol. 2010, 55, 3271. [Google Scholar] [CrossRef]
- Stensjøen, A.L.; Solheim, O.; Kvistad, K.A.; Håberg, A.K.; Salvesen, Ø.; Berntsen, E.M. Growth dynamics of untreated glioblastomas in vivo. Neuro-Oncology 2015, 17, 1402–1411. [Google Scholar] [CrossRef]
- Kong, D.S.; Kim, J.; Ryu, G.; You, H.J.; Sung, J.K.; Han, Y.H.; Shin, H.M.; Lee, I.H.; Kim, S.T.; Park, C.K.; et al. Quantitative radiomic profiling of glioblastoma represents transcriptomic expression. Oncotarget 2018, 9, 6336. [Google Scholar] [CrossRef] [PubMed]
- Kickingereder, P.; Burth, S.; Wick, A.; Götz, M.; Eidel, O.; Schlemmer, H.P.; Maier-Hein, K.H.; Wick, W.; Bendszus, M.; Radbruch, A.; et al. Radiomic profiling of glioblastoma: Identifying an imaging predictor of patient survival with improved performance over established clinical and radiologic risk models. Radiology 2016, 280, 880–889. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Tian, J.; Dong, D.; Gu, D.; Dong, Y.; Zhang, L.; Lian, Z.; Liu, J.; Luo, X.; Pei, S.; et al. Radiomics Features of Multiparametric MRI as Novel Prognostic Factors in Advanced Nasopharyngeal CarcinomaPretreatment Radiomics for Nasopharyngeal Carcinoma. Clin. Cancer Res. 2017, 23, 4259–4269. [Google Scholar] [CrossRef] [PubMed]
- Rathore, S.; Akbari, H.; Rozycki, M.; Abdullah, K.G.; Nasrallah, M.P.; Binder, Z.A.; Davuluri, R.V.; Lustig, R.A.; Dahmane, N.; Bilello, M.; et al. Radiomic MRI signature reveals three distinct subtypes of glioblastoma with different clinical and molecular characteristics, offering prognostic value beyond IDH1. Sci. Rep. 2018, 8, 5087. [Google Scholar] [CrossRef]
- Wang, S.; Martinez-Lage, M.; Sakai, Y.; Chawla, S.; Kim, S.; Alonso-Basanta, M.; Lustig, R.; Brem, S.; Mohan, S.; Wolf, R.; et al. Differentiating tumor progression from pseudoprogression in patients with glioblastomas using diffusion tensor imaging and dynamic susceptibility contrast MRI. Am. J. Neuroradiol. 2016, 37, 28–36. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, X.; Yin, L.; Zhang, X.; Li, L.; Lu, H. Relationship between glioblastoma heterogeneity and survival time: An MR imaging texture analysis. Am. J. Neuroradiol. 2017, 38, 1695–1701. [Google Scholar] [CrossRef]
- Chow, D.; Chang, P.; Weinberg, B.D.; Bota, D.A.; Grinband, J.; Filippi, C.G. Imaging Genetic Heterogeneity in Glioblastoma and Other Glial Tumors: Review of Current Methods and Future Directions. AJR. Am. J. Roentgenol. 2018, 210, 30–38. [Google Scholar] [CrossRef]
- Mazurowski, M.A.; Clark, K.; Czarnek, N.M.; Shamsesfandabadi, P.; Peters, K.B.; Saha, A. Radiogenomics of lower-grade glioma: Algorithmically-assessed tumor shape is associated with tumor genomic subtypes and patient outcomes in a multi-institutional study with The Cancer Genome Atlas data. J. Neuro-Oncol. 2017, 133, 27–35. [Google Scholar] [CrossRef]
- Liang, S.; Zhang, R.; Liang, D.; Song, T.; Ai, T.; Xia, C.; Xia, L.; Wang, Y. Multimodal 3D DenseNet for IDH genotype prediction in gliomas. Genes 2018, 9, 382. [Google Scholar] [CrossRef]
- Eichinger, P.; Alberts, E.; Delbridge, C.; Trebeschi, S.; Valentinitsch, A.; Bette, S.; Huber, T.; Gempt, J.; Meyer, B.; Schlegel, J.; et al. Diffusion tensor image features predict IDH genotype in newly diagnosed WHO grade II/III gliomas. Sci. Rep. 2017, 7, 13396. [Google Scholar] [CrossRef]
- Delfanti, R.L.; Piccioni, D.E.; Handwerker, J.; Bahrami, N.; Krishnan, A.; Karunamuni, R.; Hattangadi-Gluth, J.A.; Seibert, T.M.; Srikant, A.; Jones, K.A.; et al. Imaging correlates for the 2016 update on WHO classification of grade II/III gliomas: Implications for IDH, 1p/19q and ATRX status. J. Neuro-Oncol. 2017, 135, 601–609. [Google Scholar] [CrossRef]
- Hong, E.K.; Choi, S.H.; Shin, D.J.; Jo, S.W.; Yoo, R.E.; Kang, K.M.; Yun, T.J.; Kim, J.H.; Sohn, C.H.; Park, S.H.; et al. Radiogenomics correlation between MR imaging features and major genetic profiles in glioblastoma. Eur. Radiol. 2018, 28, 4350–4361. [Google Scholar] [CrossRef] [PubMed]
- Scherer, H. Cerebral astrocytomas and their derivatives. Am. J. Cancer 1940, 40, 159–198. [Google Scholar]
- Kros, J.M.; van Run, P.R.; Alers, J.C.; Avezaat, C.J.; Luider, T.M.; van Dekken, H. Spatial variability of genomic aberrations in a large glioblastoma resection specimen. Acta Neuropathol. 2001, 102, 103–109. [Google Scholar] [CrossRef] [PubMed]
- Woodworth, G.F.; McGirt, M.J.; Samdani, A.; Garonzik, I.; Olivi, A.; Weingart, J.D. Frameless image-guided stereotactic brain biopsy procedure: Diagnostic yield, surgical morbidity, and comparison with the frame-based technique. J. Neurosurg. 2006, 104, 233–237. [Google Scholar] [CrossRef] [PubMed]
- Steinmetz, M.P.; Barnett, G.H.; Kim, B.S.; Chidel, M.A.; Suh, J.H. Metastatic seeding of the stereotactic biopsy tract in glioblastoma multiforme: Case report and review of the literature. J. Neuro-Oncol. 2001, 55, 167–171. [Google Scholar] [CrossRef]
- Perrin, R.G.; Bernstein, M. Iatrogenic seeding of anaplastic astrocytoma following stereotactic biopsy. J. Neuro-Oncol. 1998, 36, 243–246. [Google Scholar] [CrossRef]
- Zinn, P.O.; Singh, S.K.; Kotrotsou, A.; Hassan, I.; Thomas, G.; Luedi, M.M.; Elakkad, A.; Elshafeey, N.; Idris, T.; Mosley, J.; et al. A Coclinical Radiogenomic Validation Study: Conserved Magnetic Resonance Radiomic Appearance of Periostin-Expressing Glioblastoma in Patients and Xenograft ModelsValidation of Radiomics and Radiogenomics. Clin. Cancer Res. 2018, 24, 6288–6299. [Google Scholar] [CrossRef]
- Bakas, S.; Akbari, H.; Sotiras, A.; Bilello, M.; Rozycki, M.; Kirby, J.S.; Freymann, J.B.; Farahani, K.; Davatzikos, C. Advancing the cancer genome atlas glioma MRI collections with expert segmentation labels and radiomic features. Sci. Data 2017, 4, 170117. [Google Scholar] [CrossRef]
- Lu, C.F.; Hsu, F.T.; Hsieh, K.L.C.; Kao, Y.C.J.; Cheng, S.J.; Hsu, J.B.K.; Tsai, P.H.; Chen, R.J.; Huang, C.C.; Yen, Y.; et al. Machine Learning—Based Radiomics for Molecular Subtyping of GliomasMachine Learning for Molecular Subtyping of Gliomas. Clin. Cancer Res. 2018, 24, 4429–4436. [Google Scholar] [CrossRef] [PubMed]
- Chaddad, A.; Desrosiers, C.; Hassan, L.; Tanougast, C. A quantitative study of shape descriptors from glioblastoma multiforme phenotypes for predicting survival outcome. Br. J. Radiol. 2016, 89, 20160575. [Google Scholar] [CrossRef] [PubMed]
- Jenkinson, M.; Smith, S. A global optimisation method for robust affine registration of brain images. Med. Image Anal. 2001, 5, 143–156. [Google Scholar] [CrossRef]
- Jenkinson, M.; Bannister, P.; Brady, M.; Smith, S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage 2002, 17, 825–841. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.M.; Jenkinson, M.; Woolrich, M.W.; Beckmann, C.F.; Behrens, T.E.; Johansen-Berg, H.; Bannister, P.R.; De Luca, M.; Drobnjak, I.; Flitney, D.E.; et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 2004, 23, S208–S219. [Google Scholar] [CrossRef]
- Woolrich, M.W.; Jbabdi, S.; Patenaude, B.; Chappell, M.; Makni, S.; Behrens, T.; Beckmann, C.; Jenkinson, M.; Smith, S.M. Bayesian analysis of neuroimaging data in FSL. Neuroimage 2009, 45, S173–S186. [Google Scholar] [CrossRef]
- Jenkinson, M.; Beckmann, C.F.; Behrens, T.E.; Woolrich, M.W.; Smith, S.M. Fsl. Neuroimage 2012, 62, 782–790. [Google Scholar] [CrossRef]
- Dessai, V.S.; Arakeri, M.P.; Reddy, G.R.M. A parallel segmentation of brain tumor from magnetic resonance images. In Proceedings of the 2012 Third International Conference on Computing, Communication and Networking Technologies (ICCCNT’12), Bangalore, India, 3–7 January 2012; pp. 1–6. [Google Scholar]
- Max, J. Quantizing for minimum distortion. IRE Trans. Inf. Theory 1960, 6, 7–12. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Li, Q.; Griffiths, J.G. Least squares ellipsoid specific fitting. In Proceedings of the Geometric Modeling and Processing, Beijing, China, 13–15 April 2004; pp. 335–340. [Google Scholar]
- Thibault, G.; Fertil, B.; Navarro, C.; Pereira, S.; Cau, P.; Levy, N.; Sequeira, J.; Mari, J.L. Shape and texture indexes application to cell nuclei classification. Int. J. Pattern Recognit. Artif. Intell. 2013, 27, 1357002. [Google Scholar] [CrossRef]
- Macyszyn, L.; Akbari, H.; Pisapia, J.M.; Da, X.; Attiah, M.; Pigrish, V.; Bi, Y.; Pal, S.; Davuluri, R.V.; Roccograndi, L.; et al. Imaging patterns predict patient survival and molecular subtype in glioblastoma via machine learning techniques. Neuro-Oncology 2015, 18, 417–425. [Google Scholar] [CrossRef] [PubMed]
- Collewet, G.; Strzelecki, M.; Mariette, F. Influence of MRI acquisition protocols and image intensity normalization methods on texture classification. Magn. Reson. Imaging 2004, 22, 81–91. [Google Scholar] [CrossRef] [PubMed]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man. Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Galloway, M.M. Texture analysis using gray level run lengths. Comput. Graph. Image Process. 1975, 4, 172–179. [Google Scholar] [CrossRef]
- Chu, A.; Sehgal, C.M.; Greenleaf, J.F. Use of gray value distribution of run lengths for texture analysis. Pattern Recognit. Lett. 1990, 11, 415–419. [Google Scholar] [CrossRef]
- Dasarathy, B.V.; Holder, E.B. Image characterizations based on joint gray level—Run length distributions. Pattern Recognit. Lett. 1991, 12, 497–502. [Google Scholar] [CrossRef]
- Tang, X. Texture information in run-length matrices. IEEE Trans. Image Process. 1998, 7, 1602–1609. [Google Scholar] [CrossRef]
- Thibault, G. Indices de Forme et de Texture: De la 2D vers la 3D: Application au Classement de Noyaux de Cellules. Ph.D. Thesis, Aix-Marseille 2, Marseille, France, 2009. [Google Scholar]
- Amadasun, M.; King, R. Textural features corresponding to textural properties. IEEE Trans. Syst. Man Cybern. 1989, 19, 1264–1274. [Google Scholar] [CrossRef]
- Bilello, M.; Akbari, H.; Da, X.; Pisapia, J.M.; Mohan, S.; Wolf, R.L.; O’Rourke, D.M.; Martinez-Lage, M.; Davatzikos, C. Population-based MRI atlases of spatial distribution are specific to patient and tumor characteristics in glioblastoma. NeuroImage Clin. 2016, 12, 34–40. [Google Scholar] [CrossRef]
- Hogea, C.; Biros, G.; Abraham, F.; Davatzikos, C. A robust framework for soft tissue simulations with application to modeling brain tumor mass effect in 3D MR images. Phys. Med. Biol. 2007, 52, 6893. [Google Scholar] [CrossRef]
- Hogea, C.; Davatzikos, C.; Biros, G. Brain—Tumor interaction biophysical models for medical image registration. SIAM J. Sci. Comput. 2008, 30, 3050–3072. [Google Scholar] [CrossRef]
- Hogea, C.; Davatzikos, C.; Biros, G. An image-driven parameter estimation problem for a reaction—Diffusion glioma growth model with mass effects. J. Math. Biol. 2008, 56, 793–825. [Google Scholar] [CrossRef] [PubMed]
- Binder, Z.; Bakas, S.; Wileyto, E.; Akbari, H.; Rathore, S.; Rozycki, M.; Morrissette, J.; Martinez-Lage, M.; Dahmane, N.; Davatzikos, C.; et al. Extracellular EGFR289 activating mutations confer poorer survival and exhibit radiographic signature of enhanced motility in primary glioblastoma. Neuro-Oncology 2016, 18, vi105–vi106. [Google Scholar] [CrossRef]
- Rathore, S.; Akbari, H.; Rozycki, M.; Bakas, S.; Davatzikos, C. NIMG-20. Imaging Pattern Analysis Reveals Three Distinct Phenotypic Subtypes of gbm with Different Survival Rates; Oxford University Press: Oxford, MI, USA, 2016. [Google Scholar]
- Assefa, D.; Keller, H.; Ménard, C.; Laperriere, N.; Ferrari, R.J.; Yeung, I. Robust texture features for response monitoring of glioblastoma multiforme on-weighted and-FLAIR MR images: A preliminary investigation in terms of identification and segmentation. Med. Phys. 2010, 37, 1722–1736. [Google Scholar] [CrossRef]
- Aerts, H.J.; Velazquez, E.R.; Leijenaar, R.T.; Parmar, C.; Grossmann, P.; Carvalho, S.; Bussink, J.; Monshouwer, R.; Haibe-Kains, B.; Rietveld, D.; et al. Decoding tumour phenotype by noninvasive imaging using a quantitative radiomics approach. Nat. Commun. 2014, 5, 4006. [Google Scholar] [CrossRef]
- Bakas, S.; Akbari, H.; Sotiras, A.; Bilello, M.; Rozycki, M.; Kirby, J.; Freymann, J.; Farahani, K.; Davatzikos, C. Segmentation labels and radiomic features for the pre-operative scans of the TCGA-GBM collection. Cancer Imaging Arch. 2017, 286. [Google Scholar] [CrossRef]
- Ansari, A.; Jedidi, K.; Jagpal, S. A hierarchical Bayesian methodology for treating heterogeneity in structural equation models. Mark. Sci. 2000, 19, 328–347. [Google Scholar] [CrossRef]
- Sharkey, P.; Torrats-Espinosa, G.; Takyar, D. Community and the crime decline: The causal effect of local nonprofits on violent crime. Am. Sociol. Rev. 2017, 82, 1214–1240. [Google Scholar] [CrossRef]
- Wooditch, A.; Johnson, N.J.; Solymosi, R.; Medina Ariza, J.; Langton, S. Bivariate Correlation. In A Beginner’s Guide to Statistics for Criminology and Criminal Justice Using R; Springer: Berlin/Heidelberg, Germany, 2021; pp. 227–244. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley & Sons: Hoboken, NJ, USA, 1950; Volume 1. [Google Scholar]
- Armocida, D.; Pesce, A.; Di Giammarco, F.; Frati, A.; Salvati, M.; Santoro, A. Histological, molecular, clinical and outcomes characteristics of Multiple Lesion Glioblastoma. A retrospective monocentric study and review of literature. Neurocirugia 2021, 32, 114–123. [Google Scholar] [CrossRef]
- Showalter, T.N.; Andrel, J.; Andrews, D.W.; Curran, W.J., Jr.; Daskalakis, C.; Werner-Wasik, M. Multifocal glioblastoma multiforme: Prognostic factors and patterns of progression. Int. J. Radiat. Oncol. Biol. Phys. 2007, 69, 820–824. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Holland, E.C. Glioblastoma multiforme: The terminator. Proc. Natl. Acad. Sci. USA 2000, 97, 6242–6244. [Google Scholar] [CrossRef]
- Felsher, D.W.; Bishop, J.M. Reversible tumorigenesis by MYC in hematopoietic lineages. Mol. Cell 1999, 4, 199–207. [Google Scholar] [CrossRef]
- Pelengaris, S.; Littlewood, T.; Khan, M.; Elia, G.; Evan, G. Reversible activation of c-Myc in skin: Induction of a complex neoplastic phenotype by a single oncogenic lesion. Mol. Cell 1999, 3, 565–577. [Google Scholar] [CrossRef] [PubMed]
- Chin, L.; Tam, A.; Pomerantz, J.; Wong, M.; Holash, J.; Bardeesy, N.; Shen, Q.; O’Hagan, R.; Pantginis, J.; Zhou, H.; et al. Essential role for oncogenic Ras in tumour maintenance. Nature 1999, 400, 468–472. [Google Scholar] [CrossRef] [PubMed]
- Bilgel, M.; Jedynak, B.; Wong, D.F.; Resnick, S.M.; Prince, J.L. Temporal trajectory and progression score estimation from voxelwise longitudinal imaging measures: Application to amyloid imaging. In Information Processing in Medical Imaging, Proceedings of the 24th International Conference, IPMI 2015, Sabhal Mor Ostaig, Isle of Skye, UK, 28 June– 3 July 2015; Proceedings 24; Springer: Berlin/Heidelberg, Germany, 2015; pp. 424–436. [Google Scholar]
- Li, D.; Iddi, S.; Thompson, W.K.; Donohue, M.C.; Initiative, A.D.N. Bayesian latent time joint mixed effect models for multicohort longitudinal data. Stat. Methods Med Res. 2019, 28, 835–845. [Google Scholar] [CrossRef]
- Abi Nader, C.; Ayache, N.; Frisoni, G.B.; Robert, P.; Lorenzi, M.; Initiative, A.D.N. Simulating the outcome of amyloid treatments in Alzheimer’s disease from imaging and clinical data. Brain Commun. 2021, 3, fcab091. [Google Scholar] [CrossRef] [PubMed]
- Marinescu, R.V.; Eshaghi, A.; Alexander, D.C.; Golland, P. BrainPainter: A software for the visualisation of brain structures, biomarkers and associated pathological processes. In Multimodal Brain Image Analysis and Mathematical Foundations of Computational Anatomy, Proceedings of the 4th International Workshop, MBIA 2019, and 7th International Workshop, MFCA 2019, Held in Conjunction with MICCAI 2019, Shenzhen, China, 17 October 2019; Proceedings 4; Springer: Berlin/Heidelberg, Germany, 2019; pp. 112–120. [Google Scholar]
- Burnham, S.C.; Fandos, N.; Fowler, C.; Pérez-Grijalba, V.; Dore, V.; Doecke, J.D.; Shishegar, R.; Cox, T.; Fripp, J.; Rowe, C.; et al. Longitudinal evaluation of the natural history of amyloid-β in plasma and brain. Brain Commun. 2020, 2, fcaa041. [Google Scholar] [CrossRef]
- Gromeier, M.; Lachmann, S.; Rosenfeld, M.R.; Gutin, P.H.; Wimmer, E. Intergeneric poliovirus recombinants for the treatment of malignant glioma. Proc. Natl. Acad. Sci. USA 2000, 97, 6803–6808. [Google Scholar] [CrossRef]
- Mitchell, D.A.; Fecci, P.E.; Sampson, J.H. Immunotherapy of malignant brain tumors. Immunol. Rev. 2008, 222, 70–100. [Google Scholar] [CrossRef]
- Tomaszewski, W.; Sanchez-Perez, L.; Gajewski, T.F.; Sampson, J.H. Brain tumor microenvironment and host state: Implications for immunotherapy. Clin. Cancer Res. 2019, 25, 4202–4210. [Google Scholar] [CrossRef] [PubMed]
- Hotchkiss, K.M.; Sampson, J.H. Temozolomide treatment outcomes and immunotherapy efficacy in brain tumor. J. Neuro-Oncol. 2021, 151, 55–62. [Google Scholar] [CrossRef]
- Kim, S.S.; Harford, J.B.; Pirollo, K.F.; Chang, E.H. Effective treatment of glioblastoma requires crossing the blood–brain barrier and targeting tumors including cancer stem cells: The promise of nanomedicine. Biochem. Biophys. Res. Commun. 2015, 468, 485–489. [Google Scholar] [CrossRef] [PubMed]
- Lin, K.W.; Liao, A.; Qutub, A.A. Simulation predicts IGFBP2-HIF1α interaction drives glioblastoma growth. PLoS Comput. Biol. 2015, 11, e1004169. [Google Scholar] [CrossRef] [PubMed]
- Ozdemir-Kaynak, E.; Qutub, A.A.; Yesil-Celiktas, O. Advances in glioblastoma multiforme treatment: New models for nanoparticle therapy. Front. Physiol. 2018, 9, 170. [Google Scholar] [CrossRef]
- Chow, R.D.; Guzman, C.D.; Wang, G.; Schmidt, F.; Youngblood, M.W.; Ye, L.; Errami, Y.; Dong, M.B.; Martinez, M.A.; Zhang, S.; et al. AAV-mediated direct in vivo CRISPR screen identifies functional suppressors in glioblastoma. Nat. Neurosci. 2017, 20, 1329–1341. [Google Scholar] [CrossRef]
- Decarvalho, A.C.; Kim, H.; Poisson, L.M.; Winn, M.E.; Mueller, C.; Cherba, D.; Koeman, J.; Seth, S.; Protopopov, A.; Felicella, M.; et al. Discordant inheritance of chromosomal and extrachromosomal DNA elements contributes to dynamic disease evolution in glioblastoma. Nat. Genet. 2018, 50, 708–717. [Google Scholar] [CrossRef]
- Robertson, F.L.; Marqués-Torrejón, M.A.; Morrison, G.M.; Pollard, S.M. Experimental models and tools to tackle glioblastoma. Dis. Model. Mech. 2019, 12, dmm040386. [Google Scholar] [CrossRef]
- McNutt, T.R.; Benedict, S.H.; Low, D.A.; Moore, K.; Shpitser, I.; Jiang, W.; Lakshminarayanan, P.; Cheng, Z.; Han, P.; Hui, X.; et al. Using big data analytics to advance precision radiation oncology. Int. J. Radiat. Oncol. Biol. Phys. 2018, 101, 285–291. [Google Scholar] [CrossRef]




| Radiomic Features | Parameters | Mean | Standard Deviation |
|---|---|---|---|
| Volume | Whole Tumor | 107,999.84 | 52,700.74 |
| Edema | 62,139.61 | 35,360.39 | |
| Tumor Core | 45,560.24 | 31,424.16 | |
| Non-enhancing Tumor | 15,578.29 | 17,475.42 | |
| GD-Enhancing Tumor | 29,981.94 | 22,104.20 | |
| Spatial Parameters | Spatial Frontal | 25.64 | 35.69 |
| Spatial Temporal | 42.39 | 38.89 | |
| Spatial Occipital | 4.22 | 14.13 | |
| Spatial Insula | 2.95 | 5.76 | |
| Spatial Fornix | 1.19 | 3.04 | |
| Spatial Parietal | 18.34 | 29.50 | |
| Spatial Brain Stem | 0.25 | 0.71 | |
| Histology Parameters | Occipital Cortex | 0.375 | 0.8097 |
| Temporal Cortex | 0.146 | 0.3546 | |
| Basal Ganglia | 0.681 | 1.508 | |
| Morphology | Eccentricity | 0.68 | 0.09 |
| Solidity | 0.40 | 0.14 | |
| Survival Length (in years) | 1.5 | 1.4 |
| Sample No. | Posterior Mean Volume | Probability | ||
|---|---|---|---|---|
| Estimate | 95% C.I. | Estimate | 95% C.I. | |
| 43 | 1038 | [1037.924, 1038.076] | 0.5625000 | [0.2944, 0.8306] |
| 51 | 1346 | [1345.911, 1346.089] | 0.6400000 | [0.4286, 0.8514] |
| 8 | 3528 | [3527.910, 3528.090] | 0.6944444 | [0.4643, 0.9125] |
| 65 | 5008 | [5007.907, 5008.093] | 0.7901235 | [0.6155, 0.9245] |
| 101 | 6224 | [6223.896, 6224.104] | 0.8264463 | [0.7092, 0.9408] |
| 96 | 6559 | [6558.842, 6559.158] | 0.8622449 | [0.8119, 0.9436] |
| 12 | 8587 | [8586.837, 8587.163] | 0.9070295 | [0.8732, 0.9570] |
| 38 | 8990 | [8989.836, 8990.164] | 0.9420415 | [0.9271, 0.9647] |
| 17 | 9001 | [9000.813, 9001.187] | 0.9674819 | [0.9430, 0.9771] |
| 74 | 9101 | [9100.723, 9101.277] | 0.9760488 | [0.9579, 0.9990] |
| ROIs | Spatial Features | Histology Features | ||||
|---|---|---|---|---|---|---|
| F-Stat. | p-Val. | F-Stat. | p-Val. | |||
| ED | 0.8814 | 0.2104 | 0.3445 | 0.8540 | 0.0381 | 0.3826 |
| ET | 0.8601 | 0.1083 | 0.3746 | 0.8676 | 0.0076 | 0.3638 |
| NET | 0.7899 | 0.0074 | 0.4584 | 0.8822 | 0.0154 | 0.3432 |
| TC | 0.7805 | 0.0012 | 0.4685 | - | - | - |
| WT | 0.7820 | 0.0052 | 0.4669 | - | - | - |
| Eventual Volume (In Nearest Cubic mm) | Probability That No Cancer Cells Remain Undetected | Tumor Subregion | ||
|---|---|---|---|---|
| Estimate | 95% C.I. | Estimate | 95% C.I. | |
| 9525 | [9433.78, 9616.22] | 0.9937805 | [0.9934967, 0.9940643] | ET |
| 68,592 | [68,500.78, 68,683.33] | 0.9961458 | [0.9958620, 0.9964296] | ET |
| 5899 | [5807.78, 5990.22] | 0.9556447 | [0.9553609, 0.9559285] | ET |
| 31,614 | [31,522.78, 31,705.22] | 0.9907852 | [0.9905014, 0.9910690] | NET |
| 7338 | [7246.78, 7429.22] | 0.8806554 | [0.8803716, 0.8809392] | NET |
| 17,679 | [17,587.78, 17,770.22] | 0.9778719 | [0.9775881, 0.9781557] | NET |
| 34,935 | [34,843.78, 35,026.22] | 0.9738203 | [0.9735365, 0.9741041] | ED |
| 70,998 | [70,906.78, 71,089.22] | 0.9777224 | [0.9774386, 0.9780062] | ED |
| 83,517 | [83,425.78, 83,608.22] | 0.9890068 | [0.9887230, 0.9892906] | ED |
| 117,105 | [117,013.78, 117,196.22] | 0.9839206 | [0.9836368, 0.9842044] | TC |
| 86,271 | [86,179.78, 86,362.22] | 0.9632160 | [0.9629322, 0.9634998] | TC |
| 37,513 | [37,421.78, 37,604.22] | 0.9502363 | [0.9499525, 0.9505201] | TC |
| 279,108 | [278,136.78, 281,916.22] | 0.9618206 | [0.9536135, 0.9871034] | WT |
| 196,472 | [183,412.78, 203,120.22] | 0.9931245 | [0.9910266, 0.9954483] | WT |
| 138,532 | [113,574.78, 158,964.22] | 0.9802536 | [0.9795436, 0.9871256] | WT |
| ROIs | R-Squared | AIC | C.V. Error | |||
|---|---|---|---|---|---|---|
| GLM | Bayesian | GLM | Bayesian | GLM | Bayesian | |
| ED | 0.7936 | 0.8341 | 212.56 | 179.69 | 0.3637 | 0.2931 |
| ET | 0.8924 | 0.9018 | 265.23 | 259.86 | 0.7750 | 0.7236 |
| NET | 0.8825 | 0.9341 | 338.53 | 338.38 | 2.1869 | 1.1805 |
| TC | 0.5301 | 0.5305 | 301.25 | 251.61 | 0.7304 | 0.7293 |
| WT | 0.9176 | 0.9372 | 190.46 | 187.35 | 0.3634 | 0.3130 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, A.; Ding, S.; Liu, R.; Huang, C. Quantifying the Growth of Glioblastoma Tumors Using Multimodal MRI Brain Images. Cancers 2023, 15, 3614. https://doi.org/10.3390/cancers15143614
Das A, Ding S, Liu R, Huang C. Quantifying the Growth of Glioblastoma Tumors Using Multimodal MRI Brain Images. Cancers. 2023; 15(14):3614. https://doi.org/10.3390/cancers15143614
Chicago/Turabian StyleDas, Anisha, Shengxian Ding, Rongjie Liu, and Chao Huang. 2023. "Quantifying the Growth of Glioblastoma Tumors Using Multimodal MRI Brain Images" Cancers 15, no. 14: 3614. https://doi.org/10.3390/cancers15143614
APA StyleDas, A., Ding, S., Liu, R., & Huang, C. (2023). Quantifying the Growth of Glioblastoma Tumors Using Multimodal MRI Brain Images. Cancers, 15(14), 3614. https://doi.org/10.3390/cancers15143614







