Integrated Network Pharmacology Approach for Drug Combination Discovery: A Multi-Cancer Case Study
Abstract
:Simple Summary
Abstract
1. Introduction
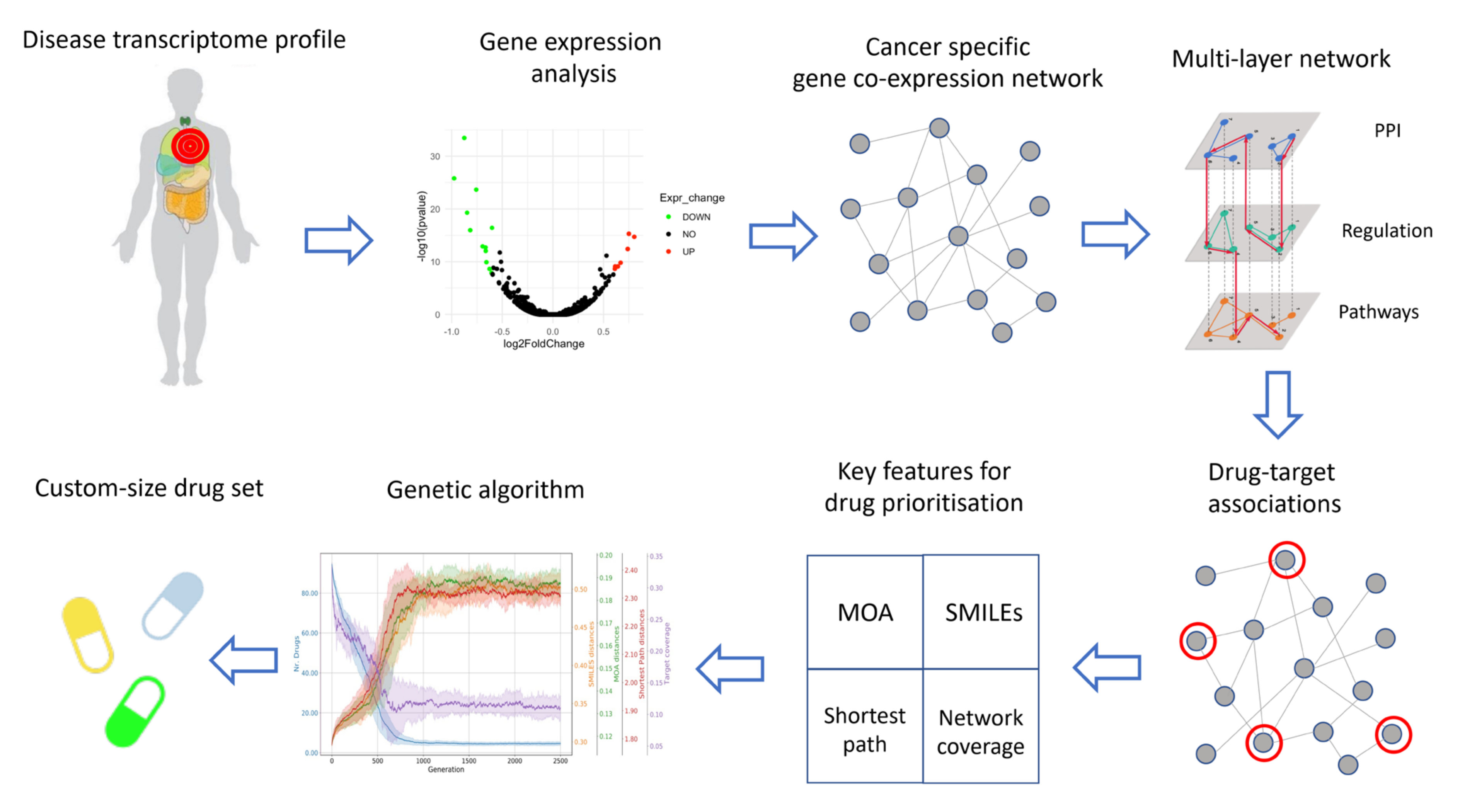
2. Materials and Methods
2.1. Data Collection
2.2. Gene Expression Analysis
2.3. Co-Expression Networks Inference
2.4. Construction of the Multi-Layer Network
2.5. Characterization of Drugs Properties
2.6. Final Drug Prioritization
- (1).
- MOA: the drugs in must have the most dissimilar mechanisms of action: , where is the average HIM distance between each pair of drugs in : , where is the number of drugs in ;
- (2).
- SMILES: the drugs in must have the most different secondary structure: , where is the average Levenshtein distance between each pair of drugs in : ;
- (3).
- TARGETS: the drugs in must target genes which are as far as possible between themselves in the cancer network: , where is the average length of the shortest paths between the sets of targets of each pair of drugs in : ;
- (4).
- COVERAGE: the drugs in must target as many genes as possible in the cancer network: ;
- (5).
- SIZE: we want the smallest subset of drugs .
3. Results and Discussion
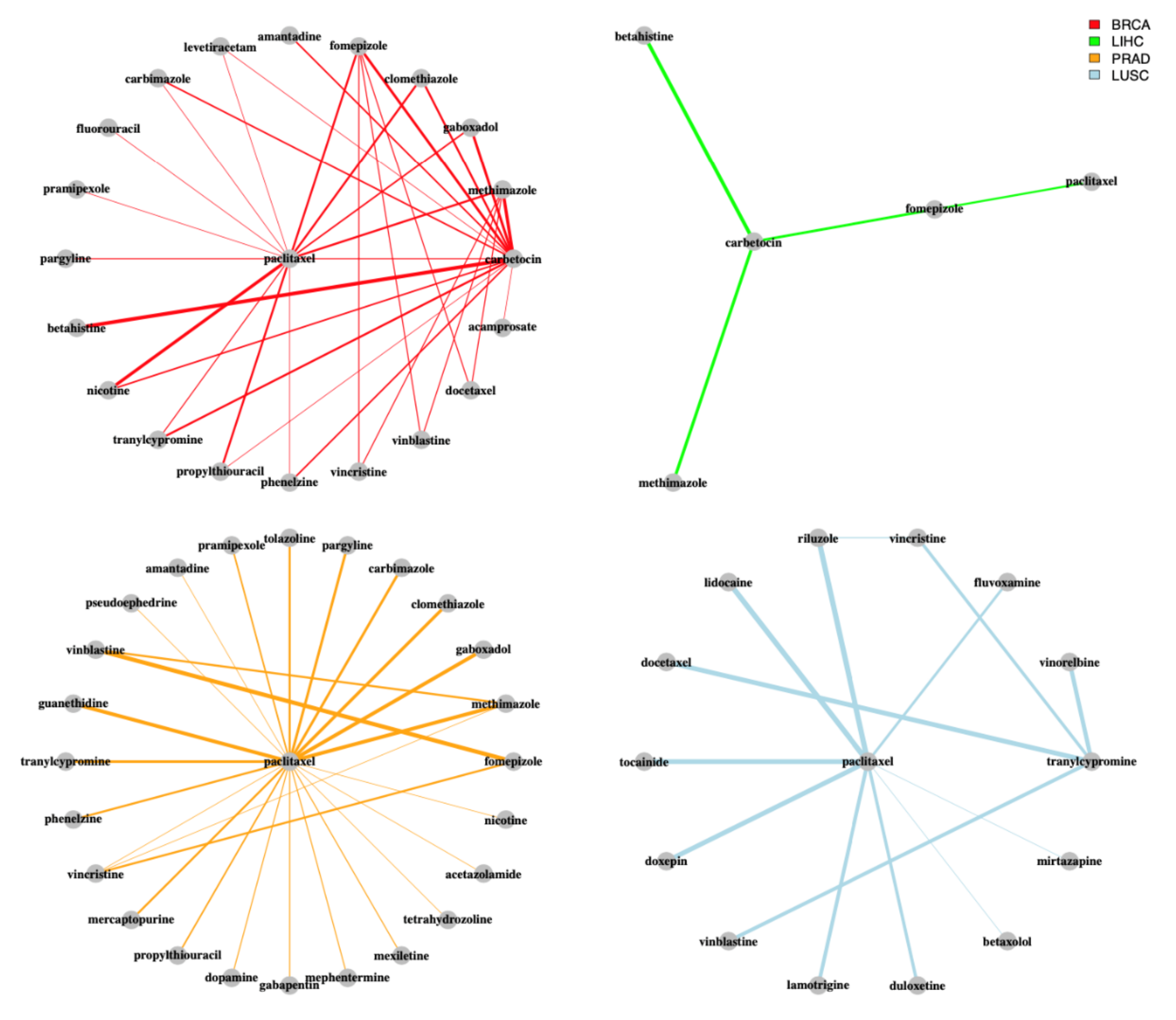
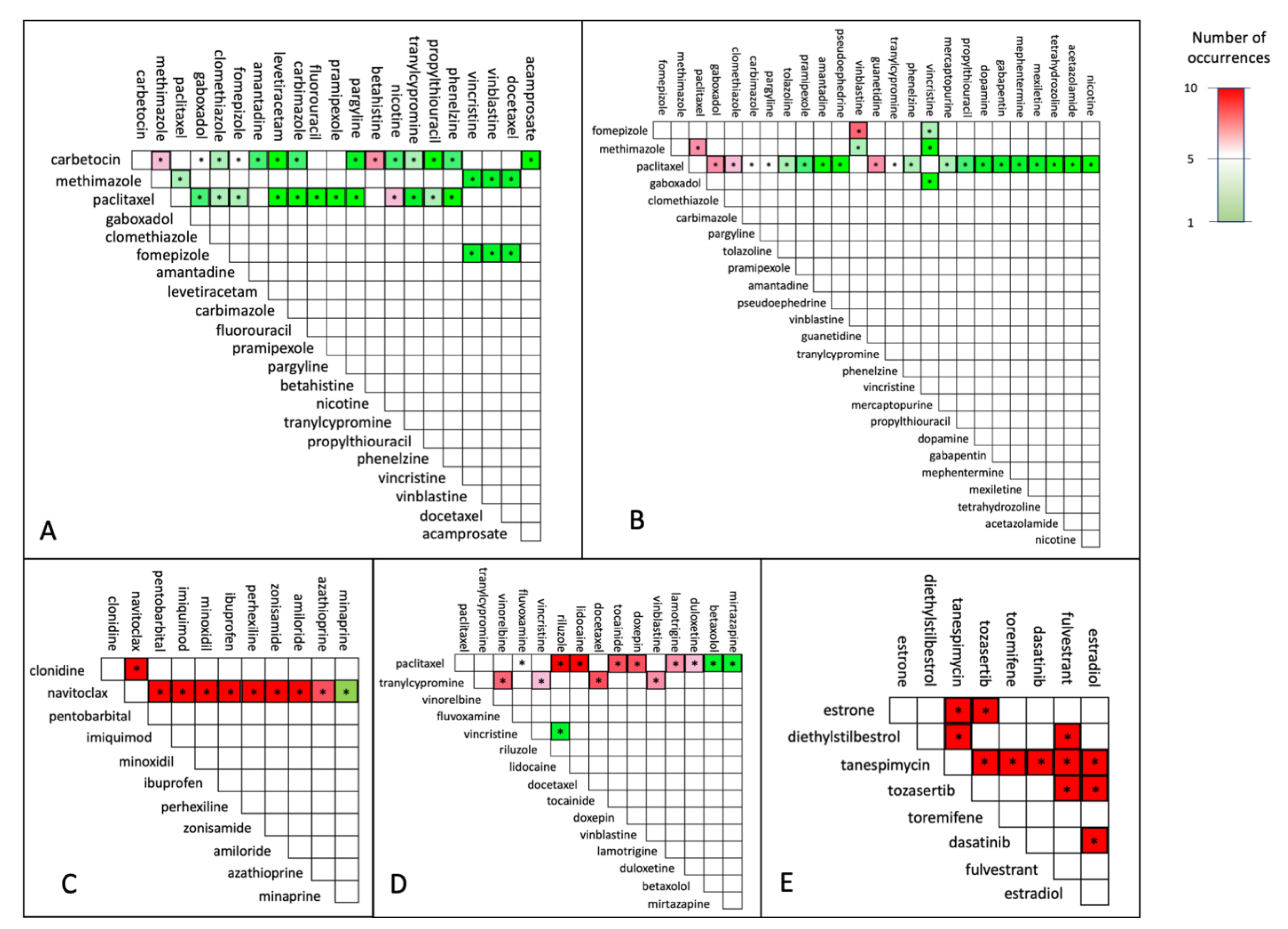
3.1. Implementation
3.2. Case Study
3.3. Robustness and Stability Evaluation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pulley, J.M.; Rhoads, J.P.; Jerome, R.N.; Challa, A.; Erreger, K.B.; Joly, M.M.; Lavieri, R.R.; Perry, K.E.; Zaleski, N.M.; Shirey-Rice, J.K.; et al. Using What We Already Have: Uncovering New Drug Repurposing Strategies in Existing Omics Data. Annu. Rev. Pharmacol. Toxicol. 2020, 60, 333–352. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Napolitano, F.; Zhao, Y.; Moreira, V.M.; Tagliaferri, R.; Kere, J.; D’Amato, M.; Greco, D. Drug repositioning: A machine-learning approach through data integration. J. Cheminform. 2013, 5, 30. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lamb, J.; Crawford, E.D.; Peck, D.; Modell, J.W.; Blat, I.C.; Wrobel, M.J.; Lerner, J.; Brunet, J.-P.; Subramanian, A.; Ross, K.N.; et al. The Connectivity Map: Using Gene-Expression Signatures to Connect Small Molecules, Genes, and Disease. Science 2006, 313, 1929–1935. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheng, F.; Desai, R.J.; Handy, D.; Wang, R.; Schneeweiss, S.; Barabasi, A.; Loscalzo, J. Network-based approach to prediction and population-based validation of in silico drug repurposing. Nat. Commun. 2018, 9, 2691. [Google Scholar] [CrossRef] [Green Version]
- Cheng, F.; Kovacs, I.A.; Barabaási, A.-L. Network-based prediction of drug combinations. Nat. Commun. 2019, 10, 1197. [Google Scholar] [CrossRef]
- Li, S.; Zhang, B.; Zhang, N. Network target for screening synergistic drug combinations with application to traditional Chinese medicine. BMC Syst. Biol. 2011, 5, S10. [Google Scholar] [CrossRef] [Green Version]
- Gayvert, K.M.; Aly, O.; Platt, J.; Bosenberg, M.W.; Stern, D.F.; Elemento, O. A Computational Approach for Identifying Synergistic Drug Combinations. PLoS Comput. Biol. 2017, 13, e1005308. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Rani, R. An integrated framework for identification of effective and synergistic anti-cancer drug combinations. J. Bioinform. Comput. Biol. 2018, 16, 1850017. [Google Scholar] [CrossRef]
- Li, Y.; Wei, Q.; Yu, G.; Gai, W.; Chen, X. DCDB 2.0: A major update of the drug combination database. Database 2014, 2014, bau124. [Google Scholar] [CrossRef]
- Wishart, D.S.; Feunang, Y.D.; Guo, A.C.; Lo, E.J.; Marcu, A.; Grant, J.R.; Sajed, T.; Johnson, D.; Li, C.; Sayeeda, Z.; et al. DrugBank 5.0: A Major Update to the DrugBank Database for 2018. Nucleic Acids Res. 2018, 46, D1074–D1082. [Google Scholar] [CrossRef]
- Held, M.A.; Langdon, C.G.; Platt, J.T.; Graham-Steed, T.; Liu, Z.; Chakraborty, A.; Bacchiocchi, A.; Koo, A.; Haskins, J.W.; Bosenberg, M.W.; et al. Genotype-Selective Combination Therapies for Melanoma Identified by High-Throughput Drug Screening. Cancer Discov. 2013, 3, 52–67. [Google Scholar] [CrossRef] [Green Version]
- Menden, M.P.; Wang, D.; Mason, M.J.; Szalai, B.; Bulusu, K.C.; Guan, Y.; Yu, T.; Kang, J.; Jeon, M.; Wolfinger, R.; et al. Community assessment to advance computational prediction of cancer drug combinations in a pharmacogenomic screen. Nat. Commun. 2019, 10, 2674. [Google Scholar] [CrossRef] [Green Version]
- Ji, X.; Tong, W.; Liu, Z.; Shi, T. Five-Feature Model for Developing the Classifier for Synergistic vs. Antagonistic Drug Combinations Built by XGBoost. Front. Genet. 2019, 10, 600. [Google Scholar] [CrossRef] [Green Version]
- Serra, A.; Önlü, S.; Coretto, P.; Greco, D. An integrated quantitative structure and mechanism of action-activity relationship model of human serum albumin binding. J. Cheminform. 2019, 11, 38. [Google Scholar] [CrossRef]
- Serra, A.; Fratello, M.; Federico, A.; Ojha, R.; Provenzani, R.; Tasnadi, E.; Cattelani, L.; del Giudice, G.; Kinaret, P.A.S.; Saarimäki, L.A.; et al. Computationally prioritized drugs inhibit SARS-CoV-2 infection and syncytia formation. Brief. Bioinform. 2022, 23, bbab507. [Google Scholar] [CrossRef]
- Colaprico, A.; Silva, T.C.; Olsen, C.; Garofano, L.; Cava, C.; Garolini, D.; Sabedot, T.S.; Malta, T.M.; Pagnotta, S.M.; Castiglioni, I.; et al. TCGAbiolinks: An R/Bioconductor package for integrative analysis of TCGA data. Nucleic Acids Res. 2016, 44, e71. [Google Scholar] [CrossRef]
- Stathias, V.; Turner, J.; Koleti, A.; Vidovic, D.; Cooper, D.; Fazel-Najafabadi, M.; Pilarczyk, M.; Terryn, R.; Chung, C.; Umeano, A.; et al. LINCS Data Portal 2.0: Next generation access point for perturbation-response signatures. Nucleic Acids Res. 2019, 48, D431–D439. [Google Scholar] [CrossRef] [Green Version]
- Rosner, B.; Glynn, R.J.; Lee, M.-L.T. The Wilcoxon Signed Rank Test for Paired Comparisons of Clustered Data. Biometrics 2005, 62, 185–192. [Google Scholar] [CrossRef]
- Marwah, V.S.; Kinaret, P.A.S.; Serra, A.; Scala, G.; Lauerma, A.; Fortino, V.; Greco, D. INfORM: Inference of NetwOrk Response Modules. Bioinformatics 2018, 34, 2136–2138. [Google Scholar] [CrossRef] [Green Version]
- Faith, J.J.; Hayete, B.; Thaden, J.T.; Mogno, I.; Wierzbowski, J.; Cottarel, G.; Kasif, S.; Collins, J.J.; Gardner, T.S. Large-Scale Mapping and Validation of Escherichia coli Transcriptional Regulation from a Compendium of Expression Profiles. PLoS Biol. 2007, 5, e8. [Google Scholar] [CrossRef]
- Margolin, A.A.; Nemenman, I.; Basso, K.; Wiggins, C.; Stolovitzky, G.; Favera, R.D.; Califano, A. ARACNE: An Algorithm for the Reconstruction of Gene Regulatory Networks in a Mammalian Cellular Context. BMC Bioinform. 2006, 7 (Suppl. S1), S7. [Google Scholar] [CrossRef] [Green Version]
- Meyer, P.E.; Kontos, K.; Lafitte, F.; Bontempi, G. Information-Theoretic Inference of Large Transcriptional Regulatory Networks. EURASIP J. Bioinform. Syst. Biol. 2007, 2007, 79879. [Google Scholar] [CrossRef] [Green Version]
- Meyer, P.E.; Lafitte, F.; Bontempi, G. minet: A R/Bioconductor Package for Inferring Large Transcriptional Networks Using Mutual Information. BMC Bioinform. 2008, 9, 461. [Google Scholar] [CrossRef]
- Schimek, M.G.; Budinská, E.; Kugler, K.G.; Svendova, V.; Ding, J.; Lin, S. TopKLists: A comprehensive R package for statistical inference, stochastic aggregation, and visualization of multiple omics ranked lists. Stat. Appl. Genet. Mol. Biol. 2015, 14, 311–316. [Google Scholar] [CrossRef] [Green Version]
- Pavel, A.; del Giudice, G.; Federico, A.; Di Lieto, A.; Kinaret, P.A.S.; Serra, A.; Greco, D. Integrated network analysis reveals new genes suggesting COVID-19 chronic effects and treatment. Briefings Bioinform. 2021, 22, 1430–1441. [Google Scholar] [CrossRef]
- Auer, S.; Kovtun, V.; Prinz, M.; Kasprzik, A.; Stocker, M.; Vidal, M.E. Towards a knowledge graph for science. In Proceedings of the 8th International Conference on Web Intelligence, Mining and Semantics—WIMS’18, Novi Sad, Serbia, 25–27 June 2018; Akerkar, R., Ivanović, M., Kim, S.-W., Manolopoulos, Y., Rosati, R., Savić, M., Badica, C., Radovanović, M., Eds.; ACM Press: New York, NY, USA, 2018; pp. 1–6. [Google Scholar]
- Nicholson, D.; Greene, C.S. Constructing knowledge graphs and their biomedical applications. Comput. Struct. Biotechnol. J. 2020, 18, 1414–1428. [Google Scholar] [CrossRef]
- Van der Loo, M.P.J. The stringdist package for approximate string matching. R J. Comput. Sci. 2014, 6, 111–122. [Google Scholar]
- Fortin, F.-A.; De Rainville, F.-M.; Gardner, M.-A.; Parizeau, M.; Gagné, C. DEAP: Evolutionary algorithms made easy. J. Mach. Learn. Res. 2012, 13, 2171–2175. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Bazeley, P. Complementary analysis of varied data sources. In Integrating Analyses in Mixed Methods Research; SAGE Publications Ltd.: Thousand Oaks, FL, USA, 2018; pp. 91–125. ISBN 9781412961868. [Google Scholar]
- OuYang, J.; Yang, F.; Yang, S.W.; Nie, Z.P. The Improved NSGA-II Approach. J. Electromagn. Waves Appl. 2008, 22, 163–172. [Google Scholar] [CrossRef]
- Serra, A.; Önlü, S.; Festa, P.; Fortino, V.; Greco, D. MaNGA: A novel multi-objective multi-niche genetic algorithm for QSAR modelling. Bioinformatics 2020, 36, 145–153. [Google Scholar] [CrossRef] [PubMed]
- Ivery, M.T.G.; Le, T. Modeling the Interaction of Paclitaxel With β-Tubulin. Oncol. Res. Featur. Preclin. Clin. Cancer Ther. 2003, 14, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Fife, C.M.; McCarroll, J.; Kavallaris, M. Movers and shakers: Cell cytoskeleton in cancer metastasis. J. Cereb. Blood Flow Metab. 2014, 171, 5507–5523. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heinhuis, K.M.; Ros, W.; Kok, M.; Steeghs, N.; Beijnen, J.H.; Schellens, J.H.M. Enhancing antitumor response by combining immune checkpoint inhibitors with chemotherapy in solid tumors. Ann. Oncol. 2019, 30, 219–235. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Zhang, L.; Xiu, Z.; Guo, J.; Wang, L.; Zhou, Y.; Jiao, Y.; Sun, M.; Cai, J. Combination of Immune Checkpoint Inhibitors with Chemotherapy in Lung Cancer. OncoTargets Ther. 2020, 13, 7229–7241. [Google Scholar] [CrossRef] [PubMed]
- Wahid, M.; Mandal, R.K.; Dar, S.A.; Jawed, A.; Lohani, M.; Areeshi, M.Y.; Akhter, N.; Haque, S.; Areeshi, M.Y. Therapeutic potential and critical analysis of trastuzumab and bevacizumab in combination with different chemotherapeutic agents against metastatic breast/colorectal cancer affecting various endpoints. Crit. Rev. Oncol. Hematol. 2016, 104, 124–130. [Google Scholar] [CrossRef] [PubMed]
- Hisam, N.S.N.; Ugusman, A.; Rajab, N.F.; Ahmad, M.F.; Fenech, M.; Liew, S.L.; Anuar, N.N.M. Combination Therapy of Navitoclax with Chemotherapeutic Agents in Solid Tumors and Blood Cancer: A Review of Current Evidence. Br. J. Pharmacol. 2021, 13, 1353. [Google Scholar] [CrossRef]
- Zhang, H.-H.; Guo, X.-L. Combinational strategies of metformin and chemotherapy in cancers. Cancer Chemother. Pharmacol. 2016, 78, 13–26. [Google Scholar] [CrossRef]
- Schott, A.F.; Goldstein, L.J.; Cristofanilli, M.; Ruffini, P.A.; McCanna, S.; Reuben, J.M.; Perez, R.P.; Kato, G.; Wicha, M. Phase Ib Pilot Study to Evaluate Reparixin in Combination with Weekly Paclitaxel in Patients with HER-2–Negative Metastatic Breast Cancer. Clin. Cancer Res. 2017, 23, 5358–5365. [Google Scholar] [CrossRef] [Green Version]
- Young, S.Z.; Bordey, A. GABA’s Control of Stem and Cancer Cell Proliferation in Adult Neural and Peripheral Niches. Physiology 2009, 24, 171–185. [Google Scholar] [CrossRef] [Green Version]
- Abdul, M.; McCray, S.D.; Hoosein, N.M. Expression of gamma-aminobutyric acid receptor (subtype A) in prostate cancer. Acta Oncol. 2008, 47, 1546–1550. [Google Scholar] [CrossRef]
- Tian, J.; Chau, C.; Hales, T.G.; Kaufman, D.L. GABAA receptors mediate inhibition of T cell responses. J. Neuroimmunol. 1999, 96, 21–28. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, R.; Zheng, Y.; Shen, J.; Xiao, D.; Li, J.; Shi, X.; Huang, L.; Tang, H.; Liu, J.; et al. Expression of gamma-aminobutyric acid receptors on neoplastic growth and prediction of prognosis in non-small cell lung cancer. J. Transl. Med. 2013, 11, 102. [Google Scholar] [CrossRef] [Green Version]
- Thaker, P.H.; Yokoi, K.; Jennings, N.B.; Li, Y.; Rebhun, R.B.; Rousseau, D.L., Jr.; Fan, D.; Sood, A.K. Inhibition of experimental colon cancer metastasis by the GABA-receptor agonist nembutal. Cancer Biol. Ther. 2005, 4, 753–758. [Google Scholar] [CrossRef] [Green Version]
- Reversi, A.; Rimoldi, V.; Marrocco, T.; Cassoni, P.; Bussolati, G.; Parenti, M.; Chini, B. The Oxytocin Receptor Antagonist Atosiban Inhibits Cell Growth via a “Biased Agonist” Mechanism. J. Biol. Chem. 2005, 280, 16311–16318. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Gruber, C.; Alewood, P.F.; Möller, A.; Muttenthaler, M. The oxytocin receptor signalling system and breast cancer: A critical review. Oncogene 2020, 39, 5917–5932. [Google Scholar] [CrossRef]
- Poyurovsky, M.; Pashinian, A.; Levi, A.; Weizman, R.; Weizman, A. The effect of betahistine, a histamine H1 receptor agonist/H3 antagonist, on olanzapine-induced weight gain in first-episode schizophrenia patients. Int. Clin. Psychopharmacol. 2005, 20, 101–103. [Google Scholar] [CrossRef]
- Rivera, E.S.; Cricco, G.P.; Engel, N.I.; Fitzsimons, C.P.; Martín, G.A.; Bergoc, R.M. Histamine as an autocrine growth factor: An unusual role for a widespread mediator. Semin. Cancer Biol. 2000, 10, 15–23. [Google Scholar] [CrossRef]
- Sieja, K.; Stanosz, S.; von Mach-Szczypiński, J.; Olewniczak, S. Concentration of histamine in serum and tissues of the primary ductal breast cancers in women. Breast 2005, 14, 236–241. [Google Scholar] [CrossRef]
- Medina, V.; Cricco, G.; Nuñez, M.; Martín, G.; Mohamad, N.; Correa-Fiz, F.; Sanchez-Jiménez, F.; Bergoc, R.; Rivera, E.S. Histamine-mediated signaling processes in human malignant mammary cells. Cancer Biol. Ther. 2006, 5, 1462–1471. [Google Scholar] [CrossRef] [Green Version]
- Stark, H. Histamine H4 Receptor: A Novel Drug Target in Immunoregulation and Inflammation; Versita: London, UK, 2013; ISBN 9788376560564. [Google Scholar]
- Von Mach-Szczypiński, J.; Stanosz, S.; Sieja, K.; Stanosz, M. Metabolism of histamine in tissues of primary ductal breast cancer. Metab. Clin. Exp. 2009, 58, 867–870. [Google Scholar] [CrossRef] [PubMed]
- Medina, V.; Croci, M.; Crescenti, E.; Mohamad, N.; Sanchez-Jiménez, F.; Massari, N.; Nuñez, M.; Cricco, G.; Martin, G.; Bergoc, R.; et al. The role of histamine in human mammary carcinogenesis: H3 and H4 receptors as potential therapeutic targets for breast cancer treatment. Cancer Biol. Ther. 2008, 7, 28–35. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Massari, N.A.; Nicoud, M.B.; Medina, V.A. Histamine receptors and cancer pharmacology: An update. Br. J. Pharmacol. 2018, 177, 516–538. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, Y.; Yu, D. Tumor microenvironment as a therapeutic target in cancer. Pharmacol. Ther. 2021, 221, 107753. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Wang, X.; Yu, J.; Ma, F.; Li, Z.; Zhou, Y.; Zeng, S.; Ma, X.; Li, Y.-R.; Neal, A.; et al. Targeting monoamine oxidase A-regulated tumor-associated macrophage polarization for cancer immunotherapy. Nat. Commun. 2021, 12, 3530. [Google Scholar] [CrossRef]
- Dimopoulos, M.-A.; Mitsiades, C.S.; Anderson, K.C.; Richardson, P.G. Tanespimycin as Antitumor Therapy. Clin. Lymphoma Myeloma Leuk. 2011, 11, 17–22. [Google Scholar] [CrossRef]
- Banerji, U. Heat Shock Protein 90 as a Drug Target: Some Like It Hot. Clin. Cancer Res. 2009, 15, 9–14. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Federico, A.; Fratello, M.; Scala, G.; Möbus, L.; Pavel, A.; del Giudice, G.; Ceccarelli, M.; Costa, V.; Ciccodicola, A.; Fortino, V.; et al. Integrated Network Pharmacology Approach for Drug Combination Discovery: A Multi-Cancer Case Study. Cancers 2022, 14, 2043. https://doi.org/10.3390/cancers14082043
Federico A, Fratello M, Scala G, Möbus L, Pavel A, del Giudice G, Ceccarelli M, Costa V, Ciccodicola A, Fortino V, et al. Integrated Network Pharmacology Approach for Drug Combination Discovery: A Multi-Cancer Case Study. Cancers. 2022; 14(8):2043. https://doi.org/10.3390/cancers14082043
Chicago/Turabian StyleFederico, Antonio, Michele Fratello, Giovanni Scala, Lena Möbus, Alisa Pavel, Giusy del Giudice, Michele Ceccarelli, Valerio Costa, Alfredo Ciccodicola, Vittorio Fortino, and et al. 2022. "Integrated Network Pharmacology Approach for Drug Combination Discovery: A Multi-Cancer Case Study" Cancers 14, no. 8: 2043. https://doi.org/10.3390/cancers14082043
APA StyleFederico, A., Fratello, M., Scala, G., Möbus, L., Pavel, A., del Giudice, G., Ceccarelli, M., Costa, V., Ciccodicola, A., Fortino, V., Serra, A., & Greco, D. (2022). Integrated Network Pharmacology Approach for Drug Combination Discovery: A Multi-Cancer Case Study. Cancers, 14(8), 2043. https://doi.org/10.3390/cancers14082043









