Prognostic Gene Discovery in Glioblastoma Patients using Deep Learning
Abstract
1. Introduction
2. Results
2.1. Deep Learning Model
2.2. Deep Learning Model Performance Comparison with Penalized Cox Regression Models
2.3. Network Node Parameters Improved the Baseline Cox Proportional Hazard Model
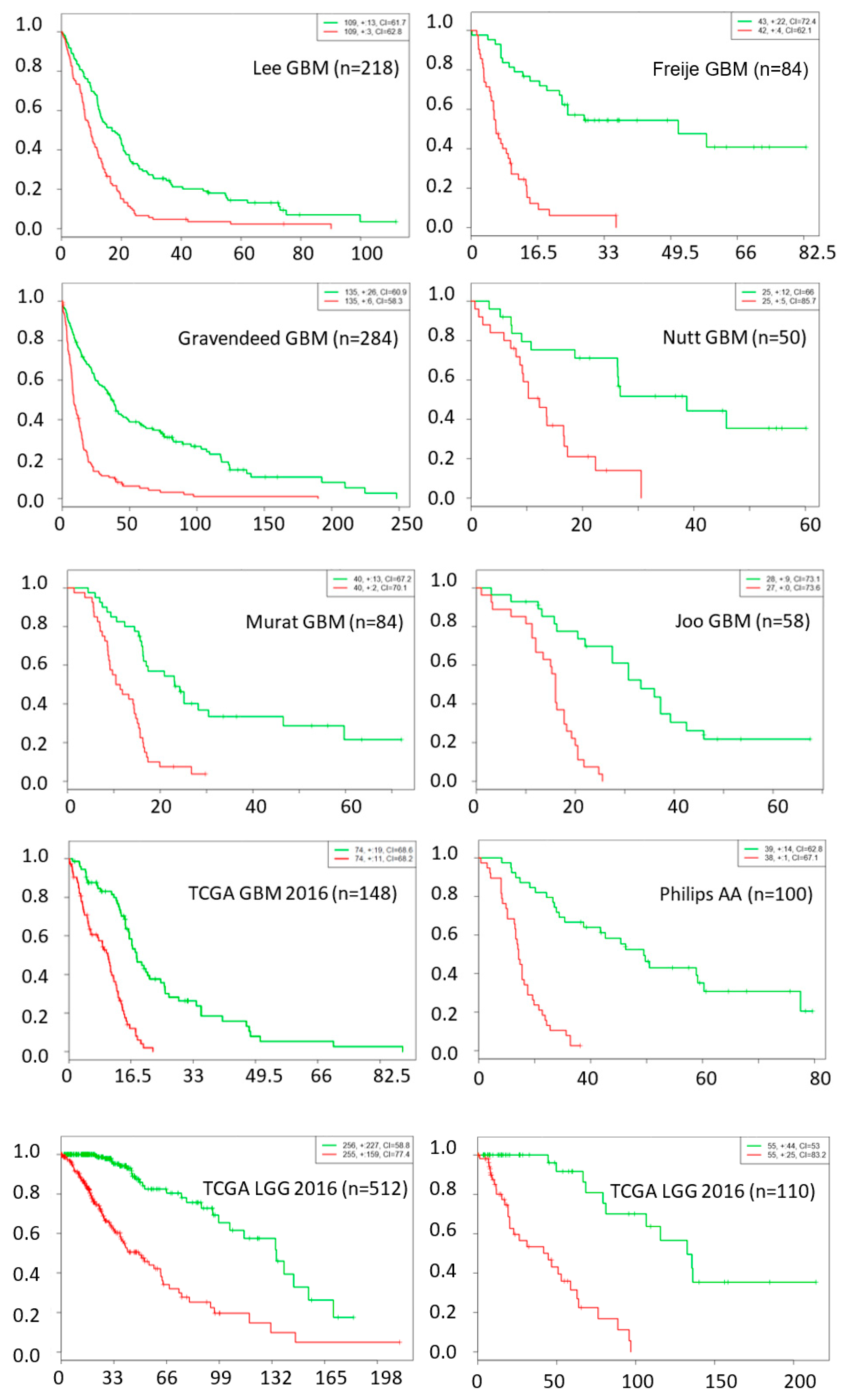
2.4. Prognostic Significance Validation of Gene Set with External Data
3. Discussion
4. Materials and Methods
4.1. Gene Expression Data Analysis
4.2. Deep Learning Model
4.3. Deep Learning Model Performance Comparison with Penalized Cox Regression Models
4.4. Impact of Deep Learning Network Features on Baseline Survival Model
4.5. Identifying Important Genes in Deep Learning Model
4.6. Prognostic Significance Validation of Gene Set with External Data
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Cheng, B.; Titterington, D.M. Neural Networks: A Review from a Statistical Perspective. Stat. Sci. 1994, 9, 2–30. [Google Scholar] [CrossRef]
- Kuan, C.M.; White, H. Artificial Neural Networks: An Econometric Perspective. Econom. Rev. 1994, 13, 1–91. [Google Scholar] [CrossRef]
- Ripley, B.D. Statistical Aspects of Neural Networks; Chapman & Hall: Boca Raton, FL, USA, 1993. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Cherkassky, V.; Friedman, J.H.; Wechsler, H. Statistics to Neural Networks: Theory and Pattern Recognition Applications; Springer: Berlin, Germany, 1994. [Google Scholar]
- Young, J.D.; Cai, C.; Lu, X. Unsupervised deep learning reveals prognostically relevant subtypes of glioblastoma. BMC Bioinform. 2017, 18, 381. [Google Scholar] [CrossRef]
- Preuer, K.; Lewis, R.P.I.; Hochreiter, S.; Bender, A.; Bulusu, K.C.; Klambauer, G. DeepSynergy: Predicting anti-cancer drug synergy with Deep Learning. Bioinformatics 2017. [Google Scholar] [CrossRef] [PubMed]
- Chaudhary, K.; Poirion, O.B.; Lu, L.; Garmire, L.X. Deep Learning based multi-omics integration robustly predicts survival in liver cancer. Clin. Cancer Res. 2017. [Google Scholar] [CrossRef] [PubMed]
- Putin, E.; Mamoshina, P.; Aliper, A.; Korzinkin, M.; Moskalev, A.; Kolosov, A.; Ostrovskiy, A.; Cantor, C.; Vijg, J.; Zhavoronkov, A. Deep biomarkers of human aging: Application of deep neural networks to biomarker development. Aging 2016, 8, 1021–1033. [Google Scholar] [CrossRef] [PubMed]
- Angermueller, C.; Lee, H.J.; Reik, W.; Stegle, O. DeepCpG: Accurate prediction of single-cell DNA methylation states using deep learning. Genome Biol. 2017, 18, 67. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Ung, M.; Cheng, C.; Greene, C.S. Unsupervised feature construction and knowledge extraction from genome-wide assays of breast cancer with denoising autoencoders. Pac. Symp. Biocomput. 2015, 132–143. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kim, Y.W.; Koul, D.; Kim, S.H.; Lucio-Eterovic, A.K.; Freire, P.R.; Yao, J.; Wang, J.; Almeida, J.S.; Aldape, K.; Yung, W.K. Identification of prognostic gene signatures of glioblastoma: A study based on TCGA data analysis. Neuro-Oncology 2013, 15, 829–839. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Bredel, M. Feature selection and survival modeling in The Cancer Genome Atlas. Int. J. Nanomed. 2013, 8 (Suppl. 1), 57–62. [Google Scholar] [CrossRef]
- Verhaak, R.G.; Hoadley, K.A.; Purdom, E.; Wang, V.; Qi, Y.; Wilkerson, M.D.; Miller, C.R.; Ding, L.; Golub, T.; Mesirov, J.P.; et al. Integrated genomic analysis identifies clinically relevant subtypes of glioblastoma characterized by abnormalities in PDGFRA, IDH1, EGFR, and NF1. Cancer Cell 2010, 17, 98–110. [Google Scholar] [CrossRef] [PubMed]
- Yousefi, S.; Amrollahi, F.; Amgad, M.; Dong, C.; Lewis, J.E.; Song, C.; Gutman, D.A.; Halani, S.H.; Velazquez Vega, J.E.; Brat, D.J.; et al. Predicting clinical outcomes from large scale cancer genomic profiles with deep survival models. Sci. Rep. 2017, 7, 11707. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Ledesma, E.; Verhaak, R.G.; Trevino, V. Identification of a multi-cancer gene expression biomarker for cancer clinical outcomes using a network-based algorithm. Sci. Rep. 2015, 5, 11966. [Google Scholar] [CrossRef]
- Kong, Y.; Yu, T. A graph-embedded deep feedforward network for disease outcome classification and feature selection using gene expression data. Bioinformatics 2018, 34, 3727–3737. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, B.; Hu, X.; Kim, H.; Squatrito, M.; Scarpace, L.; deCarvalho, A.C.; Lyu, S.; Li, P.; Li, Y.; et al. Tumor Evolution of Glioma-Intrinsic Gene Expression Subtypes Associates with Immunological Changes in the Microenvironment. Cancer Cell 2017, 32, 42–56. [Google Scholar] [CrossRef]
- Brennan, C.W.; Verhaak, R.G.; McKenna, A.; Campos, B.; Noushmehr, H.; Salama, S.R.; Zheng, S.; Chakravarty, D.; Sanborn, J.Z.; Berman, S.H.; et al. The somatic genomic landscape of glioblastoma. Cell 2013, 155, 462–477. [Google Scholar] [CrossRef] [PubMed]
- Floyd, D.H.; Kefas, B.; Seleverstov, O.; Mykhaylyk, O.; Dominguez, C.; Comeau, L.; Plank, C.; Purow, B. Alpha-secretase inhibition reduces human glioblastoma stem cell growth in vitro and in vivo by inhibiting Notch. Neuro-Oncology 2012, 14, 1215–1226. [Google Scholar] [CrossRef]
- Schnepp, P.M.; Lee, D.D.; Guldner, I.H.; O’Tighearnaigh, T.K.; Howe, E.N.; Palakurthi, B.; Eckert, K.E.; Toni, T.A.; Ashfeld, B.L.; Zhang, S. GAD1 Upregulation Programs Aggressive Features of Cancer Cell Metabolism in the Brain Metastatic Microenvironment. Cancer Res. 2017, 77, 2844–2856. [Google Scholar] [CrossRef]
- Steponaitis, G.; Skiriute, D.; Kazlauskas, A.; Golubickaite, I.; Stakaitis, R.; Tamasauskas, A.; Vaitkiene, P. High CHI3L1 expression is associated with glioma patient survival. Diagn. Pathol. 2016, 11, 42. [Google Scholar] [CrossRef] [PubMed]
- Francescone, R.A.; Scully, S.; Faibish, M.; Taylor, S.L.; Oh, D.; Moral, L.; Yan, W.; Bentley, B.; Shao, R. Role of YKL-40 in the angiogenesis, radioresistance, and progression of glioblastoma. J. Biol. Chem. 2011, 286, 15332–15343. [Google Scholar] [CrossRef] [PubMed]
- Mikheev, A.M.; Mikheeva, S.A.; Trister, A.D.; Tokita, M.J.; Emerson, S.N.; Parada, C.A.; Born, D.E.; Carnemolla, B.; Frankel, S.; Kim, D.H.; et al. Periostin is a novel therapeutic target that predicts and regulates glioma malignancy. Neuro-Oncology 2015, 17, 372–382. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Ke, S.Q.; Huang, Z.; Flavahan, W.; Fang, X.; Paul, J.; Wu, L.; Sloan, A.E.; McLendon, R.E.; Li, X.; et al. Periostin secreted by glioblastoma stem cells recruits M2 tumour-associated macrophages and promotes malignant growth. Nat. Cell Biol. 2015, 17, 170–182. [Google Scholar] [CrossRef] [PubMed]
- Park, S.Y.; Piao, Y.; Jeong, K.J.; Dong, J.; de Groot, J.F. Periostin (POSTN) Regulates Tumor Resistance to Antiangiogenic Therapy in Glioma Models. Mol. Cancer Ther. 2016, 15, 2187–2197. [Google Scholar] [CrossRef]
- Jung, J.; Kim, L.J.Y.; Wang, X.; Wu, Q.; Sanvoranart, T.; Hubert, C.G.; Prager, B.C.; Wallace, L.C.; Jin, X.; Mack, S.C.; et al. Nicotinamide metabolism regulates glioblastoma stem cell maintenance. JCI Insight 2017, 2. [Google Scholar] [CrossRef]
- Palanichamy, K.; Kanji, S.; Gordon, N.; Thirumoorthy, K.; Jacob, J.R.; Litzenberg, K.T.; Patel, D.; Chakravarti, A. NNMT Silencing Activates Tumor Suppressor PP2A, Inactivates Oncogenic STKs, and Inhibits Tumor Forming Ability. Clin. Cancer Res. 2017, 23, 2325–2334. [Google Scholar] [CrossRef]
- Clark, P.A.; Iida, M.; Treisman, D.M.; Kalluri, H.; Ezhilan, S.; Zorniak, M.; Wheeler, D.L.; Kuo, J.S. Activation of multiple ERBB family receptors mediates glioblastoma cancer stem-like cell resistance to EGFR-targeted inhibition. Neoplasia 2012, 14, 420–428. [Google Scholar] [CrossRef]
- Anlar, B.; Gunel-Ozcan, A. Tenascin-R: Role in the central nervous system. Int. J. Biochem. Cell Biol. 2012, 44, 1385–1389. [Google Scholar] [CrossRef]
- Dwyer, C.A.; Bi, W.L.; Viapiano, M.S.; Matthews, R.T. Brevican knockdown reduces late-stage glioma tumor aggressiveness. J. Neurooncol. 2014, 120, 63–72. [Google Scholar] [CrossRef]
- Lu, R.; Wu, C.; Guo, L.; Liu, Y.; Mo, W.; Wang, H.; Ding, J.; Wong, E.T.; Yu, M. The role of brevican in glioma: Promoting tumor cell motility in vitro and in vivo. BMC Cancer 2012, 12, 607. [Google Scholar] [CrossRef] [PubMed]
- Xia, S.; Lal, B.; Tung, B.; Wang, S.; Goodwin, C.R.; Laterra, J. Tumor microenvironment tenascin-C promotes glioblastoma invasion and negatively regulates tumor proliferation. Neuro-Oncology 2016, 18, 507–517. [Google Scholar] [CrossRef] [PubMed]
- Rupp, T.; Langlois, B.; Koczorowska, M.M.; Radwanska, A.; Sun, Z.; Hussenet, T.; Lefebvre, O.; Murdamoothoo, D.; Arnold, C.; Klein, A.; et al. Tenascin-C Orchestrates Glioblastoma Angiogenesis by Modulation of Pro- and Anti-angiogenic Signaling. Cell Rep. 2016, 17, 2607–2619. [Google Scholar] [CrossRef] [PubMed]
- Midwood, K.S.; Hussenet, T.; Langlois, B.; Orend, G. Advances in tenascin-C biology. Cell. Mol. Life Sci. 2011, 68, 3175–3199. [Google Scholar] [CrossRef] [PubMed]
- El Ayachi, I.; Baeza, N.; Fernandez, C.; Colin, C.; Scavarda, D.; Pesheva, P.; Figarella-Branger, D. KIAA0510, the 3′-untranslated region of the tenascin-R gene, and tenascin-R are overexpressed in pilocytic astrocytomas. Neuropathol. Appl. Neurobiol. 2010, 36, 399–410. [Google Scholar] [CrossRef] [PubMed]
- Choi, K.J.; Lee, J.H.; Kim, K.S.; Kang, S.; Lee, Y.S.; Bae, S. Identification of ELAVL4 as a modulator of radiation sensitivity in A549 non-small cell lung cancer cells. Oncol. Rep. 2011, 26, 55–63. [Google Scholar] [CrossRef] [PubMed]
- LeBlanc, M.E.; Wang, W.; Chen, X.; Caberoy, N.B.; Guo, F.; Shen, C.; Ji, Y.; Tian, H.; Wang, H.; Chen, R.; et al. Secretogranin III as a disease-associated ligand for antiangiogenic therapy of diabetic retinopathy. J. Exp. Med. 2017, 214, 1029–1047. [Google Scholar] [CrossRef]
- Hernandez, M.; Martin, R.; Garcia-Cubillas, M.D.; Maeso-Hernandez, P.; Nieto, M.L. Secreted PLA2 induces proliferation in astrocytoma through the EGF receptor: Another inflammation-cancer link. Neuro-Oncology 2010, 12, 1014–1023. [Google Scholar] [CrossRef]
- Banyard, J.; Barrows, C.; Zetter, B.R. Differential regulation of human thymosin beta 15 isoforms by transforming growth factor beta 1. Genes Chromosomes Cancer 2009, 48, 502–509. [Google Scholar] [CrossRef]
- Gautier, L.; Cope, L.; Bolstad, B.M.; Irizarry, R.A. Analysis of Affymetrix GeneChip data at the probe level. Bioinformatics 2004, 20, 307–315. [Google Scholar] [CrossRef]
- MacDonald, J.W. Affycoretools: Functions Useful for Those Doing Repetitive Analyses with Affymetrix GeneChips. Available online: https://bioconductor.org/packages/release/bioc/html/affycoretools.html (accessed on 23 September 2017).
- Wu, Z.J.; Irizarry, R.A.; Gentleman, R.; Martinez-Murillo, F.; Spencer, F. A model-based background adjustment for oligonucleotide expression arrays. J. Am. Stat. Assoc. 2004, 99, 909–917. [Google Scholar] [CrossRef]
- Pounds, S.; Morris, S.W. Estimating the occurrence of false positives and false negatives in microarray studies by approximating and partitioning the empirical distribution of p-values. Bioinformatics 2003, 19, 1236–1242. [Google Scholar] [CrossRef] [PubMed]
- Hallam, A. TensorFlow-Survival-Analysis. Available online: https://github.com/alexhallam/TensorFlow-Survival-Analysis (accessed on 23 September 2017).
- Faraggi, D.; Simon, R. A neural network model for survival data. Stat. Med. 1995, 14, 73–82. [Google Scholar] [CrossRef] [PubMed]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Wang, L.; Shen, J.; Thall, P.F. A Modified Adaptive Lasso for Identifying Interactions in the Cox Model with the Heredity Constraint. Stat. Probab. Lett. 2014, 93, 126–133. [Google Scholar] [CrossRef] [PubMed]
- Suchting, R.; Hebert, E.T.; Ma, P.; Kendzor, D.E.; Businelle, M.S. Using Elastic Net Penalized Cox Proportional Hazards Regression to Identify Predictors of Imminent Smoking Lapse. Nicotine Tob. Res. 2017. [Google Scholar] [CrossRef] [PubMed]
- Simon, N.; Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Cox’s Proportional Hazards Model via Coordinate Descent. J. Stat. Softw. 2011, 39, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Guam, X.; Olden, J.D. A new R2-based metric to shed greater insight on variable importance in artificial neural networks. Ecol. Model. 2015, 313, 307–313. [Google Scholar] [CrossRef]
- Aguirre-Gamboa, R.; Gomez-Rueda, H.; Martinez-Ledesma, E.; Martinez-Torteya, A.; Chacolla-Huaringa, R.; Rodriguez-Barrientos, A.; Tamez-Pena, J.G.; Trevino, V. SurvExpress: An online biomarker validation tool and database for cancer gene expression data using survival analysis. PLoS ONE 2013, 8, e74250. [Google Scholar] [CrossRef]
- Lee, Y.; Scheck, A.C.; Cloughesy, T.F.; Lai, A.; Dong, J.; Farooqi, H.K.; Liau, L.M.; Horvath, S.; Mischel, P.S.; Nelson, S.F. Gene expression analysis of glioblastomas identifies the major molecular basis for the prognostic benefit of younger age. BMC Med. Genom. 2008, 1, 52. [Google Scholar] [CrossRef]
- Freije, W.A.; Castro-Vargas, F.E.; Fang, Z.; Horvath, S.; Cloughesy, T.; Liau, L.M.; Mischel, P.S.; Nelson, S.F. Gene expression profiling of gliomas strongly predicts survival. Cancer Res. 2004, 64, 6503–6510. [Google Scholar] [CrossRef]
- Gravendeel, L.A.; Kouwenhoven, M.C.; Gevaert, O.; de Rooi, J.J.; Stubbs, A.P.; Duijm, J.E.; Daemen, A.; Bleeker, F.E.; Bralten, L.B.; Kloosterhof, N.K.; et al. Intrinsic gene expression profiles of gliomas are a better predictor of survival than histology. Cancer Res. 2009, 69, 9065–9072. [Google Scholar] [CrossRef] [PubMed]
- Nutt, C.L.; Mani, D.R.; Betensky, R.A.; Tamayo, P.; Cairncross, J.G.; Ladd, C.; Pohl, U.; Hartmann, C.; McLaughlin, M.E.; Batchelor, T.T.; et al. Gene expression-based classification of malignant gliomas correlates better with survival than histological classification. Cancer Res. 2003, 63, 1602–1607. [Google Scholar] [PubMed]
- Murat, A.; Migliavacca, E.; Gorlia, T.; Lambiv, W.L.; Shay, T.; Hamou, M.F.; de Tribolet, N.; Regli, L.; Wick, W.; Kouwenhoven, M.C.; et al. Stem cell-related “self-renewal” signature and high epidermal growth factor receptor expression associated with resistance to concomitant chemoradiotherapy in glioblastoma. J. Clin. Oncol. 2008, 26, 3015–3024. [Google Scholar] [CrossRef] [PubMed]
- Joo, K.M.; Kim, J.; Jin, J.; Kim, M.; Seol, H.J.; Muradov, J.; Yang, H.; Choi, Y.L.; Park, W.Y.; Kong, D.S.; et al. Patient-specific orthotopic glioblastoma xenograft models recapitulate the histopathology and biology of human glioblastomas in situ. Cell Rep. 2013, 3, 260–273. [Google Scholar] [CrossRef] [PubMed]
- Phillips, H.S.; Kharbanda, S.; Chen, R.; Forrest, W.F.; Soriano, R.H.; Wu, T.D.; Misra, A.; Nigro, J.M.; Colman, H.; Soroceanu, L.; et al. Molecular subclasses of high-grade glioma predict prognosis, delineate a pattern of disease progression, and resemble stages in neurogenesis. Cancer Cell 2006, 9, 157–173. [Google Scholar] [CrossRef] [PubMed]

| Gene | Frequency | Gene | Frequency | Gene | Frequency | Gene | Frequency |
|---|---|---|---|---|---|---|---|
| TNR | 17 | DPYSL4 | 10 | MEG3 | 9 | GRB10 | 8 |
| GAD1 | 16 | EGFR | 10 | NES | 9 | KDELR3 | 8 |
| TMSB15B | 15 | F13A1 | 10 | NPTX2 | 9 | KIF1A | 8 |
| POSTN | 15 | FBN2 | 10 | NRXN1 | 9 | LSAMP | 8 |
| SCG3 | 15 | NEFM | 10 | NTSR2 | 9 | LYPD1 | 8 |
| PLA2G2A | 14 | PTGDS | 10 | PEG3 | 9 | MMP9 | 8 |
| NNMT | 13 | RAB6B | 10 | PROM1 | 9 | MYT1L | 8 |
| CHI3L1 | 13 | RAPGEF4 | 10 | SH3GL3 | 9 | NMNAT2 | 8 |
| ELAVL4 | 13 | RUNDC3A | 10 | SOX11 | 9 | NNAT | 8 |
| TF | 13 | SERPINA3 | 10 | SPOCK1 | 9 | NOL4 | 8 |
| UGT8 | 13 | SH3GL2 | 10 | TMEM35 | 9 | NSG1 | 8 |
| AQP1 | 12 | SNAP25 | 10 | C4B | 8 | PLBD1 | 8 |
| COL6A3 | 12 | TCEAL2 | 10 | SLC16A3 | 8 | RGS1 | 8 |
| ERBB3 | 12 | TIMP4 | 10 | SOD2 | 8 | RGS17 | 8 |
| KCNQ2 | 12 | LOC101060835 | 9 | AIM1 | 8 | RGS4 | 8 |
| LTF | 12 | ADAM22 | 9 | ANXA1 | 8 | RTN1 | 8 |
| MEOX2 | 12 | BCAN | 9 | APOD | 8 | S100A2 | 8 |
| PCDH9 | 12 | C1orf61 | 9 | ATP2B2 | 8 | SLC17A7 | 8 |
| STMN2 | 12 | DDX25 | 9 | ATP6V1G2 | 8 | SRD5A1 | 8 |
| FCGR2B | 11 | ETNPPL | 9 | CFI | 8 | STC1 | 8 |
| FGFR3 | 11 | FAM107A | 9 | DSP | 8 | STEAP3 | 8 |
| SLC1A2 | 11 | GABRB1 | 9 | ENPP2 | 8 | STK32B | 8 |
| CA10 | 10 | GDF15 | 9 | FCGBP | 8 | TAC1 | 8 |
| CXCL14 | 10 | GNAO1 | 9 | FUT9 | 8 | VSNL1 | 8 |
| CXorf57 | 10 | LGI1 | 9 | FZD6 | 8 | WIF1 | 8 |
| Cox Model with Deep Learning Features | HR (95% CI) | p-Value |
|---|---|---|
| Network Node 0 | 1.26 (0.98–1.62) | 0.0718 |
| Network Node 1 | 1.13 (0.94–1.36) | 0.1996 |
| Network Node 2 | 1.03 (0.81–1.32) | 0.7931 |
| Network Node 3 | 1.15 (0.94–1.41) | 0.1681 |
| Network Node 4 | 0.73 (0.59–0.89) | 0.0022 |
| Network Node 5 | 0.95 (0.77–1.16) | 0.5935 |
| Network Node 6 | 1.13 (0.88–1.44) | 0.341 |
| Network Node 7 | 1.19 (0.97–1.46) | 0.0929 |
| Network Node 8 | 1.71 (1.40–2.08) | <0.0001 |
| Network Node 9 | 1.02 (0.81–1.29) | 0.8505 |
| Network Node 10 | ||
| ≥1.6 | 0.45 (0.25–0.81) | 0.0076 |
| <1.6 | 1 | |
| Network Node 11 | 0.80 (0.66–0.96) | 0.0197 |
| Network Node 12 | 1.36 (1.11–1.68) | 0.0034 |
| Network Node 13 | 0.93 (0.77–1.14) | 0.4994 |
| Network Node 14 | 1.12 (0.88–1.42) | 0.3495 |
| Network Node 15 | 0.86 (0.67–1.10) | 0.2324 |
| Network Node 16 | 0.57 (0.45–0.72) | <0.0001 |
| Network Node 17 | 1.35 (1.09–1.67) | 0.0056 |
| Network Node 18 | 0.80 (0.64–1.00) | 0.0478 |
| Network Node 19 | 0.78 (0.64–0.95) | 0.0132 |
| Network Node 20 | 0.91 (0.73–1.15) | 0.4437 |
| Network Node 21 | 1.34 (1.10–1.62) | 0.0035 |
| Network Node 22 | 1.16 (0.95–1.42) | 0.1575 |
| Network Node 23 | 0.77 (0.62–0.97) | 0.0281 |
| Network Node 24 | 1.87 (1.54–2.27) | <0.0001 |
| Network Node 25 | 1.41 (1.10–1.80) | 0.0063 |
| Network Node 26 | 0.80 (0.65–1.00) | 0.0476 |
| Overall Model | <0.0001 |
| Cox Model with Clinical Covariates and Deep Learning Features | HR (95% CI) | p-Value |
|---|---|---|
| Age | ||
| ≥54 years old | 1.50 (1.10–2.03) | 0.0098 |
| <54 years old | 1 | |
| Gender | ||
| Male | 1.25 (0.92–1.68) | 0.1542 |
| Female | 1 | |
| KPS | ||
| ≥60 | 0.35 (0.17–0.72) | 0.0042 |
| <60 | 1 | |
| Therapy | ||
| Chemoradiation | 0.27 (0.12–0.62) | 0.0018 |
| Chemotherapy | 1.06 (0.35–3.17) | 0.9193 |
| Radiation | 0.51 (0.22–1.17) | 0.1122 |
| Subtype | ||
| Proneural | 1.70 (1.01–2.87) | 0.0464 |
| Classical | 1.26 (0.79–2.01) | 0.3311 |
| Mesenchymal | 1.41 (0.89–2.25) | 0.1462 |
| MGMT Methylated | 1.18 (0.85–1.62) | 0.3181 |
| G-CIMP Methylated | 1.03 (0.35–3.06) | 0.9553 |
| R132C/R132G/R132H Mutation | 1.08 (0.35–3.31) | 0.8986 |
| Network Node 0 | 1.09 (0.80–1.48) | 0.5888 |
| Network Node 1 | 1.10 (0.87–1.39) | 0.4348 |
| Network Node 2 | 1.15 (0.86–1.55) | 0.3407 |
| Network Node 3 | 1.11 (0.86–1.44) | 0.4264 |
| Network Node 4 | 0.77 (0.60–0.99) | 0.0387 |
| Network Node 5 | 0.85 (0.64–1.12) | 0.2558 |
| Network Node 6 | 1.12 (0.80–1.55) | 0.514 |
| Network Node 7 | 1.12 (0.86–1.44) | 0.4041 |
| Network Node 8 | 1.73 (1.36–2.21) | <0.0001 |
| Network Node 9 | 1.07 (0.81–1.42) | 0.6384 |
| Network Node 10 | ||
| ≥1.6 | 0.44 (0.20–0.95) | 0.0363 |
| Network Node 11 | 0.86 (0.67–1.10) | 0.2336 |
| Network Node 12 | 1.27 (0.99–1.65) | 0.0645 |
| Network Node 13 | 1.04 (0.82–1.32) | 0.7484 |
| Network Node 14 | 1.10 (0.82–1.48) | 0.5313 |
| Network Node 15 | 0.79 (0.57–1.11) | 0.1711 |
| Network Node 16 | 0.64 (0.48–0.86) | 0.0029 |
| Network Node 17 | 1.55 (1.16–2.07) | 0.0027 |
| Network Node 18 | 0.79 (0.60–1.05) | 0.1049 |
| Network Node 19 | 0.86 (0.68–1.08) | 0.2001 |
| Network Node 20 | 0.74 (0.54–1.00) | 0.0528 |
| Network Node 21 | ||
| ≥1.6 | 0.96 (0.55–1.69) | 0.8937 |
| Network Node 22 | 1.22 (0.94–1.58) | 0.1327 |
| Network Node 23 | 0.75 (0.57–1.00) | 0.048 |
| Network Node 24 | 1.66 (1.30–2.12) | <0.0001 |
| Network Node 25 | 1.49 (1.10–2.01) | 0.0101 |
| Network Node 26 | 0.83 (0.64–1.07) | 0.1555 |
| Overall Model | <0.0001 |
| 39-Gene Signature | |||
|---|---|---|---|
| TNR | UGT8 | FGFR3 | PTGDS |
| GAD1 | AQP1 | SLC1A2 | RAB6B |
| TMSB15B | COL6A3 | CA10 | RAPGEF4 |
| POSTN | ERBB3 | CXCL14 | RUNDC3A |
| SCG3 | KCNQ2 | CXorf57 | SERPINA3 |
| PLA2G2A | LTF | DPYSL4 | SH3GL2 |
| NNMT | MEOX2 | EGFR | SNAP25 |
| CHI3L1 | PCDH9 | F13A1 | TCEAL2 |
| ELAVL4 | STMN2 | FBN2 | TIMP4 |
| TF | FCGR2B | NEFM | |
| Study Datasets | Samples | Source |
|---|---|---|
| Lee Nelson Glioblastoma GSE13041 GPL96 | 218 | Lee [56] |
| Freije Nelson Glioblastoma GSE4412 GPL96 | 85 | Freije [57] |
| Gravendeed French Glioblastoma GSE16011 | 284 | Gravendeel [58] |
| Nutt Louis Glioblastoma BROAD | 50 | Nutt [59] |
| Murat Hegi Glioblastoma GSE7696 | 84 | Murat [60] |
| Joo Kim Jin Kim Seol Nam Glioblastoma GSE42669 | 58 | Joo [61] |
| Philips Aldape Astrocytoma GSE4271 GPL96 | 100 | Phillips [62] |
| Brain Low Grade Glioma TCGA 2016 | 110 | TCGA |
| GBM-TCGA June 2016 | 148 | TCGA |
| LGG-TCGA-Low Grade Gliomas June 2016 | 512 | TCGA |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wong, K.K.; Rostomily, R.; Wong, S.T.C. Prognostic Gene Discovery in Glioblastoma Patients using Deep Learning. Cancers 2019, 11, 53. https://doi.org/10.3390/cancers11010053
Wong KK, Rostomily R, Wong STC. Prognostic Gene Discovery in Glioblastoma Patients using Deep Learning. Cancers. 2019; 11(1):53. https://doi.org/10.3390/cancers11010053
Chicago/Turabian StyleWong, Kelvin K., Robert Rostomily, and Stephen T. C. Wong. 2019. "Prognostic Gene Discovery in Glioblastoma Patients using Deep Learning" Cancers 11, no. 1: 53. https://doi.org/10.3390/cancers11010053
APA StyleWong, K. K., Rostomily, R., & Wong, S. T. C. (2019). Prognostic Gene Discovery in Glioblastoma Patients using Deep Learning. Cancers, 11(1), 53. https://doi.org/10.3390/cancers11010053





