A Barter Economy in Tumors: Exchanging Metabolites through Gap Junctions
Abstract
1. Trading within Biological Systems
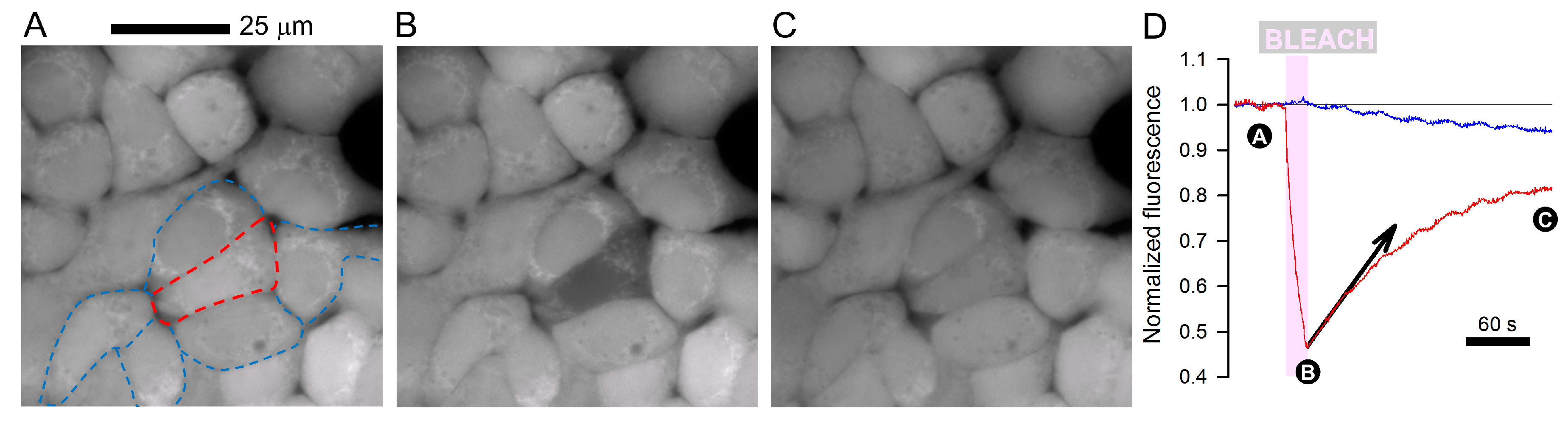
2. Gap Junctions are Conduits for Exchanging Small- to Medium-Sized Molecules
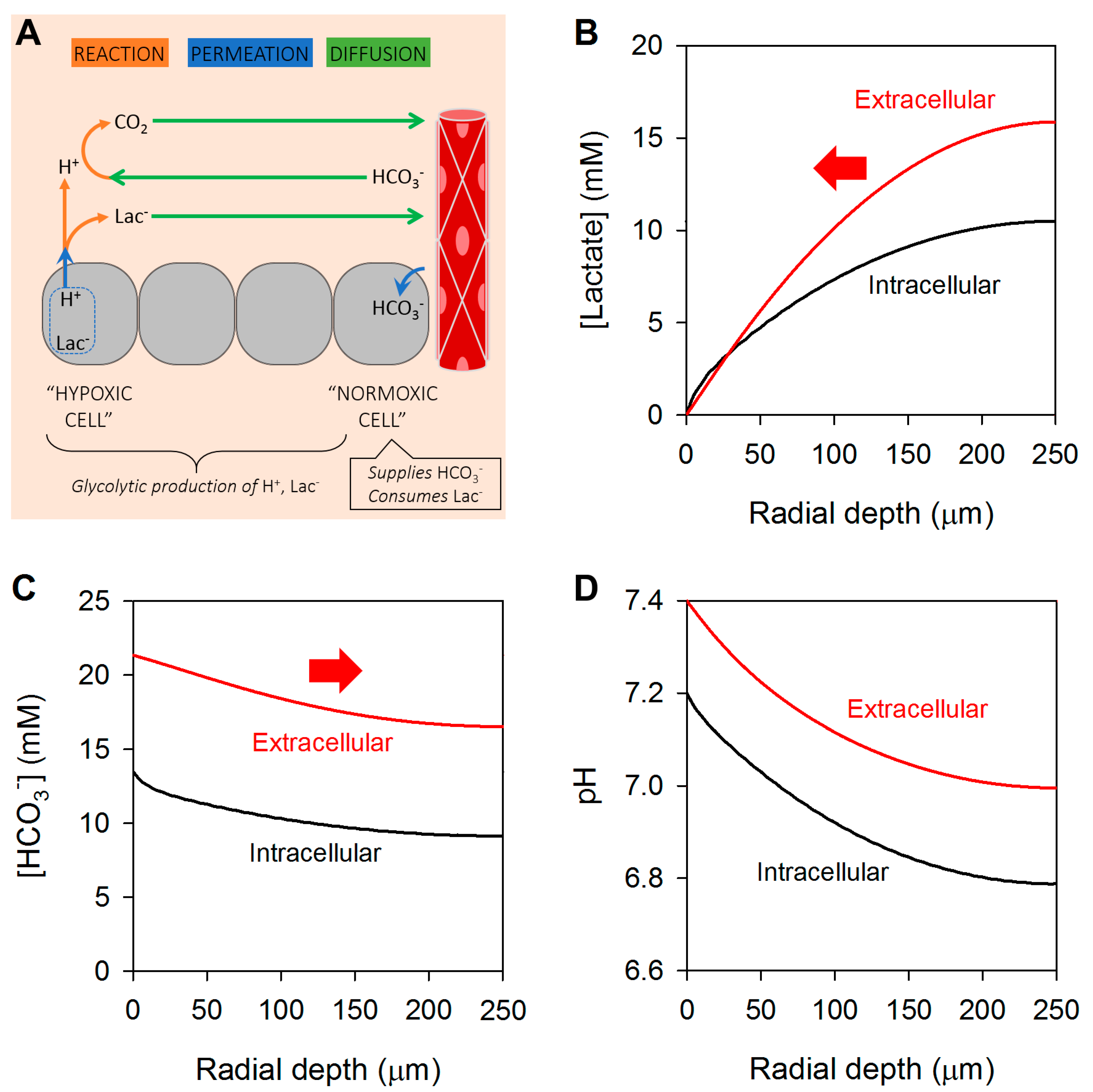
3. Glycolytic Metabolism Establishes Radial Concentration Gradients of Lactate and Bicarbonate in Solid Tumors
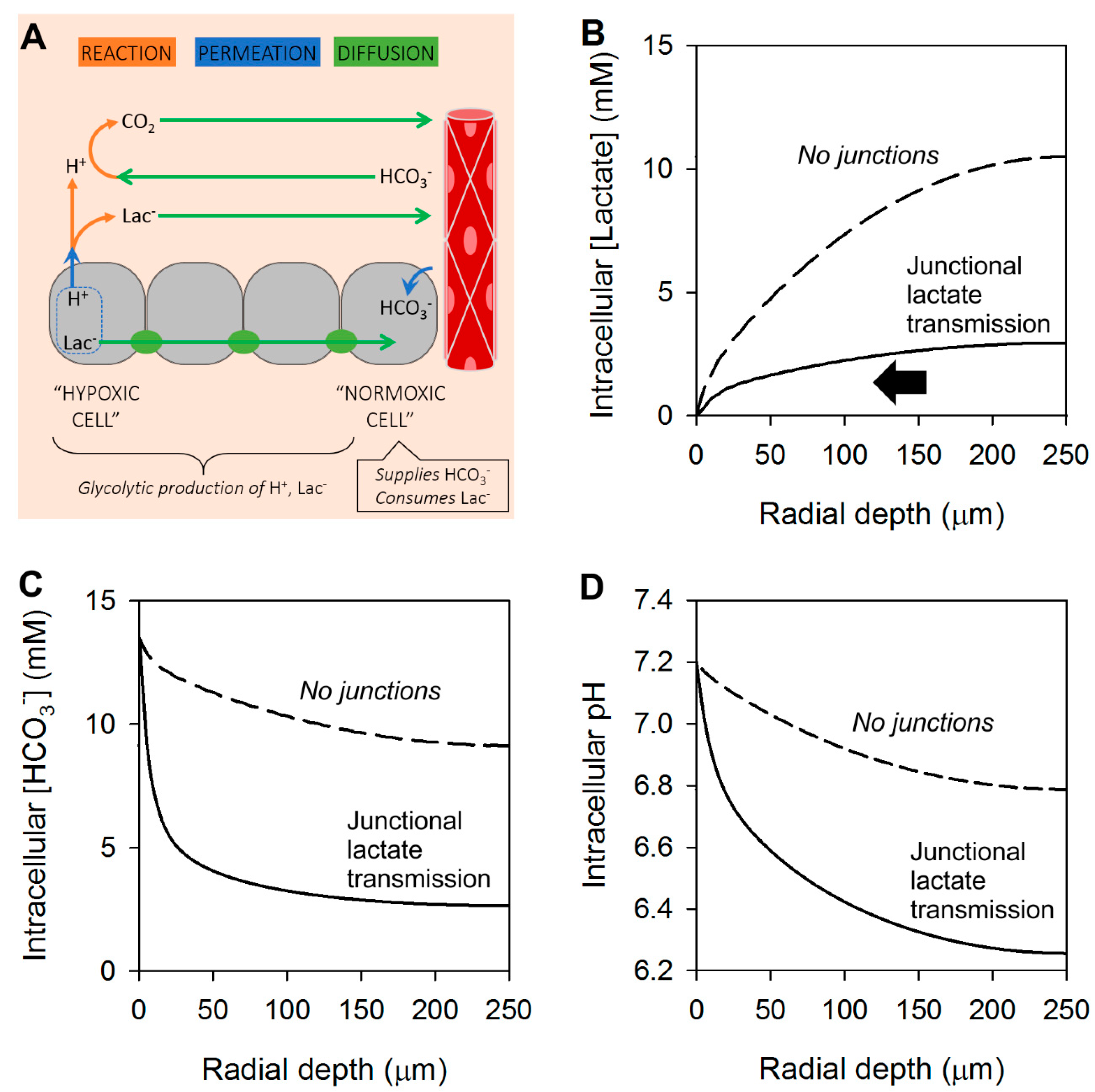
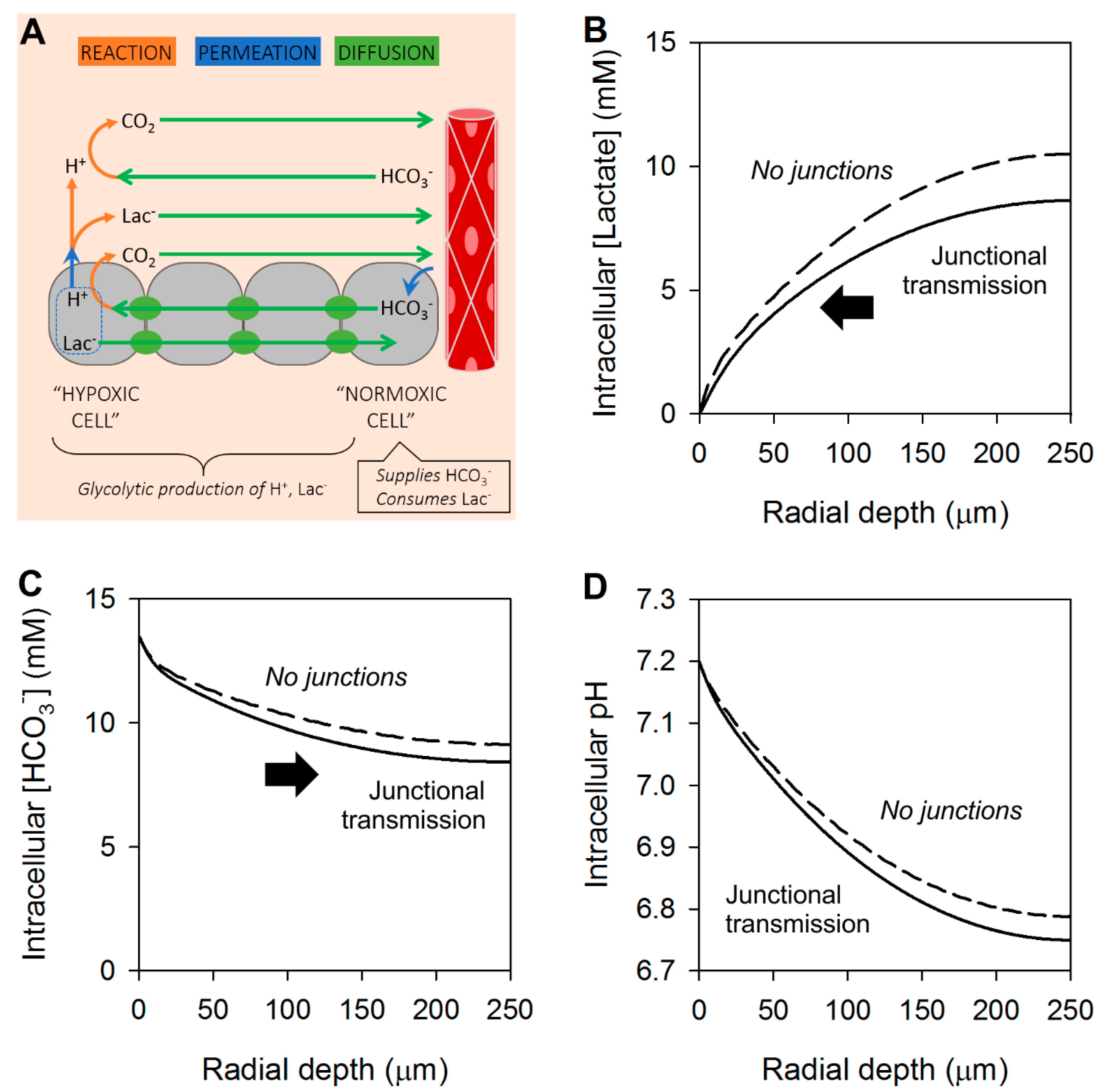
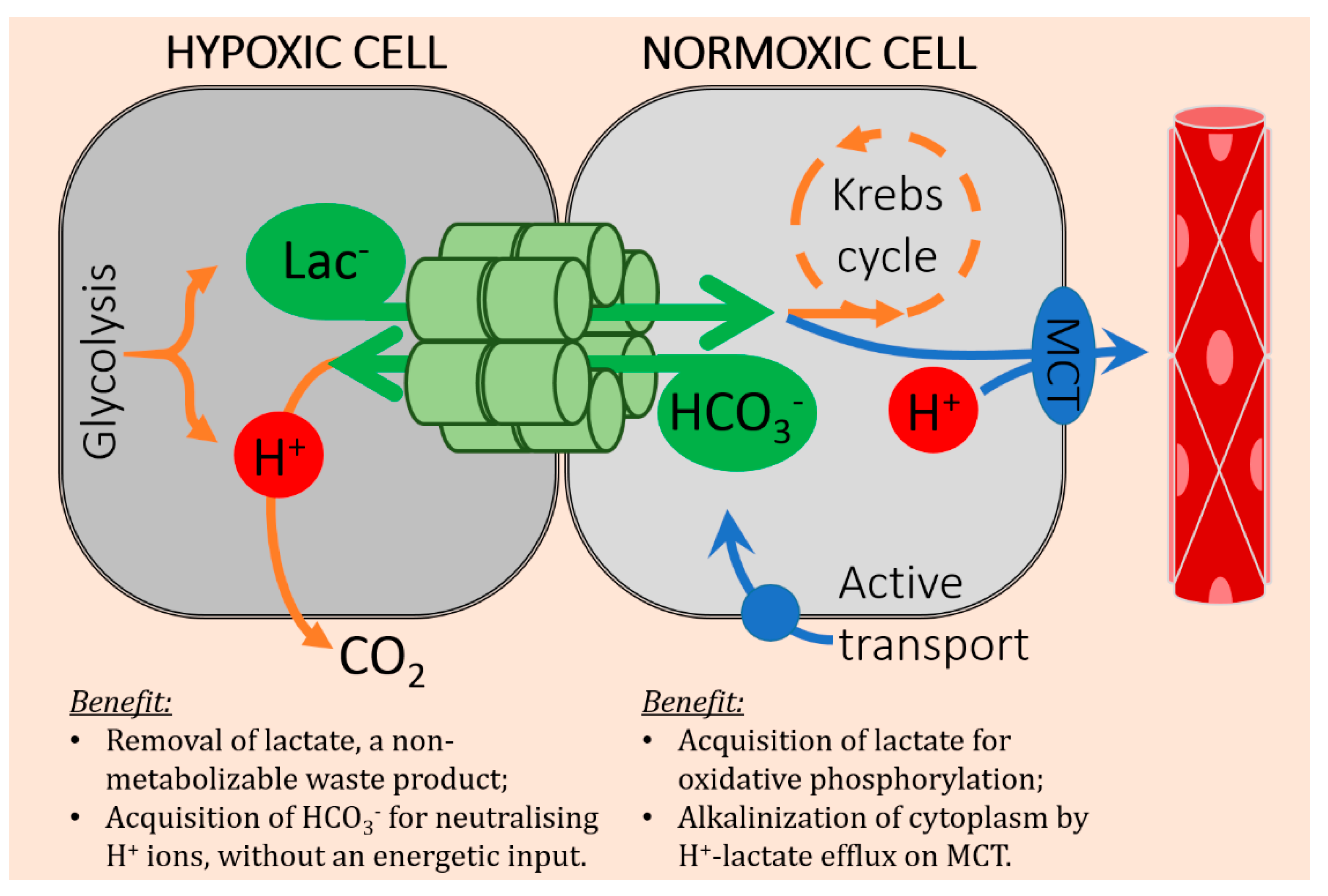
4. Cancer Cells Can Exchange Lactate and Bicarbonate Ions through Gap Junctions
5. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Graeber, D. Toward an Anthropological Theory of Value: The False Coin of our Dreams; Palgrave: Basingstoke, UK, 2001. [Google Scholar]
- Humphrey, C. Barter and Economic Disintegration. Man 1985, 20, 48–72. [Google Scholar] [CrossRef]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [PubMed]
- Gatenby, R.A.; Gillies, R.J.; Brown, J.S. Evolutionary dynamics of cancer prevention. Nat. Rev. Cancer 2010, 10, 526–527. [Google Scholar] [CrossRef] [PubMed]
- Kalluri, R.; Zeisberg, M. Fibroblasts in cancer. Nat. Rev. Cancer 2006, 6, 392–401. [Google Scholar] [CrossRef] [PubMed]
- Hanahan, D.; Coussens, L.M. Accessories to the crime: Functions of cells recruited to the tumor microenvironment. Cancer Cell 2012, 21, 309–322. [Google Scholar] [CrossRef] [PubMed]
- Loewenstein, W.R.; Socolar, S.J.; Higashino, S.; Kanno, Y.; Davidson, N. Intercellular Communication: Renal, Urinary Bladder, Sensory, and Salivary Gland Cells. Science 1965, 149, 295–298. [Google Scholar] [CrossRef] [PubMed]
- Evans, W.H. Cell communication across gap junctions: A historical perspective and current developments. Biochem. Soc. Trans. 2015, 43, 450–459. [Google Scholar] [CrossRef]
- Goodenough, D.A. Bulk isolation of mouse hepatocyte gap junctions. Characterization of the principal protein, connexin. J. Cell Biol. 1974, 61, 557–563. [Google Scholar] [CrossRef]
- Aasen, T.; Mesnil, M.; Naus, C.C.; Lampe, P.D.; Laird, D.W. Gap junctions and cancer: Communicating for 50 years. Nat. Rev. Cancer 2016, 16, 775–788. [Google Scholar] [CrossRef]
- Duffy, H.S.; Fort, A.G.; Spray, D.C. Cardiac connexins: Genes to nexus. Adv. Cardiol. 2006, 42, 1–17. [Google Scholar] [CrossRef]
- Kumar, N.M.; Gilula, N.B. The gap junction communication channel. Cell 1996, 84, 381–388. [Google Scholar] [CrossRef]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; et al. Search for magnetic monopoles in sqrt[s]=7 TeV pp collisions with the ATLAS detector. Phys. Rev. Lett. 2012, 109, 261803. [Google Scholar] [CrossRef] [PubMed]
- Graham, S.V.; Jiang, J.X.; Mesnil, M. Connexins and Pannexins: Important Players in Tumorigenesis, Metastasis and Potential Therapeutics. Int. J. Mol. Sci. 2018, 19, 1645. [Google Scholar] [CrossRef] [PubMed]
- Solan, J.L.; Hingorani, S.R.; Lampe, P.D. Changes in connexin43 expression and localization during pancreatic cancer progression. J. Membr. Biol. 2012, 245, 255–262. [Google Scholar] [CrossRef] [PubMed]
- Constantin, B.; Cronier, L. Involvement of gap junctional communication in myogenesis. Int. Rev. Cytol. 2000, 196, 1–65. [Google Scholar] [PubMed]
- Loewenstein, W.R.; Kanno, Y. Intercellular communication and the control of tissue growth: Lack of communication between cancer cells. Nature 1966, 209, 1248–1249. [Google Scholar] [CrossRef] [PubMed]
- Johnson, R.G.; Sheridan, J.D. Junctions between cancer cells in culture: Ultrastructure and permeability. Science 1971, 174, 717–719. [Google Scholar] [CrossRef]
- Borek, C.; Higashino, S.; Loewenstein, W.R. Intercellular communication and tissue growth: IV. Conductance of membrane junctions of normal and cancerous cells in culture. J. Membr. Biol. 1969, 1, 274–293. [Google Scholar] [CrossRef]
- Mesnil, M.; Crespin, S.; Avanzo, J.L.; Zaidan-Dagli, M.L. Defective gap junctional intercellular communication in the carcinogenic process. Biochim. Biophys. Acta 2005, 1719, 125–145. [Google Scholar] [CrossRef]
- McLachlan, E.; Shao, Q.; Wang, H.L.; Langlois, S.; Laird, D.W. Connexins act as tumor suppressors in three-dimensional mammary cell organoids by regulating differentiation and angiogenesis. Cancer Res. 2006, 66, 9886–9894. [Google Scholar] [CrossRef]
- Mesnil, M. Connexins and cancer. Biol. Cell 2002, 94, 493–500. [Google Scholar] [CrossRef]
- Jiang, J.X.; Penuela, S. Connexin and pannexin channels in cancer. BMC Cell Biol. 2016, 17 (Suppl. 1), 12. [Google Scholar] [CrossRef]
- Lin, J.H.; Takano, T.; Cotrina, M.L.; Arcuino, G.; Kang, J.; Liu, S.; Gao, Q.; Jiang, L.; Li, F.; Lichtenberg-Frate, H.; et al. Connexin 43 enhances the adhesivity and mediates the invasion of malignant glioma cells. J. Neurosci. Off. J. Soc. Neurosci. 2002, 22, 4302–4311. [Google Scholar] [CrossRef]
- Pollmann, M.A.; Shao, Q.; Laird, D.W.; Sandig, M. Connexin 43 mediated gap junctional communication enhances breast tumor cell diapedesis in culture. Breast Cancer Res. 2005, 7, R522–R534. [Google Scholar] [CrossRef]
- Polusani, S.R.; Kalmykov, E.A.; Chandrasekhar, A.; Zucker, S.N.; Nicholson, B.J. Cell coupling mediated by connexin 26 selectively contributes to reduced adhesivity and increased migration. J. Cell Sci. 2016, 129, 4399–4410. [Google Scholar] [CrossRef] [PubMed]
- Naus, C.C.; Laird, D.W. Implications and challenges of connexin connections to cancer. Nat. Rev. Cancer 2010, 10, 435–441. [Google Scholar] [CrossRef]
- Ezumi, K.; Yamamoto, H.; Murata, K.; Higashiyama, M.; Damdinsuren, B.; Nakamura, Y.; Kyo, N.; Okami, J.; Ngan, C.Y.; Takemasa, I.; et al. Aberrant expression of connexin 26 is associated with lung metastasis of colorectal cancer. Clin. Cancer Res. Off. J. Am. Assoc. Cancer Res. 2008, 14, 677–684. [Google Scholar] [CrossRef]
- Nomura, S.; Maeda, K.; Noda, E.; Inoue, T.; Fukunaga, S.; Nagahara, H.; Hirakawa, K. Clinical significance of the expression of connexin26 in colorectal cancer. J. Exp. Clin. Cancer Res. 2010, 29, 79. [Google Scholar] [CrossRef]
- Thuringer, D.; Berthenet, K.; Cronier, L.; Solary, E.; Garrido, C. Primary tumor- and metastasis-derived colon cancer cells differently modulate connexin expression and function in human capillary endothelial cells. Oncotarget 2015, 6, 28800–28815. [Google Scholar] [CrossRef]
- Bigelow, K.; Nguyen, T.A. Increase of gap junction activities in SW480 human colorectal cancer cells. BMC Cancer 2014, 14, 502. [Google Scholar] [CrossRef]
- Valiunas, V.; Polosina, Y.Y.; Miller, H.; Potapova, I.A.; Valiuniene, L.; Doronin, S.; Mathias, R.T.; Robinson, R.B.; Rosen, M.R.; Cohen, I.S.; et al. Connexin-specific cell-to-cell transfer of short interfering RNA by gap junctions. J. Physiol. 2005, 568, 459–468. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.W.; Kaneda, M.; Morita, I. The gap junction-independent tumor-suppressing effect of connexin 43. J. Biol. Chem. 2003, 278, 44852–44856. [Google Scholar] [CrossRef]
- Al-Ghadban, S.; Kaissi, S.; Homaidan, F.R.; Naim, H.Y.; El-Sabban, M.E. Cross-talk between intestinal epithelial cells and immune cells in inflammatory bowel disease. Sci. Rep. 2016, 6, 29783. [Google Scholar] [CrossRef] [PubMed]
- Dovmark, T.H.; Hulikova, A.; Niederer, S.A.; Vaughan-Jones, R.D.; Swietach, P. Normoxic cells remotely regulate the acid-base balance of cells at the hypoxic core of connexin-coupled tumor growths. Faseb. J. Off. Publ. Fed. Am. Soc. Exp. Biol. 2018, 32, 83–96. [Google Scholar] [CrossRef] [PubMed]
- Dovmark, T.H.; Saccomano, M.; Hulikova, A.; Alves, F.; Swietach, P. Connexin-43 channels are a pathway for discharging lactate from glycolytic pancreatic ductal adenocarcinoma cells. Oncogene 2017, 36, 4538–4550. [Google Scholar] [CrossRef]
- Kyo, N.; Yamamoto, H.; Takeda, Y.; Ezumi, K.; Ngan, C.Y.; Terayama, M.; Miyake, M.; Takemasa, I.; Ikeda, M.; Doki, Y.; et al. Overexpression of connexin 26 in carcinoma of the pancreas. Oncol. Rep. 2008, 19, 627–631. [Google Scholar] [CrossRef]
- Weber, P.A.; Chang, H.C.; Spaeth, K.E.; Nitsche, J.M.; Nicholson, B.J. The permeability of gap junction channels to probes of different size is dependent on connexin composition and permeant-pore affinities. Biophys. J. 2004, 87, 958–973. [Google Scholar] [CrossRef]
- Kanaporis, G.; Brink, P.R.; Valiunas, V. Gap junction permeability: Selectivity for anionic and cationic probes. Am. J. Physiol. Cell Physiol. 2011, 300, C600–C609. [Google Scholar] [CrossRef]
- Gillies, R.J.; Verduzco, D.; Gatenby, R.A. Evolutionary dynamics of carcinogenesis and why targeted therapy does not work. Nat. Rev. Cancer 2012, 12, 487–493. [Google Scholar] [CrossRef]
- Gatenby, R.A.; Vincent, T.L.; Gillies, R.J. Evolutionary dynamcs in carcinogenesis. Math. Models Methods Appl. Sci. 2005, 15, 1619–1638. [Google Scholar] [CrossRef]
- Gatenby, R.A.; Gillies, R.J. Why do cancers have high aerobic glycolysis? Nat. Rev. Cancer 2004, 4, 891–899. [Google Scholar] [CrossRef] [PubMed]
- Ward, P.S.; Thompson, C.B. Metabolic reprogramming: A cancer hallmark even warburg did not anticipate. Cancer Cell 2012, 21, 297–308. [Google Scholar] [CrossRef] [PubMed]
- Subak-Sharpe, H.; Burk, R.R.; Pitts, J.D. Metabolic co-operation between biochemically marked mammalian cells in tissue culture. J. Cell Sci. 1969, 4, 353–367. [Google Scholar] [PubMed]
- Koppenol, W.H.; Bounds, P.L.; Dang, C.V. Otto Warburg’s contributions to current concepts of cancer metabolism. Nat. Rev. Cancer 2011, 11, 325–337. [Google Scholar] [CrossRef]
- Vander Heiden, M.G.; Cantley, L.C.; Thompson, C.B. Understanding the Warburg effect: The metabolic requirements of cell proliferation. Science 2009, 324, 1029–1033. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Chao, M.; Wu, H. Central role of lactate and proton in cancer cell resistance to glucose deprivation and its clinical translation. Signal Transduct. Target. Ther. 2017, 2, 16047. [Google Scholar] [CrossRef]
- Hochachka, P.W.; Mommsen, T.P. Protons and anaerobiosis. Science 1983, 219, 1391–1397. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Ying, M.; Hu, X. Lactic acidosis switches cancer cells from aerobic glycolysis back to dominant oxidative phosphorylation. Oncotarget 2016, 7, 40621–40629. [Google Scholar] [CrossRef]
- Yizhak, K.; Le Devedec, S.E.; Rogkoti, V.M.; Baenke, F.; de Boer, V.C.; Frezza, C.; Schulze, A.; van de Water, B.; Ruppin, E. A computational study of the Warburg effect identifies metabolic targets inhibiting cancer migration. Mol. Syst. Biol. 2014, 10, 744. [Google Scholar] [CrossRef]
- Bailey, K.M.; Wojtkowiak, J.W.; Cornnell, H.H.; Ribeiro, M.C.; Balagurunathan, Y.; Hashim, A.I.; Gillies, R.J. Mechanisms of buffer therapy resistance. Neoplasia 2014, 16, 354–364.e1-3. [Google Scholar] [CrossRef]
- Wu, M.; Neilson, A.; Swift, A.L.; Moran, R.; Tamagnine, J.; Parslow, D.; Armistead, S.; Lemire, K.; Orrell, J.; Teich, J.; et al. Multiparameter metabolic analysis reveals a close link between attenuated mitochondrial bioenergetic function and enhanced glycolysis dependency in human tumor cells. Am. J. Physiol. Cell Physiol. 2007, 292, C125–C136. [Google Scholar] [CrossRef] [PubMed]
- Giang, A.H.; Raymond, T.; Brookes, P.; de Mesy Bentley, K.; Schwarz, E.; O’Keefe, R.; Eliseev, R. Mitochondrial dysfunction and permeability transition in osteosarcoma cells showing the Warburg effect. J. Biol. Chem. 2013, 288, 33303–33311. [Google Scholar] [CrossRef] [PubMed]
- Cheng, G.; Zielonka, J.; McAllister, D.; Tsai, S.; Dwinell, M.B.; Kalyanaraman, B. Profiling and targeting of cellular bioenergetics: Inhibition of pancreatic cancer cell proliferation. Br. J. Cancer 2014, 111, 85–93. [Google Scholar] [CrossRef] [PubMed]
- Halestrap, A.P.; Meredith, D. The SLC16 gene family-from monocarboxylate transporters (MCTs) to aromatic amino acid transporters and beyond. Pflugers Arch. 2004, 447, 619–628. [Google Scholar] [CrossRef] [PubMed]
- Ullah, M.S.; Davies, A.J.; Halestrap, A.P. The plasma membrane lactate transporter MCT4, but not MCT1, is up-regulated by hypoxia through a HIF-1alpha-dependent mechanism. J. Biol. Chem. 2006, 281, 9030–9037. [Google Scholar] [CrossRef] [PubMed]
- Hulikova, A.; Swietach, P. Rapid CO2 permeation across biological membranes: Implications for CO2 venting from tissue. Faseb. J. Off. Publ. Fed. Am. Soc. Exp. Biol. 2014, 28, 2762–2774. [Google Scholar] [CrossRef] [PubMed]
- Swietach, P.; Hulikova, A.; Vaughan-Jones, R.D.; Harris, A.L. New insights into the physiological role of carbonic anhydrase IX in tumour pH regulation. Oncogene 2010, 29, 6509–6521. [Google Scholar] [CrossRef]
- Swietach, P.; Patiar, S.; Supuran, C.T.; Harris, A.L.; Vaughan-Jones, R.D. The role of carbonic anhydrase 9 in regulating extracellular and intracellular ph in three-dimensional tumor cell growths. J. Biol. Chem. 2009, 284, 20299–20310. [Google Scholar] [CrossRef]
- Swietach, P.; Wigfield, S.; Cobden, P.; Supuran, C.T.; Harris, A.L.; Vaughan-Jones, R.D. Tumor-associated carbonic anhydrase 9 spatially coordinates intracellular pH in three-dimensional multicellular growths. J. Biol. Chem. 2008, 283, 20473–20483. [Google Scholar] [CrossRef]
- Hulikova, A.; Black, N.; Hsia, L.T.; Wilding, J.; Bodmer, W.F.; Swietach, P. Stromal uptake and transmission of acid is a pathway for venting cancer cell-generated acid. Proc. Natl. Acad. Sci. USA 2016, 113, E5344–E5353. [Google Scholar] [CrossRef]
- Hulikova, A.; Harris, A.L.; Vaughan-Jones, R.D.; Swietach, P. Regulation of intracellular pH in cancer cell lines under normoxia and hypoxia. J. Cell. Physiol. 2013, 228, 743–752. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, J.R.; Stevens, A.N.; Iles, R.A.; Gordon, R.E.; Shaw, D. 31P-NMR investigation of solid tumours in the living rat. Biosci. Rep. 1981, 1, 319–325. [Google Scholar] [CrossRef] [PubMed]
- Webb, B.A.; Forouhar, F.; Szu, F.E.; Seetharaman, J.; Tong, L.; Barber, D.L. Structures of human phosphofructokinase-1 and atomic basis of cancer-associated mutations. Nature 2015, 523, 111–114. [Google Scholar] [CrossRef] [PubMed]
- Swietach, P.; Vaughan-Jones, R.D.; Harris, A.L. Regulation of tumor pH and the role of carbonic anhydrase 9. Cancer Metastasis Rev. 2007, 26, 299–310. [Google Scholar] [CrossRef] [PubMed]
- Swietach, P.; Vaughan-Jones, R.D. Novel method for measuring junctional proton permeation in isolated ventricular myocyte cell pairs. Am. J. Physiol. Heart Circ. Physiol. 2004, 287, H2352–H2363. [Google Scholar] [CrossRef]
- Turin, L.; Warner, A. Carbon dioxide reversibly abolishes ionic communication between cells of early amphibian embryo. Nature 1977, 270, 56–57. [Google Scholar] [CrossRef] [PubMed]
- Spray, D.C.; Harris, A.L.; Bennett, M.V. Gap junctional conductance is a simple and sensitive function of intracellular pH. Science 1981, 211, 712–715. [Google Scholar] [CrossRef] [PubMed]
- Swietach, P.; Rossini, A.; Spitzer, K.W.; Vaughan-Jones, R.D. H+ ion activation and inactivation of the ventricular gap junction: A basis for spatial regulation of intracellular pH. Circ. Res. 2007, 100, 1045–1054. [Google Scholar] [CrossRef]
- Garciarena, C.D.; Malik, A.; Swietach, P.; Moreno, A.P.; Vaughan-Jones, R.D. Distinct moieties underlie biphasic H(+) gating of connexin43 channels, producing a pH optimum for intercellular communication. Faseb J. Off. Publ. Fed. Am. Soc. Exp. Biol. 2018, 32, 1969–1981. [Google Scholar] [CrossRef]
- Sonveaux, P.; Vegran, F.; Schroeder, T.; Wergin, M.C.; Verrax, J.; Rabbani, Z.N.; De Saedeleer, C.J.; Kennedy, K.M.; Diepart, C.; Jordan, B.F.; et al. Targeting lactate-fueled respiration selectively kills hypoxic tumor cells in mice. J. Clin. Investig. 2008, 118, 3930–3942. [Google Scholar] [CrossRef]
- Swietach, P.; Zaniboni, M.; Stewart, A.K.; Rossini, A.; Spitzer, K.W.; Vaughan-Jones, R.D. Modelling intracellular H(+) ion diffusion. Prog. Biophys. Mol. Biol. 2003, 83, 69–100. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swietach, P.; Monterisi, S. A Barter Economy in Tumors: Exchanging Metabolites through Gap Junctions. Cancers 2019, 11, 117. https://doi.org/10.3390/cancers11010117
Swietach P, Monterisi S. A Barter Economy in Tumors: Exchanging Metabolites through Gap Junctions. Cancers. 2019; 11(1):117. https://doi.org/10.3390/cancers11010117
Chicago/Turabian StyleSwietach, Pawel, and Stefania Monterisi. 2019. "A Barter Economy in Tumors: Exchanging Metabolites through Gap Junctions" Cancers 11, no. 1: 117. https://doi.org/10.3390/cancers11010117
APA StyleSwietach, P., & Monterisi, S. (2019). A Barter Economy in Tumors: Exchanging Metabolites through Gap Junctions. Cancers, 11(1), 117. https://doi.org/10.3390/cancers11010117




