Multimodal Radiomic Features for the Predicting Gleason Score of Prostate Cancer
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Description
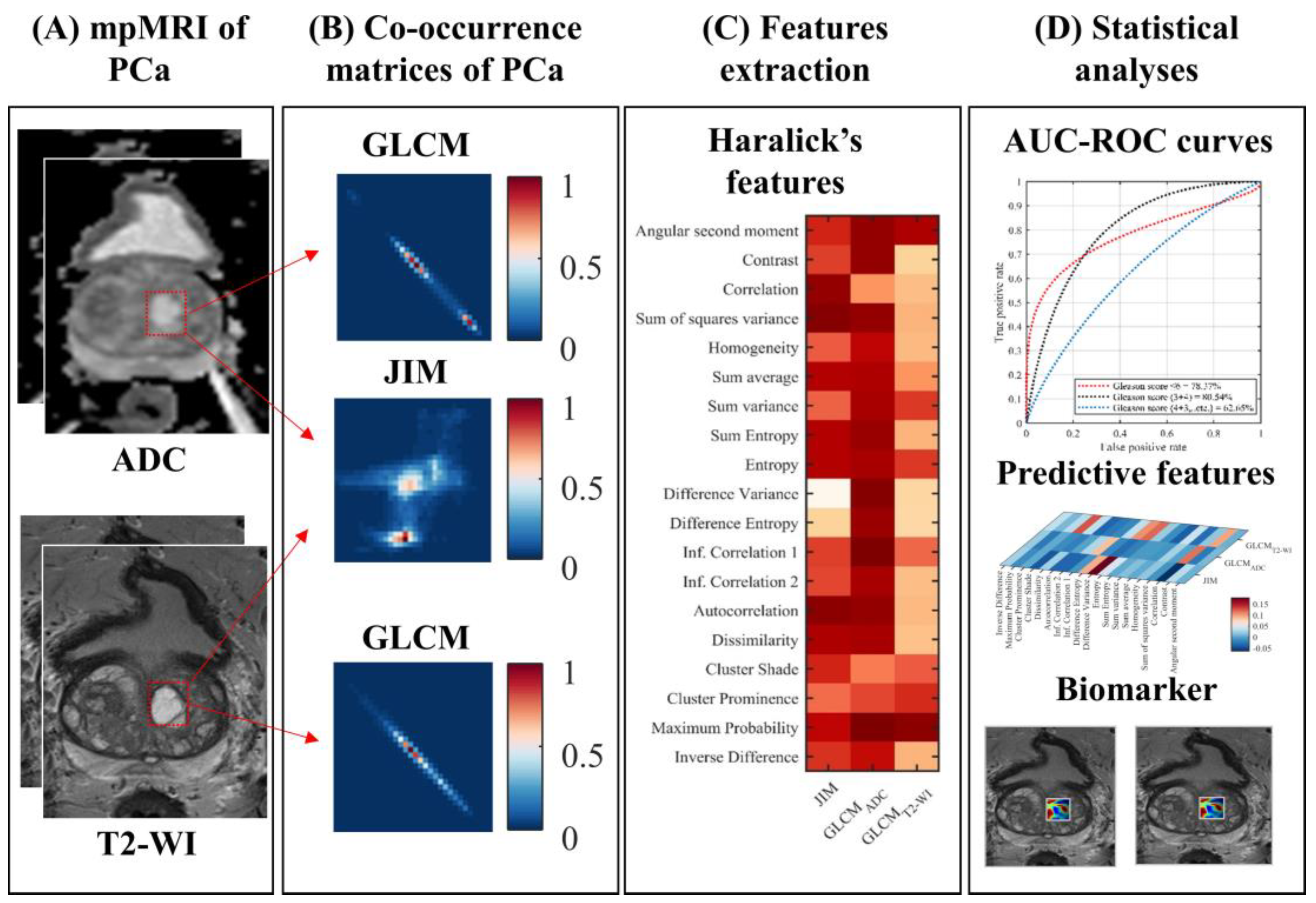
2.2. Proposed Radiomic Features
2.3. Statistical Analysis
3. Results
3.1. Patient Characteristics
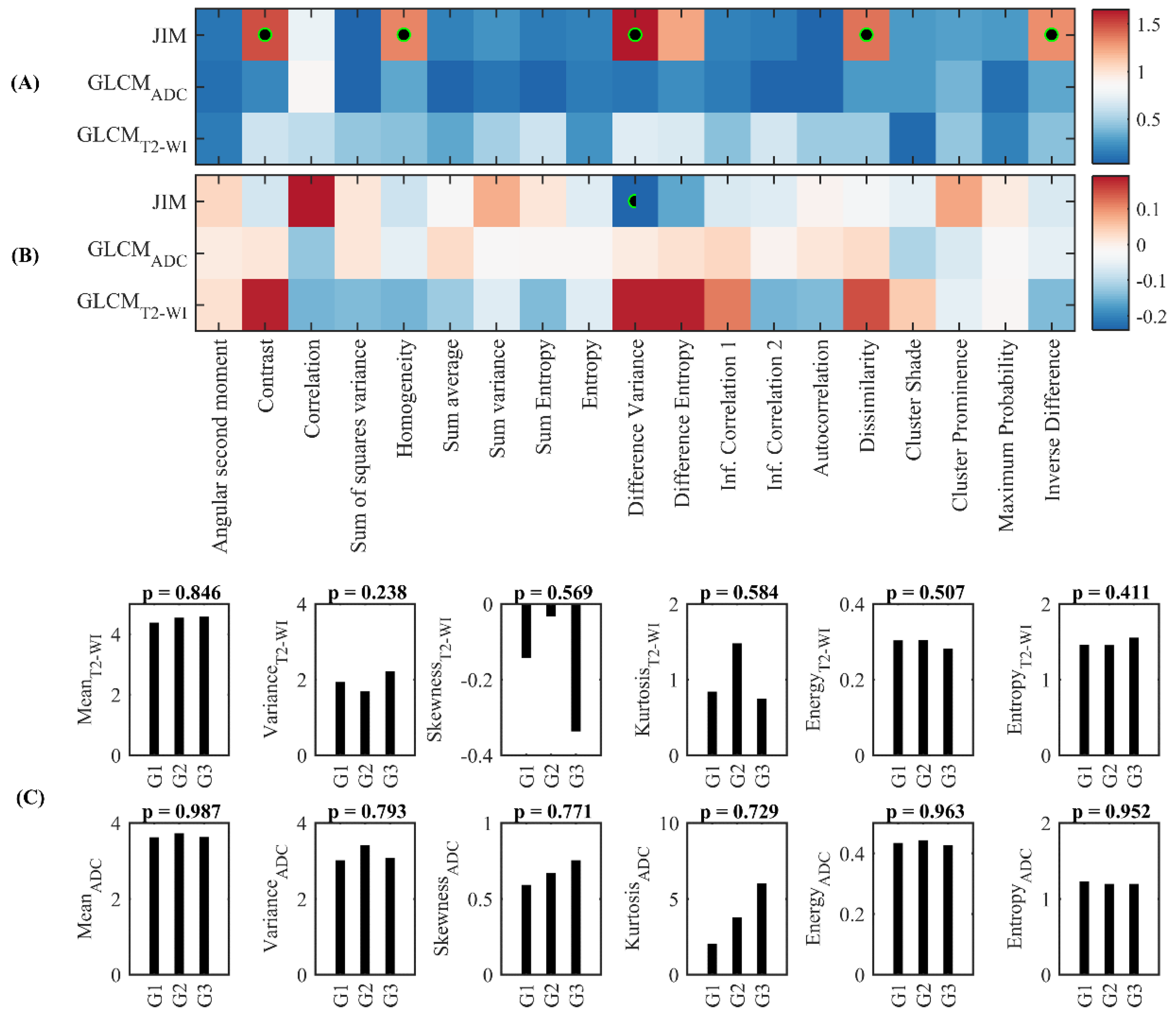
3.2. Differences and Correlation Analysis
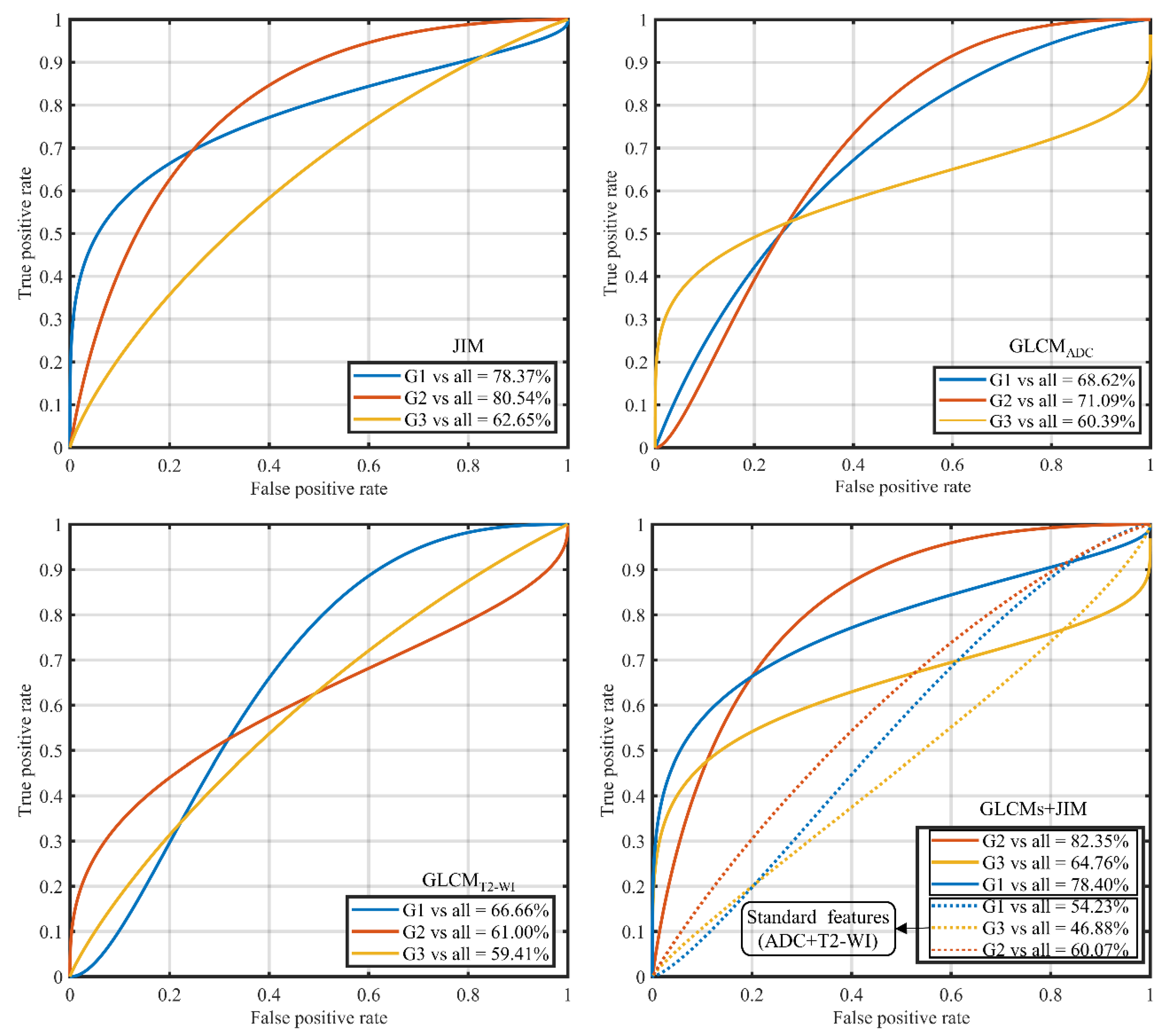
3.3. Gleason Score Prediction
3.4. Predictive Feature Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Lindenberg, M.L.; Turkbey, B.; Mena, E.; Choyke, P.L. Imaging Locally Advanced, Recurrent, and Metastatic Prostate Cancer: A Review. JAMA Oncol. 2017, 3, 1415–1422. [Google Scholar] [CrossRef] [PubMed]
- Fitzmaurice, C.; Allen, C.; Barber, R.M.; Barregard, L.; Bhutta, Z.A.; Brenner, H.; Dicker, D.J.; Chimed-Orchir, O.; Dandona, R.; Dandona, L.; et al. Global, Regional, and National Cancer Incidence, Mortality, Years of Life Lost, Years Lived With Disability, and Disability-Adjusted Life-Years for 29 Cancer Groups, 1990 to 2016: A Systematic Analysis for the Global Burden of Disease Study. JAMA Oncol. 2018. [Google Scholar] [CrossRef]
- Canadian Cancer Statistics Publication—Canadian Cancer Society. Available online: http://www.cancer.ca/en/cancer-information/cancer-101/canadian-cancer-statistics-publication/?region=on (accessed on 22 May 2018).
- Pinsky, P.F.; Parnes, H.L.; Andriole, G. Mortality and complications after prostate biopsy in the P rostate, L ung, C olorectal and O varian C ancer S creening (PLCO) trial. BJU Int. 2014, 113, 254–259. [Google Scholar] [CrossRef] [PubMed]
- Epstein, J.I. Prostate cancer grading: A decade after the 2005 modified system. Mod. Pathol. 2018, 31, S47–S63. [Google Scholar] [CrossRef] [PubMed]
- Truong, M.; Frye, T.; Messing, E.; Miyamoto, H. Historical and contemporary perspectives on cribriform morphology in prostate cancer. Nat. Rev. Urol. 2018. [Google Scholar] [CrossRef] [PubMed]
- D’Amico, A.V.; Moul, J.; Carroll, P.R.; Sun, L.; Lubeck, D.; Chen, M.-H. Cancer-specific mortality after surgery or radiation for patients with clinically localized prostate cancer managed during the prostate-specific antigen era. J. Clin. Oncol. Off. J. Am. Soc. Clin. Oncol. 2003, 21, 2163–2172. [Google Scholar] [CrossRef] [PubMed]
- Andriole, G.L.; Crawford, E.D.; Grubb, R.L.I.; Buys, S.S.; Chia, D.; Church, T.R.; Fouad, M.N.; Gelmann, E.P.; Kvale, P.A.; Reding, D.J.; et al. Mortality Results from a Randomized Prostate-Cancer Screening Trial. N. Engl. J. Med. 2009, 360, 1310–1319. [Google Scholar] [CrossRef] [PubMed]
- Schröder, F.H.; Hugosson, J.; Roobol, M.J.; Tammela, T.L.J.; Ciatto, S.; Nelen, V.; Kwiatkowski, M.; Lujan, M.; Lilja, H.; Zappa, M.; et al. Screening and Prostate-Cancer Mortality in a Randomized European Study. N. Engl. J. Med. 2009, 360, 1320–1328. [Google Scholar] [CrossRef] [PubMed]
- Heidegger, I.; Skradski, V.; Steiner, E.; Klocker, H.; Pichler, R.; Pircher, A.; Horninger, W.; Bektic, J. High risk of under-grading and -staging in prostate cancer patients eligible for active surveillance. PLoS ONE 2015, 10, e0115537. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, D.F.R.; Melia, J.; McWilliam, L.J.; Ball, R.Y.; Grigor, K.; Harnden, P.; Jarmulowicz, M.; Montironi, R.; Moseley, R.; Waller, M.; et al. A study of Gleason score interpretation in different groups of UK pathologists; techniques for improving reproducibility. Histopathology 2006, 48, 655–662. [Google Scholar] [CrossRef] [PubMed]
- Harbias, A.; Salmo, E.; Crump, A. Implications of Observer Variation in Gleason Scoring of Prostate Cancer on Clinical Management: A Collaborative Audit. Gulf J. Oncol. 2017, 1, 41–45. [Google Scholar]
- Nakai, Y.; Tanaka, N.; Shimada, K.; Konishi, N.; Miyake, M.; Anai, S.; Fujimoto, K. Review by urological pathologists improves the accuracy of Gleason grading by general pathologists. BMC Urol. 2015, 15, 70. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-J.; Chu, W.-C.; Pu, Y.-S.; Chueh, S.-C.; Shun, C.-T.; Tseng, W.-Y.I. Washout gradient in dynamic contrast-enhanced MRI is associated with tumor aggressiveness of prostate cancer. J. Magn. Reson. Imaging JMRI 2012, 36, 912–919. [Google Scholar] [CrossRef] [PubMed]
- Vos, E.K.; Litjens, G.J.S.; Kobus, T.; Hambrock, T.; Hulsbergen-van de Kaa, C.A.; Barentsz, J.O.; Huisman, H.J.; Scheenen, T.W.J. Assessment of prostate cancer aggressiveness using dynamic contrast-enhanced magnetic resonance imaging at 3 T. Eur. Urol. 2013, 64, 448–455. [Google Scholar] [CrossRef] [PubMed]
- Mehralivand, S.; Shih, J.H.; Rais-Bahrami, S.; Oto, A.; Bednarova, S.; Nix, J.W.; Thomas, J.V.; Gordetsky, J.B.; Gaur, S.; Harmon, S.A.; et al. A Magnetic Resonance Imaging–Based Prediction Model for Prostate Biopsy Risk Stratification. JAMA Oncol. 2018, 4, 678–685. [Google Scholar] [CrossRef] [PubMed]
- Hassanzadeh, E.; Glazer, D.I.; Dunne, R.M.; Fennessy, F.M.; Harisinghani, M.G.; Tempany, C.M. Prostate Imaging Reporting and Data System Version 2 (PI-RADS v2): A pictorial review. Abdom. Radiol. N.Y. 2017, 42, 278–289. [Google Scholar] [CrossRef] [PubMed]
- Donati, O.F.; Afaq, A.; Vargas, H.A.; Mazaheri, Y.; Zheng, J.; Moskowitz, C.S.; Hricak, H.; Akin, O. Prostate MRI: Evaluating tumor volume and apparent diffusion coefficient as surrogate biomarkers for predicting tumor Gleason score. Clin. Cancer Res. Off. J. Am. Assoc. Cancer Res. 2014, 20, 3705–3711. [Google Scholar] [CrossRef] [PubMed]
- Hambrock, T.; Somford, D.M.; Huisman, H.J.; van Oort, I.M.; Witjes, J.A.; Hulsbergen-van de Kaa, C.A.; Scheenen, T.; Barentsz, J.O. Relationship between apparent diffusion coefficients at 3.0-T MR imaging and Gleason grade in peripheral zone prostate cancer. Radiology 2011, 259, 453–461. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Li, H.; Yan, X.; Wu, C.-J.; Liu, X.-S.; Shi, H.-B.; Zhang, Y.-D. Histogram analysis of diffusion kurtosis magnetic resonance imaging in differentiation of pathologic Gleason grade of prostate cancer. Urol. Oncol. 2015, 33, 337.e15–337.e24. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, P.; Kurhanewicz, J.; Madabhushi, A. Multi-kernel graph embedding for detection, Gleason grading of prostate cancer via MRI/MRS. Med. Image Anal. 2013, 17, 219–235. [Google Scholar] [CrossRef] [PubMed]
- Vargas, H.A.; Akin, O.; Franiel, T.; Mazaheri, Y.; Zheng, J.; Moskowitz, C.; Udo, K.; Eastham, J.; Hricak, H. Diffusion-weighted Endorectal MR Imaging at 3 T for Prostate Cancer: Tumor Detection and Assessment of Aggressiveness. Radiology 2011, 259, 775–784. [Google Scholar] [CrossRef] [PubMed]
- Wibmer, A.; Hricak, H.; Gondo, T.; Matsumoto, K.; Veeraraghavan, H.; Fehr, D.; Zheng, J.; Goldman, D.; Moskowitz, C.; Fine, S.W.; et al. Haralick texture analysis of prostate MRI: Utility for differentiating non-cancerous prostate from prostate cancer and differentiating prostate cancers with different Gleason scores. Eur. Radiol. 2015, 25, 2840–2850. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Weng, Z.; Xu, H.; Zhang, Z.; Miao, H.; Chen, W.; Liu, Z.; Zhang, X.; Wang, M.; Xu, X.; et al. Support Vector Machines (SVM) classification of prostate cancer Gleason score in central gland using multiparametric magnetic resonance images: A cross-validated study. Eur. J. Radiol. 2018, 98, 61–67. [Google Scholar] [CrossRef] [PubMed]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Litjens, G.; Debats, O.; Barentsz, J.; Karssemeijer, N.; Huisman, H. Computer-aided detection of prostate cancer in MRI. IEEE Trans. Med. Imaging 2014, 33, 1083–1092. [Google Scholar] [CrossRef] [PubMed]
- Chaddad, A.; Daniel, P.; Desrosiers, C.; Toews, M.; Abdulkarim, B. Novel Radiomic Features based on Joint Intensity Matrices for Predicting Glioblastoma Patient Survival Time. IEEE J. Biomed. Health Inform. 2018. [Google Scholar] [CrossRef] [PubMed]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Zar, J.H. Significance Testing of the Spearman Rank Correlation Coefficient. J. Am. Stat. Assoc. 1972, 67, 578–580. [Google Scholar] [CrossRef]
- Holm, S. A Simple Sequentially Rejective Multiple Test Procedure. Scand. J. Stat. 1979, 6, 65–70. [Google Scholar]
- Archer, K.J.; Kimes, R.V. Empirical characterization of random forest variable importance measures. Comput. Stat. Data Anal. 2008, 52, 2249–2260. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How Many Trees in a Random Forest? In Machine Learning and Data Mining in Pattern Recognition; Lecture Notes in Computer Science; Springer: Berlin, Heidelberg, 2012; pp. 154–168. [Google Scholar]
- Vignati, A.; Mazzetti, S.; Giannini, V.; Russo, F.; Bollito, E.; Porpiglia, F.; Stasi, M.; Regge, D. Texture features on T2-weighted magnetic resonance imaging: New potential biomarkers for prostate cancer aggressiveness. Phys. Med. Biol. 2015, 60, 2685–2701. [Google Scholar] [CrossRef] [PubMed]
- Aerts, H.J.W.L. The Potential of Radiomic-Based Phenotyping in Precision Medicine: A Review. JAMA Oncol. 2016, 2, 1636–1642. [Google Scholar] [CrossRef] [PubMed]
- Mankoff, D.A.; Farwell, M.D.; Clark, A.S.; Pryma, D.A. Making Molecular Imaging a Clinical Tool for Precision Oncology: A Review. JAMA Oncol. 2017, 3, 695–701. [Google Scholar] [CrossRef] [PubMed]
- Siddiqui, M.M.; Rais-Bahrami, S.; Turkbey, B.; George, A.K.; Rothwax, J.; Shakir, N.; Okoro, C.; Raskolnikov, D.; Parnes, H.L.; Linehan, W.M.; et al. Comparison of MR/Ultrasound Fusion–Guided Biopsy With Ultrasound-Guided Biopsy for the Diagnosis of Prostate Cancer. JAMA 2015, 313, 390–397. [Google Scholar] [CrossRef] [PubMed]
- Chaddad, A.; Daniel, P.; Niazi, T. Radiomics Evaluation of Histological Heterogeneity Using Multiscale Textures Derived From 3D Wavelet Transformation of Multispectral Images. Front. Oncol. 2018, 8. [Google Scholar] [CrossRef] [PubMed]
- Chaddad, A.; Sabri, S.; Niazi, T.; Abdulkarim, B. Prediction of survival with multi-scale radiomic analysis in glioblastoma patients. Med. Biol. Eng. Comput. 2018, 1–14, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Chaddad, A.; Desrosiers, C.; Toews, M.; Abdulkarim, B.; Chaddad, A.; Desrosiers, C.; Toews, M.; Abdulkarim, B. Predicting survival time of lung cancer patients using radiomic analysis. Oncotarget 2017, 8, 104393–104407. [Google Scholar] [CrossRef] [PubMed]
- Viswanath, S.E.; Bloch, N.B.; Chappelow, J.C.; Toth, R.; Rofsky, N.M.; Genega, E.M.; Lenkinski, R.E.; Madabhushi, A. Central gland and peripheral zone prostate tumors have significantly different quantitative imaging signatures on 3 Tesla endorectal, in vivo T2-weighted MR imagery. J. Magn. Reson. Imaging JMRI 2012, 36, 213–224. [Google Scholar] [CrossRef] [PubMed]
- Moradi, M.; Salcudean, S.E.; Chang, S.D.; Jones, E.C.; Buchan, N.; Casey, R.G.; Goldenberg, S.L.; Kozlowski, P. Multiparametric MRI maps for detection and grading of dominant prostate tumors. J. Magn. Reson. Imaging JMRI 2012, 35, 1403–1413. [Google Scholar] [CrossRef] [PubMed]
- Madabhushi, A.; Feldman, M.D.; Metaxas, D.N.; Tomaszeweski, J.; Chute, D. Automated detection of prostatic adenocarcinoma from high-resolution ex vivo MRI. IEEE Trans. Med. Imaging 2005, 24, 1611–1625. [Google Scholar] [CrossRef] [PubMed]
- Niaf, E.; Rouvière, O.; Mège-Lechevallier, F.; Bratan, F.; Lartizien, C. Computer-aided diagnosis of prostate cancer in the peripheral zone using multiparametric MRI. Phys. Med. Biol. 2012, 57, 3833–3851. [Google Scholar] [CrossRef] [PubMed]
- Fehr, D.; Veeraraghavan, H.; Wibmer, A.; Gondo, T.; Matsumoto, K.; Vargas, H.A.; Sala, E.; Hricak, H.; Deasy, J.O. Automatic classification of prostate cancer Gleason scores from multiparametric magnetic resonance images. Proc. Natl. Acad. Sci. USA 2015, 112, E6265–6273. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, A.; Bourne, R.M.; Wang, S.; Devaraj, A.; Gallan, A.J.; Antic, T.; Karczmar, G.S.; Oto, A. Diagnosis of Prostate Cancer with Noninvasive Estimation of Prostate Tissue Composition by Using Hybrid Multidimensional MR Imaging: A Feasibility Study. Radiology 2018, 171130. [Google Scholar] [CrossRef] [PubMed]

| Gleason (n) | Gleason Score | Our Classification (n) |
|---|---|---|
| Grade Group 1 (30) | ≤6 | G1 (30) |
| Grade Group 2 (39) | 3 + 4 = 7 | G2 (39) |
| Grade Group 3 (17) | 4 + 3 = 7 | G3 (30) |
| Grade Group 4 (7) | 4 + 4 = 8; 3 + 5 = 8; 5 + 3 = 8 | |
| Grade Group 5 (6) | 9 or 10 |
| JIM Features | GS ≤ 6, n = 30 | GS = 3 + 4, n = 39 | GS ≥ 3 + 4, n = 30 | p-Value |
|---|---|---|---|---|
| Contrast | 536.5119–325.99 | 735.9059–492.77 | 438.9053–373.11 | 0.03 |
| Homogeneity | 0.1365–0.06 | 0.1117–0.08 | 0.1362–0.07 | 0.04 |
| Difference variance | 159.4869–49.76 | 188.8752–111.58 | 129.6384–65.47 | 0.02 |
| Dissimilarity | 14.5873–4.68 | 17.1876–7.19 | 13.6761–6.77 | 0.04 |
| Inverse difference | 0.2093–0.06 | 0.1827–0.08 | 0.2091–0.08 | 0.04 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaddad, A.; Kucharczyk, M.J.; Niazi, T. Multimodal Radiomic Features for the Predicting Gleason Score of Prostate Cancer. Cancers 2018, 10, 249. https://doi.org/10.3390/cancers10080249
Chaddad A, Kucharczyk MJ, Niazi T. Multimodal Radiomic Features for the Predicting Gleason Score of Prostate Cancer. Cancers. 2018; 10(8):249. https://doi.org/10.3390/cancers10080249
Chicago/Turabian StyleChaddad, Ahmad, Michael J Kucharczyk, and Tamim Niazi. 2018. "Multimodal Radiomic Features for the Predicting Gleason Score of Prostate Cancer" Cancers 10, no. 8: 249. https://doi.org/10.3390/cancers10080249
APA StyleChaddad, A., Kucharczyk, M. J., & Niazi, T. (2018). Multimodal Radiomic Features for the Predicting Gleason Score of Prostate Cancer. Cancers, 10(8), 249. https://doi.org/10.3390/cancers10080249







