Array of Resonant Electromechanical Nanosystems: A Technological Breakthrough for Uncooled Infrared Imaging
Abstract
1. Introduction
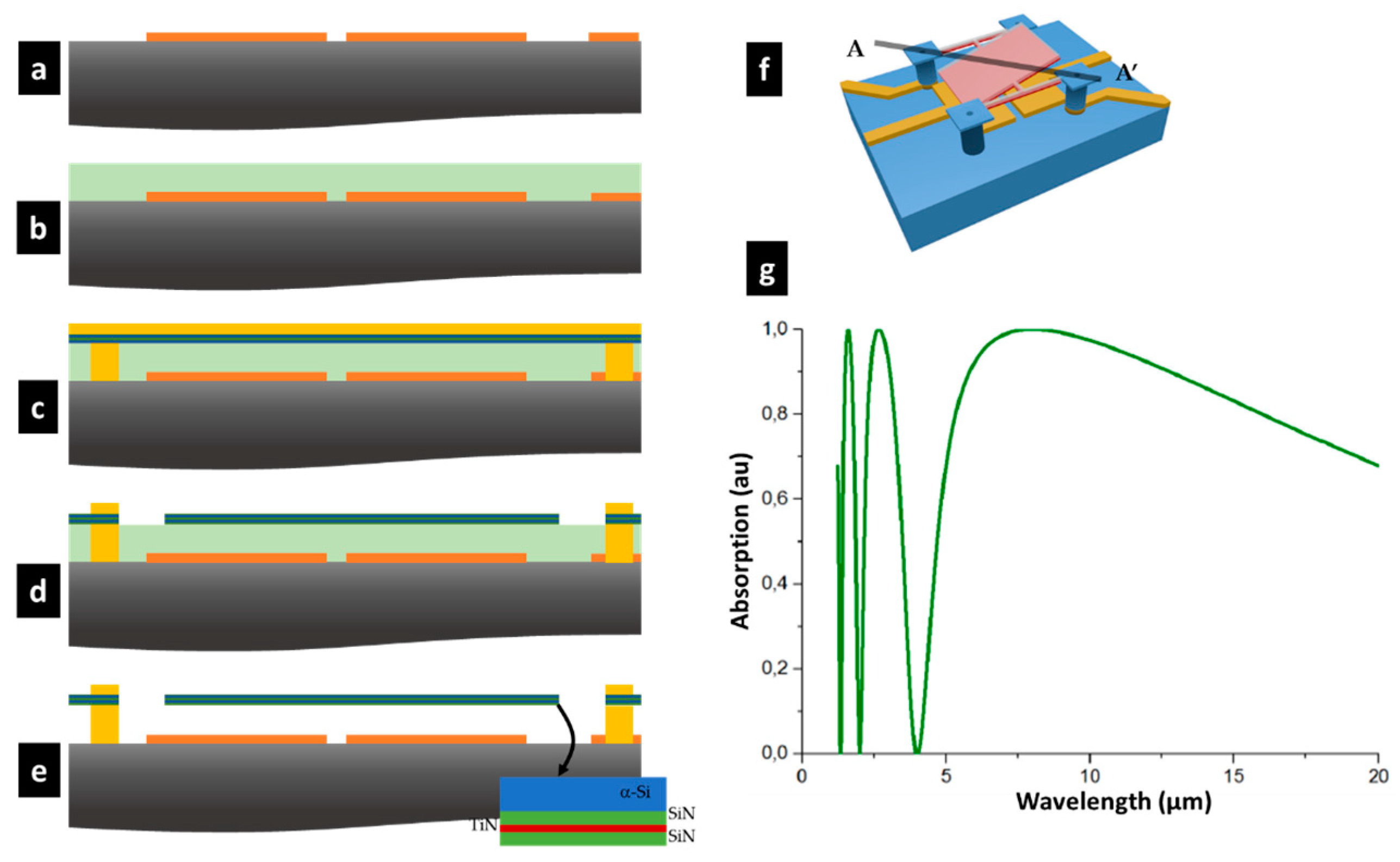
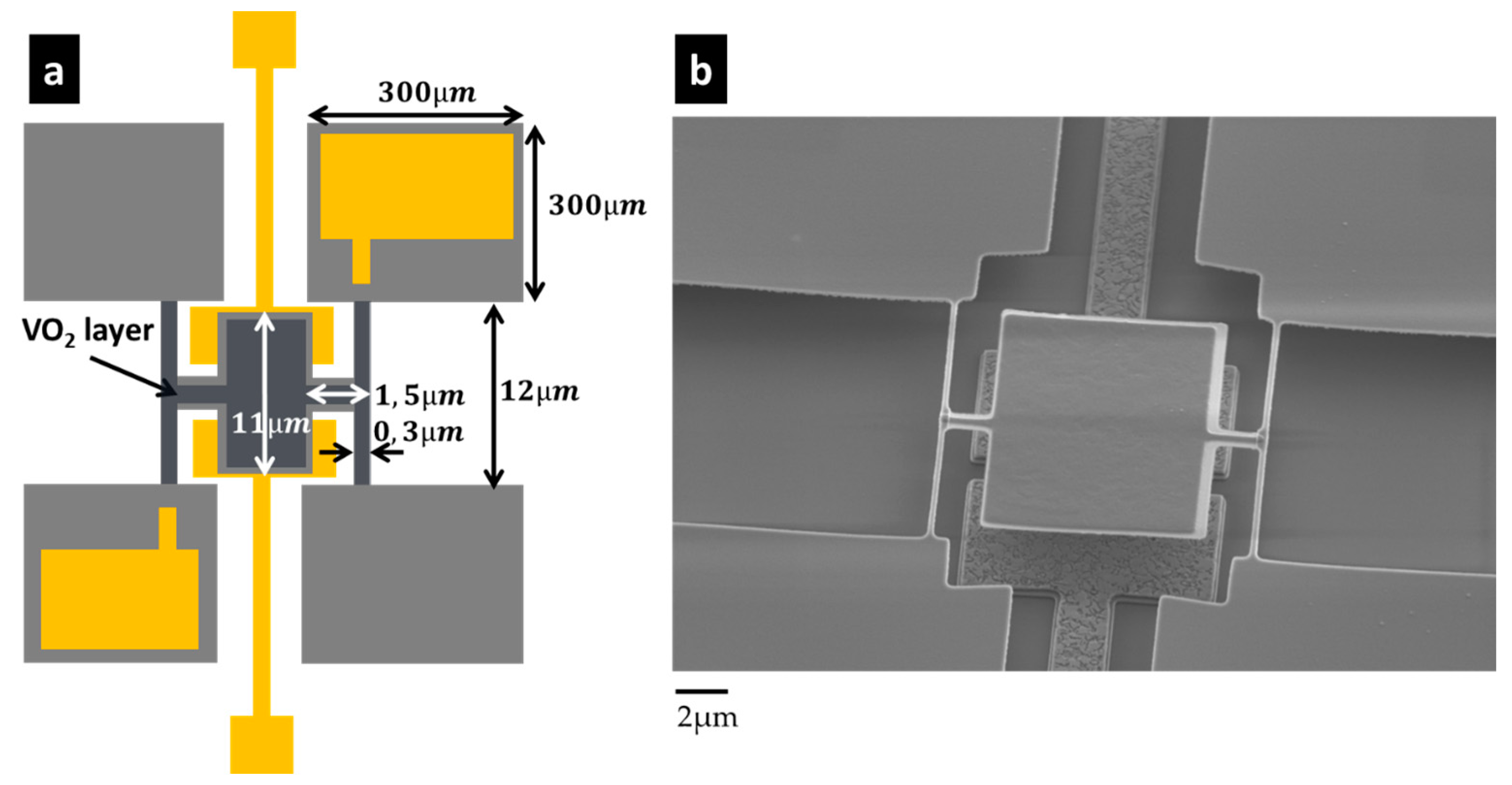
2. Design and Fabrication of Electromechanical Resonator Arrays
3. Results
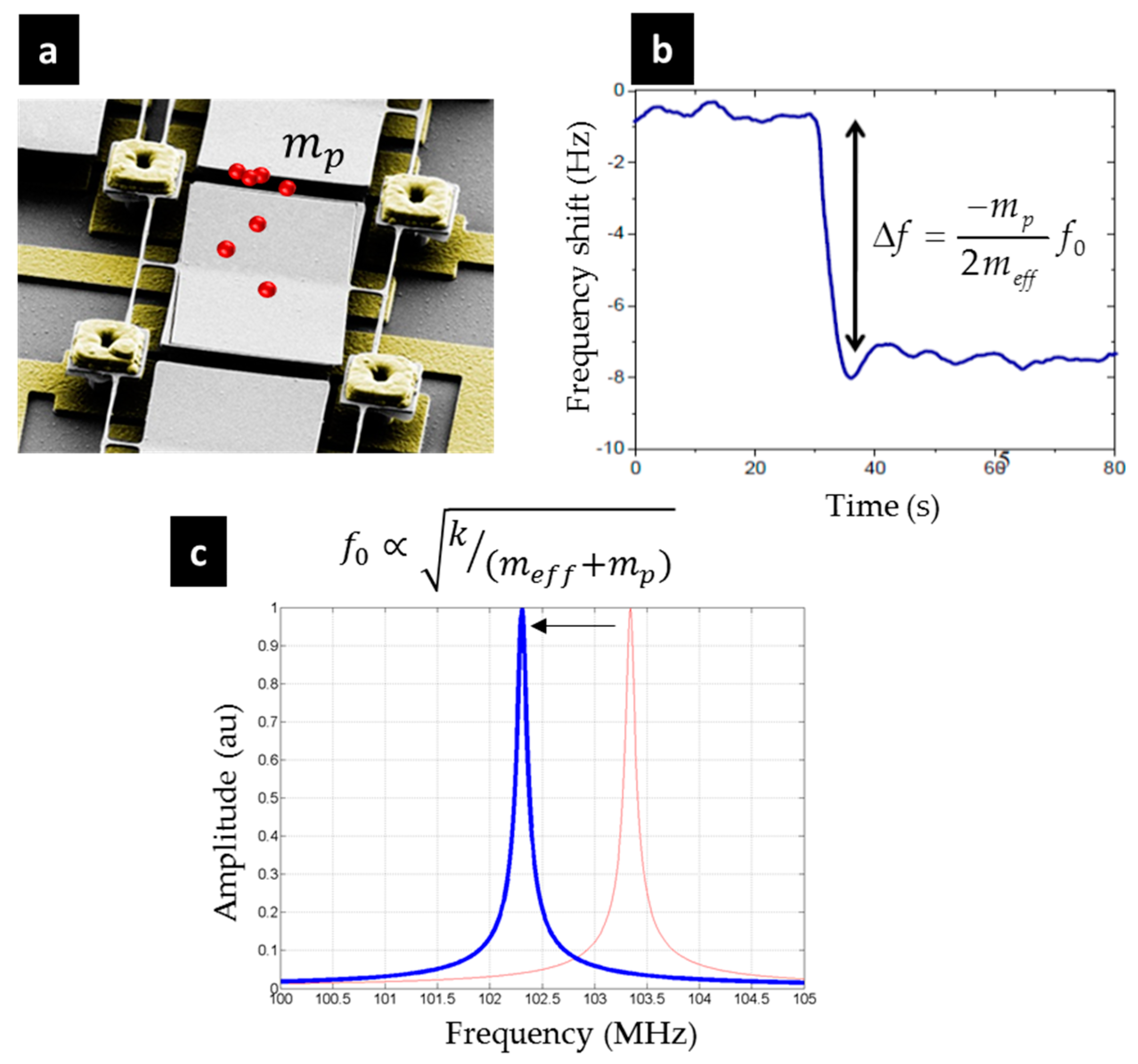
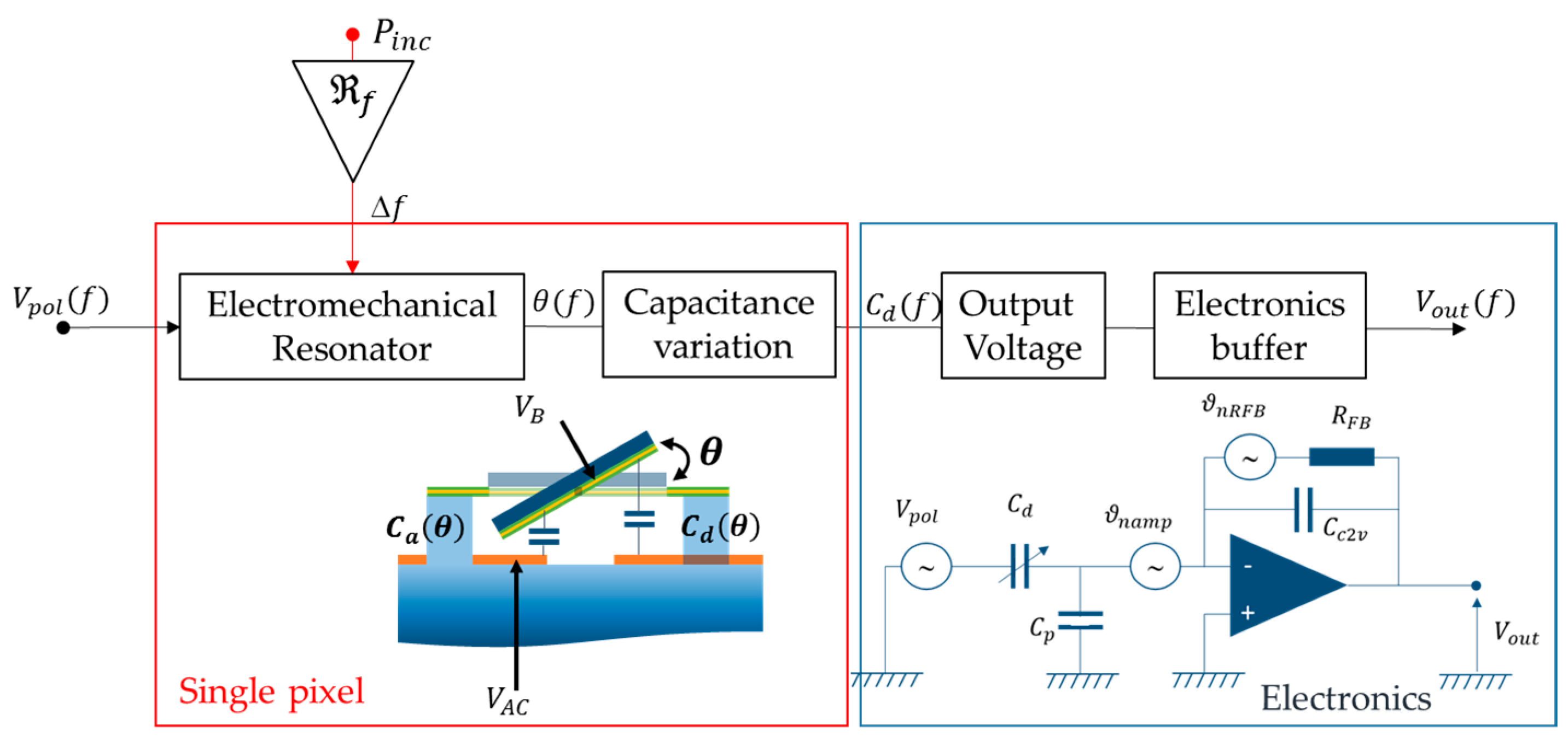
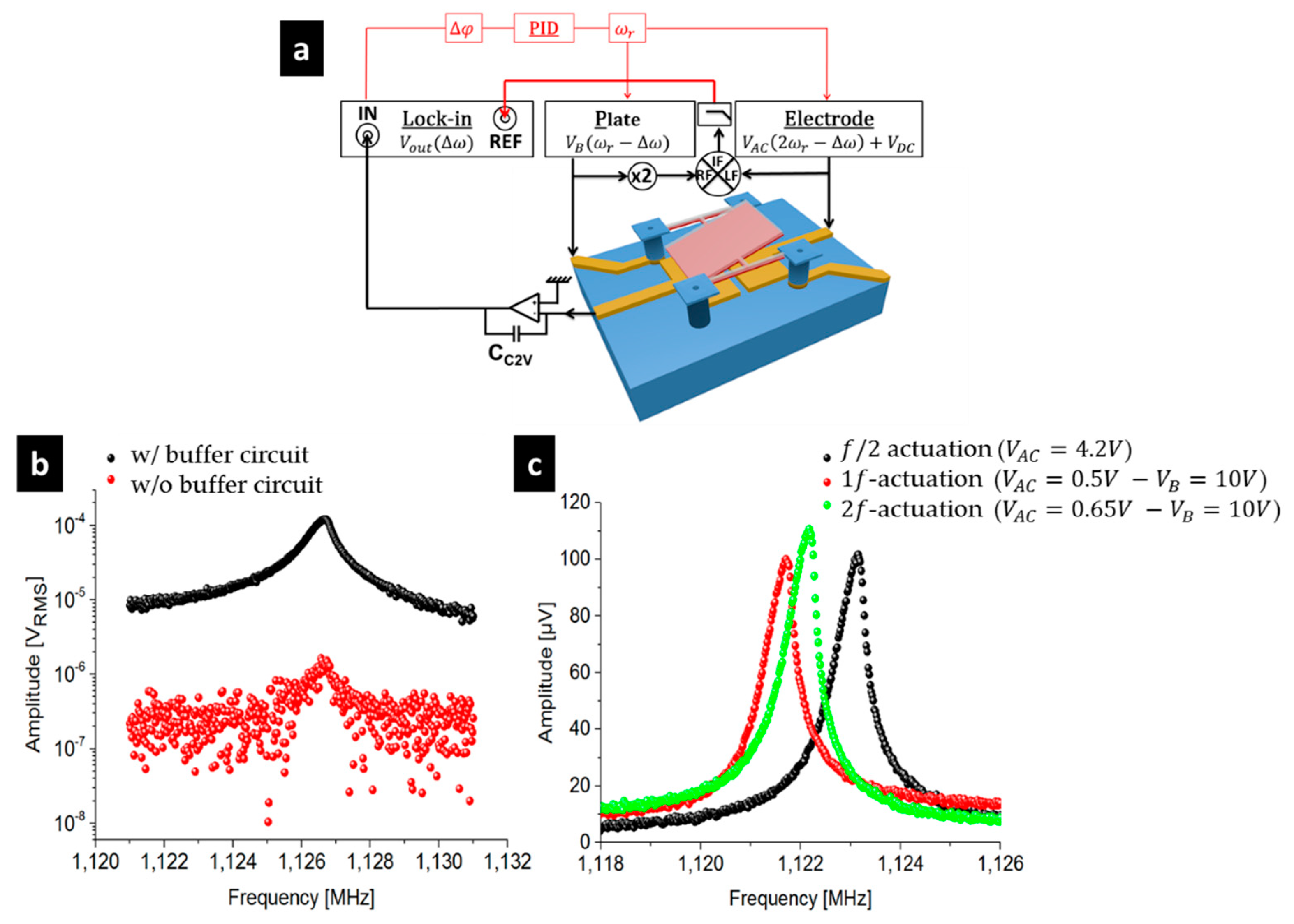
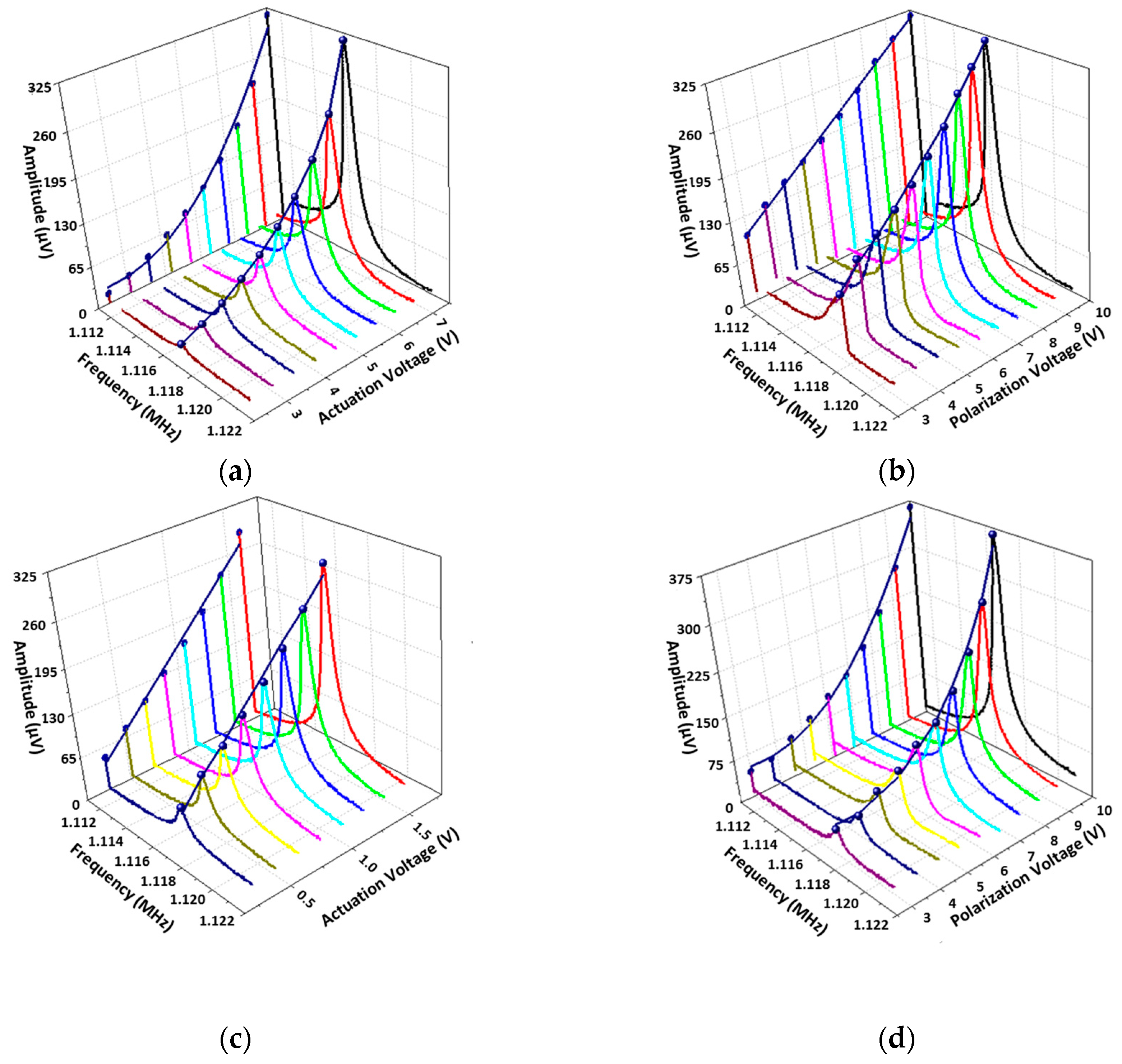
3.1. Electromechanical Characterizations
- ;
- ;
3.2. Thermal Characterizations
3.2.1. TCF & G
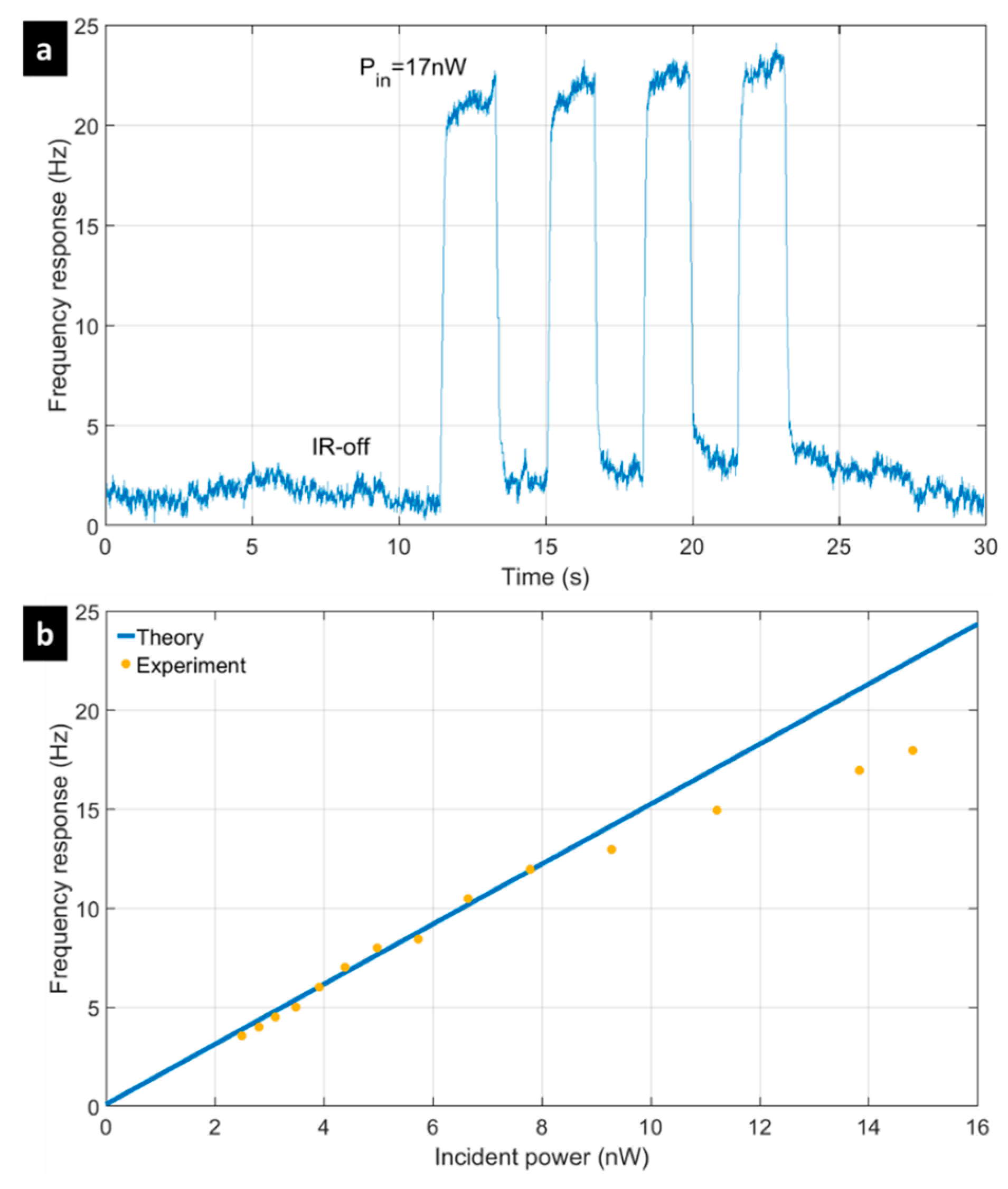
3.2.2. Thermal Response
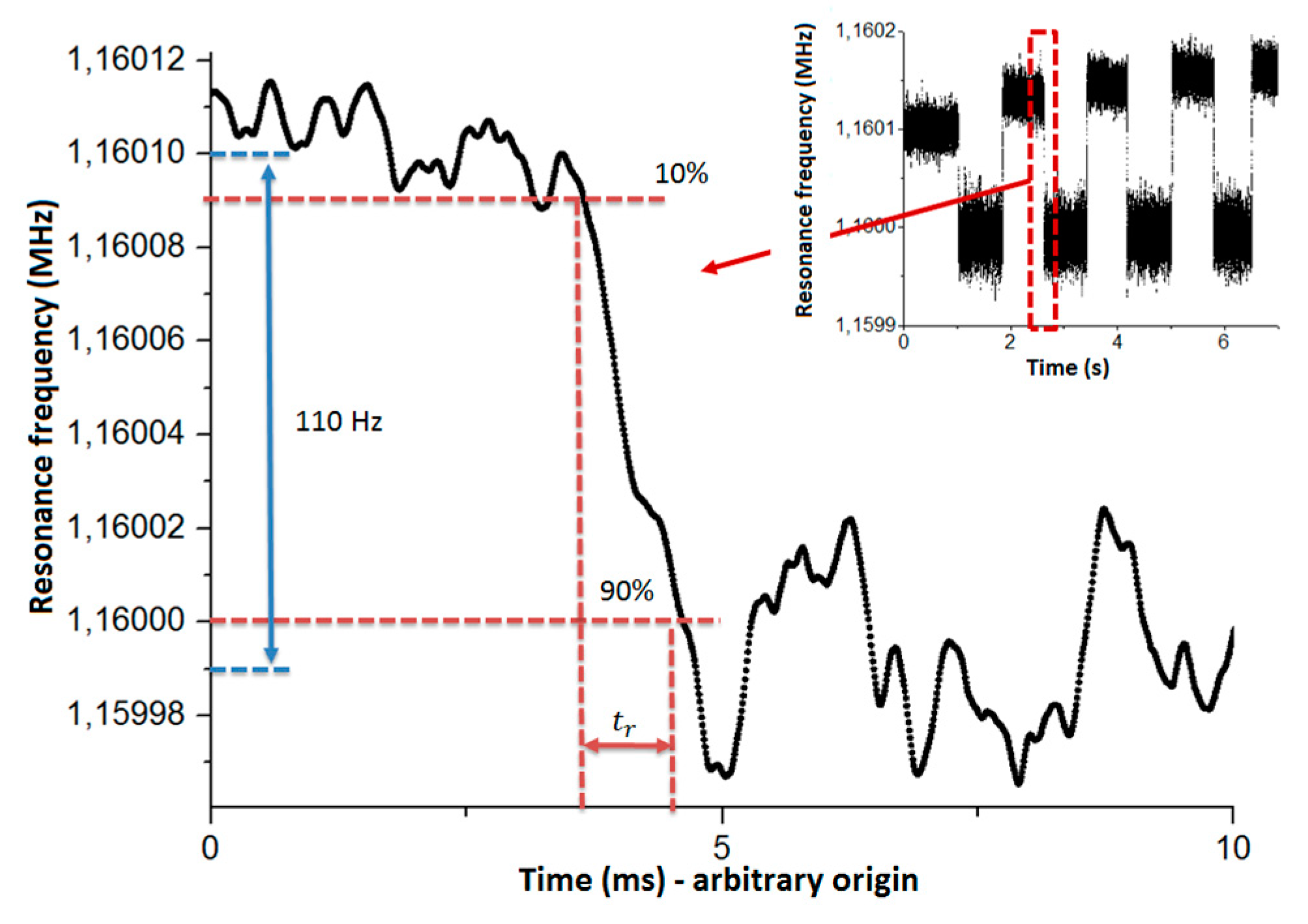
3.2.3. Response Time
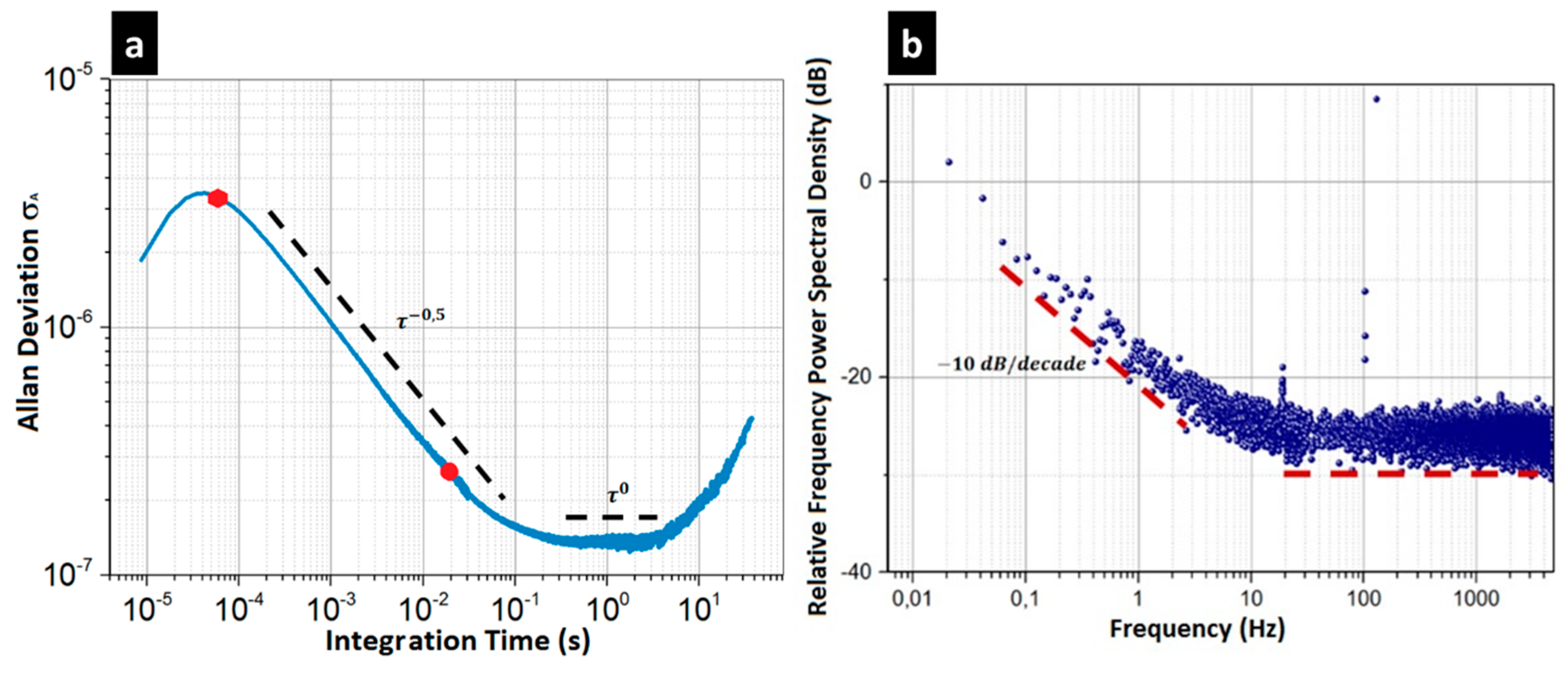
3.3. Noises and Temperature Sensitivity
4. Discussion
- Frequency stability and matrix readout strategy: A 50 Hz integration bandwidth requires an improvement of the noise amplitude of our buffer electronics close to the pixel. Lower amplitude noise levels can be reached by using self-oscillating electronics requiring only a few transistors, unlike PLL circuits. Moreover, our electronics was realized close to the pixel but this was not done through an application-specific integrated circuit (ASIC) fabricated underneath the electromechanical pixels. The low-temperature fabrication process presented above has already been used to manufacture resistive bolometer imagers on top of CMOS circuits (ROIC) by post-processing [37,55], and it should be straightforward to reuse this approach in our case. As mentioned in the introductive section of the paper, a co-integration of the readout electronics at the pixel level will reduce the parasitic capacitance down to a few fF, and will decrease the electrical noise down to a theoretical level of , or even . This approach makes the down-mixing detection scheme unnecessary, leading to a much simpler measurement chain than the strategy presented here. will be decreased by a factor of 8 with a self-oscillating IC (a gain of a factor 4 on the absolute noise, and a gain of a factor 2 on the output voltage with a the direct detection (see Equation (9))). Thus, the electronics noise will become lower than the fundamental APN () for a 700 Hz integration bandwidth. This conclusion leads us to suggest a new readout scheme consisting of reading 700/50 = 14 pixels during a 50 Hz frame rate, which allows for a larger area for the co-integrated readout. These two straightforward improvements allow us to obtain a FOM that is close to 0.75 for a (global shutter approach), which is an encouraging element.
- Thermal response: At the end, the noise floor level will be set by the APN, whatever the electronics and the readout strategy. An improvement of the signal through the thermal insulation is much trickier in our case. Indeed, this would require long and thin rods/insulations legs, and this would lower the onset of nonlinearity of (see Equation (8)), leading to a degradation of the SNRs and therefore the frequency stability .
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rugar, D.; Budakian, R.; Mamin, H.J.; Chui, B.W. Single spin detection by magnetic resonance force microscopy. Nature 2004, 430, 329. [Google Scholar] [CrossRef] [PubMed]
- Arlett, J.L.; Maloney, J.R.; Gudlewski, B.; Muluneh, M.; Roukes, M.L. Self-sensing micro- and nanocantilevers with attonewton-scale force resolution. Nano Lett. 2006, 6, 1000–1006. [Google Scholar] [CrossRef]
- Sage, E.; Brenac, A.; Alava, T.; Morel, R.; Dupré, C.; Hanay, M.S.; Roukes, L.M.; Duraffourg, L.; Masselon, C.; Hentz, S. Neutral particle mass spectrometry with nanomechanical systems. Nat. Commun. 2015, 6, 6482. [Google Scholar] [CrossRef] [PubMed]
- Hanay, M.S.; Kelber, S.; Naik, A.K.; Chi, D.; Hentz, S.; Bullard, E.C.; Colinet, L.; Duraffourg, E.; Roukes, M.L. Single-protein nanomechanical mass spectrometry in real time. Nat. Nanotechnol. 2012, 7, 602–608. [Google Scholar] [CrossRef] [PubMed]
- Bargatin, I.; Myers, E.B.; Aldridge, J.S.; Marcoux, C.; Brianceau, P.; Duraffourg, L.; Colinet, E.; Hentz, S.; Andreucci, S.; Roukes, M.L. Large-scale integration of nanoelectromechanical systems for gas sensing applications. Nano Lett. 2012, 12, 1269–1274. [Google Scholar] [CrossRef] [PubMed]
- Fahad, H.M.; Shiraki, H.; Amani, M.; Zhang, C.; Hebbar, V.S.; Gao, W.; Ota, H.; Hettick, M.; Kiriya, D.; Chen, Y.-Z.; et al. Room temperature multiplexed gas sensing using chemical-sensitive 3.5-nm-thin silicon transistors. Sci. Adv. 2017, 3, e1602557. [Google Scholar] [CrossRef] [PubMed]
- Ralph, J.E.; King, R.C.; Curran, J.E.; Page, J.S. Miniature quartz resonator thermal detector. In Proceedings of the IEEE Ultrasonics Symposium, San Francisco, CA, USA, 16–18 October 1985; p. 362. [Google Scholar]
- Cabuz, C.; Shoji, S.; Fukatsu, K.; Cabuz, E.; Minami, K.; Esashi, M. Fabrication and packaging of a resonant infrared sensor integrated in silicon. Sens. Actuators A 1994, 43, 92–99. [Google Scholar] [CrossRef]
- Zhang, X.C.; Myers, E.B.; Sader, J.E.; Roukes, M.L. Nanomechanical torsional resonators for frequency-shift infrared thermal sensing. Nano Lett. 2013, 13, 1528–1534. [Google Scholar] [CrossRef] [PubMed]
- Yamazaki, T.; Ogawa, S.; Kumagai, S.; Sasaki, M. A novel infrared detector using highly nonlinear twisting vibration. Sens. Actuators A 2014, 212, 165–172. [Google Scholar] [CrossRef]
- Jensen, K.; Kim, K.; Zettl, A. An atomic-resolution nanomechanical mass sensor. Nat. Nanotechnol. 2008, 3, 533–537. [Google Scholar] [CrossRef] [PubMed]
- Chaste, J.; Eichler, A.; Moser, J.; Ceballos, G.; Rurali, R.; Bachtold, A. A nanomechanical mass sensor with yoctogram resolution. Nat. Nanotechnol. 2012, 7, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Ruz, J.J.; Tamayo, J.; Pini, V.; Kosaka, P.M.; Calleja, M. Physics of nanomechanical spectrometry of viruses. Sci. Rep. 2014, 4, 6051. [Google Scholar] [CrossRef] [PubMed]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Metcalfe, M. Applications of cavity optomechanics. Appl. Phys. Rev. 2014, 1, 031105. [Google Scholar] [CrossRef]
- Li, B.B.; Bulla, D.; Bilek, J.; Prakash, V.; Forstner, S.; Sheridan, E.; Madsen, L.; Rubinsztein-Dunlop, H.; Foster, S.; Schäfermeier, C.; et al. Ultrasensitive and broadband magnetometry with cavity optomechanics. In Proceedings of the IEEE Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 14–19 May 2017. [Google Scholar]
- Godin, M.; Bryan, A.K.; Burg, T.P.; Babcock, K.; Manalis, S.R. Measuring the mass, density, and size of particles and cells using a suspended microchannel resonator. Appl. Phys. Lett. 2007, 91, 123121. [Google Scholar] [CrossRef]
- Agache, V.; Blanco-Gomez, G.; Baleras, F.; Caillat, P. An embedded microchannel in a MEMS plate resonator for ultrasensitive mass sensing in liquid. Lab Chip 2011, 11, 2598–2603. [Google Scholar] [CrossRef] [PubMed]
- Min, D.H.; Moreland, J. Quantitative measurement of magnetic moments with a torsional resonator: Proposal for an ultralow moment reference material. J. Appl. Phys. 2005, 97, 10R504. [Google Scholar] [CrossRef]
- Antonio, D.; Dolz, M.I.; Pastoriza, H. Micromechanical magnetometer using an all-silicon nonlinear torsional resonator. Appl. Phys. Lett. 2009, 95, 133505. [Google Scholar] [CrossRef]
- Davis, J.P.; Vick, D.; Li, P.; Portillo, S.K.N.; Fraser, A.E.; Burgess, J.A.J.; Fortin, D.C.; Hiebert, W.K.; Freeman, M.R. Nanomechanical torsional resonator torque magnetometry. J. Appl. Phys. 2011, 109, 07D309. [Google Scholar] [CrossRef]
- Perez-Morelo, D.; Pastoriza, H. Torque magnetometry in YBa2Cu3O7-δ single crystals using high sensitive micromechanical torsional oscillator. J. Phys. Conf. Ser. 2014, 568, 22038. [Google Scholar] [CrossRef]
- Degen, C.L.; Poggio, M.; Mamin, H.J.; Rettner, C.T.; Rugar, D. Nanoscale magnetic resonance imaging. Proc. Natl. Acad. Sci. USA 2009, 106, 1313–1317. [Google Scholar] [CrossRef] [PubMed]
- Loh, O.Y.; Espinosa, H.D. Nanoelectromechanical contact switches. Nat. Nanotechnol. 2012, 7, 283–295. [Google Scholar] [CrossRef] [PubMed]
- Wong, A.-C.; Nguyen, C.T.C. Micromechanical mixer-filters (‘mixlers’). J. Microelectromech Syst. 2004, 13, 100–112. [Google Scholar] [CrossRef]
- Arlett, J.L.; Myers, E.B.; Roukes, M.L. Comparative advantages of mechanical biosensors. Nat. Nanotechnol. 2011, 6, 203–215. [Google Scholar] [CrossRef] [PubMed]
- Tamayo, J.; Kosaka, P.M.; Ruz, J.J.; San Paulo, Á.; Calleja, M. Biosensors based on nanomechanical systems. Chem. Soc. Rev. 2013, 42, 1287–1311. [Google Scholar] [CrossRef] [PubMed]
- Duraffourg, L.; Arcamone, J. From MEMS to NEMS. In Nanoelectromechanical Systems, 1st ed.; Baptist, R., Duraffourg, L., Eds.; ISTE Ltd.: London, UK, 2015; Chapter 1; p. 5. ISBN 978-1-84821-669-3. [Google Scholar]
- Mile, E.; Jourdan, G.; Bargatin, I.; Labarthe, S.; Marcoux, C.; Andreucci, P.; Hentz, S.; Kharrat, C.; Colinet, E.; Duraffourg, L. In-plane nanoelectromechanical resonators based on silicon nanowire piezoresistive detection. Nanotechnology 2010, 21, 165504. [Google Scholar] [CrossRef] [PubMed]
- Colinet, E.; Duraffourg, L.; Labarthe, S.; Hentz, S.; Robert, P.; Andreucci, P. Self-oscillation conditions of a resonant nanoelectromechanical mass sensor. J. Appl. Phys. 2009, 105, 124908. [Google Scholar] [CrossRef]
- Sage, E.; Sansa, M.; Fostner, S.; Defoort, M.; Gély, M.; Naik, A.K.; Morel, R.; Duraffourg, L.; Roukes, M.L.; Alava, T.; et al. Single-particle mass spectrometry with arrays of frequency-addressed nanomechanical resonators. arXiv, 2017arXiv:1712.06694. [CrossRef]
- Endoh, T.; Tohyama, S.; Yamazaki, T.; Tanaka, Y.; Okuyama, K.; Kurashina, S.; Miyoshi, M.; Katoh, K.; Yamamoto, T.; Okuda, Y.; et al. Uncooled infrared detector with 12 μm pixel pitch video graphics array. In Proceedings of the SPIE Conference on Defense, Security, and Sensing, Baltimore, MD, USA, 11 June 2013; Volume 8704, p. 87041G. [Google Scholar]
- FLIR Boson® | FLIR Systems. Available online: http://www.flir.com/cores/boson/ (accessed on 24 February 2017).
- TWV640 Thermal Camera Core | BAE Systems | International. Available online: http://www.baesystems.com/en/product/twv640-thermal-camera-core (accessed on 24 February 2017).
- Jo, Y.; Kwon, I.-W.; Kim, D.S.; Shim, H.B.; Lee, H.C. A self-protecting uncooled microbolometer structure for uncooled microbolometer. In Proceedings of the SPIE Conference on Defense, Security, and Sensing, Orlando, FL, USA, 25–29 April 2011; Volume 8012, p. 80121O. [Google Scholar]
- Dorn, D.A.; Herrera, O.; Tesdahl, C.; Shumard, E.; Wang, Y.-W. Impacts and mitigation strategies of sun exposure on uncooled microbolometer image sensors. In Proceedings of the SPIE Conference on Defense, Security, and Sensing, Orlando, FL, USA, 25–29 April 2011; Volume 8012, p. 80123Z. [Google Scholar]
- Tissot, J.L.; Durand, A.; Garret, T.; Minassian, C.; Robert, P.; Tinnes, S.; Vilain, M. High performance uncooled amorphous silicon VGA IRFPA with 17 μm pixel-pitch. In Proceedings of the SPIE Conference on Defense, Security, and Sensing, Orlando, FL, USA, 5–9 April 2010; Volume 7660, p. 76600T. [Google Scholar]
- Fraenkel, A.; Mizrahi, U.; Bikov, L.; Adin, A.; Malkinson, E.; Giladi, A.; Seter, D.; Kopolovich, Z. VOx-based uncooled microbolometric detectors: Recent developments at SCD. In Proceedings of the SPIE Conference on Defense, Security, and Sensing, Orlando, FL, USA, 17 May 2006; Volume 6206, p. 62061C. [Google Scholar]
- Truitt, P.A.; Hertzberg, J.B.; Huang, C.C.; Ekinci, K.L.; Schwab, K.C. Efficient and Sensitive Capacitive Readout of Nanomechanical Resonator Arrays. Nano Lett. 2007, 7, 120–126. [Google Scholar] [CrossRef] [PubMed]
- Younis, M.I. MEMS Linear and Nonlinear Statics and Dynamics; Springer: Boston, MA, USA, 2011; Volume 20. [Google Scholar]
- Verbridge, S.S.; Parpia, J.M.; Reichenbach, R.B.; Bellan, L.M.; Craighead, H.G. High quality factor resonance at room temperature with nanostrings under high tensile stress. J. Appl. Phys. 2006, 99, 124304. [Google Scholar] [CrossRef]
- Kacem, N.; Hentz, S.; Pinto, D.; Reig, B.; Nguyen, V. Nonlinear dynamics of nanomechanical beam resonators: Improving the performance of NEMS-based sensors. Nanotechnology 2009, 20, 275501. [Google Scholar] [CrossRef] [PubMed]
- Kozinsky, I.; Postma, H.W.C.; Bargatin, I.; Roukes, M.L. Tuning nonlinearity, dynamic range, and frequency of nanomechanical resonators. Appl. Phys. Lett. 2006, 88, 253101. [Google Scholar] [CrossRef]
- Analog Devices, Op Amp Total Output Noise Calculations for Second-Order System. Available online: http://www.analog.com/media/en/training-seminars/tutorials/MT-050.pdf (accessed on 1 June 2016).
- Bargatin, I.; Myers, E.B.; Arlett, J.; Gudlewski, B.; Roukes, M.L. Sensitive detection of nanomechanical motion using piezoresistive signal downmixing. Appl. Phys. Lett. 2005, 86, 133109. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum Settings for Automatic Controllers. J. Dyn. Syst. Meas. Control 1993, 115, 220–222. [Google Scholar] [CrossRef]
- Laurent, L.; Yon, J.J.; Moulet, J.S.; Imperinetti, P.; Duraffourg, L. Compensation of nonlinear hardening effect in a nanoelectromechanical torsional resonator. Sensors Actuators A 2017, 263, 326–331. [Google Scholar] [CrossRef]
- Wood, R.A. Chapter 3—Monolithic Silicon Microbolometer Arrays. In Uncooled Infrared Imaging Arrays and Systems; Semiconductors and Semimetals Series; Kruse, W., Skatrud, D.D., Eds.; Elsevier: New York, NY, USA, 1997; Volume 47, p. 43. [Google Scholar]
- Robins, W.P. Phase Noise in Signal Sources: Theory and Applications; IET: London, UK, 1984. [Google Scholar]
- Cleland, A.N.; Roukes, M.L. Noise processes in nanomechanical resonators. J. Appl. Phys. 2002, 92, 2758–2769. [Google Scholar] [CrossRef]
- Allan, D.W. Time and Frequency (Time-Domain) Characterization, Estimation, and Prediction of Precision Clocks and Oscillators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1987, 34, 647–654. [Google Scholar] [CrossRef] [PubMed]
- Sansa, M.; Sage, E.; Bullard, E.C.; Gély, M.; Alava, T.; Colinet, E.; Naik, A.K.; Villanueva, L.G.; Duraffourg, L.; Roukes, M.L.; et al. Frequency fluctuations in silicon nanoresonators. Nat. Nanotechnol. 2016, 11, 552–558. [Google Scholar] [CrossRef] [PubMed]
- Kruse, P.W.; Skatrud, D.D. Uncooled Infrared Imaging Arrays and Systems; Academic Press: Cambridge, MA, USA, 1997; Volume 47. [Google Scholar]
- Skidmore, G.D.; Han, C.J.; Li, C. Uncooled microbolometers at DRS and elsewhere through 2013. In Proceedings of the SPIE Conference on Image Sensing Technologies: Materials, Devices, Systems, and Applications, Baltimore, MD, USA, 21 May 2014; Volume 9100, p. 910003. [Google Scholar]
- Tissot, J.-L.; Mottin, E.; Martin, J.-L.; Yon, J.-J.; Vilain, M. Advanced uncooled infrared focal plane development at CEA/LETI. In Proceedings of the International Conference on Space Optics, Rhodes Island, Greece, 4–8 October 2010; p. 1056902. [Google Scholar] [CrossRef]
- Schodowski, S.S. Resonator self-temperature-sensing using a dual-harmonic-mode crystal oscillator. In Proceedings of the 43rd Annual Symposium on Frequency Control, Denver, CO, USA, 31 May–2 June 1989; pp. 2–7. [Google Scholar] [CrossRef]
- Li, M.-H.; Chen, C.-Y.; Li, C.-S.; Chin, C.-H.; Li, S.-S. Design and Characterization of a Dual-Mode CMOS-MEMS Resonator for TCF Manipulation. J. Microelectromech. Syst. 2015, 24, 446–457. [Google Scholar] [CrossRef]
- Holsteen, A.; Kim, I.S.; Lauhon, L.J. Extraordinary Dynamic Mechanical Response of Vanadium Dioxide Nanowires around the Insulator to Metal Phase Transition. Nano Lett. 2014, 14, 1898. [Google Scholar] [CrossRef] [PubMed]
- Rúa, A.; Cabrera, R.; Coy, H.; Merced, E.; Sepúlveda, N.; Fernández, F.E. Phase transition behavior in microcantilevers coated with M1-phase VO2 and M2-phase VO2:Cr thin films. J. Appl. Phys. 2012, 111, 104502. [Google Scholar] [CrossRef]


| Electromechanical & Thermal Features | This Work (Figure 3c) | Bolometer [32] | Resonant MEMS [9] |
|---|---|---|---|
| Maximal Angle (°) | 21 | - | |
| Inertial Moment (kg.m2) | |||
| Torsional stiffness (N.m) | |||
| Resonant Frequency (MHz) | 1.1 | - | |
| Onset of Nonlinearity (°) (This value is computed by solving a nonlinear dynamic equation [44].) | 13.5 | - | |
| Quality Factor Q | |||
| Capacitance at Rest (fF) | 0.185 | ||
| Pitch (µm) | |||
| Thermal Conductance G (W/K) | |||
| Thermal Capacity C (J/K) | |||
| Thermal Constant (ms) | |||
| Temperature Sensitivity (/°C) |
| Transduction Method | Voltages | SBR (dB) | |
|---|---|---|---|
| - | - | ||
| -actuation | −33 | ||
| -actuation | −13 | ||
| -actuation/differential mode | 2 | ||
| -actuation/down-mixing mode | 22 | ||
| -actuation/down-mixing mode | 20 | ||
| -actuation/down-mixing mode | 22 | ||
| Pixel Types | ||||
|---|---|---|---|---|
| Typical (Figure 3c) | 55.4 | 14.6 | ||
| Butterfly (Figure 4a) | 45.2 | 3.6 | ||
| Typical with Thin Nano-Rod (Figure 4c) | 86.2 | 16.4 |
| Noise Sources | |||||||
|---|---|---|---|---|---|---|---|
| Thermodynamic | rad | ||||||
| Electronics | |||||||
| Phonon | - | ||||||
| Pixel | NETD | NETD | |||||
|---|---|---|---|---|---|---|---|
| Typical | 1.5 (0.75) | 2 (1) | |||||
| Butterfly | 4.9 (3.96) | 11.6 (9.28) | |||||
| Thin Rod | 13.7 (38.3) | - | |||||
| Resistive Pixel [1] | 16 | - | - | 0.05 | - | - | 0.05 (4) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duraffourg, L.; Laurent, L.; Moulet, J.-S.; Arcamone, J.; Yon, J.-J. Array of Resonant Electromechanical Nanosystems: A Technological Breakthrough for Uncooled Infrared Imaging. Micromachines 2018, 9, 401. https://doi.org/10.3390/mi9080401
Duraffourg L, Laurent L, Moulet J-S, Arcamone J, Yon J-J. Array of Resonant Electromechanical Nanosystems: A Technological Breakthrough for Uncooled Infrared Imaging. Micromachines. 2018; 9(8):401. https://doi.org/10.3390/mi9080401
Chicago/Turabian StyleDuraffourg, Laurent, Ludovic Laurent, Jean-Sébastien Moulet, Julien Arcamone, and Jean-Jacques Yon. 2018. "Array of Resonant Electromechanical Nanosystems: A Technological Breakthrough for Uncooled Infrared Imaging" Micromachines 9, no. 8: 401. https://doi.org/10.3390/mi9080401
APA StyleDuraffourg, L., Laurent, L., Moulet, J.-S., Arcamone, J., & Yon, J.-J. (2018). Array of Resonant Electromechanical Nanosystems: A Technological Breakthrough for Uncooled Infrared Imaging. Micromachines, 9(8), 401. https://doi.org/10.3390/mi9080401




