Acceleration Sensitivity in Bulk-Extensional Mode, Silicon-Based MEMS Oscillators
Abstract
:1. Introduction
2. Theory of Acceleration Sensitivity
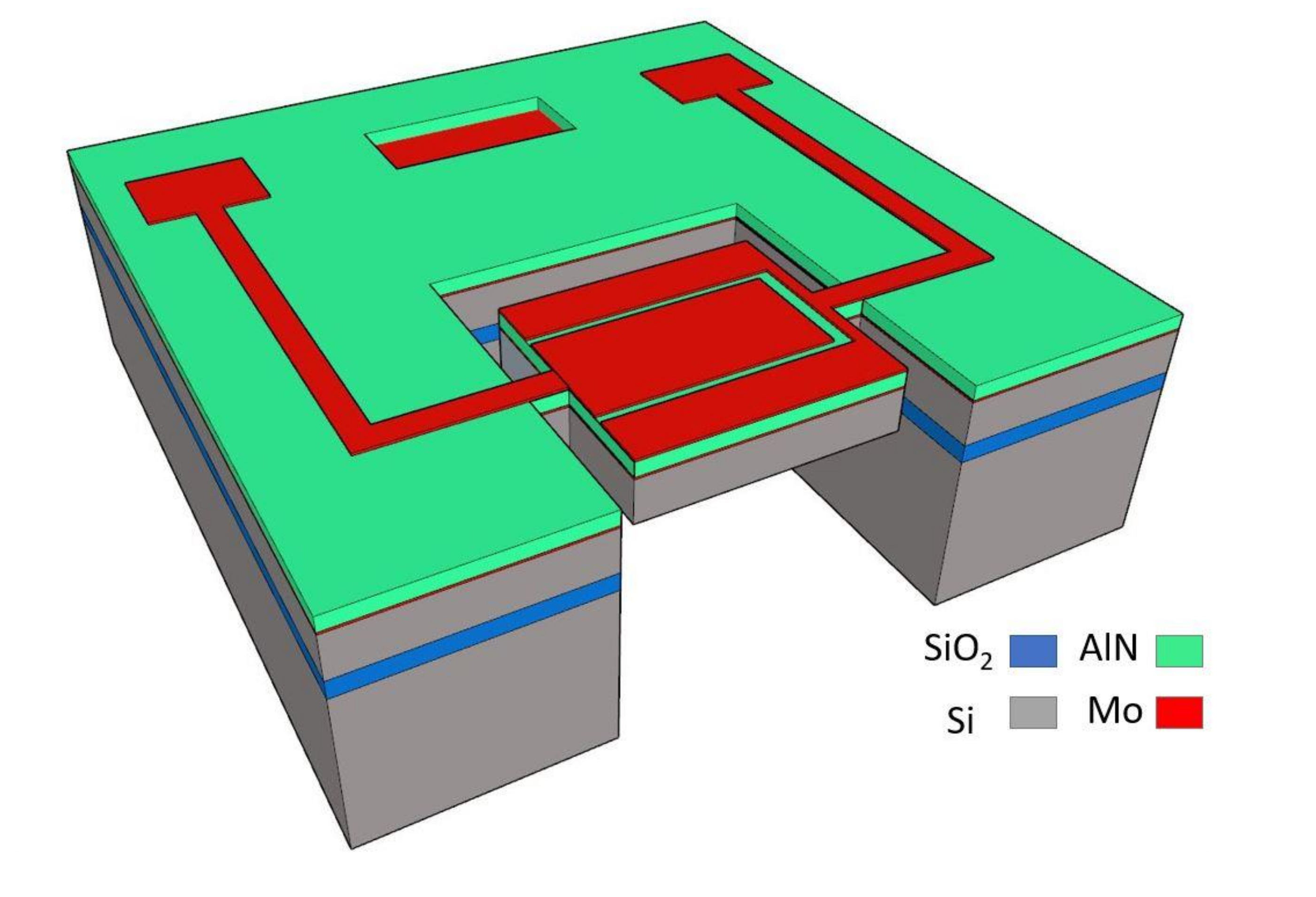
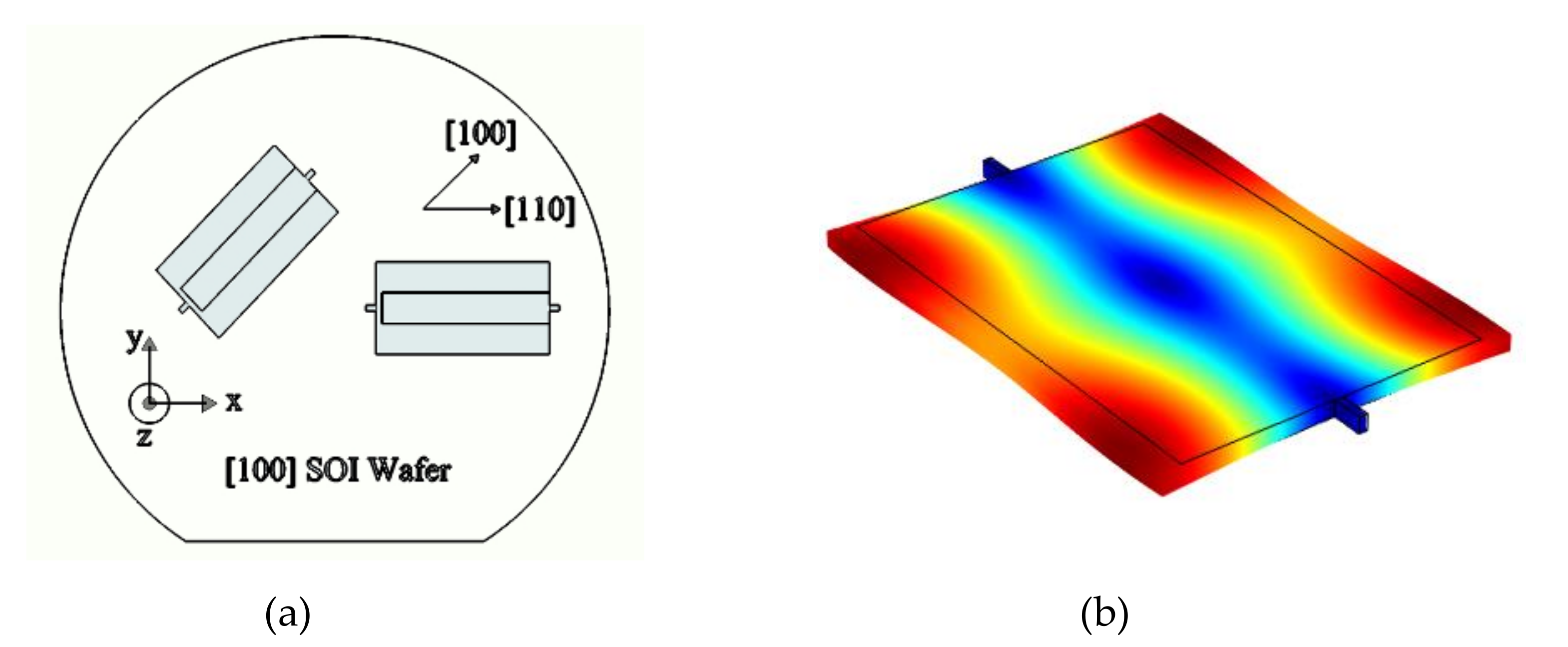
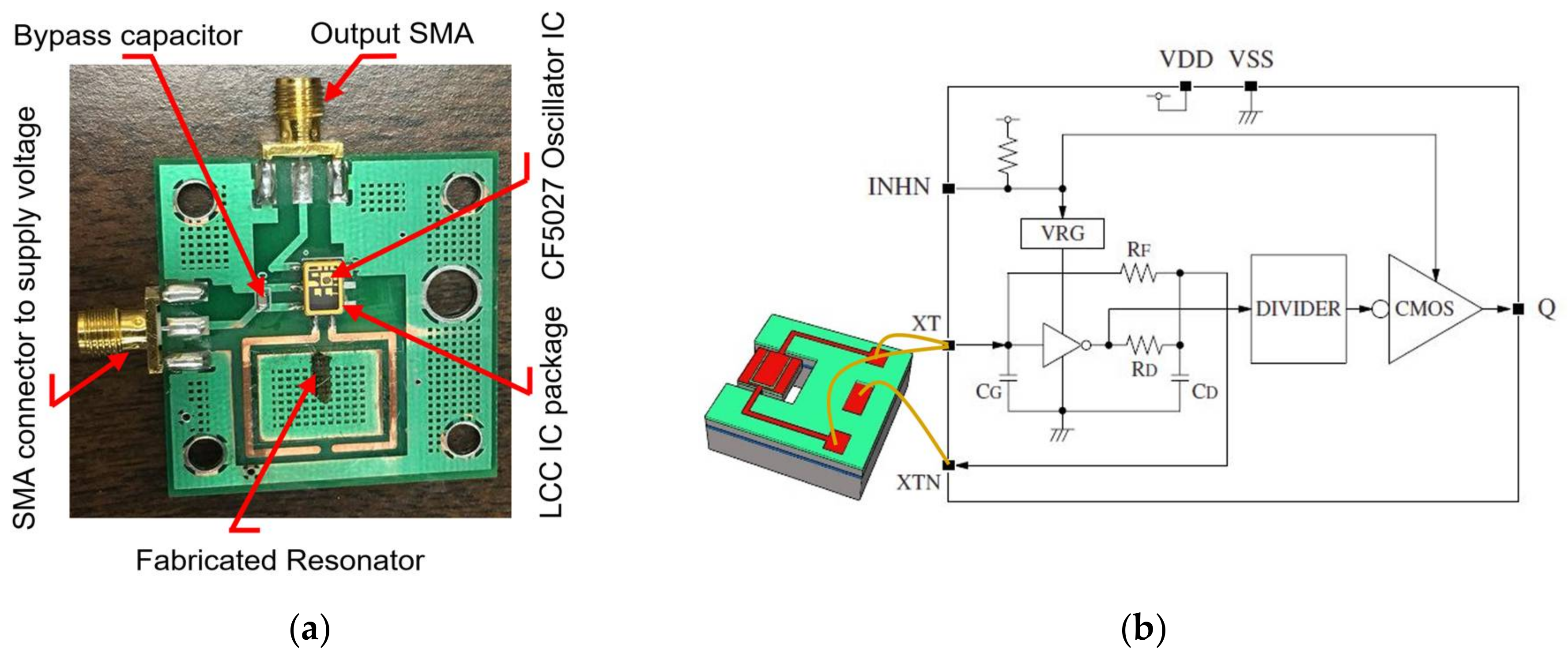
3. Resonator Design and Characterization
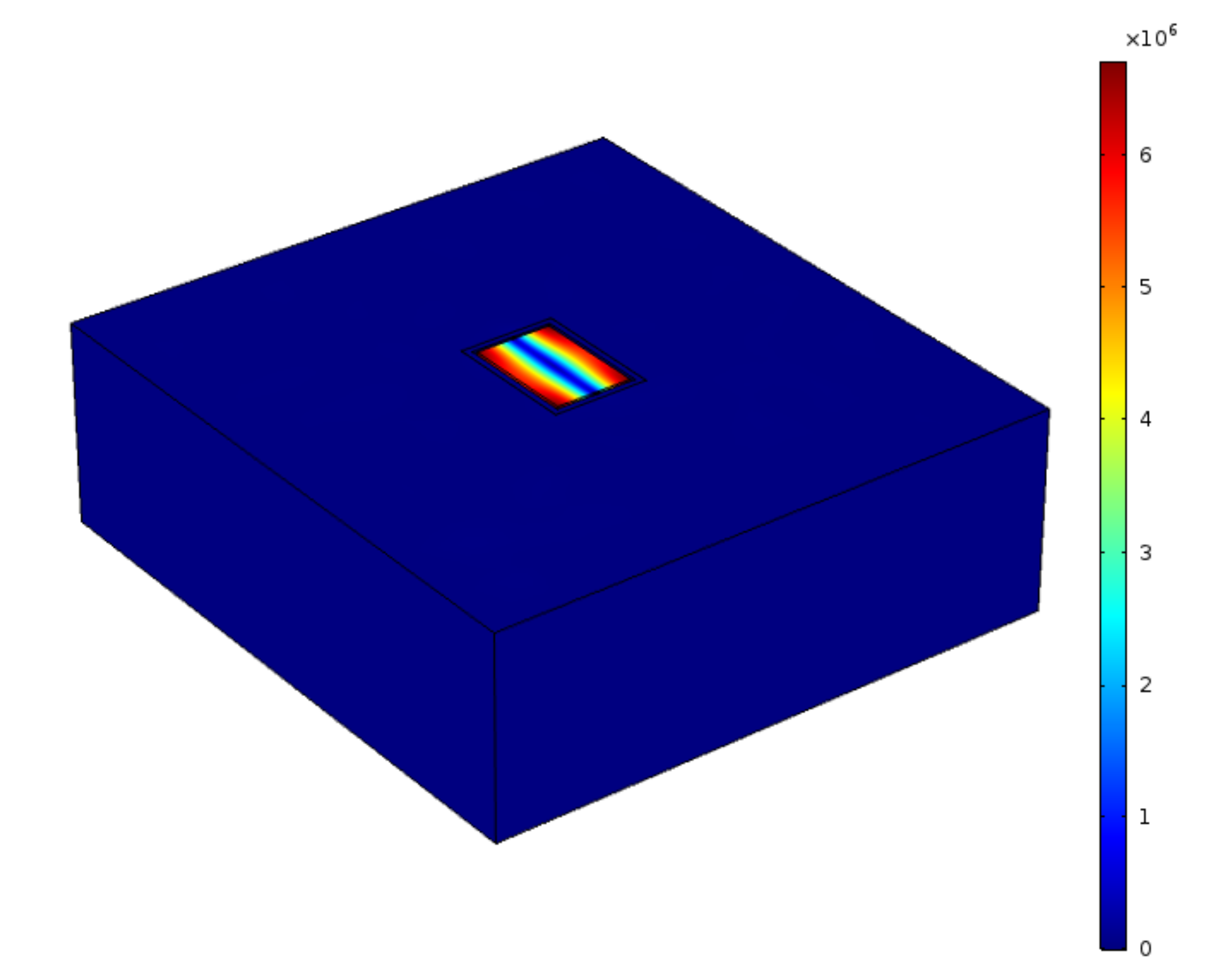
4. Finite Element Simulation
4.1. Geometric Nonlinearity
4.2. Material Nonlinearity
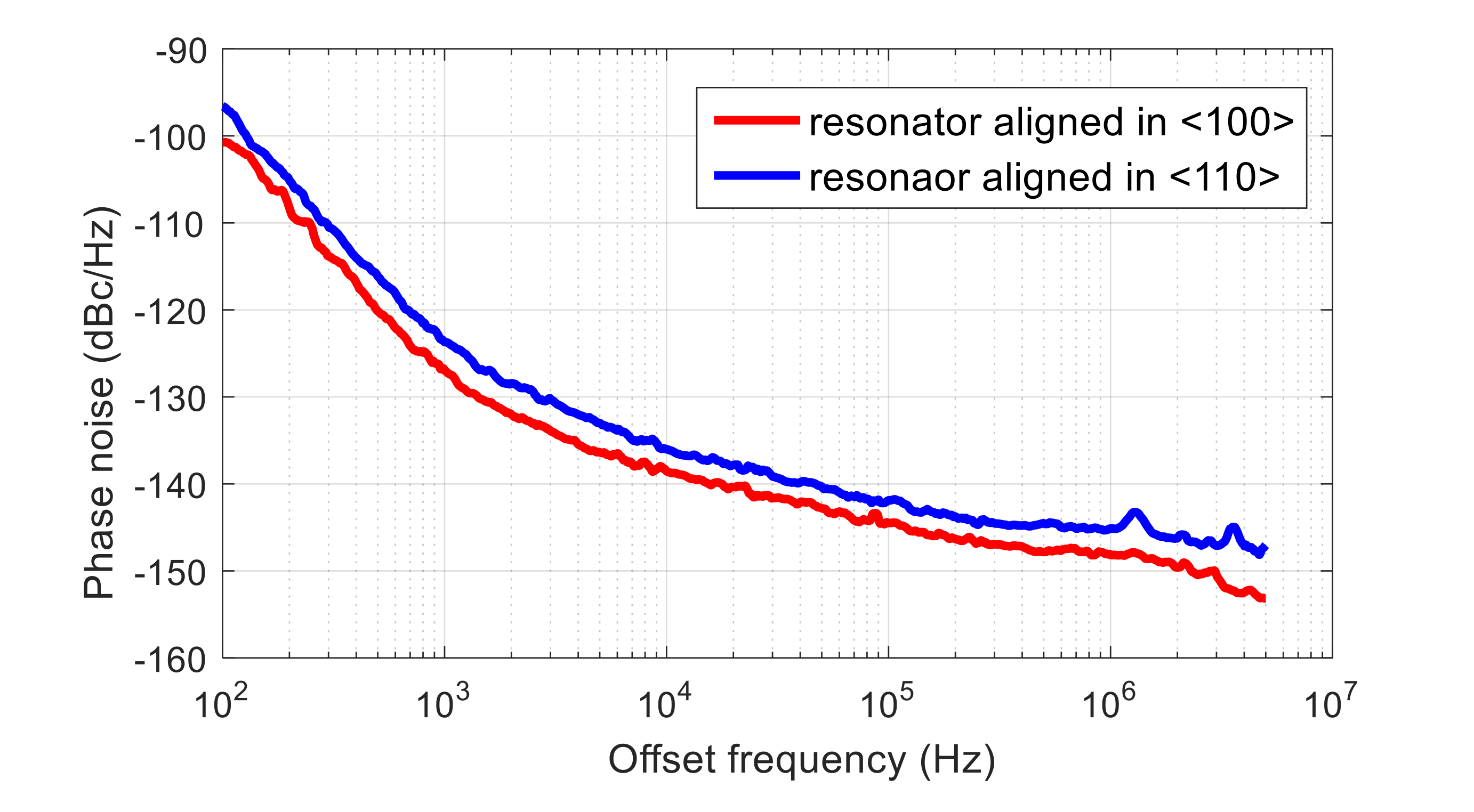
5. Measurements and Results
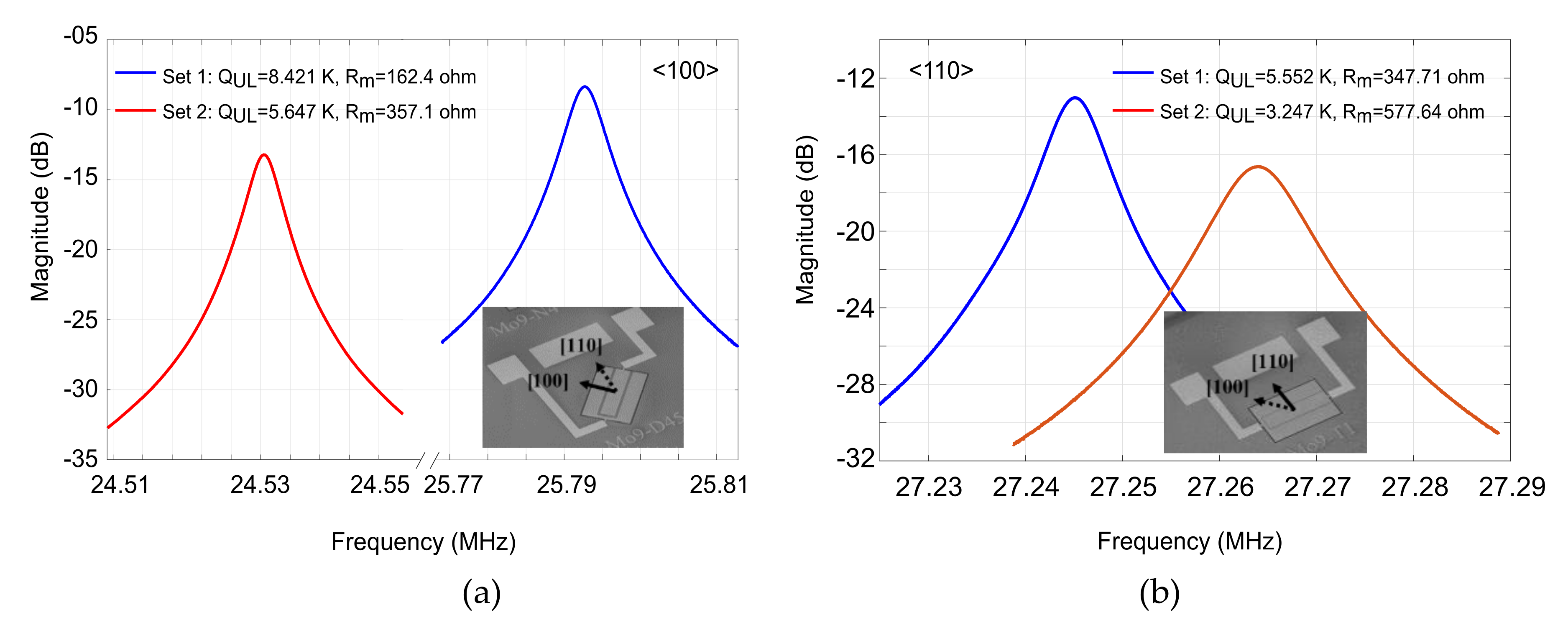
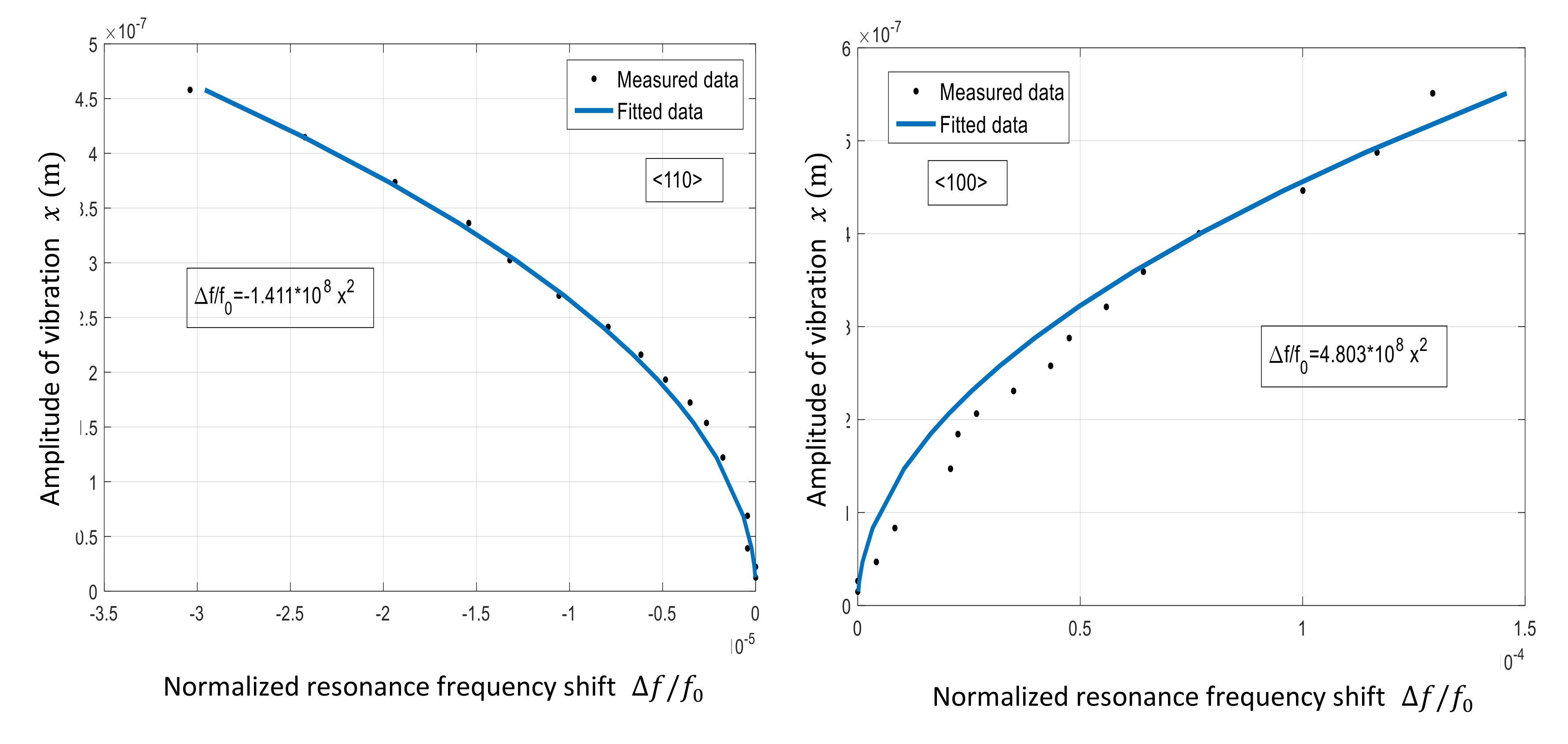
5.1. Nonlinearity Measurements
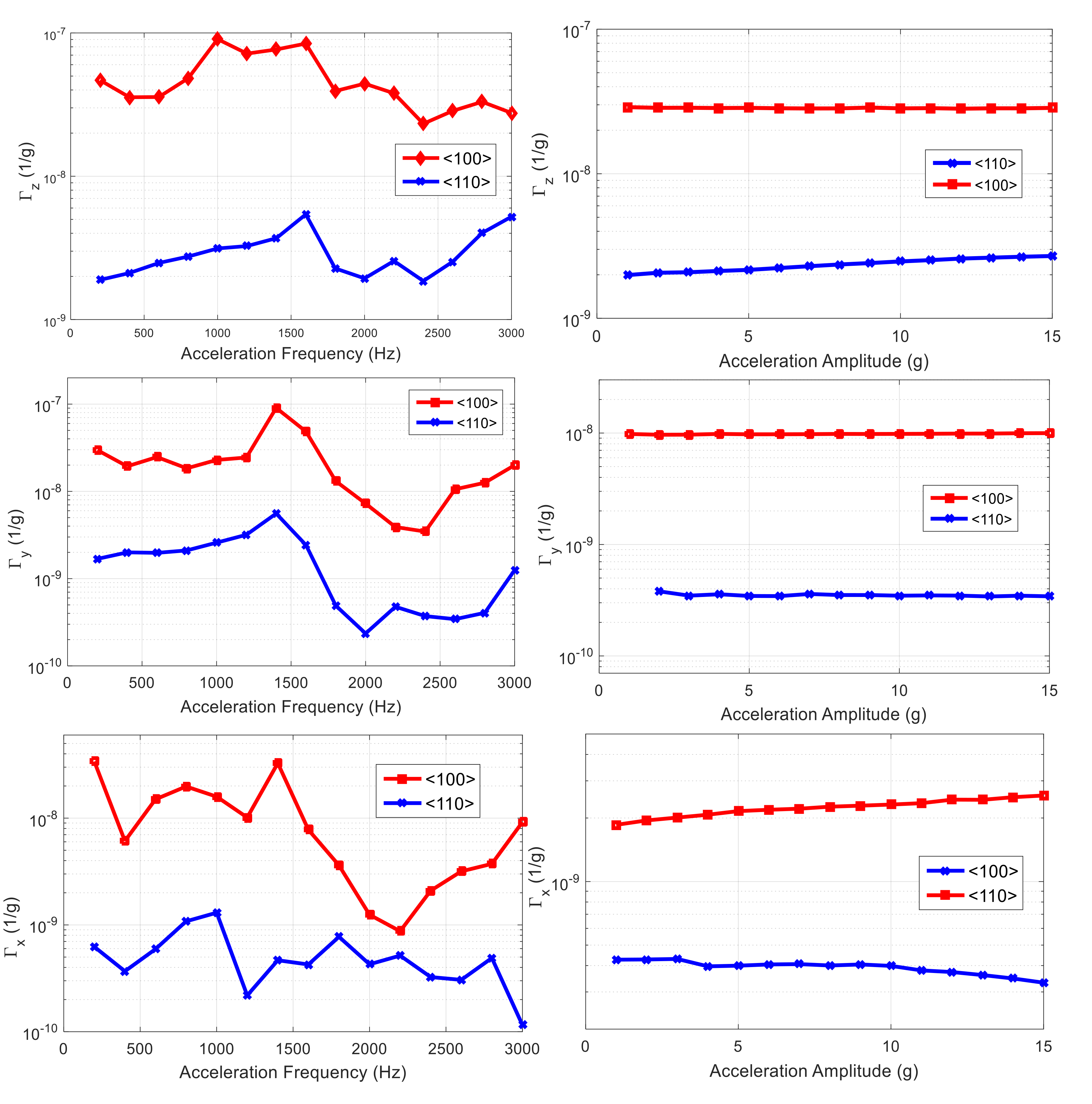
5.2. Acceleration Sensitivity Measurements
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Ng, E.; Yang, Y.; Hong, V.A.; Ahn, C.H.; Heinz, D.B.; Flader, I.; Chen, Y.; Everhart, C.L.M.; Kim, B.; Melamud, R.; et al. The long path from MEMS resonators to timing products. In Proceedings of the 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Estoril, Portugal, 18–22 January 2015; pp. 1–2. [Google Scholar]
- Abdolvand, R.; Bahreyni, B.; Lee, J.E.; Nabki, F. Micromachined resonators: A review. Micromachines 2016, 7. [Google Scholar] [CrossRef]
- Beek, J.T.M.V.; Puers, R. A review of MEMS oscillators for frequency reference and timing applications. J. Micromech. Microeng. 2011, 22, 013001. [Google Scholar] [CrossRef]
- Walls, F.L.; Gagnepain, J.-J. Environmental sensitivities of quartz oscillators. IEEE Trans. Ultrasonics Ferroelectr. Freq. Control 1992, 392, 241–249. [Google Scholar] [CrossRef] [PubMed]
- Ballato, A.; Mizan, M. Simplified expressions for the stress-frequency coefficients of quartz plates. IEEE Trans. Ultrasonics Ferroelectr. Freq. Control 1984, 311, 11–17. [Google Scholar] [CrossRef]
- Anderson, C.L.; Bagby, J.S.; Barrett, R.L.; Ungvichian, V. Acceleration charge sensitivity in AT-quartz resonators. In Proceedings of the IEEE International Frequency Control Symposium, San Francisco, CA, USA, 31 May–2 June 1995. [Google Scholar]
- Yong, Y.K.; Chen, J. Effects of initial nonlinear strains and nonlinear elastic constants in force-frequency and acceleration sensitivity of quartz resonators. In Proceedings of the IEEE International Frequency Control Symposium (IFCS), New Orleans, LA, USA, 9–12 May 2016; pp. 1–2. [Google Scholar]
- Filler, R.L. The acceleration sensitivity of quartz crystal oscillators: A review. IEEE Trans. Ultrasonics Ferroelectr. Freq. Control 1988, 35, 297–305. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Yong, Y.K.; Kubena, R.; Kirby, D.; Chang, D. On the acceleration sensitivity and its active reduction by edge electrodes in at-cut Quartz resonators. IEEE Trans. Ultrasonics Ferroelectr. Freq. Control 2015, 626, 1104–1113. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Yong, Y.K.; Kubena, R.; Kirby, D.; Chang, D. Nonlinear acceleration sensitivity of quartz resonators. In Proceedings of the Joint Conference of the IEEE International Frequency Control Symposium & the European Frequency and Time Forum, Denver, CO, USA, 12–16 April 2015; pp. 11–16. [Google Scholar]
- Fry, S.J.; Burnett, G.A. Reducing the acceleration sensitivity of AT-strip quartz crystal oscillators. In Proceedings of the International Frequency Control Symposium, Newport Beach, CA, USA, 1–4 June 2010; pp. 25–30. [Google Scholar]
- Rosati, V.R.; Filler, R.L. Reduction of the effects of vibration on SC-cut quartz crystal oscillators. In Proceedings of the IEEE 35th Annual Frequency Control Symposium, Philadelphia, PA, USA, 27–29 May 1981. [Google Scholar]
- Fruehauf, H. “g”- Compensated, Miniature, High Performance Quartz Crystal Oscillators; Frequency Electronics Inc.: New York, NY, USA, 2007. [Google Scholar]
- Bloch, M.; Mancini, O.; McClelland, T.; Terracciano, L. Acceleration “G” Compensated Quartz Crystal Oscillators; Frequency Electronics, Inc.: New York, NY, USA, 2009. [Google Scholar]
- Bhaskar, S.; Curran, J.T.; Lachapelle, G. Improving GNSS carrier-phase tracking via oscillator g-sensitivity compensation. IEEE Trans. Aerosp. Electron. Syst. 2015, 514, 2641–2654. [Google Scholar] [CrossRef]
- Hati, A.; Nelson, C.W.; Taylor, J.; Ashby, N.; Howe, D.A. Cancellation of Vibration Induced Phase Noise in Optical Fibers. IEEE Photonics Technol. Lett. 2008, 20, 1842–1844. [Google Scholar] [CrossRef]
- Walls, F.L.; Vig, J.R. Acceleration Insensitive Oscillator. U.S. Patent 4.575.690, 1985. [Google Scholar]
- Fry, S.; Bolton, W.; Esterline, J. Crystal Oscillator with Reduced Acceleration Sensitivity. U.S. Grant US8525607B2, 2008. [Google Scholar]
- Ballato, A. Resonators compensated for acceleration fields. In Proceedings of the IEEE 33rd Annual Symposium on Frequency Control, Atlantic City, NJ, USA, 30 May–1 June 1979. [Google Scholar]
- Besson, R.J.; Peier, U.R. Further advances on BVA quartz resonators. In Proceedings of the IEEE 34th Annual Symposium on Frequency Control, Philadelphia, PA, USA, 28–30 May 1980. [Google Scholar]
- Hati, A.; Nelson, C.; Howe, D. Vibration-induced PM Noise in Oscillators and its Suppression; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2009.
- Maleki, L. High Performance Optical Oscillators for Microwave and mm-wave Applications. Microw. J. 2013, 56, 106. [Google Scholar]
- Leibrandt, D.R.; Bergquist, J.C.; Rosenband, T. Cavity-stabilized laser with acceleration sensitivity below 10−12/g−1. Phys. Rev. A 2013, 87, 023829. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Hung, X.; Notcutt, M.; Zanon-Willette, T.; Foreman, S.M.; Boyd, M.M.; Blatt, S.; Ye, J. Compact, thermal-noise-limited optical cavity for diode laser stabilization at 1 × 10−15. Opt. Lett. 2007, 32, 641–643. [Google Scholar] [CrossRef] [PubMed]
- Millo, J.; Dawkins, S.; Chicireanu, R.; Magalhaes, D.V.; Mandache, C.; Holleville, D.; Lours, M.; Bize, S.; Lemonde, P.; Santarelli, G. Ultra-stable optical cavities: Design and experiments at LNE-SYRTE. In Proceedings of the IEEE International Frequency Control Symposium, Honolulu, HI, USA, 19–21 May 2008; pp. 110–114. [Google Scholar]
- Webster, S.A.; Oxborrow, M.; Gill, P. Vibration insensitive optical cavity. Phys. Rev. A 2007, 75. [Google Scholar] [CrossRef]
- Kosinski, J.A.; Ballato, A. Designing for low acceleration sensitivity. IEEE Trans. Ultrasonics Ferroelectr. Freq. Control 1993, 405, 532–537. [Google Scholar] [CrossRef] [PubMed]
- Kosinski, J.A.; Pastore, R.A. Theory and design of piezoelectric resonators immune to acceleration: Present state of the art. IEEE Trans. Ultrasonics Ferroelectr. Freq. Control 2001, 485, 1426–1437. [Google Scholar] [CrossRef]
- Ballato, A.; Eernisse, E.P.; Lukaszek, T.J. Force-Frequency Effect in Doubly Rotated Quartz Resonators; Sandia Labs: Albuquerque, NM, USA, 1977. [Google Scholar]
- Eernisse, E.P.; Lukaszek, T.J.; Ballato, A. Variational calculation of force-frequency constants of doubly rotated quartz resonators. IEEE Trans. Sonics Ultrasonics 1978, 253, 132–137. [Google Scholar] [CrossRef]
- SiTime corporation. MEMS Oscillators: Enabling Smaller, Lower Power IoT & Wearables. Available online: https://www.sitime.com/api/gated/SiTime-MEMS-Enable-Small-Low-Power-IoT-Wearables.pdf (accessed on 11 May 2018).
- SiTime corporation. Increase Automotive Reliability and Performance with High-temperature, Ultra Robust MEMS Oscillators. Available online: https://www.sitime.com/api/gated/SiTime-MEMS-Oscillators-for-Automotive-Applications.pdf (accessed on 11 May 2018).
- Kim, B.; Olsson, R.H.; Smart, K.; Wojciechowski, K.E. MEMS Resonators with Extremely Low Vibration and Shock Sensitivity. In Proceedings of the IEEE Sensors, Limerick, Ireland, 28–31 October 2011. [Google Scholar]
- Kim, B.; Akgul, M.; Lin, Y.; Li, We.; Ren, Z.; Nguyen, C.T.-C. Acceleration sensitivity of small-gap capacitive micromechanical resonator oscillators. In Proceedings of the IEEE International Frequency Control Symposium (FCS), Newport Beach, CA, USA, 1–4 June 2010. [Google Scholar]
- Khazaeili, B.; Abdolvand, R. Orientation-dependent acceleration sensitivity of silicon-based MEMS resonators. In Proceedings of the IEEE International Frequency Control Symposium (IFCS), New Orleans, LA, USA, 9–12 May 2016; pp. 1–5. [Google Scholar]
- Harrington, B.P.; Shahmohammadi, M.; Abdolvand, R. Toward ultimate performance in GHz MEMS resonators: Low impedance and high Q. In Proceedings of the IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Hong Kong, China, 24–28 January 2010; pp. 707–710. [Google Scholar]
- Fatemi, H.; Shahmohammadi, M.; Abdolvand, R. Ultra-stable nonlinear thin-film piezoelectric-on-substrate oscillators operating at bifurcation. In Proceedings of the IEEE 27th International Conference on Micro Electro Mechanical Systems (MEMS), San Francisco, CA, USA, 26–30 January 2014; pp. 1285–1288. [Google Scholar]
- Shahmohammadi, M.; Fatemi, H.; Abdolvand, R. Nonlinearity reduction in silicon resonators by doping and re-orientation. In Proceedings of the IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 793–796. [Google Scholar]
- Kosinski, J.A. The fundamental nature of acceleration sensitivity. In Proceedings of the IEEE International Frequency Control Symposium, Honolulu, HI, USA, 5–7 June 1996; pp. 439–448. [Google Scholar]
- Kim, K.Y.; Sachse, W. Nonlinear elastic equation of state of solids subjected to uniaxial homogeneous loading. J. Mater. Sci. 2000, 3513, 3197–3205. [Google Scholar] [CrossRef]
- Kaajakari, V.; Mattila, T.; Lipsanen, A.; Oja, A. Nonlinear Mechanical Effects in Silicon Longitudinal Mode Beam Resonators. Sens. Actuators A Phys. 2005, 120, 64–70. [Google Scholar] [CrossRef]
- Wortman, J.; Evans, R. Young’s modulus, shear modulus, and Poisson’s ratio in silicon and germanium. J. Appl. Phys. 1965, 361, 153–156. [Google Scholar] [CrossRef]
- Hall, J.J. Electronic Effects in the Elastic Constants of n-Type Silicon. Phys. Rev. 1967, 161. [Google Scholar] [CrossRef]
- Yang, Y.; Ng, E.J.; Hong, V.A.; Ahn, C.H.; Chen, Y.; Ahadi, E.; Dykman, M.; Kenny, T.W. Measurement of the nonlinear elasticity of doped bulk-mode MEMS resonators. In Proceedings of the Solid-State Sensors, Actuators and Microsystems Workshop, Hilton Head Island, SC, USA, 8–12 June 2014. [Google Scholar]
- Yang, Y.; Ng, E.J.; Polunin, P.M.; Chen, Y.; Flader, I.B.; Shaw, S.W.; Dykman, M.I.; Kenny, T.W. Nonlinearity of Degenerately Doped Bulk-Mode Silicon MEMS Resonators. J. Microelectromech. Syst. 2016, 255, 859–869. [Google Scholar] [CrossRef]
- Fatemi, H.; Abdolvand, R. Fracture Limit in Thin-Film Piezoelectric-on-Substrate Resonators: Silicon vs. Diamond. In Proceedings of the IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 461–464. [Google Scholar]
- Crystal Oscillator Module ICs; MSDS No. CF5027; SEIKO NPC Corporation: Tokyo, Japan, February 2010; Available online: http://www.npc.co.jp/en/products/xtal/clock-oscillator/5027-series/ (accessed on 11 May 2018).
- Meyer, D.G. A Test Set for the Accurate Measurement of Phase Noise on High-Quality Signal Sources. IEEE Trans. Instrum. Meas. 1970, 19, 215–227. [Google Scholar] [CrossRef]
- Barnes, J.A.; Mockler, R.C. The Power Spectrum and Its Importance in Precise Frequency Measurements. IRE Trans. Instrum. 1960, I-9, 149–155. [Google Scholar] [CrossRef]
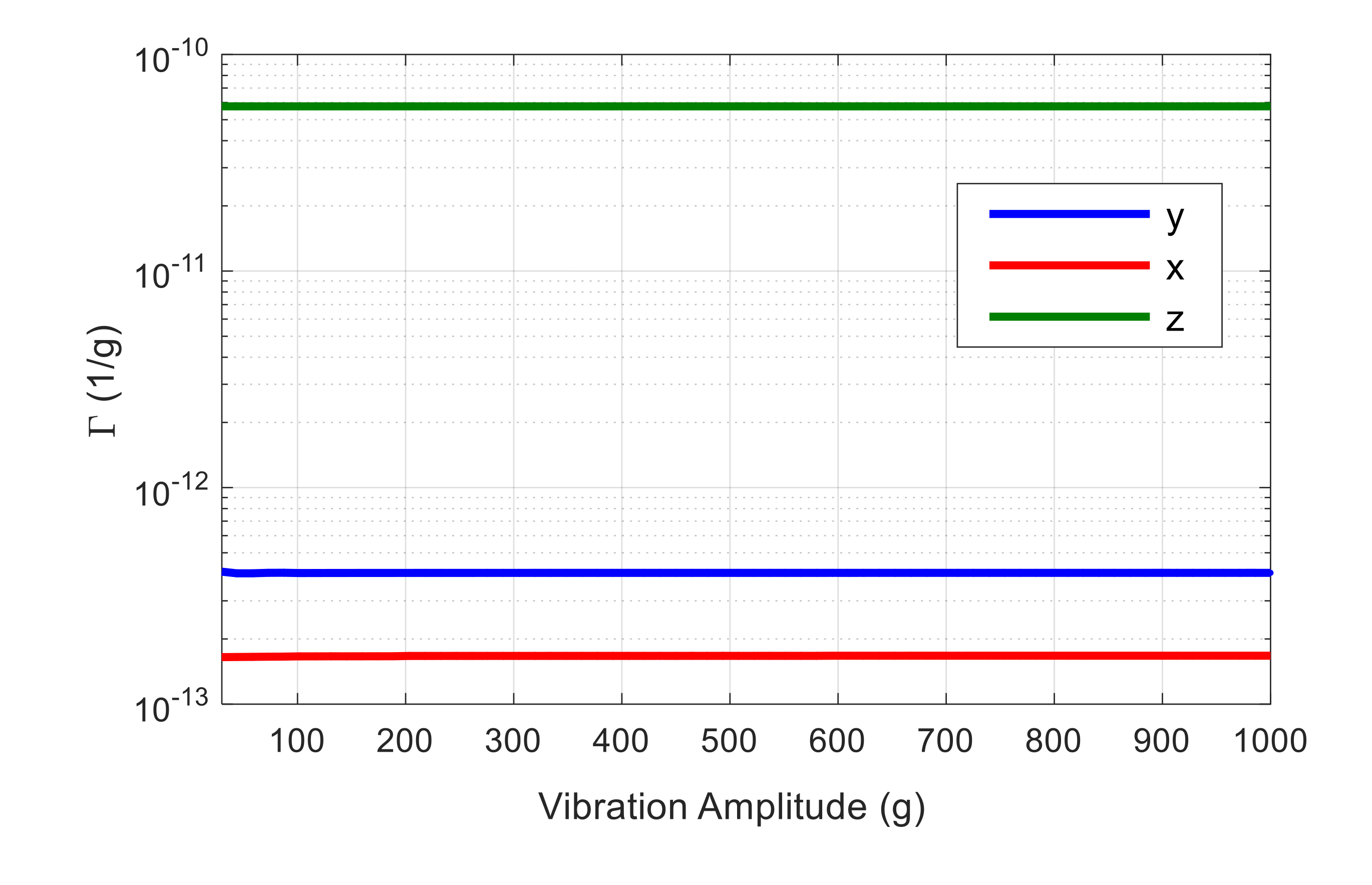
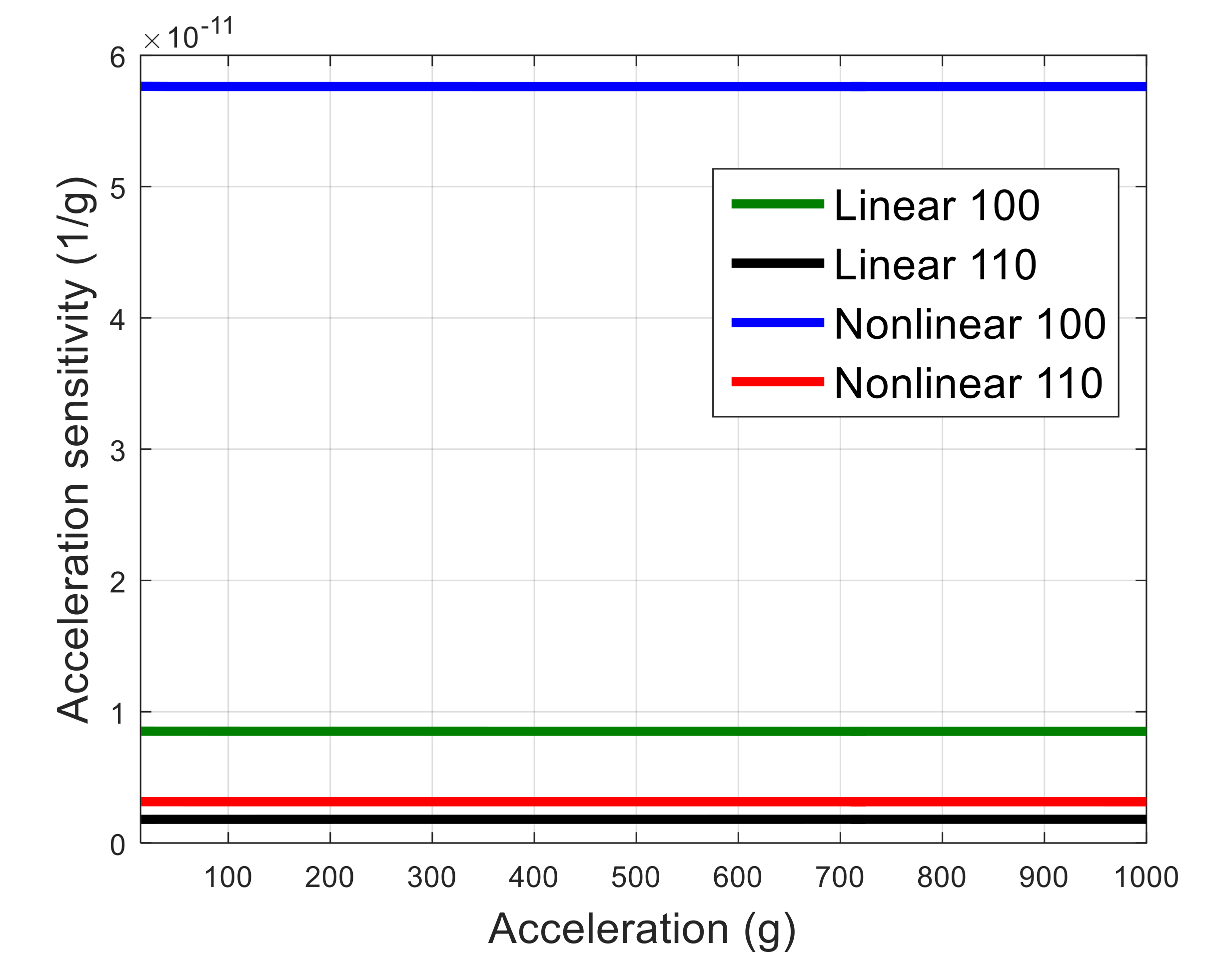
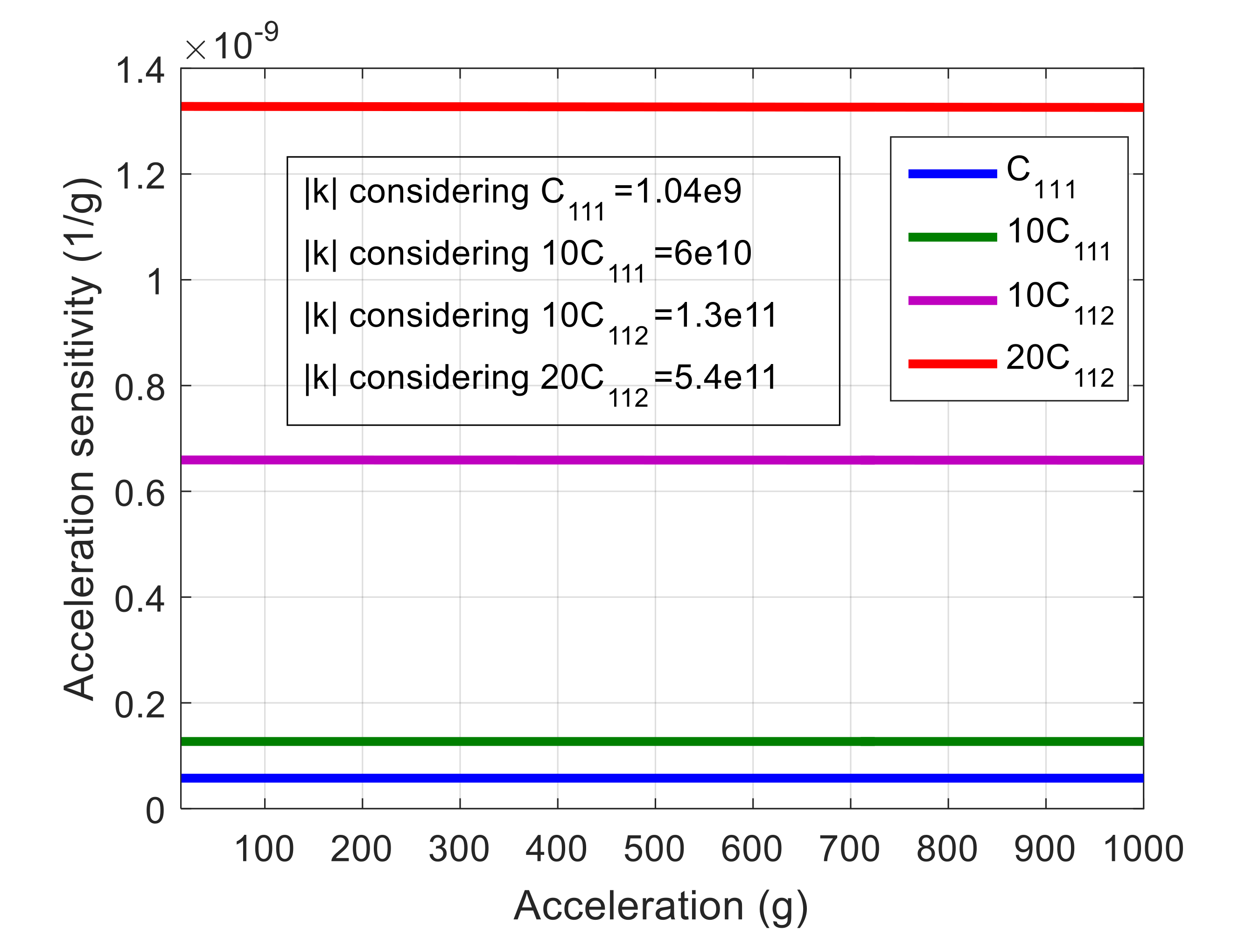
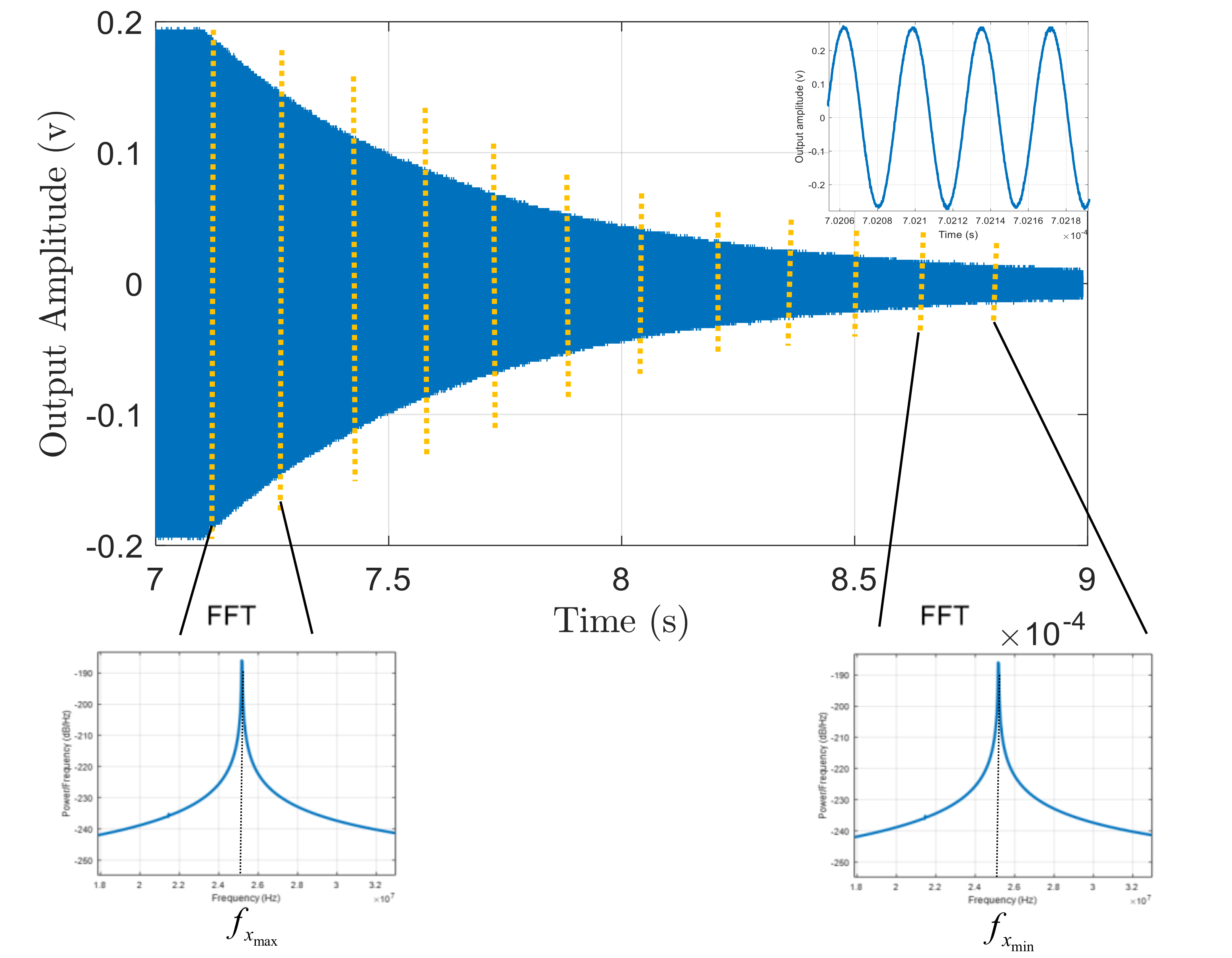



| Orientation | Гx | Гy | Гz | Гtotal | |
|---|---|---|---|---|---|
| Set 1 | <100> | 3.73 × 10−9 | 1.2 × 10−8 | 3.3 × 10−8 | 3.6 × 10−8 |
| <110> | 4.9 × 10−10 | 4.1 × 10−10 | 4 × 10−9 | 4.1 × 10−9 | |
| Set 2 | <100> | 8.5 × 10−9 | 2.5 × 10−8 | 8.1 × 10−8 | 8.5 × 10−8 |
| <110> | 3.1 × 10−10 | 6.4 × 10−9 | 4.8 × 10−9 | 8 × 10−9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khazaeili, B.; Gonzales, J.; Abdolvand, R. Acceleration Sensitivity in Bulk-Extensional Mode, Silicon-Based MEMS Oscillators. Micromachines 2018, 9, 233. https://doi.org/10.3390/mi9050233
Khazaeili B, Gonzales J, Abdolvand R. Acceleration Sensitivity in Bulk-Extensional Mode, Silicon-Based MEMS Oscillators. Micromachines. 2018; 9(5):233. https://doi.org/10.3390/mi9050233
Chicago/Turabian StyleKhazaeili, Beheshte, Jonathan Gonzales, and Reza Abdolvand. 2018. "Acceleration Sensitivity in Bulk-Extensional Mode, Silicon-Based MEMS Oscillators" Micromachines 9, no. 5: 233. https://doi.org/10.3390/mi9050233
APA StyleKhazaeili, B., Gonzales, J., & Abdolvand, R. (2018). Acceleration Sensitivity in Bulk-Extensional Mode, Silicon-Based MEMS Oscillators. Micromachines, 9(5), 233. https://doi.org/10.3390/mi9050233





