Electrowetting Using a Microfluidic Kelvin Water Dropper
Abstract
:1. Introduction
2. Methods
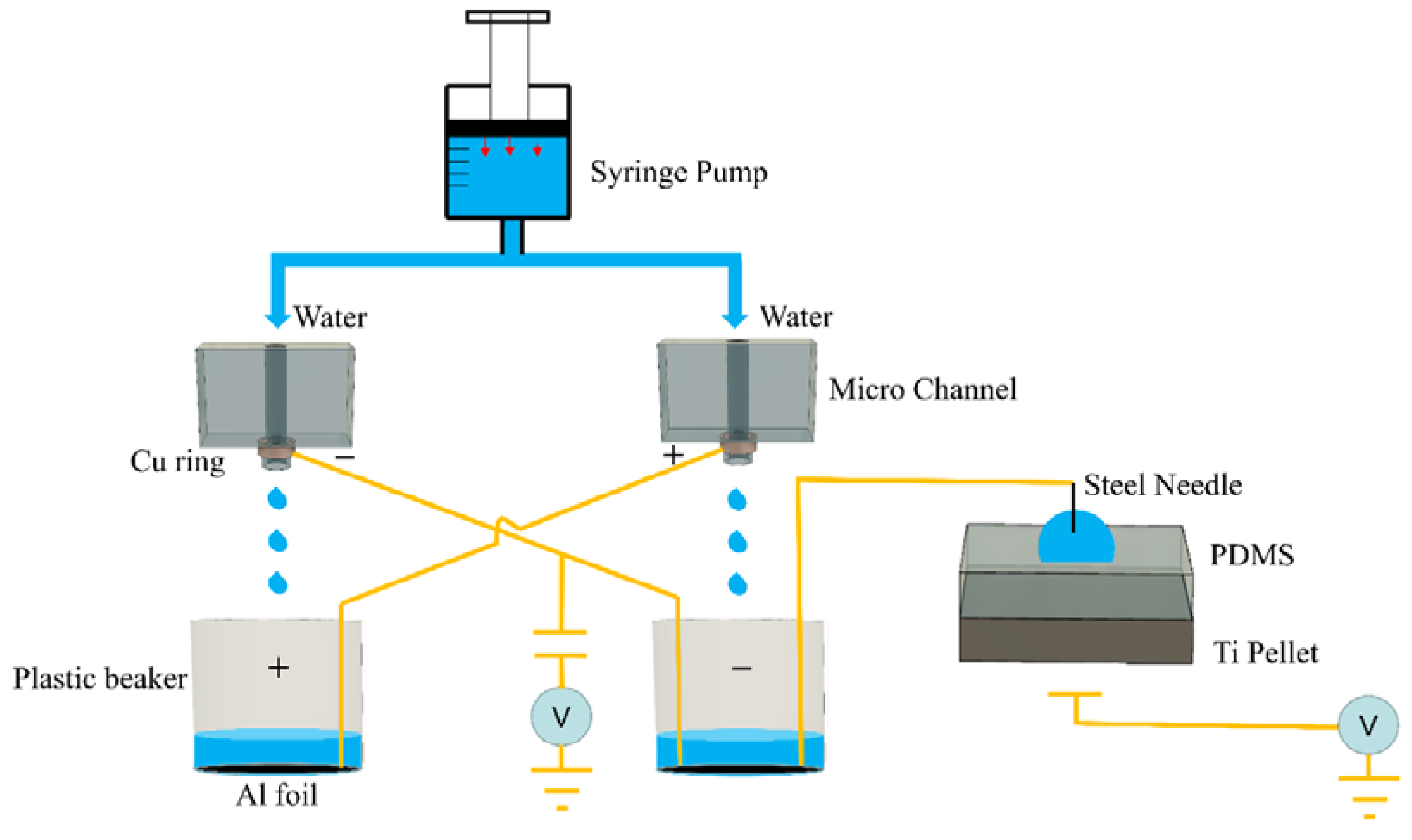
2.1. Experimental Method
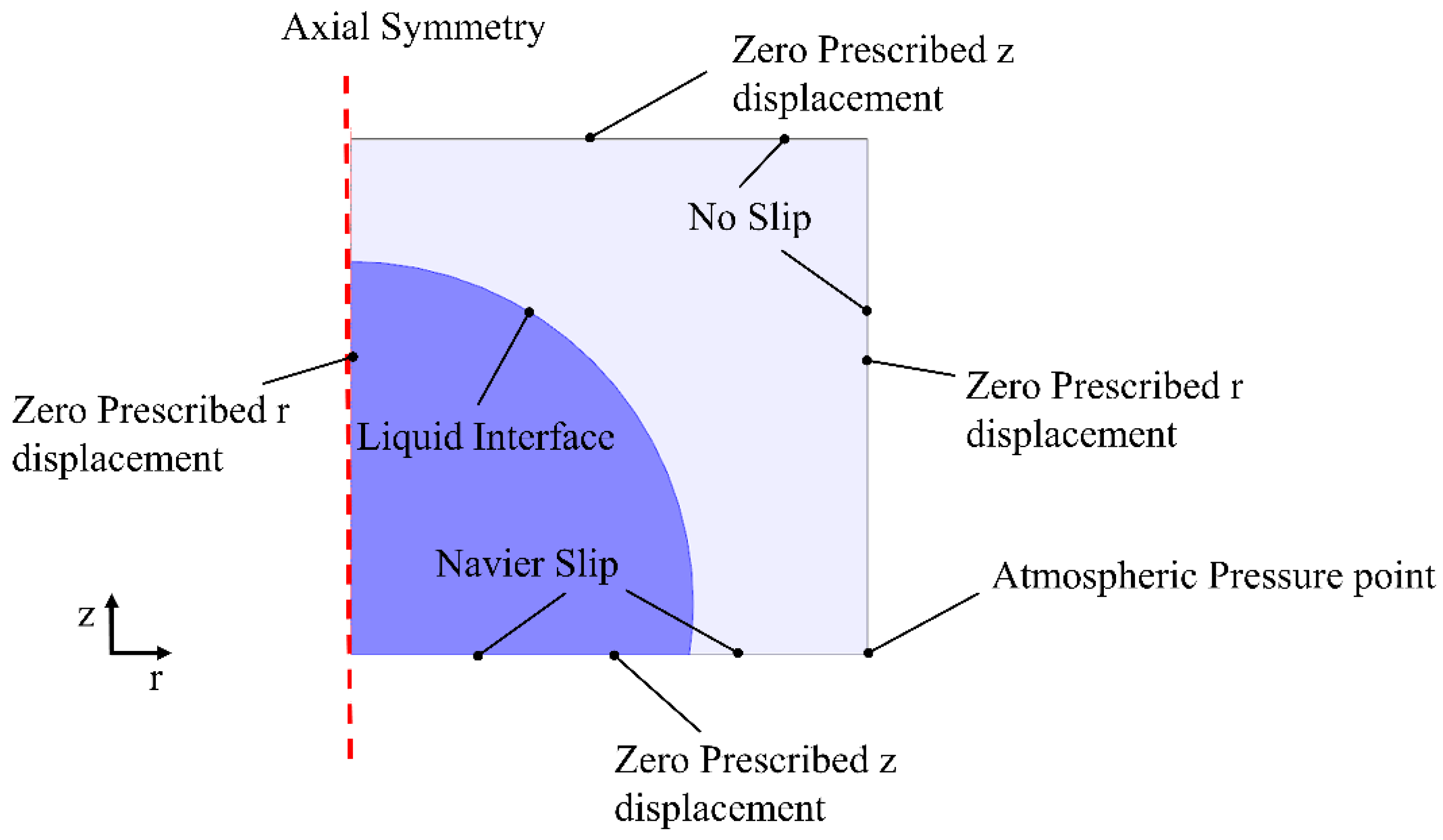
2.2. Analytical Method
3. Results and Discussion
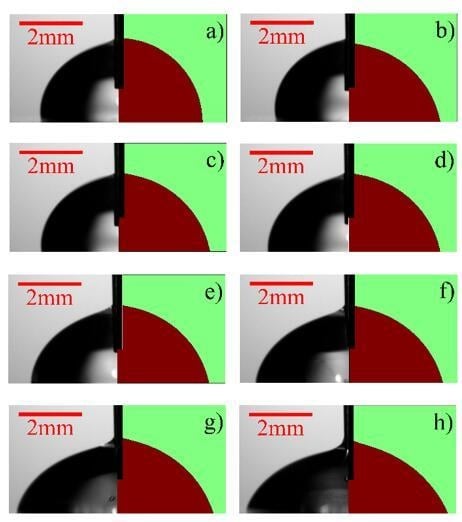
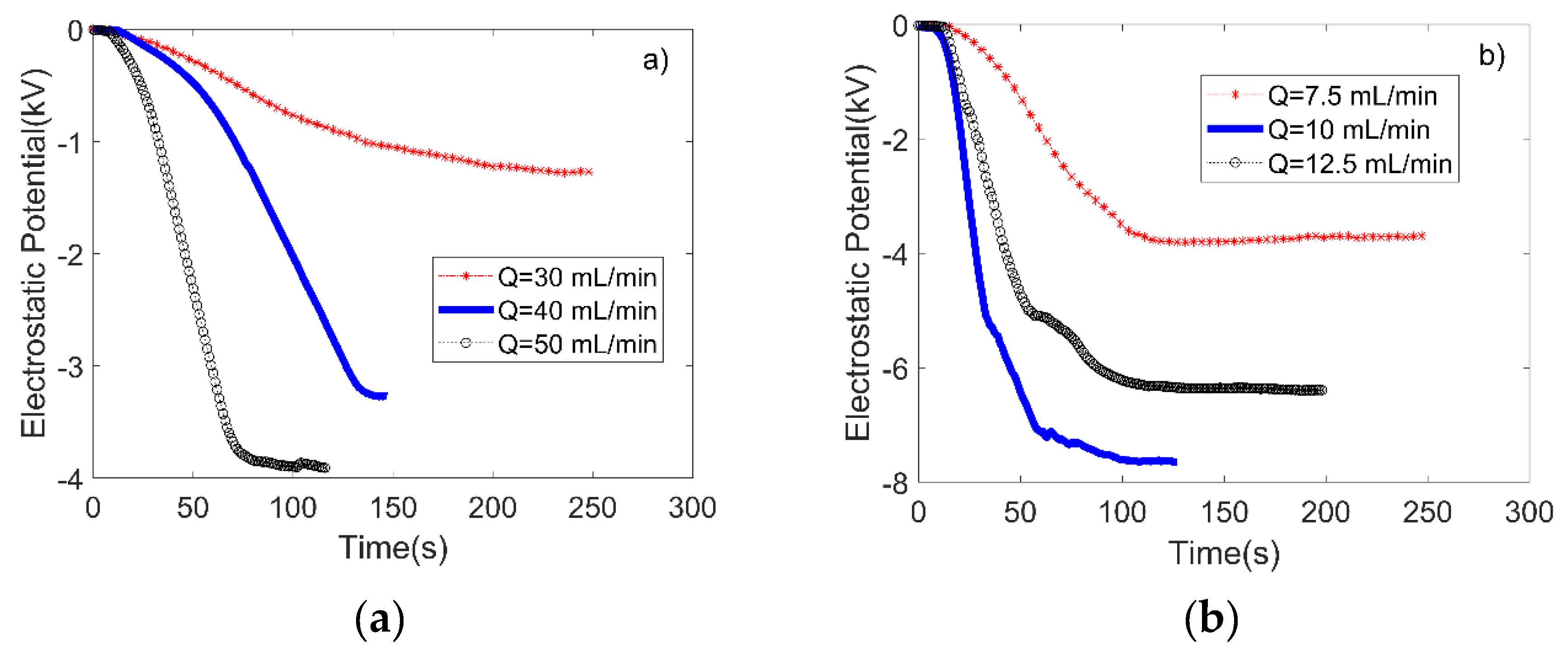
3.1. Performance Evaluation of the Microfluidic Kelvin Water Droppers (MKWDs)
3.2. Electrowetting Using the Microfluidic Kelvin Water Dropper (MKWD)
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| u | velocity field |
| mass density | |
| μ | dynamic viscosity |
| p | pressure |
| surface force per unit volume | |
| body force per unit volume | |
| I | identity matrix |
| σ | coefficient of surface tension |
| n | interface normal direction |
| direct delta function | |
| h | grid spacing |
| level set function | |
| E | electric field |
| V | electrostatic voltage |
| contact angle in experiment | |
| contact angle in simulation |
References
- Thomson, W. On a self-acting apparatus for multiplying and maintaining electric charges, with applications to illustrate the voltaic theory. Proc. R. Soc. Lond. 1867, 16, 67–72. [Google Scholar] [CrossRef]
- Zahn, M. Self-excited ac high voltage generation using water droplets. Am. J. Phys. 1973, 41, 196–202. [Google Scholar] [CrossRef]
- Xie, Y. Microfluidic Energy Conversion by Application of Two Phase Flow. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 26 September 2013. [Google Scholar]
- Xie, Y.; Bos, D.; De Vreede, L.J.; De Boer, H.L.; van der Meulen, M.J.; Versluis, M.; Sprenkels, A.J.; van den Berg, A.; Eijkel, J.C. High-efficiency ballistic electrostatic generator using microdroplets. Nat. Commun. 2014, 5, 3575. [Google Scholar] [CrossRef] [PubMed]
- Singh, G. Self-excited induction generator research—A survey. Electr. Power Syst. Res. 2004, 69, 107–114. [Google Scholar] [CrossRef]
- Desmet, S.; Orban, F.; Grandjean, F. On the kelvin electrostatic generator. Eur. J. Phys. 1989, 10, 118. [Google Scholar] [CrossRef]
- Lewin, W. Mit Open Course 8.02 Electricity and Magnetism. Available online: http://videolectures.net/mit802s02_electricity_magnetism (accessed on 24 February 2018).
- Evans, L.; Stevens, J.T. Kelvin water dropper revisited. Phys. Teach. 1977, 15, 548–549. [Google Scholar] [CrossRef]
- Sady, M. The kelvin water dropper: An elementary experience. Phys. Teach. 1984, 22, 516. [Google Scholar] [CrossRef]
- Planinšič, G.; Prosen, T. Conducting rod on the axis of a charged ring: The kelvin water drop generator. Am. J. Phys. 2000, 68, 1084–1089. [Google Scholar] [CrossRef]
- Özdemir, A.; Lin, J.-L.; Gillig, K.J.; Chen, C.-H. Kelvin spray ionization. Analyst 2013, 138, 6913–6923. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.-F. Voltage build-up time responses of kelvin’s water droplet generator: Variations due to different geometric configurations. J. Electrost. 2014, 72, 447–456. [Google Scholar] [CrossRef]
- Marín, Á.G.; van Hoeve, W.; García-Sánchez, P.; Shui, L.; Xie, Y.; Fontelos, M.A.; Eijkel, J.C.; van den Berg, A.; Lohse, D. The microfluidic kelvin water dropper. Lab Chip 2013, 13, 4503–4506. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; de Boer, H.L.; Sprenkels, A.J.; van den Berg, A.; Eijkel, J.C. Pressure-driven ballistic kelvin’s water dropper for energy harvesting. Lab Chip 2014, 14, 4171–4177. [Google Scholar] [CrossRef] [PubMed]
- Schwierz, N.; Lam, R.K.; Gamlieli, Z.; Tills, J.J.; Leung, A.; Geissler, P.L.; Saykally, R.J. Hydrogen and electric power generation from liquid microjets: Design principles for optimizing conversion efficiency. J. Phys. Chem. C 2016, 120, 14513–14521. [Google Scholar] [CrossRef]
- Mugele, F.; Baret, J.-C. Electrowetting: From basics to applications. J. Phys. Condens. Matter 2005, 17, R705. [Google Scholar] [CrossRef]
- Kim, D.Y.; Steckl, A.J. Electrowetting on paper for electronic paper display. ACS Appl. Mater. Interfaces 2010, 2, 3318–3323. [Google Scholar] [CrossRef] [PubMed]
- Eral, H.B.; de Ruiter, J.; de Ruiter, R.; Oh, J.M.; Semprebon, C.; Brinkmann, M.; Mugele, F. Drops on functional fibers: From barrels to clamshells and back. Soft Matter 2011, 7, 5138–5143. [Google Scholar] [CrossRef]
- Kuiper, S.; Hendriks, B. Variable-focus liquid lens for miniature cameras. Appl. Phys. Lett. 2004, 85, 1128–1130. [Google Scholar] [CrossRef]
- Preston, D.J.; Anders, A.; Barabadi, B.; Tio, E.; Zhu, Y.; Dai, D.A.; Wang, E.N. Electrowetting-on-dielectric actuation of a spatial and angular manipulation mems stage. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 Janauruy 2017; pp. 769–772. [Google Scholar]
- Pollack, M.G.; Fair, R.B.; Shenderov, A.D. Electrowetting-based actuation of liquid droplets for microfluidic applications. Appl. Phys. Lett. 2000, 77, 1725–1726. [Google Scholar] [CrossRef]
- Cho, S.K.; Moon, H.; Kim, C.-J. Creating, transporting, cutting, and merging liquid droplets by electrowetting-based actuation for digital microfluidic circuits. J. Microelectromech. Syst. 2003, 12, 70–80. [Google Scholar]
- Chang, H.-C.; Yeo, L.Y. Electrokinetically Driven Microfluidics and Nanofluidics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Khodayari, M.; Hahne, B.; Crane, N.B. Long life electrochemical diodes for continuous electrowetting. J. Electrochem. Soc. 2014, 161, E105–E111. [Google Scholar] [CrossRef]
- Lu, Y.; Sur, A.; Pascente, C.; Annapragada, S.R.; Ruchhoeft, P.; Liu, D. Dynamics of droplet motion induced by electrowetting. Int. J. Heat Mass Transf. 2017, 106, 920–931. [Google Scholar] [CrossRef]
- Gerratt, A.P.; Bergbreiter, S. Dielectric breakdown of pdms thin films. J. Micromech. Microeng. 2013, 23, 067001. [Google Scholar] [CrossRef]
- Satyanarayana, T.; Ajay, G.; Reddy, K.; Rajesh, V. Design and simulation of micro electro wetting liquid lens for miniature cameras. Int. J. Sci. Res. 2013, 2, 5. [Google Scholar]
- Nahar, M.M.; Bindiganavane, G.S.; Nikapitiya, J.; Moon, H. Numerical modeling of 3D electrowetting droplet actuation and cooling of a hotspot. In Proceedings of the 2015 COMSOL Conference, Boston, MA, USA, 7–9 October 2015; pp. 1–7. [Google Scholar]
- Guan, Y. A Numerical Study of Microfluidic Droplet Motions in Parallel-Plate Electrowetting-on-Dielectric (ewod) Devices. Ph.D. Thesis, The University of TexasArlington Texas, Arlington, TX, USA, 2015. [Google Scholar]
- Ai, Y.; Joo, S.W.; Jiang, Y.; Xuan, X.; Qian, S. Transient electrophoretic motion of a charged particle through a converging–diverging microchannel: Effect of direct current-dielectrophoretic force. Electrophoresis 2009, 30, 2499–2506. [Google Scholar] [CrossRef] [PubMed]
- Castañer, L.; Di Virgilio, V.; Bermejo, S. Charge-coupled transient model for electrowetting. Langmuir 2010, 26, 16178–16185. [Google Scholar] [CrossRef] [PubMed]
- Moon, H.; Cho, S.K.; Garrell, R.L.; Kim, C.-J.C. Low voltage electrowetting-on-dielectric. J. Appl. Phys. 2002, 92, 4080–4087. [Google Scholar] [CrossRef]
- Quilliet, C.; Berge, B. Electrowetting: A recent outbreak. Curr. Opin. Colloid Interface Sci. 2001, 6, 34–39. [Google Scholar] [CrossRef]
- Pallas, N.; Harrison, Y. Colloids surfaces, 43 (1990) 169. S. H&d, y. Hamnerius and 0. Nilsson. J. Appl. Phys. 1976, 47, 2433. [Google Scholar]
- Virgilio, V.D. Contactless Electrowetting. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2015. [Google Scholar]
- Gomez, A.; Tang, K. Charge and fission of droplets in electrostatic sprays. Phys. Fluid 1994, 6, 404–414. [Google Scholar] [CrossRef]
- Biegaj, K.W.; Rowland, M.G.; Lukas, T.M.; Heng, J.Y. Surface chemistry and humidity in powder electrostatics: A comparative study between tribocharging and corona discharge. ACS Omega 2017, 2, 1576–1582. [Google Scholar] [CrossRef]
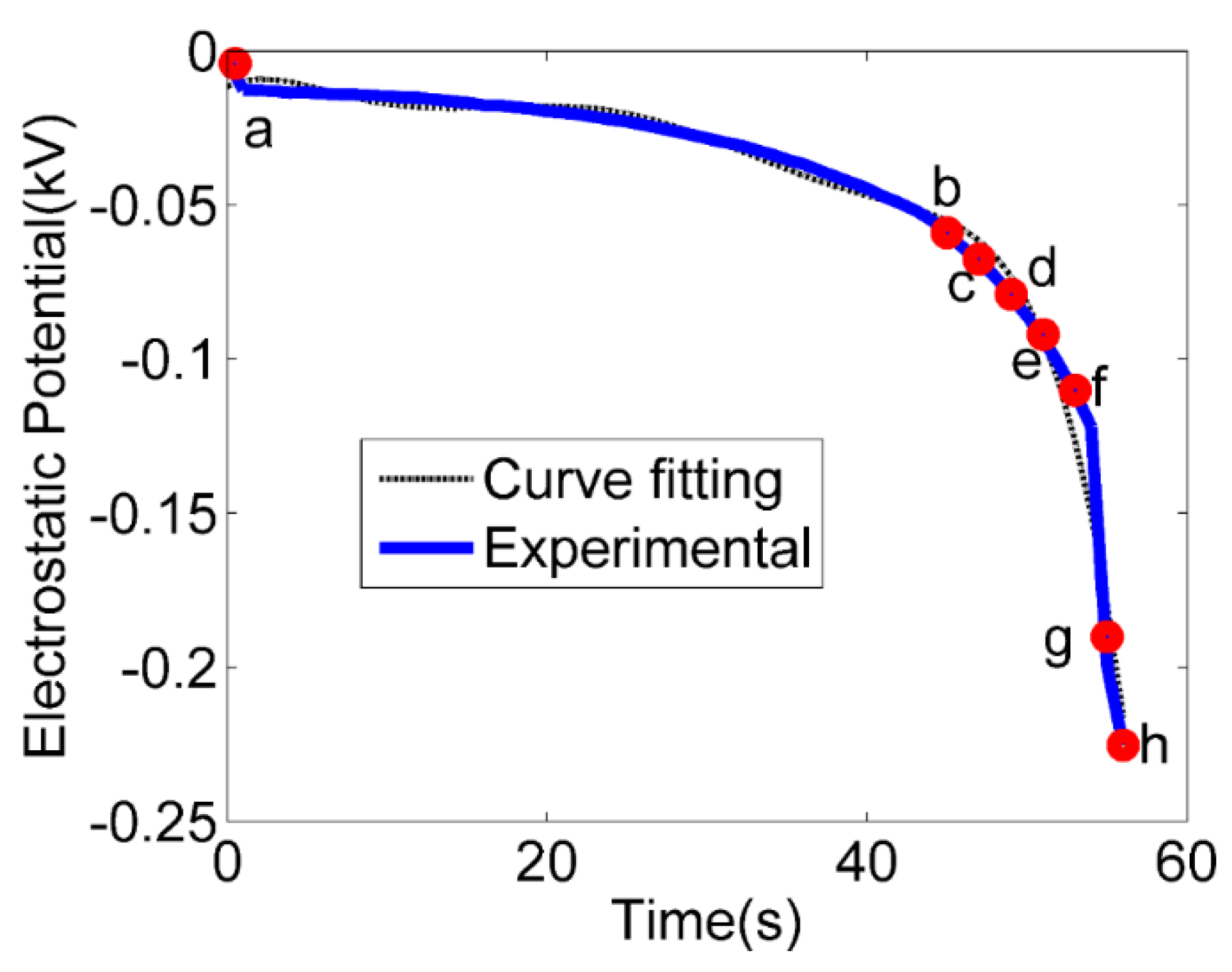

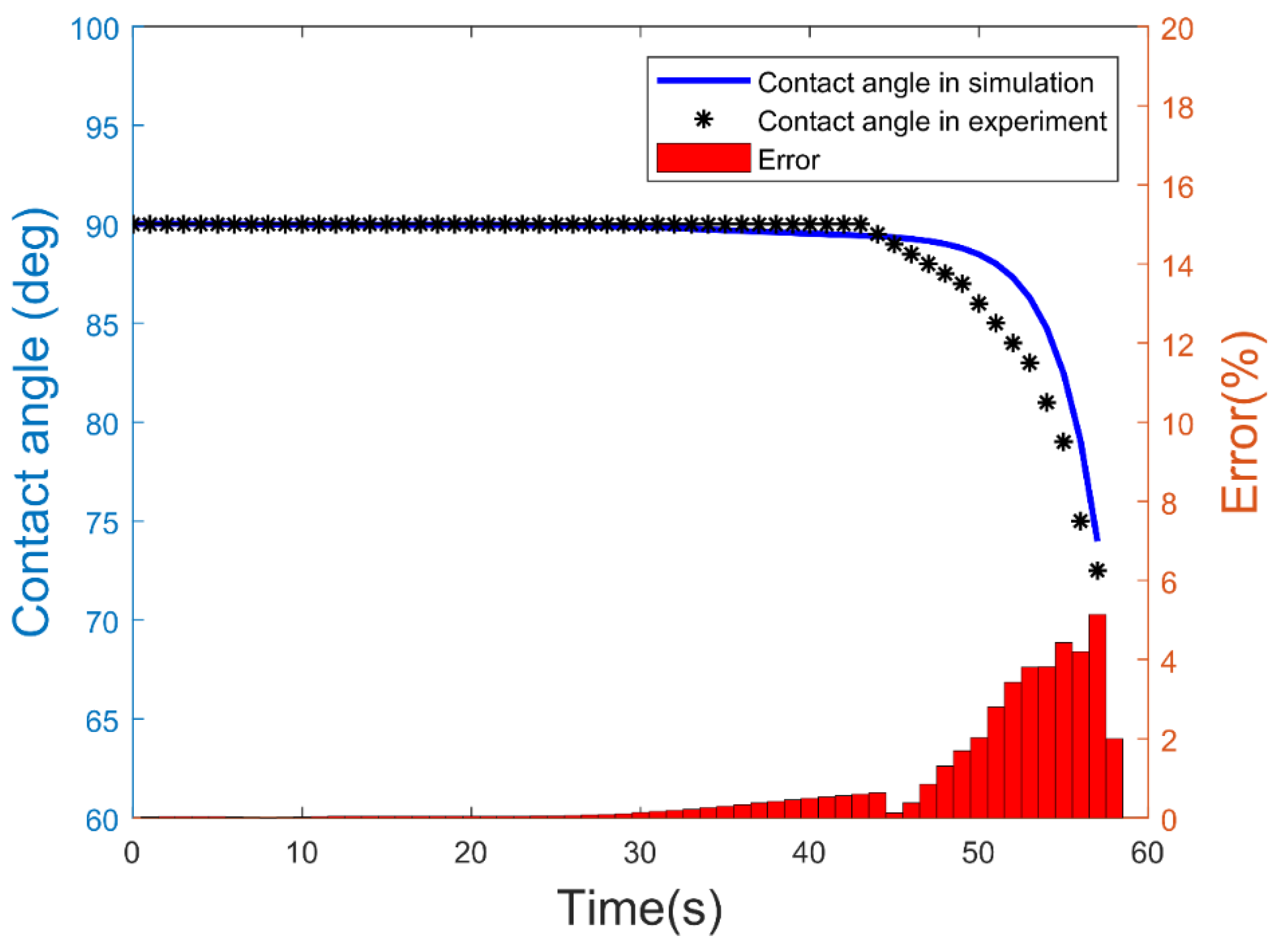
| Experimental Sets | Channel Inner Diameter (ID) (µm) | Water Flow Rate (mL/min) | Ambient Humidity (%) | Water Flow Speed (m/s) | Ambient Temperature (C) |
|---|---|---|---|---|---|
| A1 | 508 | 30 | 48 ± 3 | 2.517 | 22 |
| 40 | 3.356 | ||||
| 50 | 4.195 | ||||
| A2 | 254 | 7.5 | 48 ± 3 | 2.517 | 22 |
| 10 | 3.356 | ||||
| 12.5 | 4.195 | ||||
| B | 254 | 12.5 | 48 ± 3 | 4.195 | 22 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yazdanshenas, E.; Tang, Q.; Zhang, X. Electrowetting Using a Microfluidic Kelvin Water Dropper. Micromachines 2018, 9, 92. https://doi.org/10.3390/mi9030092
Yazdanshenas E, Tang Q, Zhang X. Electrowetting Using a Microfluidic Kelvin Water Dropper. Micromachines. 2018; 9(3):92. https://doi.org/10.3390/mi9030092
Chicago/Turabian StyleYazdanshenas, Elias, Qiang Tang, and Xiaoyu Zhang. 2018. "Electrowetting Using a Microfluidic Kelvin Water Dropper" Micromachines 9, no. 3: 92. https://doi.org/10.3390/mi9030092
APA StyleYazdanshenas, E., Tang, Q., & Zhang, X. (2018). Electrowetting Using a Microfluidic Kelvin Water Dropper. Micromachines, 9(3), 92. https://doi.org/10.3390/mi9030092