Applications of Photonic Crystal Nanobeam Cavities for Sensing
Abstract
1. Introduction
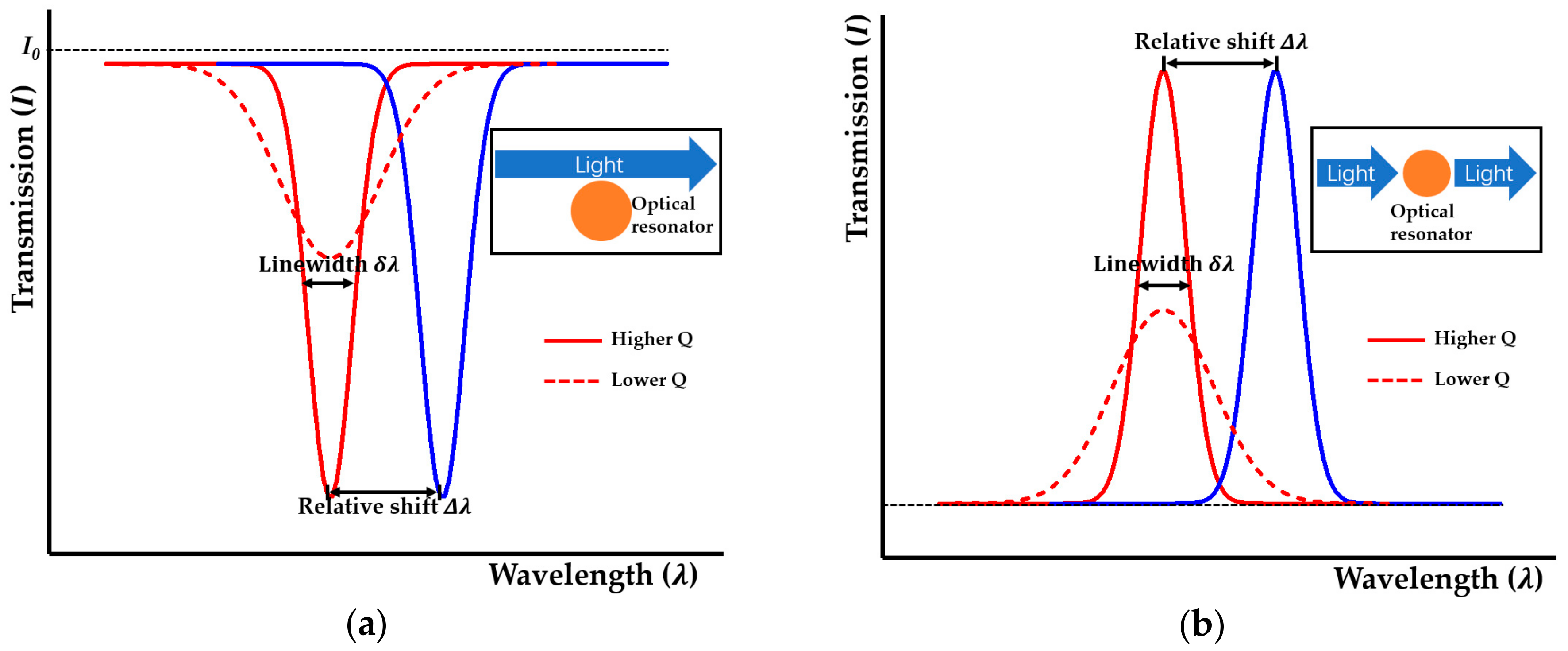
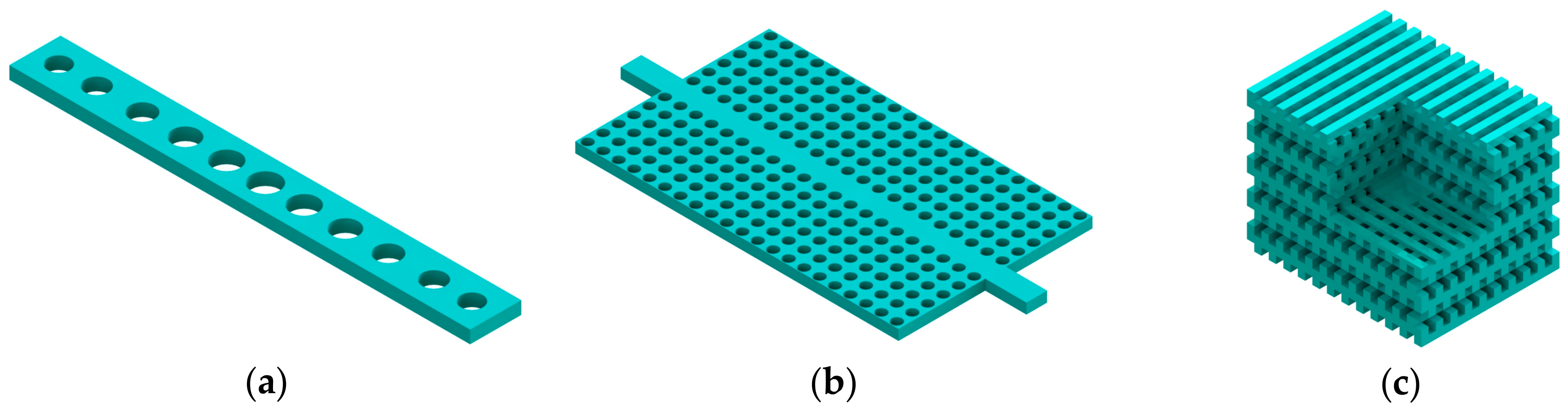
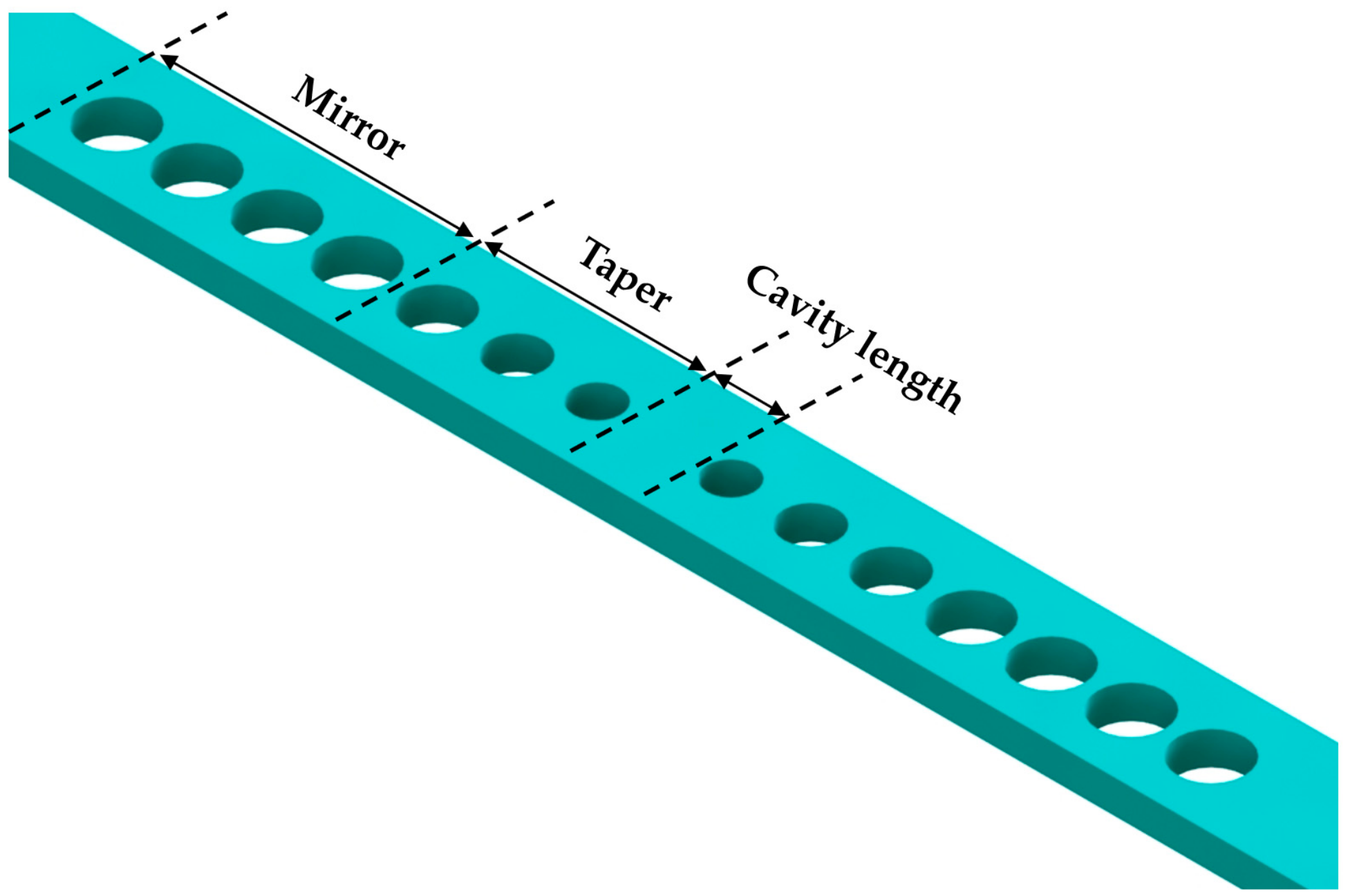
2. Optical Cavity
3. Refractive Index Sensing
3.1. Sensing Principle
3.2. Sensing Applications
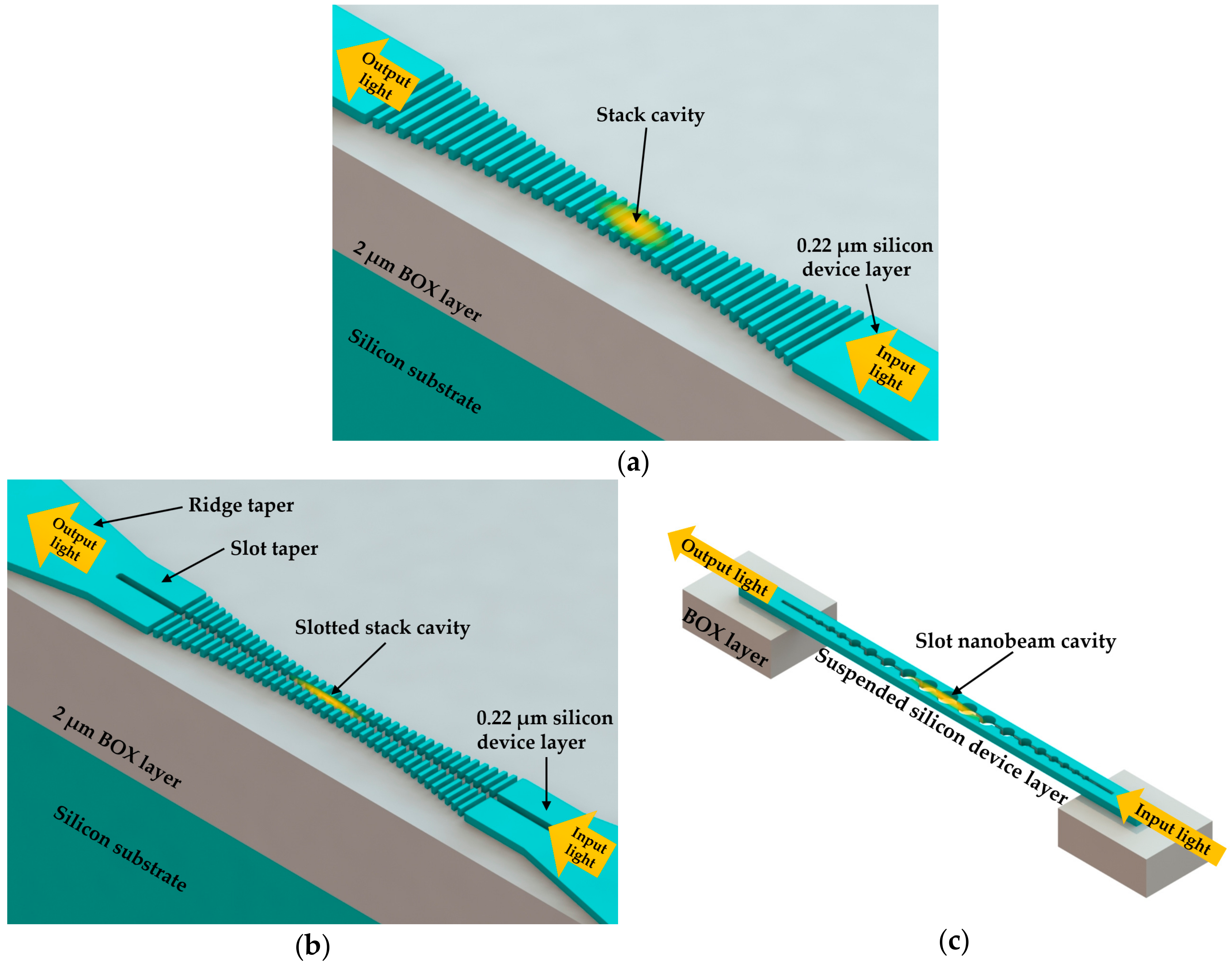
3.2.1. Efforts on Sensitivity
3.2.2. The Pursuit of Both High Q Factor and High Sensitivity
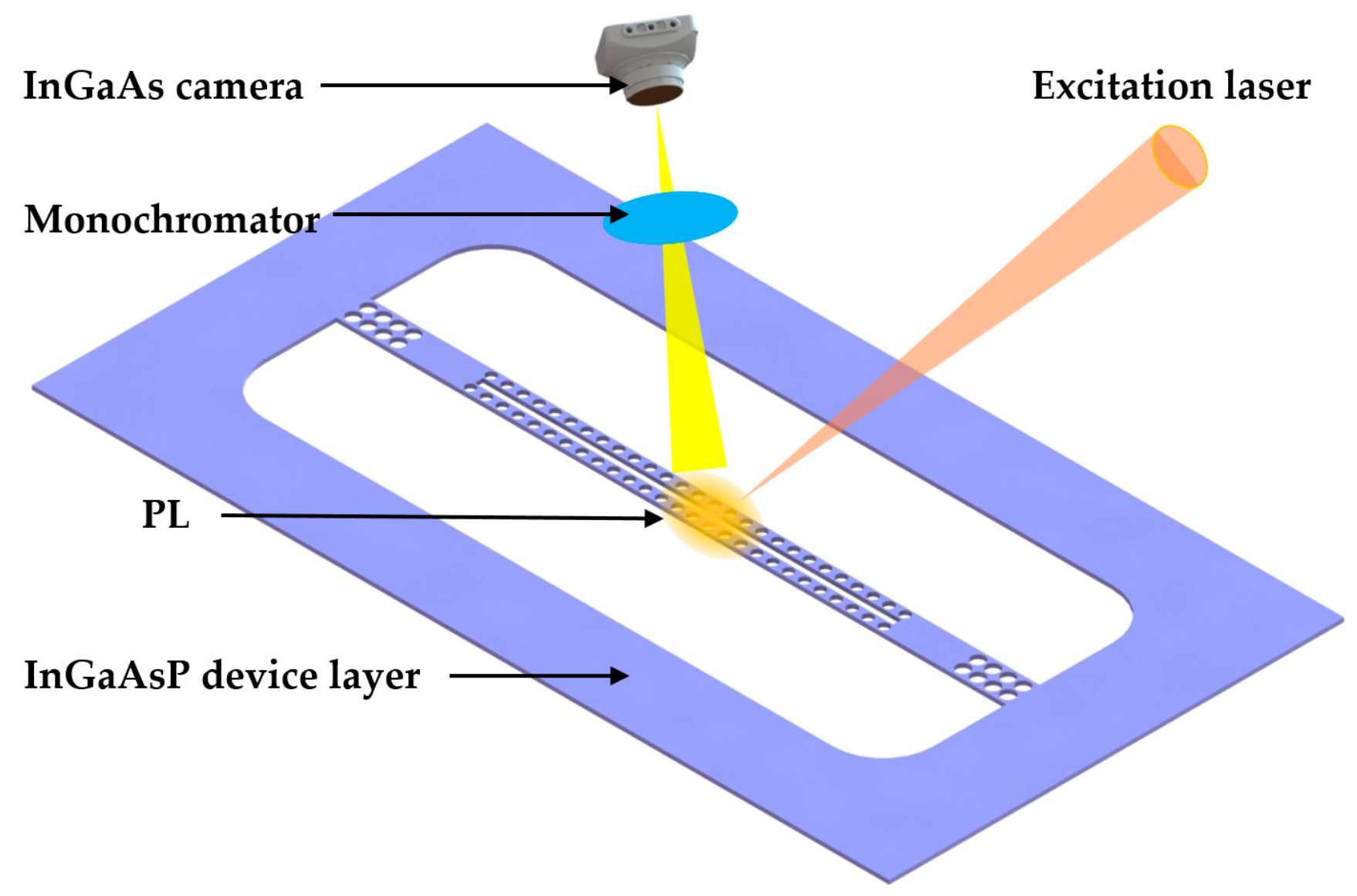
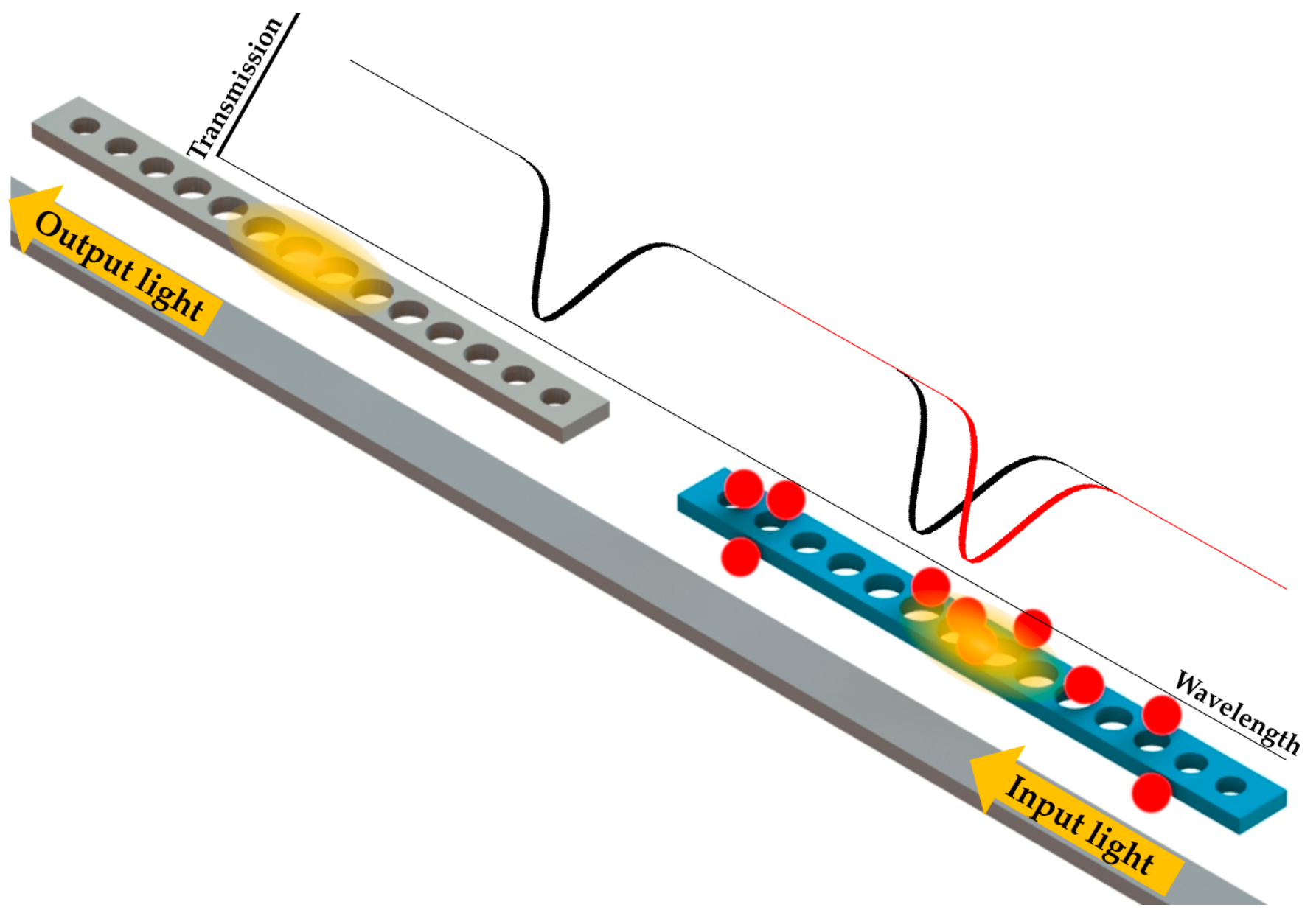
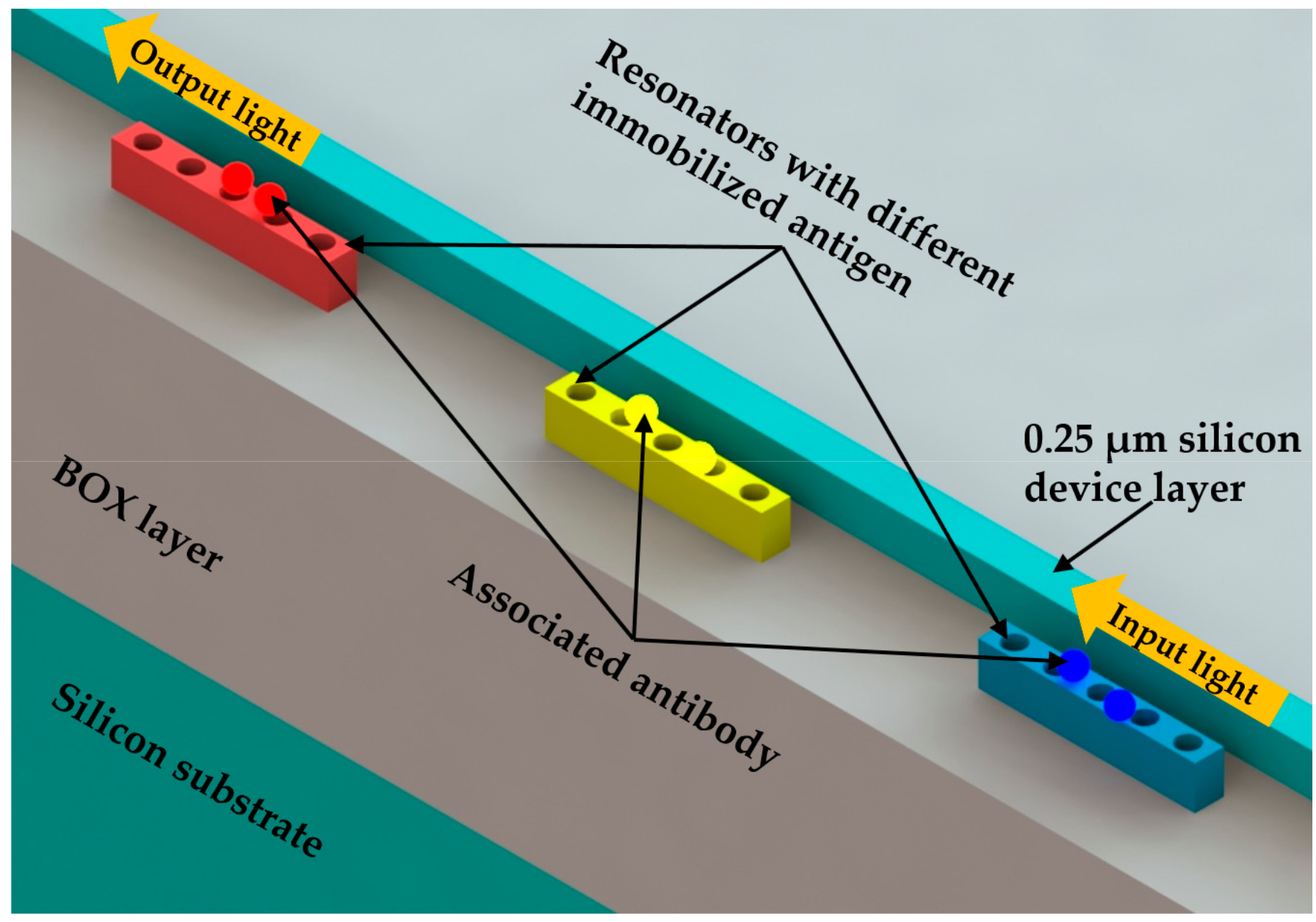
3.2.3. Multiplex RI Sensing
3.3. Discussion
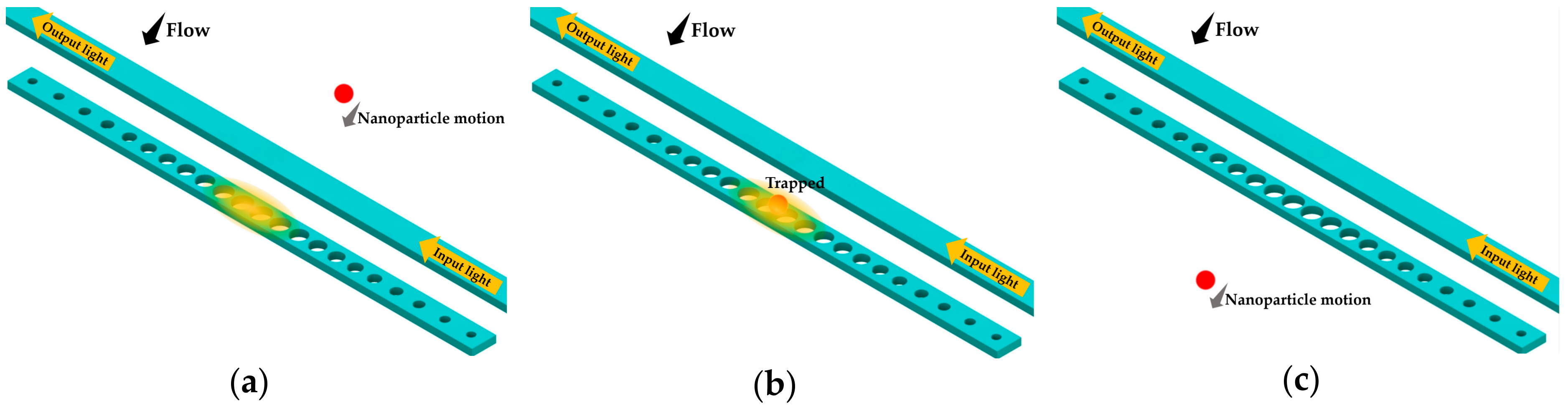
4. Nanoparticle Sensing
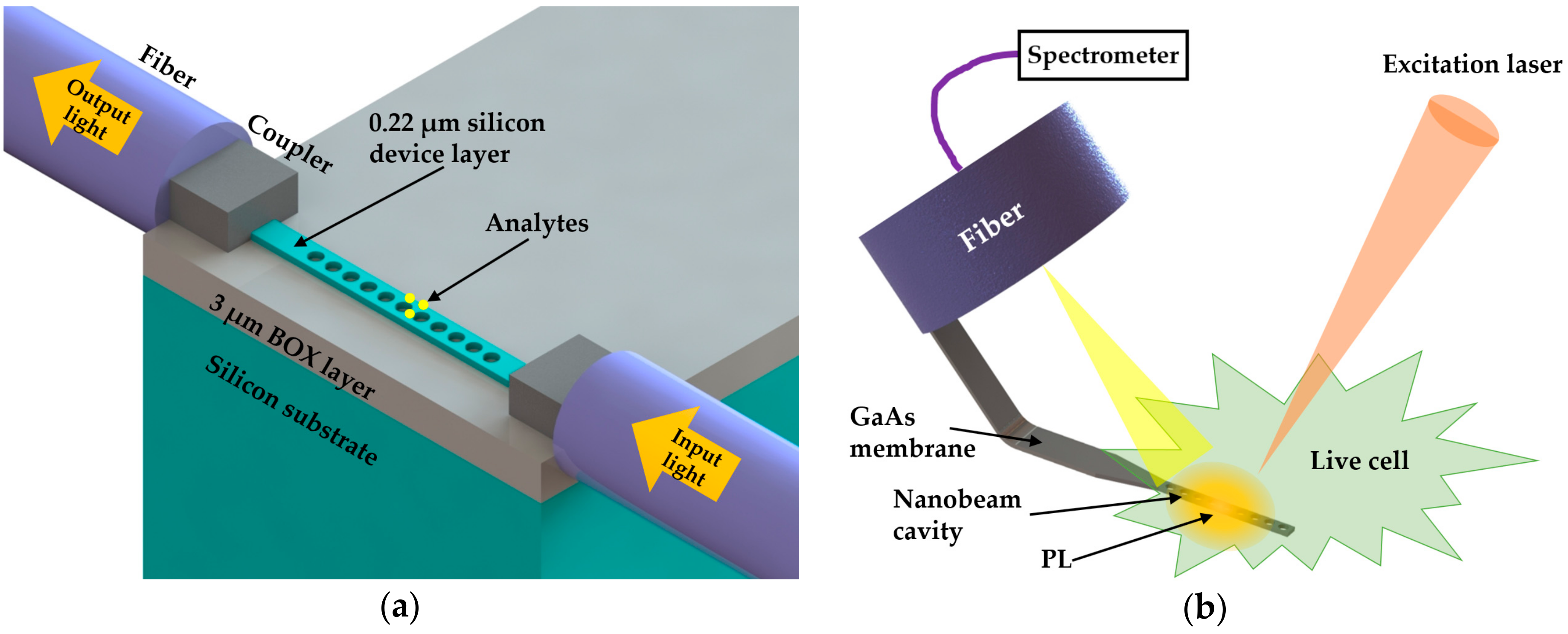
4.1. Functionalized Coating Surface
4.2. Unfunctionalized Coating Surface
4.3. Discussion
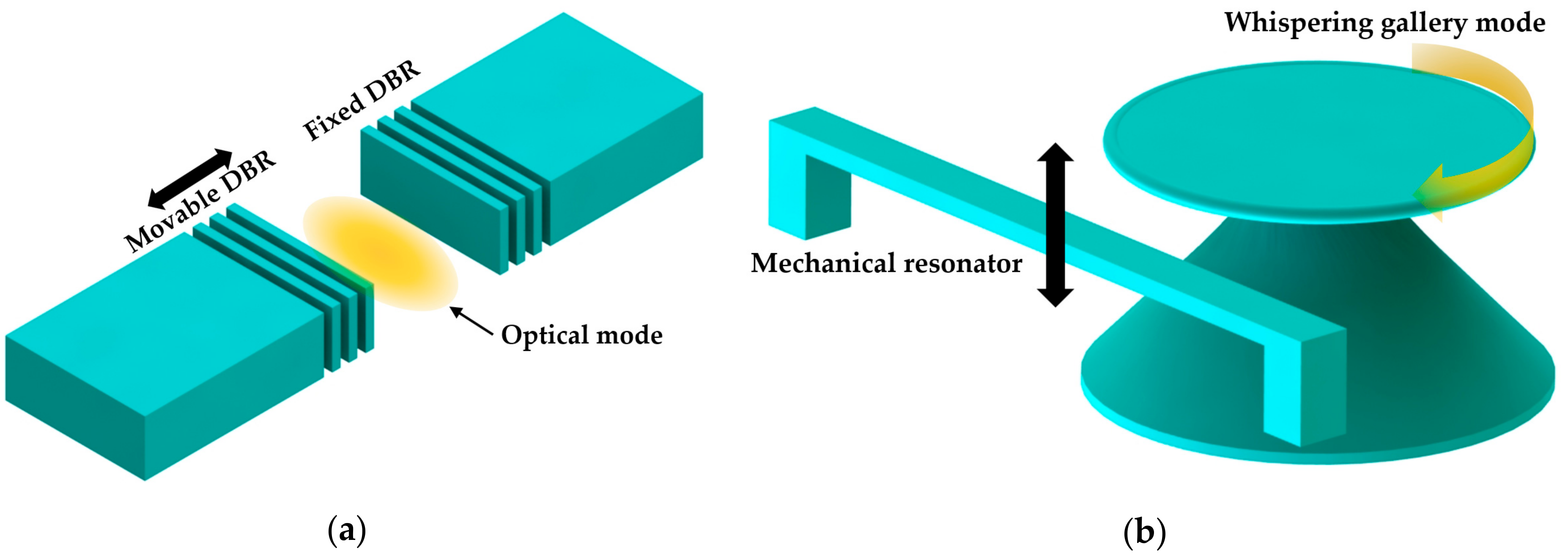
5. Optomechanical Sensors
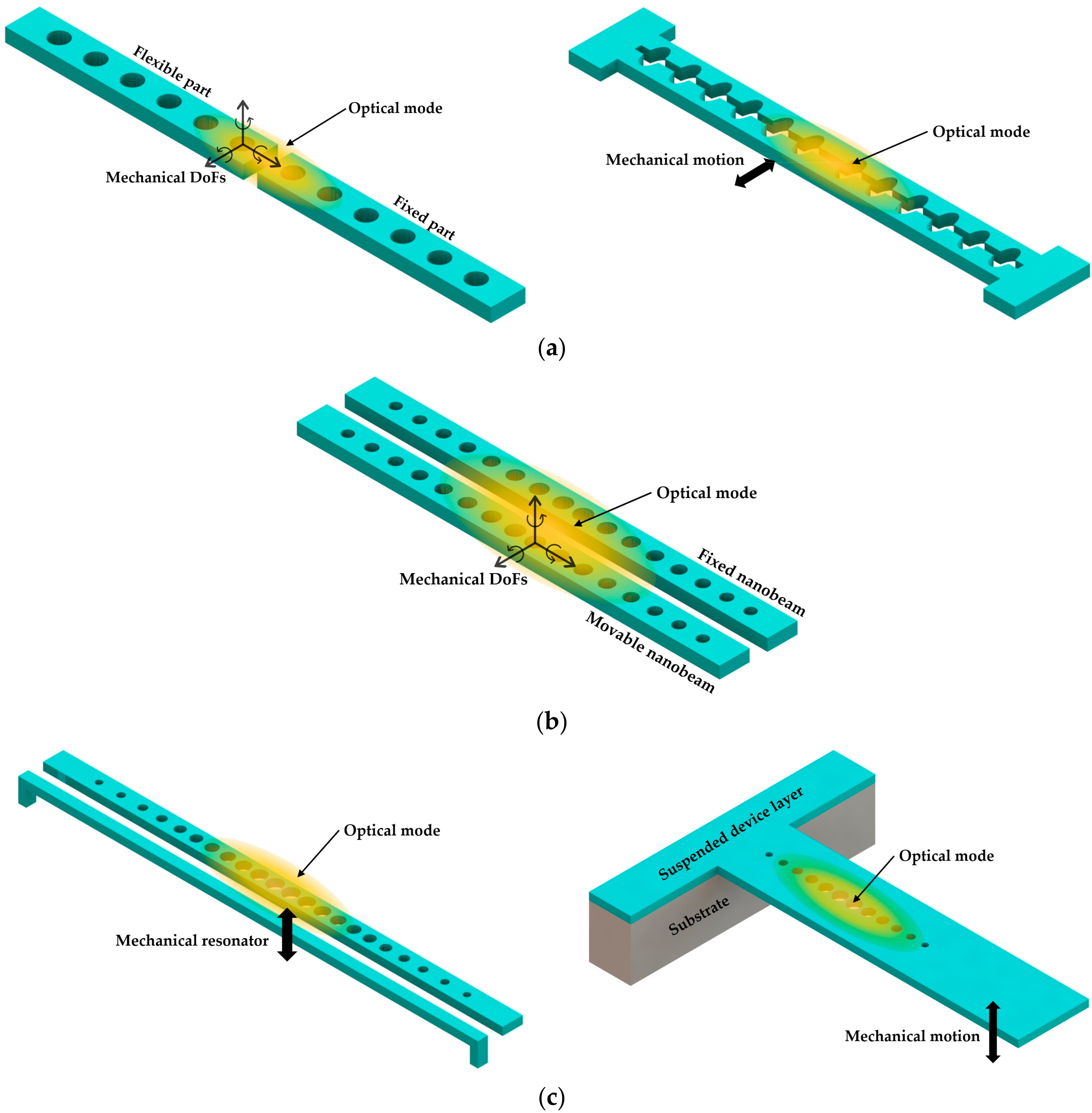
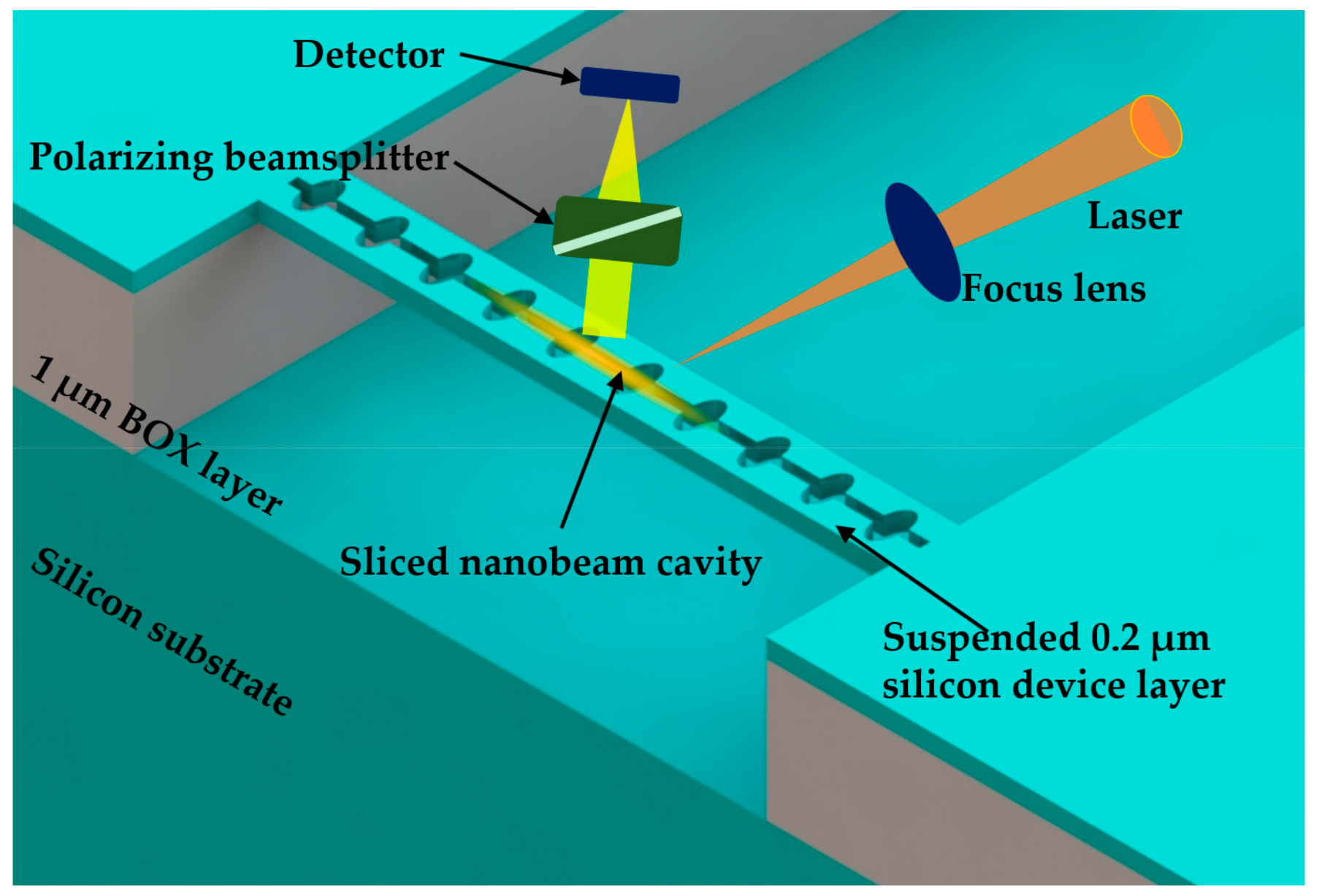
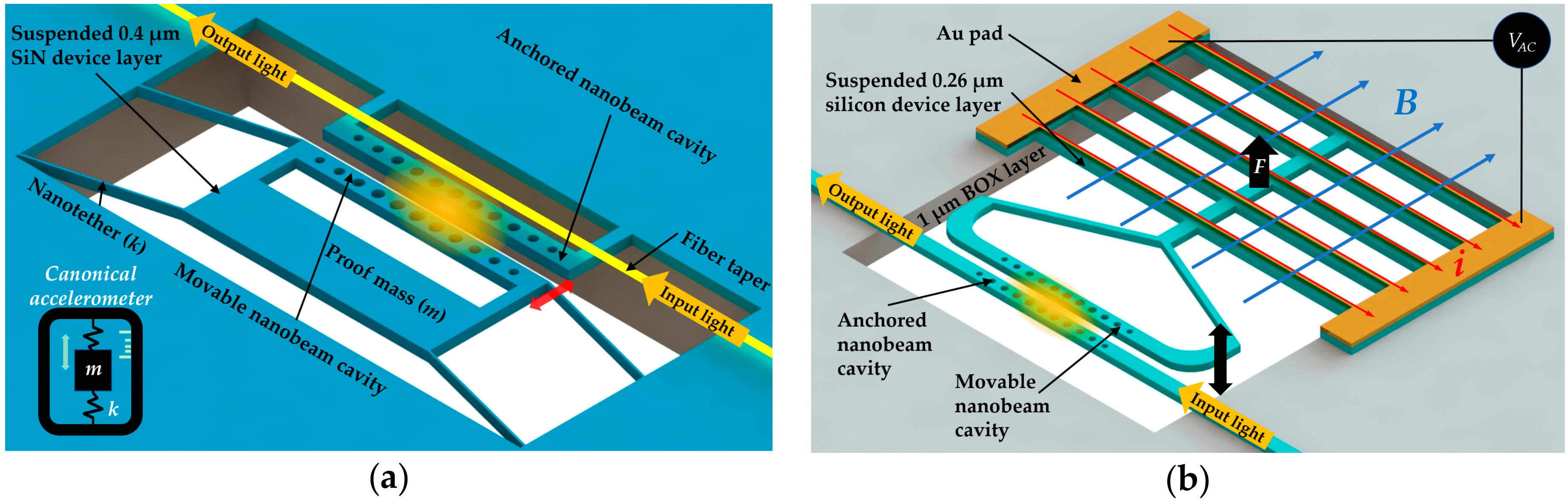
5.1. Single Nanobeam Cavity
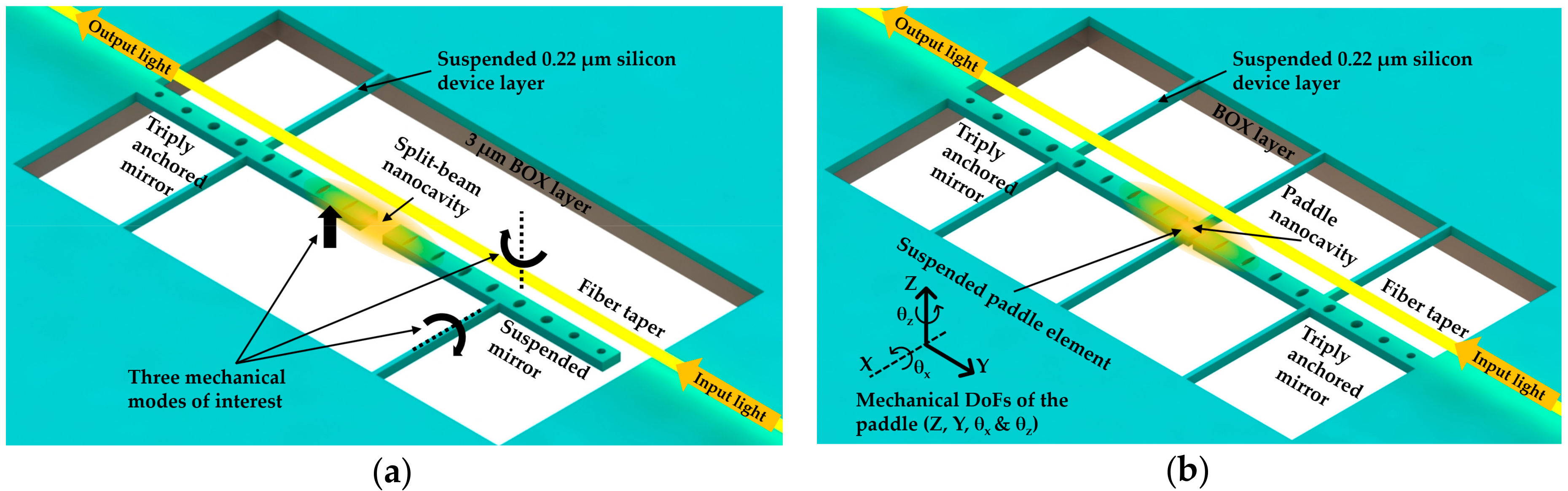
5.2. Coupled Nanobeam Cavities
5.3. Discussion
6. Temperature Sensors
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Painter, O.; Lee, R.; Scherer, A.; Yariv, A.; O’brien, J.; Dapkus, P.; Kim, I. Two-dimensional photonic band-gap defect mode laser. Science 1999, 284, 1819–1821. [Google Scholar] [CrossRef] [PubMed]
- Goyal, A.K.; Dutta, H.S.; Pal, S. Recent advances and progress in photonic crystal-based gas sensors. J. Phys. D Appl. Phys. 2017, 50, 203001. [Google Scholar] [CrossRef]
- Mandal, S.; Erickson, D. Nanoscale optofluidic sensor arrays. Opt. Express 2008, 16, 1623–1631. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Dündar, M.A.; Nötzel, R.; Karouta, F.; He, S.; van der Heijden, R.W. Photonic crystal slot nanobeam slow light waveguides for refractive index sensing. Appl. Phys. Lett. 2010, 97, 151105. [Google Scholar] [CrossRef]
- Yao, K.; Shi, Y. High-Q width modulated photonic crystal stack mode-gap cavity and its application to refractive index sensing. Opt. Express 2012, 20, 27039–27044. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Tian, H.; Ji, Y.; Quan, Q. Design of simultaneous high-Q and high-sensitivity photonic crystal refractive index sensors. J. Opt. Soc. Am. B 2013, 30, 2027–2031. [Google Scholar] [CrossRef]
- Liang, F.; Quan, Q. Detecting single gold nanoparticles (1.8 nm) with ultrahigh-Q air-mode photonic crystal nanobeam cavities. ACS Photonics 2015, 2, 1692–1697. [Google Scholar] [CrossRef]
- Yang, D.; Tian, H.; Ji, Y. High-Q and high-sensitivity width-modulated photonic crystal single nanobeam air-mode cavity for refractive index sensing. Appl. Opt. 2015, 54, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Wang, C.; Ji, Y. Silicon on-chip 1D photonic crystal nanobeam bandstop filters for the parallel multiplexing of ultra-compact integrated sensor array. Opt. Express 2016, 24, 16267–16279. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, G.; Shi, P.; Du, H.; Lin, T.; Teng, J.; Chau, F.S. On-chip integrated optofluidic complex refractive index sensing using silicon photonic crystal nanobeam cavities. Opt. Lett. 2016, 41, 1197–1200. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, B.; Almeida, V.; Manolatou, C.; Preble, S.; Lipson, M. Nanocavity in a silicon waveguide for ultrasensitive nanoparticle detection. Appl. Phys. Lett. 2004, 85, 4854–4856. [Google Scholar] [CrossRef]
- Mandal, S.; Goddard, J.M.; Erickson, D. A multiplexed optofluidic biomolecular sensor for low mass detection. Lab Chip 2009, 9, 2924–2932. [Google Scholar] [CrossRef] [PubMed]
- Liang, F.; Clarke, N.; Patel, P.; Loncar, M.; Quan, Q. Scalable photonic crystal chips for high sensitivity protein detection. Opt. Express 2013, 21, 32306–32312. [Google Scholar] [CrossRef] [PubMed]
- Quan, Q.; Floyd, D.L.; Burgess, I.B.; Deotare, P.B.; Frank, I.W.; Tang, S.K.; Ilic, R.; Loncar, M. Single particle detection in CMOS compatible photonic crystal nanobeam cavities. Opt. Express 2013, 21, 32225–32233. [Google Scholar] [CrossRef] [PubMed]
- Shambat, G.; Kothapalli, S.R.; Provine, J.; Sarmiento, T.; Harris, J.; Gambhir, S.S.; Vuckovic, J. Single-cell photonic nanocavity probes. Nano Lett. 2013, 13, 4999–5005. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Hu, J.; Kimerling, L.; Crozier, K. Design of nanoslotted photonic crystal waveguide cavities for single nanoparticle trapping and detection. Opt. Lett. 2009, 34, 3451–3453. [Google Scholar] [CrossRef] [PubMed]
- Mandal, S.; Serey, X.; Erickson, D. Nanomanipulation using silicon photonic crystal resonators. Nano Lett. 2010, 10, 99–104. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.F.; Serey, X.; Sarkar, R.; Chen, P.; Erickson, D. Controlled photonic manipulation of proteins and other nanomaterials. Nano Lett. 2012, 12, 1633–1637. [Google Scholar] [CrossRef] [PubMed]
- Eichenfield, M.; Camacho, R.; Chan, J.; Vahala, K.J.; Painter, O. A picogram-and nanometre-scale photonic-crystal optomechanical cavity. Nature 2009, 459, 550–555. [Google Scholar] [CrossRef] [PubMed]
- Krause, A.G.; Winger, M.; Blasius, T.D.; Lin, Q.; Painter, O. A high-resolution microchip optomechanical accelerometer. Nat. Photonics 2012, 6, 768–772. [Google Scholar] [CrossRef]
- Wu, M.; Hryciw, A.C.; Healey, C.; Lake, D.P.; Jayakumar, H.; Freeman, M.R.; Davis, J.P.; Barclay, P.E. Dissipative and dispersive optomechanics in a nanocavity torque sensor. Phys. Rev. X 2014, 4, 021052. [Google Scholar] [CrossRef]
- Kaviani, H.; Healey, C.; Wu, M.; Ghobadi, R.; Hryciw, A.; Barclay, P.E. Nonlinear optomechanical paddle nanocavities. Optica 2015, 2, 271–274. [Google Scholar] [CrossRef]
- Leijssen, R.; Verhagen, E. Strong optomechanical interactions in a sliced photonic crystal nanobeam. Sci. Rep. 2015, 5, 15974. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Zhou, G.; Zhao, Y.; Chen, G.; Chau, F.S. Magnetic field sensor based on coupled photonic crystal nanobeam cavities. Appl. Phys. Lett. 2017, 110, 061110. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, P.; Zhang, S.; Liu, W.; Chen, J.; Shi, Y. High sensitivity temperature sensor based on cascaded silicon photonic crystal nanobeam cavities. Opt. Express 2016, 24, 23037–23043. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Shi, Y. Simultaneous measurement of refractive index and temperature using cascaded side-coupled photonic crystal nanobeam cavities. Opt. Express 2017, 25, 28398–28406. [Google Scholar] [CrossRef]
- Armani, D.; Kippenberg, T.; Spillane, S.; Vahala, K. Ultra-high-Q toroid microcavity on a chip. Nature 2003, 421, 925–928. [Google Scholar] [CrossRef] [PubMed]
- Yablonovitch, E.; Gmitter, T.; Leung, K. Photonic band structure: The face-centered-cubic case employing nonspherical atoms. Phys. Rev. Lett. 1991, 67, 2295. [Google Scholar] [CrossRef] [PubMed]
- Yablonovitch, E.; Gmitter, T.; Meade, R.; Rappe, A.; Brommer, K.; Joannopoulos, J. Donor and acceptor modes in photonic band structure. Phys. Rev. Lett. 1991, 67, 3380–3383. [Google Scholar] [CrossRef] [PubMed]
- Kuchyanov, A.; Chubakov, P.; Plekhanov, A. Highly sensitive and fast response gas sensor based on a light reflection at the glass-photonic crystal interface. Opt. Commun. 2015, 351, 109–114. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Ogawa, S.; Imada, M.; Yoshimoto, S.; Okano, M.; Noda, S. Control of light emission by 3D photonic crystals. Science 2004, 305, 227–229. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, S.; Suzuki, K.; Okano, M.; Imada, M.; Nakamori, T.; Ota, Y.; Ishizaki, K.; Noda, S. Direct creation of three-dimensional photonic crystals by a top-down approach. Nat. Mater. 2009, 8, 721–725. [Google Scholar] [CrossRef] [PubMed]
- Foresi, J.; Villeneuve, P.R.; Ferrera, J.; Thoen, E.; Steinmeyer, G.; Fan, S.; Joannopoulos, J.; Kimerling, L.; Smith, H.I.; Ippen, E. Photonic-bandgap microcavities in optical waveguides. Nature 1997, 390, 143–145. [Google Scholar] [CrossRef]
- Purcell, E.M. Spontaneous emission probabilities at radio frequencies. In Confined Electrons and Photons; Springer: Berlin, Germany, 1995; p. 839. [Google Scholar]
- Johnson, S.G.; Fan, S.; Mekis, A.; Joannopoulos, J. Multipole-cancellation mechanism for high-Q cavities in the absence of a complete photonic band gap. Appl. Phys. Lett. 2001, 78, 3388–3390. [Google Scholar] [CrossRef]
- Palamaru, M.; Lalanne, P. Photonic crystal waveguides: Out-of-plane losses and adiabatic modal conversion. Appl. Phys. Lett. 2001, 78, 1466–1468. [Google Scholar] [CrossRef]
- Vučković, J.; Lončar, M.; Mabuchi, H.; Scherer, A. Design of photonic crystal microcavities for cavity QED. Phys. Rev. E 2001, 65, 016608. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, K.; Painter, O. Momentum space design of high-Q photonic crystal optical cavities. Opt. Express 2002, 10, 670–684. [Google Scholar] [CrossRef] [PubMed]
- Akahane, Y.; Asano, T.; Song, B.-S.; Noda, S. High-Q photonic nanocavity in a two-dimensional photonic crystal. Nature 2003, 425, 944–947. [Google Scholar] [CrossRef] [PubMed]
- Lalanne, P.; Hugonin, J.P. Bloch-wave engineering for high-Q, small-V microcavities. IEEE J. Quantum Electron. 2003, 39, 1430–1438. [Google Scholar] [CrossRef]
- Lalanne, P.; Mias, S.; Hugonin, J.-P. Two physical mechanisms for boosting the quality factor to cavity volume ratio of photonic crystal microcavities. Opt. Express 2004, 12, 458–467. [Google Scholar] [CrossRef] [PubMed]
- Sauvan, C.; Lecamp, G.; Lalanne, P.; Hugonin, J.-P. Modal-reflectivity enhancement by geometry tuning in photonic crystal microcavities. Opt. Express 2005, 13, 245–255. [Google Scholar] [CrossRef] [PubMed]
- Velha, P.; Rodier, J.-C.; Lalanne, P.; Hugonin, J.-P.; Peyrade, D.; Picard, E.; Charvolin, T.; Hadji, E. Ultra-high-reflectivity photonic-bandgap mirrors in a ridge SOI waveguide. New J. Phys. 2006, 8, 204. [Google Scholar] [CrossRef]
- Velha, P.; Picard, E.; Charvolin, T.; Hadji, E.; Rodier, J.-C.; Lalanne, P.; Peyrade, D. Ultra-high Q/V Fabry-Perot microcavity on SOI substrate. Opt. Express 2007, 15, 16090–16096. [Google Scholar] [CrossRef] [PubMed]
- McCutcheon, M.W.; Loncar, M. Design of a silicon nitride photonic crystal nanocavity with a Quality factor of one million for coupling to a diamond nanocrystal. Opt. Express 2008, 16, 19136–19145. [Google Scholar] [CrossRef] [PubMed]
- Notomi, M.; Kuramochi, E.; Taniyama, H. Ultrahigh-Q nanocavity with 1D photonic gap. Opt. Express 2008, 16, 11095–11102. [Google Scholar] [CrossRef] [PubMed]
- Zain, A.R.; Johnson, N.P.; Sorel, M.; De La Rue, R.M. Ultra high quality factor one dimensional photonic crystal/photonic wire micro-cavities in silicon-on-insulator (SOI). Opt. Express 2008, 16, 12084–12089. [Google Scholar] [CrossRef] [PubMed]
- Deotare, P.B.; McCutcheon, M.W.; Frank, I.W.; Khan, M.; Lončar, M. High quality factor photonic crystal nanobeam cavities. Appl. Phys. Lett. 2009, 94, 121106. [Google Scholar] [CrossRef]
- Kuramochi, E.; Taniyama, H.; Tanabe, T.; Kawasaki, K.; Roh, Y.G.; Notomi, M. Ultrahigh-Q one-dimensional photonic crystal nanocavities with modulated mode-gap barriers on SiO2 claddings and on air claddings. Opt. Express 2010, 18, 15859–15869. [Google Scholar] [CrossRef] [PubMed]
- Quan, Q.; Deotare, P.B.; Loncar, M. Photonic crystal nanobeam cavity strongly coupled to the feeding waveguide. Appl. Phys. Lett. 2010, 96, 203102. [Google Scholar] [CrossRef]
- Quan, Q.; Loncar, M. Deterministic design of wavelength scale, ultra-high Q photonic crystal nanobeam cavities. Opt. Express 2011, 19, 18529–18542. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Sun, F.; Dong, B.; Ma, Y.; Chang, Y.; Tian, H.; Lee, C. Deterministic aperiodic photonic crystal nanobeam supporting adjustable multiple mode-matched resonances. Opt. Lett. in press.
- Matsko, A.B.; Ilchenko, V.S. Optical resonators with whispering gallery modes I: Basics. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 3–14. [Google Scholar] [CrossRef]
- Arnold, S.; Khoshsima, M.; Teraoka, I.; Holler, S.; Vollmer, F. Shift of whispering-gallery modes in microspheres by protein adsorption. Opt. Lett. 2003, 28, 272–274. [Google Scholar] [CrossRef] [PubMed]
- Hanumegowda, N.M.; Stica, C.J.; Patel, B.C.; White, I.; Fan, X. Refractometric sensors based on microsphere resonators. Appl. Phys. Lett. 2005, 87, 201107. [Google Scholar] [CrossRef]
- Mortensen, N.A.; Xiao, S.; Pedersen, J. Liquid-infiltrated photonic crystals: Enhanced light-matter interactions for lab-on-a-chip applications. Microfluid. Nanofluid. 2008, 4, 117–127. [Google Scholar] [CrossRef]
- Rindorf, L.; Jensen, J.B.; Dufva, M.; Pedersen, L.H.; Høiby, P.E.; Bang, O. Photonic crystal fiber long-period gratings for biochemical sensing. Opt. Express 2006, 14, 8224–8231. [Google Scholar] [CrossRef] [PubMed]
- Abdulhalim, I.; Zourob, M.; Lakhtakia, A. Surface plasmon resonance for biosensing: A mini-review. Electromagnetics 2008, 28, 214–242. [Google Scholar] [CrossRef]
- White, I.M.; Fan, X. On the performance quantification of resonant refractive index sensors. Opt. Express 2008, 16, 1020–1028. [Google Scholar] [CrossRef] [PubMed]
- Chow, E.; Grot, A.; Mirkarimi, L.; Sigalas, M.; Girolami, G. Ultracompact biochemical sensor built with two-dimensional photonic crystal microcavity. Opt. Lett. 2004, 29, 1093–1095. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.; Fauchet, P.M. Two-dimensional silicon photonic crystal based biosensing platform for protein detection. Opt. Express 2007, 15, 4530–4535. [Google Scholar] [CrossRef] [PubMed]
- Johnson, S.G.; Joannopoulos, J.D. Block-iterative frequency-domain methods for Maxwell’s equations in a planewave basis. Opt. Express 2001, 8, 173–190. [Google Scholar] [CrossRef] [PubMed]
- Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 687–702. [Google Scholar] [CrossRef]
- Chen, X.; Uttamchandani, D.; Trager-Cowan, C.; O’donnell, K. Luminescence from porous silicon. Semicond. Sci. Technol. 1993, 8, 92. [Google Scholar] [CrossRef]
- Quan, Q.; Vollmer, F.; Burgess, I.B.; Deotare, P.B.; Frank, I.; Tang, S.; Illic, R.; Loncar, M. Ultrasensitive on-chip photonic crystal nanobeam sensor using optical bistability. In Proceedings of the Quantum Electronics and Laser Science Conference, Baltimore, MD, USA, 22–27 May 2011. [Google Scholar]
- Xu, T.; Zhu, N.; Xu, M.Y.-C.; Wosinski, L.; Aitchison, J.S.; Ruda, H. Pillar-array based optical sensor. Opt. Express 2010, 18, 5420–5425. [Google Scholar] [CrossRef] [PubMed]
- Almeida, V.R.; Xu, Q.; Barrios, C.A.; Lipson, M. Guiding and confining light in void nanostructure. Opt. Lett. 2004, 29, 1209–1211. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Yao, K.; Zheng, J.; Guan, X.; Shi, Y. Slotted photonic crystal nanobeam cavity with parabolic modulated width stack for refractive index sensing. Opt. Express 2013, 21, 26908–26913. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Zhang, P.; Tian, H.; Ji, Y.; Quan, Q. Ultrahigh- Q and Low-Mode-Volume Parabolic Radius-Modulated Single Photonic Crystal Slot Nanobeam Cavity for High-Sensitivity Refractive Index Sensing. IEEE Photonics J. 2015, 7, 1–8. [Google Scholar]
- Sherry, L.J.; Chang, S.-H.; Schatz, G.C.; Van Duyne, R.P.; Wiley, B.J.; Xia, Y. Localized surface plasmon resonance spectroscopy of single silver nanocubes. Nano Lett. 2005, 5, 2034–2038. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.G.A.; Velha, P.; Richard, M.; Johnson, N.P. Silicon-on-insulator (soi) nanobeam optical cavities for refractive index based sensing. In Proceedings of the Optical Sensing and Detection II, Brussels, Belgium, 16–19 April 2012. [Google Scholar]
- Yang, D.; Kita, S.; Liang, F.; Wang, C.; Tian, H.; Ji, Y.; Lončar, M.; Quan, Q. High sensitivity and high Q-factor nanoslotted parallel quadrabeam photonic crystal cavity for real-time and label-free sensing. Appl. Phys. Lett. 2014, 105, 063118. [Google Scholar] [CrossRef]
- Huang, L.; Zhou, J.; Sun, F.; Fu, Z.; Tian, H. Optimization of One Dimensional Photonic Crystal Elliptical-Hole Low-Index Mode Nanobeam Cavities for On-Chip Sensing. J. Light. Technol. 2016, 34, 3496–3502. [Google Scholar] [CrossRef]
- Bartlett, J.M.; Stirling, D. A short history of the polymerase chain reaction. In PCR Protocols; Springer: Berlin, Germany, 2003; pp. 3–6. [Google Scholar]
- Yaseen, M.T.; Yang, Y.C.; Shih, M.H.; Chang, Y.C. Optimization of high-Q coupled nanobeam cavity for label-free sensing. Sensors 2015, 15, 25868–25881. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Tian, H.; Huang, L.; Fu, Z.; Sun, F.; Ji, Y. Parabolic tapered coupled two photonic crystal nanobeam slot cavities for high-FOM biosensing. IEEE Photonics Technol. Lett. 2017, 29, 1281–1284. [Google Scholar] [CrossRef]
- Meng, Z.-M.; Li, Z.-Y. Control of Fano resonances in photonic crystal nanobeams side-coupled with nanobeam cavities and their applications to refractive index sensing. J. Phys. D Appl. Phys. 2018, 51, 095106. [Google Scholar] [CrossRef]
- Peng, F.; Wang, Z.; Guan, L.; Yuan, G.; Peng, Z. High-Sensitivity Refractive Index Sensing Based on Fano resonances in a Photonic Crystal Cavity-Coupled Microring Resonator. IEEE Photonics J. 2018, 1. [Google Scholar] [CrossRef]
- Lin, T.; Zhang, X.; Zhou, G.; Siong, C.F.; Deng, J. Design of an ultra-compact slotted photonic crystal nanobeam cavity for biosensing. J. Opt. Soc. Am. B 2015, 32, 1788–1791. [Google Scholar] [CrossRef]
- Sun, F.; Zhou, J.; Huang, L.; Fu, Z.; Tian, H. High quality factor and high sensitivity photonic crystal rectangular holes slot nanobeam cavity with parabolic modulated lattice constant for refractive index sensing. Opt. Commun. 2017, 399, 56–61. [Google Scholar] [CrossRef]
- Saha, P.; Sen, M. A slotted photonic crystal nanobeam cavity for simultaneous attainment of ultra-high Q-factor and sensitivity. IEEE Sens. J. 2018, 18, 3602–3609. [Google Scholar] [CrossRef]
- Yu, P.; Qiu, H.; Yu, H.; Wu, F.; Wang, Z.; Jiang, X.; Yang, J. High-Q and high-order side-coupled air-mode nanobeam photonic crystal cavities in silicon. IEEE Photonics Technol. Lett. 2016, 28, 2121–2124. [Google Scholar] [CrossRef]
- Liu, W.; Yan, J.; Shi, Y. High sensitivity visible light refractive index sensor based on high order mode Si3N4 photonic crystal nanobeam cavity. Opt. Express 2017, 25, 31739–31745. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Yu, Z.; Shen, X.; Dai, S. High quality factor and high sensitivity chalcogenide 1D photonic crystal microbridge cavity for mid-infrared sensing. Opt. Commun. 2017, 382, 361–365. [Google Scholar] [CrossRef]
- Deng, C.-S.; Li, M.-J.; Peng, J.; Liu, W.-L.; Zhong, J.-X. Simultaneously high-Q and high-sensitivity slotted photonic crystal nanofiber cavity for complex refractive index sensing. J. Opt. Soc. Am. B 2017, 34, 1624–1631. [Google Scholar] [CrossRef]
- Velha, P.; Rodier, J.-C.; Lalanne, P.; Hugonin, J.-P.; Peyrade, D.; Picard, E.; Charvolin, T.; Hadji, E. Ultracompact silicon-on-insulator ridge-waveguide mirrors with high reflectance. Appl. Phys. Lett. 2006, 89, 171121. [Google Scholar] [CrossRef]
- Yang, D.; Wang, B.; Chen, X.; Wang, C.; Ji, Y. Ultracompact on-chip multiplexed sensor array based on dense integration of flexible 1-D photonic crystal nanobeam cavity with large free spectral range and high Q-factor. IEEE Photonics J. 2017, 9, 1–12. [Google Scholar] [CrossRef]
- Wang, J.; Fu, Z.; Sun, F.; Wang, Z.; Wang, C.; Tian, H. Multiplexing dual-parameter sensor using photonic crystal multimode nanobeam cavities. Opt. Commun. 2018, 427, 382–389. [Google Scholar] [CrossRef]
- Yang, D.; Wang, C.; Ji, Y. Silicon on-chip 1D photonic crystal nanobeam bandgap filter integrated with nanobeam cavity for accurate refractive index sensing. IEEE Photonics J. 2016, 8, 1–8. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, D.; Ji, Y. Ultra-compact photonic crystal integrated sensor formed by series-connected nanobeam bandstop filter and nanobeam cavity. In Proceedings of the High Power Lasers, High Energy Lasers, and Silicon-based Photonic Integration, Beijing, China, 19 October 2016. [Google Scholar]
- Sun, F.; Fu, Z.; Wang, C.; Ding, Z.; Wang, C.; Tian, H. Ultra-compact air-mode photonic crystal nanobeam cavity integrated with bandstop filter for refractive index sensing. Appl. Opt. 2017, 56, 4363–4368. [Google Scholar] [CrossRef] [PubMed]
- Tian, F.; Zhou, G.; Du, Y.; Chau, F.S.; Deng, J.; Tang, X.; Akkipeddi, R. Energy-efficient utilization of bipolar optical forces in nano-optomechanical cavities. Opt. Express 2013, 21, 18398–18407. [Google Scholar] [CrossRef] [PubMed]
- Vollmer, F.; Yang, L. Review Label-free detection with high-Q microcavities: A review of biosensing mechanisms for integrated devices. Nanophotonics 2012, 1, 267–291. [Google Scholar] [CrossRef] [PubMed]
- Armani, A.M.; Kulkarni, R.P.; Fraser, S.E.; Flagan, R.C.; Vahala, K.J. Label-free, single-molecule detection with optical microcavities. Science 2007, 317, 783–787. [Google Scholar] [CrossRef] [PubMed]
- Vollmer, F.; Arnold, S.; Keng, D. Single virus detection from the reactive shift of a whispering-gallery mode. Proc. Natl. Acad. Sci. USA 2008, 105, 20701–20704. [Google Scholar] [CrossRef] [PubMed]
- Wark, A.W.; Lee, H.J.; Corn, R.M. Long-range surface plasmon resonance imaging for bioaffinity sensors. Anal. Chem. 2005, 77, 3904–3907. [Google Scholar] [CrossRef] [PubMed]
- Homola, J. Surface plasmon resonance sensors for detection of chemical and biological species. Chem. Rev. 2008, 108, 462–493. [Google Scholar] [CrossRef] [PubMed]
- Ymeti, A.; Greve, J.; Lambeck, P.V.; Wink, T.; van Hövell, S.W.; Beumer, T.A.; Wijn, R.R.; Heideman, R.G.; Subramaniam, V.; Kanger, J.S. Fast, ultrasensitive virus detection using a young interferometer sensor. Nano Lett. 2007, 7, 394–397. [Google Scholar] [CrossRef] [PubMed]
- Brandenburg, A. Differential refractometry by an integrated-optical Young interferometer. Sens. Actuators B Chem. 1997, 39, 266–271. [Google Scholar] [CrossRef]
- Scullion, M.; Di Falco, A.; Krauss, T. Slotted photonic crystal cavities with integrated microfluidics for biosensing applications. Biosens. Bioelectron. 2011, 27, 101–105. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Ozdemir, S.K.; Xiao, Y.-F.; Li, L.; He, L.; Chen, D.-R.; Yang, L. On-chip single nanoparticle detection and sizing by mode splitting in an ultrahigh-Q microresonator. Nat. Photonics 2010, 4, 46–49. [Google Scholar] [CrossRef]
- Shao, L.; Jiang, X.F.; Yu, X.C.; Li, B.B.; Clements, W.R.; Vollmer, F.; Wang, W.; Xiao, Y.F.; Gong, Q. Detection of single nanoparticles and lentiviruses using microcavity resonance broadening. Adv. Mater. 2013, 25, 5616–5620. [Google Scholar] [CrossRef] [PubMed]
- Shen, B.-Q.; Yu, X.-C.; Zhi, Y.; Wang, L.; Kim, D.; Gong, Q.; Xiao, Y.-F. Detection of single nanoparticles using the dissipative interaction in a high-Q microcavity. Phys. Rev. Appl. 2016, 5, 024011. [Google Scholar] [CrossRef]
- Vörös, J. The density and refractive index of adsorbing protein layers. Biophys. J. 2004, 87, 553–561. [Google Scholar] [CrossRef] [PubMed]
- Vollmer, F.; Braun, D.; Libchaber, A.; Khoshsima, M.; Teraoka, I.; Arnold, S. Protein detection by optical shift of a resonant microcavity. Appl. Phys. Lett. 2002, 80, 4057–4059. [Google Scholar] [CrossRef]
- Chen, Y.; Fegadolli, W.S.; Jones, W.M.; Scherer, A.; Li, M. Ultrasensitive gas-phase chemical sensing based on functionalized photonic crystal nanobeam cavities. ACS Nano 2014, 8, 522–527. [Google Scholar] [CrossRef] [PubMed]
- Duhr, S.; Braun, D. Why molecules move along a temperature gradient. Proc. Natl. Acad. Sci. USA 2006, 103, 19678–19682. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Crozier, K.B. Trapping-assisted sensing of particles and proteins using on-chip optical microcavities. ACS Nano 2013, 7, 1725–1730. [Google Scholar] [CrossRef] [PubMed]
- Hu, J. Ultra-sensitive chemical vapor detection using micro-cavity photothermal spectroscopy. Opt. Express 2010, 18, 22174–22186. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Yi, Z.; Hu, J. Double resonance 1-D photonic crystal cavities for single-molecule mid-infrared photothermal spectroscopy: Theory and design. Opt. Lett. 2012, 37, 1304–1306. [Google Scholar] [CrossRef] [PubMed]
- Ilchenko, V.S.; Paxton, A.H.; Kudryashov, A.V.; Poust, S.; Armani, A.M.; Shen, X.; Kovach, A.; Chen, D. Environmentally stable integrated ultra-high-Q optical cavities. Proc. SPIE 2018. [Google Scholar] [CrossRef]
- Grutter, K.E.; Davanço, M.I.; Balram, K.C.; Srinivasan, K. Invited Article: Tuning and stabilization of optomechanical crystal cavities through NEMS integration. APL Photonics 2018, 3, 100801. [Google Scholar] [CrossRef]
- Lu, T.; Lee, H.; Chen, T.; Herchak, S.; Kim, J.-H.; Fraser, S.E.; Flagan, R.C.; Vahala, K. High sensitivity nanoparticle detection using optical microcavities. Proc. Natl. Acad. Sci. USA 2011, 108, 5976–5979. [Google Scholar] [CrossRef] [PubMed]
- Ament, I.; Prasad, J.; Henkel, A.; Schmachtel, S.; Sonnichsen, C. Single unlabeled protein detection on individual plasmonic nanoparticles. Nano Lett. 2012, 12, 1092–1095. [Google Scholar] [CrossRef] [PubMed]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Hu, Y.-W.; Xiao, Y.-F.; Liu, Y.-C.; Gong, Q. Optomechanical sensing with on-chip microcavities. Front. Phys. 2013, 8, 475–490. [Google Scholar] [CrossRef]
- Pruessner, M.W.; Stievater, T.H.; Khurgin, J.B.; Rabinovich, W.S. Integrated waveguide-DBR microcavity opto-mechanical system. Opt. Express 2011, 19, 21904–21918. [Google Scholar] [CrossRef] [PubMed]
- Zandi, K.; Wong, B.; Zou, J.; Kruzelecky, R.V.; Jamroz, W.; Peter, Y.-A. In-plane silicon-on-insulator optical MEMS accelerometer using waveguide fabry-perot microcavity with silicon/air bragg mirrors. In Proceedings of the 2010 IEEE 23rd International Conference on Micro Electro Mechanical Systems (MEMS), Hong Kong, China, 24–28 January 2010; pp. 839–842. [Google Scholar]
- Jiang, X.; Lin, Q.; Rosenberg, J.; Vahala, K.; Painter, O. High-Q double-disk microcavities for cavity optomechanics. Opt. Express 2009, 17, 20911–20919. [Google Scholar] [CrossRef] [PubMed]
- Anetsberger, G.; Arcizet, O.; Unterreithmeier, Q.P.; Rivière, R.; Schliesser, A.; Weig, E.M.; Kotthaus, J.P.; Kippenberg, T.J. Near-field cavity optomechanics with nanomechanical oscillators. Nat. Phys. 2009, 5, 909–914. [Google Scholar] [CrossRef]
- Gavartin, E.; Verlot, P.; Kippenberg, T.J. A hybrid on-chip optomechanical transducer for ultrasensitive force measurements. Nat. Nanotechnol. 2012, 7, 509–514. [Google Scholar] [CrossRef] [PubMed]
- Gavartin, E.; Braive, R.; Sagnes, I.; Arcizet, O.; Beveratos, A.; Kippenberg, T.J.; Robert-Philip, I. Optomechanical coupling in a two-dimensional photonic crystal defect cavity. Phys. Rev. Lett. 2011, 106, 203902. [Google Scholar] [CrossRef] [PubMed]
- Safavi-Naeini, A.H.; Alegre, T.M.; Chan, J.; Eichenfield, M.; Winger, M.; Lin, Q.; Hill, J.T.; Chang, D.E.; Painter, O. Electromagnetically induced transparency and slow light with optomechanics. Nature 2011, 472, 69–73. [Google Scholar] [CrossRef] [PubMed]
- Eichenfield, M.; Chan, J.; Camacho, R.M.; Vahala, K.J.; Painter, O. Optomechanical crystals. Nature 2009, 462, 78–82. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Thillaigovindan, J.; Chen, C.-C.; Chen, X.T.; Chao, Y.-T.; Tao, S.; Xiang, W.; Yu, A.; Feng, H.; Lo, G. Si nanophotonics based cantilever sensor. Appl. Phys. Lett. 2008, 93, 113113. [Google Scholar] [CrossRef]
- Lee, C.; Radhakrishnan, R.; Chen, C.-C.; Li, J.; Thillaigovindan, J.; Balasubramanian, N. Design and modeling of a nanomechanical sensor using silicon photonic crystals. J. Light. Technol. 2008, 26, 839–846. [Google Scholar] [CrossRef]
- Thompson, J.; Zwickl, B.; Jayich, A.; Marquardt, F.; Girvin, S.; Harris, J. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature 2008, 452, 72–75. [Google Scholar] [CrossRef] [PubMed]
- Sankey, J.C.; Yang, C.; Zwickl, B.M.; Jayich, A.M.; Harris, J.G. Strong and tunable nonlinear optomechanical coupling in a low-loss system. Nat. Phys. 2010, 6, 707–712. [Google Scholar] [CrossRef]
- Srinivasan, K.; Miao, H.; Rakher, M.T.; Davanco, M.; Aksyuk, V. Optomechanical transduction of an integrated silicon cantilever probe using a microdisk resonator. Nano Lett. 2011, 11, 791–797. [Google Scholar] [CrossRef] [PubMed]
- Hryciw, A.C.; Barclay, P.E. Optical design of split-beam photonic crystal nanocavities. Opt. Lett. 2013, 38, 1612–1614. [Google Scholar] [CrossRef] [PubMed]
- Lipfert, J.; Kerssemakers, J.W.; Jager, T.; Dekker, N.H. Magnetic torque tweezers: Measuring torsional stiffness in DNA and RecA-DNA filaments. Nat. Methods 2010, 7, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Weiss, T.; Nunnenkamp, A. Quantum limit of laser cooling in dispersively and dissipatively coupled optomechanical systems. Phys. Rev. A 2013, 88, 023850. [Google Scholar] [CrossRef]
- Anetsberger, G.; Gavartin, E.; Arcizet, O.; Unterreithmeier, Q.P.; Weig, E.M.; Gorodetsky, M.L.; Kotthaus, J.P.; Kippenberg, T.J. Measuring nanomechanical motion with an imprecision below the standard quantum limit. Phys. Rev. A 2010, 82, 061804. [Google Scholar] [CrossRef]
- Chan, J.; Eichenfield, M.; Camacho, R.; Painter, O. Optical and mechanical design of a “zipper” photonic crystal optomechanical cavity. Opt. Express 2009, 17, 3802–3817. [Google Scholar] [CrossRef] [PubMed]
- Kippenberg, T.J.; Vahala, K.J. Cavity opto-mechanics. Opt. Express 2007, 15, 17172–17205. [Google Scholar] [CrossRef] [PubMed]
- Fleming, W.J. Overview of automotive sensors. IEEE Sens. J. 2001, 1, 296–308. [Google Scholar] [CrossRef]
- Li, H.-N.; Li, D.-S.; Song, G.-B. Recent applications of fiber optic sensors to health monitoring in civil engineering. Eng. Struct. 2004, 26, 1647–1657. [Google Scholar] [CrossRef]
- Jolesz, F.A. MRI-guided focused ultrasound surgery. Annu. Rev. Med. 2009, 60, 417–430. [Google Scholar] [CrossRef] [PubMed]
- Woo, X.Y.; Nagy, Z.K.; Tan, R.B.; Braatz, R.D. Adaptive concentration control of cooling and antisolvent crystallization with laser backscattering measurement. Cryst. Growth Des. 2008, 9, 182–191. [Google Scholar] [CrossRef]
- Strouse, G. Standard platinum resistance thermometer calibrations from the Ar TP to the Ag FP. NIST Spec. Publ. 2008, 250, 81. [Google Scholar] [CrossRef]
- Kim, G.-D.; Lee, H.-S.; Park, C.-H.; Lee, S.-S.; Lim, B.T.; Bae, H.K.; Lee, W.-G. Silicon photonic temperature sensor employing a ring resonator manufactured using a standard CMOS process. Opt. Express 2010, 18, 22215–22221. [Google Scholar] [CrossRef] [PubMed]
- Rabiei, P. Electro-Optic and Thermo-Optic Polymer Micro-Ring Resonators and Their Applications; University of Southern California: Los Angeles, CA, USA, 2002. [Google Scholar]
- Klimov, N.N.; Mittal, S.; Berger, M.; Ahmed, Z. On-chip silicon waveguide Bragg grating photonic temperature sensor. Opt. Lett. 2015, 40, 3934–3936. [Google Scholar] [CrossRef] [PubMed]
- Kwon, M.-S.; Steier, W.H. Microring-resonator-based sensor measuring both the concentration and temperature of a solution. Opt. Express 2008, 16, 9372–9377. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-T.; Yu, M. Cascaded ring resonator-based temperature sensor with simultaneously enhanced sensitivity and range. Opt. Express 2016, 24, 9501–9510. [Google Scholar] [CrossRef] [PubMed]
- Klimov, N.N.; Purdy, T.; Ahmed, Z. Fabrication and characterization of on-chip integrated silicon photonic Bragg grating and photonic crystal cavity thermometers. In Proceedings of the 2015 TechConnect World Innovation Conference, Washington, DC, USA, 15–18 June 2015. [Google Scholar]
- Klimov, N.N.; Purdy, T.P.; Ahmed, Z. On-Chip Integrated Silicon Photonic Thermometers. Sens. Transducers J. 2015, 191, 67–71. [Google Scholar]
- Teng, J.; Dumon, P.; Bogaerts, W.; Zhang, H.; Jian, X.; Han, X.; Zhao, M.; Morthier, G.; Baets, R. Athermal Silicon-on-insulator ring resonators by overlaying a polymer cladding on narrowed waveguides. Opt. Express 2009, 17, 14627–14633. [Google Scholar] [CrossRef] [PubMed]
- Desiatov, B.; Goykhman, I.; Levy, U. Parabolic tapered photonic crystal cavity in silicon. Appl. Phys. Lett. 2012, 100, 041112. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, S.; Zhang, S.; Liu, P.; Shi, Y. High-Q and High-Sensitivity Photonic Crystal Cavity Sensor. IEEE Photonics J. 2015, 7, 1–6. [Google Scholar] [CrossRef]
- Ahn, B.-H.; Kang, J.-H.; Kim, M.-K.; Song, J.-H.; Min, B.; Kim, K.-S.; Lee, Y.-H. One-dimensional parabolic-beam photonic crystal laser. Opt. Express 2010, 18, 5654–5660. [Google Scholar] [CrossRef] [PubMed]
- Karnutsch, C.; Smith, C.L.; Graham, A.; Tomljenovic-Hanic, S.; McPhedran, R.; Eggleton, B.J.; O’Faolain, L.; Krauss, T.F.; Xiao, S.; Mortensen, N.A. Temperature stabilization of optofluidic photonic crystal cavities. Appl. Phys. Lett. 2009, 94, 231114. [Google Scholar] [CrossRef]
- Hagino, H.; Takahashi, Y.; Tanaka, Y.; Asano, T.; Noda, S. Effects of fluctuation in air hole radii and positions on optical characteristics in photonic crystal heterostructure nanocavities. Phys. Rev. B 2009, 79, 085112. [Google Scholar] [CrossRef]
- Lim, A.E.-J.; Liow, T.-Y.; Song, J.-F.; Yu, M.-B.; Li, C.; Tu, X.-G.; Chen, K.-K.; Tern, R.P.-C.; Huang, Y.; Luo, X.-S. Path to Silicon Photonics Commercialization: The Foundry Model Discussion. In Silicon Photonics III; Springer: Berlin, Germany, 2016; pp. 191–215. [Google Scholar]
- O’Brien, P.; Carrol, L.; Eason, C.; Lee, J.S. Packaging of silicon photonic devices. In Silicon Photonics III; Springer: Berlin, Germany, 2016; pp. 217–236. [Google Scholar]





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, Q.; Xia, J.; Lee, C.; Zhou, G. Applications of Photonic Crystal Nanobeam Cavities for Sensing. Micromachines 2018, 9, 541. https://doi.org/10.3390/mi9110541
Qiao Q, Xia J, Lee C, Zhou G. Applications of Photonic Crystal Nanobeam Cavities for Sensing. Micromachines. 2018; 9(11):541. https://doi.org/10.3390/mi9110541
Chicago/Turabian StyleQiao, Qifeng, Ji Xia, Chengkuo Lee, and Guangya Zhou. 2018. "Applications of Photonic Crystal Nanobeam Cavities for Sensing" Micromachines 9, no. 11: 541. https://doi.org/10.3390/mi9110541
APA StyleQiao, Q., Xia, J., Lee, C., & Zhou, G. (2018). Applications of Photonic Crystal Nanobeam Cavities for Sensing. Micromachines, 9(11), 541. https://doi.org/10.3390/mi9110541






