Accurate Extraction of the Self-Rotational Speed for Cells in an Electrokinetics Force Field by an Image Matching Algorithm
Abstract
:1. Introduction
2. Theory
3. Materials and Methods
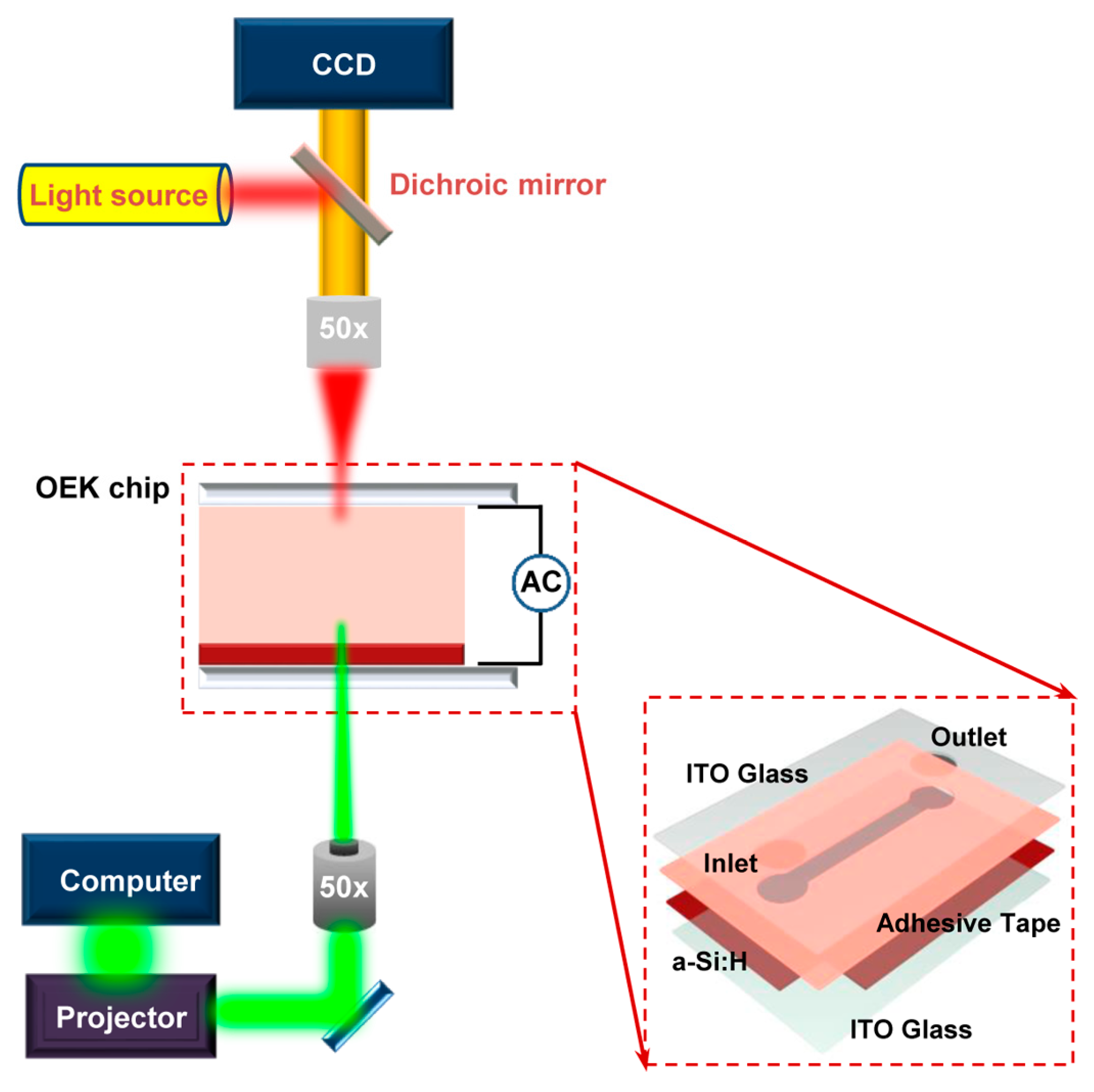
3.1. Experimental Setup and Working Principle
3.2. Cell Preparation
3.3. Self-Rotational Speed Extraction
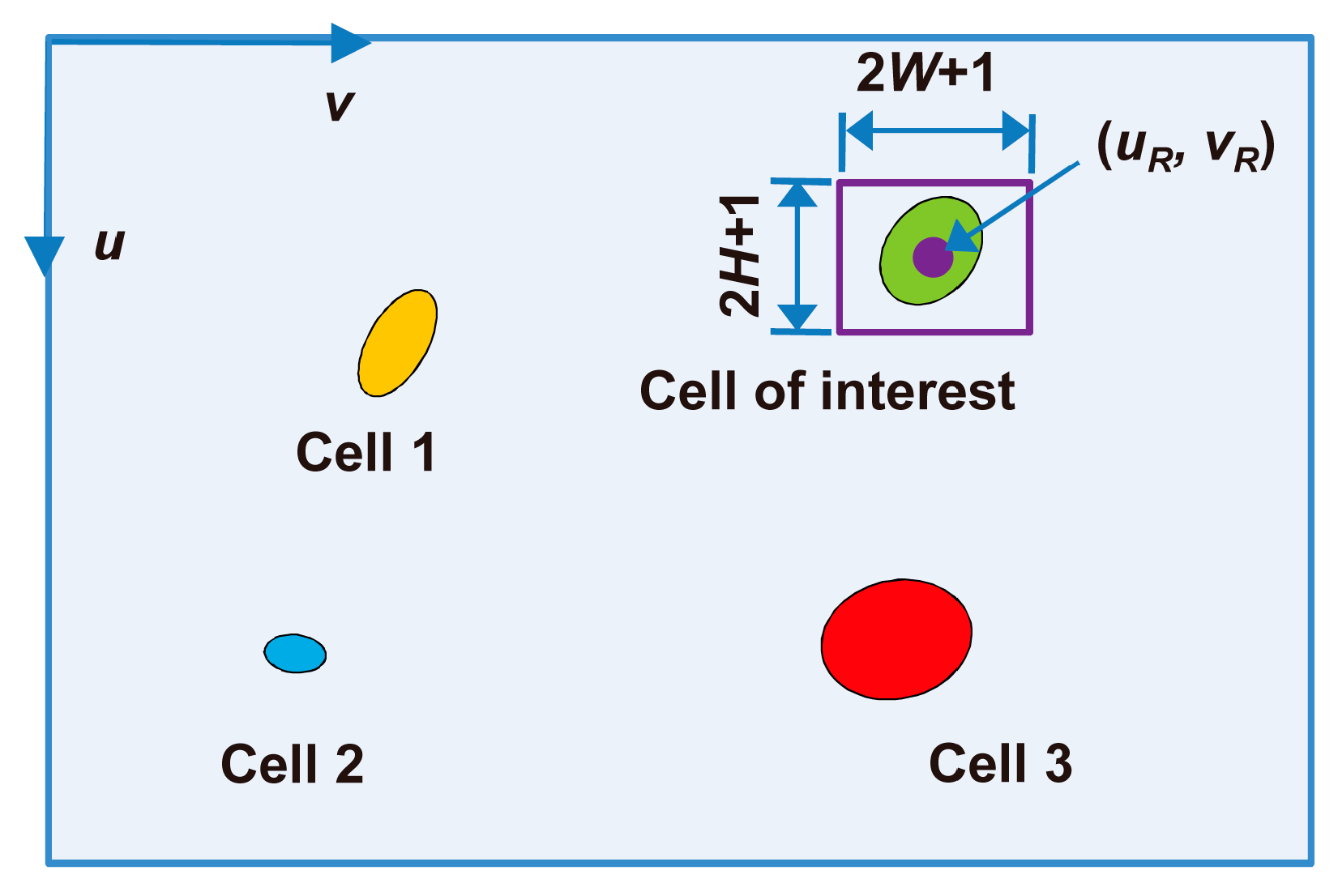
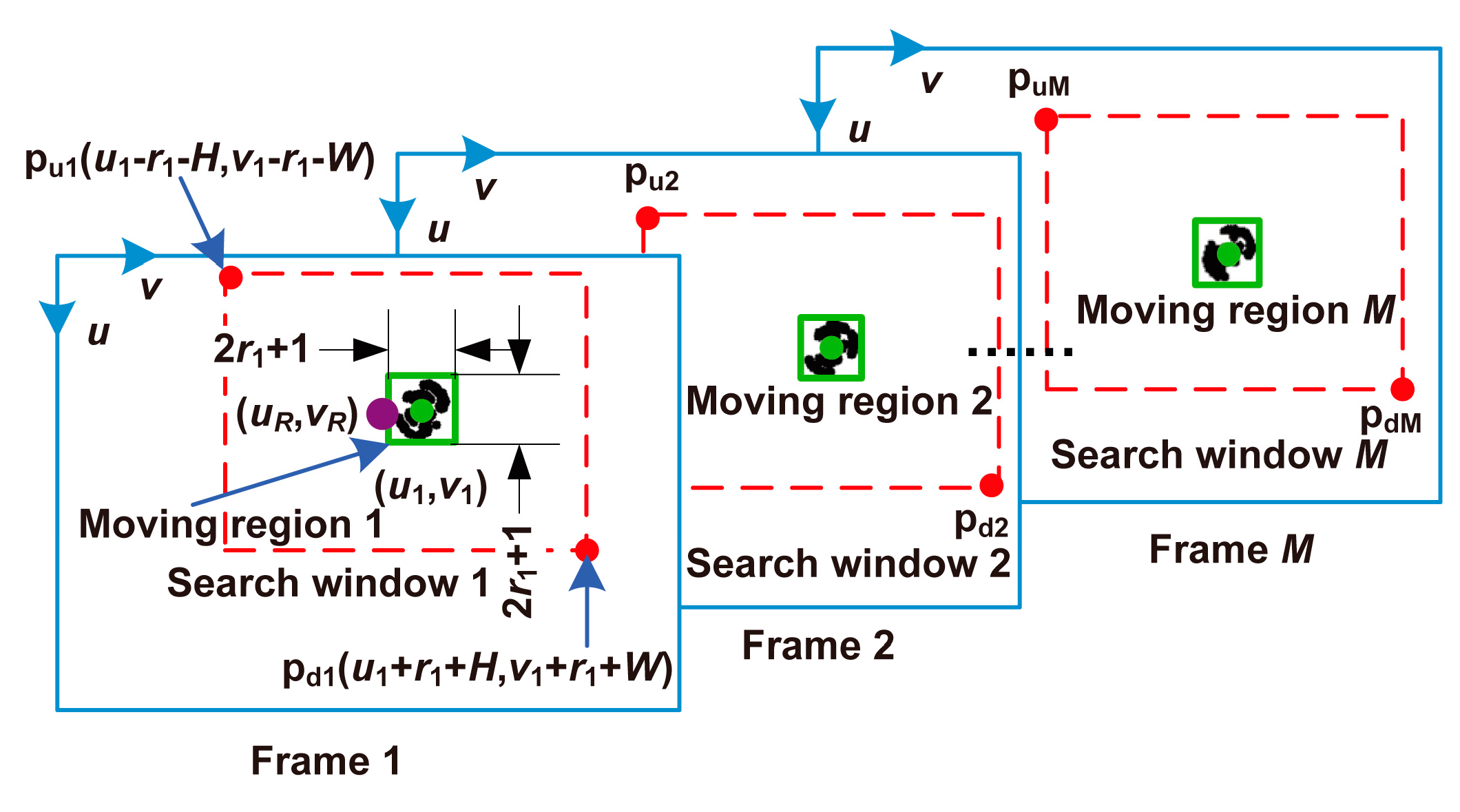
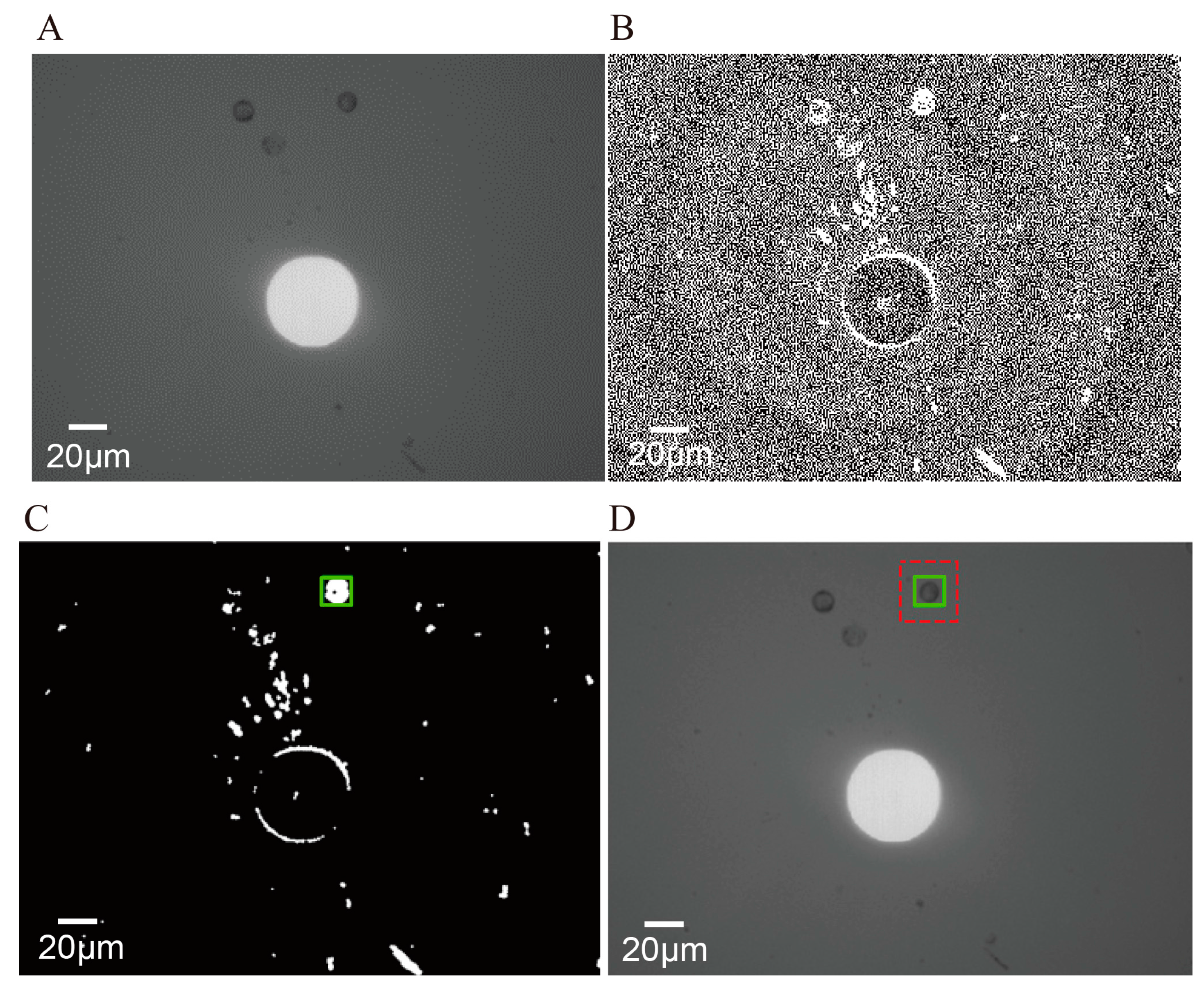
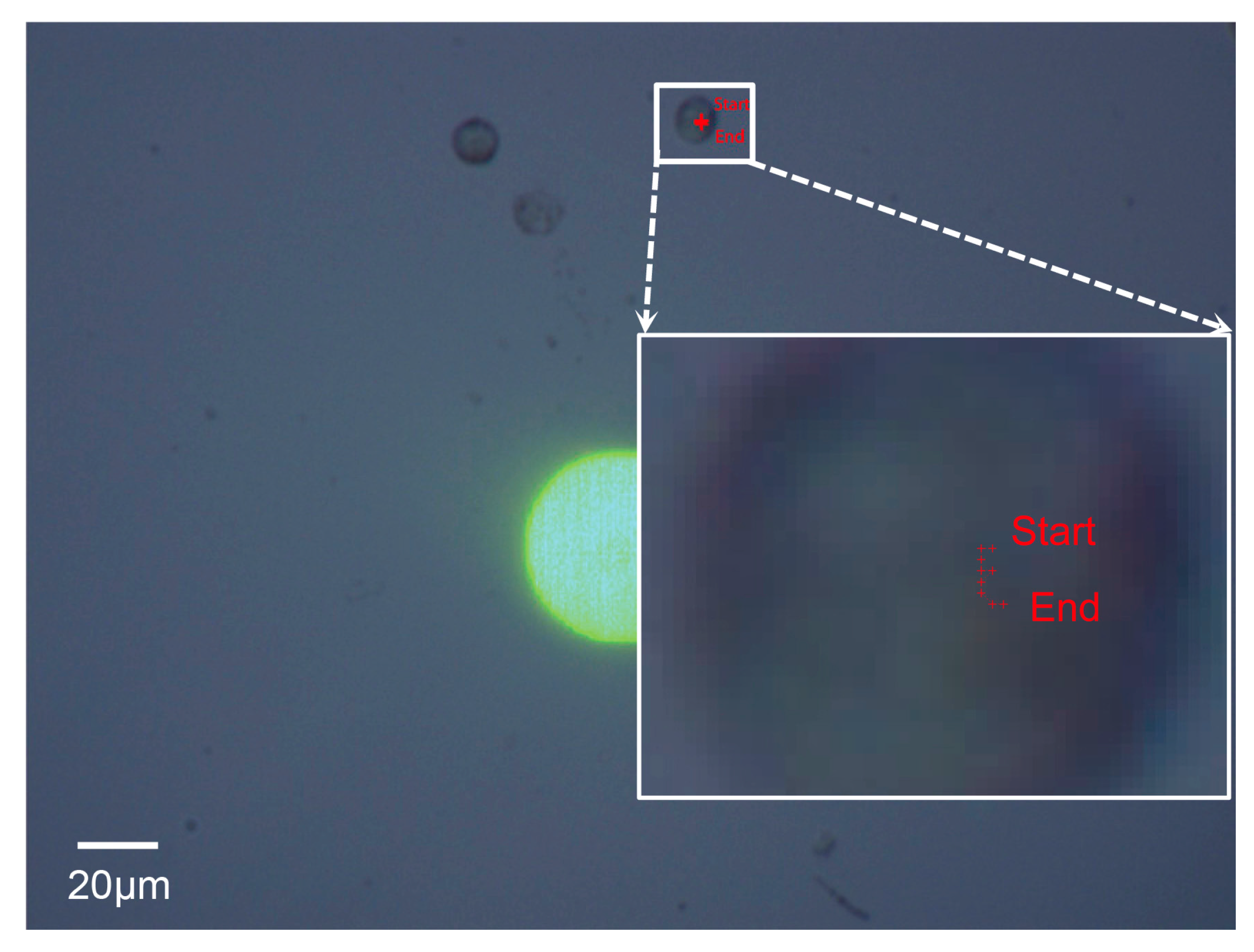
3.3.1. Selection of a Cell of Interest in the First Frame
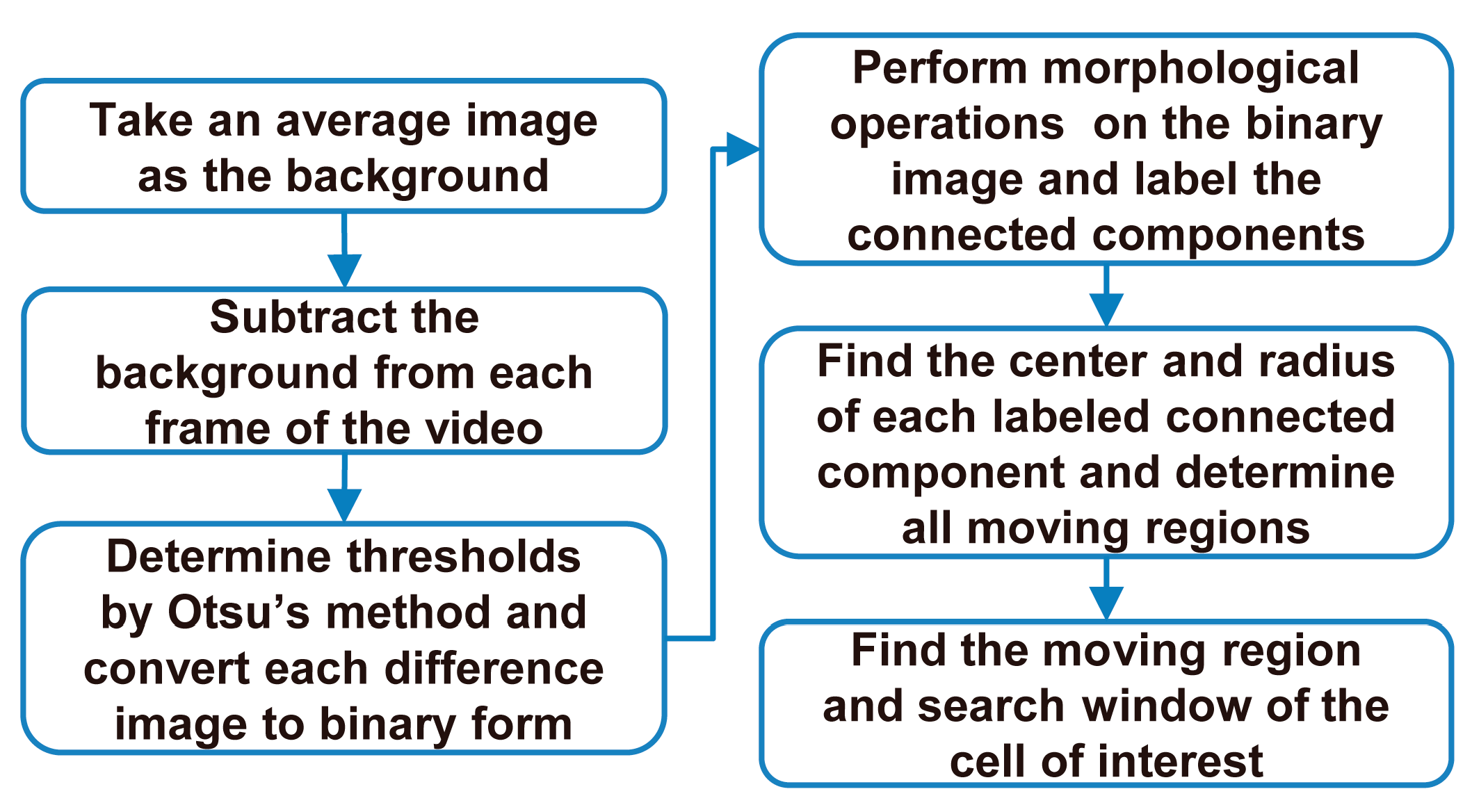
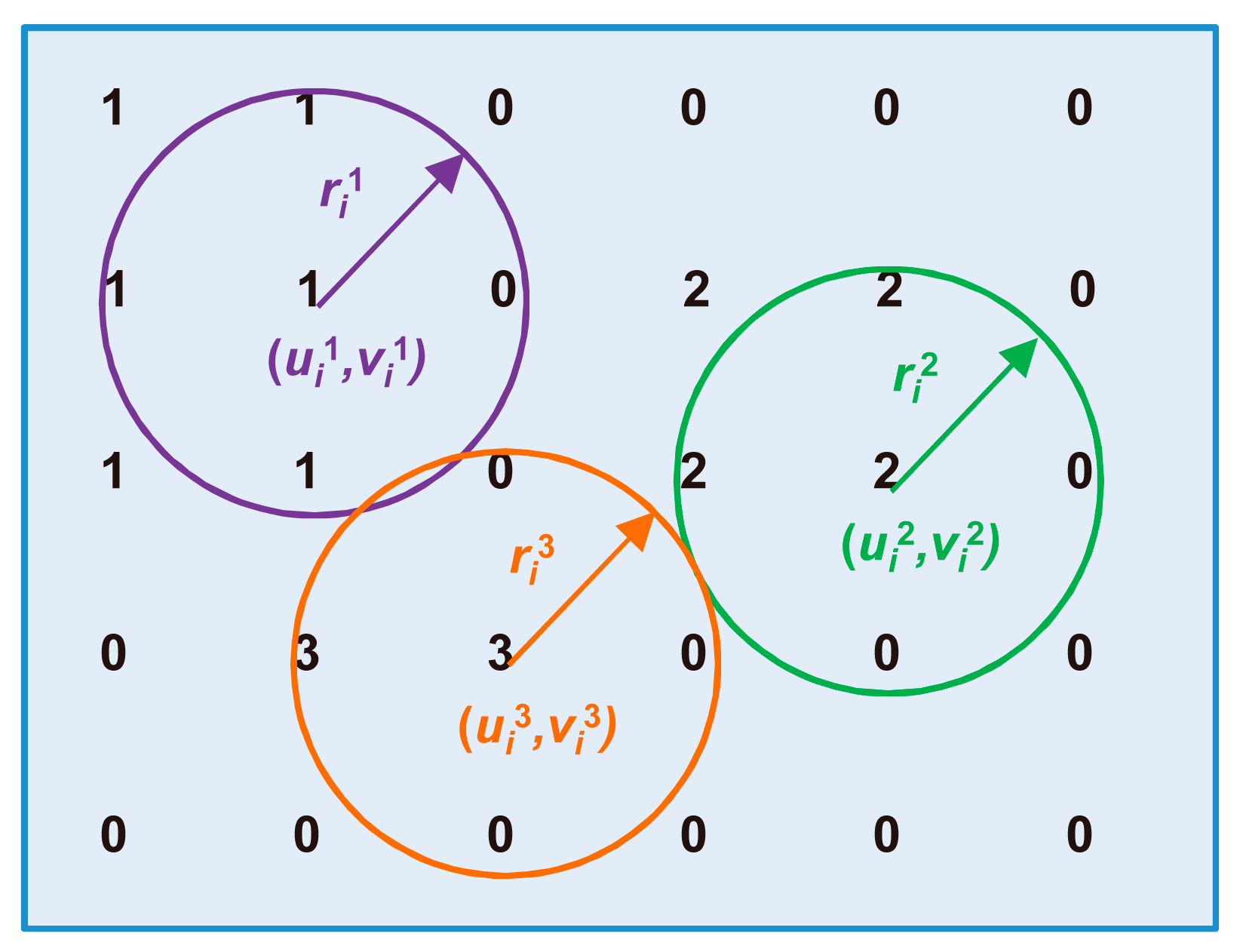
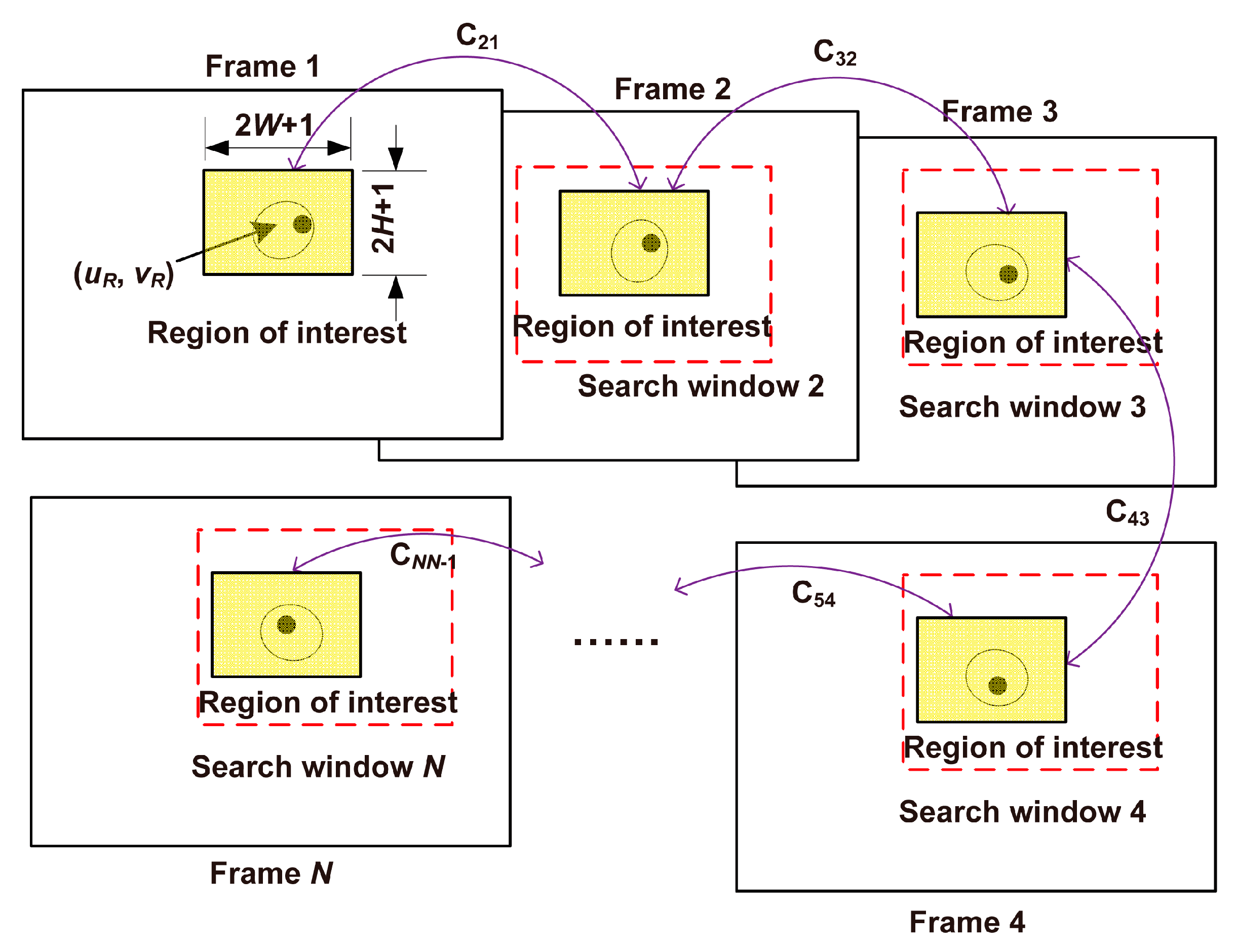
3.3.2. Tracking the Cell of Interest
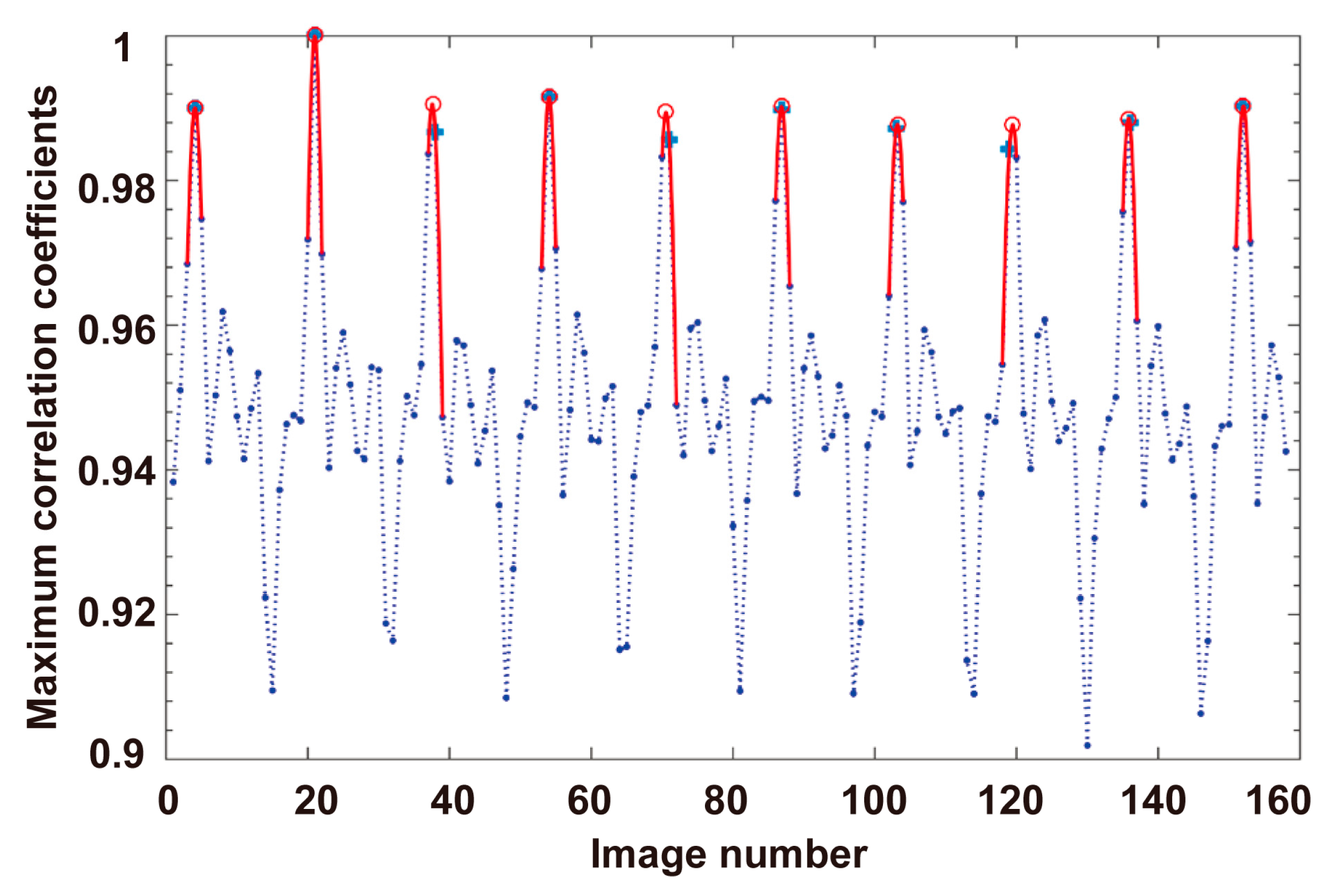
3.3.3. Determination of the Reference Frame
3.3.4. Calculation of the Self-Rotational Speed
4. Results and Discussions
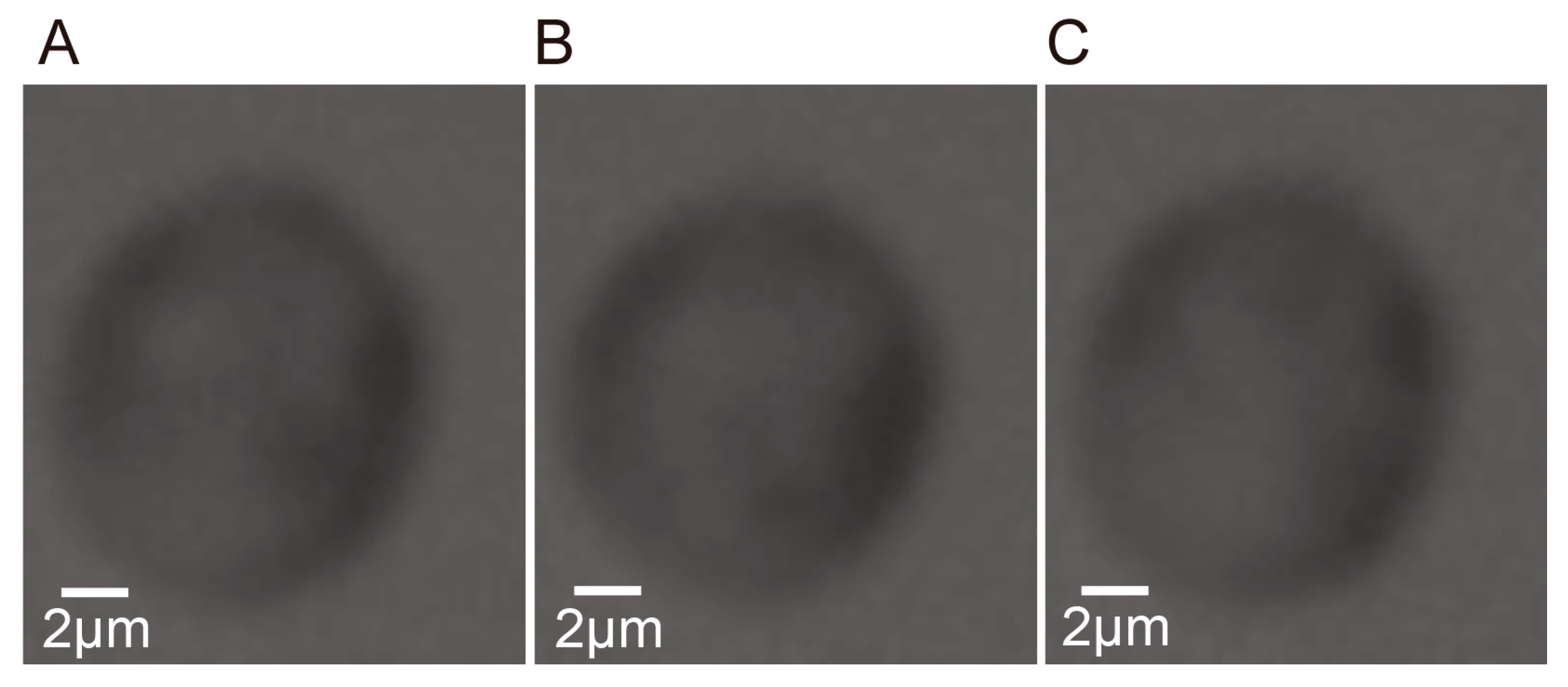
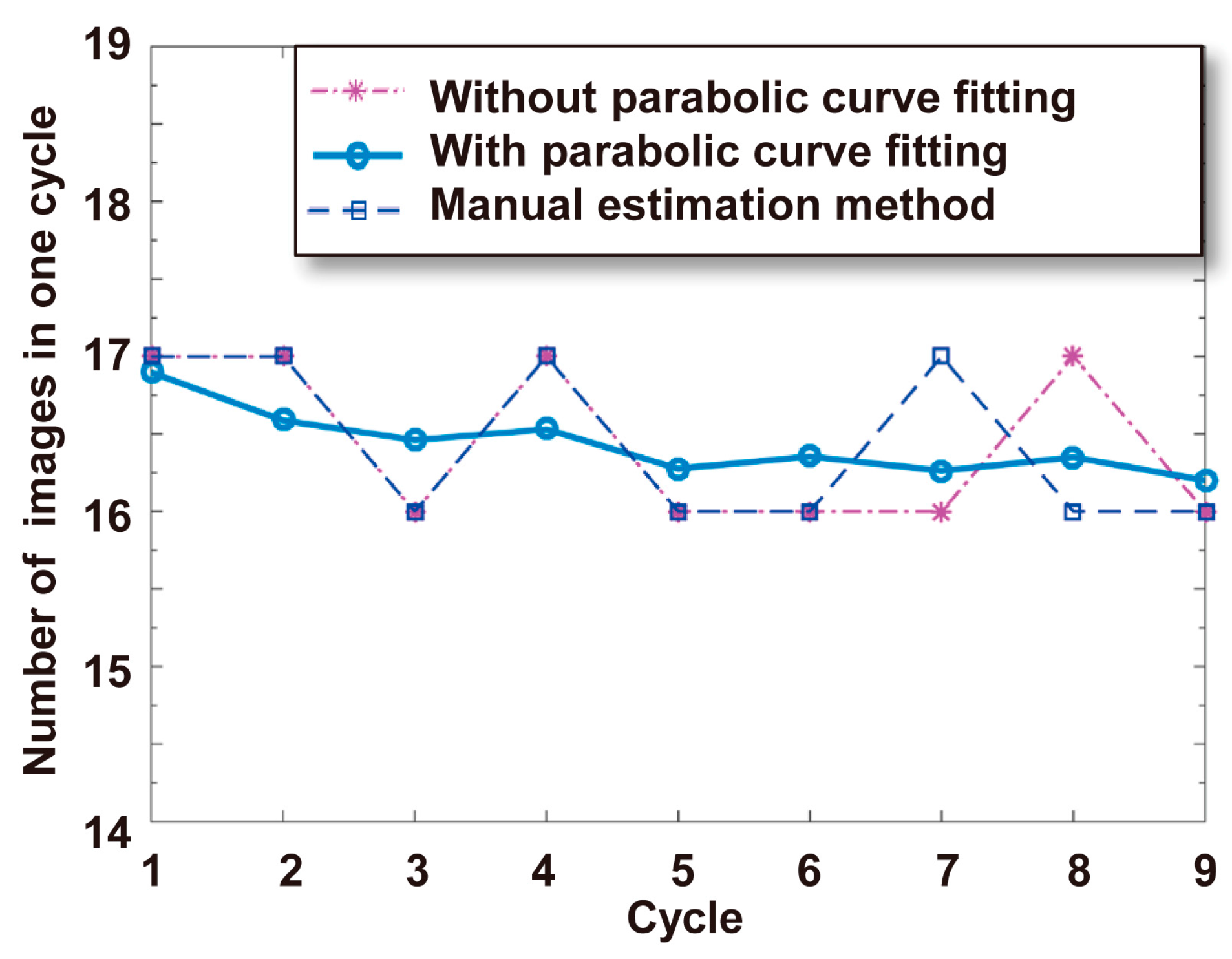
4.1. Self-Rotational Speed of a Raji Cell under Given AC Bias Parameters
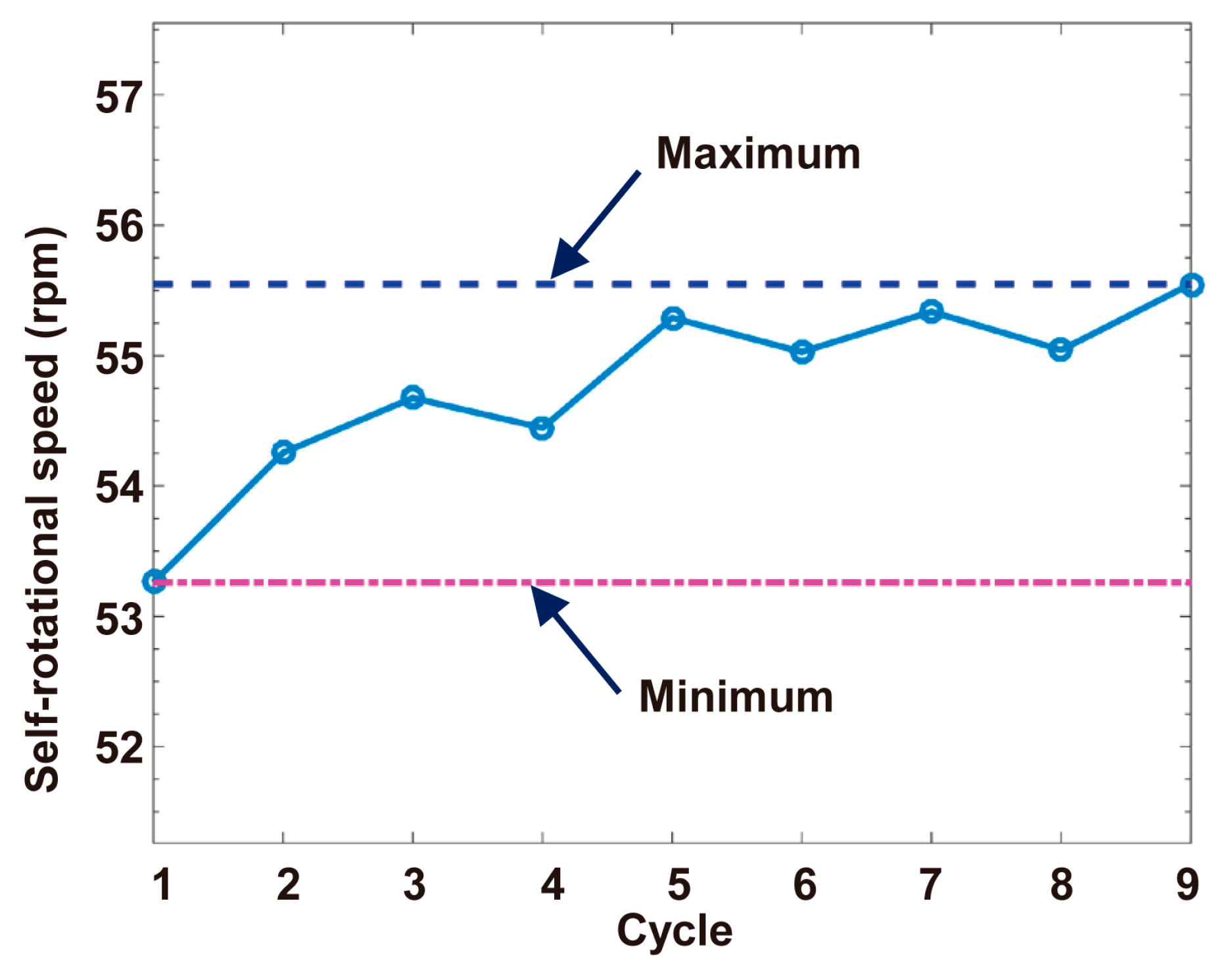
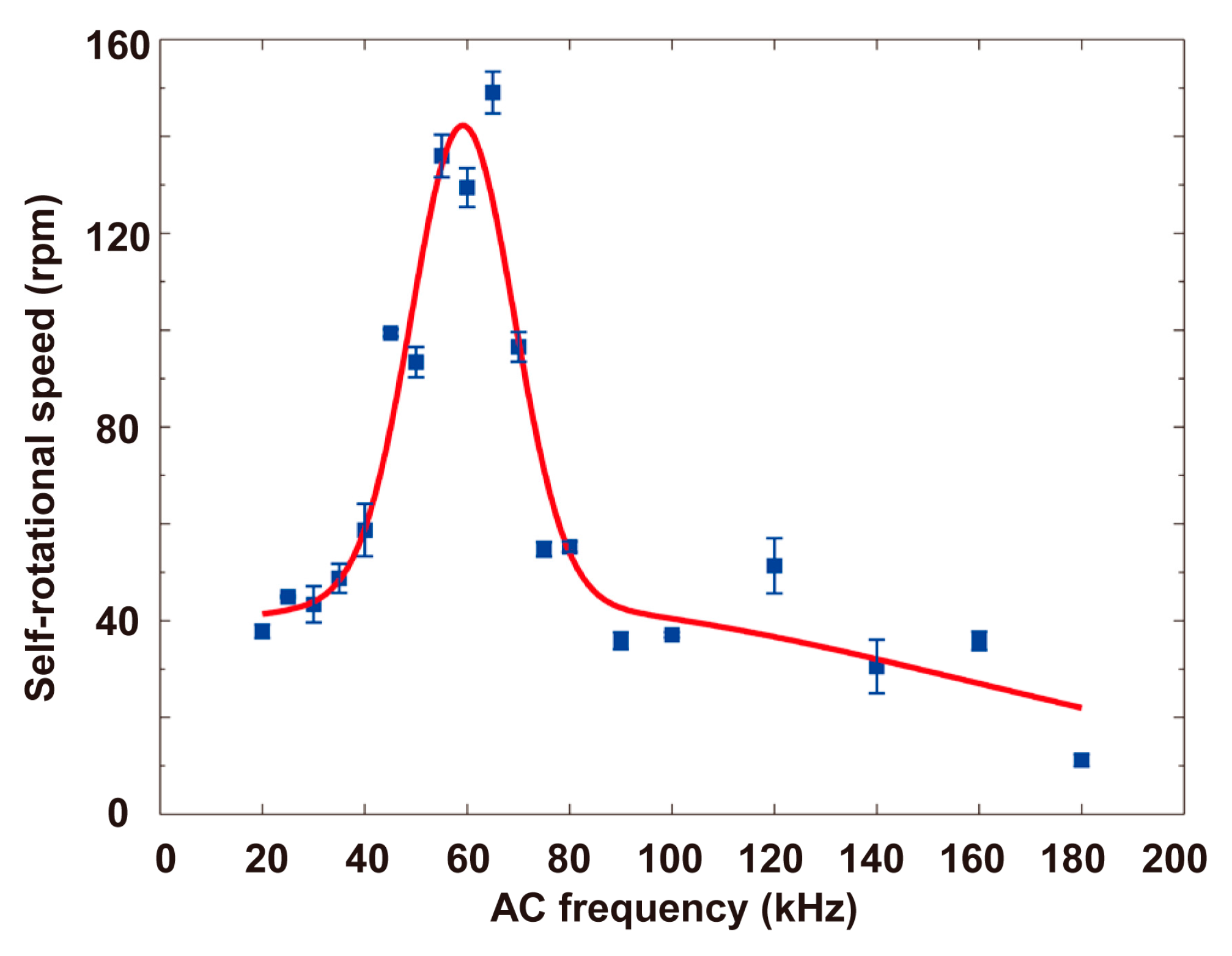
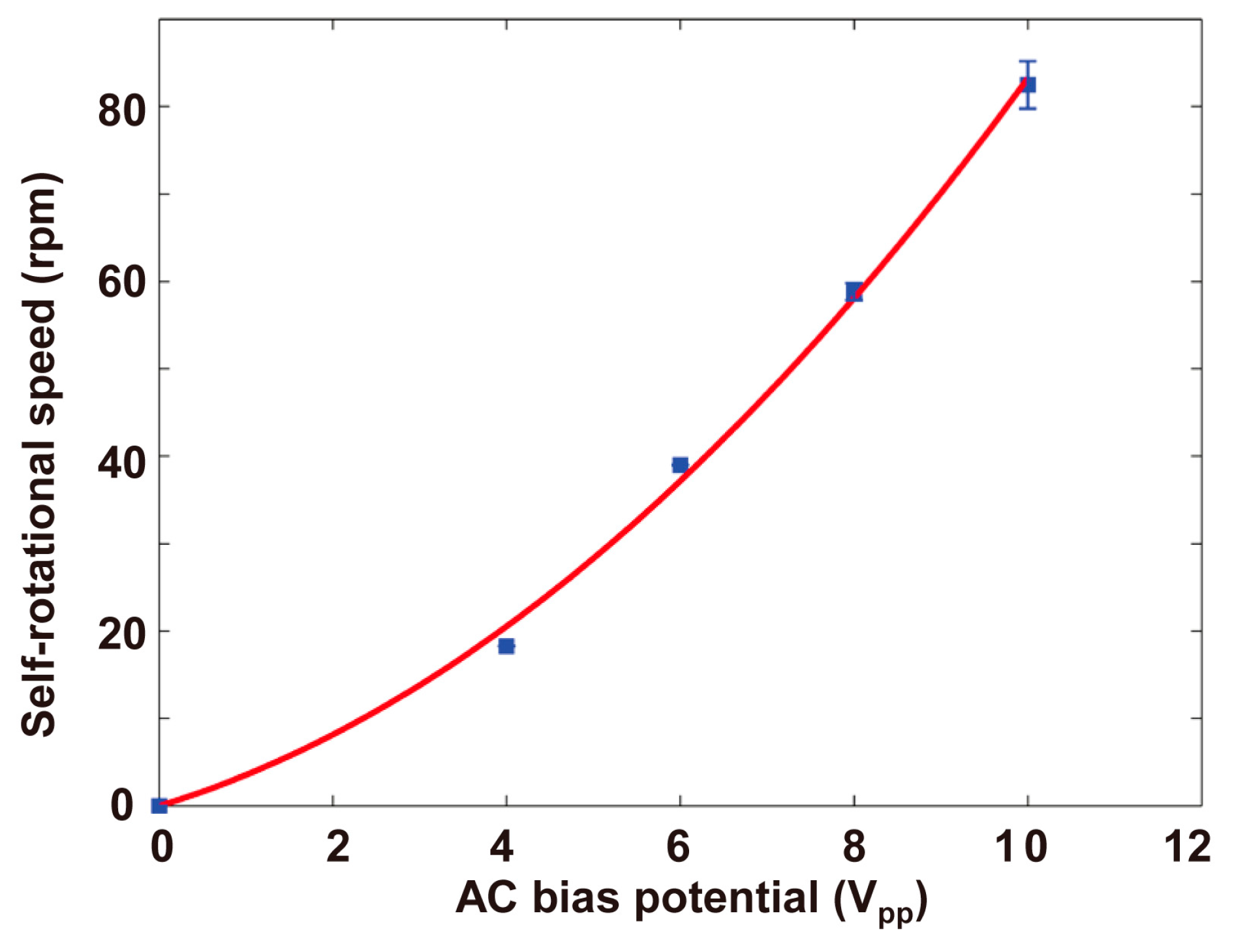
4.2. Self-Rotational Speed of Raji Cells under Various AC Bias Parameters
4.3. Discussions
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kodandaramaiah, S.B.; Franzesi, G.T.; Chow, B.Y.; Boyden, E.S.; Forest, C.R. Automated whole-cell patch-clamp electrophysiology of neurons in vivo. Nat. Methods 2012, 9, 585–587. [Google Scholar] [CrossRef] [PubMed]
- Khan, Z.S.; Vanapalli, S.A. Probing the mechanical properties of brain cancer cells using a microfluidic cell squeezer device. Biomicrofluidics 2013, 7, 11806. [Google Scholar] [CrossRef] [PubMed]
- Adams, T.N.G.; Turner, P.A.; Janorkar, A.V.; Zhao, F.; Minerick, A.R. Characterizing the dielectric properties of human mesenchymal stem cells and the effects of charged elastin-like polypeptide copolymer treatment. Biomicrofluidics 2014, 8, 054109. [Google Scholar] [CrossRef] [PubMed]
- Jain, R.K.; Martin, J.D.; Stylianopoulos, T. The role of mechanical forces in tumor growth and therapy. Annu. Rev. Biomed. Eng. 2014, 16, 321–346. [Google Scholar] [CrossRef] [PubMed]
- Swaminathan, V.; Mythreye, K.; O’Brien, E.T.; Berchuck, A.; Blobe, G.C.; Superfine, R. Mechanical stiffness grades metastatic potential in patient tumor cells and in cancer cell lines. Cancer Res. 2011, 71, 5075–5080. [Google Scholar] [CrossRef] [PubMed]
- Bagnaninchi, P.O.; Drummond, N. Real-time label-free monitoring of adipose-derived stem cell differentiation with electric cell-substrate impedance sensing. Proc. Natl. Acad. Sci. USA 2011, 108, 6462–6467. [Google Scholar] [CrossRef] [PubMed]
- González-Cruz, R.D.; Fonseca, V.C.; Darling, E.M. Cellular mechanical properties reflect the differentiation potential of adipose-derived mesenchymal stem cells. Proc. Natl. Acad. Sci. USA 2012, 109, 1523–1529. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zheng, Y.; Tan, Q.; Shojaei-Baghini, E.; Zhang, Y.L.; Li, J.; Prasad, P.; You, L.; Wu, X.Y.; Sun, Y. Classification of cell types using a microfluidic device for mechanical and electrical measurement on single cells. Lab. Chip 2011, 11, 3174. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Lanry Yung, L.Y.; Lim, K.M. Dielectrophoretic capture voltage spectrum for measurement of dielectric properties and separation of cancer cells. Biomicrofluidics 2012, 6, 14113. [Google Scholar] [CrossRef] [PubMed]
- Salmanzadeh, A.; Sano, M.B.; Gallo-Villanueva, R.C.; Roberts, P.C.; Schmelz, E.M.; Davalos, R.V. Investigating dielectric properties of different stages of syngeneic murine ovarian cancer cells. Biomicrofluidics 2013, 7, 011809. [Google Scholar] [CrossRef] [PubMed]
- Han, S.I.; Joo, Y.D.; Han, K.H. An electrorotation technique for measuring the dielectric properties of cells with simultaneous use of negative quadrupolar dielectrophoresis and electrorotation. Analyst 2013, 138, 1529–1537. [Google Scholar] [CrossRef] [PubMed]
- El-Gaddar, A.; Frénéa-Robin, M.; Voyer, D.; Aka, H.; Haddour, N.; Krähenbühl, L. Assessment of 0.5 T static field exposure effect on yeast and hek cells using electrorotation. Biophys. J. 2013, 104, 1805–1811. [Google Scholar] [CrossRef] [PubMed]
- Arnold, W.M.; Zimmermann, U. Electro-rotation: Development of a technique for dielectric measurements on individual cells and particles. J. Electrostat. 1988, 21, 151–191. [Google Scholar] [CrossRef]
- Cen, E.G.; Dalton, C.; Li, Y.; Adamia, S.; Pilarski, L.M.; Kaler, K.V.I.S. A combined dielectrophoresis, traveling wave dielectrophoresis and electrorotation microchip for the manipulation and characterization of human malignant cells. J. Microbiol. Meth. 2004, 58, 387–401. [Google Scholar] [CrossRef] [PubMed]
- Sancho, M.; Martínez, G.; Muñoz, S.; Sebastián, J.L.; Pethig, R. Interaction between cells in dielectrophoresis and electrorotation experiments. Biomicrofluidics 2010, 4, 022802. [Google Scholar] [CrossRef] [PubMed]
- Trainito, C.I.; Bayart, E.; Subra, F.; Français, O.; Le Pioufle, B. The electrorotation as a tool to monitor the dielectric properties of spheroid during the permeabilization. J. Membr. Biol. 2016, 249, 593–600. [Google Scholar] [CrossRef] [PubMed]
- Quincke, G. Ueber rotationen im constanten electrischen felde. Ann. Phys. 1896, 295, 417–486. [Google Scholar] [CrossRef]
- Pohl, H.A.; Crane, J.S. Dielectrophoresis of cells. Biophys. J. 1971, 11, 711–727. [Google Scholar] [CrossRef]
- Chuang, C.H.; Hsu, Y.M.; Yeh, C.C. The effects of nanoparticles uptaken by cells on electrorotation. Electrophoresis 2009, 30, 1449–1456. [Google Scholar] [CrossRef] [PubMed]
- De Gasperis, G.; Wang, X.B.; Yang, J.; Becker, F.F.; Gascoyne, P.R.C. Automated electrorotation: Dielectric characterization of living cells by real-time motion estimation. Meas. Sci. Technol. 1998, 9, 518. [Google Scholar] [CrossRef]
- Huang, C.; Chen, A.; Guo, M.; Yu, J. Membrane dielectric responses of bufalin-induced apoptosis in hl-60 cells detected by an electrorotation chip. Biotechnol. Lett. 2007, 29, 1307–1313. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, M.; Ki Cheung, C.W.; Liang, W.; Mai, J.D.; Keung, L.W.; Jung, L.W. Inducing self-rotation of cells with natural and artificial melanin in a linearly polarized alternating current electric field. Biomicrofluidics 2013, 7, 054112. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Ouyang, M.; Mai, J.; Li, W.J.; Liu, W.K. Automated rotation rate tracking of pigmented cells by a customized block-matching algorithm. J. Lab. Autom. 2013, 18, 161–170. [Google Scholar] [CrossRef] [PubMed]
- Chau, L.H.; Liang, W.; Cheung, F.W.K.; Liu, W.K.; Li, W.J.; Chen, S.C.; Lee, G.B. Self-rotation of cells in an irrotational ac e-field in an opto-electrokinetics chip. PLoS ONE 2013, 8, e51577. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Liang, W.; Zhang, G.; Mai, J.D.; Liu, L.; Lee, G.B.; Li, W.J. Distinguishing cells by their first-order transient motion response under an optically induced dielectrophoretic force field. Appl. Phys. Lett. 2013, 103, 183702. [Google Scholar] [CrossRef]
- Liang, W.; Zhao, Y.; Liu, L.; Wang, Y.; Dong, Z.; Li, W.J.; Lee, G.B.; Xiao, X.; Zhang, W. Rapid and label-free separation of burkitt’s lymphoma cells from red blood cells by optically-induced electrokinetics. PLoS ONE 2014, 9, e90827. [Google Scholar] [CrossRef] [PubMed]
- Liang, W.; Zhang, K.; Yang, X.; Liu, L.; Yu, H.; Zhang, W. Distinctive translational and self-rotational motion of lymphoma cells in an optically induced non-rotational alternating current electric field. Biomicrofluidics 2015, 9, 014121. [Google Scholar] [CrossRef] [PubMed]
- Liang, W.; Wang, S.; Dong, Z.; Lee, G.-B.; Li, W.J. Optical spectrum and electric field waveform dependent optically-induced dielectrophoretic (ODEP) micro manipulation. Micromachines 2012, 3, 492–508. [Google Scholar] [CrossRef]
- Liang, W.; Liu, L.; Lai, S.H.; Wang, Y.; Lee, G.-B.; Li, W.J. Rapid assembly of gold nanoparticle-based microstructures using optically-induced electrokinetics. Opt. Mater. Express 2014, 4, 2368–2380. [Google Scholar] [CrossRef]
- Huang, S.B.; Wu, M.H.; Lin, Y.H.; Hsieh, C.H.; Yang, C.L.; Lin, H.C.; Tseng, C.P.; Lee, G.-B. High-purity and label-free isolation of circulating tumor cells (CTCs) in a microfluidic platform by using optically-induced-dielectrophoretic (ODEP) force. Lab. Chip 2013, 13, 1371–1383. [Google Scholar] [CrossRef] [PubMed]
- Jone, T.B. Electromechanics of Particles; Cambridge University Press: New York, NY, USA, 1995; pp. 17–20. [Google Scholar]
- Mischel, M.; Lamprecht, I. Rotation of cells in nonuniform alternating fields. J. Biol. Phys. 1983, 11, 43–44. [Google Scholar] [CrossRef]
- Turcu, I. Electric field induced rotation of spheres. J. Phys. A-Math. Gen. 1987, 20, 3301–3307. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. St. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Torino, S.; Iodice, M.; Rendina, I.; Coppola, G.; Schonbrun, E. A microfluidic approach for inducing cell rotation by means of hydrodynamic forces. Sensors 2016, 16, 1326. [Google Scholar] [CrossRef] [PubMed]
- Soffe, R.; Tang, S.Y.; Baratchi, S.; Nahavandi, S.; Nasabi, M.; Cooper, L.M.; Mitchell, A.; Khoshmanesh, K. Controlled rotation and vibration of patterned cell clusters using dielectrophoresis. Anal. Chem. 2015, 87, 2389–2395. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Feng, C.; Muruganandam, R.; Ang, W.T.; Tan, W.Y.M.; Latt, W.T. Three-dimensional cell rotation with fluidic flow-controlled cell manipulating device. IEEE/ASME Trans. Mech. 2016, 21, 1995–2003. [Google Scholar] [CrossRef]
- Huang, L.; Tu, L.; Zeng, X.; Mi, L.; Li, X.; Wang, W. Study of a microfluidic chip integrating single cell trap and 3D stable rotation manipulation. Micromachines 2016, 7, 141. [Google Scholar] [CrossRef]
- Shetty, R.M.; Myers, J.R.; Sreenivasulu, M.; Teller, W.; Vela, J.; Houkal, J.; Chao, S.-H.; Johnson, R.H.; Kelbauskas, L.; Wang, H.; et al. Characterization and comparison of three microfabrication methods to generate out-of-plane microvortices for single cell rotation and 3D imaging. J. Micromech. Microeng. 2016, 27, 015004. [Google Scholar] [CrossRef]
- Ahmed, D.; Ozcelik, A.; Bojanala, N.; Nama, N.; Upadhyay, A.; Chen, Y.; Hanna-Rose, W.; Huang, T.J. Rotational manipulation of single cells and organisms using acoustic waves. Nat. Commun. 2016, 7, 11085. [Google Scholar] [CrossRef] [PubMed]
- Bernard, I.; Doinikov, A.A.; Marmottant, P.; Rabaud, D.; Poulain, C.; Thibault, P. Controlled rotation and translation of spherical particles or living cells by Surface Acoustic Waves. Lab. Chip 2017, 17, 2470–2480. [Google Scholar] [CrossRef] [PubMed]
- Läubli, N.; Shamsudhin, N.; Ahmed, D.; Nelson, B.J. Controlled three-dimensional rotation of single cells using acoustic waves. Procedia CIRP 2017, 65, 93–98. [Google Scholar] [CrossRef]
- Ozcelik, A.; Nama, N.; Huang, P.H.; Kaynak, M.; McReynolds, M.R.; Hanna-Rose, W.; Huang, T.H. Acoustofluidic rotational manipulation of cells and organisms using oscillating solid structures. Small 2016, 12, 5120–5125. [Google Scholar] [CrossRef] [PubMed]
- Habaza, M.; Gilboa, B.; Roichman, Y.; Shaked, N.T. Tomographic phase microscopy with 180 rotation of live cells in suspension by holographic optical tweezers. Opt. Lett. 2015, 40, 1881–1884. [Google Scholar] [CrossRef] [PubMed]
- Xie, M.; Mills, J.K.; Wang, Y.; Mahmoodi, M.; Sun, D. Automated translational and rotational control of biological cells with a robot-aided optical tweezers manipulation system. IEEE Trans. Autom. Sci. Eng. 2016, 13, 543–551. [Google Scholar] [CrossRef]
- Cao, B.; Kelbauskas, L.; Chan, S.; Shetty, R.M.; Smith, D.; Meldrum, D.R. Rotation of single live mammalian cells using dynamic holographic optical tweezers. Opt. Laser. Eng. 2017, 92, 70–75. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Niu, X.; Liu, Z.; Zhao, Y.; Zhang, G.; Liang, W.; Li, W.J. Accurate Extraction of the Self-Rotational Speed for Cells in an Electrokinetics Force Field by an Image Matching Algorithm. Micromachines 2017, 8, 282. https://doi.org/10.3390/mi8090282
Yang X, Niu X, Liu Z, Zhao Y, Zhang G, Liang W, Li WJ. Accurate Extraction of the Self-Rotational Speed for Cells in an Electrokinetics Force Field by an Image Matching Algorithm. Micromachines. 2017; 8(9):282. https://doi.org/10.3390/mi8090282
Chicago/Turabian StyleYang, Xieliu, Xihui Niu, Zhu Liu, Yuliang Zhao, Guanglie Zhang, Wenfeng Liang, and Wen Jung Li. 2017. "Accurate Extraction of the Self-Rotational Speed for Cells in an Electrokinetics Force Field by an Image Matching Algorithm" Micromachines 8, no. 9: 282. https://doi.org/10.3390/mi8090282
APA StyleYang, X., Niu, X., Liu, Z., Zhao, Y., Zhang, G., Liang, W., & Li, W. J. (2017). Accurate Extraction of the Self-Rotational Speed for Cells in an Electrokinetics Force Field by an Image Matching Algorithm. Micromachines, 8(9), 282. https://doi.org/10.3390/mi8090282




